Proposal and validation of a modified Simulated annealing algorithm for solving optimization problems

Resumen

Durante las últimas décadas, los métodos de optimización heurísticos basados en imitar procesos naturales, biológicos, sociales o culturales a nivel computacional han despertado el interés de la comunidad científica debido a su capacidad para explorar eficientemente espacios de soluciones multimodales y multidimensionales. A pesar de todos los trabajos publicados en la literatura internacional, la mayoría de los algoritmos heurísticos todavía presentan baja precisión y exactitud. En este contexto, se propone y se valida un algoritmo Simulated annealing modificado (ASAM) para la solución de problemas de optimización. La evaluación del desempeño se realizó en funciones de pruebas (benchmark functions) con y sin restricciones reportadas en la literatura internacional y en problemas prácticos de diseño en ingeniería civil. En todos los casos analizados ASAM obtuvo iguales o mejores resultados que los reportados por otros autores, ilustrando la aplicabilidad del algoritmo propuesto.

Abstract

Over the last decades, heuristic optimization methods based on imitating natural, biological, social or cultural processes on a computational level have aroused the interest of the scientific community due to their ability to effectively explore multimodal and multidimensional solution spaces. Despite all the papers published in the international literature, most heuristic algorithms still have low precision and accuracy. In this context, a modified Simulated annealing algorithm (MSAA) is proposed and validated for solving optimization problems. Performance evaluation was performed on test functions (benchmark functions) with and without restrictions reported in the international literature and practical design problems in civil engineering. In all cases analyzed MSAA obtained equal or better results than those reported by other authors, illustrating the applicability of the proposed algorithm.

Palabras clave

Algoritmo Simulated annealing ; Optimización ; Métodos heurísticos

Keywords

Simulated annealing algorithm ; Optimization ; Heuristic methods

1. Introducción

Simulated annealing (SA) pertenece a la clase de algoritmos de búsqueda local que permiten movimientos ascendentes para evitar quedar atrapado prematuramente en un óptimo local. Estos algoritmos juegan un rol especial dentro del campo de la optimización por 2 razones: en primer lugar, sus resultados han sido muy exitosos cuando se han aplicado a un amplio espectro de problemas prácticos; en segundo lugar, poseen una componente estadística que facilita su convergencia. El origen de esta técnica estocástica y la elección del criterio de aceptación de la nueva solución generada se basan en el proceso físico de enfriamiento del metal propuesto por Metropolis et al. [1] en los años cincuenta. Treinta años más tarde se creó el algoritmo actual [2] . El enfriamiento es un proceso termal a través del cual se alcanzan estados de energía mínima de un sólido en un baño de calor, y consiste en 2 pasos: primero se incrementa la temperatura en el baño de calor hasta un valor máximo al que se funde el sólido; luego se disminuye la temperatura cuidadosamente hasta que las partículas del sólido se reorganizan para conformar un reticulado altamente estructurado y la energía del sistema es mínima [3] .

Actualmente, los problemas complejos de optimización multidimensional, no lineal y altamente multimodales pueden encontrarse en ingeniería, en economía, en geofísica y en prácticamente todos los campos de la ciencia. Los objetivos de este trabajo son presentar un algoritmo Simulated annealing modificado (ASAM) para la resolución de problemas continuos con o sin restricciones que se encuentran en el área de la ingeniería civil, y realizar una evaluación del desempeño de dicho algoritmo para abordar este tipo de problemas.

En su primera parte, este trabajo presenta el ASAM, sus fundamentos y los parámetros que la controlan. Como segunda parte, se describen los problemas por analizar. Finalmente se muestran los resultados de la implementación del ASAM y se comparan con resultados de artículos de la literatura internacional.

2. Algoritmo Simulated annealing modificado

El funcionamiento del SA se puede describir de la siguiente manera: comienza con un cierto estado S . A través de un proceso único crea un estado vecino S ′ al estado inicial. Si la energía o la evaluación del estado S ′ son menores que el estado S cambia el estado S por S ′. Si la evaluación de S ′ es mayor que la de S puede estar empeorando, por lo que elige S ′ en vez de S con una cierta probabilidad que depende de las diferencias en las evaluaciones y la temperatura del sistema T . La probabilidad de aceptar un estado peor se calcula por la siguiente ecuación:

$P(\Delta f,T)=e^{\left(\Delta f/T\right)}$

( 1)

donde:

• P: probabilidad de aceptar el nuevo estado.
• Δf: diferencia de las evaluaciones de la función para cada estado.
• T: temperatura del sistema.
• e: número de Euler.

Inicialmente, con valores grandes para T, frecuentemente se aceptan soluciones con un mayor valor de función objetivo; a medida que el valor de T disminuye, tal tipo de soluciones raramente se aceptan, y cuando T se acerca a cero, solo se aceptan aquellas soluciones que mejoran la anterior. Varios estudios teóricos demuestran que si T decrece con la suficiente lentitud, el proceso converge a la solución óptima [4] . La función para reducción de temperatura más utilizada es: T_k+1  = T_k α, donde T_k+1 es el nuevo valor ajustado de T, T_k corresponde al previo valor de T, y α es una constante que está comprendida en el intervalo [0,8-0,99]. Por tanto, podemos definir un algoritmo básico de SA para problemas de optimización, como se indica en la figura 1 .

Figura 1. Algoritmo básico SA.

SA comienza con una solución inicial escogida aleatoriamente en el espacio de búsqueda y la compara con otra que también se selecciona estocásticamente en el espacio de búsqueda, lo que afecta al algoritmo cuando se tienen funciones altamente dimensionales y modales generando mayores tiempos de búsqueda y soluciones subóptimas. Además, la probabilidad de aceptación de una solución peor se encuentra en un intervalo de entre 0 y 1, lo cual causa que a temperaturas iniciales el algoritmo acepte un gran número de soluciones de peor calidad (aumentando el riesgo de quedar atrapado en un óptimo local). Por tales razones, el nuevo algoritmo propuesto en este estudio tiene 3 características fundamentales que lo diferencian del SA básico (fig. 1 ). Dichas características son las siguientes:

2.1. Exploración preliminar

En esta etapa el algoritmo realiza una exploración en todo el espacio de búsqueda (fig. 2 ) que viene dado por la siguiente matriz:

$X_{pxN}=I_{pxN}X_{min}+rand_{pxN}(X_{max}-X_{min)}$

( 2)

donde:

• P: número de puntos (estados) que se desean en el espacio de búsqueda.
• N: número de dimensiones del problema.
• I_PxN: matriz identidad de tamaño PxN.
• X_min: límite inferior del problema.
• X_max: límite superior del problema.
• rand_PxN: matriz PxN de números aleatorios (aleatoriedad pura) entre 0 y 1.

Figura 2. Exploración en el campo de búsqueda.

Para comenzar el proceso de optimización con ASAM se evalúan todos los puntos generados con la ecuación (2) mediante la función objetivo del problema y se escoge el que tenga menor valor (en el caso de estar buscando el valor mínimo de la función) como punto inicial de la búsqueda.

2.2. Paso de búsqueda

A partir del punto inicial determinado en la etapa anterior, se genera un paso de búsqueda para determinar el estado vecino. Este paso depende de un radio de acción que se reduce gradualmente a medida que desciende la temperatura del sistema (ec. 3). Es decir, cuando el algoritmo está en determinada temperatura, con radio de acción definido por la ecuación 3 para esa temperatura, la transición del punto inicial al nuevo punto (paso de búsqueda) se realiza mediante la adición al punto inicial de números aleatorios que están comprendidos entre cero y el valor del radio. Esto permite que el algoritmo realice una exploración global a temperaturas altas y una exploración local a temperaturas bajas, dando un equilibrio entre la exploración y la explotación del algoritmo.

$R_{i+1}=R_{i}\cdot \alpha$

( 3)

donde:

• R_i: radio inicial ciclo.
• α: coeficiente de reducción del radio.

2.3. Probabilidad de aceptación

En esta propuesta la probabilidad de aceptación de una solución (estado) peor viene dada por:

$P={\frac {1}{1+e^{\left(\Delta f/T\right)}}}$

( 4)

donde:

• P: probabilidad de aceptar el nuevo estado.
• Δf: diferencia de las evaluaciones de la función para cada estado.
• T: temperatura del sistema.
• e: número de Euler.

Esta probabilidad se encuentra en un intervalo entre 0 y ½, lo que permite al algoritmo tener un rango menor de aceptación de peores soluciones.

En resumen, las 3 modificaciones propuestas aquí tienen la finalidad de mejorar la exploración inicial, permitir un balance entre exploración inicial y final, y controlar la convergencia en la etapa final de la búsqueda.

3. Evaluación del desempeño del algoritmo Simulated annealing modificado

En esta sección se describen los problemas seleccionados (sin y con restricciones) para la aplicación y el análisis del comportamiento del algoritmo propuesto. La descripción incluye un conjunto importante de problemas bien conocidos de optimización combinatoria y numérica. Todos estos problemas han sido estudiados a través de la aplicación de diferentes enfoques, desde métodos tradicionales hasta las modernas técnicas estocásticas. Para evaluar el desempeño del ASAM, se elaboró un código con el paquete computacional Matlab^® .

3.1. Problemas sin restricciones

Los problemas seleccionados para evaluar el potencial y las limitaciones del ASAM se encuentran en [5]  ;  [6] , donde hay una gran variedad de funciones para validar algoritmos estocásticos de optimización global. En la tabla 1 se encuentran resumidas dichas funciones.

Tabla 1. Funciones de prueba sin restricciones

Problema	Nombre de la función	Valor óptimo	Dimensión n
1	Función Rosenbrock (R)	0,000	50
2	Función Dixon (DX)	0,000	10
3	Función Ackley (AK)	0,000	50
4	Función Schwefek (SW)	–8.379,672	20
5	Función Sphere (SP)	0,000	50
6	Función Neumaier (NM)	–210,000	10

Teniendo en cuenta que el algoritmo estudiado en este trabajo es de naturaleza estocástica, a continuación se describen los criterios para evaluar su desempeño. La desviación estándar de las funciones analíticas se utilizó para medir la precisión y la estabilidad del método. Se dice que un método heurístico de optimización que es estable y preciso si su desviación estándar es baja. Se cataloga exactitud en el método cuando la diferencia entre la media de las pruebas y el valor óptimo analítico (conocido, para la función de prueba) es pequeño. El algoritmo se puede describir como robusto si cuando se aplica en diferentes problemas presenta precisión y exactitud. En este trabajo, cada corrida del algoritmo se realizó 100 veces y el mejor valor de la función (MF), el peor valor de la función (PF), el promedio de los valores de la función (MEF), la desviación estándar de los valores de la función (DF) y el tiempo de ejecución promedio (TP) se muestran en la tabla 2 . Adicionalmente, en la tabla 3 se presenta una comparativa entre los algoritmos ASAM y SA básico en cuanto a tiempo de ejecución promedio (TP), número de iteraciones realizadas (NI) y mejor valor de la función (MF). Cabe recordar que para estas evaluaciones se utilizó un computador de escritorio con las siguientes características: procesador INTEL Core™2 Duo, 1,33 GHz y 2 Gb de RAM.

Tabla 2. Desempeño de ASAM en las funciones sin restricciones

	Funciones de prueba
Estadística	R	DX	AK	SW	SP	NM
MF	0,021	0,000	0,000	–8.379,672	0,000	–209,999
PF	0,038	0,000	0,000	–8.379,678	0,000	–209,994
MEF	0,035	0,000	0,000	–8.379,673	0,000	–209,996
DF	1,42E-05	7,11E-06	3,72E-05	1,80E-05	2,96E-05	9,84E-04
TP	350,1 s	3,5 s	31,2 s	26,3 s	5,7 s	58,0 s

Tabla 3. Comparativa entre los algoritmos ASAM y SA básico

		ASAM			SA básico
Función	Valor óptimo	MF	TP	NI	MF	TP	NI
R	0,000	0,021	350,1 s	6.200.000	1.528,478	51,5 s	624.000
DX	0,000	0,000	3,5 s	155.000	16,313	25,4 s	520.000
AK	0,000	0,000	31,2 s	520.000	18,395	73,2 s	572.000
SW	–8.379,672	–8.379,672	26,3 s	468.000	–5534,207	80,5 s	312.000
SP	0,000	0,000	5,7 s	155.000	62,178	16,2 s	260.000
NM	–210,000	–209,999	58,0 s	260.000	–1.253,802	17,4 s	290.000

Se puede considerar que ASAM es un algoritmo muy rápido debido a la velocidad de convergencia que presenta. Además, es un algoritmo muy estable, capaz de obtener resultados consistentes y razonables. En cuanto a la robustez, el algoritmo encontró el óptimo global en todas las funciones. Por lo tanto, ASAM puede ser considerado como un algoritmo de optimización robusto. Por otro lado, se puede afirmar que ASAM muestra una gran capacidad para escapar de óptimos locales cuando se trata de funciones multimodales (SW, AK). Igualmente, mostró potencial de búsqueda al manejar funciones unimodales difíciles de resolver (R, NM). Finalmente, se observa que el SA básico queda atrapado en óptimos locales, haciendo que converja de manera rápida y no encuentre el valor mínimo de la función. Lo contrario ocurrió con la nueva propuesta, donde se empleó más costo computacional y mayor número de iteraciones, pero las soluciones obtenidas fueron iguales o muy cercanas al óptimo.

3.2. Problemas con restricciones

Con el objeto de probar la eficiencia de los algoritmos propuestos se adoptó un conjunto estándar de funciones de prueba disponibles en la literatura [7] . Todas estas funciones se refieren a problemas de optimización numérica global resueltas previamente con técnicas evolutivas y con técnicas clásicas. Este conjunto de funciones de prueba incluye problemas con restricciones de desigualdad y de igualdad, espacios de búsqueda de alta y baja dimensionalidad y espacios convexos y no convexos, además de zonas factibles disjuntas y/o muy pequeñas.

En la tabla 4 se resumen las características de las 13 funciones de prueba adoptadas para evaluar los algoritmos propuestos. LI indica el número de desigualdades lineales, NI el número de desigualdades no lineales, LE el número de igualdades lineales, NE el número de igualdades no lineales, n el número de variables de decisión y ρ representa una estimación del tamaño de la región factible con respecto a todo el espacio de búsqueda, y se obtiene generando un millón de soluciones aleatorias y evaluando qué porcentaje de ellas son factibles.

Tabla 4. Funciones de prueba con restricciones

Problema	Valor óptimo	n	Función	ρ	LI	NI	LE	NE
g01	–15,000	13	Cuadrática	0,00%	9	0	0	0
g02	–0,803	20	No lineal	100,00%	1	1	0	0
g03	–1,000	10	No lineal	0,00%	0	0	0	1
g04	–30665,530	5	Cuadrática	27,01%	0	6	0	0
g05	5.126,490	4	No lineal	0,00%	2	0	0	3
g06	–6.961,814	2	No lineal	0,01%	0	2	0	0
g07	24,306	10	Cuadrática	0,00%	3	5	0	0
g08	–0,096	2	No lineal	0,86%	0	2	0	0
g09	680,630	7	No lineal	0,52%	0	4	0	0
g10	7.049,250	8	Lineal	0,00%	3	3	0	0
g11	0,750	2	Cuadrática	0,10%	0	0	0	1
g12	–1,000	3	Cuadrática	4,77%	0	9	0	0
g13	0,054	5	No lineal	0,00%	0	0	1	2

Puede observarse que hay funciones que tienen la zona factible muy pequeña, como en el caso de g05, g07, g13, en las que ρ = 0,00%, es decir, no se encuentra ningún individuo factible de manera aleatoria, lo que implica que en esos casos resultará desafiante el llegar siquiera a la zona factible. Existen otros casos, como en g02, donde la zona de factible es muy grande pero resulta muy complicado llegar al óptimo, ya que esta función tiene muchos óptimos locales; g02, g03 y g12 son problemas de maximización y los casos restantes son problemas de minimización. Sin embargo, para facilitar la presentación de resultados todos los problemas se manejarán como problemas de minimización. Para el análisis de resultados se aplicó la misma estadística que para las funciones sin restricciones, y están resumidos en la tabla 5 .

Tabla 5. Desempeño de ASAM en las funciones con restricciones

	Funciones de prueba
Estadística	g01	g02	g03	g04	g05	g06
MF	–15,000	–0,803	–1,005	–30.665,538	5.073,911	–6.961,812
PF	–14,999	–0,785	–1,005	–30.665,527	5.114,438	–6.961,796
MEF	–14,999	–0,800	–1,005	–30.665,534	5.091,353	–6.961,806
DF	2,72E-04	5,94E-03	2,79E-05	2,92E-03	1,12E + 01	3,75E-03
TP	59,2 s	231,5 s	320,5 s	2,4 s	1,4 s	3,3 s

	Funciones de prueba
Estadística	g07	g08	g09	g10	g11	g12	g13
MF	24,308	–0,096	680,630	7.251,654	0,750	–1,000	0,049
PF	24,381	–0,096	680,646	8.253,390	0,750	–0,952	0,527
MEF	24,336	–0,096	680,634	7.582,715	0,750	–0,988	0,247
DF	1,94E-02	1,11E-04	2,93E-03	8,45E + 02	3,94E-05	1,36E-02	1,98E-01
TP	164,8 s	27,5 s	17,1 s	61,2 s	4,5 s	467,2 s	10,8 s

En las tablas puede verse que ASAM alcanza el óptimo en varios problemas y converge al óptimo en otros. Además, se puede observar que el algoritmo propuesto puede lidiar con problemas que contienen restricciones moderadas (g06); problemas con alto número de restricciones (g01, g04); con dimensionalidad baja (g06, g08), moderada (g09) y alta (g01, g02, g03, g07); con diferentes tipos de restricciones y sus combinaciones (lineales, no lineales, igualdad y desigualdad); con regiones factibles grandes (g02), muy pequeñas (g05, g13) o disjuntas (g12); y más aún, con problemas donde el óptimo global se encuentra en la frontera de la región factible (g01, g02, g04, g06, g07, g09). Los 2 problemas en los que el algoritmo tuvo mayor dificultad fueron g05 y g13, debido a que tienen zonas de factibilidad muy pequeñas y además restricciones de igualdad, por lo que encontrar soluciones es un paso grande del algoritmo.

Teniendo en cuenta los resultados presentados en las Tabla 2 , Tabla 3  ;  Tabla 5 se procedió a evaluar el desempeño del algoritmo ASAM para la solución de problemas de ingeniería reportados en la literatura relevante. Los problemas por analizar se presentan en la siguiente sección.

4. Problemas de ingeniería

Para probar el desempeño se utilizaron 3 funciones que representan problemas de ingeniería. Los resultados se compararon con soluciones encontradas por otros autores, y dichas funciones fueron las siguientes:

4.1. Problema Welded Beam Design[8]

Este problema consiste en diseñar una viga soldada con mínimo costo y sujeta a restricciones de esfuerzo cortante, restricciones de tamaño, deflexión final y carga en la barra (fig. 3 ). Existen 4 variables de diseño:

• h (X₁ ): espesor de la soldadura.
• l (X₂ ): longitud de empotramiento de la viga.
• t (X₃ ): altura de la viga.
• b (X₄ ): espesor de la viga.

Figura 3. Estructura viga soldada [8] .

4.2. Problema Pressure Vessel Design[9]

Se trata de minimizar el costo del material, la forma y la soldadura de un recipiente cilíndrico con tapas hemisféricas. Hay 4 variables de diseño:

• X₁ (Ts ): espesor del cuerpo.
• X₂ (Th ): espesor de la tapa.
• X₃ (R): radio del recipiente.
• X₄ (L): longitud del recipiente.

Además, las variables X₁ y X₂ tienen que ser mayores o iguales a 1,1 y 0,6, respectivamente, y también tienen que ser múltiplos de 0,0625. En la figura 4 se puede observar dicho problema.

Figura 4. Esquema recipiente cilíndrico [9] .

4.3. Problema Tension/Compression Spring Design[10]

Consiste en minimizar el peso de un resorte de tensión/compresión sujeto a restricciones de mínima deflexión, tensión de corte, frecuencia de ondulamiento, límites de diámetro exterior y en las variables de diseño. Existen 3 variables:

• X₁ (d ): diámetro del resorte.
• X₂ (D ): diámetro del cable.
• X₃ (N ): número de vueltas del resorte.

Los rangos de las variables se acotaron según Mezura [11] . En la figura 5 se ilustra el problema.

Figura 5. Esquema resorte tensión/compresión [10] .

5. Resultados

5.1. Problema Welded Beam Design

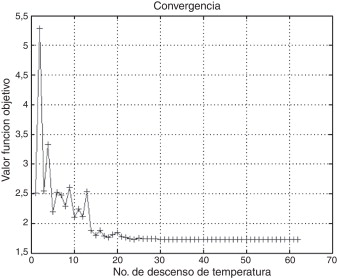
Deb [8] , Coello [12]  ;  [13] y Hwang y He [14] resolvieron este problema utilizando algoritmos genéticos (GA). Adicionalmente, Mezura [11] encontró resultados empleando una técnica multiobjetivo. Sidall [15] usó diferentes técnicas de optimización y Ragsdell [16] utilizó programación geométrica. Lee y Geem [17] obtuvieron soluciones utilizando el algoritmo Harmony Search, y Liu et al. [18] emplearon un algoritmo híbrido denominado PSO-DE (Particle swarm optimization-differential evolution). En la tabla 6 se muestra una comparación de los resultados obtenidos con ASAM y los obtenidos por los autores mencionados anteriormente. Además, en la figura 6 se puede apreciar como el valor de la función objetivo se va minimizando a medida que va descendiendo la temperatura.

Tabla 6. Resultados óptimos para Welded Beam Design

Variables de diseño	Mejor solución encontrada
	Este estudio	Deb [8]	Mezura [11]	Coello [12]
X1(h)	0,2057	0,2489	0,2671	0,2088
X2(l)	3,4705	6,1730	4,8997	3,4205
X3(t)	9,0366	8,1789	5,4567	8,9975
X4(b)	0,2057	0,2533	0,7834	0,2100
g1(X)	–0,0195	–5.758,6030	–1.384,5104	–0,3378
g2(X)	–0,1211	–255,5769	–8.392,8299	–353,9026
g3(X)	0,0000	–0,0044	–0,5163	–0,0012
g4(X)	–3,4333	–2,9828	–1,1057	–3,4118
g5(X)	–0,0807	–0,1239	–0,1421	–0,0838
g6(X)	–0,2355	–0,2341	–0,2328	–0,2356
g7(X)	–0,0281	–4.465,2710	–221.184,6600	–363,2323
f(X)	1,7248	2,4331	4,2730	1,7483

Variables de diseño	Mejor solución encontrada
	Coello [13]	Hwang y He [14]	Sidall [15]	Ragsdell y Phillips [16]	Lee y Geem [17]	Liu et al. [18]
	0,1829	0,2231	0,2444	0,2450	0,2442	0,2057
X1(h)	4,0483	1,5815	6,2189	6,1960	6,2231	3,4704
X2(l)	9,3666	12,8468	8,2915	8,2730	8,2915	9,0366
X3(t)	0,2059	0,2245	0,2444	0,2455	0,2443	0,2057
X4(b)	–408,7328	N/A	–5.743,5020	–5.743,8260	N/A	N/A
g1(X)	–2.105,9140	N/A	–4,0152	–4,7151	N/A	N/A
g2(X)	–0,0231	N/A	0,0000	0,0000	N/A	N/A
g3(X)	–3,3215	N/A	–3,0225	–3,0203	N/A	N/A
g4(X)	–0,0579	N/A	–0,1194	–0,1205	N/A	N/A
g5(X)	–0,2370	N/A	–0,2342	–0,2342	N/A	N/A
g6(X)	–160,5865	N/A	–3.490,4690	–3.604,2750	N/A	N/A
g7(X)	1,8246	2,2500	2,3815	2,3859	2,3807	1,7248
f(X)

Figura 6. Gráfica de convergencia para Welded Beam Design.

5.2. Problema Pressure Vessel Design

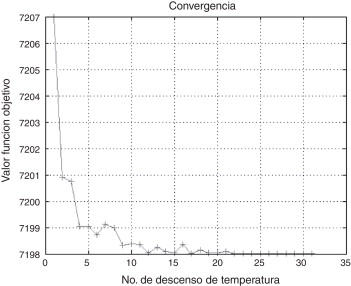
Este problema fue resuelto por Mezura [11] , empleando una técnica multiobjetivo; por Lee y Geem [17] , usando el algoritmo Harmony Search; por Wu y Chow [19] , a través de una propuesta de GA; por Sandgren [20] , con el método Branch and bound , y por último por Kannan y Kramer [9] , mediante multiplicadores de Lagrange. En la tabla 7 se puede ver que el ASAM arrojó mejores resultados, y la figura 7 muestra la gráfica de convergencia.

Tabla 7. Resultados óptimos para Pressure Vessel Design

Variables de diseño	Mejor solución encontrada
	Este estudio	Kannan y Kramer [9]	Mezura [11]	Lee y Geem [17]	Wu y Chow [19]	Sandgren [20]
X1(Ts)	1,1250	1,1250	1,5481	1,1250	1,1250	1,1250
X2(Th)	0,6250	0,6250	2,3609	0,6250	0,6250	0,6250
X3(R)	58,2901	58,2910	57,1299	58,2789	58,1978	48,9700
X4(L)	43,6927	43,6900	155,5212	43,7549	44,2930	106,7200
g1(X)	0,0000	0,0000	–0,4455	–0,0002	–0,0018	–0,1799
g2(X)	–0,0006	–0,0689	–1,8159	–0,0690	–0,0698	–0,1578
g3(X)	–0,0005	–21,2201	–1.079.706,5	–3,7163	–974,3000	97,7600
g4(X)	–1,9630	–96,3100	–84,4788	–196,2450	–195,7070	–133,2800
f(X)	7.198,0074	7.198,0428	26.159,2366	7.198,4330	7.207,4940	7.980,8940

Figura 7. Gráfica de convergencia para Pressure Vessel Design.

5.3. Problema Tension/Compression Spring Design

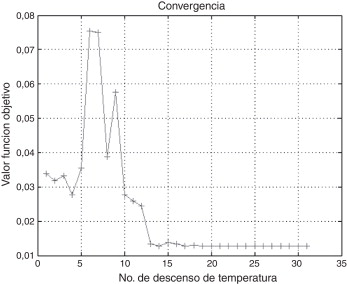
Este problema fue resuelto por Belegundu [21] con 8 técnicas diferentes de optimización matemática. Arora [10] también resolvió este problema con una técnica de optimización numérica llamada CCC (Constraint Correction at constant Cost) . Además, Coello [22] resolvió este problema mediante el uso de GA. En la tabla 8 se muestran los resultados obtenidos con ASAM, y en la figura 8 se presenta la convergencia.

Tabla 8. Resultados óptimos para Tension/Compression Spring Design

Variables de diseño	Mejor solución encontrada
	Este estudio	Arora [10]	Liu et al. [18]	Belegundu [21]	Coello [22]
X1(d)	0,05180	0,05339	0,05168	0,05000	0,05199
X2(D)	0,35948	0,39918	0,35671	0,31590	0,36397
X3(N)	11,12875	9,18540	11,28931	14,25000	10,89052
g1(X)	0,00000	0,00002	N/A	–0,00014	–0,00001
g2(X)	0,00000	–0,00002	N/A	–0,00378	–0,00002
g3(X)	–4,05920	–4,12383	N/A	–3,93830	–4,06134
g4(X)	–0,72581	–0,69828	N/A	–0,75607	–0,72270
f(X)	0,012666	0,012730	0,012665	0,012833	0,012681

Figura 8. Gráfica de convergencia para Tension/Compression Spring Design.

6. Conclusiones

En este trabajo se ha introducido una propuesta (ASAM) para la optimización de problemas de ingeniería (con o sin restricciones). Las principales modificaciones propuestas son: exploración en el espacio de búsqueda, paso de búsqueda y probabilidad de aceptación.

Se ha evaluado el desempeño de ASAM en un total de 19 funciones de prueba (benchmark functions). En los 2 grupos de funciones estudiadas (sin y con restricciones) el algoritmo presentó alta precisión, exactitud y robustez, como se evidencia en las Tabla 2 , Tabla 3  ;  Tabla 5 .

En los 3 problemas de optimización en ingeniería resueltos con ASAM se han comparado los resultados obtenidos con los generados por otros autores utilizando diversas técnicas heurísticas (Harmony Search, algoritmos genéticos, optimización con enjambre de partículas, entre otras) que están reportadas en la literatura. En todas las pruebas ASAM arrojó iguales o mejores resultados (Tabla 6 , Tabla 7  ;  Tabla 8 ). De esta manera se demuestra la aplicabilidad del trabajo aquí presentado.

Agradecimientos

Los autores agradecen a la Universidad Industrial de Santander la financiación de esta investigación. De igual forma damos las gracias al grupo de investigación INME y a la Escuela de Ingeniería Civil-UIS por el apoyo ofrecido.

Bibliografía

1. [1] N. Metropolis, A. Rosenbluth, M. Rosenbluth, A. Teller, E. Teller; Equation of state calculations by fast computing machines; J. Chem. Phys., 21 (6) (1953), pp. 1087–1092
2. [2] S. Kirkpatrick, C.D. Gelatt, M.P. Vecchi; Optimization by simulated annealing; Science, 220 (4598) (1983), pp. 671–680
3. [3] A. Corana, M. Marchesi, C. Martini, S. Ridella; Minimizing multimodal functions of continuous variables with the Simulated Annealing Algorithm; ACM Trans. on Math. Software, 13 (3) (1983), pp. 262–280
4. [4] K.A. Dowsland, B.A. Díaz; Diseño de heurística y fundamentos del Simulated Annealing; Revista Iberoamericana de IA, 19 (2003), pp. 93–102
5. [5] M.M. Ali, C. Khompatraporn, Z.B. Zabinsky; A numerical evaluation of several stochastic algorithms on selected continuous global optimization test problems; J. Global Optim., 31 (2005), pp. 635–672
6. [6] A. Hedar. Studies on Metaheuristics for Continuous Global Optimization Problems. Ph.D Tesis, Kyoto University, Japan, 2004.
7. [7] T.P. Runarsson, X. Yao; Stochastic ranking for constrained evolutionary optimization; IEEE Trans. Evol. Comput., 4 (3) (2000), pp. 284–294
8. [8] K. Deb; Optimal design of a welded beam via genetic algorithms; AIAA Journal, 29 (11) (1991), pp. 2013–2015
9. [9] B.N. Kannan, S.N. Kramer; An augmented Lagrange multiplier based method for mixed integer discrete continuous optimization and its applications to mechanical design; J. Mech. Des., 116 (1994), pp. 405–411
10. [10] J.S. Arora; Introduction to Optimum Design, McGraw-Hill series in Mechanical Engineering; McGraw-Hill, New York, USA (1989)
11. [11] E. Mezura. Uso de una técnica multiobjetivo (Niched Pareto Genetic Algorithm) para el manejo de restricciones en un algoritmo genético. Resultados preliminares. En: Technical Report LANIA-RI-2000-09, Xalapa, 2000, pp. 1-9.
12. [12] C. Coello; Constraint-handling using an evolutionary multiobjective optimization technique; Gordon and Breach Science Publishers, 17 (2000), pp. 319–346
13. [13] C. Coello; Use of a self-adaptive penalty approach for engineering optimization problems; Comput. Ind., 41 (2) (2000), pp. 113–127
14. [14] S. Hwang, R. He; A hybrid real-parameter genetic algorithm for function optimization; Adv. Eng. Inf., 20 (2006), pp. 7–21
15. [15] J. Sidall; Analytical Decision-Marketing in Engineering Design; Englewood Cliffs, New Jersey, USA (1972)
16. [16] K. Ragsdell, D. Phillips; Optimal design of a class of welded structures using geometric programming; Trans. ASME J. of Engi. for Industry, 98 (3) (1976), pp. 1021–1025
17. [17] G. Lee, Z. Geem; A new meta-heuristic algorithm for continuous engineering optimization-harmony search theory and practice; Comput. Meth. Appl. Mech. Eng., 194 (2004), pp. 3902–3933
18. [18] H. Liu, Z. Cai, Y. Wang; Hybridizing particle swarm optimization with differential evolution for constrained numerical and engineering optimization; Appl. Soft Comput., 10 (2010), pp. 629–640
19. [19] S. Wu, P.T. Chow; Genetic algorithms for nonlinear mixed discrete-integer optimization problems via meta-genetic parameter optimization; Eng. Optim., 24 (1995), pp. 137–159
20. [20] E. Sandgren; Nonlinear Integer and discrete programming in mechanical design; J. Mech. Des., 112 (1990), pp. 223–229
21. [21] A.D. Belegundu; A study of mathematical programming methods for structural optimization-Part II: Numerical results; Int. J. Numer. Methods Eng., 21 (1985), pp. 1601–1623
22. [22] C. Coello; Constraint-handling in genetic algorithms through the use of dominance-based tournament selection; Adv. Eng. Inf., 16 (2002), pp. 193–203