Characterization of a submarine landslide in Santa María del Oro lake using a numerical model
Diego A. Pantoja, Anatoliy Filonov, Noel Gutiérrez
Departamento de Física
Universidad de Guadalajara, CUCEI
Direccion postal
Guadalajara, Mex. 44430
e-mail: diego.pantoja@academicos.udg.mx,
afilonov@prodigy.net.mx,
nogutier@ucsd.edu
Abstract
During summer of 2016 an event was register in the volcanic lake of Santa María del Oro, a perturbation that triggers a considerable rise of amplitude on the lake system for at least two days. Due to the scarce observations in the lake, yet it is not definitive what event took place, a storm, a landslide or other. Based on numerical modelling a series of experiments were carry out in order to determine the kind of forcing that created those anomalies. This study is focused in characterizing a submarine landslide and the effects of the wind valley breeze. The results indicate that the lake acts as a dynamical membrane resonating to frequencies at 3.2 min (external seiche) and in a band of the 2-8 hrs (internal seiches) with the 2.64 hrs the most intense. After every forcing the water starts to oscillate uniformly and in a clockwise sense until the energy is dissipated by friction at the internal seiches frequencies.
KeyWords. Internal and external Seiches, Crater Lake, Delft3D model.
INTRODUCTION
Long standing waves oscillations in enclosed water bodies, or seiches [1], are forced movements provoked mainly by atmospheric (storms) or topographic (seismic motion) perturbations. These oscillations that can span from a few minutes to several hours strongly depend on the shape of the basin and less in the intensity of the disturbed processes. The modal structure of the membrane-like movements losses its energy by dissipating mechanisms until the system came at rest if the external forcing ceases, [1]. In volcanic lakes those oscillations are typically caused by wind burst or other situation like landslides due to the conic-shape of the basin. In august 18 of 2006 a device deployment in the Lake Santa Maria del Oro recorded a sudden perturbation on the background ambient configuration for a pair of days. In order to shed some light in what could be happened, the numerical approach was used to simulated the typical behaviour of the lake due to an external rapid forcing. The lake of Santa Maria del Oro, (21 22' N and 104 34' W, Nayarit, México), is a volcanic lake located 750 m over sea level, with nearly a circular shape of 2 km of diameter and a maximum depth of 65 m near the center. The lateral slopes are pronounce, except at the west coast where they end smoothly at a bay, Fig. 1. The atmospheric forcing of the lake comprises a valley breeze circulation due to the mountain chain of 200-300 m high that runs east-west in the northern and southern section of the region. At daylight the wind blows to the west and at night time the wind blows to east [2], Fig.1. The summer stratification of the lake range from 29 C on the surface to 22 C at the bottom. The thermocline (where there is an abrupt jump of temperature) lies around 15 m deep [2], Fig. 1.![Bathymetry of Santa María del Oro Lake [m] (upper), temperature profile for summer (right) and typical wind valley breeze (bottom).](/wd/images/thumb/8/89/Draft_Pantoja_832101244-Fig1.png/600px-Draft_Pantoja_832101244-Fig1.png)
|
| Figure 1: Bathymetry of Santa María del Oro Lake [m] (upper), temperature profile for summer (right) and typical wind valley breeze (bottom). |
According to [3], a possible landslide took place near the bay at the western section of the lake during august of 2006. The observed perturbations co-oscillated with the background system with a periods between 2 and 6 hrs.
MODEL
Delft3D is an open-source numerical model developed by WL/Delft Hydraulics and the Delft University of Technology [4]. It includes implementations of several mathematical models for different physical phenomena (currents, transport, wave propagation, morphological developments, etc.). In the present study, it is used to predict the circulation in a lake system. The Delft3D model solves the Navier-Stokes equations for an incompressible fluid, under the shallow water and the Boussinesq assumptions using a finite difference scheme (see [5]). The model includes the depth-averaged horizontal momentum equations, (shown here in Cartesian coordinates for the sake of clarity):
|
the depth-averaged continuity equation:
|
|
(3) |
and the vertical momentum equation, which reduces to the hydrostatic pressure relationship via the Boussinesq approximation:
|
|
(4) |
where are the depth-averaged velocity in the and directions, is the Chézy coefficient, is the water depth, is the free surface elevation above the reference plane (at ), is a two dimensional current vector, whose Euclidean norm is , are sinks or sources of water, is Coriolis force, is Reynolds stress, is the gravity, is the horizontal eddy viscosity, is the pressure and the water density. In the horizontal direction, the model uses orthogonal curvilinear grids, which support both cartesian and spherical coordinates. Both coordinate systems permit the management of geometrically complex domains. In the vertical direction, Delft3D uses the or the z coordinate systems. The z coordinate system is made up of layers with predefined depths. In this particular study, the spherical and z-coordinate system are used without boundary conditions. All the simulations were ran for only six days within a mesh of 156 x 126 number of cell in the (x,y)-directions, respectively, m, with 20 z-layer in the vertical distributed according to [10 6 4 3 2] % of the water column, where the first value is assigned to the bottom layer and the last value is assigned to the upper layer (surface). In every cell the number of layers is variable depending on the water depth. The time step used was seg.
MODEL RESULTS
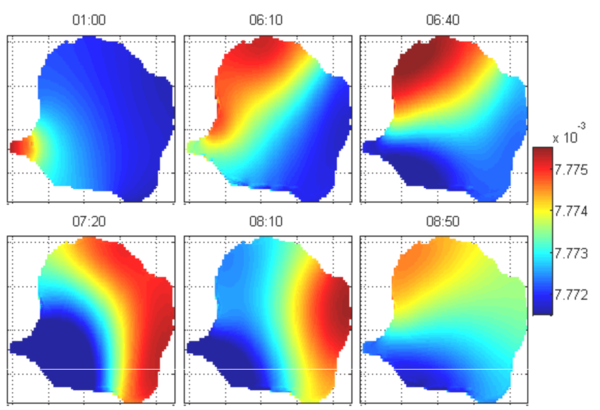
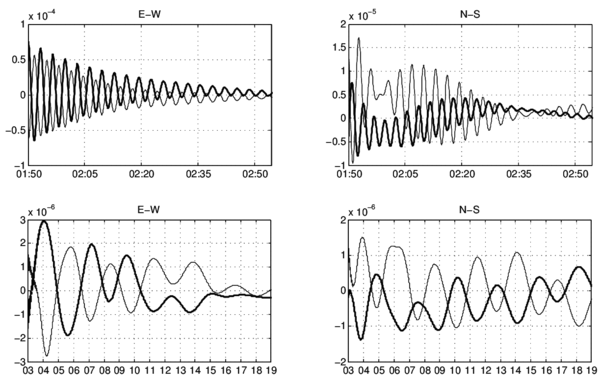
In order to investigate the possible causes that appears in those of the observational data, three scenarios were set-up for the early stage of the perturbation. A Landslide-forced simulation (Ls), a Wind-forced simulation (Ws), and a Landslide- and Wind-forced simulation (LWs). The Ls is a configuration that characterizes a landslide which comprise an equivalent flux of water displaced by the sediment. Remembering that the intensity of the forcing is not as important as the geometrical shape of the basin, then the input of energy here was chosen rather arbitrary. The Ws is the typical configuration as the lake develops day by day in response of the valley breeze wind, and the LWs is the combination of both forcing. The numerical event (landslide) for the Ls was configured to happen at hr 1 in the day 2. After the impulsive forcing the water level was set in motion in a back- and forward movement rotating counter-clockwise, Fig. 2.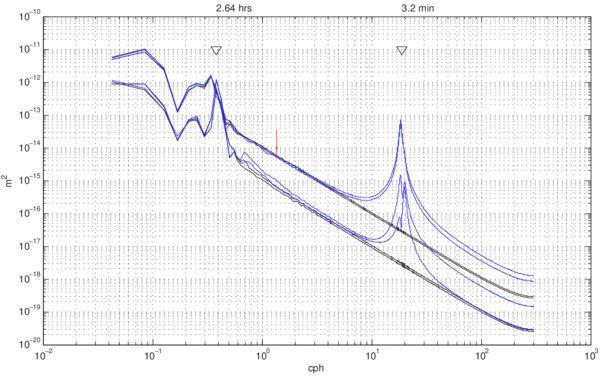
|
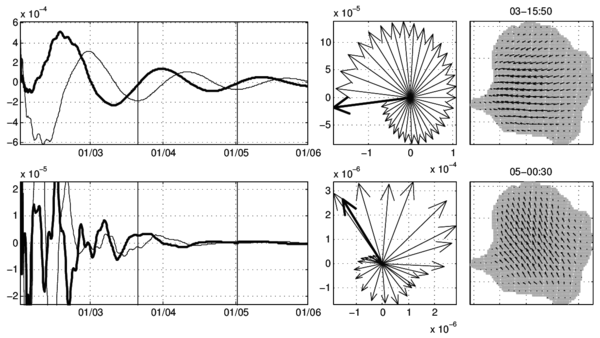
| Figure 6: Same as Fig. 5, for Ws (Black lines) and LWs (Blue lines). |
SUMMARY AND DISCUSSION
Lake Santa María del Oro can be considered as a circular basin which according to the 2D structure modal configuration, obeys the following standing oscillation from the seiches motion ([1]):
|
|
(5) |
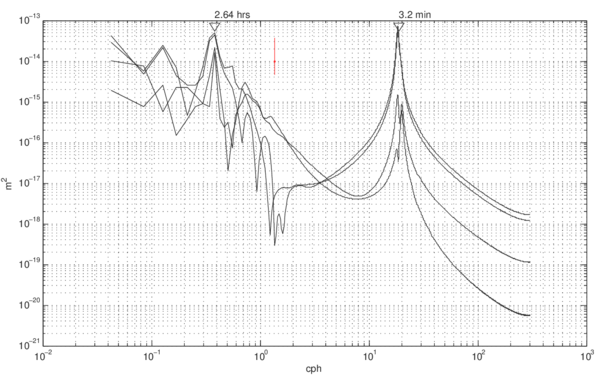
For a basin with radius r, where , and the polar angle. is the Bessel function of order s, and are arbitrary constants and , with the roots of given the normal modes of the system. The period of oscillation of the first external model correspond to , where g is the gravity and H the mean depth. If the lake was considered homogeneous in temperature, the first mode of oscillation (external mode) will remain between 2-3 min, whereas for an stratified lake, the first internal mode remains between 2.1-4.5 hrs ([2,8]). As shown by the combined configuration (Fig. 6), the resonant internal modes can coexist in the same simulation, and in the same band of frequency (2-8 hrs), so there is not a very clear contribution of which forcing caused the sudden perturbation on the observational data. Both simulations, wind and submarine landslide, can cause resonant amplification on the lake. Then, with the information at hand from the numerical outputs we can not confirm that effectively was a landslide that perturb the lake system, there is more work to do in order to support the idea of a topographical perturbation.
Acknowledgements
This work was supported by the Mexican Secretaría de Educación Publica (SEP) through the Program for Teachers PRODEP of DAP. The AF acknowledge the support of CONACyT.
REFERENCES
[1] A. B. Rabinovich, "Seiches and harbor oscillations", Handbook of coastal and ocean engineering, (2009).
[2] D. Serrano, A. Filonov and I. Tereshchenko, "Dynamic response to valley breeze circulation in Santa María del Oro, a volcanic lake in México", Geophysical Research Letters, Vol. 29(131649), pp. 27-1-27-4, (2002).
[3] N. Gutierrez, "In-situ measuments of the coupling between internal waves submarine landslides in a volcanic lake", Tesis de Licenciatura en Física (In spanish), Universidad de Guadalajara, CUCEI, Guadalajara, Mexico, (2017).
[4] G.R. Lesser, "Development and validation of a three-dimensional morphological model", Coast. Eng. Vol. 51, pp. 883–915, (2004). [5] Deltares, "Delft3D-FLOW, User Manual", The Netherlands, (2013).
[6] A. Filonov, I. Tereshchenko, "Thermal lenses and internal solitones in the shallow lake Chapala, Mexico", Chinese Journal of Oceanology and Limnology, Vol. 17, pp. 308-314, (1999).
[7] A. Filonov, I. Tereshchenko, J. Alcocer, "Dynamic response to mountain breeze circulation in Alchichica, a crater lake in Mexico", Geophysical Research Letters, Vol. 33, L07404, (2006).
[8] D. Serrano, "Procesos termodinamicos en el lago volcanico de Santa Maria del Oro, Nayarit", Tesis de Doctorado, UNAM, (2004).
Document information
Published on 17/11/17
Submitted on 16/11/17
Volume 1, 2017
Licence: CC BY-NC-SA license