Assessment of the minimum value of photovoltaic electricity in Italy

Abstract

We investigate the value of solar photovoltaic (PV) power in the Italian wholesale electricity market (IPEX). A model is developed and applied to simulate and predict the monthly average electricity prices in peak hours, as well as to simulate scenarios without PV generation. The computed merit-order effect of the PV generation in Italy, around −2.9 €/MWh per each additional GWh of PV production, as well as the greater −4.5 €/MWh absolute value evaluated under the hypothesis of stationary electricity demand, are in line with the upper values found in related studies of near mature renewable energy markets. A strong relationship of the value of PV electricity in the IPEX with the electricity demand is clearly evident, leading to important policy implications in terms of possible actions on the granted subsidies, electrification of energy end use, and promotion of specific PV technologies. The anomalous temporal behavior of the IPEX, shown by high off-peak electricity prices that followed the installation of Italys large PV park, partly offsets the beneficial effect of PV generation.

Introduction

In a world of ever more uncertain fossil fuels market due to both geopolitical instability and steadily reducing gap between economically viable crude oil supply and demand [1], renewable energy sources (RES) can represent an effective way to reduce energy dependence, to ensure energy security and dramatically reduce pollution and the impact on climate of energy generation. There is a general consensus about the steadily declining Energy Return on Energy Investment (ERoEI) of crude until todays values below 10, namely the safe threshold to consider oil as a sustainable energy source for todays complex societies and their respective industrial and welfare economies oil [1].

The aim of this article is the assessment of the value of the photovoltaic (PV) electricity in Italy, considered as an economically viable energy source in the medium and long term. Two recent studies based on life cycle assessment (LCA) analysis collocate the ERoEI of PV technologies either in the range 19–38 [2] or below 4 [3]. Raugei subsequently pointed out the basic calculation mistakes and the wrong working hypotheses underlying the calculation of the latter poor ERoEI value [4].

However, these studies certainly do not refer to state-of-the-art PV technology. First, even in the most favorable case for PVs ERoEI [2], the 14% module efficiency considered is in the low end of the PV modules installed at least since the year 2012 (state-of-the-art monocrsytalline Si modules have >21% efficiency; and polycrystalline Si modules have now surpassed the 18% efficiency threshold), and completely neglects sun-tracking systems which are known to push the production up by 30% or even 40% (depending on latitude and local climate). Furthermore, it is not clear why said LCA-based studies limit the lifetime of PV modules and systems to 25 or 30 years, respectively, when the efficiency of PV modules degrades less than 20% after 40 years [5] (the accepted value for the median value of the measured degradation rate of existing PV modules or systems is around 0.5%/year).

Since the early years of 21st century, many Governments in the European Union have implemented financial incentives to PV generation via the Feed-in-Tariff (FiT) scheme first conceived by Hermann Scheer in Germany [6]. Significant costs faced by all electricity consumers led to raising criticisms about the economic viability of the transition to low-carbon emission power generation, mostly in countries such as Germany, Spain, and Italy, where FiT schemes were adopted earlier when the capital cost of PV installations was very high.

However, the FiT scheme in these countries led to more than 30 GW of PV power installed in Germany by the end of 2012 (from less than 0.1 GW in 2000); and to about 18 GW in Italy by Summer 2013 (it was 87 MW by the end of 2007). As a result in 2011, Germany and Italy accounted for over half the global cumulative capacity, followed by Japan, Spain, the United States, and China [7]. In detail, the GSE officially reports on its website (www.gse.it) that as of 31 October 2013, Italys solar subsidy plan, introduced in 2005 and having gone through five consecutive revisions, has driven the installation of 549,576 solar PV plants with 17.493 GW of installed power.

Following Spain and Portugal, which stopped granting new subsidies in 2012, Italy thus ceased granting FiT for new installations after 6 July 2013 because the annual cost of existing or approved PV plants reached its limit of 6.7 billion euros on 6 June 2013 and law restricts further expenditure for solar energy a month after the threshold is reached.

On the other hand, the efforts carried by those countries allowed a two orders of magnitude increase in solar cells production, today mostly based in China, as well as the rapid introduction of new PV technologies of lower cost [8]. This, coupled with the astonishing reduction in the PV capital costs following very steep learning curves [9], led to a fall in the retail price of PV modules from 6–7 USD/W in 2000 to 0.5–0.6 $/W currently [10], turning PV modules into a commodity benefiting low-income countries such as Bangladesh where off-grid PV plants today provide over six million families in rural areas with clean electricity.

In brief, PV electricity has now reached grid parity in many countries, including Italy [11]. This requires evaluating the economic sustainability of PV stimulation policies in liberalized electricity markets on the basis of the impact of additional PV electricity generation into the energy markets; and specifically in terms of its direct impact to the wholesale electricity price.

To the best of our knowledge no specific studies assessing the quantitative impact of the PV generation on the prices formed over the Italian wholesale electricity market (IPEX) have been published. In 2002, the seminal work [12] of Jensen and Skytte first suggested that an increase in RES deployment results in decreasing electricity prices due to low or null marginal costs of renewable energy generation that, contrary to conventional energy sources and technologies, does not require the use of fuels such as oil, natural gas, and coal.

In the following after a short description of the Italian electricity market, we first ('Materials and Methods') identify the datasets and present the model for the peak price and its performance. In 'Results and Discussion', we discuss the results in terms of the difference in peak and off-peak unit electricity price with and without the PV generation, as well as the monthly and cumulated savings. These findings lead to policy implications that are summarized in the Conclusions.

Materials and Methods

The Italian electricity market

The structure of the Italian electricity market followed the liberalization dictated by the European Commission with the Directive 96/92/EC. Since 2004, the power exchange in the Italian Energy Market (IPEX) is fully operational under the lead of the Manager of the Italian Energy Markets (GME). Still preserving some degree of the former monopolistic nature in the form of oligopoly [13], Italys electricity market is integrated with the other EU power markets [14]. The IPEX has been deeply studied, including the formation of the price on the basis of the merit-order effect, as well as the wholesale electricity prices integration process in the main European markets including the IPEX [15].

What is relevant to the present study is that a unique national hourly wholesale electricity price (PUN) is formed on the day-ahead market starting from the separate prices formed in several interconnected zones including the problematic large islands of Sicily and Sardinia suffering from poor interconnections and frequent congestion. Therefore, the PUN is affected both in the short term by occasional congestion, and in the medium and long term by major works aimed at the revamping and refurbishment of the interconnections involving the most critical zones, which are difficult to include in a long-term power price model. We remind here that generation of energy from RES impacts the merit-order scheme of electricity price formation; a growth in RES power bid into the wholesale market drives the marginal plants (the most costly power generation plants) out of the market, therefore shifting the supply curve to the right and resulting in lower electricity prices [16].

We remind here that the installed electric power in Italy in 2010 was 105 GW, about 50% higher than the 50–55 GW peak of a typical December day, when power demand from the gird reaches its maximum. The base load is usually supplied by large coal-based thermal plants that run for long periods and have the lowest generating cost. Intermediate demand is instead met by smaller plants with higher generating costs, while peak demand is provided by expensive gas-fired plants and, where available by hydroelectric power plants, capable in each case to respond in seconds or minutes to the sudden variation in demand.

Selection of datasets

The analysis has been limited to the so called “peak hours,” that is, 8 am to 8 pm CET during the working days around the year, while neither weekends nor national holidays were included due to the much lower power demand which, by means of the usual merit order mechanism, leads to the PUN formation quite similar to night time, therefore adding inhomogeneity to the following analysis. The contribution of the discarded daylight hours to the price effect of PV generation is very small, however, because practically only base load generation plants (geothermal, hydro and coal power) will be called into operation besides solar PV and wind. The hourly PUN series since January 2006 till September 2013, was collected from the GME datasets [17] providing the monthly average PUN during the peak hours (hereinafter “peak PUN”) along with the monthly number of peak hours.

The monthly national electricity demand was retrieved from the same easily manageable and openly distributed datasets as average hourly demand over the peak hours. Forcing terms for the power prices consisting of the national electricity demand, the PV and wind power generation, and the oil price, are included as monthly averages.

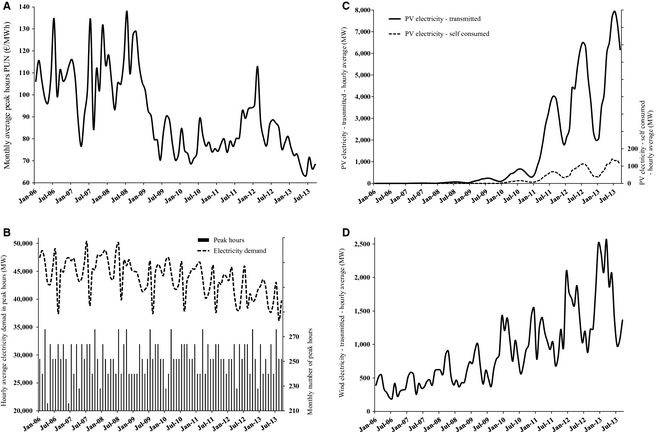
The PV and wind electricity monthly generated and fed into the transmission grid was obtained from the Manager of the Italian electricity transmission grid (TERNA) datasets [18]. The wind power is totally fed into the transmission grid (small wind installations are negligible so far in Italy), yet a small but significant fraction of the PV power is self-consumed by in situ loads. Such fraction was derived by comparison with the total PV generation data drawn from the GSE datasets. The graphs in Figure 1 show the evolution of the above dataset in the January 2006 to September 2013 period.

Figure 1. Monthly average peak PUN (A), hourly average electricity demand in peak hours and monthly number of peak hours (B), hourly average transmitted and self-consumed PV electricity (C), and hourly average wind electricity (D).

Following the financial crisis started in late 2008, the peak PUN series underwent a sudden and substantial shift from ample oscillations around an average value approximately equal to 110 €/MWh till 2008 (Fig. 1A) to a much more stable averaging to just less than 80 €/MWh during the subsequent 2 years (July 2009 to July 2011). Eventually, as the recession of Italys economy continued and PV installed power rose to an astonishing 18 GW, the PUN fell down to less than 70 €/MWh in Spring 2013. Overall, since 2008 the unit electricity price in the peak hours has lost about 40% of its original value.

Moreover, the peak PUN series appears to be linearly autocorrelated with maximum explained variance (about 58%) and maximum significance (much greater than 99.99% according to the usual F-statistics) at the 1-month lag, suggesting to include such 1-month lag autocorrelation into the model of peak PUN series; such lag-1 autocorrelation was found also in previous studies, despite they used daily series of electricity price data [19].

Figure 1B shows that the electricity demand in Italy began a steady fall in late 2008, with an apparent acceleration since mid-2012, losing more than 10%. The boom of the PV generation, in its turn, is apparent when comparing the seasonal peaks in 2010 and 2011, with a sixfold increase in 1 year. Since then, the PV electricity transmitted into the grid doubled again, with about 4% of the overall PV generation consumed on-site (Fig. 1C).

Finally, the wind electricity generation in Italy increased about 2.5 times in 4 years since 2009 (Fig. 1D). It is interesting to note that seasonality of the wind electricity generation is out of phase by about 6 months with regard to the PV generation, therefore in late Spring and even more in Summer months of year 2013 the PV generation has become about seven times greater than the wind power generation.

In 2013, natural gas accounted 58–65% of the electricity generation from Italys thermoelectric plants (about 35–45% of the total generation), about 3.5–4 times more than coal, with oil representing only a tiny fraction of the mix [20]. More importantly, natural gas powers all the marginal thermoelectric plants traditionally dictating the PUN in most of the peak hours according to the merit-order price scheme, particularly the “Turbogas” plants, namely open-cycle gas turbines that, while enjoying a very fast start needed to follow the grids peak loads [21], suffer from very low efficiencies (around 30%) and thus very high production costs. Unfortunately, the prices of natural gas for electricity generation in Italy are marked as “Confidential” and therefore undisclosed [22].

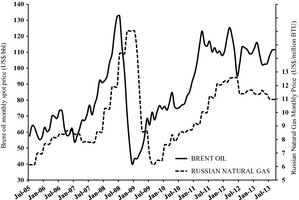
In order to check the hypothesis that the Brent oil monthly average price series could be an effective indicator (proxy data) set for the price of natural gas for electricity generation in Italy, the series of Russian Natural Gas border price in Germany [23] has been compared with the Brent spot oil price [24], finding that the Brent oil price series, in US$ per barrel (US$/bbl), explains as much as 75% of the variance of the Russian Natural Gas price series, in US$ per Million Metric British Thermal Unit (US$/million BTU). Figure 2 shows the two price series in the July 2005 to September 2013 period. The oil price lags 6 months before the natural gas price. In other words, the Brent oil price at a given time is a very effective predictor for the Russian natural gas price after about 6 months.

Figure 2. Monthly average prices of Brent oil and Russian natural gas.

Therefore, the Brent spot oil price can be used with good confidence as a useful forcing term for the power price on the IPEX, provided that the most effective lag is identified, as shown in the following.

The peak PUN model

A multivariate regression model was chosen for the peak PUN series due to its simplicity, repeatability, stability, and successful use in related studies [19, 25].

Forcing terms specific to the monthly time basis and the available series used in this study were introduced, with the aim to explain as much of the variance as possible. The peak PUN series itself with 1-month lag is used as forcing term due to the autocorrelation of the series mentioned in the section 'Selection of datasets'. The Brent oil price series shown to be most effective when used unchanged but with an optimal lag equal to 4 months, that is, the peak PUN price shows to respond elastically to the oil price lagging behind by 4 months, all other conditions being the same. Furthermore, the price units of €/bbl for Brent oil proved to be marginally more effective than US$/bbl. Therefore, the official currency exchange rates were applied to convert the original price series in dollar per barrel. Again, this is in agreement with the findings of Wurzburg and coworkers [19] who reported that when converted into homogeneous units, at least the European merit-order effects are quite comparable in size (the homogeneous units referred to are €/MWh per each additional GWh of renewable production).

The forcing term connected to the electricity demand is more subtle. The formation of the peak PUN hourly price on the basis of the merit-order effect [14] suggests that its response to the electricity demand should be substantially faster than proportional. Moreover, the PV electricity fed into the grid (Fig. 1C) as well as the wind electricity (Fig. 1D) should be subtracted from the total demand (Fig. 1B) because such contributions incur no fuel cost and do not contribute to the merit-order scheme. Few common functions of the residual demand were used into the multivariate regression model, that is, square, fourth power, and exponential. The exponential law in equation (1) performed substantially better than the others in terms of both explained variance and significance:

$F_{D}=e^{D-PV_{t}-W}$

(1)

In equation (1), F_D is the forcing term, D is the total electricity demand over the grid, PV_t is the PV electricity fed into the grid (i.e., transmitted), and W is the wind electricity. All the demand terms are expressed in units of 10⁴ MW to obtain manageable values.

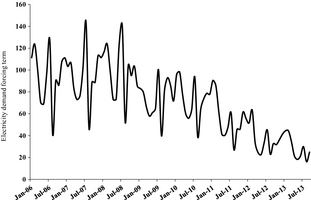
Figure 3 shows the series of the F_D forcing term; both the short-term variability and the longer term decrease trend starting in late 2008 and accelerating since mid-2012 are amplified as a result of both the subtraction of the PV and wind electricity and the use of an exponential function (eq. (1)).

Figure 3. Electricity demand forcing term series used in the peak PUN model.

The model for the monthly average peak PUN time series is a multivariate regression model shown mathematically in equation (2):

${\begin{array}{rl}peak\_PUN(t)=&\left(1.35\pm 6.90\right)+\left(0.50\pm 0.06\right)\cdot \\peak\_PUN\left(t-1\right)+\left(0.36\pm 0.04\right)\cdot \\&F_{D}\left(t\right)++\left(0.29\pm 0.07\right)\cdot \\&Brent\_Oil\left(t-4\right)\end{array}}$

(2)

where peak_PUN is the monthly average peak PUN in units €/MWh, peak_PUN(t − 1) is the observed one lagging 1 month before, F_D is the electricity demand forcing term (eq. (1)), Brent_Oil is the Brent spot oil price, in units €/bbl and t is time expressed in months. The standard errors of the regression coefficients are indicated, while the computed standard error on the estimated quantity is about 9 €/MWh.

The mathematical method above, despite a difference in the aggregation time, is similar to the multivariate regression model recently used to describe the German–Austrian market, in which the daily electricity price is correlated to the load (electricity demand), fuel price and RES generation as basic predictors [19].

The model of equation (2) explains about 78% of the variance of the observed peak PUN series and significance much greater than 99.99% according to the usual F statistics. The inclusion of the autoregressive term prevents the independence of the predicted series from the predictor series. Therefore, in order to check the real significance of the other terms, that is, electricity demand forcing and Brent oil price, another multivariate regression model was used, which does not include the autoregressive term. The latter model still explains about 60% of the variance of the observed peak PUN series, again with a significance much greater than 99.99% according to the usual F statistics.

On the basis of these findings, the model represented in equation (2) appears better suited to describe the phenomenon, while its 18% gain in terms of explained variance adds substantially to the model accuracy. It is also interesting to note that the abovementioned levels of explained variance locate our regression model in the upper range among those reported by related recent work [19].

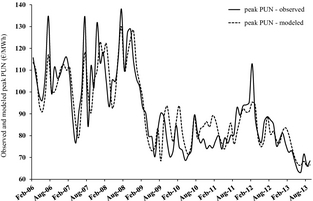
Figure 4 shows the series of the observed and modeled peak PUN values in the February 2006 to August 2013 time interval. Besides the overall and specific good agreement, sometimes the autoregressive term appears to force a shift of the modeled peak PUN 1-month ahead, especially until the first months of year 2009. The model, furthermore, appears generally limited in replicating the large Summer oscillation with high prices in July and low prices in August (due to the consecutive occurrence of the highest and lowest monthly demand) that took place until 2009.

Figure 4. Observed and modeled peak PUN series in the 2006–2013 period.

Results and Discussion

Impact of the PV generation on the peak PUN

The objective of the modeling effort described in the section 'The peak PUN model' is to compare the peak PUN formed when the PV electricity is fed into the grid with the peak PUN formed without such contribution but still taking into account both wind energy (which is completely fed into the grid) and the small fraction of the PV electricity that is consumed in situ. Modeling the peak PUN without PV generation requires, first, to use a predictive model starting from a specific initial condition, that is, from a peak PUN observed at a given initial time, because the peak PUN observed at later times is assumed to be affected by the PV generation itself. The expression of the forcing term for the electricity demand to be used in Eq. (2) therefore evolves from equation (1) into equation (3):

${F_{D}}^{'}=e^{D-W+PV_{c}}$

(3)

where F_D ′ is the forcing term, D is the total electricity demand over the grid, W is the wind electricity, PV_c is the PV electricity consumed in situ (and thus not transmitted), all the demand terms being expressed in units of 10⁴ MW to obtain manageable values.

In other words, after removing the wind electricity, the total demand without the PV electricity would be as great as that observed with the addition of the self-consumed PV electricity. Of course, the other forcing term, that is, the oil price, can be used unchanged.

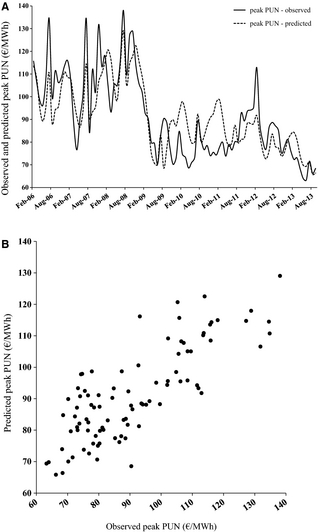
As a consequence of the first requirement to model the peak PUN without PV generation, also the peak PUN including PV generation must be modeled starting from a specific initial condition, that is, from a peak PUN observed at the same initial time as its counterpart without PV generation. The comparison between the observed peak PUN series and its prediction including PV generation is shown by the two graphs in Figure 5. The 2006–2013 period is the same considered above.

Figure 5. Monthly average observed and predicted peak PUN including PV generation: time series (A) and scatter diagram (B).

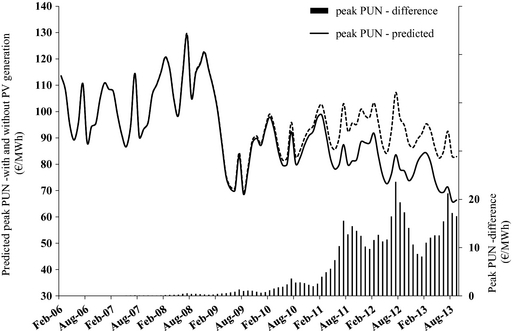
The agreement is still quite good and as much as 65% of the variance of the original series is explained by the predicted one, which is still 5% greater than the variance explained without the use of the autoregressive term. Figure 6 shows the peak PUN predicted with and without PV generation, as well as the respective difference (histograms).

Figure 6. Peak PUN series predicted with and without PV generation, as well as the respective difference, in the 2006–2013 period.

While a very tiny effect is apparent as of 2009, a large increase in the peak PUN difference is apparent from 2010 to 2011, followed by a smaller increase in 2012. Despite the further remarkable increase in the PV generation in 2013, the difference between the two prices seems to have stopped its growth (or even to have undergone a marginal decrease) in the Summer months of 2013. Such evidence is not surprising, and can be completely ascribed to the abovementioned acceleration of the decreasing trend in the electricity demand. It could therefore be reverted by an inversion of the economic trend and therefore of the electricity demand itself.

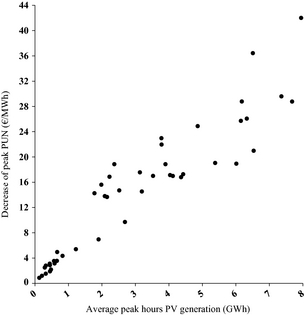
With this caveat in mind, it is now possible to extract the extent of the merit-order effect (MOE) to be ascribed to the PV generation in the IPEX, according to the homogeneous units referred to in the 'Introduction' section. This is represented by the decrease in the monthly average peak PUN, in units €/MWh, per unit increment of average hourly PV generation in the peak hours expressed in GWh.

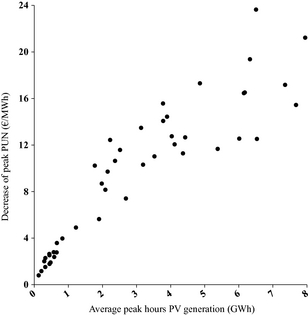
Figure 7 shows the relationship between the two abovementioned quantities in the January 2010 to September 2013 period, and the numerical result from the linear regression of the data shown in Figure 7 assuming that the peak PUN is unchanged with null PV generation. The value of the linear regression is −2.9 €/MWh per each additional GWh of PV production, which lies in upper tail of the range estimated for other large European markets [19].

Figure 7. Scatter diagram of the decrease in monthly average peak PUN and the average PV generation during the peak hours; data points correspond to the January 2010 to September 2013 period.

Due to the counteracting effect of the decreasing electricity demand, the above result of the MOE due to the PV generation is likely to become substantially greater in the future, in the event of new economic growth. In order therefore to provide a quantitative estimation of the peak PUN reduction under the hypothesis that the economy recovers to the 2007 values, the monthly series of the electricity demand observed in the year 2007 has been artificially reproduced for subsequent years, until September 2013.

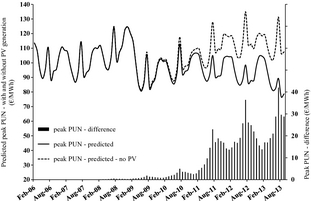
Figure 8 shows the peak PUN predicted with and without PV generation, as well as the respective difference, under this hypothesis. The MOE produced by the PV generation is apparently much greater and monotonically growing on an annual basis, as expected.

Figure 8. Same as Figure 6, under the hypothesis that the monthly electricity demand observed in 2007 repeats in all following years.

Figure 9, in its turn, shows the relationship between the decrease in peak PUN and the hourly average PV generation in the January 2010 to September 2013 period, under the hypothesis that the monthly electricity demand observed in 2007 repeats in all following years. The numerical result from the linear regression of the data shown in Figure 9, assuming that the peak PUN is unchanged with null PV generation, is −4.5 €/MWh per each additional GWh of PV production, that is, as much as 55% higher than the value computed using the observed data for electricity demand in Italy.

Figure 9. Same as Figure 7, under the hypothesis that the monthly electricity demand observed in 2007 repeats in all following years.

While the results derived for the impact of the PV generation on the prices formed on the IPEX under the MOE are in line with other studies [19], the strong dependence of such price impact on the overall electricity demand, therefore on the status of the economy, must be emphasized. The results of the present simulation show that, without the recession or in the presence of a reduced economic contraction, the impact of the PV generation on the peak PUN would have been greater in the Italian wholesale market than in others having similar size. Italy indeed has suffered a greater and accelerating economic contraction in comparison to Germany, Austria, and other countries taken into consideration in said studies, that in their turn hardly include data after year 2011.

PV-induced savings in the peak hours

The estimated monthly financial savings on the consumers' side due to the PV generation can be computed by simply multiplying the monthly electricity demand by the monthly average peak PUN difference with and without PV generation, as obtained after applying to the model described by equation (2) the forcing terms described in equation (1) and equation (3), respectively, the series of such differences having being displayed in Figure 6.

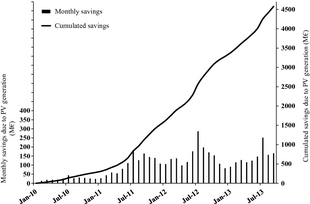
As a result of the above described computation, Figure 10 shows the monthly and cumulated direct financial savings due to the PV electricity generation, in the 2010–2013 time interval. Until September 2013, the total estimated savings amounted to about 4600 M€, with an average annual value in the last 12 months (September 2012 to September, 2013) greater than 1600 M€/year, that is, about 30% of the 6500 M€ per year total amount of the Italian FiT charged on the consumers' electricity bill estimated in September 2013 [26].

Figure 10. Monthly and cumulated direct financial savings on the consumers' side due to the PV generation, in the 2010–2013 period.

In other words, the net cost of Italian solar FiT is 30% lower than the charge listed in the electricity bill, which is a little greater than, but consistent with, the findings of other recent studies [25].

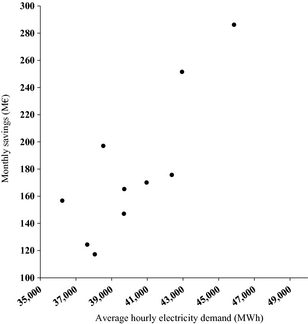
The sensitivity of said monthly savings to the electricity demand can be appreciated considering the Summer months (May–September) of 2012 and 2013. Figure 11 indeed shows the fastest increase in the savings due to PV generation with the increasing demand (scattering is partly due to the monthly variability and the increase in PV generation).

Figure 11. Scatter diagram of the monthly savings due to PV generation and monthly average hourly electricity demand; data points correspond to the months May to September in the years 2012 and 2013.

In the event of a new economic growth, in example up to the levels of the years 2006–2008 when the hourly average electricity demand in Italy was greater than 43,000 MWh in any Summer months except August (and with peaks over 50,000 MWh in July), the savings due to the PV generation would rapidly increase in comparison to the 2013 Summer with the same PV generation.

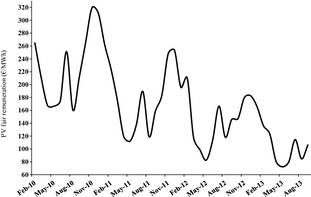
Figure 12 shows the graphical outcome of the division of the monthly financial savings shown in Figure 10 by the corresponding PV generation fed into the grid (Fig. 1C). Such straightforward calculation provides an objective assessment of the minimum value of the PV electricity for Italian customers on a monthly basis, which could be translated into the remuneration level that is exactly compensated by the respective monthly saving.

Figure 12. Monthly series of the estimated minimum objective value of the PV electricity for the Italian customers, in the 2010–2013 time range.

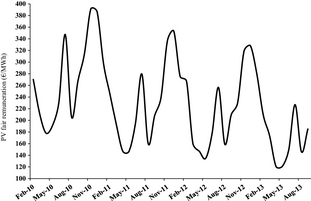
In comparison to 2010, the computed minimum value of the PV electricity approximately halves in 2013 due to the decreasing electricity demand and to the stationary or slightly decreasing monthly savings in 2012–2013. Moreover, in the same period the strong monthly oscillations dampen, while retaining local minimums in May and August, a local maximum in July and the absolute maximum in November or December.

We have artificially set constant the electricity demand observed in the year 2007 for all following years until September 2013, and plotted in Figure 13 the monthly series of the estimated minimum value of the PV electricity for Italys electricity customers in the 2010–2013 period. While the decreasing trend of Figure 12 is confirmed, the absolute values are about 75% higher, while the calculated minimum value of the PV electricity in 2013 is now only 35% lower than in 2010.

Figure 13. Same as Figure 12, under the hypothesis that the monthly electricity demand observed in 2007 repeats in all following years.

Under this hypothesis of economic recovery, the total estimated savings until September 2013, would amount to nearly 6900 M€, with an average annual value in the last 12 months of 2800 M€/year, namely about 47% of the total amount of the Italian FiT charged on the consumers' electricity bill.

Anomalous IPEX trends

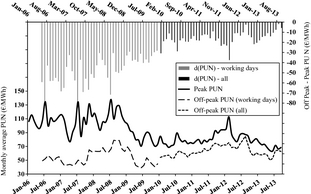
It is perhaps not surprising, in front of 18 GW installed PV solar power, to notice that the IPEX is showing an anomalous behavior. Figure 14 portrays the monthly series in the 2006–2013 time interval of the peak PUN, the off-peak PUN (only working days till 2009, all off-peak hours since 2010), and the respective differences. After nearly 3 years with small overall change, a first consistent reduction in the (absolute) difference value occurs with the economic downfall in 2009, when PV generation in Italy was still very small.

Figure 14. Monthly series of peak PUN, off-peak PUN, and their difference, in the 2006–2013 period.

In subsequent years, however, the curves of peak PUN and off-peak PUN continue to get closer with a further dramatic acceleration since Spring 2012, when PV generation in Italy had become relevant.

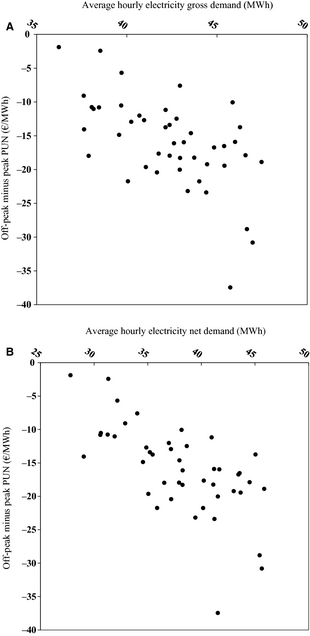
To check whether this trend was connected either to the increasing PV generation or only to the decrease in the gross (total) electricity demand in peak hours, the scatter plot of the monthly series of such difference against gross and net electricity demand (where “net” means after subtraction of PV and wind generation) are shown in Figure 15 for the January 2010 to September 2013 period.

Figure 15. Scatter plot of the off-peak minus peak PUN against the average hourly gross (A) and net (B) electricity demand, on a monthly basis in the January 2010 to September 2013 period.

The substantially greater dispersion along the vertical axis in Figure 15A (gross demand) compared to that in Figure 15B (net demand) shows, at least qualitatively, that the PV generation plays a significant role in this anomalous phenomenon (the trend of the off-peak electricity price) that partially offsets the advantages brought by the PV generation in peak hours. The above conclusion about the significant role of the PV in affecting the trend of peak to off-peak PUN difference appears reinforced by the further consideration that the off-peak gross electricity demand is strongly correlated with its counterpart in peak hours with an explained variance about 84% (not shown); in other words, using the off-peak electricity demand would add little information, if any, to the above picture.

Conclusions and Policy Implications

The impact of the PV generation on the prices formed in the IPEX has been assessed on a quantitative basis in terms of units homogeneous to other studies in order to allow comparability. The main result is the −2.9 €/MWh value in price reduction per each additional GWh of PV production, a figure in good agreement with other studies concerning electricity markets of large size such as the German–Austrian market where the 2010 impact of RES generation was comprised between −5 and −6 €/MWh; [19, 25] from the −7.8 €/MWh value found by Sensfuß and coworkers who first described [16] the impact of PV generation in a near mature RES market considering both wind and solar PV generation as a whole, namely the case of Germany in year 2006. We also demonstrate that the impact of PV generation has been dampened by the steep fall of the electricity demand exactly during the time interval in which the PV installed power quickly grew from a few MW to 18,000 MW. If the electricity demand of the year 2007 had repeated in the following years the above impact would have been as great as −4.5 €/MWh.

The overall cost of the electricity sold in the IPEX market in the January 2010 to September 2013 time framework, has diminished by 4600 M€, of which more than 1600 M€/year in the last 12 months of the considered period (corresponding to 30% of the total yearly amount of the Italian FiT). Again, in the hypothetical absence of the fall in the electricity demand after year 2007, the above figures would have been, respectively, 6900 M€ and 2800 M€/year (47% of the total amount of Italys FiT).

The series of estimated minimum objective monthly value of the PV electricity (Figs. 12 and 13) suggest a number of straightforward policy options. Since the Italian FiT stimulation scheme ceased on July 2013, and presently only fiscal incentives are granted, an option would be to increase or extend such tax relief measures. Another option would be to restore a special FiT scheme, for ground-mounted sun-tracking PV installations which allow higher levels of electricity generation in the late Fall and Winter months when the PV generation presently enjoys the highest absolute unit value for consumers. The objective assessment of the minimum value of the PV electricity for Italian customers of this study will help Italys Government to shape a monthly based fair remuneration for said PV electricity.

A third policy measure for Italys Government, ruling a country where solar plants cumulating over 17 GW power are installed and will be perfectly working for at least the next 18 years, will be to stimulate the electrification of most of the end use of energy such as heating and mobility (electric vehicles), for example, by means of fiscal incentives, in order to increase the electricity demand and therefore the impact of the PV generation on the peak PUN. As the solar revolution continues with electrification of transportation now taking place in Germany, France, and other large EU countries [27], we believe that this will be the straightforward and convenient option for years to come.

Acknowledgments

This article is dedicated to Natan Hogrebe on the occasion of his familys travel to Sicily in Autumn 2013, 20 years after Leiden 1993. The authors gratefully acknowledge Giuseppe Artizzu (Cautha Srl) and Carlo Durante (APER), who first unveiled the impact of PV generation on the electricity prices in Italy, for fruitful discussion and invaluable suggestions.

Conflict of Interest

None declared.

References

1. Heun, M. K., and M. de Wit. 2012. Energy return on (energy) invested (EROI), oil prices, and energy transitions. Energy Policy40:147–158.
2. Raugei, M., P. Fullana-i-Palmer, and V. Fthenakis. 2012. The energy return on energy investment (EROI) of photovoltaics: methodology and comparisons with fossil fuel life cycles. Energy Policy45:576–582.
3. Weißbach, D., G. Ruprecht, A. Huke, K. Czerski, S. Gottlieb, and A. Hussein. 2013. Energy intensities, EROIs (energy returned on invested), and energy payback times of electricity generating power plants. Energy52:210–221.
4. Raugei, M.2013. Comments on “Energy intensities, EROIs (energy returned on invested), and energy payback times of electricity generating power plants”—Making clear of quite some confusion. Energy59:781–782.
5. Jordan, D. C., and S. R. Kurtz. 2013. Photovoltaic degradation rates - an analytical review. Prog. Photovoltaics Res. Appl.21:12–29.
6. Jenner, S., F. Groba, and J. Indvik. 2013. Assessing the strength and effectiveness of renewable electricity feed-in tariffs in European Union countries. Energy Policy52:385–401.
7. IEA. 2013. IEA - solar (PV and CSP). Available at http://www.iea.org/topics/solarpvandcsp/ (accessed 1 November 2013).
8. Pagliaro, M., R. Ciriminna, and G. Palmisano. 2008. Flexible solar cells. ChemSusChem1:880–891.
9. Haas, R., G. Lettner, H. Auer, and N. Duic. 2013. The looming revolution: how photovoltaics will change electricity markets in Europe fundamentally. Energy57:38–43.
10. Schachinger, M. 2013. (pvXchange) “Module price index October 2013: New low price suppliers.” Available at www.pv-magazine.com/investors/module-price-index/#ixzz2jlBHuDP9 (accessed 5 November 2013).
11. Breyer, C., and A. Gerlach. 2013. Global overview on grid-parity. Prog. Photovoltaics Res. Appl.21:121–136.
12. Jensen, S. G., and K. Skytte. 2002. Interactions between the power and green certificate markets. Energy Policy30:425–435.
13. Floro, D.2009. Selecting oligopolistic models in the Italian wholesale electricity market. Pp. 1–6inIEEEXplore, Proceedings of the 6th International Conference on the European Energy Market (EEM2009). IEEE, Leuven.
14. Bonenti, F., G. Oggioni, E. Allevi, and G. Marangoni. 2013. Evaluating the EU ETS impacts on profits, investments and prices of the Italian electricity market. Energy Policy59:242–256.
15. Bollino, C. A., D. Ciferri, and P. Polinori. 2013. Integration and convergence in European electricity markets. MPRA Paper No. 44704. Available at http://mpra.ub.uni-muenchen.de/44704/ (accessed 5 November 2013).
16. Sensfuß, F., M. Ragwitz, and M. Genoese. 2008. The merit-order effect: a detailed analysis of the price effect of renewable electricity generation on spot market prices in Germany. Energy Policy36:3086–3094.
17. GME. 2013. GME - Manager of the Italian Energy Markets. Available at http://www.mercatoelettrico.org/En/Default.aspx (accessed 5 November 2013).
18. TERNA. 2013. TERNA - Manager of the Italian power transmission grid. Available at http://www.terna.it/Default.aspx?tabid=101 (accessed 5 November 2013).
19. Würzburg, K., X. Labandeira, and P. Linares. 2013. Renewable generation and electricity prices: taking stock and new evidence for Germany and Austria. Energy Econ.40:S159–S171.
20. TERNA. 2013. Impianti di Generazione, 2013. Available at http://www.terna.it/default/Home/SISTEMA_ELETTRICO/statistiche/dati_statistici.aspx (accessed 5 November 2013).
21. Pelacchi, P., and D. Poli. 2010. The influence of wind generation on power system reliability and the possible use of hydrogen storages. Electr. Power Syst. Res.80:249–255.
22. EIA. 2013a. EIA - U.S. Energy Information Administration. Natural Gas Prices for Electricity Generation for Selected Countries. Available at http://www.eia.gov/countries/prices/natgasprice_elecgen.cfm (accessed 5 November 2013).
23. Indexmundi. 2013. Indexmundi - Russian Natural Gas Monthly Price [WWW Document]. Available at http://www.indexmundi.com/commodities/?commodity=russian-natural-gas&months=120 (accessed 5 November 2013).
24. EIA. 2013b. EIA - U.S. Energy Information Administration. Petroleum & other liquids. Available at http://www.eia.gov/dnav/pet/pet_pri_spt_s1_m.htm (accessed 5 November 2013).
25. Tveten, Å. G., T. F. Bolkesjø, T. Martinsen, and H. Hvarnes. 2013. Solar feed-in tariffs and the merit order effect: a study of the German electricity market. Energy Policy61:761–770.
26. GSE. 2013. Contatore fotovoltaico GSE: aggiornamento del costo indicativo annuo degli impianti ammessi al Primo Registro del Quinto Conto Energia. Available at http://www.gse.it/it/salastampa/news/Pages/Contatore-fotovoltaico-GSE-aggiornamento-costo-indicativo-annuo-impianti-ammessi-Primo-Registro-Quinto-Conto-Energia.aspx (accessed 5 November 2013).
27. European Commission. 2013. European Commission, Communication on Clean Power for Transport, 24 January 2013. Available at http://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=COM:2013:0017:FIN:EN:PDF (accessed 5 November 2013).

References

1. Heun, M. K., and M. de Wit. 2012. Energy return on (energy) invested (EROI), oil prices, and energy transitions. Energy Policy40:147–158.
2. Raugei, M., P. Fullana-i-Palmer, and V. Fthenakis. 2012. The energy return on energy investment (EROI) of photovoltaics: methodology and comparisons with fossil fuel life cycles. Energy Policy45:576–582.
3. Weißbach, D., G. Ruprecht, A. Huke, K. Czerski, S. Gottlieb, and A. Hussein. 2013. Energy intensities, EROIs (energy returned on invested), and energy payback times of electricity generating power plants. Energy52:210–221.
4. Raugei, M.2013. Comments on “Energy intensities, EROIs (energy returned on invested), and energy payback times of electricity generating power plants”—Making clear of quite some confusion. Energy59:781–782.
5. Jordan, D. C., and S. R. Kurtz. 2013. Photovoltaic degradation rates - an analytical review. Prog. Photovoltaics Res. Appl.21:12–29.
6. Jenner, S., F. Groba, and J. Indvik. 2013. Assessing the strength and effectiveness of renewable electricity feed-in tariffs in European Union countries. Energy Policy52:385–401.
7. IEA. 2013. IEA - solar (PV and CSP). Available at http://www.iea.org/topics/solarpvandcsp/ (accessed 1 November 2013).
8. Pagliaro, M., R. Ciriminna, and G. Palmisano. 2008. Flexible solar cells. ChemSusChem1:880–891.
9. Haas, R., G. Lettner, H. Auer, and N. Duic. 2013. The looming revolution: how photovoltaics will change electricity markets in Europe fundamentally. Energy57:38–43.
10. Schachinger, M. 2013. (pvXchange) “Module price index October 2013: New low price suppliers.” Available at www.pv-magazine.com/investors/module-price-index/#ixzz2jlBHuDP9 (accessed 5 November 2013).
11. Breyer, C., and A. Gerlach. 2013. Global overview on grid-parity. Prog. Photovoltaics Res. Appl.21:121–136.
12. Jensen, S. G., and K. Skytte. 2002. Interactions between the power and green certificate markets. Energy Policy30:425–435.
13. Floro, D.2009. Selecting oligopolistic models in the Italian wholesale electricity market. Pp. 1–6inIEEEXplore, Proceedings of the 6th International Conference on the European Energy Market (EEM2009). IEEE, Leuven.</̋Ɍ��