Published in Comput. Meth. Appl. Mech. Engng., Vol. 293, pp. 191-206, 2015
10.1016/j.cma.2013.12.009
Abstract
We present a 3-noded triangle and a 4-noded tetrahedra with a continuous linear velocity and a discontinuous linear pressure field formed by the sum of an unknown constant pressure field and a prescribed linear field that satisfies the steady state momentum equations for a constant body force. The elements are termed P1/P0+ as the “effective” pressure field is linear, although the unknown pressure field is piecewise constant within each element. The elements have an excellent behaviour for incompressible viscous flow problems with discontinuous material properties formulated in either Eulerian or Lagrangian descriptions. The necessary numerical stabilization for dealing with the inf-sup condition imposed by the incompressibility constraint and high convective effects (in Eulerian flows) is introduced via the Finite Calculus (FIC) approach. For the sake of clarity, the element derivation is presented first for the simpler Stokes equations written in the standard Eulerian frame. The extension of the formulation to the Navier-Stokes equations written in the Eulerian and Lagrangian frameworks is straightforward and is presented in the second part of the paper.
The efficiency and accuracy of the new P1/P0+ triangle is verified by solving a set of incompressible multifluid flow problems using a Lagrangian approach and a classical Eulerian description. The excellent performance of the new triangular element in terms of mass conservation and general accuracy for analysis of fluids with discontinuous material properties is highlighted.
Keywords: P1/P0+ elements, Incompressible flow, Discontinuous material properties, Multifluids
1 INTRODUCTION
Preservation of mass is a great challenge in the numerical study of incompressible flow problems. Mass losses can be introduced by the so-called stabilization terms which are typically added to the discretized forms of the momentum and mass balance equations in order to account for large values of the convective acceleration terms in the momentum equations in high Reynolds number flows and to satisfy the inf-sup condition imposed by the incompressibility constraint when equal order interpolation of the velocities and the pressure are used in mixed finite element methods [4,11,39].
Mass loss also typically occurs in the numerical study of free-surface incompressible flow problems using Eulerian and Lagrangian descriptions. In both cases, the inaccuracy in capturing the free surface can lead to considerable mass losses unless special numerical schemes are used [22].
An additional source of mass loss occurs in the numerical analysis of the so-called multifluid problems with discontinuous changes in the viscosity and/or the density in parts of the domain. Most numerical methods have difficulties for accurately capturing the jumps in the pressure and/or the pressure gradient at the interfaces between the different fluids [20,21,25].
The numerical study of multifluids via the FEM and similar computational techniques has been the subject of much research in last decades. Several authors have proposed alternative stabilized FEM procedures for accounting for the discontinuity in the pressure (and/or the pressure gradient) at the interface of fluids with different viscosity (and/or pressure). Among these formulations we note those based in injecting a discontinuous pressure field within the appropriate elements [2] and those based on using a stabilized formulation based on the introduction of stabilization terms including the jumps in the pressure and the viscous terms at the element boundaries [3,5,6,7,9,12,14,17,23].
In this work we present a new 3-noded triangle (and the 4-noded tetrahedron counterpart) with a continuous linear velocity and a discontinuous linear pressure field formed by the sum of an unknown constant pressure field and a prescribed linear field that satisfies the steady state momentum equations for a constant body force. The so-called P1/P0+ elements have an excellent behaviour for incompressible viscous flow problems formulated in Eulerian and Lagrangian descriptions. For the sake of clarity, the elements derivation is presented first for the simpler Stokes equations written in the standard Eulerian frame. The extension of the formulation to the Navier-Stokes equations written in the Eulerian and Lagrangian frameworks is straightforward and is presented in the second part of the paper. A motivation of this work is the study of multifluids problems using a Lagrangian formulation via the Particle Finite Element Method (PFEM) [10],[18]–[21],[25,32],[36]–[38] and similar procedures.
The success of the P1/P0+ formulation lays in the consistent derivation of a residual-based expression of the mass balance equation using the Finite Calculus (FIC) technique. The FIC approach in mechanics is based on expressing the equations of balance of mass and momentum in a domain of finite size and retaining higher order terms in the Taylor series expansion typically used for expressing the change in the transported variables within the balance domain. In addition to the standard terms of infinitesimal theory, the FIC forms of the balance equations contain derivatives of the classical differential equations in mechanics multiplied by characteristic distances in space and time. Examples of stabilized FIC-FEM formulations in fluid and solid mechanics can be found in [26]–[31],[33]–[35]. In our work we use the FIC forms of the mass balance equation in space and time for obtaining a variational residual form useful for finite element analysis.
The discretized stabilized variational form for the mass balance equation using a P1/P0+ approximation for the velocity/pressure variables involves the jumps in the viscous stresses, the pressure, the surface tractions and the acceleration term in the normal direction to each side (or face) of the elements. These stabilization terms resemble those proposed by other authors for similar fluid flow problems [3,9,12,14,17,23]. The method presented in this paper yields a consistent and extended form of the stabilization terms that has proven to give a superior behaviour in terms of mass conservation and overall stability in multifluids problems.
The lay-out of the paper is the following. In the next section we present the basic equations for an incompressible Stokes fluid. Next we derive the stabilized variational FIC form of the mass balance equation. Then the P1/P0+ finite element discretization for the 3-noded triangle and the 4-noded tetrahedron is presented and the key matrices and vectors of the discretized system of equations are given. Details of the solution of the FEM equations are given.
The extension of the general stabilized FIC-FEM formulation to Navier-Stokes flows using a standard Eulerian approach and a Lagrangian description is outlined.
The efficiency and accuracy of the new P1/P0+ triangle is verified by solving a set of transient incompressible multifluid flow problems using a Lagrangian approach and a steady state problem via a classical Eulerian description. The excellent performance of the P1/P0+ triangle in terms of mass conservation and general accuracy for fluid flow problems with discontinuous material properties is highlighted.
2 BASIC EQUATIONS
We write the governing equations for an incompressible Stokes flow problem as follows.
Momentum equations
|
|
(1) |
In Eq.(1), and are the velocity and body force components along the th Cartesian axis, is the number of space dimension (i.e. for a 3D problem), is the analysis domain and are the Cauchy stresses that are split in the deviatoric () and pressure () components as
|
|
(2) |
where is the Kronecker delta. Note that the pressure is assumed to be positive for a tension state.
Summation of terms with repeated indices is assumed in Eq.(1) and in the following, unless otherwise specified.
Constitutive equation and volumetric strain rates
The relationship between the deviatoric stresses and the strain rates has the standard form for a Newtonian fluid,
|
|
(3) |
where the strain rates are related to the velocities by
|
|
(4) |
In Eq.(4) is the volumetric strain rate defined as
|
|
(5) |
Substituting Eqs.(2) and (4) into (1) gives a useful form of the momentum equations as
|
|
(6) |
Boundary conditions
The boundary conditions at the Dirichlet () and Neumann/traction () boundaries are
|
|
(7.a) |
|
|
(7.b) |
where and , are the prescribed velocities and prescribed tractions on the and boundaries, respectively.
Mass balance equation
The mass balance equation for an incompressible fluid is written as
|
|
(8) |
Stabilized FEM techniques are needed for solving the general momentum equations in fluid mechanics when they are written in the Eulerian description. This is due to the effect of the convective acceleration terms that lead to loss of stability of standard Galerkin FEM. For Stokes flows (or for fluid flows formulated in the Lagrangian description) the convective terms vanish from the momentum equations and, consequently, the equations can be solved with the Galerkin FEM.
The problem, however, remains for obtaining stable solution for incompressible flows when an equal order interpolation is used for the velocities and the pressure, as it is the case for the element derived in the paper. This situation violates the so called inf-sup (or LBB) condition and, hence, there is a need to use stabilization techniques for solving the mass balance equation with the FEM [11,39].
3 STABILIZED FIC FORMS OF THE MASS BALANCE EQUATION
In our work the stabilized form of the mass balance equation is obtained using the Finite Calculus (FIC) procedure [26]–[31],[33]–[35]. We will use both the second order form of the mass balance equation for an incompressible fluid obtained using the FIC method in space, as well as the FIC form of the mass balance equation in time. These forms have the following expressions.
Second order FIC mass balance equation in space
|
|
(9) |
FIC mass balance equation in time
|
|
(10) |
Eq.(9) is obtained by expressing the balance of mass in a rectangular domain of finite size (with space dimensions for 2D problems) and retaining higher order terms in the Taylor series expansions than those typically used in the infinitesimal theory for expressing the change of mass along the sides of the balance domain. The characteristic lengths are related to the finite element sizes in the discretized problem, as it will be explained later.
Eq.(10), on the other hand, is obtained by expressing the balance of mass in a domain of infinitesimal size in space and of finite dimension in time, where is a characteristic time value.
In Eqs.(9) and (10) the terms involving and play the role of stabilization terms respectively. The form of the and parameters will be defined later. Note that for and the standard expression of the mass balance equation (8) is recovered in all cases.
The derivation of Eqs.(9) and (10) for a 1D problem are shown in [37].
4 FIC FORM OF THE MASS BALANCE EQUATION IN TERMS OF THE MOMENTUM EQUATIONS
We will derive next a more useful FIC form of the stabilized mass balance equation expressed in terms of the momentum equations.
From the momentum equations (6) we obtain (neglecting the space changes of the viscosity in the term involving )
|
|
(11) |
From the last equation we deduce
|
|
(12) |
In the last two equations is a static momentum term defined as
|
|
(13) |
Let us introduce from Eq.(12) intro Eq.(9). This gives, after small algebra
|
|
(14) |
Observing the term involving the time derivative of in Eq.(14) gives
|
|
(15) |
Substituting Eq.(15) into (14) gives
|
|
(16) |
On the other hand, from Eq.(10) we deduce
|
|
(17) |
Substituting Eq.(17) into (16) gives
|
|
(18) |
In the following we will assume where is a characteristic length that will be related to a typical average dimension of each finite element in the mesh. Multiplying Eq.(18) by gives, after grouping some terms,
|
|
(19) |
where is a stabilization parameter given by
|
|
(20) |
Eq.(19) is the FIC form of the stabilized mass balance equation. This equation will be taken as the starting point for deriving the stabilized FIC-FEM formulation. Note again that for , the standard form of the incompressibility condition (8) is obtained.
5 VARIATIONAL EQUATIONS
5.1 Variational expression of the momentum equation
Multiplying Eq.(1) by arbitrary test functions (with dimension of velocity) and integrating over the analysis domain gives the standard weighted residual form of the momentum equations as
|
|
(21) |
Integrating by parts the term involving and making use of the Neumann boundary conditions (7.b), yields the standard principle of virtual power as [4,39]
|
|
(22) |
where is an arbitrary (virtual) strain rate field.
Substituting the expression of the stresses from Eq.(2) into (22) gives
|
|
(23) |
Eq.(23) can be written in matrix form as
|
|
(24) |
In Eq.(24) are vectors containing the weighting functions, the velocities and the strain rates, respectively; and are body force and surface tractions vectors, respectively; is the viscous constitutive matrix and is an auxiliary vector. These vectors are defined as (for 3D problems)
|
|
(25) |
The 2D form of above expressions is straightforward. For instance, the 2D expression of matrix is obtained by deleting the rows and columns 3, 5 and 6 in Eq.(25).
Remark 1. From the definition of and and Eqs.(2), (3) and (5) we deduce
|
|
(26) |
where are the stress and deviatoric stress vectors, respectively.
5.2 Variational expression of the stabilized mass balance equation
Multiplying equation (19) by arbitrary test functions (with dimension of pressure) defined over the analysis domain and integrating over gives
|
|
(27) |
Let us integrate by parts the second integral in Eq.(27) over a mesh of elements each one with area and boundary . This yields
|
|
(28) |
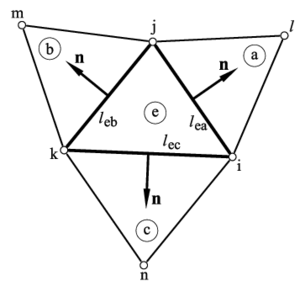
where are the components of the unit normal vector to the element boundary . Note that is a side for a 3-noded triangle and a face for a 4-noded tetrahedron.
Remark 2. In Eq.(28), the second integral over the domain involving is zero for a piecewise constant approximation of the weighting function over the elements. This situation occurs for the P1/P0+ elements presented in this work.
From the definition of of Eqs.(13) and (1) we deduce
|
|
(29) |
Multiplying by the normal components gives
|
|
(30) |
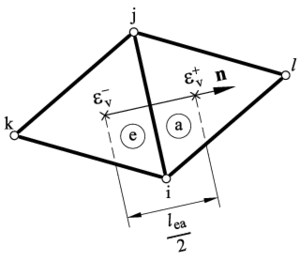
where is the projection of the velocity in the direction of the normal to the element boundary and is the derivative of in the normal direction.
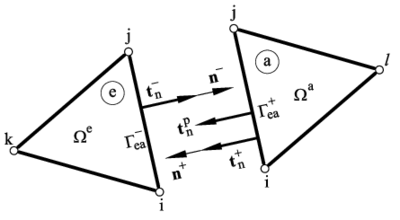
The term at an element boundary connecting elements and can be computed as
|
|
(31) |
where and denote the values of the relevant magnitude at the external and internal points adjacent to the element boundary, respectively and is the characteristic length of the boundary. For triangles is taken as the side lenght (Figure 1). For 4-noded tetrahedra where is the area of the triangular face connecting elements and .
Eq.(31) is just a simple (yet effective) model for computing at the element boundary. Indeed, more sophisticated procedures can be used [9].
From the Neumann boundary conditions (7b) and Eq.(31) we deduce
|
where indices and – denote values at the external and internal sides and of the element boundary, respectively. In Eqs.(5.2) and are the normal tractions respectively acting at and (Figure 1c).
Substituting Eqs.(5.2) into (31) gives
|
|
(33) |
where denotes the jump of the magnitude across the element boundary , i.e. .
From the equilibrium of tractions at the element boundaries we obtain
|
|
(34) |
where is the external normal traction acting on the element side in the direction of the normal to (Figure 1). Clearly for unloaded boundaries and, consequently, .
We note that above derivations are independent of the choice of and .
Substituting Eq.(33) into (30) and this one into (28) gives the final stabilized variational form of the mass balance equation as
|
|
(35) |
where are the lengths of the element sides.
For element boundaries laying on the Dirichlet boundary , and the boundary term vanishes from Eq.(35). This is justified by the fact that both and are zero at .
Remark 3. At element boundaries laying on an external Neumann boundary , , and, hence, at .
Remark 4. The boundary integral in Eq.(35) resembles the jump stabilization terms across element sides proposed by different authors for fluid flow problems [3,9,12,14,17,23]. It is remarkable that Eq.(35) emanates naturally from the FIC formulation. Also, the form of Eq.(35) introduces the effect of the acceleration in the normal direction to the element side, as well as the effect of the external surface tractions acting on the element side. These two terms have proven to be important for the improved mass conservation and overall stability of the numerical solution of the multifluid problems solved in this paper and also for free surface homogeneous fluid flows [37].
Remark 5. For steady state problems the acceleration term vanishes from the boundary integral in Eq.(35).
6 FEM DISCRETIZATION
We discretize the analysis domain into a mesh of finite elements in the standard manner. In our work we will choose simple 3-noded triangles (for 2D problems) and 4-noded tetrahedra (for 3D problems). The velocity is linearly interpolated in terms of the nodal values, while a discontinuous linear interpolation for the pressure over each element is chosen, i.e.
|
|
(36) |
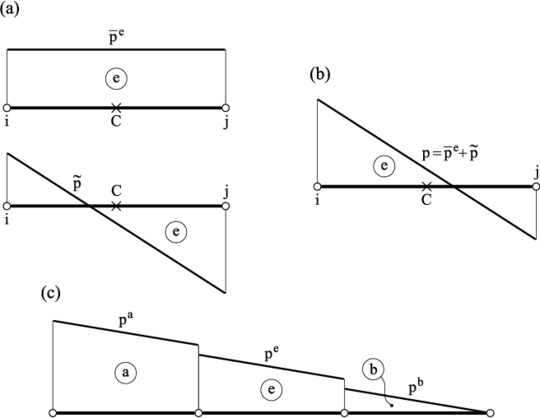
where are the standard linear shape functions for simplicial elements, is the number of element nodes ( for 2D/3D problems), denotes the value of the th velocity component for the th node of an element, is a constant pressure field over each element and is a discontinuous linear pressure field chosen as (Figure 2)
|
|
(37) |
where are the coordinates of the element midpoint.
Note that satisfies the steady state form of the momentum equation for a linear velocity field and constant body forces , i.e.
|
|
(38) |
The actual unknowns of the problem are the nodal velocities and the constant pressure field for each element (Figure 3).
We will choose now piecewise constant unit weighting functions so that and if and if . With these assumptions the variational form (35) for the stabilized mass balance equation simplifies for 3-noded triangles to
|
|
(39) |
where the sum in the second term extends over the three sides of each triangular element and is the length of the th element side.
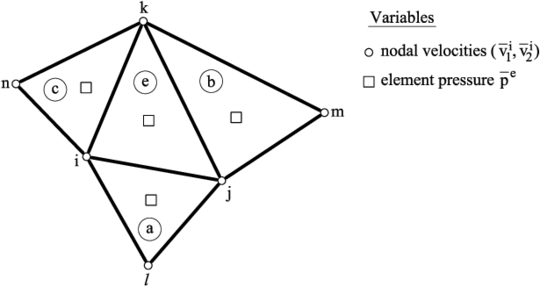
|
| Figure 3: Nodal velocities and element pressure variables at a patch of four 3-noded triangles |
Remark 6. For 4-noded tetrahedra the sum in Eq.(39) extends over the four faces of the tetrahedra and is a characteristic distance for the th face with area computed as where is the area of the face.
Substituting the approximation (36) into Eqs.(39) and (24) and choosing a Galerkin form with gives the discretized expression of the momentum and (stabilized) mass balance equations as
|
|
(40.a) |
|
|
(40.b) |
with
|
|
(40.c) |
where is the number of nodes in the mesh. The different matrices and vectors in Eqs.(6a,b) are assembled from the element contributions given in Box 1 for 3-noded triangles.
|
Remark 7. The FEM approximation (36) yields the strain rates and the stresses within an element in terms of the nodal velocities and pressure as
|
|
(41) |
where is given in Box 1 for 2D problems.
7 SOLUTION OF THE DISCRETIZED EQUATIONS
The discretized form in time of the system of Eqs.(6) is expressed as
|
|
(42.a) |
|
|
(42.b) |
A symmetric monolithic form of Eq.(7) can be written as
|
|
(43) |
The steady state form of Eq.(43) is simply
|
|
(44) |
Note that the terms involving the normal velocity to the element, the normal tractions to the side and the term emanating form the side discontinuous linear pressure field have been incorporated into the force vector in Eq.(40.b). An obvious alternative will be to add the contribution of these terms to matrices and in the l.h.s. of this equation.
Remark 8. The stabilization parameter of Eq.(20) is computed at each element boundary connecting elements and as
|
|
(45.a) |
where is a characteristic length of the element boundary. For triangles is taken as the side length. For 4-noded tetrahedra , where is the area of the face connecting elements and . The material parameters and are computed as
|
|
(45.b) |
where indices and denote the element where the material parameter is computed.
Remark 9. For the steady state case the stabilization parameter of Eq.(45.a) is computed as
|
|
(46) |
with being the velocity vector of the mid-point of the boundary connecting elements and .
The above expressions of the stabilization parameter are similar to those used by many stabilization methods [11,39].
8 EXTENSION TO THE NAVIER-STOKES EQUATIONS
The momentum equations for Navier-Stokes flows are written in the Eulerian framework as
|
|
(47) |
Note that the difference with Eq.(1) is that the convective acceleration terms are now accounted for in Eq.(47).
The constitutive equation and the boundary conditions are identical to Eqs.(2)–(4) and (7), respectively.
The mass balance equation is given by Eq.(8). The stabilized form is given by Eq.(19).
The FEM solution of the Navier-Stokes equation for incompressible fluids requires a stabilized numerical method that can capture the internal layers introduced by the convective acceleration terms, as well as for satisfying the inf-sup condition introduced by the incompressibility constraint. Different stabilization procedures have been proposed in the past two decades. An overview can be found in [11,39]. In our work we use the FIC approach for obtaining stabilized FEM solutions for the Navier-Stokes equations [26]–[31],[33]–[35].
In the FIC method the momentum equations are derived in a balance domain of finite size. This yields a non-local form of the equations. For the th momentum equation we have
|
|
(48) |
where are characteristic distances that define the balance domain [28]–[30].
For consistency reasons, in the FIC method the Neumann boundary conditions expressing balance of tractions at the boundary are also derived in a finite domain adjacent to the boundary. The modified Neumann boundary conditions are written as
|
|
(49) |
where .
Applying the standard weighted residual procedure to Eq.(48) we obtain
|
|
(50) |
where are standard weighting functions.
Integrating by parts the second integral in (50) assuming that on and using the modified Neumann boundary conditions (49) we obtain
|
|
(51) |
The characteristic distances can be defined in a number of ways. For instance choosing
|
|
(52) |
where is a characteristic distance for element , reproduces the standard SUPG method [11,39].
The effect of sharp internal gradients in the solution can be introduced by defining as
|
|
(53) |
The first term in the r.h.s. of Eq.(53) introduces the SUPG stabilization while the second term introduces a shock-capturing type of stabilization. In Eq.(53) and are appropriate characteristic distances for 1D elements . The simplest choice for simplicial 2D and 3D elements is .
As for the treatment of the mass balance equation, the same procedure explained in Section 5.2 has been applied. Hence, the stabilized mass balance expression is identical to Eq.(19). Also, the corresponding variational form of the mass balance equation coincides with Eq.(35).
The final system of discretized equations using P1/P0+ elements is identical to Eq.(6). For 3-noded triangles, all matrices and vectors coincide with the expressions of Box 1 except and which are now given by (for each element)
|
|
(54) |
In Eq.(54) is the viscous contribution coinciding with the expression of of Box 1 and and are the convective and stabilization contributions for the element given by
|
|
(55.a) |
where is the unit matrix and
|
|
(55.b) |
In Eq.(54) coincides with the expression of in Box 1 and is the contribution from the stabilization terms given by
|
|
(56) |
The general form of of Eq.(53) can be used in (56) to introduce SUPG and/or shock capturing effects in the stabilized formulation, as appropriate.
For the problems we are solving in this work the velocity field is free from internal layers. Therefore, good results are obtained with the standard Galerkin form of the momentum equations neglecting the stabilization term. The full stabilized formulation expressed by Eq.(51), with given by Eq.(53), should however be used for the general solution of Navier-Stokes problems involving high gradients of the velocity.
9 PARTICULARIZATION FOR LAGRANGIAN FLOWS
The formulation presented in Sections 2–6 for Stokes flows in an Eulerian framework can be easily particularized for analysis of a viscous fluid flow using a Lagrangian description of the motion [4].
The relevant change is the definition of the acceleration term in the momentum equations. In the updated Lagrangian formulation these are written as [4]
|
|
(57) |
where is the material derivative of the th velocity component of a material point with coordinates at time . Also, the Cauchy stresses , the body forces and the coordinates are referred to the updated configuration at time [4].
The material derivative of the velocity in the Lagrangian formulation is typically approximated as
|
|
(58) |
where denotes the value of the th velocity component of the material point at time , etc.
Remark 10. The material derivative in an Eulerian description is expressed in a fixed control domain as
|
|
(59) |
Eq.(59) is the form used in the Eulerian formulation of the Navier-Stokes equations (see Eq.(47)). Neglecting the convective acceleration term in Eq.(59) yields the expression used in Eq.(1) for Stokes flows.
A difficulty in the Lagrangian formulation of flow problems is the need for tracking the motion of the material points in space and time. The authors have developed in recent years a particular class of Lagrangian method for analysis of fluid flow problems termed the Particle Finite Element Method (PFEM, www.cimne.com/pfem). The PFEM treats the nodes in a continuum as virtual particles that can freely move and even separate from the main domain representing, for instance, the effect of water drops in a splashing fluid or soil particles in an excavation problem. A finite element mesh connects the nodes defining the discretized domain where the governing equations are solved using the FEM. An advantage of the Lagrangian formulation in the PFEM is that the convective terms disappear from the fluid equations. The difficulty is however transferred to the problem of adequately (and efficiently) moving the mesh node using a fast mesh regeneration procedure at each time step. The theory and applications of the PFEM are reported in [1,8],[18]–[21],[25,32],[36]–[38].
The particularization of the formulation of the P1/P0+ triangle presented in Sections 2–6 to the Lagrangian analysis of viscous flows is straightforward and simply implies computing the acceleration term with the expression given by Eq.(58). The rest of the terms are identical to those given in those sections.
In this work we have applied the Lagrangian formulation of the P1/P0+ triangle to the study of multifluid problems with relatively small changes of the geometry of the fluid domain. The application of the P1/P0+ triangle and tetrahedra to a wider class of Lagrangian flow problems using the PFEM will be the subject of further work of the authors.
10 EXAMPLES
In this section we present the solutions obtained by the FIC method for four benchmark problems. The first two examples are steady state problems formulated in the Eulerian framework. The last two examples are transient problems formulated in the Lagrangian framework. In all these examples, the pressure solution has a strong discontinuity across the interface where the fluid viscosities are relevant and distinct. These pressure jumps occur either due to a relevant normal derivative of the velocity or in its absence due to a prescribed over-pressure force at the interface.
|
|
| (a) Eulerian extrusion problem. | (b) Zhong's problem. |
| Figure 4: Description of the steady-state examples. (a) fixed-mesh (Eulerian) extrusion problem and (b) the Zhong's problem. | |
10.1 Fixed-mesh (Eulerian) extrusion problem
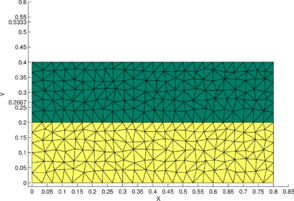
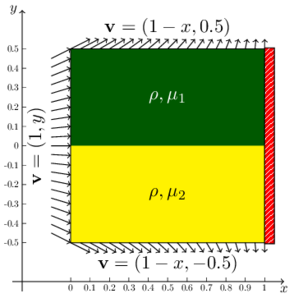
This example deals with a flow entering a rectangular 2D domain from the left boundary with a unit normal velocity and moving to the right where it finds an impermeable slip wall that deviates the flow upwards and downwards [20]. The 2D domain occupies the region: (Figure 4a). The upper-half and lower-half of the domain are occupied by two immiscible fluids which have the same density (), but with distinct viscosities (). This problem has an analytical solution which can be expressed as follows.
|
|
(60) |
As the pressure solution is known up to a constant, in Eq. (60) the later is chosen such that the pressure has a zero mean value over the domain. At the interface (), due to a jump in the viscosities and a relevant directional derivative of the velocity along its normal, the pressure field has a jump across it.
Remark 11. This is a steady state example involving the solution of the Navier-Stokes equations solved in the Eulerian framework (Section 8). Generally, the presence of the convective term in the momentum equation triggers both global and local numerical instabilities which needs to be stabilized. However, these instabilities are manifested only when the solution of the continuous problem involves layers. In examples like the current one velocity field does not contain layers. Hence, in this problem, we can obtain a good numerical approximation to the velocity even without convective stabilization.
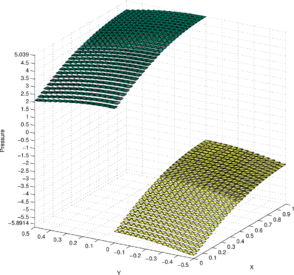
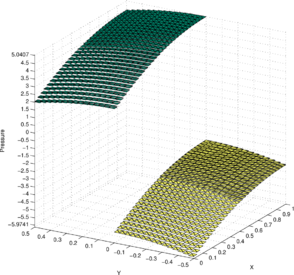
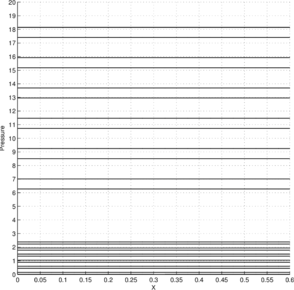
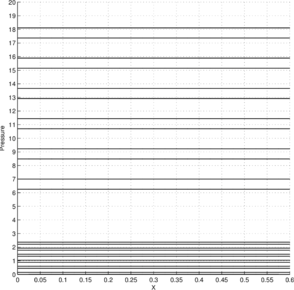
Figure 5a illustrates the pressure solution obtained by the P1-P0+ triangle. The domain is discretized using a symmetric structured mesh of elements. The material properties are chosen to be: , and . The velocity boundary conditions are chosen to be of Dirichlet (essential) type, taking values given by the expression in Eq. (60). The indeterminacy of the pressure solution is removed by imposing the zero-mean pressure condition [11]. The nonlinear convective terms in the Navier-Stokes equations are linearized using the Newton–Raphson method (Appendix A) and they converge in just two iterations for a tolerance of .
Figure 5b illustrates the best approximation to the exact pressure solution given in Eq. (60) from the discrete pressure space of piecewise constant pressure values over the elements of the considered mesh. The best approximation is chosen from using the norm () as the metric. Thus, is the projection of onto . It can be obtained as follows: Find , such that
|
|
(61) |
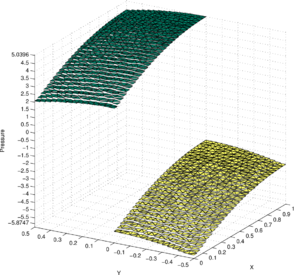
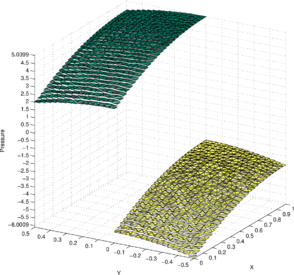
Figure 5c illustrates the constant pressure solution (termed in Section 6) obtained by the new P1-P0+ triangle and using an unstructured mesh. The unstructured mesh is generated by small random perturbations of the interior nodes (excluding the nodes on the interface) of the structured mesh followed by a Delaunay tessellation. Figure 5d illustrates the best approximation obtained using the same mesh.
|
|
| (a) Fixed-mesh (Eulerian) extrusion problem. | (b) Zhong's problem. |
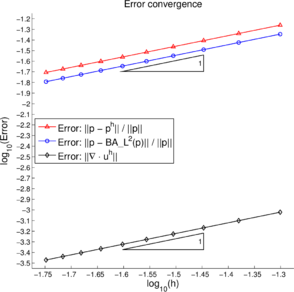
| Figure 6: Error convergence in the norm on mesh refinement for and . | |
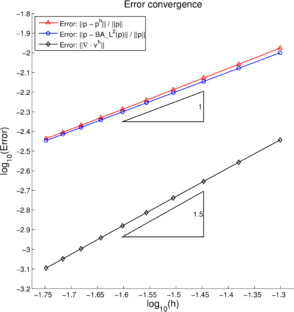
Figure 6a shows the convergence of the error in the norm with respect to mesh refinement. This error is compared with the best approximation error . To measure the convergence rate the domain is discretized by a sequence of symmetrical structured meshes of elements, using . The relative error in the pressure solutions are measured as follows.
|
|
(62) |
As expected for a piecewise constant pressure approximation, the convergence rate is found to be one for both solutions. Further, the error line of the numerical solution is found to be close to the error line of the best approximation , indicating the good accuracy of the obtained solution. Additionally, in Figure 6a the convergence in the norm of the divergence of the velocity is also shown. As the exact solution is solenoidal, this error is measured as follows.
|
|
(63) |
where is the velocity solution obtained with the P1/P0+ triangle. The convergence rate for is found to be close to , which is more than the expected first-order rate. This super-convergence for could be due to the smooth (linear, cf. Eq. (60)) solution profile for the velocity.
10.2 Zhong's problem: buoyant Stokes flow with a columnar viscosity structure
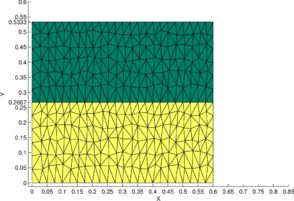
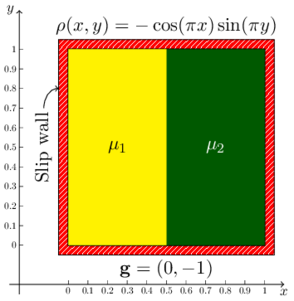
This example deals with the buoyancy-driven Stokes flow of a fluid with a columnar viscosity structure and was first presented in [40]. It has been previously used as a benchmark in [13,24]. It is an idealization of the mantle convection and the plate dynamics that occur in the subduction zones of the Earth. The temperature of the subducted plates are much colder than the ambient mantle which in turn leads to sharp lateral variations in the viscosity. The 2D domain (cf. Figure 4b) is a unit square: . The left-half and right-half of the domain have viscosities given by and , respectively. The density and the acceleration due to gravity are specified as and , respectively. Free-slip boundary conditions are imposed everywhere on the domain boundary.
The evaluation 1 of the analytical solution is described in [40] using the method of separation of variables (used earlier in [16]) and the propagator matrix techniques [15]. The constant to fix the pressure is chosen such that the latter has a zero mean value over the domain. Due to a jump in the viscosities at the viscosity boundary () and a non-zero directional derivative of the velocity along its normal, the pressure field acquires a jump across it. The expression for the pressure jump at the viscosity boundary can be written as follows.
|
|
(64) |
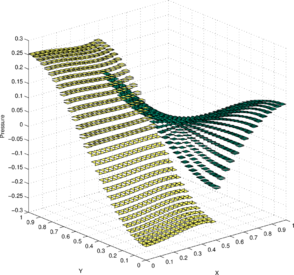
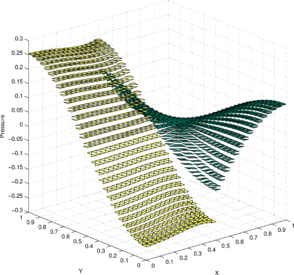
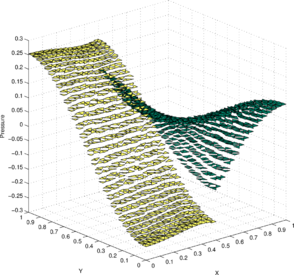
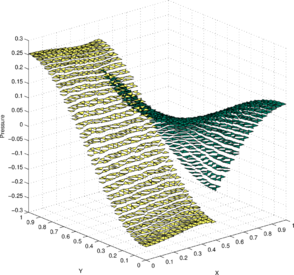
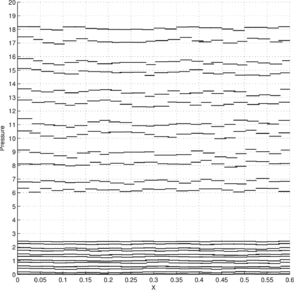
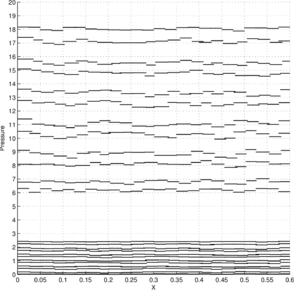
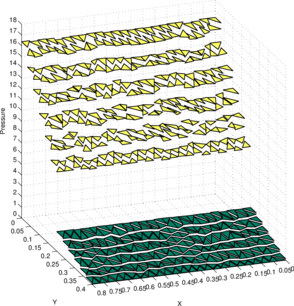
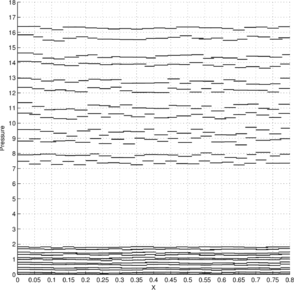
Figures 7a and 7c show the pressure solution obtained by the P1-P0+ triangle using a structured mesh ( elements) and an unstructured mesh ( elements), respectively. The corresponding best approximations in the norm are shown in Figures 7b and 7d, respectively.
Figure 6b shows the convergence of the error in the norm with respect to mesh refinement. This error is compared with the best approximation error . As expected for a piecewise constant pressure approximation, the convergence rate is found to be one for both solutions. Further, the error line for the numerical solution is found to be close to the error line of the best approximation , indicating the good accuracy of the obtained solution. Additionally, in Figure 6b the convergence in the norm of the divergence of the velocity is also shown. As expected for a piecewise linear velocity approximation, a first-order convergence rate is found for .
(1) The algebraic work involved to arrive at a closed form analytical expression of the solution is very tedious which includes the symbolic inversion of a matrix. Thus, the analytical solution is often computed numerically for a specified problem data.
10.3 Moving-mesh (Lagrangian) extrusion problem
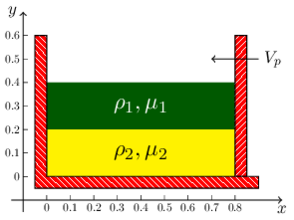
This is a transient example where the initial configuration is a rectangular 2D domain occupied by two immiscible fluids contained (due to the action of gravity) in a region bounded with sufficiently high walls (Figure 8a). Both the walls and the floor are considered to be slippery. The floor and the left wall are fixed while the right wall is pushed towards left at a constant prescribed velocity . This is a free surface problem with an interface between the two immiscible fluids and the shape of the domain varies due to the action of the right wall. The numerical solution is sought using a Lagrangian formulation of the problem (Section 9).
The fluid viscosities are chosen as and . The fluid densities are chosen as and . The acceleration due to gravity is taken as and the prescribed velocity . The 2D domain has an initial length and height . The upper-half of the domain is occupied by the fluid with properties . For these data, the dynamics is dominated by the viscous term and hence in the exact solution the inertial effects can be neglected.
As a shorthand notation, we denote by and as the positions of an arbitrary fluid particle at times and , respectively. Similar notation is used for the rest of the dependent variables in the Lagrangian description, e.g. and . Using this notation and the expressions and , the exact solution to this problem can be expressed as follows.
|
|
(65) |
|
|
(66) |
|
|
(67) |
where denotes the acceleration of the fluid particle and is the y-coordinate of the trajectory . The constant in the pressure solution given by Eq. (67) is chosen such that it takes a value zero at the free surface. In the numerical solution, no boundary conditions are imposed for the velocity at the free surface. On the rest of the boundary, Dirichlet (essential) conditions are imposed for the velocity. As the velocity boundary conditions are not exclusively of the Dirichlet type, no further conditions need to be imposed for the pressure. For the sake of simplicity the discretized (Lagrangian) equations are linearized using the Picard (Fixed-point) method. The configuration is updated at every iteration. The time integration is done using the Newmark method with the choice and (zero dissipation; second-order accuracy). The time increment is chosen as s (Appendix B).
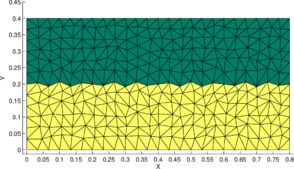
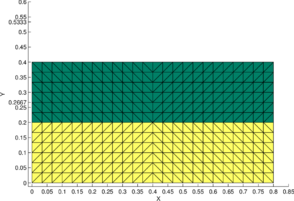
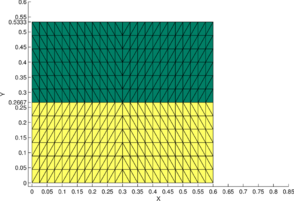
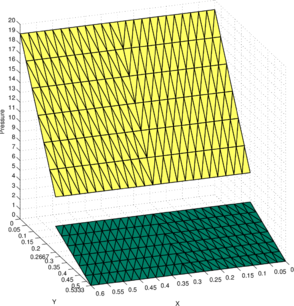
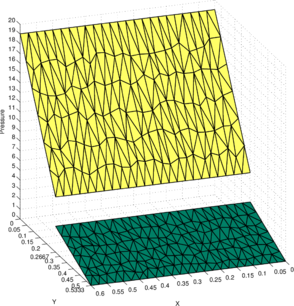
Figure 9b illustrates the final configuration (at time ) obtained with the P1-P0+ triangle using a symmetric structured mesh of elements. The initial configuration is shown in Figure 9a. Figures 9c and 9d show the initial and final configurations when using an unstructured mesh. For the initial domain area to be conserved the interface and the free surface should raise to a height of and , respectively. This is indeed observed in Figures 9b and 9d showing the good area conservation properties for the P1/P0+ triangle.
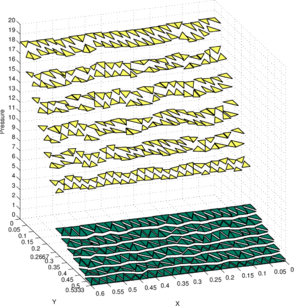
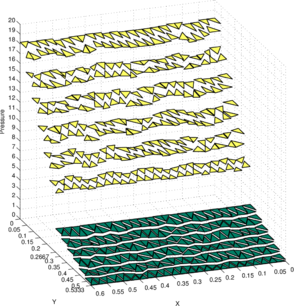
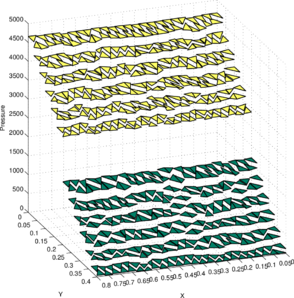
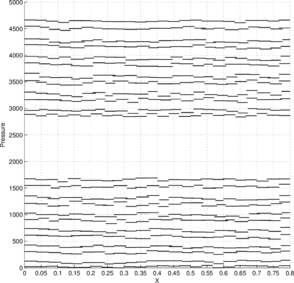
Figure 10a shows the pressure solution obtained using the structured mesh. As the two fluids have distinct densities, it leads to a jump in both the pressure and its gradient at the interface. Figure 10b shows the projection of the exact pressure given in Eq. (67) onto the discrete pressure space and is denoted as . For the sake of comparison, the constants in the discrete pressure solutions and are chosen a posteriori such that the minimum value on the free surface is zero. Likewise, Figures 10c and 10d show the pressure solutions and obtained on the unstructured mesh.
Figure 11 presents the same results as shown in Figure 10 but with the solutions projected onto the plane. In this view, the inter-element jumps in the obtained solution can be better compared with those in the best approximation . We see that on both meshes the obtained solution is in good agreement with the best approximation .
Figures 12a and 12b illustrate the effective pressure solution obtained with the P1/P0+ triangle using the structured and the unstructured meshes, respectively. Recall that the effective pressure solution includes a prescribed linear field defined over each element given by Eq.(37). A nearly identical figure is obtained by plotting the exact pressure solution given by Eq.(67), thus indicating the good accuracy of the method.
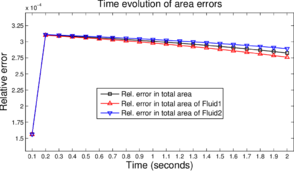
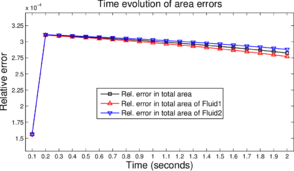
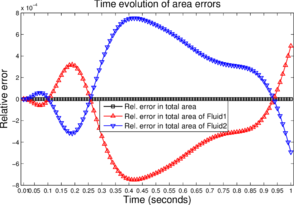
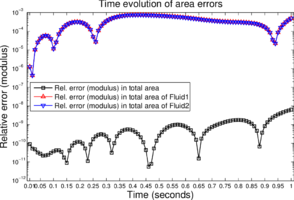
Finally, in Figure 13 we present the time evolution of the error in the area for all the cases discussed in this section. The relative error in the area is measured in three different ways
|
|
(68) |
where and represent the initial and current (at time ) areas of an element with index . and denote the regions occupied by the two immiscible fluids, respectively and is the domain. The indices and refer to the upper-half and lower-half regions of the domain. is the relative error in the total area of both fluids. and are the relative errors in the total area of the fluids occupying the regions and , respectively. For the simulated time period (s), the maximum relative error is below for , and .
10.4 Lagrangian example with fixed-walls and an unstable interface
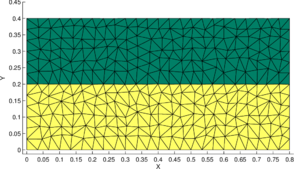
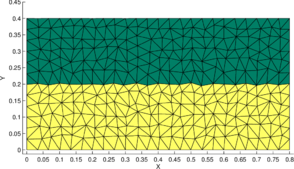
Finally, we present another transient example where the two-fluid interface initially has a serrated profile (thus unstable) and becomes straight in due course. This configuration (Figure 8b) is obtained by meshing the domain with an unstructured mesh and identifying the elements that occupy the upper-half of the domain to represent a fluid with lower density and the remaining elements to represent the other fluid with a higher density.
To observe the interface evolution in a reasonable time period, fluid-pairs with low viscosities are chosen. Further, to avoid sloshing-like effects that arise due to the low viscosities, all the walls of the domain are fixed and are considered slippery. Thus, there are only buoyancy driven low-speed motions in the fluid due to its initial unstable configuration.
Due to the small viscosities and low-speed motions, the pressure has a negligible jump across the interface. In order to have a visible pressure jump, we prescribe a fictitious over-pressure force at the interface given by the expression . Here represents the outward normal to the interface with respect to the heavier fluid and represents the prescribed jump in the pressure value across the interface.
This problem is solved considering two fluid-pairs. For the first fluid-pair, the material properties of the fluids on top and bottom are taken as and , respectively. At the interface, the over-pressure force is taken as . The second fluid-pair consists of sunflower oil on the top and water at the bottom. The material properties for sunflower oil and water at are (in International units) and , respectively. At the oil–water interface, the over-pressure force is taken as . The initial configuration is the same for both fluid-pairs, cf. figure 8b. The time integration is done by the Newmark method with the choice and (zero-dissipation; second-order accuracy). The time increment is chosen as s. As no re-meshing is done, the simulation is stopped after time steps, i.e. a simulation time of s, to avoid numerical difficulties associated with severe mesh deformations.
Due to the small viscosities, the profile of the interface will have an oscillatory behavior (possibly damped due to momentum distribution in all directions) and a steady state can be expected in due course. We use the total length of the interface as a metric to measure the “distance” of the perturbed state of the interface from the stable horizontal profile. For an oscillating interface profile, the interface length will have an oscillatory behavior and will take a minimum value equal to (horizontal length of the domain) whenever the interface profile is horizontal.
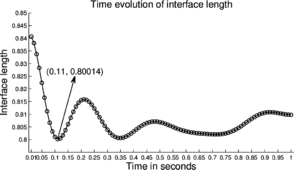
Within the simulated time period, the P1-P0+ triangle is able to reproduce this oscillatory behavior of the interface for the first fluid-pair, cf. Figure 14a. The interface length first attains a minimum value of in eleven time steps (at s). The interface at this instant attains a horizontal profile as shown in Figure 14c. However, near the end of the simulation we observe an unphysical increase in the interface length. This could be due to the numerical difficulties associated to mesh-distortion (recall that no re-meshing is done here).
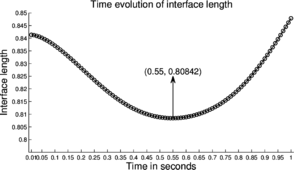
As the viscosities in the second fluid-pair (oil–water) are three orders of magnitude greater than those for the first fluid-pair, it is reasonable to expect a greater time scale for the former. Figure 14b shows that the oil–water interface length gradually reduces (i.e. the interface flattens) and takes a minimum value of at s. The interface at this instant attains a nearly horizontal profile as shown in Figure 14d. Past s, the interface length gradually returns back to its initial value. However, the trend near the end of the simulation shows an unphysical increase in the interface length, which again could be due to the numerical difficulties associated to mesh-distortion.
Figure 15 shows the pressure solutions obtained for the considered fluid-pairs when their interfaces first attain a minimum length. We observe jumps in the pressure across the interface equivalent to the prescribed over-pressure forces, i.e. for the first fluid-pair (Figure 15a) and for the oil–water fluid-pair (Figure 15c). Figures 15b and 15d present the same result as shown in Figures 15a and 15c, respectively, but with the solutions projected onto the plane. In this view, all the inter-element jumps in the obtained pressure solutions are better seen.
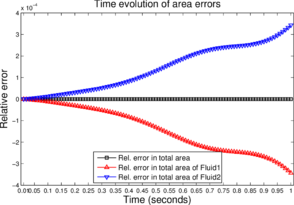
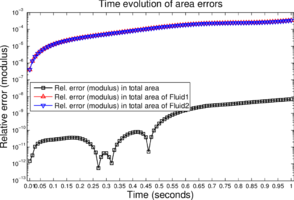
The time evolution of the area-errors is shown in Figure 16 (both signed and absolute relative errors). The area-errors are measured in the same way as it is done earlier in section 10.3, i.e. using the expressions given in Eq. (68). For the simulated time period and the first fluid-pair, we find , and . Likewise for the oil–water fluid-pair we find , and . These results indicate the good area preservation property of the P1-P0+ triangle.
11 CONCLUDING REMARKS
We have presented a 3-noded triangle and a 4-noded tetrahedra with a continuous linear velocity and a discontinuous linear pressure field formed by the sum of an unknown constant pressure field and a prescribed linear field that satisfies the steady state momentum equations for a constant body force. In the so called P1/P0+ elements the “effective” pressure field is linear, although the unknown pressure field is piecewise constant within each element. The P1/P0+ elements have shown an excellent behaviour in terms of accuracy and mass conservation for incompressible viscous flow problems with discontinuous material properties formulated in either Eulerian or Lagrangian descriptions.
ACKNOWLEDGEMENTS
This research was supported by project HFLUIDS of the Ministerio de Educación y Ciencia of Spain and projects SAFECON and REALTIME of the European Research Council.
The authors are grateful to Prof. Shijie Zhong and Dr. Thibault Duretz for sharing their codes to evaluate the analytical solution of the buoyant Stokes flow example with a columnar viscosity structure.
APPENDIX A. LINEARIZATION OF THE NAVIER-STOKES EQUATIONS
Consider the steady Navier–Stokes equations described in an Eulerian framework. The stabilized momentum and mass balance equations discretized in space by the FEM lead to the following system of equations,
|
|
(A.1) |
It is assumed that the stabilization terms in matrices and and vector are linear, i.e. they do not depend on the solution. The only nonlinear term that remains is, therefore, matrix obtained from the Galerkin FEM discretization of the convective term (Eq.(55a)).
The Newton–Raphson linearization of Eq.(1) gives the following system of equations.
|
|
(A.2) |
with
|
|
(A.3) |
where matrices and are given in Eqs.(54) and (8) and
|
|
(A.4) |
In Eq.(2) index denotes the iterations. Hence,
|
|
(A.5) |
The Picard linearization of Eq.(1) yields the following system of equations
|
|
(A.6) |
APPENDIX B. TIME INTEGRATION IN THE LAGRANGIAN FRAMEWORK
The momentum and the stabilized mass balance equations discretized in space by the FEM leads to the following system of equations in the Lagrangian framework
|
where, the matrices and vectors with sub-scripts are the ones that appear due to the stabilization of the mass balance equation. Let denote the vector of unknown nodal accelerations. The momentum balance equation, i.e. Eq.(B.1), is a dynamic equation. On the contrary, the stabilized mass balance equation, i.e. Eq.(B.2), is a quasi-static equation.
Using the Newmark algorithm the balance equations given in Eqs.(B.1) and (B.2) are integrated in time () as follows
|
REFERENCES
[1] R. Aubry, S.R. Idelsohn, E. Oñate, Particle finite element method in fluid mechanics including thermal convection–diffusion, Comput. Struct. 83 (2004) 1459–-75.
[2] R.F. Ausas , G.C. Buscaglia, S.R. Idelsohn, A new enrichment space for the treatment of discontinuous pressures in multi-fluid flows, Int. J. Numer. Meth. Fluids 70 (7) (2012) 829–850.
[3] R. Araya, G.R. Barrechea, F. Valentin, Stabilized finite element methods based on multiscale enrichment for the Stokes problem, Siam J. Numer. Anal. 44 (1) (2006) 322–-348.
[4] T. Belytschko, W.K. Liu, B. Moran, Non linear finite element for continua and structures, 2d Edition, Wiley, 2013.
[5] E. Burman, M. Fernández, P. Hansbo, Edge stabilizatio n for the incompressible Navier–Stokes equations: a continuous interior penalty finite element method, Tech. Report RR-5349, INRIA, Le Chesnay, France, 2004.
[6] E. Burman, P. Hansbo, A unified stabilized method for Stokes’ and Darcy equations, Tech. Report 2002-15, Chalmers Finite Element Center, Göteborg, Sweden, 2002.
[7] A. Caiazzo, M.A. Fernández, V. Martin, Analysis of a stabilized finite element method for fluid flows through a porous interface, Applied Mathematics Letters 24 (2011) 2124–2127.
[8] J.M. Carbonell, E. Oñate, B. Suárez, Modelling of tunnelling processes and cutting tool wear with the Particle Finite Element Method (PFEM), Accepted in Comput. Mech. (2013) DOI:10.1007/s00466-013-0835-x.
[9] R. Codina, S. Badia, On the design of discontinuous Galerkin methods for elliptic problems based on hybrid formulation, Comput. Methods Appl. Mech. Engrg. (2013) http://dx.doi.org/10.1016/j.cma.2013.05.004.
[10] F. Del Pin, S.R. Idelsohn, E. Oñate, R. Aubry, The ALE/Lagrangian Particle Finite Element Method: A new approach to computation of free-surface flows and fluid–object interactions, Computers & Fluids 36 (1) (2007) 27–38.
[11] J. Donea, A. Huerta, Finite element method for flow problems, J. Wiley & Sons, 2003, pp. 362.
[12] J. Douglas, J. Wang, An absolutely stabilized finite element method for the Stokes problem, Math. Comp. 52 (186) (1989) 495–508.
[13] T. Duretz, D. A. May, T. V. Gerya, P. J. Tackley, Discretization errors and free surface stabilization in the finite difference and marker-in-cell method for applied geodynamics: A numerical study, Geochemistry, Geophysics, Geosystems 12 (7) (2011).
[14] M.A. Fernández, J.-F. Gerbeau, V. Martin, Numerical simulation of blood flows through a porous interface, ESAIM: Mathematical Modelling and Numerical Analysis 42 (2008) 961–990.
[15] F. Gilbert, G. E. Backus, Propagator matrices in elastic wave and vibration problems, Geophysics 31 (2) (1966) 326–332.
[16] B. H. Hager, R. J. O'Connell, A simple global model of plate dynamics and mantle convection, Journal of Geophysical Research 86 (B6) (1981) 4843–4867.
[17] T.J.R. Hughes, L.P. Franca, A new finite element formulation for computational fluid dynamics: VII. The Stokes problem with various well-posed boundary conditions: Symmetric formulations that converge for all velocity/pressure spaces, Comput. Methods Appl. Mech. Engrg. 65 (1987) 85–-96.
[18] S.R. Idelsohn, E. Oñate, F. Del Pin, The particle finite element method: a powerful tool to solve incompressible flows with free-surfaces and breaking waves, Int. J. Numer. Methods Engrg. 61 (2004) 964–989.
[19] S.R. Idelsohn, E. Oñate, F. Del Pin, Fluid-structure interaction with the Particle Finite Element Method, Comput. Methods Appl. Mech. Engrg. 195 (2006) 2100–2113.
[20] S.R. Idelsohn, M. Mier-Torrecilla, E. Oñate, Multi-fluid flows with the Particle Finite Element Method, Comput Methods Appl Mech Engrg. 198 (2009) 2750–2767.
[21] S.R. Idelsohn, M. Mier-Torrecilla, R. Nigro, E. Oñate, On the analysis of heterogeneous fluids with jumps in the viscosity using a discontinuous pressure field, Comput. Mech. 46 (1) (2010) 115–124
[22] S.R. Idelsohn, E. Oñate, The challenge of mass conservation in the solution of free-surface flows with the fractional-step method: Problems and solutions, Int. J. Numer. Meth. Biomed. Engng. 26 (2010) 1313–-1330.
[23] N. Kechar, D. Silvester, Analysis of a locally stabilized mixed finite element method for the Stokes problem, Math. Comp. 58 (1992) 1–-10.
[24] M. Kronbichler, T. Heister, W. Bangerth, High accuracy mantle convection simulation through modern numerical methods, Geophysical Journal International 191 (1) (2012) 12–29.
[25] M. Mier-Torrecilla, S.R. Idelsohn, E. Oñate, Advances in the simulation of multi-fluid flows with the particle finite element method. Application to bubble dynamics, Int. J. Numer. Meth. Fluids 67 (2011) 1516–-1539.
[26] E. Oñate, Derivation of stabilized equations for advective-diffusive transport and fluid flow problems, Comput. Meth. Appl. Mech. Engng. 151 (1998) 233–267.
[27] E. Oñate, A stabilized finite element method for incompressible viscous flows using a finite increment calculus formulation, Comput Methods Appl Mech Engrg. 182 (1–2) (2000) 355–370.
[28] E. Oñate, J. García, A finite element method for fluid-structure interaction with surface waves using a finite calculus formulation, Comput. Meth. Appl. Mech. Engrg. 191 (2001) 635–660.
[29] E. Oñate, Multiscale computational analysis in mechanics using finite calculus: an introduction, Comput. Meth. Appl. Mech. Engrg. 192(28-30) (2003) 3043–3059.
[30] E. Oñate, Possibilities of finite calculus in computational mechanics, Int. J. Num. Meth. Engng. 60 (1) (2004) 255–281.
[31] E. Oñate, J. Rojek, R.L. Taylor, O.C. Zienkiewicz, Finite calculus formulation for incompressible solids using linear triangles and tetrahedra, Int. J. Numer. Meth. Engng. 59 (11) (2004a) 1473–1500.
[32] E. Oñate, S.R. Idelsohn, F. Del Pin, R. Aubry, The particle finite element method. An overview, Int. J. Comput. Methods 1 (2) (2004b) 267–307.
[33] E. Oñate, A. Valls, J. García, FIC/FEM formulation with matrix stabilizing terms for incompressible flows at low and high Reynold's numbers, Comput. Mech. 38 (4-5) (2006) 440–455.
[34] E. Oñate, J. García, S.R. Idelsohn, F. Del Pin, Finite calculus formulation for finite element analysis of incompressible flows. Eulerian, ALE and Lagrangian approaches, Comput. Meth. Appl. Mech. Engng. 195 (2006b) 3001–3037.
[35] E. Oñate, A. Valls, J. García, Computation of turbulent flows using a finite calculus-finite element formulation, Int. J. Numer. Meth. Engng. 54 (2007) 609–637.
[36] E. Oñate, M.A. Celigueta, S.R. Idelsohn, F. Salazar, B. Suárez, Possibilities of the particle finite element method for fluid-soil-structure interaction problems, Comput. Mech. 48(3) (2011) 307–318.
[37] E. Oñate, A. Franci, J.M. Carbonell, A FIC-based stabilized Lagrangian formulation with negligible mass losses for incompressible fluids. Application to free-surface flows using PFEM, Publication CIMNE, No. PI394. Submitted to Int. J. Num. Meth. Fluids, 2013.
[38] P. Ryzhakov, R. Rossi, S.R. Idelsohn, E. Oñate, A monolithic Lagrangian approach for fluid-structure interaction problems, Comput. Mech. 46 (6) 2010 883–899.
[39] O.C. Zienkiewicz, R.L. Taylor, P. Nithiarasu, The finite element method for fluid dynamics, Elsevier, 2006.
[40] S. Zhong. Analytic solutions for Stokes’ flow with lateral variations in viscosity, Geophysical Journal International 124 (1) 1996 18–28.
Document information
Published on 01/01/2015
DOI: 10.1016/j.cma.2013.12.009
Licence: CC BY-NC-SA license