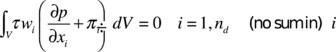Presented in the "XI ICOLD BENCHMARK WORKSHOP ON NUMERICAL ANALYSIS OF DAMS", Valencia, October 20-21, 2011 - Invited Session
Summary
We present some developments in the Particle Finite Element Method (PFEM) for analysis of coupled problems in mechanics involving fluid-soil-structure interaction (FSSI). The PFEM uses an updated Lagrangian description to model the motion of material points in both the fluid and the solid domains (the later including soil/rocks and structures). A mesh connects the particles (nodes) defining the discretized domain where the governing equations for each of the constituent materials are solved as in the standard FEM. The procedure to model frictional contact conditions and material erosion at fluid-solid and solid-solid interfaces is described. We present several examples of application of the PFEM to solve FSSI problems such as the motion of rocks by water streams, the erosion of river beds, the stability of breakwaters and constructions under sea waves, the falling of landslides on houses and into a reservoir and the failure of rockfill dams in overspill situations.
1. Introduction
The analysis of problems involving the interaction of fluids, soil/rocks and structures is of relevance in many areas of engineering. Examples are common in the study of landslides and their effect on reservoirs and adjacent structures, off-shore and harbour structures under large waves, constructions hit by floods and tsunamis, soil erosion and stability of rock-fill dams in overspill situations, etc.
The authors have developed in previous works a particular class of Lagrangian formulation for solving problems involving the interaction between free surface fluids and solids. The so-called particle finite element method (PFEM, www.cimne.com/pfem), treats the mesh nodes in the fluid and solid domains as particles which can freely move and even separate from the main fluid domain representing, for instance, the effect of water drops. A mesh connects the nodes discretizing the domain where the governing equations are solved using a stabilized FEM.
An advantage of the PFEM is that, as a Lagrangian formulation, the convective terms disappear from the fluid equations [4,25]. The difficulty is however transferred to the problem of adequately (and efficiently) moving the mesh nodes. We use a mesh regeneration procedure blending elements of different shapes using an extended Delaunay tesselation with special shape functions [8]. The theory and applications of the PFEM are reported in [2,3,9-22].
In this paper we describe recent advances of the PFEM for fluid-soil-structure interaction (FSSI) problems and present several examples of application to the study of the motion of rocks by water streams, the stability of breakwaters and constructions under sea waves, the falling of landslides on houses and into a reservoir and the failure of a rockfill dam in an overspill situation.
2. The Basis of the Particle Finite Element method
In the PFEM both the fluid and the solid domains are modelled using an updated Lagrangian formulation [9,11,16,25]. That is, all variables are assumed to be known in the current configuration at time . The new set of variables in both domains are sought for in the next or updated configuration at time . The finite element method (FEM) is used to solve the equations of continuum mechanics for each of the subdomains. Hence a mesh discretizing these domains must be generated in order to solve the governing equations for each subdomain in the standard FEM fashion. The quality of the numerical solution depends on the discretization chosen as in the standard FEM. Adaptive mesh refinement techniques can be used to improve the solution in zones where large motions of the fluid or the structure occur.
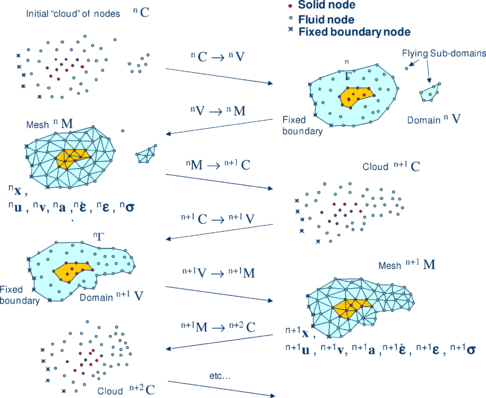
A typical solution with the PFEM involves the following steps.
1. The starting point at each time step is the cloud of points (particles) in the fluid and solid domains. For instance denotes the cloud at time (Fig. 1).
2. Identify the boundaries for both the fluid and solid domains defining the analysis domain in the fluid and the solid. This is an essential step as some boundaries (such as the free surface in fluids) may be severely distorted during the solution, including separation and re-entering of nodes. The Alpha Shape method [6,9,17] is used for the boundary definition.
3. Discretize the fluid and solid domains with a finite element mesh . We use an innovative mesh generation scheme based on the extended Delaunay tesselation [8].
4. Solve the coupled Lagrangian equations of motion for the fluid and the solid domains. Compute the state variables at the next (updated) configuration for : velocities, pressure and viscous stresses in the fluid and displacements, stresses and strains in the solid.
5. Move the mesh nodes to a new position where denotes the time , in terms of the time increment size.
6. Go back to step 1 and repeat the process for the next time step to obtain (Fig. 1).
3. FIC/FEM formulation for a Lagrangian continuum
3.1. Governing equations
The equations to be solved are the standard ones in continuum mechanics, written in the Lagrangian frame of reference:
Momentum:
|
|
(1) |
Pressure-velocity relationship:
|
|
(2) |
In above equations is the velocity along the ith global (cartesian) axis, is the pressure (assumed to be positive in compression) and are the density and bulk modulus of the material, respectively, and are the body forces and the (Cauchy) stresses. Equations 1 and 2 are completed with the constitutive relationships. For details see [11,24,25].
3.2 Discretization of the equations
A key problem in the solution of Equations 1--2 is the satisfaction of the mass balance condition for the incompressible case (i.e. ). A number of procedures to solve his problem exist in the finite element literature [4,25]. In our approach we use a stabilized formulation based in the so-called finite calculus procedure [15]. The essence of this method is the solution of a modified mass balance equation which is written as
|
(5) |
where are weighting functions, is a stabilization parameter. 6 are auxiliary pressure projection variables chosen so as to ensure that the second term in Equation 6 can be interpreted as weighted sum of the residuals of the momentum equations and therefore it vanishes for the exact solution. The set of governing equations is completed by adding the following constraint equation
|
(6) |
where are arbitrary weighting functions.
The rest of the integral equations are obtained by applying the standard weighted residual technique to the governing equations (1), (2), (3) and (5) and the corresponding boundary conditions [11,18,21]. We interpolate next in the standard finite element fashion (for 3D problems) the three velocities , the pressure and the three pressure gradient projections . In our work we use equal order linear interpolation for all variables over meshes of 3-noded triangles (in 2D) and 4-noded tetrahedra (in 3D). The resulting set of discretized equations using the standard Galerkin technique has the following form
Momentum:
|
|
(7) |
Pressure-velocity relationship:
|
|
(8) |
Pressure gradient projection:
|
|
(9) |
In Eqs.(7)-(9) denotes nodal variables, .
The solution of Eqs.(7)-(9) can be performed using any time integration scheme typical of the updated Lagrangian FEM. Details of the element matrices and the solution procedure can be found in [11,18,21].
4. Generation of a new mesh
One of the key points for the success of the PFEM is the fast regeneration of a mesh at every time step on the basis of the position of the nodes in the space domain. Indeed, any fast meshing algorithm can be used for this purpose. In our work the mesh is generated at each time step using the so called extended Delaunay tesselation (EDT) presented in [8].
As a general rule for large 3D problems meshing consumes around 15% of the total CPU time for each time step, while the solution of the equations (with typically 3 iterations to reach convergence within a time step) and the assembling of the system consume approximately 70% and 15% of the CPU time for each time step, respectively. These figures refer to solutions obtained in a standard single processor Pentium IV PC for all the computations and prove that the generation of the mesh has an acceptable cost in the PFEM [21].
5. Identification of boundary surfaces
One of the main tasks in the PFEM is the correct definition of the boundary domain. Boundary nodes are sometimes explicitly identified. In other cases, the total set of nodes is the only information available and the algorithm must recognize the boundary nodes.
In our work we use an extended Delaunay partition for recognizing boundary nodes [8,16]. Considering that the nodes follow a variable distribution, where is typically the minimum distance between two nodes. All nodes on an empty sphere with a radius greater than are considered as boundary nodes. In practice is a parameter close to, but greater than one. Values of ranging between 1.3 and 1.5 have been found to be optimal in all examples analyzed. This criterion is coincident with the Alpha Shape concept [6].
The boundary recognition method is also useful for detecting isolated fluid particle outside the main fluid domain and contact conditions between the fluid domain and a fixed boundary, as well as between different interacting solids.
6. Treatment of contact conditions in the PFEM
6.1 Contact between the fluid and a fixed boundary
The condition of prescribed velocities at the fixed boundaries in the PFEM are applied in strong form to the boundary nodes. Nodes might belong to fixed external boundaries or to moving boundaries linked to the interacting solids. Contact between fluid particles and fixed boundaries is accounted for by the incompressibility condition which naturally prevents the fluid nodes to penetrate into the solid boundaries [3,17,18,19,21].
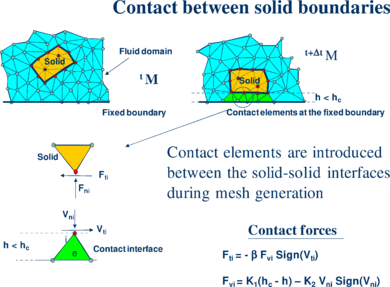
6.2 Contact between solid-solid interfaces
The contact between two solid interfaces is treated by introducing a layer of contact elements between the two interacting solid interfaces. This layer is created during the mesh generation step by prescribing a minimum distance ( ) between two solid boundaries. If the distance exceeds the minimum value ( ) then the generated elements are treated as fluid elements. Otherwise the elements are treated as contact elements where a relationship between the tangential and normal forces and the displacements is introduced (Fig. 2).
This algorithm can also be used effectively to model frictional contact conditions between rigid or elastic solids in structural mechanics applications [2].
7. Modeling of bed erosion
Prediction of bed erosion and sediment transport in open channel flows are important tasks in many areas of river and environmental engineering. Modeling of bed erosion is also relevant for predicting the evolution of surface material dragged in earth dams in overspill situations. Bed erosion is one of the main causes of environmental damage in floods.
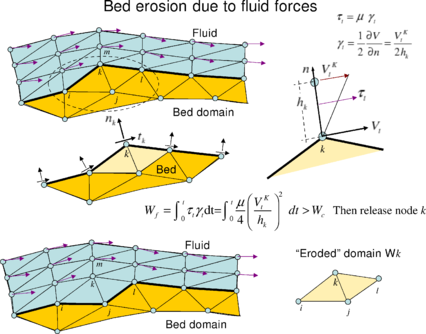
The algorithm for modeling the erosion of soil/rock particles at the fluid bed is the following:
1. Compute at every point of the bed surface the resultant tangential stress induced by the fluid motion. In 3D problems where and are the tangential stresses in the plane defined by the normal direction at the bed node. The value of for 2D problems can be estimated as shown in Fig.3.
2. Compute the frictional work due to the tangential stresses at the bed surface (Fig. 3).
3. The onset of erosion at a bed point occurs when the frictional work exceeds a critical threshold value . Then the node is detached from the bed region and it is allowed to move with the fluid flow. As a consequence, the mass of the patch of bed elements surrounding the bed node vanishes in the bed domain and it is transferred to the new fluid node. This mass is transported with the fluid.
4. Sediment deposition can be modeled by an inverse process to that described above. Hence, a suspended node adjacent to the bed surface with a velocity below a threshold value is attached to the bed surface.
Details of the bed erosion algorithm described can be found in [17,18].
8. Examples
8.1 Dragging of rocks by a water stream
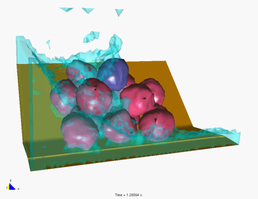
Predicting the speed at which a rock will be dragged by a water stream is of importance in many problems in hydraulic, harbour, civil and environmental engineering.
Figure 4 shows the study of the motion of a 1Tn quasi-spherical rock due to a water stream. Frictional conditions between the analyzed rock and the rest of the rocks (assumed to be rigid) are assumed. Figure 4a shows that a water stream of 1m/s can not displace the individual rock. An increase of the water speed to 2m/s induces the motion of the rock (Figure 4b).
8.2 Impact of sea waves on piers and breakwaters
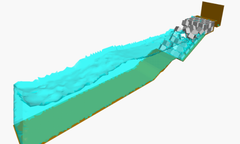
Figure 5 shows the analysis of the effect of breaking waves on two different sites of a breakwater containing reinforced concrete blocks (each one of m). The figures correspond to the study of Langosteira harbour in A Coruña, Spain using PFEM.
8.3 Soil erosion problems
Figure 6 shows the capacity of the PFEM to modelling soil erosion, sediment transport and material deposition in a river bed. The soil particles are first detached from the bed surface under the action of the jet stream. Then they are transported by the flow and eventually fall down due to gravity forces into the bed surface at a downstream point.
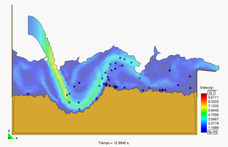
Figure 7 shows the progressive erosion of the unprotected part of a breakwater slope in the Langosteira harbour in A Coruña, Spain. The non protected upper shoulder zone is progressively eroded under the sea waves.
Other applications of the PFEM to bed erosion problems can be found in [17,18,21].
8.4 Falling of a lorry into the sea by sea wave erosion of the road slope
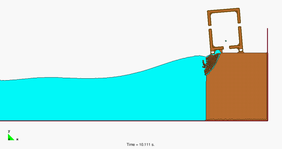
Figure 8 shows a representative example of the progressive erosion of a soil mass adjacent to the shore due to sea waves and the subsequent falling into the sea of a 2D object representing the section of a lorry. The object has been modeled as a rigid solid.
8.5 Simulation of landslides
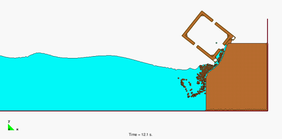
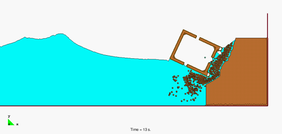
Figure 9 shows a 3D simulation with the PFEM of a landslide falling on adjacent constructions. The landslide material has been modelled as a viscous incompressible fluid.
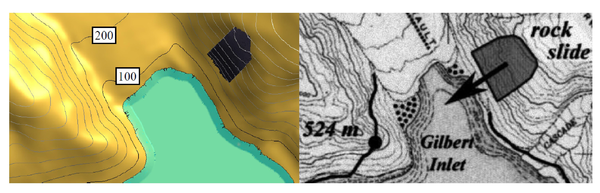
8.6 The landslide in Lituya Bay
We present some results of the 3D analysis of the landslide produced in Lituya Bay (Alaska) on July 9th 1958 (Fig. 10). The landslide was originated by an earthquake and movilized 90 millions tons of rocks that fell on the bay originating a large wave that reached a hight on the opposed slope of 524 m.
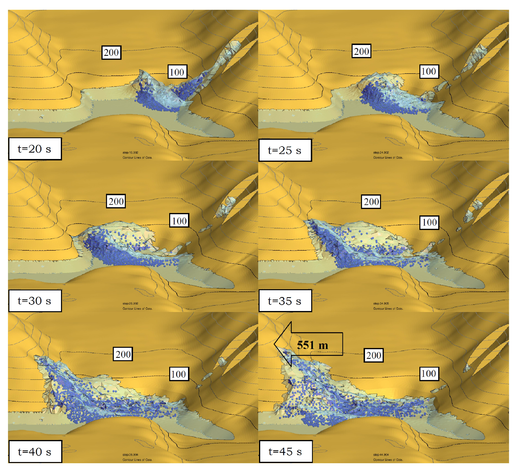
Figures 11 show images of the simulation of the landslide with PFEM. The sliding mass has been modelled as a continuum with a prescribed shear modulus. No frictional effect between the sliding mass and the underneath soil has been considered. The analysis has not taken into account the erosion and dragging of soil material induced by the landslide mass.
PFEM results have been compared with observed values of the maximum water level in the north hill adjacent to the reservoir. The maximum water level in this hill obtained with PFEM was 551 m. This is 5% higher than the observed value of 524 m. [7]. The maximum height location differs in 300 m from the observed value. In the south slope the maximum water height observed was 208 m, while the PFEM result (not shown here) was 195 m (6% error).
More information on the PFEM solutions of this example can be found in [20,22].
8.7 Failure of a rockfill dam due to an overspill
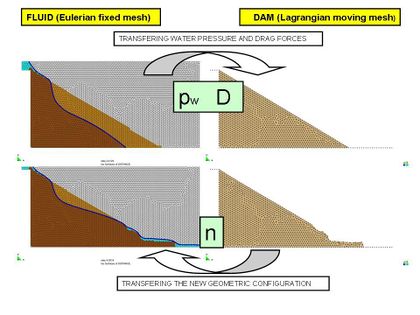
The PFEM has been used in combination with the classical (Eulerian) FEM for the analysis of the seapage and eventual failure of rockfill dams under overspill situations.
The evolution of the free surface of the fluid within the dam and over the rockfill slope is calculated using an Eulerian fixed mesh approach. A level set technique is used to track the evolution of the free surface. The Navier-Stokes equations for the fluid are modified to consider the presence of the porous media via a nonlinear (quadratic) Darcy law using Ergun coefficients that automatically go to zero when the flow exits the porous material. The balance equations are solved in term of Darcy velocity.
The structural response is evaluated using a continuum visco-rigid model and a Mohr-Coulomb failure criterion (with no cohesion) via the PFEM. Its specific features make it appropriate to treat the rockfill material undergoing large deformations and shape changes.
An alternative algorithm for projecting variables between non-matching meshes has been developed for passing information between the fixed mesh for the fluid and the moving mesh for the dams. Figure 12 shows a scheme of the algorithm. For more details see [13,14].
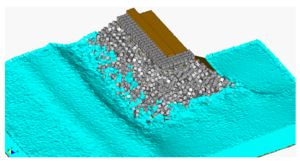
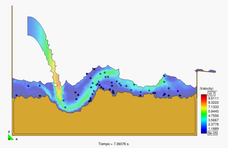
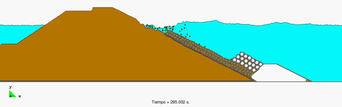
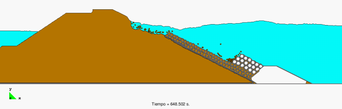
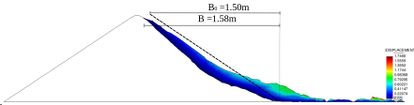
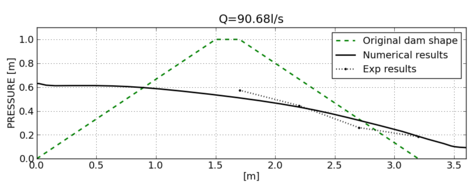
Prototype dams like the one shown in Figure 13 have been analyzed and monitored during their failing process. Results are compared with experiments carried at the Technical University of Madrid (UPM) and the Center for Hydrographic studies of CEDEX. The bottom pressure distribution is registered when the failure achieves its stationary value for a given incoming discharge. The length of failure is also measured. Both these parameters are compared to numerical results (Figures 14 and 15).

|

|
|

|
Acknowledgements
This research was supported by projects SEDUREC of the Consolider Programme of the Ministerio de Educación y Ciencia of Spain, SAFECON of the European Research Council of European Commission (EC) and the X-PRES and E-DAMS projects of the R+D National Plan of the Spanish Ministry for Science and Innovation [5,23]. Thanks are given to the Spanish construction company Dragados for financial support for the study of harbour engineering problems with PFEM.
References
- [1] Aubry, R., Idelsohn, S.R. & Oñate, E. (2005). Particle finite element method in fluid mechanics including thermal convection-diffusion, Comput. & Struct. 83(17-18), 1459-1475.
- [2] Carbonell, J.M., Oñate, E. & Suárez, B. (2010). Modeling of ground excavation with the Particle Finite Element Method. Journal of Engineering Mechanics (ASCE) 136(4), 455-463.
- [3] Del Pin F., Idelsohn, S.R., Oñate, E. & Aubry, R. (2007). The ALE/Lagrangian particle finite element method: A new approach to computation of free-surface flows and fluid-object interactions. Computers & Fluids 36, 27-38
- [4] Donea, J. & Huerta, A. (2003). Finite element method for flow problems. J. Wiley, 350 pp.
- [5] E-DAMS. Numerical and experimental techniques for safety assessment and protection of embankment dams in overtopping scenarios. Project of National Plan for TRD of the Spanish Ministry for Science and Innovation BIA2010-21350-C03-00, 2010-2013.
- [6] Edelsbrunner, H. & Mucke, E.P. (1999). Three dimensional alpha shapes. ACM Trans. Graphics 13, 43.
- [7] Fritz, H.M., Hager, W.H. & Minor, H.E. (2001). Lituya Bay Case: Rockslide impact and wave run-up. Science of Tsunami Hazards 19(1), 3-22.
- [8] Idelsohn, S.R., Calvo, N. & Oñate, E. (2003c). Polyhedrization of an arbitrary point set. Comput. Method Appl. Mech. Engng. 192(22-24), 2649-2668.
- [9] Idelsohn, S.R., Oñate, E. & Del Pin, F. (2004). The particle finite element method: a powerful tool to solve incompressible flows with free-surfaces and breaking waves. Int. J. Num. Meth. Engng. 61, 964-989.
- [10] Idelsohn, S.R., Oñate, E., Del Pin, F. & Calvo, N. (2006). Fluid-structure interaction using the particle finite element method. Comput. Meth. Appl. Mech. Engng. 195, 2100-2113.
- [11] Idelsohn, S.R., Marti, J., Limache, A., Oñate, E. (2008). Unified Lagrangian formulation for elastic solids and incompressible fluids: Application to fluid-structure interaction problems via the PFEM. Comput Methods Appl Mech Engrg. 197, 1762-1776.
- [12] Idelsohn, S.R., Mier-Torrecilla, M. & Oñate, E. (2009). Multi-fluid flows with the Particle Finite Element Method. Comput Methods Appl Mech Engrg. 198, 2750-2767.
- [13] Larese, A., Rossi, R., Oñate, E. & Idelsohn, S.R. (2008). Validation of the Particle Finite Element Method (PFEM) for simulation of free surface flows. Engng. Comput. 25(4), 385-425.
- [14] Larese, A., Rossi, R., Oñate, E. & Toledo, M.A. (2010). Physical and Numerical Modelization of the Behavior of rockfill dams during overtopping scenarios. Dam Maintenance and Rehabilitation II. CRCpress Balkema.
- [15] Oñate, E. (2004). Possibilities of finite calculus in computational mechanics. Int. J. Num. Meth. Engng. 60(1), 255-281.
- [16] Oñate, E., Idelsohn, S.R., Del Pin, F. & Aubry, R. (2004b). The particle finite element method. An overview. Int. J. Comput. Methods 1(2), 267-307.
- [17] Oñate, E., Celigueta, M.A. & Idelsohn, S.R. (2006c). Modeling bed erosion in free surface flows by the Particle Finite Element Method, Acta Geotechnia 1(4), 237-252.
- [18] Oñate, E., Idelsohn, S.R., Celigueta, M.A. & Rossi, R. (2008). Advances in the particle finite element method for the analysis of fluid-multibody interaction and bed erosion in free surface flows. Comput. Meth. Appl. Mech. Engng. 197(19-20), 1777-1800.
- [19] Oñate, E., Rossi, R., Idelsohn, S.R. & Butler, K. (2010). Melting and spread of polymers in fire with the Particle Finite Element Method. Int. J. Numerical Methods Engng., 81(8), 1046-1072.
- [20] Oñate, E., Salazar, F. & Morán, R. (2011). Modeling of landslides into reservoirs with the Particle Finite Element Method. Research Report CIMNE No. PI355. Submitted to Int. J. Numerical Methods in Geomechanics.
- [21] Oñate, E., Celigueta, M.A., Idelsohn, S.R., Salazar, F. & Suárez, B. (2011). Possibilities of the Particle Finite Element Method for fuid-soil-structure interaction problems. Computational Mechanics. Accepted for publication.
- [22] Salazar, F., Oñate, E. & Morán, R. (2011). Modelación numérica de deslizamientos de ladera en embalses mediante el método de partículas y elementos finitos (PFEM). Rev. Int. Mét. Num. Cálc. Dis. Ing. Accepted for publication
- [23] XPRES. Development of a method for study of the failure process of rockfill dams in overtopping situations combining particle based method and finite element method. National Plan for RTD of Spanish Ministry for Science and Innovation I+D BIA2007-68120-C03-01, 2007-2010.
- [24] Zienkiewicz, O.C. & Taylor, R.L. (2005). The finite element method for solid and structural mechanics, Elsevier.
- [25] Zienkiewicz, O.C., Taylor, R.L. & Nithiarasu, P. (2006). The finite element method for fluid dynamics, Elsevier.
(1) CIMNE, Universitat Politècnica de Catalunya (UPC), Barcelona, Spain.
(2) ICREA Research Professor at CIMNE.
(3) CIMNE-UPM-Classroom. School of Civil Engineering. Universidad Politécnica de Madrid, Spain.
Document information
Published on 01/01/2012
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?