Possibilities of the particle finite element method for fluid-soil-structure interaction problems

Abstract

We present some developments in the Particle Finite Element Method (PFEM) for analysis of complex coupled problems in mechanics involving fluid-soil-structure interaction (FSSI). The PFEM uses an updated Lagrangian description to model the motion of nodes (particles) in both the fluid and the solid domains (the later including soil/rock and structures). A mesh connects the particles (nodes) defining the discretized domain where the governing equations for each of the constituent materials are solved as in the standard FEM. The stabilization for dealing with an incompressibility continuum is introduced via the finite calculus (FIC) method. An incremental iterative scheme for the solution of the non linear transient coupled FSSI problem is described. The procedure to model frictional contact conditions and material erosion at fluid-solid and solid-solid interfaces is described. We present several examples of application of the PFEM to solve FSSI problems such as the motion of rocks by water streams, the erosion of a river bed adjacent to a bridge foundation, the stability of breakwaters and constructions sea waves and the study of landslides.

1 Introduction

The analysis of problems involving the interaction of fluids, soil/rocks and structures is of relevance in many areas of engineering. Examples are common in the study of landslides and their effect on reservoirs and adjacent structures, off-shore and harbour structures under large waves, constructions hit by floods and tsunamis, soil erosion and stability of rock-fill dams in overspill situations, etc.

These studies can be considered as an extension of the so-called fluid-structure interaction (FSI) problems [46]. Typical difficulties of FSI analysis in free surface flows using the FEM both the Eulerian or ALE formulation include the treatment of the convective terms and the incompressibility constraint in the fluid equations, the modelling and tracking of the free surface in the fluid, the transfer of information between the fluid and the moving solid domains via the contact interfaces, the modeling of wave splashing, the possibility to deal with large motions of multi-bodies within the fluid domain, the efficient updating of the finite element meshes for both the structure and the fluid, etc. Examples of 3D analysis of FSI problems using ALE and space-time FEM are reported in [4,6,26,27,31,34,40].

Most of the above problems disappear if a Lagrangian description is used to formulate the governing equations of both the solid and the fluid domains. In the Lagrangian formulation the motion of the individual particles are followed and, consequently, nodes in a finite element mesh can be viewed as moving material points (hereforth called “particles”). Hence, the motion of the mesh discretizing the total domain (including both the fluid and solid parts) is followed during the transient solution.

A powerful Lagrangian method for FSI analysis is the so-called Soboran Grid CIP technique, which has been successfully applied to different class of 3D problems [44].

The authors have successfully developed in previous works a particular class of Lagrangian formulation for solving problems involving complex interactions between (free surface fluids) and solids. The method, called the particle finite element method (PFEM,www.cimne.com/pfem), treats the mesh nodes in the fluid and solid domains as particles which can freely move and even separate from the main fluid domain representing, for instance, the effect of water drops. A mesh connects the nodes discretizing the domain where the governing equations are solved using a stabilized FEM.

An advantage of the Lagrangian formulation is that the convective terms disappear from the fluid equations [11,48]. The difficulty is however transferred to the problem of adequately (and efficiently) moving the mesh nodes. We use a mesh regeneration procedure blending elements of different shapes using an extended Delaunay tesselation with special shape functions [17,19]. The theory and applications of the PFEM are reported in [2,7,10,18,20,21,23,26,32,34,35,36,37,38,39].

The FEM solution of (incompressible) fluid flow problem implies solving the momentum and incompressibility equations. This is not a simple problem as the incompressibility condition limits the choice of the FE approximations for the velocity and pressure to overcome the well known ${\textstyle div}$-stability condition [11,48]. In our work we use a stabilized mixed FEM based on the Finite Calculus (FIC) approach which allows for a linear approximation for the velocity and pressure variables [15,29,30,31,33,34]. Among the other stabilized FEM with similar features we mention the PSPG method [41], multiscale methods [3,6,8,9] and the CBS method [9,48].

The aim of this paper is to describe recent advances of the PFEM for fluid-soil-structure interaction (FSSI) problems. These problems are of relevance in many areas of civil, hydraulic, marine and environmental engineering, among others. It is shown that the PFEM provides a general analysis methodology for treat such complex problems in a simple and efficient manner.

The layout of the paper is the following. In the next section the key ideas of the PFEM are outlined. Next the basic equations for a compressible/incompressible continuum using a Lagrangian description and the FIC formulation are schematically presented. Then an algorithm for the transient solution is briefly described. The treatment of the coupled FSSI problem and the methods for mesh generation and for identification of the free surface nodes are outlined. The procedure for treating the frictional contact interaction between fluid, soil and structure interfaces is explained. We present several examples of application of the PFEM to solve FSSI problems such as the motion of rocks by water streams, the erosion of a river bed adjacent to a bridge foundation, the stability of breakwaters and constructions under sea waves and the study of landslides falling into reservoirs.

2 The basis of the particle finite element method

Let us consider a domain containing both fluid and solid subdomains (the solid subdomain may include soil/rock materials and/or structural elements). The moving fluid particles interact with the solid boundaries thereby inducing the deformation of the solid which in turn affects the flow motion and, therefore, the problem is fully coupled.

In the PFEM both the fluid and the solid domains are modelled using an updated Lagrangian formulation [47]. That is, all variables are assumed to be known in the current configuration at time ${\textstyle t}$. The new set of variables in both domains are sought for in the next or updated configuration at time ${\textstyle t+\Delta t}$. The finite element method (FEM) is used to solve the equations of continuum mechanics for each of the subdomains. Hence a mesh discretizing these domains must be generated in order to solve the governing equations for each subdomain in the standard FEM fashion.

The quality of the numerical solution depends on the discretization chosen as in the standard FEM. Adaptive mesh refinement techniques can be used to improve the solution in zones where large motions of the fluid or the structure occur.

2.1 Basic steps of the PFEM

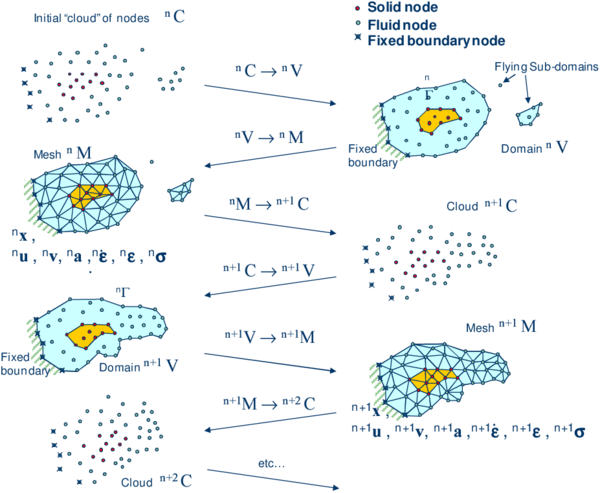
For clarity purposes we will define the collection or cloud of nodes (C) pertaining to the fluid and solid domains, the volume (V) defining the analysis domain for the fluid and the solid and the mesh (M) discretizing both domains.

A typical solution with the PFEM involves the following steps.

1. The starting point at each time step is the cloud of points in the fluid and solid domains. For instance ${\textstyle {}^{n}C}$ denotes the cloud at time ${\textstyle t=t_{n}}$ (Figure 1).
2. Identify the boundaries for both the fluid and solid domains defining the analysis domain ${\textstyle {}^{n}V}$ in the fluid and the solid. This is an essential step as some boundaries (such as the free surface in fluids) may be severely distorted during the solution, including separation and re-entering of nodes. The Alpha Shape method [12] is used for the boundary definition.
3. Discretize the fluid and solid domains with a finite element mesh ${\textstyle {}^{n}M}$. In our work we use an innovative mesh generation scheme based on the extended Delaunay tesselation [17,19,20].
4. Solve the coupled Lagrangian equations of motion for the fluid and the solid domains. Compute the state variables in both domains at the next (updated) configuration for ${\textstyle t+\Delta t}$: velocities, pressure and viscous stresses in the fluid and displacements, stresses and strains in the solid.
5. Move the mesh nodes to a new position ${\textstyle {}^{n+1}C}$ where ${\textstyle n+1}$ denotes the time ${\textstyle t_{n}+\Delta t}$, in terms of the time increment size. This step is typically a consequence of the solution process of step 4.
6. Go back to step 1 and repeat the solution process for the next time step to obtain ${\textstyle {}^{n+2}C}$ (Figure 1).

Figure 1: Sequence of steps to update a “cloud” of nodes representing a domain containing a fluid and a solid part from time $n$ ($t=t_{n}$) to time $n+2$ ($t=t_{n}+2\Delta t$)

3 FIC/FEM formulation for a Lagrangian continuum

3.1 Governing equations

The equations to be solved are the standard ones in continuum mechanics, written in the Lagrangian frame of reference:

Momentum

$\rho {\partial v_{i} \over \partial t}={\partial \sigma _{ij} \over \partial x_{j}}+b_{i}\qquad {\hbox{in }}V$

(1)

Pressure-velocity relationship

${\frac {1}{K}}{\partial p \over \partial t}-{\partial v_{i} \over \partial x_{i}}=0\qquad {\hbox{in }}V$

(2)

In above equations ${\textstyle v_{i}}$ is the velocity along the ith global (cartesian) axis, ${\textstyle p}$ is the pressure (assumed to be positive in compression) ${\textstyle \rho }$ and ${\textstyle K}$ are the density and bulk modulus of the material, respectively, ${\textstyle b_{i}}$ and ${\textstyle \sigma _{ij}}$ are the body forces and the (Cauchy) stresses. Eqs.(1) and (2) are completed with the constitutive relationships:

Incompressible continuum

${}^{t+1}\sigma _{ij}=2\mu {\dot {\varepsilon }}_{ij}-{}^{t+1}p\delta _{ij}$

(3)

Compressible/quasi-incompressible continuum

${}^{t+1}s_{ij}={}^{t}{\hat {\sigma }}_{ij}+2\mu {\dot {\varepsilon }}_{ij}+\lambda {\dot {\varepsilon }}_{ii}\delta _{ij}$

(4.a)

where ${\textstyle {\hat {\sigma }}_{ij}}$ are the component of the stress tensor ${\textstyle [{\hat {\sigma }}]}$

$[{\hat {\sigma }}]={\frac {1}{J}}{F}^{T}{S}{F}$

(4.b)

where ${\textstyle {S}}$ is the second Piola-Kirchhoff stress tensor, ${\textstyle {F}}$ is the deformation gradient tensor and ${\textstyle J=\det {F}}$ [22,47]. Parameters ${\textstyle \mu }$ and ${\textstyle \lambda }$ take the following values for a fluid or solid material:

Fluid: ${\textstyle \mu }$: viscosity; ${\textstyle \lambda =\Delta tK-{\frac {2\mu }{3}}}$

Solid: ${\textstyle \displaystyle \mu ={\frac {\Delta tG}{J}}}$; ${\textstyle \displaystyle \lambda ={\frac {2G\nu \Delta t}{J(1-2\nu )}}}$, where ${\textstyle \nu }$ is the Poisson ration, ${\textstyle G}$ is the shear modulus and ${\textstyle \Delta t}$ the time increment.

In Eqs.(3) and (4), ${\textstyle s_{ij}}$ are the deviatoric stresses, ${\textstyle {\dot {\varepsilon }}_{ij}}$ is the rate of deformation, ${\textstyle \mu }$ is the viscosity and ${\textstyle \delta _{ij}}$ is the Kronecker delta. ${\textstyle {}^{t}(\cdot )}$ denotes values at time ${\textstyle t}$.

Indexes in Eqs.(1)–(4) range from ${\textstyle i,j=1,n_{d}}$, where ${\textstyle n_{d}}$ is the number of space dimensions of the problem (i.e. ${\textstyle n_{d}=2}$ for 2D problems). These equations are completed with the standard boundary conditions of prescribed velocities and surface tractions in the mechanical problem [11,36,47,48].

3.2 Discretization of the equations

A key problem in the numerical solution of Eqs.(1)–(3.1) is the satisfaction of the mass balance condition for the incompressible case (i.e. ${\textstyle K=\infty }$ in Eq.(2)). A number of procedures to solve his problem exist in the finite element literature [11,48]. In our approach we use a stabilized formulation based in the so-called finite calculus procedure [15,29,30,31,33,34]. The essence of this method is the solution of a modified mass balance equation which is written as

${\frac {1}{K}}{\partial p \over \partial t}-{\partial v_{i} \over \partial x_{i}}-\sum \limits _{i=1}^{3}\tau {\partial q \over \partial x_{i}}\left[{\partial p \over \partial x_{i}}+\pi _{i}\right]=0$

(5)

where ${\textstyle q}$ are weighting functions, ${\textstyle \tau }$ is a stabilization parameter given by [34]

$\tau =\left({\frac {2\rho \vert \mathbf {v} \vert }{h}}+{\frac {8\mu }{3h^{2}}}\right)^{-1}$

(6)

In the above, ${\textstyle h}$ is a characteristic length of each finite element and ${\textstyle \vert \mathbf {v} \vert }$ is the modulus of the velocity vector. In Eq.(5) ${\textstyle \pi _{i}}$ are auxiliary pressure projection variables chosen so as to ensure that the second term in Eq.(5) can be interpreted as weighted sum of the residuals of the momentum equations and therefore it vanishes for the exact solution. The set of governing equations is completed by adding the following constraint equation [32,36]

$\int _{V}\tau w_{i}\left({\partial p \over \partial x_{i}}+\pi _{i}\right)dV=0\quad i=1,n_{d}\quad {\hbox{(no sum in )}}i$

(7)

where ${\textstyle w_{i}}$ are arbitrary weighting functions.

The rest of the integral equations are obtained by applying the standard weighted residual technique to the governing equations (1), (2), (3) and (5) and the corresponding boundary conditions [11,22,48].

We interpolate next in the standard finite element fashion the set of problem variables. For 3D problems these are the three velocities ${\textstyle v_{i}}$, the pressure ${\textstyle p}$, the temperature ${\textstyle T}$ and the three pressure gradient projections ${\textstyle \pi _{i}}$. In our work we use equal order linear interpolation for all variables over meshes of 3-noded triangles (in 2D) and 4-noded tetrahedra (in 3D). The resulting set of discretized equations using the standard Galerkin technique has the following form

Momentum

$\mathbf {M} {\dot {\bar {v}}}+\mathbf {K} {\bar {v}}-\mathbf {G} {\bar {p}}={f}$

(8)

Pressure-velocity relationship

${\bar {M}}{\dot {\bar {p}}}-\mathbf {G} {\bar {v}}-\mathbf {L} {\bar {p}}-\mathbf {Q} {\bar {\boldsymbol {\pi }}}=\mathbf {0}$

(9)

Pressure gradient projection

${\hat {M}}{\bar {\boldsymbol {\pi }}}+\mathbf {Q} ^{T}{\bar {p}}=\mathbf {0}$

(10)

In Eqs.(8)–(10) ${\textstyle {\bar {(\cdot )}}}$ denotes nodal variables, ${\textstyle {\dot {\bar {(\cdot )}}}={\partial \over \partial t}{\bar {(\cdot )}}}$. The different matrices and vectors are given in [22,34,36].

The solution in time of Eqs.(8)–(10) can be performed using any time integration scheme typical of the updated Lagrangian FEM [36,47]. A basic algorithm following the conceptual process described in Section 2 is presented in Box I.

Box I. Basic PFEM algorithm for a Lagrangian continuum

1. LOOP OVER TIME STEPS, ${\textstyle t=1}$, NTIME Known values ${\textstyle ^{t}{\bar {x}},{}^{t}{\bar {v}},{}^{t}{\bar {p}},{}^{t}{\bar {\boldsymbol {\pi }}},{}^{t}{\bar {T}},{}^{t}\mu ,{}^{t}{f},{}^{t}\mathbf {q} ,{}^{t}C,{}^{t}V,{}^{t}M}$

2. LOOP OVER NUMBER OF ITERATIONS, ${\textstyle i=1}$, NITER

${\textstyle \bullet }$ Compute nodal velocities by solving Eq.(8)

${\textstyle \displaystyle \left[{\frac {1}{\Delta t}}\mathbf {M} +\mathbf {K} \right]{}^{t+1}{\bar {v}}^{i+1}={}^{t+1}\mathbf {f} +G{}^{t+1}{\bar {p}}^{i}+{\frac {1}{\Delta t}}\mathbf {M} {}^{t}{\bar {v}}}$

${\textstyle \bullet }$ Compute nodal pressures from Eq.(9)

${\textstyle \displaystyle \left[{\frac {1}{\Delta t}}-{L}{\bar {M}}\right]{}^{t+1}{\bar {p}}^{i+1}=\mathbf {G} {}^{T}{}^{t+1}{\bar {v}}^{i+1}+\mathbf {Q} {}^{t+1}{\bar {\boldsymbol {\pi }}}^{i}+{\frac {1}{\Delta t}}{\bar {M}}{}^{t}{\bar {p}}}$

${\textstyle \bullet }$ Compute nodal pressure gradient projections from Eq.(10)

${\textstyle {}^{n+1}{\bar {\boldsymbol {\pi }}}^{i+1}=-{\hat {M}}_{D}^{-1}\left[\mathbf {Q} ^{T}\right]{}^{t+1}{\bar {p}}^{i+1}{\begin{array}{ccc}{}&{,}&{{\hat {M}}_{D}=diag\left[{\hat {M}}_{D}\right]}\end{array}}}$

${\textstyle \bullet }$ Update position of analysis domain nodes:

${\textstyle {}^{t+\Delta t}{\bar {x}}^{i+1}={}^{t}\mathbf {x} ^{i}+{}^{t+\Delta t}\mathbf {v} ^{i+1}\Delta t}$

Define new “cloud” of nodes ${\textstyle {}^{t+1}C^{i+1}}$

${\textstyle \bullet }$ Update strain rate and strain values

${\textstyle \bullet }$ Update stress values

Check convergence ${\textstyle \rightarrow }$ NO ${\textstyle \rightarrow }$ Next iteration ${\textstyle i\to i+1}$

${\textstyle \downarrow }$ YES

Next time step ${\textstyle t\to t+1}$

${\textstyle \bullet }$ Identify new analysis domain boundary: ${\textstyle {}^{t+1}V}$

${\textstyle \bullet }$ Generate mesh:${\textstyle {}^{t+1}M}$

Go to 1

4 Generation of a new mesh

One of the key points for the success of the PFEM is the fast regeneration of a mesh at every time step on the basis of the position of the nodes in the space domain. Indeed, any fast meshing algorithm can be used for this purpose. In our work the mesh is generated at each time step using the so called extended Delaunay tesselation (EDT) presented in [17,19].

The CPU time required for meshing grows linearly with the number of nodes. The CPU time for solving the equations exceeds that required for meshing as the number of nodes increases. This situation has been found in all the problems solved with the PFEM. As a general rule for large 3D problems meshing consumes around 15% of the total CPU time for each time step, while the solution of the equations (with typically 3 iterations to reach convergence within a time step) and the assembling of the system consume approximately 70% and 15% of the CPU time for each time step, respectively. These figures refer to solutions obtained in a standard single processor Pentium IV PC for all the computations and prove that the generation of the mesh has an acceptable cost in the PFEM. The cost of remeshing is similar to that reported in [24]. Indeed considerable speed can be gained using parallel computation techniques.

5 Identification of boundary surfaces

One of the main tasks in the PFEM is the correct definition of the boundary domain. Boundary nodes are sometimes explicitly identified. In other cases, the total set of nodes is the only information available and the algorithm must recognize the boundary nodes.

In our work we use an extended Delaunay partition for recognizing boundary nodes [19]. Considering that the nodes follow a variable ${\textstyle h(x)}$ distribution, where ${\textstyle h(x)}$ is typically the minimum distance between two nodes. All nodes on an empty sphere with a radius greater than $\alpha h$, are considered as boundary nodes. In practice ${\textstyle \alpha }$ is a parameter close to, but greater than one. Values of ${\textstyle \alpha }$ ranging between 1.3 and 1.5 have been found to be optimal in all examples analyzed. This criterion is coincident with the Alpha Shape concept [12].

Once a decision has been made concerning which nodes are on the boundaries, the boundary surface is defined by all the polyhedral surfaces (or polygons in 2D) having all their nodes on the boundary and belonging to just one polyhedron.

The method described also allows one to identify isolated fluid particles outside the main fluid domain. These particles are treated as part of the external boundary where the pressure is fixed to the atmospheric value. We recall that each particle is a material point characterized by the density of the solid or fluid domain to which it belongs. The mass which is lost when a boundary element is eliminated due to departure of a node from the main analysis domain is again regained when the “flying” node falls down and a new boundary element is created by the Alpha Shape algorithm.

The boundary recognition method is also useful for detecting contact conditions between the fluid domain and a fixed boundary, as well as between different solids interacting with each other as detailed in the next section.

We emphasize that the main difference between the PFEM and the classical FEM is just the remeshing technique and the identification of the domain boundary at each time step.

6 Treatment of contact conditions in the PFEM

6.1 Contact between the fluid and a fixed boundary

The condition of prescribed velocities at the fixed boundaries in the PFEM is applied in strong form to the boundary nodes. These nodes might belong to fixed external boundaries or to moving boundaries linked to the interacting solids. Contact between the fluid particles and the fixed boundaries is accounted for by the incompressibility condition which naturally prevents the fluid nodes to penetrate into the solid boundaries [32,36].

6.2 Contact between solid-solid interfaces

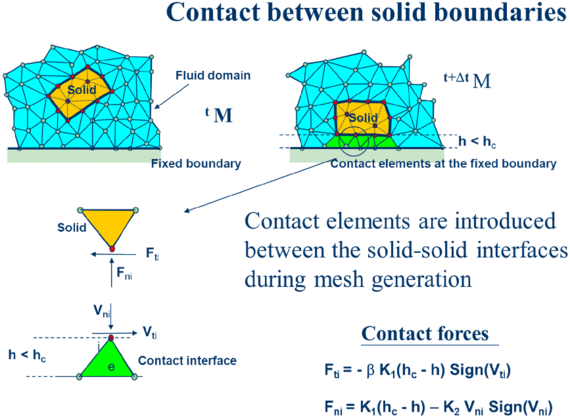
The contact between two solid interfaces is simply treated by introducing a layer of contact elements between the two interacting solid interfaces. This layer is automatically created during the mesh generation step by prescribing a minimum distance (${\textstyle h_{c}}$) between two solid boundaries. If the distance exceeds the minimum value (${\textstyle h_{c}}$) then the generated elements are treated as fluid elements. Otherwise the elements are treated as contact elements where a relationship between the tangential and normal forces and the corresponding displacement is introduced (Figure 2).

Figure 2: Modelling of contact conditions at a solid-solid interface with the PFEM

This algorithm has proven to be very effective and it allows to identifying and modeling complex frictional contact conditions between two or more interacting bodies moving in water in an extremely simple manner.

This algorithm can also be used effectively to model frictional contact conditions between rigid or elastic solids in structural mechanics applications [7,36].

7 Modeling of bed erosion

Prediction of bed erosion and sediment transport in open channel flows are important tasks in many areas of river and environmental engineering. Bed erosion can lead to instabilities of the river basin slopes. It can also undermine the foundation of bridge piles thereby favouring structural failure. Modeling of bed erosion is also relevant for predicting the evolution of surface material dragged in earth dams in overspill situations. Bed erosion is one of the main causes of environmental damage in floods.

Bed erosion models are traditionally based on a relationship between the rate of erosion and the shear stress level [25]. In a recent work we have proposed an extension of the PFEM to model bed erosion [35,36]. The erosion model is based on the frictional work at the bed surface originated by the shear stresses in the fluid. The resulting erosion model resembles Archard law typically used for modeling abrasive wear in surfaces under frictional contact conditions [1].

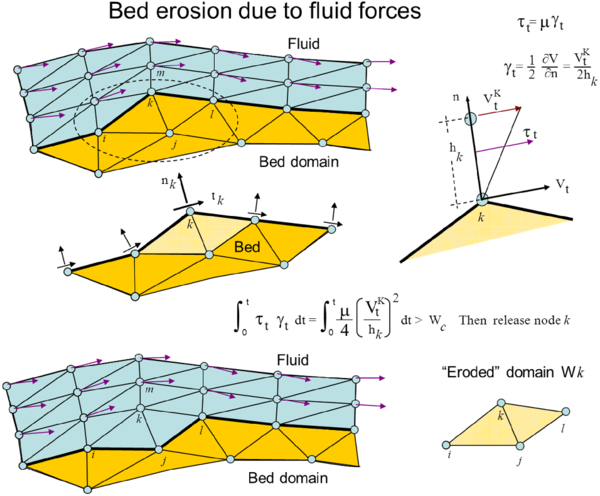
The algorithm for modeling the erosion of soil/rock particles at the fluid bed is the following:

1. Compute at every point of the bed surface the resultant tangential stress ${\textstyle \tau }$ induced by the fluid motion. In 3D problems ${\textstyle \tau =(\tau _{s}^{2}+\tau _{t})^{2}}$ where ${\textstyle \tau _{s}}$ and ${\textstyle \tau _{t}}$ are the tangential stresses in the plane defined by the normal direction ${\textstyle {n}}$ at the bed node. The value of ${\textstyle \tau }$ for 2D problems can be estimated as follows:

   $\tau _{t}=\mu \gamma _{t}\quad {\hbox{with}}\quad \gamma _{t}={1 \over 2}{\partial v_{t} \over \partial n}={v_{t}^{k} \over 2h_{k}}$

   (11)

where ${\textstyle v_{t}^{k}}$ is the modulus of the tangential velocity at the node ${\textstyle k}$ and ${\textstyle h_{k}}$ is a prescribed distance along the normal of the bed node ${\textstyle k}$. Typically ${\textstyle h_{k}}$ is of the order of magnitude of the smallest fluid element adjacent to node ${\textstyle k}$ (Figure 3).

2. Compute the frictional work originated by the tangential stresses at the bed surface as

   $W_{f}=\int _{\circ }^{t}\tau _{t}\gamma _{t}\,dt=\int _{\circ }^{t}{\mu \over 4}\left({v_{t}^{k} \over h_{k}}\right)^{2}dt$

   (12)

Eq.(12) is integrated in time as

${}^{n}W_{f}={}^{n-1}W_{f}+\tau _{t}\gamma _{t}\,\Delta t$

(13)

3. The onset of erosion at a bed point occurs when ${\textstyle {}^{n}W_{f}}$ exceeds a critical threshold value ${\textstyle W_{c}}$.

1. If ${\textstyle {}^{n}W_{f}>W_{c}}$ at a bed node, then the node is detached from the bed region and it is allowed to move with the fluid flow. As a consequence, the mass of the patch of bed elements surrounding the bed node vanishes in the bed domain and it is transferred to the new fluid node. This mass is subsequently transported with the fluid.
2. Sediment deposition can be modeled by an inverse process to that described in the previous step. Hence, a suspended node adjacent to the bed surface with a velocity below a threshold value is attached to the bed surface.

Figure 3 shows an schematic view of the bed erosion algorithm described.

Figure 3: Modeling of bed erosion with the PFEM by dragging of bed material

8 Examples

8.1 Dragging of rocks by a water stream

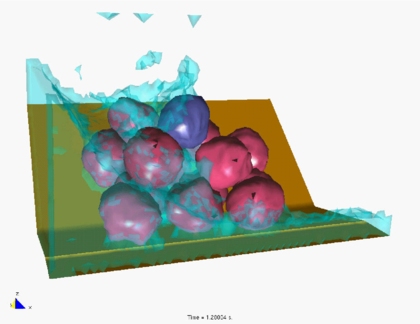
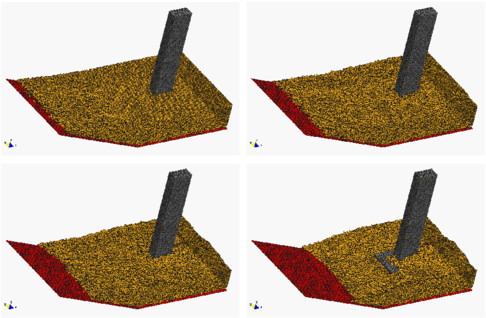
Predicting the critical speed at which a rock will be dragged by a water stream is of great importance in many problems in hydraulic, harbour, civil and environmental engineering.

The PFEM has been successfully applied to the study of the motion of a 1Tn quasi-spherical rock due to a water stream. The rock lays on a collection of rocks that are kept rigid. Frictional conditions between the analyzed rock and the rest of the rocks have been assumed. Figure 4a shows that a water stream of 1m/s is not able to displace the individual rock. An increase of the water speed to 2m/s induces the motion of the rock as shown in Figure 4b.

(a) Water speed of 1m/s. The individual rock can not be dragged by the stream	(b) Water speed of 2m/s. The individual rock is dragged by the stream
Figure 4: Study of the drag of an individual rock of 1Tn under a water stream at speeds of (a) 1m/s and (b) 2m/s

8.2 Impact of sea waves on piers and breakwaters

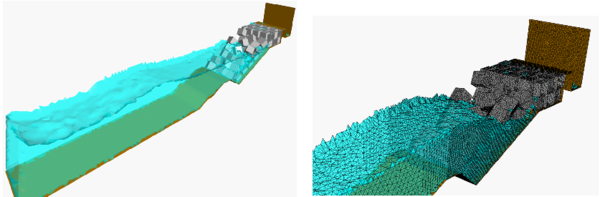
Figures 5 and 6 show the analysis of the effect of breaking waves on two different sites of a breakwater containing reinforced concrete blocks (each one of ${\textstyle 4\times 4}$ mts). The figures correspond to the study of Langosteira harbour in A Coruña, Spain using PFEM.

Figure 5: Breaking waves on breakwater slope containing reinforced concrete blocks. Mesh of 4-noded tetrahedra near the slope

Figure 6: Study of breaking waves on the edge of a breakwater structure formed by reinforced concrete blocks

8.3 Soil erosion problems

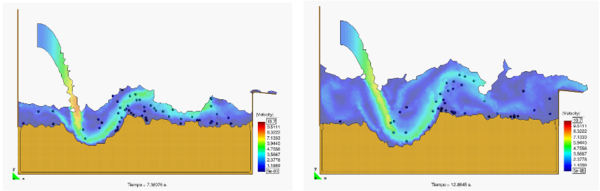
Figure 7 shows the capacity of the PFEM for modelling soil erosion, sediment transport and material deposition in a river bed. The soil particles are first detached from the bed surface under the action of the jet stream. Then they are transported by the flow and eventually fall down due to gravity forces into the bed surface at a downstream point.

Figure 8 shows the progressive erosion of the unprotected part of a breakwater slope in the Langosteira harbour in A Coruña, Spain. The non protected upper shoulder zone is progressively eroded under the sea waves.

Figure 9 displays the progressive erosion and dragging of soil particles in a river bed adjacent to the foot of bridge pile due to the water stream (water is not shown in the figure). Note the disclosure of the bridge foundation as the adjacent soil particles are removed due to erosion.

Other applications of the PFEM to bed erosion problems can be found in [35,36].

Figure 7: Erosion, transport and deposition of soil particles at a river bed due to an impacting jet stream

Figure 8: Erosion of an unprotected shoulder of a breakwater due to sea waves

Figure 9: Erosion and dragging of soil particles in a river bed adjacent to the foot of a bridge pile due to a water stream. Water is not shown

8.4 Falling of a lorry into the sea by sea wave erosion of the road slope

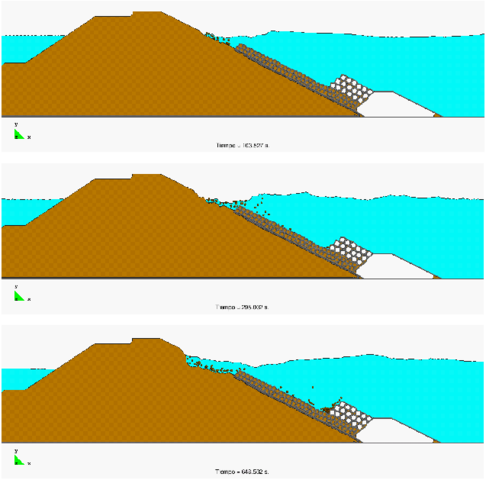
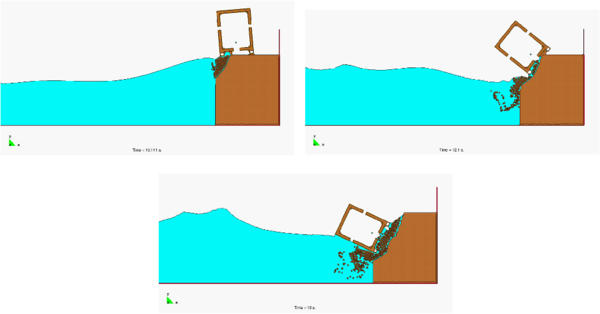
Figure 10 shows a representative example of the progressive erosion of a soil mass adjacent to the shore due to sea waves and the subsequent falling into the sea of a 2D object representing the section of a lorry. The object has been modeled as a rigid solid.

This example, although still quite simple and schematic, shows the possibility of the PFEM for modeling complex FSSI problems involving soil erosion, free surface waves and rigid/deformable structures.

Figure 10: Erosion of a soil mass due to sea waves and the subsequent falling into the sea of an adjacent lorry

8.5 Simulation of landslides

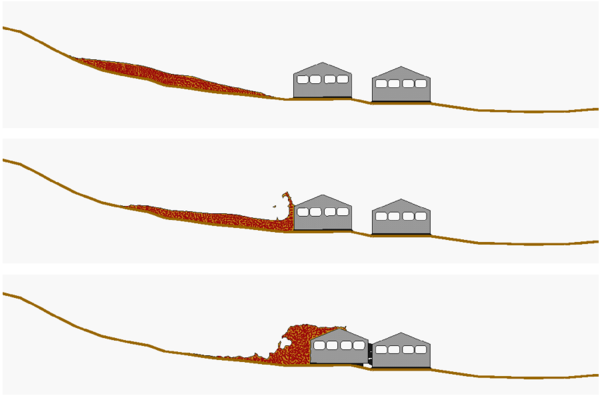
The PFEM is particularly suited for modelling and simulation of landslides and their effect in the surrounding structures. Figure 11 shows an schematic 2D simulation of a landslide falling on two adjacent constructions. The landslide material has been modelled as a viscous incompressible fluid.

Figure 11: Landslide falling on two constructions 2D simulation using PFEM

8.6 The landslide in Lituya Bay

A case of much interest is when the landslide occurs in the vicinity of a reservoir [43]. The fall of debris material into the reservoir typically induces large waves that can overtop the dam originating an unexpected flooding that can cause severe damage to the constructions and population in the downstream area.

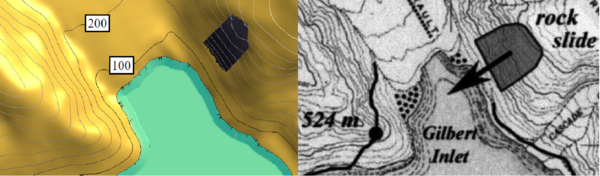
In the example, we present some results of the 3D analysis of the landslide produced in Lituya Bay (Alaska) on July 9th 1958 (Figure 12). The landslide was originated by an earthquake and movilized 90 millions tons of rocks that fell on the bay originating a large wave that reached a hight on the opposed slope of 524 mts.

]

Figure 12: Lituya Bay landslide. Left: Geometry for the simulation. Right: Landslide direction and maximum wave level [13,14]

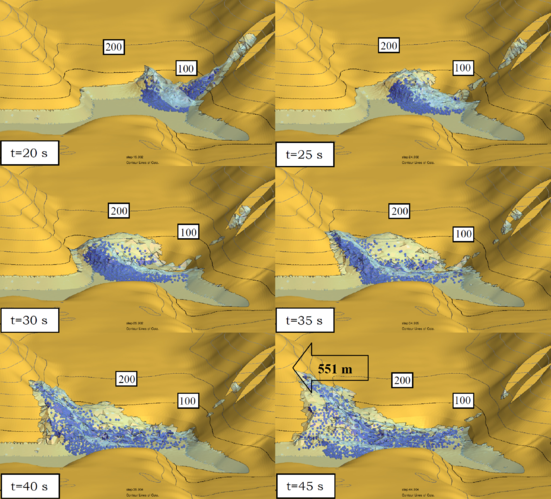
Figure 13: Lituya Bay landslide. Evolution of the landslide into the reservoir obtained with the PFEM. Maximum level of generated wave (551 mts) in the north slope

Figure 13 shows images of the simulation of the landslide with PFEM. The sliding mass has been modelled as a quasi-incompressible continuum with a prescribed shear modulus. No frictional effect between the sliding mass and the underneath soil has been considered. Also the analysis has not taken into account the erosion and dragging of soil material induced by the landslide mass during motion.

PFEM results have been compared with observed values of the maximum water level in the north hill adjacent to the reservoir. The maximum water level in this hill obtained with PFEM was 551 mts. This is 5% higher than the value of 524 mts. observed experimental by [13,14]. The maximum height location differs in 300 mts from the observed value [13,14]. In the south slope the maximum water height observed was 208 mts, while the PFEM result (not shown here) was 195 mts (6% error).

More information on the PFEM solutions of this example can be found in [38,39].

9 Conclusions

The particle finite element method (PFEM) is a promising numerical technique for solving fluid-soil-structure interaction (FSSI) problems involving large motion of fluid and solid particles, surface waves, water splashing, frictional contact situations between fluid-solid and solid-solid interfaces and bed erosion, among other complex phenomena. The success of the PFEM lies in the accurate and efficient solution of the equations of an incompressible continuum using an updated Lagrangian formulation and a stabilized finite element method allowing the use of low order elements with equal order interpolation for all the variables. Other essential solution ingredients are the efficient regeneration of the finite element mesh, the identification of the boundary nodes using the Alpha-Shape technique and the simple algorithm to treat frictional contact conditions and erosion/wear at fluid-solid and solid-solid interfaces via mesh generation. The examples presented have shown the potential of the PFEM for solving a wide class of practical FSSI problems in engineering.

Acknowledgements

This research was partially supported by project SEDUREC of the Consolider Programme of the Ministerio de Educación y Ciencia (MEC) of Spain and the projects SAFECON and REALTIME of the European Research Council of the European Commission (EC). Thanks are also given to the Spanish construction company Dragados for financial support for the study of harbour engineering problems with the PFEM .

Bibliography

[1] Archard JF (1953) Contact and rubbing of flat surfaces. J. Appl. Phys. 24(8):981–988

[2] Aubry R, Idelsohn SR, Oñate E (2005) Particle finite element method in fluid mechanics including thermal convection-diffusion, Computer & Structures 83(17-18):1459–1475

[3] Badia S, Codina R (2009) On a multiscale approach to the transient Stokes problem. Transient subscales and anisotropic space-time discretizations. Applied Mathematics and Computation 207:415–423

[4] Baiges J, Codina R (2010) The fixed-mesh ALE approach applied to solid mechanics and fluid-structure interaction problems. Int. J. Num. Meth. Engrg. 81:1529–1557

[5] Bazilevs Y, Calo VM, Cottrell JA, Hughes TJR, Reali A, Scovazzi G (2007) Variational multiscale residual-based turbulence modeling for large eddy simulation of incompressible flows. Comp. Meth. Appl. Mech Engrg. 197:173–201

[6] Bazilevs Y, Hsu M-C, Zhang Y, Wang W, Liang X, Kvamsdal T, Brekken R, Isaksen J (2010) A fully coupled fluid-structure interaction simulation of cerebral aneurysms. Computational Mechanics 46:3–16

[7] Carbonell JM, Oñate E, Suárez B (2010) Modeling of ground excavation with the Particle Finite Element Method. Journal of Engineering Mechanics (ASCE) 136(4):455–463

[8] Codina R (2002) Stabilized finite element approximation of transient incompressible flows using subscales. Comput. Meth. Appl. Mech. Engrg. 191: 4295–4321

[9] Codina R, Coppola-Owen H, Nithiarasu P, Liu CB (2006) Numerical comparison of CBS and SGS as stabilization techniques for the incompressible Navier-Stokes equations. Int. J. Num. Meth. Engrg. 66:1672–1689

[10] Del Pin F, Idelsohn SR, Oñate E, Aubry R (2007) The ALE/Lagrangian particle finite element method: A new approach to computation of free-surface flows and fluid-object interactions. Computers & Fluids 36:27–38

[11] Donea J, Huerta A (2003) Finite element method for flow problems. J. Wiley

[12] Edelsbrunner H, Mucke EP (1999) Three dimensional alpha shapes. ACM Trans. Graphics 13:43–72

[13] Fritz, HM, Hager WH, Minor HE (2001) Lituya Bay Case: Rockslide impact and wave run-up. Science of Tsunami Hazards 19(1):3–22

[14] Fritz, HM, Hager WH, Minor HE (2004) Near field characteristics of landslide generated impulse waves. Journal of Waterway, Port, Coastal and Ocean Engineering. ASCE 130(6):287–302

[15] García J, Oñate E (2003) An unstructured finite element solver for ship hydrodynamic problems. J. Appl. Mech. 70:18–26

[16] Idelsohn SR, Oñate E, Del Pin F, Calvo N (2002) Lagrangian formulation: the only way to solve some free-surface fluid mechanics problems. 5th World Congress on Comput. Mechanics, HA Mang, FG Rammerstorfer, J Eberhardsteiner (Eds), July 7–12, Viena, Austria

[17] Idelsohn SR, Oñate E, Calvo N, Del Pin F (2003a) The meshless finite element method. Int. J. Num. Meth. Engng. 58(6):893–912

[18] Idelsohn SR, Oñate E, Del Pin F (2003b) A lagrangian meshless finite element method applied to fluid-structure interaction problems. Comput. and Struct. 81:655–671

[19] Idelsohn SR, Calvo N, Oñate E (2003c) Polyhedrization of an arbitrary point set. Comput. Method Appl. Mech. Engng. 192(22-24):2649–2668

[20] Idelsohn SR, Oñate E, Del Pin F (2004) The particle finite element method: a powerful tool to solve incompressible flows with free-surfaces and breaking waves. Int. J. Num. Meth. Engng. 61:964–989

[21] Idelsohn SR, Oñate E, Del Pin F, Calvo N (2006) Fluid-structure interaction using the particle finite element method. Comput. Meth. Appl. Mech. Engng. 195:2100–2113

[22] Idelsohn SR, Marti J, Limache A, Oñate E (2008) Unified Lagrangian formulation for elastic solids and incompressible fluids: Application to fluid-structure interaction problems via the PFEM. Comput Methods Appl Mech Engrg. 197:1762–1776

[23] Idelsohn SR, Mier-Torrecilla M, Oñate E (2009) Multi-fluid flows with the Particle Finite Element Method. Comput Methods Appl Mech Engrg. 198:2750–2767

[24] Johnson AA, Tezduyar TE (1999) Advanced mesh generation and update methods for 3D flow simulations. Computational Mechanics 23:130–143

[25] Kovacs A, Parker G (1994) A new vectorial bedload formulation and its application to the time evolution of straight river channels. J. Fluid Mech. 267:153–183

[26] Larese A, Rossi R, Oñate E, Idelsohn SR (2008) Validation of the Particle Finite Element Method (PFEM) for simulation of free surface flows. Engineering Computations 25(4):385–425

[27] Löhner R (2008) Applied CFD Techniques. J. Wiley

[28] Löhner R, Yang Ch, Oñate E (2007) Simulation of flows with violent free surface motion and moving objects using unstructured grids. Int. J. Num. Meth. Fluids 153:1315–1338

[29] Oñate E (1998) Derivation of stabilized equations for advective-diffusive transport and fluid flow problems. Comput. Meth. Appl. Mech. Engng. 151:233–267

[30] Oñate E (2004) Possibilities of finite calculus in computational mechanics. Int. J. Num. Meth. Engng. 60(1):255–281

[31] Oñate E, García J (2001) A finite element method for fluid-structure interaction with surface waves using a finite calculus formulation. Comput. Meth. Appl. Mech. Engrg. 191:635–660

[32] Oñate E, Idelsohn SR, Del Pin F, Aubry R (2004b) The particle finite element method. An overview. Int. J. Comput. Methods 1(2):267–307

[33] Oñate E, Valls A, García J (2006a) FIC/FEM formulation with matrix stabilizing terms for incompressible flows at low and high Reynold's numbers. Computational Mechanics 38 (4-5):440–455

[34] Oñate E, García J, SR Idelsohn, F. Del Pin (2006b) FIC formulations for finite element analysis of incompressible flows. Eulerian, ALE and Lagrangian approaches. Comput. Meth. Appl. Mech. Engng. 195(23-24):3001–3037

[35] Oñate E, M.A. Celigueta, Idelsohn SR (2006c) Modeling bed erosion in free surface flows by the Particle Finite Element Method, Acta Geotechnia 1(4):237–252

[36] Oñate E, Idelsohn SR, Celigueta MA, Rossi R (2008) Advances in the particle finite element method for the analysis of fluid-multibody interaction and bed erosion in free surface flows. Comput. Meth. Appl. Mech. Engng. 197(19-20):1777–-1800

[37] Oñate E, Rossi R, Idelsohn SR, Butler K (2010) Melting and spread of polymers in fire with the particle finite element method. Int. J. Numerical Methods in Engineering, 81(8):1046–1072

[38] Oñate, E, Salazar F, Morán R (2011) Modeling of landslides into reservoir with the Particle Finite Element Method. Research Report CIMNE No. PI355. Submitted to Int. J. Numerical Methods in Geomechanics

[39] Salazar F, Oñate E, Morán R (2011) Modelación numérica de deslizamientos de ladera en embalses mediante el método de partículas y elementos finitos (PFEM). Rev. Int. Mét. Num. Cálc. Dis. Ing. Acepted for publication

[40] Takizawa K, Tezduyar TE (2011) Multiscale space-time fluid-structure interaction techniques. Computational Mechanics, Published online, DOI:10.1007/s00466-011-0571-z

[41] Tezduyar TE, Mittal S, Ray SE, Shih R (1992) Incompressible flow computations with stabilized bilinear and linear equal-order-interpolation velocity-pressure elements. Comput. Meth. Appl. Mech. Engng. 95:221–242

[42] Tezduyar TE (2007) Finite elements in fluids: special methods and enhanced solution techniques. Computers & Fluids 36:207–223

[43] Wan CF, Fell R (2004) Investigation of erosion of soils in embankment dams. J. Geotechnical and Geoenvironmental Engineering 130:373–380

[44] Yabe T, Takizawa K, Tezduyar TE, Im H-N (2007) Computation of fluid-solid and fluid-fluid interfaces with the CIP method based on adaptive Soroban Grids. An overview. Int. J. Num. Meth. in Fluids 54:841–853

[45] Zienkiewicz OC, Jain PC, Oñate E (1978) Flow of solids during forming and extrusion: Some aspects of numerical solutions. Int. Journal of Solids and Structures 14:15–38

[46] Zienkiewicz OC, Taylor RL, Zhu JZ (2005) The finite element method. Its basis and fundamentals, Elsevier

[47] Zienkiewicz OC, Taylor RL (2005) The finite element method for solid and structural mechanics, Elsevier

[48] Zienkiewicz OC, Taylor RL, Nithiarasu P (2006) The finite element method for fluid dynamics, Elsevier