Melting and spread of polymer in fire with the particle finite element method

Abstract

A new computational procedure for analysis of the melting and flame spread of polymers under fire conditions is presented. The method, termed Particle Finite Element Method (PFEM), combines concepts from particle-based techniques with those of the standard finite element method (FEM). The key feature of the PFEM is the use of an updated Lagrangian description to model the motion of nodes (particles) in the thermoplastic material. Nodes are viewed as material points which can freely move and even separate from the main analysis domain representing, for instance, the effect of melting and dripping of polymer particles. A mesh connects the nodes defining the discretized domain where the governing equations are solved as in the standard FEM. An incremental iterative scheme for the solution of the nonlinear transient coupled thermal-flow problem, including loss of mass by gasification, is used. Examples of the possibilities of the PFEM for the modelling and simulation of the melting and flame spread of polymers under different fire conditions are described. Numerical results are compared with experimental data provided by NIST.

Keywords: Melting, dripping, polymers, Particle Finite Element Method, PFEM

1 INTRODUCTION

Thermoplastic polymer objects, including mattresses, upholstered furniture, and molded objects such as electronic housings and automobile parts, respond to fire by melting and dripping onto the surface below. The flow of polymer material affects heat and mass transport within the object, and the accumulating melt pool below the object extends the flaming zone and increases the overall rate of heat release [1]–[3]. If the fire from the object and the pool fire interact, the intensity of the fire is enhanced even further. The spread rate of the melt pool and its burning behavior (including whether it is even able to sustain ignition) are affected by the flooring material as well as by the properties of the melt.

Computer modeling and simulation of the melting flow and flame spread of thermoplastics is extremely complex involving fluid flow, heat transfer, material degradation, flame chemistry, surface tension, and complex material properties [1]. In addition, the drastic changes in shape pose a severe challenge to traditional modelling methods. Attempts to model melt flow of polymeric material in fire using the volume of fluid (VOF) method have encountered difficulties with numerical instabilities and excessive runtimes [4].

The Particle Finite Element Method (PFEM) [5]–[11] presented in this work is a powerful technique for modelling and analysis of complex multidisciplinary problems in fluid and solid mechanics involving coupled thermal effects, fragmentation and separation of fluid particles and fluid-structure interaction effects, among others. The PFEM combines Lagrangian particle-based techniques with the advantages of the integral formulation of the finite element method [15]. A key advantage of the Lagrangian formulation in the PFEM is the elimination of the convective terms in the fluid flow and thermal equations, which favours the simplicity (and symmetry) of the formulation, as well as computational efficiency.

In the PFEM, the particles represent the nodes of a finite element mesh. The particles can move freely according to the velocity field, transporting their momentum and physical properties. A robust and efficient remeshing algorithm connects the nodes into a finite element grid for solution of the state variables in the new configuration. The PFEM has been used to solve a variety of free surface, fluid-structure interaction, and multiphase problems, including breaking waves in harbours, ship hydrodynamics, dam bursting and metal casting, among many others [5,6], [8]–[11].

This paper describes the key aspects of the PFEM for analysis of the melting, flow and flame spread of polymer objects including loss of mass by gasification. The underlying ideas of the paper follow the original work of the authors in this field as presented in [Buetal07,Roetal07]. The recent developments of the PFEM described in this paper demonstrate its potential for solving complex melting flow problems for two and three dimensional heated polymer objects accounting for frictional contact and self-contact situations.

The paper is structured as follows. In the next section the basis of the PFEM is summarized. The essential governing equations and an overview of the discretization procedure and the general solution scheme are given. The potential of the PFEM for the simulation of the melt flow and spread of thermoplastic objects in fire is shown in examples of its application for different heated samples,including a rectangular slab, a triangular slab, polymer melt spreading over a surface, a chair, and a candle. Numerical results for the rectangular slab and the spreading melt are compared with experimental data obtained at NIST [4].

2 THE PARTICLE FINITE ELEMENT METHOD. AN OVERVIEW

2.1 Basic steps of the PFEM

In the PFEM the analysis domain is modeled with an updated Lagrangian formulation [6,8,11]. The analysis domain can include solid and fluid subdomains. As an example, we can model one or several thermoplastic objects and the surrounding air as forming part of the analysis domain. All variables in the fluid and solid domains are assumed to be known in the current configuration at time ${\textstyle t}$. The new set of variables in both domains is sought in the next configuration at time ${\textstyle t+\triangle t}$. The finite element method (FEM) is used to solve the continuum equations in both domains. Hence a mesh discretizing these domains must be generated in order to solve the governing equations for both the fluid and solid problems in the standard FEM fashion. To do this, the nodes discretizing the analysis domain are treated as material particles whose motion is tracked during the transient solution. This is useful to model the separation of particles from a solid domain, such as in the dripping of melt particles from a thermoplastic object, and to follow their subsequent motion as individual particles with a known density, an initial acceleration and velocity, and subject to gravity forces. Every node is a material point and hence is characterized by the density of the polymer material. The mass of a given domain is obtained by integrating the density at the different material points over the domain.

In this paper, we will consider the analysis domain to be formed of polymer material only, i.e. the surrounding hot air is not included as part of the analysis domain. Melted drips of the polymer material separating from the main body of the heated object will be treated as independent analysis domains.

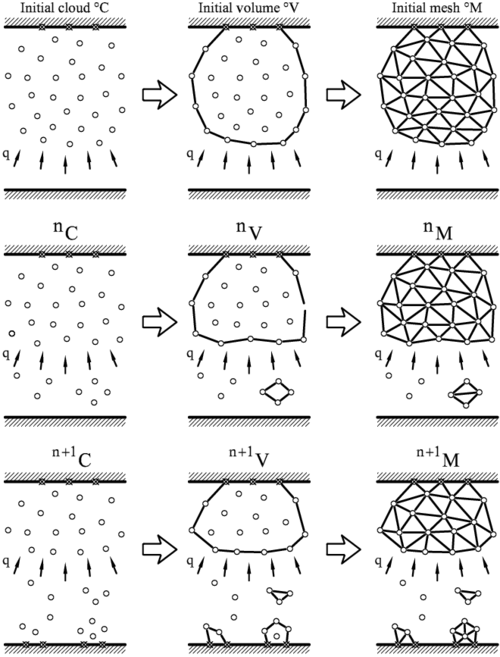
The way the PFEM solution process operates for the problems we are solving in this paper is schematically shown in Figure 1. The figure represents a polymer object hanging from a wall and subjected to an incoming heat flux ${\textstyle q}$ acting at the lower part of the object.

The collection or cloud of nodes pertaining to the polymer analysis domain will be defined as (${\textstyle C}$), the volume defining the thermoplastic analysis domain as (${\textstyle V}$), and the mesh discretizing this domain as (${\textstyle M}$).

A typical solution with the PFEM involves the following steps:

1. The starting point at each time step is the cloud of points in the polymer domain. For instance, ${\textstyle ^{\circ }C}$ and ${\textstyle ^{n}C}$ are the clouds at the initial time and at time ${\textstyle t=t_{n}}$, respectively (Figure 1).
2. Identify the boundaries defining the analysis domain ${\textstyle ^{n}V}$. This is an essential step as some boundaries, such as the free surface in the melting zone, may be severely distorted during the solution process. Some nodes may even separate from the boundary. The Alpha-Shape method [14] is used for the boundary definition. Note that the analysis domain can include different subdomains formed by the main polymer object and the dripping and spread zones (Figure 1).
3. Discretize the polymer analysis domain with a finite element mesh ${\textstyle ^{n}M}$. In our work an innovative mesh generation scheme based on the extended Delaunay tessellation is typically used [7].
4. Solve the coupled Lagrangian equations of motion for the polymer domains. Compute the relevant state variables at the next (updated) configuration for ${\textstyle t+\triangle t}$: velocities, strain rates, strains, pressure, viscous stresses and temperature in the polymer.
5. Move the mesh nodes to a new position ${\textstyle ^{n+1}C}$, where ${\textstyle n+1}$ denotes the time ${\textstyle t_{n}+\triangle t}$, in terms of the time increment size. For the fully Lagrangian application discussed here, the nodes are moved according to the forces determined in step 4.
6. Go back to step 1 and repeat the solution process for the next time step.

Figure 1: Polymer object subjected to a heat flux $q$ applied to its lower boundary (arrows indicate incoming heat flux). Sequence of steps to update the “cloud” of nodes representing the object in time using the PFEM

It is important to note that the quality of the numerical solution depends on the discretization chosen as in the standard FEM. Adaptive mesh refinement techniques can therefore be used to refine the mesh at the onset of the solution for each the step in order to improve the solution in zones where large motions of the fluid or the structure occur. Indeed, remeshing implies the introduction of new nodes in the mesh for which the state variables must be assigned via a projection method. The error introduced by the projection is corrected using an implicit algorithm which sought for a converged solution at the next configuration at time. In the examples shown in this paper the number of nodes during the transient solution has been kept constant.

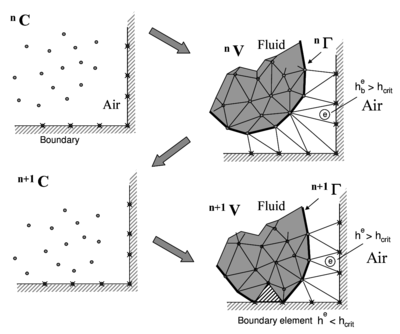
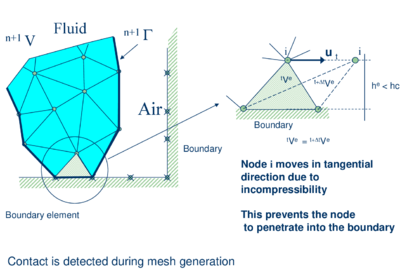
Two distinct features of the PFEM are its capability to model the separation of material fragments from the main body of the object and its ability to model frictional contact situations. The contact between two solid interfaces is treated by introducing a layer of contact elements between the two interacting domains. This layer is automatically created during the mesh generation step by prescribing a minimum distance (${\textstyle h_{c}}$) between the two interacting boundaries that controls the accuracy of the contact model. If the distance is greater than the minimum value (${\textstyle h_{c}}$) then the generated elements are given the properties of air and treated as standard fluid elements, or else they are removed from the analysis domain (Figure 2). Otherwise, the elements are treated as contact elements where a relationship between the tangential and normal forces and the corresponding displacements (or velocities) is introduced so as to model frictional contact effects. This technique also prevents nodes in a fluid domain from crossing over rigid boundaries [8,11].

The PFEM has proven to be very effective for modeling complex frictional contact conditions between two or more interacting rigid or deformable bodies or between fluid and solid interfaces in an extremely simple manner. Examples of applications of the PFEM can be found in [6]–[13].

Figure 2: Modelling of contact between the melting object and a fixed boundary

2.2 Governing equations

It is assumed that the polymer melt flow is governed by the equations of an incompressible fluid with a temperature dependent viscosity. A quasi-rigid behaviour of the polymer object at room temperature is reproduced by setting the viscosity to a sufficiently high value that the unheated polymer moves a negligible distance over the duration of the problem. As temperature increases in the thermoplastic object due to heat exposure, the viscosity decreases by several orders of magnitude as a function of temperature. This induces the melt and flow of the particles in the heated zone. The key equations to be solved in the polymer melt flow problem, written in the Lagrangian frame of reference, are the following:

Momentum

$\rho {\frac {dv_{i}}{dt}}={\frac {\partial \sigma _{ij}}{\partial x_{j}}}+b_{i}\quad {\hbox{in }}\Omega$

(1)

Mass balance

${\frac {\partial v_{i}}{\partial x_{i}}}=0\quad {\hbox{in }}\Omega$

(2)

Heat transport

$\rho c{\frac {dT}{dt}}={\frac {\partial }{\partial x_{i}}}\left(k_{i}{\frac {\partial T}{\partial x_{i}}}\right)+Q\quad {\hbox{in }}\Omega$

(3)

In the above equations ${\textstyle v_{i}}$ is the velocity along the ith global (cartesian) axis, ${\textstyle T}$ is the temperature, ${\textstyle \rho }$, ${\textstyle c}$ and ${\textstyle k_{i}}$ are the density (assumed constant), the specific heat and the conductivity of the material along the ith coordinate direction, respectively, ${\textstyle b_{i}}$ and ${\textstyle Q}$ are the body forces and the heat source per unit volume, respectively, and ${\textstyle \sigma _{ij}}$ are the (Cauchy) stresses related to the velocities by the standard constitutive equation (for an incompressible Newtonian fluid)

$\sigma _{ij}=s_{ij}-p\delta _{ij}$

(4.a)

$s_{ij}=2\mu \varepsilon _{ij}\quad ,\quad \varepsilon _{ij}={\frac {1}{2}}\left({\partial v_{i} \over \partial x_{j}}+{\partial v_{j} \over \partial x_{i}}\right)$

(4.b)

In Eqs.(4) ${\textstyle s_{ij}}$ are the deviatoric stresses, ${\textstyle p}$ is the pressure (assumed to be positive in compression), ${\textstyle \varepsilon _{ij}}$ is the rate of deformation and ${\textstyle \mu }$ is the viscosity. In the following we will assume ${\textstyle k_{i}=k}$ and the viscosity ${\textstyle \mu }$ to be a known function of temperature, i.e. ${\textstyle \mu =\mu (T)}$.

In Eqs. (1) – (3) ${\textstyle {\frac {d\varphi }{dt}}}$ means the total (material) derivative of any variable ${\textstyle \varphi }$ with respect to time.

Indexes in Eqs.(1) – (4) range from ${\textstyle i,j=1,n_{d}}$, where ${\textstyle n_{d}}$ is the number of space dimensions of the problem (i.e. ${\textstyle n_{d}=2}$ for two-dimensional problems).

Eqs.(1) – (4) are completed with the standard boundary conditions of prescribed velocities and surface tractions in the mechanical problem and prescribed temperature and prescribed normal heat flux in the thermal problem [6,8,9,10]. For surfaces exposed to fire conditions, energy losses due to radiation and convection must be taken into account, and the thermal boundary condition is:

$k{\frac {\partial T}{\partial n}}+{\bar {q}}_{n}=0$

(5.a)

with

${\bar {q}}_{n}=q_{n}+\epsilon \sigma (T^{4}-T_{0}^{4})+\alpha _{c}(T-T_{0})\quad {\hbox{in }}\Gamma _{q}$

(5.b)

where ${\textstyle {\frac {\partial T}{\partial n}}}$ is the derivative of temperature within the object along the direction normal to the Neumann boundary ${\textstyle \Gamma _{q}}$, ${\textstyle q_{n}}$ is the outgoing heat flux per unit area along the normal to the boundary surface, and the last two terms of Eqs.(5.b) are the radiative and convective heat losses respectively, where ${\textstyle T_{0}}$ is the reference temperature, ${\textstyle \epsilon }$ is the emissivity, ${\textstyle \sigma }$ is the Stefan-Boltzmann constant, and ${\textstyle \alpha _{c}}$ is the convection coefficient.

We note that Eqs.(1) – (4) are the standard ones for modeling the deformation of viscoplastic materials using the so-called “flow approach” [19,20]. In our work we have limited the viscosity to be a non linear function of the temperature. Other dependencies of the viscosity with the shear rate and the yield stress, typical of the non-Newtonian flow of solids, can be easily incorporated in the model, thus broadening its applicability to other materials.

2.3 Discretization of the equations

A key problem in the numerical solution of (1) – (4) is the satisfaction of the incompressibility condition (Eq.(2)). A number of procedures to solve this problem exist in the finite element literature [11]. In our approach, we use a stabilized formulation based on the so-called finite calculus procedure [16,17,18]. The essence of this method is the solution of a modified mass balance equation that is written as

${\partial v_{i} \over \partial x_{i}}+\sum \limits _{i=1}^{3}\tau \left[{\partial p \over \partial x_{i}}+\pi _{i}\right]=0$

(6)

where ${\textstyle \tau }$ is a stabilization parameter given by [17]

$\tau =\left({\frac {2\rho \vert \mathbf {v} \vert }{h}}+{\frac {8\mu }{3h^{2}}}\right)^{-1}$

(7)

In the above, ${\textstyle h}$ is a characteristic length of each finite element (such as ${\textstyle [A^{(e)}]^{1/2}}$ for 2D elements), and ${\textstyle \vert \mathbf {v} \vert }$ is the modulus of the velocity vector. Also in Eq.(5) ${\textstyle \pi _{i}}$ are auxiliary pressure projection variables chosen so as to ensure that in the second term in Eq.(6) ${\textstyle \pi _{i}}$ can be interpreted as a weighted sum of the residuals of the momentum equations and therefore it vanishes for the exact solution. The set of governing equations for the velocities, the pressure and the ${\textstyle \pi _{i}}$ variables is completed by adding the following constraint equation to the set of governing equations

$\int _{V}\tau w_{i}\left({\partial p \over \partial x_{i}}+\pi _{i}\right)dV=0\quad ,\quad i=1,n_{d}$

(8)

where ${\textstyle w_{i}}$ are arbitrary weighting functions.

The rest of the integral equations are obtained by applying the standard Galerkin technique to the governing equations (1), (2) and (3) and the appropriate boundary conditions for the numerical and thermal problems[8,10,11].

We interpolate in the standard finite element fashion the set of problem variables. For 3D problems these are the three velocities ${\textstyle v_{i}}$, the pressure ${\textstyle p}$, the temperature ${\textstyle T}$ and the three pressure gradient projections ${\textstyle \pi _{i}}$. In our work we use an equal order linear interpolation for all variables over meshes of 3-noded triangles (in 2D) and 4-noded tetrahedra (in 3D) [8,11,15]. The resulting set of discretized equations has the following form

Momentum

${\boldsymbol {M}}{\dot {\bar {\boldsymbol {v}}}}+{\boldsymbol {K}}(\mu ){\bar {\boldsymbol {v}}}-{\boldsymbol {G}}{\bar {\boldsymbol {p}}}={\boldsymbol {f}}$

(9)

Mass balance

${\boldsymbol {G}}^{T}{\bar {\boldsymbol {v}}}+{\boldsymbol {L}}{\bar {\boldsymbol {p}}}+{\boldsymbol {Q}}^{T}{\bar {\boldsymbol {\pi }}}={\boldsymbol {0}}$

(10)

Pressure gradient projections

${\hat {\boldsymbol {M}}}{\bar {\boldsymbol {\pi }}}+{\boldsymbol {Q}}^{T}{\bar {\boldsymbol {p}}}={\boldsymbol {0}}$

(11)

Heat transfer

${\boldsymbol {C}}{\dot {\bar {\boldsymbol {T}}}}+{\boldsymbol {H}}{\bar {\boldsymbol {T}}}={\boldsymbol {q}}$

(12)

In Eqs.(9) – (12) ${\textstyle {\bar {(\cdot )}}}$ denotes nodal variables, ${\textstyle {\dot {\bar {(\cdot )}}}={\frac {d}{dt}}{\bar {(\cdot )}}}$. The different matrices and vectors are given in the Appendix.

The solution in time of Eqs.(9) – (12) can be performed using any time integration scheme typical of the updated Lagrangian finite element method. A basic algorithm following the conceptual process described in Section 2.1 is presented in Box I [6,8,9,10,15]. In Box I ${\textstyle ^{t+1}{\bar {\boldsymbol {a}}}^{i+1}}$ denotes the values of the nodal variables ${\textstyle {\bar {\boldsymbol {a}}}}$ at time ${\textstyle t+\Delta t}$ and iteration ${\textstyle i+1}$. Note that the position of the analysis domain in the next equilibrium configuration at time ${\textstyle t+\Delta t}$ is also an output of the solution, as is typical in updated Lagrangian methods. We also recall the coupling of the flow and thermal equations via the dependence of the viscosity ${\textstyle \mu }$ with the temperature. The convergence of the solution process at each time step ensures the stability and consistency of the formulation. Within a time step (once the discretization is fixed) the mass and volume are conserved in a variational sense. Upon remeshing, the volume is not conserved in a strict sense, but the alpha-shape method provides such conservation in a statistical sense [6,8].

3 ACCOUNTING FOR GASIFICATION EFFECTS

The effect of gasification can be introduced by adding a (nonlinear) energy loss term in the energy equation. This term represents the energy that migrates from the condensed phase object to the gas due to the gasification of a part of the material during the heating process. The volumetric gasification heat flux has the following form

1. LOOP OVER TIME STEPS, $t=1$, NTIME

Known values

${~}^{t}{\bar {\boldsymbol {x}}},{~}^{t}{\bar {\boldsymbol {v}}},{~}^{t}{\bar {\boldsymbol {p}}},{~}^{t}{\bar {\boldsymbol {\pi }}},{~}^{t}{\bar {\boldsymbol {T}}},{~}^{t}\mu ,{~}^{t}{\boldsymbol {f}},{~}^{t}{\boldsymbol {q}},{~}^{t}C,{~}^{t}V,{~}^{t}M$

2. LOOP OVER NUMBER OF ITERATIONS, $i=1$, NITER

$\bullet$ Compute the nodal velocities by solving Eq. (9)

$\displaystyle \left[{\frac {1}{\Delta t}}{\boldsymbol {M}}+{\boldsymbol {K}}\right]{~}^{t+1}{\bar {\boldsymbol {v}}}^{i+1}={~}^{t+1}{\boldsymbol {f}}+{\boldsymbol {G}}{~}^{t+1}{\bar {\boldsymbol {p}}}^{i}+{\frac {1}{\Delta t}}{\boldsymbol {M}}{~}^{t}{\bar {\boldsymbol {v}}}$

$\bullet$ Compute nodal pressures from Eq.(10)

${\boldsymbol {L}}{~}^{t+1}{\bar {\boldsymbol {p}}}^{i+1}=-{\boldsymbol {G}}^{T}{~}^{t+1}{\bar {\boldsymbol {v}}}^{i+1}-{\boldsymbol {Q}}{~}^{t+1}{\bar {\boldsymbol {\pi }}}^{i}$

$\bullet$ Compute nodal pressure gradient projections from Eq. (11)

${~}^{t+1}{\bar {\boldsymbol {\pi }}}^{i+1}=-{\hat {\boldsymbol {M}}}_{D}[{\boldsymbol {Q}}^{T}]{~}^{t+1}{\bar {\boldsymbol {p}}}^{i+1}\quad ,\quad {\hat {\boldsymbol {M}}}_{D}=diag[{\hat {\boldsymbol {M}}}]$

$\bullet$ Compute nodal temperatures from Eq.(12)

$\displaystyle \left[{\frac {1}{\Delta t}}{\boldsymbol {C}}+{\boldsymbol {H}}\right]{~}^{t+1}{\bar {\boldsymbol {T}}}^{i+1}={~}^{t+1}{\boldsymbol {q}}-{\frac {1}{\Delta t}}{\boldsymbol {C}}{~}^{t}{\bar {\boldsymbol {T}}}$

$\bullet$ Update position of analysis domain nodes:

${~}^{t+1}{\bar {\boldsymbol {x}}}^{i+1}={~}^{t}{\boldsymbol {x}}^{i}+{~}^{t+1}{\boldsymbol {v}}^{i+1}\Delta t$

Define new “cloud” of nodes $^{t+1}{C}^{i+1}$

$\bullet$ Update viscosity values in terms of temperature

${~}^{t+1}\mu =\mu (^{t+1}{\bar {\boldsymbol {T}}}^{i+1})$

Check convergence for all variables $\to$ NO $\to$ Next iteration $i\to i+1$

$~~~~~~~~~~\downarrow$ YES

Next time step $t\to t+1$

$\bullet$ Identify new analysis domain boundary: $^{t+1}V$

$\bullet$ Generate mesh: ${~}^{t+1}M$

Go to 1

Box I. Flow chart of basic PFEM algorithm for the polymer domain

$q_{gas}=\rho H{\bar {\varepsilon }}_{v}$

(13)

where ${\textstyle H}$ is the enthalpy of vaporization,

${\bar {\varepsilon }}_{v}=f(T)$

(14)

where ${\textstyle f(T)}$ expresses the (generally nonlinear) relation between the rate of volume variation due to the temperature, ${\textstyle {\bar {\varepsilon }}_{v}}$, and the temperature itself. In our work, the following Arrhenius function is chosen, consistent with single-step, first-order thermal decomposition kinetics [4]

$f(T)=-Ae^{-{\frac {E}{RT}}}$

(15)

where ${\textstyle A}$ is the pre-exponential function, ${\textstyle E}$ is the activation energy, ${\textstyle R}$ is the universal gas constant, and ${\textstyle T}$ is the absolute temperature expressed in Kelvin.

Once the temperature field is known at each iteration of a time step, the rate of volume variation ${\textstyle {\bar {\varepsilon }}_{v}}$ is fixed at every point of the mesh. This allows defining a continuum distribution of the term ${\textstyle {\bar {\varepsilon }}_{v}}$ over the whole polymer domain.

The computed mass loss rate has to be included in the problem to ensure that the volume variation of the sample is correctly modeled. The approach is thus to solve the momentum and heat transfer equations, prescribing as constraints the local rate of volume variation and the gasification heat flux.

From a practical point of view this simply implies adding the gasification heat flux as an additional volumetric heat source term in vector ${\textstyle \mathbf {q} }$ in the heat transfer equations (see Appendix) and adding the volumetric deformation rate ${\textstyle {\bar {\varepsilon }}_{v}}$ into the stabilized mass balance equation (6) as

${\partial v_{i} \over \partial x_{i}}-{\bar {\varepsilon }}_{v}+\sum \limits _{i=1}^{3}\tau _{i}\left[{\partial p \over \partial x_{i}}+\pi _{i}\right]=0$

(16)

The new discretized mass balance equation is

${\boldsymbol {G}}^{T}{\bar {\boldsymbol {v}}}+{\boldsymbol {L}}{\bar {\boldsymbol {p}}}+{\boldsymbol {Q}}{\bar {\boldsymbol {\pi }}}={\boldsymbol {f}}_{g}$

(17)

where ${\textstyle {\boldsymbol {f}}_{g}}$ with ${\textstyle f_{g_{i}}=\int _{V^{e}}N_{i}{\bar {\varepsilon }}_{v}dV}$ is the forcing term contributed by the gasification heat flux.

An example of the effects of gasification will be shown in the following section.

4 NUMERICAL EXAMPLES

The examples were run in the PFIRE code in which the formulation described above has been implemented using the Kratos software platform [23].

4.1 Validation of the gasification model

A simple computational test has been chosen to verify the accuracy of the gasification algorithm.

A ${\textstyle 5\times 10}$ cms horizontal slab is insulated along its sides and bottom by an impermeable wall and is subjected to a heat flux of 30 kW/m${\textstyle ^{2}}$ acting on the free boundary. The properties of the material are shown in Table I. The analysis was carried out with several meshes of 3-noded triangles.

The example is approximately equivalent to a 1D gasification model for which the possibility exist of finding an accurate semi-analytical solution using Mathematica. The horizontal setup guarantees that the only mass loss is induced by the gasification term as no flow is allowed to leave the sample due to the presence of the impermeable boundaries [12].

The results of mass versus time for the different meshes considered are represented in Figure 3.

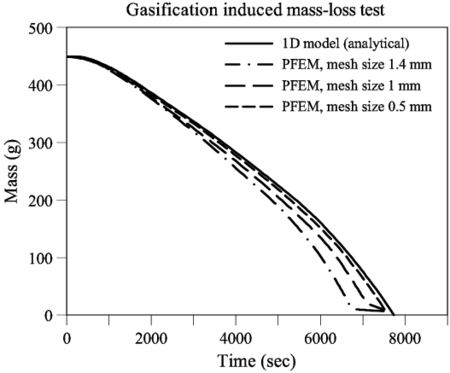
Figure 3: Gasification of a rectangular slab ($5\times 10$ cms) Analytical (1D model) and PFEM results for different mesh sizes.

Results for the finer mesh show a sufficiently close agreement between the numerical results and the analytical 1D solution, confirming the correctness of the gasification approach used.

Some screenshots of the sample geometry at different times for the finer mesh are shown in Figure 4.

Although the results are satisfactory, it is important to observe that a high mesh density is required in the vicinity of the free surface to capture accurately the analytical solution. This is due to the sharp gradient exhibited by the Arrhenius function in the proximity of the free surface, which needs to be accurately resolved. Such situation calls for an adaptive mesh refinement algorithm. This possibility will be implemented in forthcoming works.

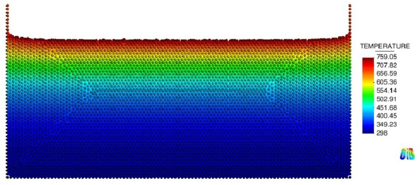
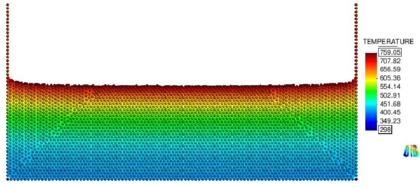
Figure 4: Gasification of a heated slab. Initial geometry and mesh and slab shapes at 2000s, 4000s and 6000s after onset of gasification.

4.2 Melting and flow of a rectangular slab

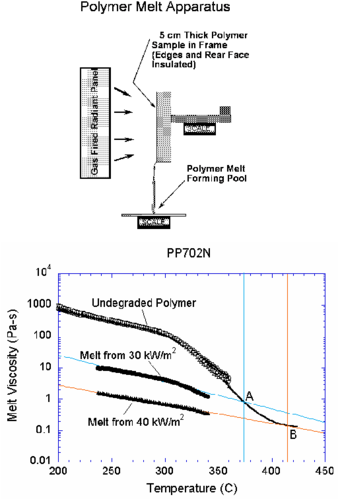
In the next example shown, the PFEM is used to simulate an experiment performed at NIST in which a slab of polymeric material is mounted vertically and exposed to uniform radiant heating on one face. Degradation of the polymer decreases its viscosity by several orders of magnitude and produces fuel gases. Polymer melt is captured by a pan below the sample.

A schematic of the apparatus used in the experiments is shown in Figure 5. A rectangular polymeric sample of dimensions 10 cm high by 10 cm wide by 5 cm thick is mounted upright and exposed to uniform heating on one face from a radiant cone heater placed on its side. The sample is insulated on its lateral and rear faces. The melt flows down the heated face of the sample and drips onto a surface below. A load cell monitors the mass of polymer remaining in the sample, and a laboratory balance measures the mass of polymer falling onto the catch surface. Details of the experimental setup are given in previous publications [4,?,13]. The first computational representation of this problem is a 2-D rectangle with steady heat flux applied to one side and adiabatic and no-slip conditions applied to the opposite side, top and bottom. The heated side is defined as a free surface, and is subject to radiative and convective losses. Gasification is not considered in this first example. Material properties except for viscosity are taken as constant, with values as given in Table I.

For polymer melts, viscosity is a function of both temperature and molecular weight distribution, which changes as the polymer bonds break during heating. This model uses an approach that incorporates this degradation into a simple description of viscosity as a function of temperature alone [22]. Figure 5 shows three curves of viscosity vs. temperature for the polypropylene type PP702N, a low viscosity commercial injection molding resin formulation. The relationship used in the model, as shown by the black line, connects the curve for the undegraded polymer to points A and B extrapolated from the viscosity curve for each melt sample to the temperature at which the sample was formed. The viscosity at room temperature is set to ${\textstyle 10^{6}}$ Pa-s to maintain rigidity, and viscosity changes linearly between ${\textstyle T=25}$ ${\textstyle ^{\circ }}$C and ${\textstyle T=200}$ ${\textstyle ^{\circ }}$C. The result is an empirical viscosity-temperature curve that implicitly accounts for molecular weight changes. The analytical definition of this curve is given in Box II.

Figure 5: Polymer melt experiment. Viscosity vs. temperature for PP702N polypropylene in its initial undegraded form and after exposure to 30 kW/m$^{2}$ and 40 kW/m$^{2}$ heat fluxes. The black curve follows the extrapolation of viscosity to high temperatures.

An initial spacing of 2.0 mm between nodes results in a finite element model of 1537 nodes and 2818 three-noded triangular elements for a 2D representation of the geometry, while a spacing of 1.4 mm results in 3098 nodes and 5832 elements. No nodes are added during the course of the analysis in this and all the other examples shown in the paper.

The addition of a catch pan to capture the dripping polymer melt tests the ability of the PFEM model to recover mass when a particle or set of particles reaches the catch surface. For this problem, heat flux was only applied to free surfaces above the midpoint between the catch pan and the base of the sample. However, every free surface is subject to radiative and convective heat losses. The problem was studied for three heat flux levels of 20, 30 and 40 kW/m${\textstyle ^{2}}$. The catch pan is set to 250 ${\textstyle ^{\circ }}$C, a temperature that is high enough to keep the melt fluid. The thickness of the sample is reduced to 2.5 cm to achieve results more quickly, and the height of 25 cm reflects the dimensions of an earlier experiment [22].

Table. 1 Parameter values for polypropylene type PP702N taken from [22]. The value of $\epsilon =1.0$ for the emissivity has been assumed

Parameter	Symbol	Value	Units
Density	$\rho$	900	kg/m${\textstyle ^{3}}$
Thermal conductivity	$k$	0.25	W/m-K
Specific heat	$c$	2400	J/kg-K
Reference temperature	$T_{0}$	298	K
Emissivity	$\epsilon$	1.0	-
Convective heat transfer coefficient	$\alpha _{c}$	8	W/m${\textstyle ^{2}}$-K
Heat of vaporization	$H$	$8\times 10^{5}$	J/kg
Pre-exponential function	$A$	$2.18\times 10^{12}$	s${\textstyle ^{-1}}$
Activation energy divided by universal
gas constant	$E/R$	24400	K
Stefan-Boltzmann constant	$\sigma$	5.67${\textstyle \times 10^{-8}}$	W/m${\textstyle ^{2}}$- K${\textstyle ^{4}}$

Tc: Temperature in degrees Celsius; T: Temperature in Kelvins

def f1(Tc):
    return 10**(14.48 - 0.13858*Tc + 5.5960e-4*Tc*Tc - 7.8665e-7*Tc*Tc*Tc)

def f2(Tc):
    return 10**(53.19 - 0.2542*Tc + 2.9879e-4*Tc*Tc)

def AuxFunction(T):

    Tc = T - 273
    if( Tc <= 25):
        mu = 1e6
    elif (Tc > 25 and  Tc <= 200):
          mu = 1e6*(200-Tc)/175 + f1(200)
    elif(Tc > 200 and Tc <= 350):
         mu = f1(Tc)
    elif(Tc > 350 and Tc < 425 ):
         mu = f2(Tc)
    else:
         mu = f2(425)

    return mu

Box II. Definition of the viscosity-temperature dependence for the polymer melt experiment of Figure 5

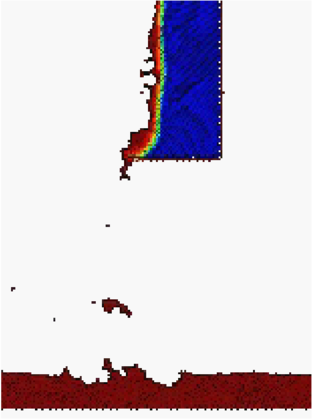
Figure 6a shows four snapshots of the time evolution of the melt flow into the catch pan using the finer grid and a heat flux level of 20 kW/m${\textstyle ^{2}}$. A detail of the flow of the melt as it drips into the pan at two different times is shown in Figure 6b.

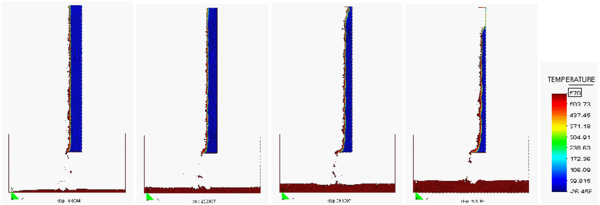
Figure 6.(a): Evolution of the melt flow into the catch pan at t = 400s, 550s, 700s and 1000s

Figure 6. (b): Detail of the flow of the melt as it drips into the pan at $t=550$ and 1000s

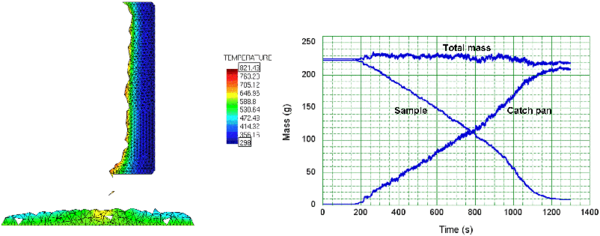
Figure 7 (left) shows the flow into the catch pan at time ${\textstyle t=600}$ s. Directly below the base of the sample where the melt is dripping, the temperature of the melt is higher. On the catch pan away from this point, the top of the melt has cooled below 325 ${\textstyle ^{\circ }}$C, the temperature of the catch pan surface in this case. The melt spreads to either side from the point at which the dripping melt contacts the catch pan.

Figure 7 (right) shows the mass of the sample, the mass of the melt on the catch pan, and their sum. After a heating time of about 170 s, the mass begins to be transferred from the sample to the catch pan. The total mass reflects a conservation of mass within ${\textstyle \pm 5\%}$. Note that because of the way nodes are eliminated and recreated at surfaces in the PFEM, the total mass at times exceeds 100% of the initial mass. Holes in the melt flow on the catch plate are occasionally generated by the Alpha-Shape method. Both types of error can be reduced by increasing the number of particles (nodes), as in the standard FEM.

Figure 7: Melt flow into catch pan at t = 600s. Mass vs time for polymer in sample, in catch pan, and total mass

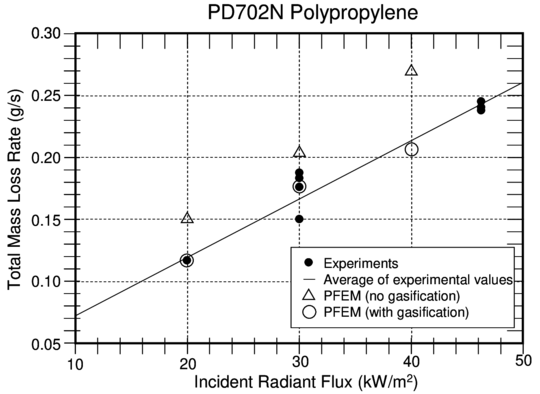
Figure 8 compares the mass loss rate of the quasi-steady period with that obtained from experiments at three levels of heat flux performed at NIST [22]. The mass loss rate follows the same trend, although the values are about 25% higher than the experimental data. Note that this solution includes only melt flow in response to heating at a steady heat flux with radiative and convective losses.

4.3 Inclusion of gasification effects

The same problem was solved next including gasification effects. The parameters in the gasification heat flux model chosen for the computations (Eqs.(13) – (15)) are given in Table I.

The general trend of the numerical results including gasification is not very different from the results shown in Figures 6 and 7. Gasification effects however have an influence on the mass loss rate.

Results for the mass loss rate including gasification are also plotted in Figure 8. The computational results fall within experimental error for the range of heat fluxes considered. This shows the importance of accounting for gasification effects in this type of problem. The decrease in mass loss rate when gasification is added to flow demonstrates two competing effects: the loss of additional mass as gas is released and the cooling caused by the endothermic process of polymer decomposition.

Note that this model is not yet complete, since phenomena such as in-depth absorption, the melting of the crystalline fraction of the polymer, and the temperature dependence of other material properties are not yet included. However, these phenomena are not difficult to add to the model and will be included in future development.

The solution of this melt flow problem took 2 CPU hours in a standard Pentium 4 PC.

Figure 8: Comparison of PFEM results to experiments for mass loss rate as a function of incident radiant flux

4.4 3D polymer melt flow

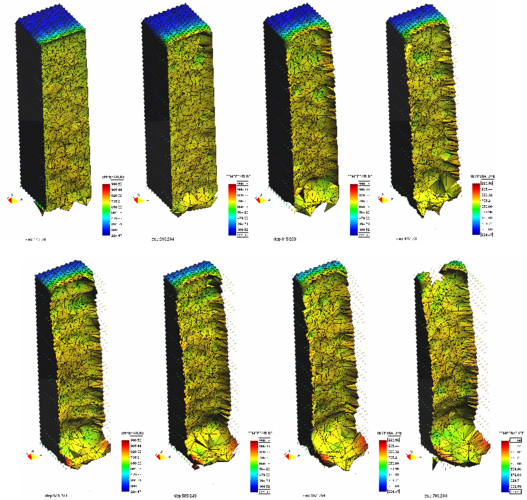
To test the ability of the PFEM to solve polymer melt flow problems in three dimensions, a 3D heated sample was studied. The same boundary conditions are used as in the 2D problem illustrated in Figure 5, but the initial dimensions of the sample are reduced to ${\textstyle 10}$ cm ${\textstyle \times 10}$ cm ${\textstyle \times 2.5}$ cm thick. The initial discretization has 22475 nodes and 97600 four-noded tetrahedra, and the runtime for this problem was slightly over 8 hours in a Pentium 4 PC. The shape of the surface and temperature field at different times after heating begins are shown in Figure 9.

Figure 9: Solution of a 3D polymer melt problem with the PFEM. Melt flow from a heated prismatic sample at different times.

Edge effects in the 3D model slow the rate of flow along the side walls, resulting in a thicker sample there throughout the melt flow process. This has also been observed in the experiments. Although the resolution for this problem is not fine enough to achieve high accuracy, the qualitative agreement of the 3D model with 2D flow and the ability to carry out this problem in a reasonable amount of time indicate that the PFEM can be used to model melt flow and spread of complex 3D polymer geometry.

4.5 Melting and flow of a triangular slab

Figure 10 shows results for the analysis of the melting of a triangular thermoplastic object with a base of ${\textstyle 5}$ cm and a height of ${\textstyle 5\times 5}$ cms. The solution is symmetrical about the ${\textstyle x=0}$ axis. All free surfaces are heated at a heat flux of 30 kW/m${\textstyle ^{2}}$. The material properties for the polymer are the same as for the previous 2D example. The potential of the PFEM for simulating the progressive detachment and flow of the polymer particles from the object surface towards the underlying floor is clearly demonstrated.

A similar but more complex analysis is shown in Figure 11. Here the problem is the simulation of the melt flow of the same triangular thermoplastic object into a catch pan. The PFEM succeeds in predicting in a very realistic manner the progressive melting and slip of the polymer particles along the vertical wall separating the triangular object and the catch pan. The analysis follows until the whole object has fully melted and its mass is transferred to the catch pan. The total mass was preserved with an accuracy of 0.5% in both these studies. Gasification, in-depth absorption and radiation were not taken into account in these examples.

Figure 10: Simulation of the melt flow of a heated triangular thermoplastic object

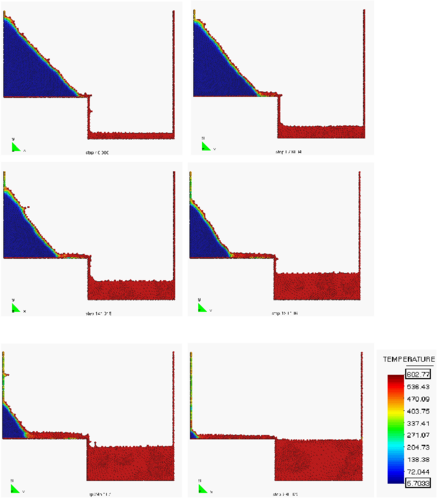
Figure 11: Melt flow of a heated triangular object into a catch pan

4.6 Study of melt spread

In the 2D PFEM model of the melt spread experiment, the initial computational space is an upright rectangle representing the thermoplastic object mounted above a rectangular catch plate, as illustrated in Figure 12. The catch plate may be tilted with respect to the horizontal line, although the catch plate always extends along the x-axis for ease of defining the distinction between the melt belonging to the object and that in the melt pool.

The left surface of the object and the top surface of the catch plate are designated as free surfaces, which are subject to heat losses from radiation and convection. A steady heat flux is applied only to the free surface of the object, whose drips are distinguished from the melt on the catch plate by location above a specified height. All other faces in the problem, identified by dark lines in Figure 12, obey no-slip conditions. These faces are adiabatic, except for the bottom surface of the catch plate, which is maintained at a fixed heater temperature of ${\textstyle 235}$ ${\textstyle ^{\circ }}$C. The thermoplastic object is initially at room temperature, and the linear temperature distribution within the catch plate balances the heat losses from the upper surface. The temperature of the top surface, given the heater temperature and the thermal conductivity of the catch plate, was found to agree with the experimental value [21].

Thermophysical material properties for the polymer are the same as for the other examples in this paper. The viscosity of the dripping object follows the curve for the undegraded polymer in Figure 5. For the flow of melt on the catch plate, a straight line is fitted to the viscosity-temperature relationship for this polymer after it has been degraded at a heat flux of 22 kW m${\textstyle ^{2}}$. This relationship is obtained by rheological measurements of the melt deposited on the catch plate, and is not shown in Figure 5. The ceramic catch plate is assigned the thermal properties reported by the manufacturer. Neither gasification, in-depth absorption, nor radiation were taken into account in this study.

The spatial resolution of the finite element mesh is initially uniform throughout the thermoplastic object. Results are reported for a grid with initial spacing of 1.0 mm. For the catch plate, the mesh size at the top surface must be small enough to catch the particles dripping from the object, but the mesh can be coarser further in-depth since only thermal diffusion needs to be resolved.

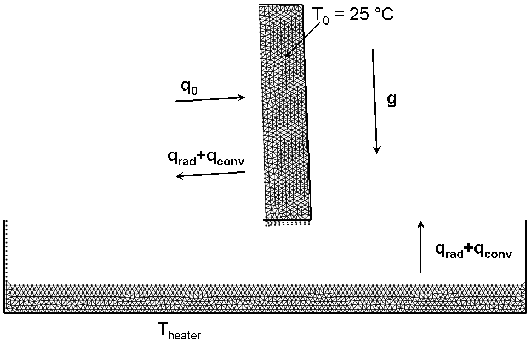
Figure 12: Initial conditions for melt spread problem

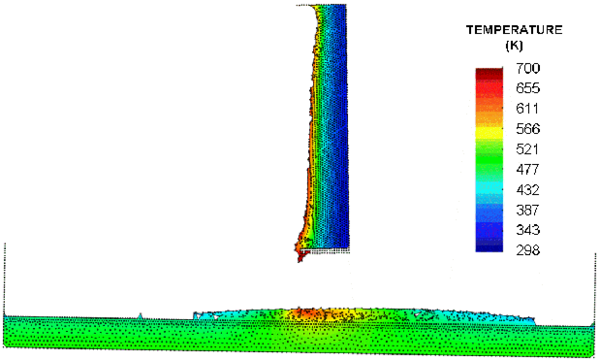
Figure 13 shows a snapshot of flow onto a horizontal catch plate at time ${\textstyle t=600}$ s. Directly below the base of the object where the polymer melt is dripping, the temperature of the melt pool is around 340 ${\textstyle ^{\circ }}$C. This equals the set temperature of the melt feeder used in the experiments. The temperature of the melt pool cools as it flows away from the line of dripping and loses heat to the catch plate and to the surroundings. At far enough distances the surface temperature of the melt pool drops below the temperature of the catch plate. If the plate was not heated, the polymer would continue to cool, until its viscosity may be high enough to interfere with the flow.

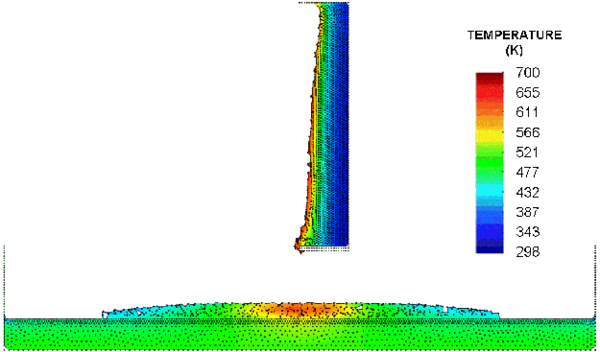
Figure 13: Thermoplastic object dripping into horizontal catch pan at $t=600$ s

Figure 14 shows the evolution of the melt pool with time as the object continues to drip. The spread rate is determined by a balance between the potential energy caused by the accumulation of melt under the drip line, the kinetic energy of the flow and the viscous drag on the melt as it moves over the catch plate.

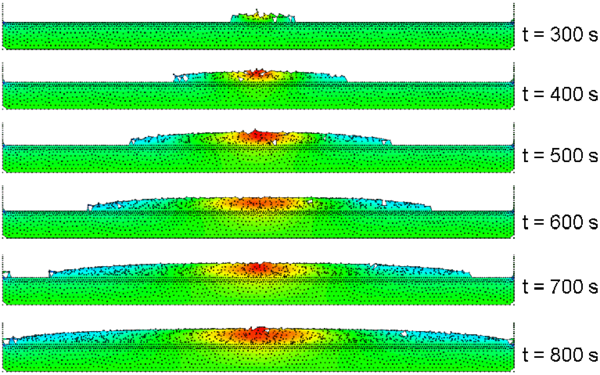
Figure 14: Spread of melt pool over horizontal catch plate

In Figure 15 the catch plate has been tilted at an angle of 1.8 degrees. The slope of the plate adds to the potential energy of the melt, and the spread rate increases in the downslope direction while it decreases in the upstream direction where the accumulation of fluid must counter the potential energy due to the slope. A study of the movement of the melt front with time for horizontal and tilted catch plates is reported in [21]. PFEM spread rates are within ${\textstyle 10\%}$ of experimental results when the continuing degradation over the surface of the heated catch plate is taken into account.

Figure 15: Thermoplastic object dripping into tilted catch plate at $t=600$ s

4.7 Melting of a thermoplastic chair

This example and the example that follows demonstrate the capabilities of the PFEM to model the fire behavior of polymers of more complex shapes.

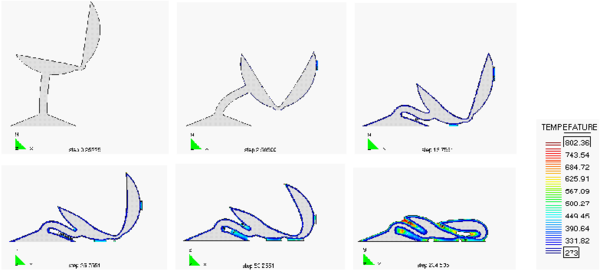
The example shown in Figure 16 is the simulation of the melt flow of a thermoplastic object resembling a chair modeled as a 2D solid. The images show the progressive melting of the chair exposed to a heat flux of 30 kW/m${\textstyle ^{2}}$ on all surfaces except the base. The ability of the PFEM to model self-contact situations as the shape of the chair changes with time due to melting is demonstrated.

Figure 16: Melting of a heated chair modeled as a 2D object. Note self-contact between chair surfaces as melting evolves

4.8 Melting of a candle

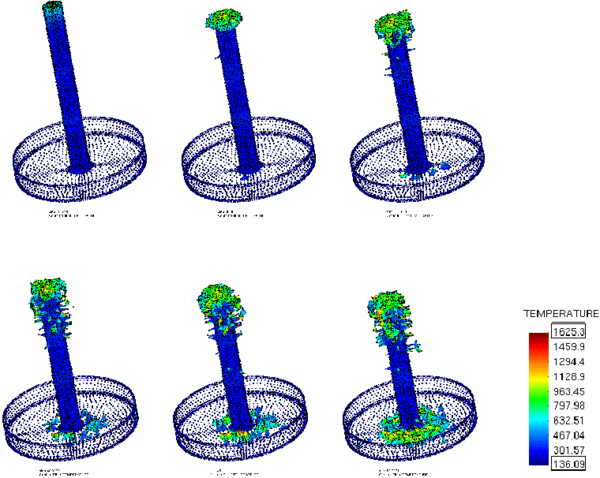
The last example shown in Figure 17 and 18 is the simulation of the melting of a cylindrical candle. Heat flux is applied at the top surface of the candle at a rate of 30 KW/m${\textstyle ^{2}}$. This induces the progressive melting and dripping of the candle particles along the cylindrical wall until they eventually hit and spread over the underlying pan surface.

Figure 17: Melting of a cylindrical candle with the PFEM

Figure 18: Melting of candle. Detail of melted zone and pan surface at a certain instant

5 CONCLUDING REMARKS

The PFEM is a powerful technique to model the melting, flow and flame spread of thermoplastic objects in fire situations. The method allows to track the motion of the polymer particles as they melt, flow over the surface of the object and fall towards and on the underlying floor. The PFEM can also predict the spread of the flame in the floor for different ambient temperature conditions and effect of gasification, in-depth absorption and radiation problems.

The simulation of the melting of a simplified chair of arbitrary shape and a candle has shown the potential of the PFEM to model the drastic change of shape of objects as they melt, drip and spread, including self-contact situations.

Developments in progress include coupling the PFEM formulation with the surrounding hot air and the external heat source, inclusion of elastic effects in the polymer material and increasing the computational efficiency of the method.

ACKNOWLEDGMENTS

The authors thank Dr. T. Ohlemiller at NIST for providing experimental results for the 2D rectangular slab problem [22]. Special thanks are given to Mr. P. Ryzhakov and to Drs. J. Marti and F. del Pin from CIMNE for their advice during this research. The support of Dr. P. Dadvand in the development of the PFIRE code using the Kratos software platform [23] is acknowledged.

REFERENCES

[1] Zhang J, Shields TJ, Silcock GWH. Effect of melting behaviour on flame spread of thermoplastics. Fire & Materials 1997; 21(1):1–6.

[2] Fleischmann CM, Hill GR. Burning behaviour of upholstered furniture. Interflam 2004; 907–916.

[3] Sherratt J, Drysdale D. The effect of the melt-flow process on the fire behaviour of thermoplastics. Interflam 2001; 149–159.

[4] Butler KM, Ohlemiller TJ, Linteris GT. A progress report on numerical modeling of experimental polymer melt flow behavior. Interflam 2004; pp. 937–948.

[5] Idelsohn SR, Oñate E, Del Pin F. A lagrangian meshless finite element method applied to fluid-structure interaction problems. Computer and Structures 2003b; 81:655–671.

[6] Idelsohn SR, Oñate E, Del Pin F. The particle finite element method: a powerful tool to solve incompressible flows with free-surfaces and breaking waves. International Journal for Numerical Methods in Engineering 2004; 61:964–989.

[7] Idelsohn SR, Oñate E, Calvo N, Del Pin F. The meshless finite element method. International Journal for Numerical Methods in Engineering 2003a; 58(6): 893–912.

[8] Oñate E, Idelsohn SR, Del Pin F, Aubry R. The particle finite element method. An overview. International Journal of Computational Methods 2004; 1(2):267–307.

[9] Aubry R, Idelsohn SR, Oñate E. Particle finite element method in fluid-mechanics including thermal convection-diffusion. Computers and Structures 2005; 83(17-18):1459–1475.

[10] Aubry R, Idelsohn SR, Oñate E. Fractional step like schemes for free surface problems with thermal coupling using the Lagrangian PFEM. Computational Mechanics 2006; 38(4-5):294–309.

[11] Oñate E, Idelsohn SR, Celigueta MA, Rossi R. Advances in the particle finite element method for the analysis of fluid-multibody interaction and bed erosion in free surface flows. Computer Methods in Applied Mechanics and Engineering 2008; 197(19-20):1777–1800.

[12] Butler KM, Oñate E, Idelsohn SR, Rossi R. Modeling polymer melt flow using the particle finite element method. 11th International Interflam Conference (Interflam'07), September 3–5 2007, London, England, Volume 2, pp. 929–940.

[13] Rossi R, Butler KM, Oñate E, Idelsohn SR. Modeling polymer melt flow using the Particle Finite Element Method. Advanced Research Workshop on Fire Computer Modeling, Gijón, Spain, October 18-20, 2007.

[14] Edelsbrunner H, Mucke EP. Three dimensional alpha shapes. ACM Trans. Graphics 1999; 13:43–72.

[15] Zienkiewicz OC, Taylor RL, Nithiarasu N. The Finite Element Method. Vol. 3 Fluid Mechanics, Elsevier, 2005.

[16] Oñate E. Derivation of stabilized equations for numerical solution of advective-diffusive transport and fluid flow problems. Computer Methods in Applied Mechanics and Engineering 1998; 151:233-265.

[17] Oñate E. A stabilized finite element method for incompressible viscous flows using a finite increment calculus formulation. Computer Methods in Applied Mechanics and Engineering 2000; 182(3-4):355-370.

[18] Oñate E. Possibilities of finite calculus in computational mechanics. International Journal for Numerical Methods in Engineering 2004; 60(1):255–281.

[19] Zienkiewicz OC, Jain P C, Oñate E. Flow of solids during forming and extrusion: Some aspects of numerical solutions. International Journal of Solids and Structures 1978; 14:15–38.

[20] Zienkiewicz OC, Oñate E, Heinrich JC. A general formulation for the coupled thermal flow of metals using finite elements. International Journal for Numerical Methods in Engineering 1981; 17:1497–1514.

[21] Butler KM. A model of melting and dripping thermoplastic objects in fire. Fire and Materials 2009, San Francisco, USA, January 26–28, 2009, pp. 341–352.

[22] Ohlemiller TJ, Shields JR. Aspects of the Fire Behavior of Thermoplastic Materials. NIST Technical Note 1493 2008.

[23] Davdand P, Rossi R, Oñate E. An object-oriented environment for developing finite element codes for multi-disciplinary applications. Archives of Computational Methods in Engineering 2009, accepted for publication.

APPENDIX

The matrices and vectors in Eqs.(9) – (12) for a 4-noded tetrahedron are:

$\mathbf {M} _{ij}=\int _{V^{e}}\rho \mathbf {N} _{i}^{T}\mathbf {N} _{j}dV\quad ,\quad \mathbf {K} _{ij}=\int _{V^{e}}\mathbf {B} _{i}^{T}\mathbf {D} \mathbf {B} _{j}dV$

$\mathbf {G} _{ij}=\int _{V^{e}}\mathbf {B} _{i}^{T}\mathbf {m} \mathbf {N} _{j}dV\quad ,\quad \mathbf {f} _{i}=\int _{V^{e}}\mathbf {N} _{i}^{T}\mathbf {b} dV+\int _{\Gamma ^{e}}\mathbf {N} _{i}^{T}\mathbf {t} d\Gamma$

${L}_{ij}=\int _{V^{e}}{\boldsymbol {\nabla }}^{T}N_{i}\tau {\boldsymbol {\nabla }}N_{j}dV\quad ,\quad {\boldsymbol {\nabla }}=\left[{\partial \over \partial x_{1}},{\partial \over \partial x_{2}},{\partial \over \partial x_{3}}\right]^{T}$

${\boldsymbol {Q}}=[{\boldsymbol {Q}}_{1},{\boldsymbol {Q}}_{2},{\boldsymbol {Q}}_{3}]\quad ,\quad [\mathbf {Q} _{k}]_{ij}=\int _{V^{e}}\tau _{k}{\partial N_{i} \over \partial x_{k}}\mathbf {N} _{j}dV\quad ,\quad {\hbox{no sum in }}k$

${\hat {\boldsymbol {M}}}=\left[{\hat {\boldsymbol {M}}}_{1},{\hat {\boldsymbol {M}}}_{2},{\hat {\boldsymbol {M}}}_{3}\right]\,,\,[{\hat {\boldsymbol {M}}}_{i}]_{kl}=\left(\int _{V^{e}}\tau _{k}{\boldsymbol {N}}_{i}{\boldsymbol {N}}_{j}dV\right)\delta _{kl}\quad ,\quad k,l=1,2,3$

${\boldsymbol {B}}=[{\boldsymbol {B}}_{1},{\boldsymbol {B}}_{2},{\boldsymbol {B}}_{3},{\boldsymbol {B}}_{4}];\,{\boldsymbol {B}}_{i}=\left[{\begin{matrix}\displaystyle {\partial N_{i} \over \partial x}&0&0\\0&\displaystyle {\partial N_{i} \over \partial y}&0\\0&0&\displaystyle {\partial N_{i} \over \partial z}\\\displaystyle {\partial N_{i} \over \partial y}&\displaystyle {\partial N_{i} \over \partial x}&0\\\\\displaystyle {\partial N_{i} \over \partial z}&0&\displaystyle {\partial N_{i} \over \partial x}\\\\0&\displaystyle {\partial N_{i} \over \partial z}&\displaystyle {\partial N_{i} \over \partial y}\end{matrix}}\right];\,\,{\boldsymbol {D}}=\mu \left[{\begin{matrix}2&0&0&0&0&0\\0&2&0&0&0&0\\0&0&2&0&0&0\\0&0&0&1&0&0\\0&0&0&0&1&0\\0&0&0&0&0&1\end{matrix}}\right]$

${\boldsymbol {N}}=[{\boldsymbol {N}}_{1},{\boldsymbol {N}}_{2},{\boldsymbol {N}}_{3},{\boldsymbol {N}}_{4}]\quad ,\quad {\boldsymbol {N}}_{i}={N}_{i}{\boldsymbol {I}}_{3}\quad ,\quad {\boldsymbol {I}}_{3}\quad {\hbox{is the }}3\times 3{\hbox{ unit matrix}}$

${C}_{ij}=\int _{V^{e}}\rho {c}{N}_{i}{N}_{j}dV\quad ,\quad {H}_{ij}=\int _{V^{e}}{\boldsymbol {\nabla }}^{T}{\boldsymbol {N}}_{i}[k]{\boldsymbol {\nabla }}{\boldsymbol {N}}_{j}dV$

$[k]=\left[{\begin{matrix}k_{1}&0&0\\0&k_{2}&0\\0&0&k_{3}\end{matrix}}\right]\quad ,\quad q_{i}=\int _{V^{e}}N_{i}(Q+q_{gas})dV-\int _{\Gamma _{q}^{e}}N_{i}{\bar {q}}_{n}d\Gamma$

In above equations indexes ${\textstyle i,j}$ run from 1 to the number of element nodes (4 for a tetrahedron), ${\textstyle q_{n}}$ is the heat flow prescribed at the external boundary ${\textstyle \Gamma }$, t is the surface traction vector ${\textstyle \mathbf {t} =[t_{x},t_{y},t_{z}]^{T}}$ and ${\textstyle V^{e}}$ and ${\textstyle \Gamma ^{e}}$ are the element volume and the element boundary, respectively.