Membrane Structures Formed by Low Pressure Inflatable tubes. New Analysis Methods and Recent Constructions

Published in Textile Composites and Inflatable Structures II, E. Oñate and B. Kröplin (eds.), pp. 163-196, 2008
DOI: 10.1007/978-1-4020-6856-0

Abstract

This paper shows applications of a recently developed thin shell element adequate for the analysis of membrane and inflatable structures. The element is a three node triangle with only translational degrees of freedom that uses the configuration of the three adjacent elements to evaluate the strains in terms of the nodal displacements only. This allows to compute (constant) bending strains and (linear) membrane strains using a total Lagrangian formulation. Several examples, including inflation and deflation of membranes and some practical applications to the analysis, design and construction of membrane structures formed by low pressure inflatable tubes are presented.

Keywords shell elements, rotation free shell triangle, membrane structures, inflatable structures, low pressure inflatable tubes

1 Introduction

Inflatable structures have unique features. Because of their foldability and air- or helium pneumatic stabilisation they cannot be compared to any classical structural concepts.

Inflatable structures have become increasingly popular in recent years for a wide range of applications in architecture, civil engineering, aeronautic and airspace situations.

The use of inflatable structures can be found in temporary and/or foldable structures to cover large spaces or to support other elements, in permanent roofs or shelters with a high degree of transparency, in mobile buildings as temporary housing in civil logistic missions (e.g. environmental disasters and rescue situations), in the construction of tunnels and dams, in antennas for both ground and aerospace applications, as well as in extremely light airship structures among other uses [1-11].

Some efforts have been made in the past years to develop inflated structures formed by assembly of high pressure tubes. The obvious disadvantages of these structures are the design of the joints and their big vulnerability to air losses. In general, high pressure inflated structures are difficult to maintain and repair and have a high cost.

Inflatable structures formed by an assembly of self-supported low pressure tubular membrane elements are ideal to cover large space areas. They also adapt easily to any design shape and have minimal maintenance requirements, other than keeping a constant low internal pressure accounting for the air losses through the material pores and the seams.

The simulation of the inflation of membrane structures is normally performed with membrane finite elements, i.e. no bending stiffness included. The formulation of such elements is simple as they only require ${\textstyle C^{0}}$ continuity [12], in contrast with elements based on thin shell theory where ${\textstyle C^{1}}$ continuity implies important obstacles [13] in the development of conforming elements. Triangular elements are naturally preferred as they can easily adapt to arbitrary geometries and due to the robustness of the associated mesh generators.

Membrane structures components have some, although small, bending stiffness that in most cases is disregarded. However in many applications it is convenient to include bending energy in the model due to the important regularization effect it introduces. Shell elements are typically more complex and expensive due the increase in degrees of freedom (rotations) and integration points (through the thickness). In the last few years shell elements without rotation degrees of freedom have been developed [14-22], which make shell elements more efficient for both implicit and explicit integration schemes.

When only the final configuration of the membrane is of interest implicit schemes are normally used, including special algorithms due to the lack of stiffness of the membrane when no tensile stresses are yet present. When the inflation/deflation process is of interest, the explicit integration of the momentum equations is largely preferred. Modeling of complex deformation with constant strain shell triangles, such as those occuring in the inflation-deflation process of inflatable membranes accounting for frictional contact conditions typically require fine discretizations. These type of simulations can be time consuming due to the time increment limitations. In this paper a rotation-free triangular shell element with similar convergence properties to the linear strain triangle, but without its drawbacks, is used.

The outline of this chapter is as follows. Next two section summarizes the rotation-free shell triangle used. Section 4 summarices the procedure for aeroelastic analysis. Section 5 presents examples of application to the analysis of inflatable membranes. The paper concludes with practical examples inflatable structures formed by low pressure inflatable tubes designed and analyzed using the technology described in the paper. Finally Section 6 summarizes some conclusions.

2 Formulation of the Rotation Free Shell Triangle

2.1 Shell Kinematics

A summary of the most relevant hypothesis related to the kinematic behaviour of a thin shell are presented. Further details may be found in the wide literature dedicated to this field [21-23].

Consider a shell with undeformed middle surface occupying the domain ${\textstyle \Omega ^{0}}$ in ${\textstyle R^{3}}$ with a boundary ${\textstyle \Gamma ^{0}}$. At each point of the middle surface a thickness ${\textstyle h^{0}}$ is defined. The positions ${\textstyle \mathbf {x} ^{0}}$ and ${\textstyle \mathbf {x} }$ of a point in the undeformed and the deformed configurations can be respectively written as a function of the coordinates of the middle surface ${\textstyle {\boldsymbol {\varphi }}}$ and the normal ${\textstyle \mathbf {t} _{3}}$ at the point as

$\mathbf {x} ^{0}\left(\xi _{1},\xi _{2},\zeta \right)={\boldsymbol {\varphi }}^{0}\left(\xi _{1},\xi _{2}\right)+\lambda \mathbf {t} _{3}^{0}$ (1) $\mathbf {x} \left(\xi _{1},\xi _{2},\zeta \right)={\boldsymbol {\varphi }}\left(\xi _{1},\xi _{2}\right)+\zeta \lambda \mathbf {t} _{3}$ (2)

where ${\textstyle \xi _{1},\xi _{2}}$ are arc-length curvilinear principal coordinates defined over the middle surface of the shell and ${\textstyle \zeta }$ is the distance from the point to the middle surface in the undeformed configuration. The product ${\textstyle \zeta \lambda }$ is the distance from the point to the middle surface measured on the deformed configuration. The parameter ${\textstyle \lambda }$ relates the thickness at the present and initial configurations as:

$\lambda ={\frac {h}{h^{0}}}$

(3)

This approach implies a constant strain in the normal direction. Parameter ${\textstyle \lambda }$ will not be considered as an independent variable and will be computed from purely geometrical considerations (isochoric behaviour) via a staggered iterative update. Besides this, the usual plane stress condition of thin shell theory will be adopted.

A convective system is computed at each point as

$\mathbf {g} _{i}\left(\mathbf {\xi } \right)={\frac {\partial \mathbf {x} }{\partial \xi _{i}}}\qquad i=1,2,3$ (4) $\mathbf {g} _{\alpha }\left(\mathbf {\xi } \right)={\frac {\partial \left(\mathbf {\boldsymbol {\varphi }} \left(\xi _{1},\xi _{2}\right)+\zeta \lambda \mathbf {t} _{3}\right)}{\partial \xi _{\alpha }}}={\boldsymbol {\varphi }}_{^{\prime }\alpha }+\zeta \left(\lambda \mathbf {t} _{3}\right)_{^{\prime }\alpha }\quad \alpha =1,2$ (5) $\mathbf {g} _{3}\left(\mathbf {\xi } \right)={\frac {\partial \left(\mathbf {\boldsymbol {\varphi }} \left(\xi _{1},\xi _{2}\right)+\zeta \lambda \mathbf {t} _{3}\right)}{\partial \zeta }}=\lambda \mathbf {t} _{3}$ (6)

This can be particularized for the points on the middle surface as

$\mathbf {a} _{\alpha }=\mathbf {g} _{\alpha }\left(\zeta =0\right)={\boldsymbol {\varphi }}_{^{\prime }\alpha }$ (7) $\mathbf {a} _{3}=\mathbf {g} _{3}\left(\zeta =0\right)=\lambda \mathbf {t} _{3}$ (8)

The covariant (first fundamental form) metric tensor of the middle surface is

$a_{\alpha \beta }=\mathbf {a} _{\alpha }\cdot \mathbf {a} _{\beta }={\boldsymbol {\varphi }}_{^{\prime }\alpha }\cdot {\boldsymbol {\varphi }}_{^{\prime }\beta }$

(9)

The Green-Lagrange strain vector of the middle surface points (membrane strains) is defined as

${\boldsymbol {\varepsilon }}_{m}=[\varepsilon _{m_{11}},\varepsilon _{m_{12}},\varepsilon _{m_{12}}]^{T}$

(10)

with

$\varepsilon _{m_{ij}}={\frac {1}{2}}(a_{ij}-a_{ij}^{0})$

(11)

The curvatures (second fundamental form) of the middle surface are obtained by

$\kappa _{\alpha \beta }={\frac {1}{2}}\left({\boldsymbol {\varphi }}_{^{\prime }\alpha }\cdot \mathbf {t} _{3^{\prime }\beta }+{\boldsymbol {\varphi }}_{^{\prime }\beta }\cdot \mathbf {t} _{3^{\prime }\alpha }\right)=-\mathbf {t} _{3}\cdot {\boldsymbol {\varphi }}_{{\prime }\alpha \beta }\quad ,\quad \alpha ,\beta =1,2$

(12)

The deformation gradient tensor is

$\mathbf {F=} [{\boldsymbol {x}}_{{\prime }1},{\boldsymbol {x}}_{{\prime }2},{\boldsymbol {x}}_{{\prime }3}]=\left[{\begin{array}{ccc}{\boldsymbol {\varphi }}_{^{\prime }1}+\zeta \left(\lambda \mathbf {t} _{3}\right)_{^{\prime }1}&{\boldsymbol {\varphi }}_{^{\prime }2}+\zeta \left(\lambda \mathbf {t} _{3}\right)_{^{\prime }2}&\lambda \mathbf {t} _{3}\end{array}}\right]$

(13)

The product ${\textstyle \mathbf {F} ^{T}\mathbf {F=U} ^{2}=\mathbf {C} }$ (where ${\textstyle \mathbf {U} }$ is the right stretch tensor, and ${\textstyle \mathbf {C} }$ the right Cauchy-Green deformation tensor) can be written as

$\mathbf {U} ^{2}=\left[{\begin{array}{ccc}a_{11}+2\kappa _{11}\zeta \lambda &a_{12}+2\kappa _{12}\zeta \lambda &0\\a_{12}+2\kappa _{12}\zeta \lambda &a_{22}+2\kappa _{22}\zeta \lambda &0\\0&0&\lambda ^{2}\end{array}}\right]$

(14)

In the derivation of expression (14) the derivatives of the thickness ratio ${\textstyle \lambda _{^{\prime }a}}$ and the terms associated to ${\textstyle \zeta ^{2}}$ have been neglected.

Equation (14) shows that ${\textstyle \mathbf {U} ^{2}}$ is not a unit tensor at the original configuration for curved surfaces (${\textstyle \kappa _{ij}^{0}\neq {0}}$). The changes of curvature of the middle surface are computed by

$\chi _{ij}=\kappa _{ij}-\kappa _{ij}^{0}$

(15)

Note that ${\textstyle \delta \chi _{ij}=\delta \kappa _{ij}}$.

For computational convenience the following approximate expression (which is exact for initially flat surfaces) will be adopted

$\mathbf {U} ^{2}=\left[{\begin{array}{ccc}a_{11}+2\chi _{11}\zeta \lambda &a_{12}+2\chi _{12}\zeta \lambda &0\\a_{12}+2\chi _{12}\zeta \lambda &a_{22}+2\chi _{22}\zeta \lambda &0\\0&0&\lambda ^{2}\end{array}}\right]$

(16)

This expression is useful to compute different Lagrangian strain measures. An advantage of these measures is that they are associated to material fibres, what makes it easy to take into account material anisotropy. It is also useful to compute the eigen decomposition of ${\textstyle \mathbf {U} }$ as

$\mathbf {U=} \sum _{\alpha =1}^{3}\lambda _{\alpha }\mathbf {r} _{\alpha }\otimes \mathbf {r} _{\alpha }$

(17)

where ${\textstyle \lambda _{\alpha }}$ and ${\textstyle \mathbf {r} _{\alpha }}$ are the eigenvalues and eigenvectors of ${\textstyle \mathbf {U} }$.

The resultant stresses (axial forces and bending moments) are obtained by integrating across the original thickness the second Piola-Kirchhoff stress vector ${\textstyle {\boldsymbol {\sigma }}}$ using the actual distance to the middle surface for evaluating the bending moments. This gives

${\boldsymbol {\sigma }}_{m}\equiv \lbrack N_{11},N_{22},N_{12}]^{T}=\int _{h^{0}}{\boldsymbol {\sigma }}d\zeta$

(18)

${\boldsymbol {\sigma }}_{b}\equiv \lbrack M_{11},M_{22},M_{12}]^{T}=\int _{h^{0}}{\boldsymbol {\sigma }}\lambda \zeta d\zeta$

(19)

With these values the virtual work can be written as

$\iint _{A^{0}}\left[\delta {\boldsymbol {\varepsilon }}_{m}^{T}{\boldsymbol {\sigma }}_{m}+\delta {\boldsymbol {\kappa }}^{T}{\boldsymbol {\sigma }}_{b}\right]dA=\iint _{A^{0}}\delta \mathbf {u} ^{T}\mathbf {t} dA$

(20)

where ${\textstyle \delta \mathbf {u} }$ are virtual displacements, ${\textstyle \delta {\boldsymbol {\varepsilon }}_{m}}$ is the virtual Green-Lagrange membrane strain vector, ${\textstyle \delta {\boldsymbol {\kappa }}}$ are the virtual curvatures and ${\textstyle \mathbf {t} }$ are the surface loads. Other load types can be easily included into (20).

2.2 Constitutive Models

In order to treat non linear material behaviour at finite strains an adequate stress-strain pair must be used. The Hencky measures will be adopted here. The (logarithmic) strains are defined as

$\mathbf {E} _{\ln }\mathbf {=} \left[{\begin{array}{ccc}\varepsilon _{11}&\varepsilon _{21}&0\\\varepsilon _{12}&\varepsilon _{22}&0\\0&0&\varepsilon _{33}\end{array}}\right]=\sum _{\alpha =1}^{3}\ln \left(\lambda _{\alpha }\right)\mathbf {r} _{\alpha }\otimes \mathbf {r} _{\alpha }$

(21)

The use of a logarithmic strain measure reasonably allows to adopt an additive decomposition of elastic and non-linear (plastic) strain components as

$\mathbf {E} _{\ln }\mathbf {=E} _{\ln }^{e}+\mathbf {E} _{\ln }^{p}$

(22)

A constant linear relationship between the (plane) Hencky stresses and the logarithmic elastic strains is chosen giving

$\mathbf {T} =\mathbf {H} \mathbf {E} _{\ln }^{e}$

(23)

where ${\textstyle {\boldsymbol {H}}}$ is the constitutive matrix.

The constitutive equations are integrated using a standard return algorithm. Details of an specific constitutive model for rubber-type materials can be found in [21,22]. The Hencky stress tensor ${\textstyle \mathbf {T} }$ can be easily particularized for the plane stress case.

We define the rotated Hencky and second Piola-Kirchhoff stress tensors as

$\mathbf {T} _{L}=\mathbf {R} _{L}^{T}\;\mathbf {T\;R} _{L}$ (24) $\mathbf {S} _{L}=\mathbf {R} _{L}^{T}\;\mathbf {S\;R} _{L}$ (25)

where ${\textstyle \mathbf {R} _{L}}$ is the rotation tensor obtained from the eigenvectors of ${\textstyle \mathbf {U} }$ given by

$\mathbf {R} _{L}=\left[{\begin{array}{ccc}\mathbf {r} _{1}\quad ,&\mathbf {r} _{2}\quad ,&\mathbf {r} _{3}\end{array}}\right]$

(26)

The relationship between the rotated Hencky and Piola-Kirchhoff stresses is ${\textstyle \left(\alpha ,\beta =1,2\right)}$

$\left[S_{L}\right]_{\alpha \alpha }={\frac {1}{\lambda _{\alpha }^{2}}}\left[T_{L}\right]_{\alpha \alpha }$ $\left[S_{L}\right]_{\alpha \beta }={\frac {\ln \left(\lambda _{\alpha }/\lambda _{\beta }\right)}{{\frac {1}{2}}\left(\lambda _{\alpha }^{2}-\lambda _{\beta }^{2}\right)}}\left[T_{L}\right]_{\alpha \beta }$

(27)

The second Piola-Kirchhoff stress tensor can be computed by

$\mathbf {S=} \sum _{\alpha =1}^{2}\sum _{\beta =1}^{2}\left[S_{L}\right]_{\alpha \beta }\mathbf {r} _{\alpha }\otimes \mathbf {r} _{\beta }$

(28)

The second Piola-Kirchhoff stress vector ${\textstyle {\boldsymbol {\sigma }}}$ used in Eqs.(18–19) can be readily extracted from the ${\textstyle \mathbf {S} }$ tensor.

3 Enhanced Basic Shell Triangle

The main features of the element formulation (termed EBST for Enhanced Basic Shell Triangle) are the following:

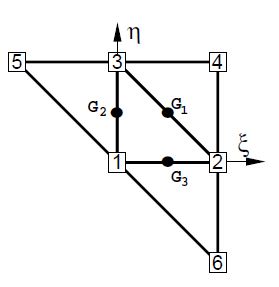
1. The geometry of the patch formed by an element and the three adjacent elements is quadratically interpolated from the position of the six nodes in the patch (Fig.1).
2. The membrane strains are assumed to vary linearly within the central triangle and are expressed in terms of the (continuous) values of the deformation gradient at the mid side points of the triangle.
3. An assumed constant curvature field within the central triangle is chosen. This is computed in terms of the values of the (continuous) deformation gradient at the mid side points.

Details of the derivation of the EBST element are given below.

(a)	(b)
Figure 1: (a) Patch of three node triangular elements including the central triangle (M) and three adjacent triangles (1, 2 and 3); (b) Patch of elements in the isoparametric space

3.1 Definition of the Element Geometry and Computation of Membrane Strains

A quadratic approximation of the geometry of the four elements patch is chosen using the position of the six nodes in the patch. It is useful to define the patch in the isoparametric space using the nodal positions given in the Table 1 (see also Fig.1).

Table. 1 Isoparametric coordinates of the six nodes in the patch of Fig.1

	1	2	3	4	5	6
${\textstyle \xi }$	0	1	0	1	-1	1
${\textstyle \eta }$	0	0	1	1	1	-1

The quadratic interpolation is defined by

${\boldsymbol {\varphi }}=\sum _{i=1}^{6}N_{i}{\boldsymbol {\varphi }}_{i}$

(29)

with (${\textstyle \zeta =1-\xi -\eta }$)

${\begin{array}{ccc}N_{1}=\zeta {+\xi }\eta &&N_{4}=\displaystyle {\frac {\zeta }{2}}\left(\zeta {-1}\right)\\[.15cm]N_{2}=\xi {+\eta }\zeta &&N_{5}=\displaystyle {\frac {\xi }{2}}\left(\xi {-1}\right)\\[.15cm]N_{3}=\eta {+\zeta }\xi &&N_{6}=\displaystyle {\frac {\eta }{2}}\left(\eta {-1}\right)\end{array}}$

(30)

This interpolation allows to computing the displacement gradients at selected points in order to use an assumed strain approach. The computation of the gradients is performed at the mid side points of the central element of the patch denoted by ${\textstyle G_{1}}$, ${\textstyle G_{2}}$ and ${\textstyle G_{3}}$ in Fig. 1. This choice has the following advantages.

• Gradients at the three mid side points depend only on the nodes belonging to the two elements adjacent to each side. This can be easily verified by sampling the derivatives of the shape functions at each mid-side point.

• When gradients are computed at the common mid-side point of two adjacent elements, the same values are obtained, as the coordinates of the same four points are used. This in practice means that the gradients at the mid-side points are independent of the element where they are computed. A side-oriented implementation of the finite element will therefore lead to a unique evaluation of the gradients per side.

The Cartesian derivatives of the shape functions are computed at the original configuration by the standard expression

$\left[{\begin{array}{c}N_{i,1}\\N_{i,2}\end{array}}\right]=\mathbf {J} ^{-1}\left[{\begin{array}{c}N_{i,\xi }\\N_{i,\eta }\end{array}}\right]$

(31)

where the Jacobian matrix at the original configuration is

$\mathbf {J=} \left[{\begin{array}{cc}\mathbf {\boldsymbol {\varphi }} _{^{\prime }\xi }^{0}\cdot \mathbf {t} _{1}&\mathbf {\boldsymbol {\varphi }} _{^{\prime }\eta }^{0}\cdot \mathbf {t} _{1}\\\mathbf {\boldsymbol {\varphi }} _{^{\prime }\xi }^{0}\cdot \mathbf {t} _{2}&\mathbf {\boldsymbol {\varphi }} _{^{\prime }\eta }^{0}\cdot \mathbf {t} _{2}\end{array}}\right]$

(32)

The deformation gradients on the middle surface, associated to an arbitrary spatial Cartesian system and to the material cartesian system defined on the middle surface are related by

$\left[{\boldsymbol {\varphi }}_{^{\prime }1},\mathbf {\boldsymbol {\varphi }} _{^{\prime }2}\right]=\left[\mathbf {\boldsymbol {\varphi }} _{^{\prime }\xi },\mathbf {\boldsymbol {\varphi }} _{^{\prime }\eta }\right]\mathbf {J} ^{-1}$

(33)

The membrane strains within the central triangle are obtained using a linear assumed strain field ${\textstyle {\hat {\boldsymbol {\varepsilon }}}_{m}}$, i.e.

${\boldsymbol {\varepsilon }}_{m}={\hat {\boldsymbol {\varepsilon }}}_{m}$

(34)

with

${\hat {\boldsymbol {\varepsilon }}}_{m}=(1-2\zeta ){\boldsymbol {\varepsilon }}_{m}^{1}+(1-2\xi ){\boldsymbol {\varepsilon }}_{m}^{2}+(1-2\eta ){\boldsymbol {\varepsilon }}_{m}^{3}=\sum _{i=1}^{3}{\bar {N}}_{i}{\boldsymbol {\varepsilon }}_{m}^{i}$

(35)

where ${\textstyle {\boldsymbol {\varepsilon }}_{m}^{i}}$ are the membrane strains computed at the three mid side points ${\textstyle G_{i}}$ (${\textstyle i=1,2,3}$ see Fig.1). In Eq.(35) ${\textstyle {\bar {N}}_{1}=(1-2\zeta )}$, etc.

The gradient at each mid side point is computed from the quadratic interpolation (29):

$\left({\boldsymbol {\varphi }}_{^{\prime }\alpha }\right)_{G_{i}}={\boldsymbol {\varphi }}_{^{\prime }\alpha }^{i}=\left[\sum _{j=1}^{3}N_{j,\alpha }^{i}{\boldsymbol {\varphi }}_{j}\right]+N_{i+3,\alpha }^{i}{\boldsymbol {\varphi }}_{i+3}\quad ,\quad \alpha =1,2\quad ,\quad i=1,2,3$

(36)

Substituting Eq.(11) into (35) and using Eq.(9) gives the membrane strain vector as

${\boldsymbol {\varepsilon }}_{m}=\sum _{i=1}^{3}{\frac {1}{2}}{\bar {N}}_{i}\left\{{\begin{array}{c}{\boldsymbol {\varphi }}_{^{\prime }1}^{i}\cdot \mathbf {\boldsymbol {\varphi }} _{^{\prime }1}^{i}-1\\{\boldsymbol {\varphi }}_{^{\prime }2}^{i}\cdot \mathbf {\boldsymbol {\varphi }} _{^{\prime }2}^{i}-1\\2{\boldsymbol {\varphi }}_{^{\prime }1}^{i}\cdot \mathbf {\boldsymbol {\varphi }} _{^{\prime }2}^{i}\end{array}}\right\}$

(37)

and the virtual membrane strains as

$\delta {\boldsymbol {\varepsilon }}_{m}=\sum _{i=1}^{3}{\bar {N}}_{i}\left\{{\begin{array}{c}{\boldsymbol {\varphi }}_{^{\prime }1}^{i}\cdot \delta \mathbf {\boldsymbol {\varphi }} _{^{\prime }1}^{i}\\{\boldsymbol {\varphi }}_{2}^{i}\cdot \delta \mathbf {\boldsymbol {\varphi }} _{^{\prime }2}^{i}\\\delta {\boldsymbol {\varphi }}_{^{\prime }1}^{i}\cdot \mathbf {\boldsymbol {\varphi }} _{^{\prime }2}^{i}+{\boldsymbol {\varphi }}_{^{\prime }1}^{i}\cdot \delta \mathbf {\boldsymbol {\varphi }} _{2}^{i}\end{array}}\right\}$

(38)

We note that the gradient at each mid side point ${\textstyle G_{i}}$ depends only on the coordinates of the three nodes of the central triangle and on those of an additional node in the patch, associated to the side ${\textstyle i}$ where the gradient is computed.

Combining Eqs.(38), (36) and (29) gives

$\delta {\boldsymbol {\varepsilon }}_{m}=\mathbf {B} _{m}\delta {\bar {\boldsymbol {u}}}^{p}$

(39.a)

with

${\underset {18\times 1}{\delta {\bar {\boldsymbol {u}}}^{p}}}=[\delta {\bar {\boldsymbol {u}}}_{1}^{T},\delta {\bar {\boldsymbol {u}}}_{2}^{T},\delta {\bar {\boldsymbol {u}}}_{3}^{T},\delta {\bar {\boldsymbol {u}}}_{4}^{T},\delta {\bar {\boldsymbol {u}}}_{5}^{T},\delta {\bar {\boldsymbol {u}}}_{6}^{T}]^{T}$

(39.b)

where ${\textstyle \delta {\bar {\boldsymbol {u}}}^{p}}$ is the patch displacement vector, ${\textstyle \delta {\bar {\boldsymbol {u}}}_{i}}$ contains the three virtual displacement of node ${\textstyle i}$ and ${\textstyle \mathbf {B} _{m}}$ is the membrane strain matrix. An explicit form of ${\textstyle \mathbf {B} _{m}}$ is given in [21,22].

Note that the membrane strains within the EBST element are a function of the displacements of the six patch nodes.

3.2 Computation of Curvatures

We will assume the following constant curvature field within each element

$\kappa _{\alpha \beta }={\hat {\kappa }}_{\alpha \beta }$

(40)

where ${\textstyle {\hat {\kappa }}_{\alpha \beta }}$ is the assumed constant curvature field defined by

${\hat {\kappa }}_{\alpha \beta }=-{\frac {1}{A_{M}^{0}}}\int _{A_{M}^{0}}\mathbf {t} _{3}\cdot {\boldsymbol {\varphi }}_{^{\prime }\beta \alpha }\;dA^{0}$

(41)

where ${\textstyle A_{M}^{0}}$ is the area (in the original configuration) of the central element in the patch.

Substituting Eq.(41) into (40) and integrating by parts the area integral gives the curvature vector within the element in terms of the following line integral

${\boldsymbol {\kappa }}=\left\{{\begin{array}{c}\kappa _{11}\\\kappa _{22}\\2\kappa _{12}\end{array}}\right\}={\frac {1}{A_{M}^{0}}}{\displaystyle \oint _{\Gamma _{M}^{0}}}\left[{\begin{array}{cc}-n_{1}&0\\0&-n_{2}\\-n_{2}&-n_{1}\end{array}}\right]\left[{\begin{array}{c}\mathbf {t} _{3}\cdot {\boldsymbol {\varphi }}_{^{\prime }1}\\\mathbf {t} _{3}\cdot {\boldsymbol {\varphi }}_{^{\prime }2}\end{array}}\right]d\Gamma$

(42)

where ${\textstyle n_{i}}$ are the components (in the local system) of the normals to the element sides in the initial configuration ${\textstyle \Gamma _{M}^{0}}$. The integration by parts of Eq.(41) is typical in finite volume methods for computing second derivatives over volumes by line integrals of gradient terms [16,17,19,21,22]. For the definition of the normal vector ${\textstyle \mathbf {t} _{3}}$, the linear interpolation over the central element is used. In this case the tangent plane components are

${\boldsymbol {\varphi }}_{^{\prime }\alpha }=\sum _{i=1}^{3}L_{i,\alpha }^{M}{\boldsymbol {\varphi }}_{i}\quad ,\quad \alpha =1,2$

(43.a)

$\mathbf {t} _{3}={\frac {{\boldsymbol {\varphi }}_{\prime {1}}\times {\boldsymbol {\varphi }}_{\prime {2}}}{\left\vert {\boldsymbol {\varphi }}_{\prime {1}}\times {\boldsymbol {\varphi }}_{\prime {2}}\right\vert }}=\lambda \;{\boldsymbol {\varphi }}_{1}\times {\boldsymbol {\varphi }}_{2}$

(43.b)

From these expressions it is also possible to compute in the original configuration the element area ${\textstyle A_{M}^{0}}$, the outer normals ${\textstyle \left(n_{1},n_{2}\right)^{i}}$ at each side and the side lengths ${\textstyle l_{i}^{M}}$. Equation (43.b) also allows to evaluate the thickness ratio ${\textstyle \lambda }$ in the deformed configuration and the actual normal ${\textstyle \mathbf {t} _{3}}$.

The numerical evaluation of the line integral in Eq.(42) results in a sum over the integration points at the element boundary which are, in fact, the same points used for evaluating the gradients when computing the membrane strains. As one integration point is used over each side, it is not necessary to distinguish between sides (${\textstyle i}$) and integration points (${\textstyle G_{i}}$). In this way the curvatures can be computed by

${\boldsymbol {\kappa }}={\frac {1}{A_{M}^{0}}}\sum _{i=1}^{3}l_{i}^{M}\left[{\begin{array}{cc}-n_{1}&0\\0&-n_{2}\\-n_{2}&-n_{1}\end{array}}\right]\left[{\begin{array}{c}\mathbf {t} _{3}\cdot {\boldsymbol {\varphi }}_{^{\prime }1}\\\mathbf {t} _{3}\cdot {\boldsymbol {\varphi }}_{^{\prime }2}\end{array}}\right]d\Gamma$

(44)

Eq.(44) is now expressed in terms of the shape functions of the 3-noded triangle ${\textstyle L_{i}^{M}}$ (which coincide with the area coordinates [23]). Noting the property of the area coordinates

$\nabla L_{i}^{M}=\left[{\begin{array}{c}L_{i,x}^{M}\\L_{i,y}^{M}\end{array}}\right]=-{\frac {l_{i}^{M}}{2A_{M}}}\left[{\begin{array}{c}n_{x}^{i}\\n_{y}^{i}\end{array}}\right]$

(45)

the expression for the curvature can be expressed as

${\boldsymbol {\kappa }}=2\sum _{i=1}^{3}\left[{\begin{array}{cc}L_{i,1}^{M}&0\\0&L_{i,2}^{M}\\L_{i,2}^{M}&L_{i,1}^{M}\end{array}}\right]\left[{\begin{array}{c}\mathbf {t} _{3}\cdot {\boldsymbol {\varphi }}_{^{\prime }1}^{i}\\\mathbf {t} _{3}\cdot {\boldsymbol {\varphi }}_{^{\prime }2}^{i}\end{array}}\right]$

(46)

The gradient ${\textstyle \mathbf {\boldsymbol {\varphi }} _{\prime \alpha }^{i}}$ is evaluated at each side ${\textstyle G_{i}}$ from the quadratic interpolation

$\left[{\begin{array}{c}{\boldsymbol {\varphi }}_{\prime {1}}^{i}\\{\boldsymbol {\varphi }}_{\prime {2}}^{i}\end{array}}\right]=\left[{\begin{array}{cccc}N_{1,1}^{i}&N_{2,1}^{i}&N_{3,1}^{i}&N_{i+3,1}^{i}\\N_{1,2}^{i}&N_{2,2}^{i}&N_{3,2}^{i}&N_{i+3,2}^{i}\end{array}}\right]\left[{\begin{array}{c}{\boldsymbol {\varphi }}_{1}\\{\boldsymbol {\varphi }}_{2}\\{\boldsymbol {\varphi }}_{3}\\{\boldsymbol {\varphi }}_{i+3}\end{array}}\right]$

(47)

This is a basic difference with respect of the computation of the curvature field in the original Basic Shell Triangle (BST) where the gradient at the side mid-point is computed as the average value between the values at two adjacent elements [17,19,21,22].

Note again than at each side the gradients depend only on the positions of the three nodes of the central triangle and of an extra node (${\textstyle i+3}$), associated precisely to the side (${\textstyle G_{i}}$) where the gradient is computed.

Direction t${\textstyle _{3}}$ in Eq.(46) can be seen as a reference direction. If a different direction than that given by Eq.(43.b) is chosen at an angle ${\textstyle \theta }$ with the former, this has an influence of order ${\textstyle \theta ^{2}}$ in the projection. This justifies Eq.(43.b) for the definition of t${\textstyle _{3}}$ as a function exclusively of the three nodes of the central triangle, instead of using the 6-node isoparametric interpolation.

The variation of the curvatures can be expressed as

$\delta {\boldsymbol {\kappa }}=2\sum _{i=1}^{3}\left[{\begin{array}{cc}L_{i,1}^{M}&0\\0&L_{i,2}^{M}\\L_{i,2}^{M}&L_{i,1}^{M}\end{array}}\right]\left\{\sum _{i=1}^{3}\left[{\begin{array}{c}N_{j,1}^{i}(\mathbf {t} _{3}\cdot \delta {\bar {\boldsymbol {u}}}_{j})\\N_{j,2}^{i}(\mathbf {t} _{3}\cdot \delta {\bar {\boldsymbol {u}}}_{j})\end{array}}\right]+\left[{\begin{array}{c}N_{i+3,1}^{i}(\mathbf {t} _{3}\cdot \delta {\bar {\boldsymbol {u}}}^{i+3})\\N_{i+3,2}^{i}(\mathbf {t} _{3}\cdot \delta {\bar {\boldsymbol {u}}}^{i+3})\end{array}}\right]\right\}-$ $-\sum _{i=1}^{3}\left[{\begin{array}{c}(L_{i,1}^{M}\rho _{11}^{1}+L_{i,2}^{M}\rho _{11}^{2})\\(L_{i,1}^{M}\rho _{22}^{1}+L_{i,2}^{M}\rho _{22}^{2})\\(L_{i,1}^{M}\rho _{12}^{1}+L_{i,2}^{M}\rho _{12}^{2})\end{array}}\right](\mathbf {t} _{3}\cdot \delta {\bar {\boldsymbol {u}}}_{i})=\mathbf {B} _{b}\delta {\bar {\boldsymbol {u}}}^{p}$

(48)

In Eq.(48)

$\mathbf {B} _{b}=[\mathbf {B} _{b_{1}},\mathbf {B} _{b_{2}},\cdots ,\mathbf {B} _{b_{6}}]$

(49)

Details of the derivation of the curvature matrix ${\textstyle \mathbf {B} _{b}}$ are given in [21,22,26].

3.3 The EBST1 Element

A simplified and yet very effective version of the EBST element can be obtained by using one point quadrature for the computation of all the element integrals. This element is termed EBST1. Note that this only affects the membrane stiffness matrices and it is equivalent to using a assumed constant membrane strain field defined by an average of the metric tensors computed at each side [21,22].

Numerical experiments have shown that both the EBST and the EBST1 elements are free of spurious energy modes [21,22].

3.4 Boundary Conditions

Elements at the domain boundary, where an adjacent element does not exist, deserve a special attention. The treatment of essential boundary conditions associated to translational constraints is straightforward, as they are the natural degrees of freedom of the element. The conditions associated to the normal vector are crucial in the bending formulation. For clamped sides or symmetry planes, the normal vector ${\textstyle \mathbf {t} _{3}}$ must be kept fixed (clamped case), or constrained to move in the plane of symmetry (symmetry case). The former case can be seen as a special case of the latter, so we will consider symmetry planes only. This restriction can be imposed through the definition of the tangent plane at the boundary, including the normal to the plane of symmetry ${\textstyle {\boldsymbol {\varphi }}_{^{\prime }n}^{0}}$ that does not change during the process.

Figure 2: Local Cartesian system for the treatment of symmetry boundary conditions

The tangent plane at the boundary (mid-side point) is expressed in terms of two orthogonal unit vectors referred to a local-to-the-boundary Cartesian system (see Fig.2) defined as

$\left[{\boldsymbol {\varphi }}_{^{\prime }n}^{0},\;{\bar {\boldsymbol {\varphi }}}_{^{\prime }s}\right]$

(50)

where vector ${\textstyle {\boldsymbol {\varphi }}_{^{\prime }n}^{0}}$ is fixed during the process while direction ${\textstyle {\bar {\boldsymbol {\varphi }}}_{^{\prime }s}}$ emerges from the intersection of the symmetry plane with the plane defined by the central element (${\textstyle M}$). The plane (gradient) defined by the central element in the selected original convective Cartesian system (${\textstyle \mathbf {t} _{1},\mathbf {t} _{2}}$) is

$\left[{\boldsymbol {\varphi }}_{^{\prime }1}^{M},\;{\boldsymbol {\varphi }}_{^{\prime }2}^{M}\right]$

(51)

the intersection line (side ${\textstyle i}$) of this plane with the plane of symmetry can be written in terms of the position of the nodes that define the side (${\textstyle j}$ and ${\textstyle k}$) and the original length of the side ${\textstyle l_{i}^{M}}$, i.e.

${\boldsymbol {\varphi }}_{^{\prime }s}^{i}={\frac {1}{l_{i}^{M}}}\left({\boldsymbol {\varphi }}_{k}-{\boldsymbol {\varphi }}_{j}\right)$

(52)

That together with the outer normal to the side ${\textstyle \mathbf {n} ^{i}=\left[n_{1},n_{2}\right]^{T}=\left[\mathbf {n\cdot t} _{1},\mathbf {n\cdot t} _{2}\right]^{T}}$ (resolved in the selected original convective Cartesian system) leads to

$\left[{\begin{array}{c}{\boldsymbol {\varphi }}_{^{\prime }1}^{iT}\\{\boldsymbol {\varphi }}_{^{\prime }2}^{iT}\end{array}}\right]=\left[{\begin{array}{cc}n_{1}&-n_{2}\\n_{2}&n_{1}\end{array}}\right]\left[{\begin{array}{c}{\boldsymbol {\varphi }}_{^{\prime }n}^{iT}\\{\boldsymbol {\varphi }}_{^{\prime }s}^{iT}\end{array}}\right]$

(53)

where, noting that ${\textstyle \lambda }$ is the determinant of the gradient, the normal component of the gradient ${\textstyle {\boldsymbol {\varphi }}_{^{\prime }n}^{i}}$ can be approximated by

${\boldsymbol {\varphi }}_{^{\prime }n}^{i}={\frac {{\boldsymbol {\varphi }}_{^{\prime }n}^{0}}{\lambda |{\boldsymbol {\varphi }}_{^{\prime }s}^{i}|}}$

(54)

For a simple supported (hinged) side, the problem is not completely defined. The simplest choice is to neglect the contribution to the side rotations from the adjacent element missing in the patch in the evaluation of the curvatures via Eq.(42) [17,19,21,22]. This is equivalent to assume that the gradient at the side is equal to the gradient in the central element, i.e.

$\left[{\boldsymbol {\varphi }}_{^{\prime }1}^{i},\;{\boldsymbol {\varphi }}_{^{\prime }2}^{i}\right]=\left[{\boldsymbol {\varphi }}_{^{\prime }1}^{M},\;{\boldsymbol {\varphi }}_{^{\prime }2}^{M}\right]$

(55)

More precise changes can be however introduced to account for the different natural boundary conditions. One may assume that the curvature normal to the side is zero, and consider a contribution of the missing side to introduce this constraint. As the change of curvature parallel to the side is also zero along the hinged side, this obviously leads to zero curvatures in both directions.

We note finally that for the membrane formulation of the EBST element, the gradient at the mid-side point of the boundary is assumed equal to the gradient of the main triangle.

More details on the specification of the boundary conditions on the EBST element can be found in [21,22].

3.5 Explicit Solution Scheme

For simulations presenting large geometrical and/or material non-linearities, involving frictional contact conditions on complex geometries, convergence is difficult to achieve with implicit schemes. In these cases an explicit solution algorithm is typically most advantageous. The explicit scheme provides the solution for dynamic problems and also for quasi-static problems if an adequate damping is chosen.

The dynamic equations of motion to solve are of the form

$\mathbf {r} ({\bar {\boldsymbol {u}}})+\mathbf {D} {\dot {\bar {\mathbf {u} }}}+\mathbf {M} {\ddot {\bar {\mathbf {u} }}}=0$

(56)

where ${\textstyle {\bar {\boldsymbol {u}}}}$ is the nodal displacement vector for the whole mesh, ${\textstyle \mathbf {M} }$ is the mass matrix, ${\textstyle \mathbf {D} }$ is the damping matrix and the dot means the time derivative. The solution is performed using the central difference method. To make the method competitive a diagonal (lumped) ${\textstyle \mathbf {M} }$ matrix is typically used and ${\textstyle \mathbf {D} }$ is taken proportional to ${\textstyle \mathbf {M} }$. As usual, mass lumping is performed by assigning one third of the triangular element mass to each node in the central element.

The explicit solution scheme can be summarized as follows. At each time step ${\textstyle n}$ where the displacements u have been computed:

1. Compute the residual forces ${\textstyle \mathbf {r} ^{n}}$. This follows the steps described in Box 1.
2. Compute the accelerations at time ${\textstyle t_{n}}$

   ${\ddot {\bar {\boldsymbol {u}}}}^{n}={\boldsymbol {M}}_{d}^{-1}[\mathbf {r} ^{n}-\mathbf {D} {\dot {\bar {\mathbf {u} }}}^{n-1/2}]$

   (57)

where ${\textstyle {\boldsymbol {M}}_{d}}$ is the diagonal (lumped) mass matrix.

3. Compute the velocities at time ${\textstyle t_{n+1/2}}$

   ${\dot {\bar {\boldsymbol {u}}}}^{n+1/2}={\dot {\bar {\boldsymbol {u}}}}^{n-1/2}+{\ddot {\bar {\boldsymbol {u}}}}^{n}\delta t$

   (58)

4. Compute the displacements at time ${\textstyle t_{n+1}}$

   ${\bar {\boldsymbol {u}}}^{n+1}={\bar {\mathbf {u} }}^{n}+{\dot {\bar {\mathbf {u} }}}^{n+1/2}\delta t$

   (59)

5. Update the shell geometry
6. Check frictional contact conditions

Generate the actual configuration ${\textstyle \mathbf {\boldsymbol {\varphi }} ^{n+1}=\mathbf {\boldsymbol {\varphi }} ^{n}+\Delta {\bar {\mathbf {u} }}^{n}}$ Compute the metric tensor ${\textstyle a_{\alpha \beta }^{n+1}\mathbf {} }$and the curvatures ${\textstyle \kappa _{\alpha \beta }^{n+1}}$. Then at each layer ${\textstyle k}$ compute the (approximate) right Cauchy-Green tensor. From (14) $\mathbf {C} _{k}^{n+1}=\mathbf {a} ^{n+1}+z_{k}{\boldsymbol {\chi }}^{n+1}$ (60) Compute the total (21) and elastic (22) deformations at each layer ${\textstyle k}$ ${\boldsymbol {\varepsilon }}_{k}^{n+1}={\frac {1}{2}}\ln {\mathbf {C} _{k}^{n+1}}$ (61) $\left[{\boldsymbol {\varepsilon }}_{e}\right]_{k}^{n+1}={\boldsymbol {\varepsilon }}_{k}^{n+1}-\left[{\boldsymbol {\varepsilon }}_{p}\right]_{k}^{n}$ Compute the trial Hencky elastic stresses (23) at each layer ${\textstyle k}$ $\mathbf {T} _{k}^{n+1}=\mathbf {H} \left[{\boldsymbol {\varepsilon }}_{e}\right]_{k}^{n+1}$ (62) Check the plasticity condition and return to the plasticity surface. If necessary correct the plastic strains ${\textstyle \left[{\boldsymbol {\varepsilon }}_{p}\right]_{k}^{n+1}}$ at each layer Compute the second Piola-Kirchhoff stress vector ${\textstyle {\boldsymbol {\sigma }}_{k}^{n+1}}$ and the generalized stresses ${\begin{array}{l}{\boldsymbol {\sigma }}_{m}^{n+1}&={\frac {h^{0}}{N_{L}}}\sum _{k=1}^{N_{L}}{\boldsymbol {\sigma }}_{k}^{n+1}w_{k}\\{\boldsymbol {\sigma }}_{b}^{n+1}&={\frac {h^{0}}{N_{L}}}\sum _{k=1}^{N_{L}}{\boldsymbol {\sigma }}_{k}^{n+1}z_{k}w_{k}\end{array}}$ (63) Where ${\textstyle w_{k}}$ is the weight of the through-the-thickness integration point and ${\textstyle N_{L}}$ is the number of layers (integration points) across the thickness. Recall that ${\textstyle z_{k}}$ is the current distance of the layer to the mid-surface and not the original distance. However, for small strain plasticity this distinction is not important. This computation of stresses is exact for an elastic problem. Compute the residual force vector for each element from $\mathbf {r} _{i}^{e}=\iint _{A}L_{i}{\boldsymbol {t}}\,dA-\iint _{A^{\circ }}({\boldsymbol {B}}_{m_{i}}^{T}{\boldsymbol {\sigma }}_{m}+{\boldsymbol {B}}_{b_{i}}^{T}{\boldsymbol {\sigma }}_{b})dA$ (64)

Box 1. Computation of the residual forces vector for an elasto-plastic material

The formulation of the EBST element described above has been implemented in the explicit dynamic code STAMPACK [31]. This code has been used for the structural analysis computations shown in the examples section.

For further details see [21,22].

4 Aeroelastic Analysis

Wind loading analysis is mandatory in outdoor membrane structures such as inflatable structures formed by low pressure inflatable tubes. Aeroelastic forces can induce the instability and failure of the structure. The accurate computation of wind forces is also essential for the correct design of the anchoring system. A simple weakly coupled staggered aeroelastic scheme has been implemented for the EBST rotation-free shell triangle described in the previous sections. The computation of the wind forces on the membrane structure is performed at each time step using the Tdyn fluid-dynamic code based on the solution of the Navier-Stokes equations for a viscous flow using a stabilized finite element formulation [33]. Wind forces are used to compute the membrane deformations via the EBST element. This naturally introduces changes in the geometry of the domain where the aerodynamic analysis is performed. These changes are taken into account in the fluid-dynamic analysis at the next time step and so on. The transfer of data between the aerodynamic and structural analysis codes is performed via “ad-hoc” interface for data interchange in fluid-structure interaction problems [27, 28, 32].

5 Examples

All units in the examples are given in the international unit system.

5.1 Inflation of a Sphere

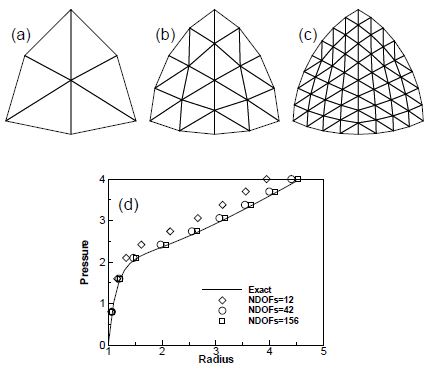
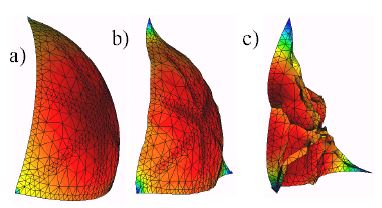
As the EBST element uses a quadratic interpolation of geometry, the existance of membrane locking must be assessed. For this example an originally curved surface is considered, where a standard linear strain triangle would lead to membrane locking. The example is the inflation of a spherical shell under internal pressure. An incompressible Mooney-Rivlin constitutive material have been considered [21, 22]. The three meshes of EBST elements considered to evaluate convergence are shown in Fig. 3.a-c. The value of the actual radius as a function of the internal pressure is plotted in Fig. 3.d for the different meshes and is also compared with the analytical solution. It can be seen that with a few degrees of freedom it is possible to obtain an excellent agreement for the range of strains considered. The final value corresponds to a thickness radius ratio of ${\textstyle h/R=0.00024}$. No membrane locking has therefore been detected in this problem. For more details see [21, 22, 29].

Figure 3: Inflation of sphere of Mooney-Rivlin material. (a)-(c) EBST meshes used in the analysis (d)Radius as a function of the internal pressure

5.2 Inflation of a Square Airbag Against a Spherical Object

The next example is the inflation of a square airbag supporting a spherical object. The lower surface part of the airbag is limited by a rigid plane and on the upper part a spherical dummy object is set to study the interaction between the airbag and the object. The material properties are given in [21, 22, 30].

The airbag geometry is initially square with an undeformed side length of ${\textstyle 0.643}$. Only one quarter of the geometry has been modelled due to symmetry. The thickness considered is ${\textstyle h=0.00075}$ and the inflation pressure is ${\textstyle 250000}$. Using a density ${\textstyle \delta =1000}$, pressure is linearly increased from 0 to the final value in ${\textstyle t=0.15}$. The spherical object has a radius ${\textstyle r=0.08}$ and a mass of ${\textstyle 4.8}$ (one quarter), and is subjected to gravity load during all the process.

Figure 4: Inflation of a square airbag against an spherical object. Deformed configurations for different times. Left figure: results obtained with the full bending formulation. Right figure: results obtained with a pure membrane solution

The mesh has 8192 EBST elements and 4225 nodes on the surface of the airbag. Figure 4 shows the deformed configurations for three different times. The sequence on the left figure corresponds to an analysis including full bending effects and the sequence on the right is the result of a pure membrane analysis. Note that the membrane solution presents artificial (numerical) wrinkles which dissappear when using the full bending formulation presented in this paper.

5.3 Inflation/Deflation of a Closed Tube

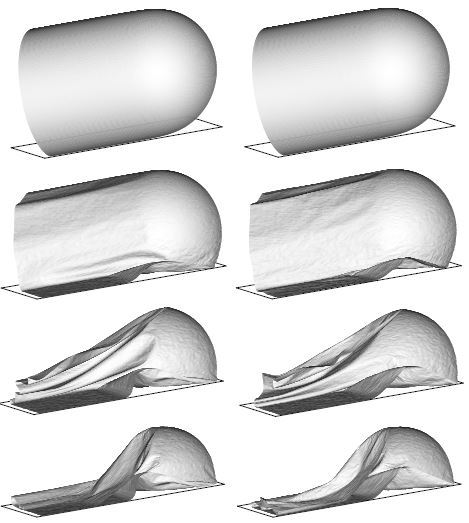
This problem studies the inflating and de-inflating of a tube with a semi-spherical end cap. The tube diameter is ${\textstyle D=2}$, its total length is ${\textstyle L=6}$ and the thickness ${\textstyle h=5\times 10^{-4}}$. The material has the following properties ${\textstyle E=4\times 10^{8}}$, ${\textstyle \nu =0.35}$, ${\textstyle \varrho =2\times 10^{3}}$. The tube is inflated fast until a pressure of ${\textstyle 10^{4}}$ and when pressure is released the tube de-inflates and falls under self weight. The analysis is performed with a mesh of 16704 EBST elements and 8501 nodes modelling a quarter of the geometry. A rigid frictionless base is assumed. Self contact is also included to avoid penetrations. The evolution of the tube walls during the de-inflating process are shown in Fig. 5. For this very thin shell, the differences between a full bending solution and a pure membrane solution are less marked.

Figure 5: Inflation and deflation of a closed tube. $L=6$, $D=2$, $h=5\times 10^{-4}$. Left figure: results obtained with the full bending formulation. Right figure: results obtained with a pure membrane solution

5.4 Inflation of a Tubular Arch

The next example is the analysis of a tubular arch. This kind of archs are joined together to form large inflatable structures for a wide range of applications as shown in the following examples. The tubular arch has a internal diameter of ${\textstyle 0.9}$; is total length is ${\textstyle 11.0}$ and the heigth is ${\textstyle 4.5}$. The tube thickness is ${\textstyle 3\times 10^{-4}}$, the constitutive material is polyamid with Young modulus ${\textstyle E=2.45\times 10^{8}}$ and Poisson ratio ${\textstyle \nu =0.35}$. Due to geometric symmetrys one quarter of the tube was discretized with 33600 triangular elements (17061 nodes). The simulation includes two stages. First the tube is left fall down under gravity action. Second an internal pressure of ${\textstyle p=883}$ is applied in a short time and kept constant afterwards until the full inflation of the tube is reached.

Figure 6 shows deformed configurations for different instants of the process.

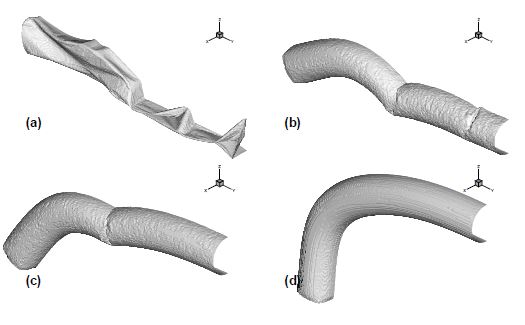
Figure 6: Inflation of a tubular arch. (a) Deflated tube. (b),(c) Deformed configurations during the inflation process. (d) Final inflated configuration

5.5 Impact of Rigid Spheres on an Inflated Pavilion

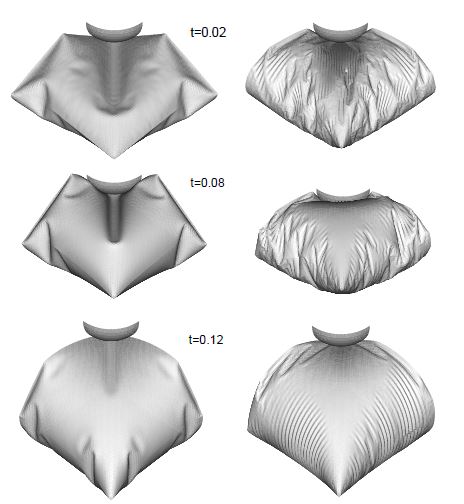
Figure 7 shows the impact of two rigid spheres on an inflatable structure ressembling a mushroom. The surface has been discretized with a relative coarse mesh of EBST elements. This example simulates the effect of children jumping or walking on an inflatable structure. Frictional contact conditions and elastic material properties are assumed. The pavilion structure is inflated to a low pressure. The sphere on the top of the pavilion is linked to the structure. The bouncing sphere was shot to the structure. The results observed agree very well with the expected behaviour.

A numerical experiment was performed next for reproducing the inflating and deflating process of the mushroom shape pavilion. Figure 8 represents the inflating process.

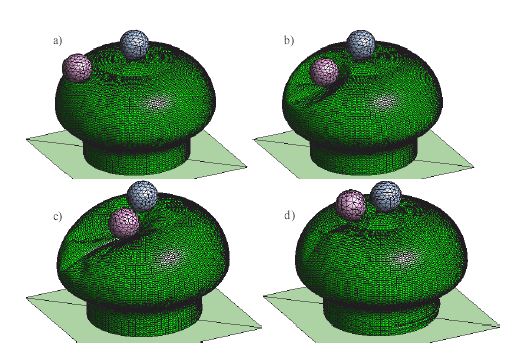
Figure 7: Impact of two spheres on a inflatable structure. Deformed shape at different times

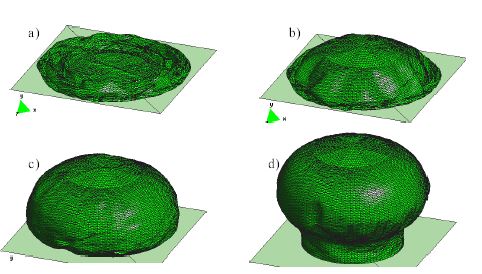
Figure 8: Inflation of a membrane structure. Geometry at different times during the inflating process

5.6 Deployment of a Spinnaker Sail

Figure 9 shows the simulation of the deployment of a spinnaker sail under the wind action. An elastic material (Naylon) is used with a coarse mesh of 730 EBST elements. The material properties used are ${\textstyle E=5000}$, ${\textstyle \nu =0.3}$, ${\textstyle t=5\times 10^{-4}}$. The wind pressure force is obtained using the Tdyn CFD code [33]. The apparent wind velocity used is 4. The sail deployment process agrees very well to the real behaviour. The objective was to determine the stress level on the sail.

5.7 Examples of Practical Constructions of Membrane Structures with Low Pressure Inflatable Tubes

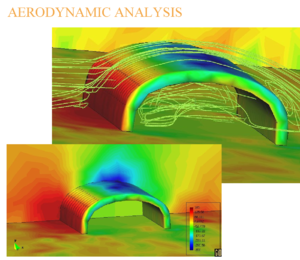
Figure Figure 10 presents a pavilion of 150 m${\textstyle ^{2}}$ for a telecommunication company in Spain. The pavilion is made by assembling some 70 low pressure tubes like the one showed in Figure Figure 6. The tubes are joined together to create the pavilion space. The complexity of the shape required extensive aerodynamic analysis to guarantee the stability of the structure. This pavilion visited some 15 cities in Spain during 2005.

Figure 9: Spinnaker sail. Sequence of deployment

Figure 10: Inflated pavilion for a telecommunication exhibition built by assembly of low pressure inflatable tubes. Triangular mesh on the pavilion surface and results of the aerodynamic analysis

Figure 11: Cadillac style exhibition pavilion built by assembly of low pressure analysis tubes. Geometry and results of the aerodynamic analysis

Figure 12: Exhibition hall in Barcelona built by assembly of low pressure inflatable tubes. Images of the design project

Figure 13: Inflatable exhibition hall in Barcelona harbour. Images of the construction of the different modules, transport, lay-out and inflating operations

Figure 14: Inflatable exhibition hall in Barcelona harbour. Images of outside and inside spaces. Lower frame shows the first and third authors of the paper (from right to left)

Figure 11 shows an inflated pavilion of some 200 m${\textstyle ^{2}}$ simulating and old cadillac automotive for and itinerant exhibition in Spain (2005). The flat geometry of the ceiling was a challenge for the designers. Extensive structural and aerodynamic analysis were performed using the Tdyn code [33] to guarantee the integrity of the structure.

Figure 12 shows the design shape of a relative large inflatable exhibition hall (1600m${\textstyle ^{2}}$) built in the harbour area of the city of Barcelona on December 2004. Figure 13 shows some stages of the construction of the different inflatable modules of the pavilion and images of the transport, lay-out and inflating operations. Note the simplicity of the transport logistics, compared with the dimensions of the structure, involving a few bags easily carried in a mid-size vehicle. Figure 14 shows images of the outside and inside spaces of the pavilion containing a display of innovative concepts and products in modern art, fashion and information technologies.

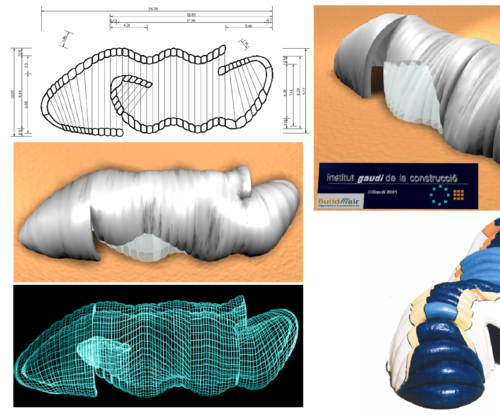
Figure 15 shows images of a mid-size inflatable pavilion (250m${\textstyle ^{2}}$) built for an itinerant exhibition on Gaudi. The exhibition visited some 20 cities in Spain in 2002. Some images of the outside and inside of the pavilion are shown in Fig 16. More details are given in [25].

Figure 17 shows images of an inflatable pavilion of ${\textstyle \approx 1000{\hbox{m}}^{2}}$ formed by assembling of 6 cylindrical halls. The pavilion was built in an old train station in Barcelona in December 2004 for an exhibition on the history of Civil Engineering in Catalonia. Some views of the pavilion entrance and the inside are shown in Fig.18. For more details of this inflatable pavilion see [25].

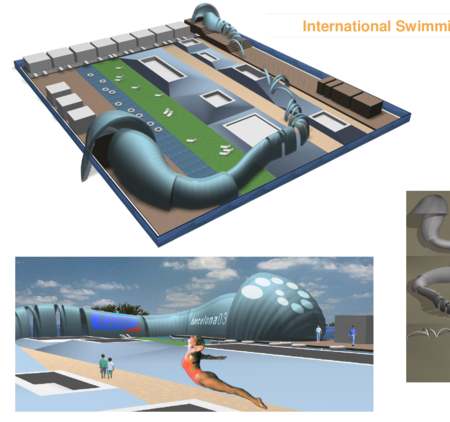
Figures 19 and 20 finally show images of designs of innovative inflatable pavilions and halls formed by low pressure inflatable tubes. The versatility of the tube assembly process allows the design and construction of quite complex shapes of artistic and architectural value in a simple and economical manner.

Figure 15: Pavilion for an itinerant Gaudi Exhibition in Spain. Geometry and lay-out of the inflation process

Figure 16: Inflatable pavilion for Gaudi Exhibition. Images of outside and inside spaces

Figure 17: Inflatable exhibition hall in Barcelona. Original design. Results of the aerodynamic analysis. Sewing of membrane patterns and final construction

Figure 18: Images of inflatable exhibition hall in Barcelona

Figure 19: Projects of low pressure inflatable pavilions. Above: pavilion for an international swimming competition. Below: mobile opera theatre

6 Concluding Remarks

We have presented in the paper the formulation of a rotation-free enhanced basic shell triangle (EBST) for analysis of thin membranes and inflatable structures. The element is based on an assumed constant curvature field expressed in terms of the nodal deflections of a patch of four elements and an assumed linear membrane strain field for the in-plane behaviour. A simple and economic version of the element using a single integration point has been presented. The element has proven to be an excellent candidate for solving practical problems in the design and analysis of low pressure inflatable structures under different loading conditions as demonstrated in the examples of application shown.

A large variety of membrane structures built by assembly of low pressure inflatable tubes has been presented showing the versalitiy and potential of this type of constructions in practice.

Acknowledgments

The second author is a member of the scientific staff of the Science Research Council of Argentina (CONICET). The financial support of CIMNE, CONICET and Agencia Córdoba Ciencia S.E. and the support of the companies QUANTECH ATZ SA (http://www.quantech.es/) and COMPASS Ingeniería y Sistemas SA (http://www.compassis.com/) providing the codes STAMPACK [31] and Tdyn [33] are gratefully acknowledged. Thanks are also given to BuildAir Ingeniería y Arquitectura SA (http://www.buildair.com/) for providing photographs of practical constructions of inflatable structures.

Figure 20: Projects of pavilions formed by low pressure inflatable tubes

References

[1] Inflatable structures for engineering and architecture applications. BuildAir Ingeniería y Arquitectura SA, www.buildair.com, 2007

[2] Plant RH, Liapis S, Telionis DP (1996) Flood Protection using Inflatable Dams. Natural Disaster Reduction Conference. Washington December 3-5:264-265

[3] Rehmet M, Bauder C, Schäfer, I Kröplin BH (1994) Solar Powered Airship Project. International Conference Remotely Piloted Vehicles, Bristol

[4] Beukers A, Molder OV, Vermeeren CAJR (2001) Inflatable Structures in Space Engineering. Journal of the IASS

[5] ILC Dover, World leader in innovative flexible solutions (2000). http://www.ilcdover.com

[6] New Methodologies for Design and Manufacturing of Inflated Structures (INFLAST) (Brite-Euram Contract NAº BRPR-CT97-0448). Consortium: CIMNE: BAZAN, S.A., CASA, S.A., NOVURANIA, S.p.A., IRD a/s, Universitat Stutt-gart, Airship Technologies, GmbH. Project finished on May 2000

[7] Sadeh WZ, Criswell ME A generic inflatable structure for a lunar/martian base. Proceeding of the Ebgineering, Construction and Operations in Space IV 1146-1156

[8] Nowak PS, Sadeh WZ, Morroni LA (1992), Geometric modeling of inflatable structures for lunar base. Journal of Aerospace Engineering 5(3):311-322

[9] Oñate E, Kröplin B (Eds.) (2003) Proceedings of the 1st. International Conference on Textile Composites and Inflatable Structures I, CIMNE, Barcelona

[10] Oñate E, Kröplin B (Eds.) (2005) Textile Composites and Inflatable Structures I, Springer, Netherlands

[11] Oñate E, Kröplin B (Eds.) (2005) Proceedings of the 2nd. International Conference on Textile Composites and Inflatable Structures II, CIMNE, Barcelona

[12] Taylor RL (2001) Finite element analysis of membrane structures. Publication 203, CIMNE, Barcelona

[13] Oñate E (1994) A review of some finite element families for thick and thin plate and shell analysis. Publication 53, CIMNE, Barcelona

[14] Hampshire JK, Topping BHV, Chan HC (1992) Three node triangular elements with one degree of freedom per node. Engng. Comput. 9:49–62,

[15] Phaal R, Calladine CR (1992) A simple class of finite elements for plate and shell problems. II: An element for thin shells with only translational degrees of freedom. Int. J. Num. Meth. Engng. 35:979–996

[16] Oñate E, Cervera M (1993) Derivation of thin plate bending elements with one degree of freedom per node. Engineering Computations 10:553–561

[17] Oñate E, Zárate F (2000) Rotation-free plate and shell triangles. Num. Meth. Engng. 47:557–603

[18] Cirak F, Ortiz M (2000) Subdivision surfaces: A new paradigm for thin-shell finite element analysis. Int. J Num. Meths. Engng. 47:2039–2072

[19] Flores FG, Oñate E (2001) A basic thin shell triangle with only translational DOFs for large strain plasticity. Int. J. Num. Meths. Engng. 51:57–83.

[20] Cirak F, Ortiz M (2001) Fully $C^{1}$-conforming subdivision elements for finite deformations thin-shell analysis. Num. Meths. Engng. 51:813–833

[21] Flores FG, Oñate E (2005) Improvements in the membrane behaviour of the three node rotation-free BST shell triangle using an assumed strain approach. Comput. Meth. Appl. Mech. Engng. 194(6–8):907–932

[22] Oñate E, Flores FG (2005) Advances in the formulation of the rotation-free basic shell triangle. Comput. Meth. Appl. Mech. Engng. 194(21-24):2406-2443

[23] Zienkiewicz OC, Taylor RL (2005) The finite element method. Vol II: Solid Mechanics, Oxford, Elsevier

[24] Ogden RW (1972) Large deformation isotropic elasticity: on the correlation of theory and experiments for incompressible rubberlike solids. Proc. Royal Society London A. 326:565–584

[25] Marcipar J, Oñate E, Miquel J (2005) Experiences in the design analysis and construction of low pressure inflatable structures. Textile Composites and Inflatable Structures I, E. Oñate and B. Kröplin (Eds.), Springer

[26] Flores F, Oñate E (2005) Applications of a rotation-free triangular element for finite strain analysis of thin shells and membranes. Textile Composites and Inflatable Structures I, E. Oñate and B. Kröplin (Eds.), Springer

[27] Pons J, Oñate E, Flores F, García J, Ribó R, Marcipar J (2005) Numerical and experimental values comparison for an inflatable structure. Textile Composites and Inflatable Structures II, E. Oñate and B. Kröplin (Eds.), CIMNE, Barcelona

[28] GiD. The personal pre/postprocessor (2007), CIMNE, Barcelona,

www.gidhome.com

[29] Needleman A (1977) Inflation of spherical rubber ballons. Solids and Structures 13:409–421

[30] Marklund PO, Nilsson L (2002) Simulation of airbag inflation processes using a coupled fluid structure approach. Computational Mechanics 29:289–297

[31] STAMPACK (2007) An explicit dynamic code for sheet stamping analysis. Quantech ATZ SA (www.quantech.es)

[32] A communication library for fluid-structure interaction analysis (2007). Compass Ingeniería y Sistemas SA, www.compassis.com

[33] Tdyn (2007) Finite element code for fluid dynamics and thermal analysis. Compass Ingeniería y Sistemas SA, www.compassis.com