Extended rotation-free plate and beam elements with shear deformation effects

Published in Int. Journal for Numerical Methods in Engineering Vol. 83 (2), pp.196-227, 2010
doi: 10.1002/nme.2836

Abstract

The paper describes a methodology for extending rotation-free plate and beam elements in order to accounting for transverse shear deformation effects. The ingredients for the element formulation are: a Hu-Washizu type mixed functional, a linear interpolation for the deflection and the shear angles over standard finite elements and a finite volume approach for computing the bending moments and the curvatures over a patch of elements. As a first application of the general procedure we present an extension of the 3-noded rotation-free basic plate triangle (BPT) originally developed for thin plate analysis to accounting for shear deformation effects of relevance for thick plates and composite laminated plates. The nodal deflection degrees of freedom (DOFs) of the original BPT element are enhanced with the two shear deformation angles. This allows to computing the bending and shear deformation energies leading to a simple triangular plate element with 3 DOFs per node (termed BPT+ element). For the thin plate case the shear angles vanish and the element reproduces the good behaviour of the original thin BPT element. As a consequence the element is applicable to thick and thin plate situations without exhibiting shear locking effects. The numerical solution for the thick case can be found iteratively starting from the deflection values for the Kirchhoff theory using the original thin BPT element. A 2-noded rotation-free beam element termed CCB+ applicable to slender and thick beams is derived as a particular case of the plate formulation. The examples presented show the robustness and accuracy of the BPT+ and the CCB+ elements for thick and thin plate and beam problems.

Keywords: Rotation-free triangle, rotation-free beam, thick and thin plates and beams, finite elements, shear deformation

1 INTRODUCTION

In past years some authors have derived a number of thin plate and shell triangular elements free of rotational degrees of freedom (DOFs) based on Kirchhoff theory [1]–[24]. This idea goes back to the original attempts to solve thin plate bending problems using finite difference schemes with the deflection as the only nodal variable [25]–[27]. In essence all methods attempt to express the curvature field over an element in terms of the displacements of a collection of nodes belonging to a patch of adjacent elements. Oñate and Cervera [6] proposed a general procedure of this kind combining finite element and finite volume concepts for deriving thin plate triangles and quadrilaterals with the deflection as the only nodal variable and presented a simple and competitive rotation-free three DOFs triangular element termed BPT (for Basic Plate Triangle). These ideas were extended in [12] to derive a number of rotation-free thin plate and shell triangles. The basic ingredients of the method are a mixed Hu-Washizu formulation, a standard discretization into three-noded triangles, a linear finite element interpolation of the displacement field within each triangle and a finite volume type approach for computing constant curvature and bending moment fields within appropriate non-overlapping control domains. The so called cell-centered and cell-vertex triangular domains yield different families of rotation-free plate and shell triangles. Both the BPT plate element and its extension to shell analysis (termed BST for Basic Shell Triangle) can be derived from the cell-centered formulation. Here the control domain is an individual triangle. The constant curvature field within a triangle is computed in terms of the displacements of the six nodes belonging to the four element patch formed by the chosen triangle and the three adjacent triangles. In the cell-vertex approach the control volume is the tributary domain of a node and this leads to a different family of rotation-free plate and shell triangles. The detailed derivation of the different rotation-free triangular plate and shell element families can be found in [12]. The three-noded BST element has been successfully extended to non-linear shell problems involving frictional-contact situations and dynamics [15,19,20]. Practical applications of the BST element to sheet stamping analysis are reported in [9,10,11,24].

The paper describes an extension of the original rotation-free thin BPT element to accounting for transverse shear deformation effects of relevance for thick plates and composite laminated plates. The nodal deflection DOFs of the original BPT element are enhanced with the two shear deformation angles. This allows to computing the bending and shear deformation energies leading to a simple triangular plate element with 3 DOFs per node (termed BPT+ element). For the thin plate case the shear angles vanish and the element reproduces the good behaviour of the original thin BPT element. As a consequence the element is applicable to thick and thin plate situations without exhibiting shear locking. It is interesting that the thick plate solution can be found iteratively starting from the deflection values obtained using the standard Kirchhoff theory and the original thin BPT element. The ingredients of the formulation are: a Hu-Washizu type mixed functional, a linear interpolation for the deflection and the shear angles over 3-noded triangles and a finite volume approach for computing the bending moments and the curvatures over a patch of elements. Details of the element formulation are given in the paper.

The rotation-free formulation described for the BPT+ element is taken as the starting point for deriving a two-noded rotation-free beam element with shear deformation effects (termed CCB+ element). The examples presented in the last part of the paper show the robustness and accuracy of the BPT+ and the CCB+ elements for thick and thin plate and beam problems.

2 BASIC THEORY

2.1 Reissner-Mindlin plate theory

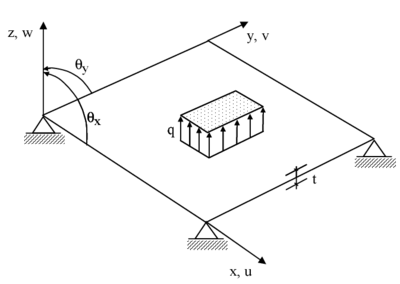
Let us consider the plate of Figure 1. We will assume Reissner-Mindlin conditions to hold, i.e.

$u(x,y,z)=-z\theta _{x}(x,y)\quad ,\quad v(x,y,z)=-z\theta _{y}(x,y)\quad ,\quad w(x,y,z)=w(x,y)$

(1)

with

$\theta _{x}={\partial w \over \partial x}+\phi _{x}\quad ,\quad \theta _{y}={\partial w \over \partial y}+\phi _{y}$

(2.a)

or

${\boldsymbol {\theta }}=[\theta _{x},\theta _{y}]^{T}={\boldsymbol {\nabla }}w+{\boldsymbol {\phi }}$

(2.b)

with

${\boldsymbol {\nabla }}=\left[{\partial \over \partial x},{\partial \over \partial y}\right]^{T}\quad {\hbox{and}}\quad {\boldsymbol {\phi }}=[\phi _{x},\phi _{y}]^{T}$

(2.c)

where ${\textstyle u,v,w}$ are the cartesian displacements ${\textstyle \theta _{x}}$, ${\textstyle \theta _{y}}$ are the rotations and ${\textstyle \phi _{x}}$, ${\textstyle \phi _{y}}$ are angles coinciding with the transverse shear deformations as shown below.

Figure 1: Sign convenion for the deflection and the rotations in a plate

The generalized bending and shear strain vectors are defined as [29,30]

${\boldsymbol {\varepsilon }}_{b}=[\kappa _{x},\kappa _{y},\kappa _{xy}]^{T}={\begin{bmatrix}\displaystyle {\partial \theta _{x} \over \partial x},&\displaystyle {\partial \theta _{y} \over \partial y},&\displaystyle \left({\partial \theta _{x} \over \partial y}+{\partial \theta _{y} \over \partial x}\right)\end{bmatrix}}^{T}={\boldsymbol {L}}_{b}{\boldsymbol {\theta }}$

(3.a)

${\boldsymbol {\varepsilon }}_{s}=[\gamma _{xz},\gamma _{yz}]^{T}={\begin{bmatrix}\displaystyle {\partial w \over \partial x}-\theta _{x},&\displaystyle {\partial w \over \partial y}-\theta _{y}\end{bmatrix}}^{T}={\boldsymbol {L}}_{s}{\boldsymbol {u}}$

(3.b)

where ${\textstyle [\kappa _{x},\kappa _{y},\kappa _{xy}]}$ and ${\textstyle [\gamma _{xz},\gamma _{yz}]}$ denote the bending strains (typically called curvatures) and the transverse shear strains, respectively and

${\boldsymbol {L}}_{b}={\begin{bmatrix}\displaystyle {\partial \over \partial x}&0\\[.3cm]0&\displaystyle {\partial \over \partial y}\\[.3cm]\displaystyle {\partial \over \partial y}&\displaystyle {\partial \over \partial x}\\\end{bmatrix}}\quad ,\quad {\boldsymbol {L}}_{s}={\begin{bmatrix}\displaystyle {\partial \over \partial x}&-1&0\\[.3cm]\displaystyle {\partial \over \partial y}&0&-1\\\end{bmatrix}}\quad ,\quad {\boldsymbol {u}}=\left\{{\begin{array}{c}w\\\theta _{x}\\\theta _{y}\end{array}}\right\}$

(4)

Substituting Eq.(2.a) into (3.b) gives

$\gamma _{xz}=-\phi _{x}\quad \quad ,\quad \quad \gamma _{yz}=-\phi _{y}$

(5)

i.e. the angles ${\textstyle \phi _{x}}$, ${\textstyle \phi _{y}}$ coincide (with opposite sign) with the transverse shear deformations. In the following ${\textstyle \phi _{x}}$ and ${\textstyle \phi _{y}}$ will be called“shear angles”.

The set of governing equations can be expressed in integral form starting from the following Hu-Washizu type functional [12,28]

${\begin{array}{ll}\Pi =&\displaystyle {1 \over 2}\left[\iint _{A}{\boldsymbol {\varepsilon }}_{b}^{T}{\boldsymbol {D}}_{b}{\boldsymbol {\varepsilon }}_{b}\,dA+\iint _{A}{\boldsymbol {\varepsilon }}_{s}^{T}{\boldsymbol {\sigma }}_{s}\,dA\right]+\iint _{A}[{\boldsymbol {L}}_{b}{\boldsymbol {\theta }}-{\boldsymbol {\varepsilon }}_{b}]^{T}{\boldsymbol {\sigma }}_{b}\,dA-\\&-\iint _{A}(qw+{\boldsymbol {\theta }}^{T}{\boldsymbol {m}})dA-\sum \limits _{i=1}^{n_{c}}w_{i}P_{i}\end{array}}$

(6)

where ${\textstyle q}$ is the distributed vertical loading, ${\textstyle {\boldsymbol {m}}=[m_{x},m_{y}]^{T}}$ are distributed bending moments, ${\textstyle P_{i}}$ is the vertical force acting at point ${\textstyle i}$, ${\textstyle n_{c}}$ is the number of points with external concentrated forces and ${\textstyle A}$ is the area of the plate. Concentrated bending moments have been excluded for simplicity.

In Eq.(6) ${\textstyle {\boldsymbol {\sigma }}_{b}=[M_{x},M_{y},M_{xy}]^{T}}$ is the bending moment vector, ${\textstyle {\boldsymbol {\sigma }}_{s}=[Q_{x},Q_{y}]^{T}}$ is the shear force vector and ${\textstyle {\boldsymbol {D}}_{b}}$ is the bending constitutive matrix given by (for the isotropy case)

${\boldsymbol {D}}_{b}=\displaystyle {{E}t^{3} \over 12(1-\nu ^{2})}\left[{\begin{array}{ccc}1&\nu &0\\\nu &1&0\\0&0&{1-\nu \over 2}\\\end{array}}\right]$

(7.a)

The shear forces and the shear strains are assumed to be related point-wise by the standard constitutive equation

${\boldsymbol {\sigma }}_{s}={\boldsymbol {D}}_{s}{\boldsymbol {\varepsilon }}_{s}\quad {\hbox{with}}\quad {\boldsymbol {D}}_{s}=\alpha Gt\left[{\begin{array}{cc}1&0\\0&1\\\end{array}}\right]$

(7.b)

In Eqs.(7) ${\textstyle t}$ is the plate thickness and ${\textstyle E,\nu }$ and ${\textstyle G}$ are the Young modulus, the Poisson's ratio and the shear modulus, respectively and ${\textstyle \alpha }$ is the shear correction factor; ${\textstyle \alpha =5/6}$ is taken for an isotropic plate.

2.2 Using the deflection and the shear angles as main variables

Let us express Eqs.(3)–(6) in terms of the deflection ${\textstyle w}$ and the shear angles ${\textstyle \phi _{x}}$ and ${\textstyle \phi _{y}}$. The resulting Reissner-Mindlin theory contains the standard expressions of Kirchhoff thin plate theory plus additional transverse shear deformation terms.

Substituting Eq.(2) into Eqs.(3) gives

${\boldsymbol {\varepsilon }}_{b}={\boldsymbol {L}}_{b}{\boldsymbol {\theta }}=\left[{\frac {\partial ^{2}w}{\partial x^{2}}}+{\partial \phi _{x} \over \partial x},{\frac {\partial ^{2}w}{\partial y^{2}}}+{\partial \phi _{y} \over \partial y},2{\frac {\partial ^{2}w}{x\partial y}}+\left({\partial \phi _{x} \over \partial y}+{\partial \phi _{y} \over \partial x}\right)\right]^{T}={\boldsymbol {L}}_{w}w+{\boldsymbol {L}}_{b}{\boldsymbol {\phi }}$ ${\boldsymbol {\varepsilon }}_{s}={\boldsymbol {L}}_{s}{\boldsymbol {u}}=[-\phi _{x},-\phi _{y}]^{T}=-{\boldsymbol {\phi }}$

(8)

with

${\boldsymbol {L}}_{w}=\left[{\frac {\partial ^{2}}{\partial x^{2}}},{\frac {\partial ^{2}}{\partial y^{2}}},2{\frac {\partial ^{2}}{x\partial y}}\right]^{T}$

(9)

Substituting Eqs.(2.b) and (8) into the functional of Eq.(6) gives

${\begin{array}{ll}\Pi =&\!\!\!\!\displaystyle {1 \over 2}\left[\iint _{A}{\boldsymbol {\varepsilon }}_{b}^{T}{\boldsymbol {D}}_{b}{\boldsymbol {\varepsilon }}_{b}\,dA-\iint _{A}{\boldsymbol {\phi }}^{T}{\boldsymbol {\sigma }}_{s}\right]+\iint _{A}[{\boldsymbol {L}}_{w}w+{\boldsymbol {L}}_{b}{\boldsymbol {\phi }}-{\boldsymbol {\varepsilon }}_{b}]^{T}{\boldsymbol {\sigma }}_{b}\,dA+\\[.4cm]&\displaystyle -\!\!\iint _{A}[qw+({\boldsymbol {\nabla }}w+{\boldsymbol {\phi }})^{T}{\boldsymbol {m}}]dA-\!\sum \limits _{i=1}^{n_{c}}w_{i}P_{i}\end{array}}$

(10)

Note that by making the shear angles ${\textstyle {\boldsymbol {\phi }}}$ equal to zero we recover precisely the variational form of standard Kirchhoff thin plate theory [29].

Variation of ${\textstyle \Pi }$ with respect to ${\textstyle {\boldsymbol {\varepsilon }}_{b}}$, ${\textstyle {\boldsymbol {\sigma }}_{b}}$, ${\textstyle w}$ and ${\textstyle {\boldsymbol {\phi }}}$ leads to the following equations:

Bending constitutive equation

$\iint _{A}\delta {\boldsymbol {\varepsilon }}_{b}^{T}[{\boldsymbol {D}}_{b}{\boldsymbol {\varepsilon }}_{b}-{\boldsymbol {\sigma }}_{b}]\,dA=0$

(11)

Relationship between bending strains, deflection and shear angles

$\iint _{A}\delta {\boldsymbol {\sigma }}_{b}^{T}[{\boldsymbol {L}}_{w}w+{\boldsymbol {L}}_{b}{\boldsymbol {\phi }}-{\boldsymbol {\varepsilon }}_{b}]\,dA=0$

(12)

Equilibrium equations

$\iint _{A}[{\boldsymbol {L}}_{w}\delta w]^{T}{\boldsymbol {\sigma }}_{b}\,dA-\iint _{A}[\delta wq+({\boldsymbol {\nabla }}\delta w)^{T}{\boldsymbol {m}}]\,dA-\sum \limits _{i=1}^{n_{c}}\delta w_{i}P_{i}=0$ (13.a) $\iint _{A}\left[({\boldsymbol {L}}_{b}\delta {\boldsymbol {\phi }})^{T}{\boldsymbol {\sigma }}_{b}-\delta {\boldsymbol {\phi }}^{T}{\boldsymbol {\sigma }}_{s}\right]dA-\iint _{A}\delta {\boldsymbol {\phi }}^{T}{\boldsymbol {m}}\,dA=0$ (13.b)

These integral expressions, completed with the constitutive equation for the shear forces (Eq.(7.b)), are the basis for deriving the element equations.

3 THREE-NODED BASIC ROTATION-FREE PLATE TRIANGLE WITH SHEAR DEFORMATION EFFECTS

Let us consider an arbitrary discretization of the plate into standard three-noded triangles. We assume a linear interpolation of the deflection ${\textstyle w}$ and the shear angles ${\textstyle {\boldsymbol {\phi }}}$ within each element in terms of the nodal values in the standard manner [28]

$w=\sum \limits _{i=1}^{3}N_{i}{\bar {w}}_{i}\quad ,\quad {\boldsymbol {\phi }}=\left\{{\begin{array}{c}\phi _{x}\\\phi _{y}\end{array}}\right\}=\sum \limits _{i=1}^{3}\mathbf {N} _{i}{\bar {\boldsymbol {\phi }}}_{i}={\boldsymbol {N}}_{\phi }{\bar {\boldsymbol {\phi }}}^{e}$

(14)

where ${\textstyle N_{i}}$ are the linear shape functions of the three-noded triangle [28,30], ${\textstyle {\bar {(\cdot )}}}$ denotes nodal variables and

$\mathbf {N} _{\phi }=[\mathbf {N} _{1},\mathbf {N} _{2},\mathbf {N} _{3}]\quad ,\quad \mathbf {N} _{i}=N_{i}{\boldsymbol {I}}_{2}\quad ,\quad \mathbf {I} _{2}=\left[{\begin{array}{cc}1&0\\0&1\\\end{array}}\right]$

(15.a)

${\bar {\boldsymbol {\phi }}}^{e}=\left\{{\begin{array}{c}{\bar {\boldsymbol {\phi }}}_{1}\\{\bar {\boldsymbol {\phi }}}_{2}\\{\bar {\boldsymbol {\phi }}}_{3}\\\end{array}}\right\}\quad ,\quad {\bar {\boldsymbol {\phi }}}_{i}=\left\{{\begin{array}{c}{\bar {\phi }}_{x_{i}}\\{\bar {\phi }}_{y_{i}}\end{array}}\right\}$

(15.b)

with

${\begin{array}{c}N_{i}=\displaystyle {1 \over 2A^{e}}(a_{i}^{e}+b_{i}^{e}x+c_{i}^{e}y),\\[.3cm]a_{i}^{e}=x_{j}^{e}y_{k}^{e}-x_{k}^{e}y_{j}^{e}\,,\,b_{i}^{e}=y_{jk}\,,\,c_{i}^{e}=x_{kj}\quad {\hbox{with }}y_{jk}=y_{j}^{e}-y_{k}^{e}\,,\,x_{kj}=x_{k}^{e}-x_{j}^{e}\quad i,j,k=1,2,3\end{array}}$

(15.c)

and ${\textstyle A^{e}}$ is the element area [28]. In the above expressions and in the following super-index ${\textstyle e}$ denotes element values.

Note that the introduction of the linear approximation for ${\textstyle w}$ into the variational form (13a) will give a vanishing of the virtual bending energy term involving second derivatives of ${\textstyle w}$. This problem is overcome by “relaxing” further the weak form using an assumed constant value for the curvatures and bending moments over the triangle and computing the curvatures from the integral of the slopes along the element sides as explained next.

3.1 Assumed curvatures and bending moments field

We describe the bending moments ${\textstyle {\boldsymbol {\sigma }}_{b}}$ and the curvatures ${\textstyle {\boldsymbol {\varepsilon }}_{b}}$ (and their virtual values) by constant fields within the triangle, i.e.

${\begin{array}{ccc}{\boldsymbol {\sigma }}_{b}={\boldsymbol {\sigma }}_{b}^{e}&,&{\boldsymbol {\varepsilon }}_{b}={\boldsymbol {\varepsilon }}_{b}^{e}\\\delta {\boldsymbol {\sigma }}_{b}=\delta {\boldsymbol {\sigma }}_{b}^{e}&,&\delta {\boldsymbol {\varepsilon }}_{b}=\delta {\boldsymbol {\varepsilon }}_{b}^{e}\end{array}}$

(16)

where ${\textstyle (\cdot )^{e}}$ denotes constant values within the triangle.

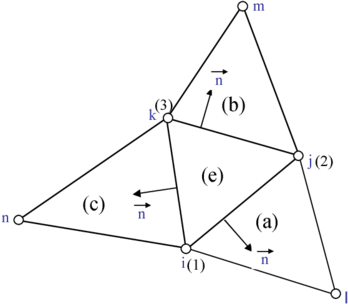
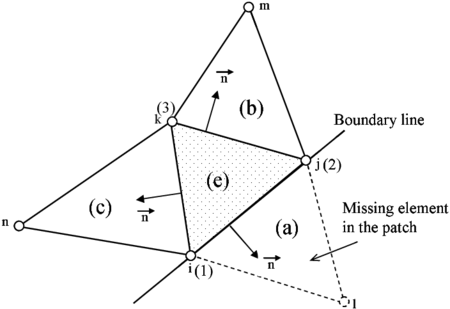
We define the term “patch of triangular elements”. This is typically formed by four elements: a central triangle and the three adjacent triangles. Central triangles adjacent to a boundary lack the element adjacent to the boundary side (Figure 2).

Eqs.(16) are introduced into the governing integral equations (11)–(13) which are modified as follows.

Constitutive equation for the bending moments

$\sum \limits _{e}\iint _{A^{e}}(\delta {\boldsymbol {\varepsilon }}_{b}^{e})^{T}[{\boldsymbol {D}}_{b}{\boldsymbol {\varepsilon }}_{b}^{e}-{\boldsymbol {\sigma }}_{b}^{e}]\,dA=0$

(17)

Recalling that the virtual curvatures are arbitrary we obtain the following constitutive equations for the assumed (constant) bending moments for each element

${\boldsymbol {\sigma }}_{b}^{e}={\boldsymbol {D}}_{b}^{e}{\boldsymbol {\varepsilon }}_{b}^{e}\quad ,\quad {\boldsymbol {D}}_{b}^{e}={1 \over A^{e}}\iint _{A}{\boldsymbol {D}}_{b}\,dA$

(18)

where ${\textstyle {\boldsymbol {D}}_{b}^{e}}$ is the average bending constitutive matrix for the triangular element.

Relationship between the bending strains, the deflection and the shear angles

Substituting Eqs.(16) into Eq.(12) gives

$\sum \limits _{e}\iint _{A^{e}}(\delta {\boldsymbol {\sigma }}_{b}^{e})^{T}[{\boldsymbol {L}}_{w}w+{\boldsymbol {L}}_{b}{\boldsymbol {\phi }}-{\boldsymbol {\varepsilon }}_{b}^{e}]\,dA=0$

(19)

(a)	(b)
Figure 2: Triangular element patches. (a) Standard four element patch; (b) Three element boundary patch. Numbers 1,2,3 in brackets denote local node numbers for the element

As the virtual bending moments are arbitrary and ${\textstyle {\boldsymbol {\varepsilon }}_{b}^{e}}$ is constant within each element we get

${\boldsymbol {\varepsilon }}_{b}^{e}={1 \over A^{e}}\iint _{A^{e}}[{\boldsymbol {L}}_{w}w+{\boldsymbol {L}}_{b}{\boldsymbol {\phi }}]\,dA$

(20)

The term ${\textstyle {\boldsymbol {L}}_{w}w}$ in Eq.(20) is integrated by parts to give

$\displaystyle {\boldsymbol {\varepsilon }}_{b}^{e}={1 \over A^{e}}\left[\int _{\Gamma ^{e}}{\boldsymbol {T}}{\boldsymbol {\nabla }}w\,d\Gamma +\iint _{A^{e}}{\boldsymbol {L}}_{b}{\boldsymbol {\phi }}\,dA\right]$

(21)

where

${\boldsymbol {T}}={\begin{bmatrix}n_{x}&0\\0&n_{y}\\n_{y}&n_{x}\end{bmatrix}}$

(22)

and ${\textstyle n_{x},n_{y}}$ are the components to the outward unit normal ${\textstyle {\boldsymbol {n}}}$ to the boundary of the element ${\textstyle \Gamma ^{e}}$ (Figure 2). The transformation of the integral of the curvature field over the element domain into the integral of the deflection gradient along the element boundary is a distinct feature of the BPT formulation [6,12,15,19,20].

Eq.(21) defines the bending strains as the sum of the integral of the deflection gradient along the boundary of the element and the integral over the element of the term ${\textstyle {\boldsymbol {L}}_{b}{\boldsymbol {\phi }}}$ including the gradients of the shear deformation angles. This term is constant within each element for a linear interpolation of ${\textstyle {\boldsymbol {\phi }}}$.

Shear forces-shear angles relationship

Making ${\textstyle {\boldsymbol {\varepsilon }}_{s}=-{\boldsymbol {\phi }}}$ (Eq.(8)) and substituting the approximation for ${\textstyle {\boldsymbol {\phi }}}$ of Eq.(14) into Eq.(7.b) gives

${\boldsymbol {\sigma }}_{s}={\boldsymbol {D}}_{s}{\boldsymbol {\varepsilon }}_{s}=-{\boldsymbol {D}}_{s}{\boldsymbol {\phi }}=-{\boldsymbol {D}}_{s}{\boldsymbol {N}}_{\phi }{\bar {\boldsymbol {\phi }}}^{e}$

(23)

Equilibrium equations

Integrating by parts the first integral in Eq.(13.a) and recalling that the bending moments are constant within each element and the additive property of the element integrals in the FEM, allows us to write Eqs.(13) as

$\sum \limits _{e}\left(\int _{\Gamma ^{e}}{\boldsymbol {T}}({\boldsymbol {\nabla }}\delta w)^{T}\,d\Gamma \right){\boldsymbol {\sigma }}_{b}^{e}-\iint _{A}\left[\delta wq+\left({\boldsymbol {\nabla }}\delta w\right)^{T}{\boldsymbol {m}}\right]\,dA+\sum \limits _{i=1}^{n_{c}}\delta w_{i}P_{i}=0$ (24) $\sum \limits _{e}\left\{\left(\iint _{A^{e}}({\boldsymbol {L}}_{b}{\boldsymbol {\phi }})^{T}dA\right){\boldsymbol {\sigma }}_{b}^{e}-\iint _{A^{e}}\delta {\boldsymbol {\phi }}^{T}{\boldsymbol {\sigma }}_{s}dA\right\}-\iint _{A}\delta {\boldsymbol {\phi }}^{T}{\boldsymbol {m}}\,dA=0$ (25)

The sum in above expressions extends over all the elements in the mesh.

Bending strain matrices

Substituting the linear interpolation for ${\textstyle w}$ and ${\textstyle {\boldsymbol {\phi }}}$ of Eqs.(14) into the integral expressions for the constant bending strain field of Eq.(21) gives

${1 \over A^{e}}\int _{\Gamma ^{e}}{\boldsymbol {T}}{\boldsymbol {\nabla }}wd\Gamma ={\boldsymbol {B}}_{w}{\bar {\boldsymbol {w}}}^{e}$

(26.a)

${1 \over A^{e}}\iint _{A^{e}}{\boldsymbol {L}}_{b}{\boldsymbol {\phi }}dA={\boldsymbol {B}}_{\phi }{\bar {\boldsymbol {\phi }}}^{e}$

(26.b)

and, therefore

${\boldsymbol {\varepsilon }}_{b}^{e}={\boldsymbol {B}}_{w}{\bar {\boldsymbol {w}}}^{e}+{\boldsymbol {B}}_{\phi }{\bar {\boldsymbol {\phi }}}^{e}$

(27)

where ${\textstyle {\boldsymbol {B}}_{w}}$ and ${\textstyle {\boldsymbol {B}}_{\phi }}$ are generalized bending strain matrices and ${\textstyle {\bar {\boldsymbol {w}}}^{e}}$ and ${\textstyle {\bar {\boldsymbol {\phi }}}^{e}}$ are nodal deflection and nodal shear angles vectors for the element. The expression for ${\textstyle {\bar {\boldsymbol {\phi }}}^{e}}$ is given in Eq.(15.b). The expression for ${\textstyle {\bar {\boldsymbol {w}}}^{e}}$ is given below (Eq.(31)).

The computation of ${\textstyle {\boldsymbol {B}}_{\phi }}$ is straightforward from the second integral of Eq.(21) as

${\boldsymbol {B}}_{\phi }=[{\boldsymbol {B}}_{\phi _{1}},{\boldsymbol {B}}_{\phi _{2}},{\boldsymbol {B}}_{\phi _{3}}]\qquad {\hbox{with }}\qquad {\boldsymbol {B}}_{\phi _{i}}={1 \over A^{e}}\iint _{A^{e}}{\boldsymbol {L}}_{b}{N}_{i}\,d\Omega$

(28)

Recalling that ${\textstyle N_{i}}$ are linear shape functions gives (using Eq.(15.c))

${\boldsymbol {B}}_{\phi _{i}}={\begin{bmatrix}\displaystyle {\partial N_{i} \over \partial x}&0\\[.25cm]0&\displaystyle {\partial N_{i} \over \partial x}\\[.45cm]\displaystyle {\partial N_{i} \over \partial y}&\displaystyle {\partial N_{i} \over \partial x}\\\end{bmatrix}}={1 \over 2A^{e}}{\begin{bmatrix}b_{i}^{e}&0\\0&c_{i}^{e}\\c_{i}^{e}&b_{i}^{e}\\\end{bmatrix}}$

(29)

The computation of ${\textstyle {\boldsymbol {B}}_{w}^{e}}$ in Eq.(26.a) requires integrating the product of the components of the normal vector and the deflection slopes along the element sides. For the 3-noded triangle this is not so straightforward as ${\textstyle {\boldsymbol {\nabla }}w}$ is discontinuous at the element sides for a linear approximation of ${\textstyle w}$. A simple way to overcoming this problem is to compute the deflection gradients at the

${\boldsymbol {B}}_{w}={1 \over A^{e}}\left[{\begin{matrix}y_{ij}{\bar {b}}_{i}^{b}+y_{ki}{\bar {b}}_{i}^{d}&y_{ij}{\bar {b}}_{j}^{b}+y_{jk}{\bar {b}}_{j}^{c}&y_{jk}{\bar {b}}_{k}^{c}+y_{ki}{\bar {b}}_{k}^{d}\\-x_{ij}{\bar {c}}_{i}^{b}-x_{ki}{\bar {c}}_{i}^{d}&-x_{ij}{\bar {c}}_{j}^{b}-x_{jk}{\bar {c}}_{j}^{c}&-x_{jk}{\bar {c}}_{k}^{c}-x_{ki}{\bar {c}}_{k}^{d}\\[][y_{ij}{\bar {c}}_{i}^{b}-x_{ij}{\bar {b}}_{i}^{b}&[y_{ij}{\bar {c}}_{j}^{b}-x_{jk}{\bar {b}}_{j}^{b}&[y_{jk}{\bar {c}}_{k}^{c}-x_{jk}{\bar {b}}_{k}^{c}\\+y_{ki}{\bar {c}}_{i}^{d}-x_{ki}{\bar {b}}_{i}^{d}]&+y_{jk}{\bar {c}}_{j}^{c}-x_{jk}{\bar {b}}_{j}^{c}]&+y_{ki}{\bar {c}}_{k}^{d}-x_{ki}{\bar {b}}_{k}^{d}]\end{matrix}}\right.$

$\left.{\begin{matrix}y_{ij}{\bar {b}}_{l}^{b}&y_{jk}{\bar {b}}_{m}^{c}&y_{ki}{\bar {b}}_{n}^{d}\\-x_{ij}{\bar {c}}_{l}^{b}&-x_{jk}{\bar {c}}_{m}^{c}&-x_{ki}{\bar {c}}_{n}^{d}\\y_{ij}{\bar {c}}_{l}^{b}-x_{ij}{\bar {b}}_{l}^{b}&y_{jk}{\bar {c}}_{m}^{c}-x_{jk}{\bar {b}}_{m}^{c}&y_{ki}{\bar {c}}_{n}^{d}-x_{ki}{\bar {c}}_{n}^{d}\\\end{matrix}}\right]$

${\bar {b}}_{i}^{p}={{b_{i}^{p}} \over 2A^{p}},\quad {\bar {c}}_{i}^{p}={{c_{i}^{p}} \over 2A^{p}},\quad b_{i}^{p}=y_{j}^{p}-y_{k}^{p}\quad c_{i}^{p}=x_{k}^{p}-x_{j}^{p},{\hbox{etc.}},\quad p=a,b,c\quad i,j,k=1,2,3$

element sides as the average value of the gradients contributed by the two triangles adjacent to the side [6,12]. This gives

${1 \over A^{e}}\int _{\Gamma ^{e}}{\boldsymbol {T}}{\boldsymbol {\nabla }}wd\Gamma ={1 \over A^{e}}\sum \limits _{j=1}^{3}{l_{j}^{e} \over 2}{\boldsymbol {T}}_{j}\left[\sum \limits _{i=1}^{3}{\boldsymbol {\nabla }}N_{i}^{e}w_{i}^{e}+\sum \limits _{i=1}^{3}{\boldsymbol {\nabla }}N_{i}^{p}w_{i}^{p}\right]_{j}={\boldsymbol {B}}_{w}{\bar {\boldsymbol {w}}}^{e}$

(30)

with

${\bar {\boldsymbol {w}}}^{e}=[{\bar {w}}_{i}^{e},{\bar {w}}_{j}^{e},{\bar {w}}_{k}^{e},{\bar {w}}_{l}^{e},{\bar {w}}_{m}^{e},{\bar {w}}_{n}^{e}]^{T}$

(31)

The sum in Eq.(30) extends over the three sides of an element ${\textstyle e}$, ${\textstyle {\boldsymbol {T}}_{j}}$ is the transformation matrix of Eq.(22) for side ${\textstyle j}$, ${\textstyle l_{j}^{e}}$ are the lengths of the element sides and superindex ${\textstyle p}$ refers to each of the three triangles ${\textstyle a,b,c}$ adjacent to the central triangle ${\textstyle e}$ with ${\textstyle p=a,b,c}$ for ${\textstyle j=1,2,3}$ (Figure 2). Sides are assigned the number of the opposite node. Thus, side ${\textstyle l_{3}^{e}}$ is opposite to node 3, etc.

Note that ${\textstyle {\boldsymbol {B}}_{w}}$ is a ${\textstyle 3\times 6}$ matrix relating the three bending strains with the deflections at the six nodes of the patch of triangles linked to element ${\textstyle e}$. The explicit form of matrix ${\textstyle {\boldsymbol {B}}_{w}}$ is given in Box I. This matrix coincides with the curvature matrix of the original BPT element, as presented in [12].

Substituting Eq.(27) into (18) gives the relationship between the bending moments and the nodal values of the deflection and the shear angles for the element as

${\boldsymbol {\sigma }}_{b}^{e}={\boldsymbol {D}}_{b}^{e}[{\boldsymbol {B}}_{w}{\bar {\boldsymbol {w}}}^{e}+{\boldsymbol {B}}_{\phi }{\bar {\boldsymbol {\phi }}}^{e}]$

(32)

Stiffness matrices and nodal force vectors

Substituting Eqs.(14), (23), (26) and (32) into the equilibrium equations (24) and (25) yields

$\sum \limits _{e}(\delta {\bar {\boldsymbol {w}}}^{e})^{T}{\boldsymbol {B}}_{w}^{T}{\boldsymbol {D}}_{b}^{e}\left[{\boldsymbol {B}}_{w}{\bar {\boldsymbol {w}}}^{e}+{\boldsymbol {B}}_{\phi }{\bar {\boldsymbol {\phi }}}^{e}\right]A^{e}-$ $-\iint _{A}\left[\left(\sum \limits _{i=1}^{3}N_{i}\delta {\bar {w}}_{i}\right)q+\left(\sum \limits _{i=1}^{3}{\boldsymbol {\nabla }}N_{i}\delta {\bar {w}}_{i}\right)^{T}{\boldsymbol {m}}\right]\,dA+\sum \limits _{i=1}^{n_{c}}\delta {\bar {w}}_{i}P_{i}=0$

(33.a)

$\sum \limits _{e}(\delta {\bar {\boldsymbol {\phi }}}^{e})^{T}\left\{{\boldsymbol {B}}_{\phi }^{T}{\boldsymbol {D}}_{b}^{e}\left[{\boldsymbol {B}}_{w}{\bar {\boldsymbol {w}}}^{e}+{\boldsymbol {B}}_{\phi }{\bar {\boldsymbol {\phi }}}^{e}\right]A^{e}+\left(\iint _{A^{e}}{\boldsymbol {N}}_{\phi }^{T}{\boldsymbol {D}}_{s}{\boldsymbol {N}}_{\phi }dA\right){\bar {\boldsymbol {\phi }}}^{e}\right\}-$ $-\iint _{A}\left(\sum \limits _{i=1}^{3}{\boldsymbol {N}}_{i}\delta {\bar {\boldsymbol {\phi }}}_{i}\right)^{T}{\boldsymbol {m}}\,dA=0$

(33.b)

After simplification of the virtual nodal deflections and the virtual nodal shear angles we obtain finally the matrix system of equilibrium equations

${\begin{array}{c}{\boldsymbol {K}}_{w}{\bar {\boldsymbol {w}}}+{\boldsymbol {K}}_{w\phi }{\bar {\boldsymbol {\phi }}}={\boldsymbol {f}}_{w}\\[.4cm]{\boldsymbol {K}}_{w\phi }^{T}{\bar {\boldsymbol {w}}}+{\boldsymbol {K}}_{\phi }{\bar {\boldsymbol {\phi }}}={\boldsymbol {f}}_{\phi }\end{array}}$

(34)

where vectors ${\textstyle {\bar {\boldsymbol {w}}}}$ and ${\textstyle {\bar {\boldsymbol {\phi }}}}$ contain the nodal deflections and the nodal shear angles for the whole mesh and the rest of the matrices and vectors are assembled from the element contributions given by

${\begin{array}{l}{\boldsymbol {K}}_{w_{ij}}^{e}=\displaystyle {\boldsymbol {B}}_{w_{i}}^{T}{\boldsymbol {D}}_{b}^{e}{\boldsymbol {B}}_{w_{j}}A^{e}\quad ,\quad {\boldsymbol {K}}_{w\phi _{ij}}^{e}={\boldsymbol {B}}_{w_{i}}^{T}{\boldsymbol {D}}_{b}^{e}{\boldsymbol {B}}_{\phi _{j}}A^{e}\\[.4cm]{\boldsymbol {K}}_{\phi _{ij}}^{e}=\displaystyle {\boldsymbol {B}}_{\phi _{i}}^{T}{\boldsymbol {D}}_{b}^{e}{\boldsymbol {B}}_{\phi _{j}}A^{e}+\iint _{A^{e}}{\boldsymbol {N}}_{i}^{T}{\boldsymbol {D}}_{s}{\boldsymbol {N}}_{j}\,dA\end{array}}$

(35)

The element stiffness matrices ${\textstyle {\boldsymbol {K}}_{w}^{e}}$ and ${\textstyle {\boldsymbol {K}}_{w\phi }^{e}}$ can be explicitly computed from the strain and constitutive matrices for the element. The exact computation of the integral in the expression of ${\textstyle {\boldsymbol {K}}_{\phi }}$ requires a 3 Gauss point quadrature. Excellent results have been obtained in all examples analyzed using a reduced one point integration rule for ${\textstyle {\boldsymbol {K}}_{\phi }}$ which indicates no advantage in using a full quadrature for ${\textstyle \mathbf {K} _{\phi }}$. The simple one point quadrature allows computing all the element stiffness matrices in Eq.(34) explicitly.

The equivalent nodal force vectors for the element are

${f}_{w_{i}}^{e}=\iint _{A^{e}}[N_{i}q+({\boldsymbol {\nabla }}N_{i})^{T}{\boldsymbol {m}}]dA\quad ;\quad \displaystyle {\boldsymbol {f}}_{\phi _{i}}^{e}=\iint _{A^{e}}\mathbf {N} _{i}{\boldsymbol {m}}dA$

(36)

For a uniform distribution of ${\textstyle q}$ and ${\textstyle {\boldsymbol {m}}}$

${\begin{array}{l}\displaystyle {f}_{w_{i}}^{e}={qA^{e} \over 3}+{1 \over 2}(b_{i}^{e}m_{x}+c_{i}^{e}m_{y})\\[.4cm]\displaystyle {\boldsymbol {f}}_{\phi _{i}}^{e}={A^{e} \over 3}[m_{x},m_{y}]^{T}\end{array}}$

(37)

where ${\textstyle b_{i}^{e}}$ and ${\textstyle c_{i}^{e}}$ are given in Eq.(15).

The vertical load ${\textstyle P_{i}}$ acting at a node ${\textstyle i}$ contributes the following terms to the ${\textstyle i}$th component of the global force vector ${\textstyle {\boldsymbol {f}}_{w}}$

${f}_{w_{i}}=P_{i}$

(38)

The reactions (the vertical force and the bending moment) can be computed at the prescribed nodes from the nodal displacement and rotations field in the usual manner.

Remark 1 . Each node has three DOFs: the deflection ${\textstyle {\bar {w}}_{i}}$ and the two shear angles ${\textstyle {\bar {\phi }}_{x_{i}}}$ and ${\textstyle {\bar {\phi }}_{y_{i}}}$ at the node. The size of all the element stiffness matrices in Eqs.(35) is ${\textstyle 6\times 6}$. This means that the effective DOFs for each element are in fact the nodal deflections of the patch of four elements assigned to each element (typically six nodal deflections except for boundary elements) and the six nodal shear angles, i.e. two shear angles for each of the three nodes of the element.

3.3 Iterative computation of the deflection and the shear angles at the nodes

Despite that the solution for the ${\textstyle {\bar {\boldsymbol {w}}}}$ and ${\textstyle {\bar {\boldsymbol {\phi }}}}$ variables can be found simultaneously by solving Eqs.(34), the following iterative algorithm is recommended for computing ${\textstyle {\bar {\boldsymbol {w}}}}$ and ${\textstyle {\bar {\boldsymbol {\phi }}}}$

$\displaystyle {\boldsymbol {K}}_{w}{\bar {\boldsymbol {w}}}^{i}\!\!\!=\!\!\!{\boldsymbol {f}}_{w}-{\boldsymbol {K}}_{w\phi }{\bar {\boldsymbol {\phi }}}^{i-1}\rightarrow {\bar {\boldsymbol {w}}}^{i}$ (39.a) $\displaystyle {\boldsymbol {K}}_{\phi }{\bar {\boldsymbol {\phi }}}^{i}\!\!\!=\!\!\!{\boldsymbol {f}}_{\phi }-{\boldsymbol {K}}_{w\phi }^{T}{\bar {\boldsymbol {w}}}^{i}\rightarrow {\bar {\boldsymbol {\phi }}}^{i}$ (39.b)

where superindex ${\textstyle i}$ denotes the number of iterations. The iterative scheme of Eqs.(39) continues until convergence for the nodal deflection and the nodal shear deformation angles is achieved. Convergence is typically measured by the ${\textstyle L_{2}}$ norm of vectors ${\textstyle {\bar {\boldsymbol {w}}}}$ and ${\textstyle {\bar {\boldsymbol {\phi }}}}$ (Eqs.(58) and (59)). An advantage of the above iterative scheme is that for ${\textstyle i=1}$ and ${\textstyle {\boldsymbol {\phi }}^{0}={\boldsymbol {0}}}$ the value of ${\textstyle {\bar {\boldsymbol {w}}}^{1}}$ corresponds to the thin plate solution of Kirchhoff theory which is accurate enough for many practical cases. The effect of shear deformation is introduced progressively with the number of iterations. Shear deformation effects are negligible for thin plates and hence the ${\textstyle {\bar {\boldsymbol {\phi }}}}$ variables tend rapidly to zero in this case.

3.4 Improved iterative scheme

An enhanced iterative scheme can be devised by performing a smoothing of the shear angles field as follows.

Step 1 Computation of the nodal deflections ̄w¹

${\boldsymbol {K}}_{w}{\bar {\boldsymbol {w}}}^{1}={\boldsymbol {f}}_{w}\to {\bar {\boldsymbol {w}}}^{1}\quad {\hbox{(Kirchhoff thin plate solution)}}$

(40)

Step 2 Compute ̄ϕⁱ, i ≥ 1

$\displaystyle {\boldsymbol {K}}_{\phi }{\bar {\boldsymbol {\phi }}}^{i}={\boldsymbol {f}}_{\phi }-{\boldsymbol {K}}_{w\phi }^{T}{\bar {\boldsymbol {w}}}^{i}\qquad \rightarrow {\bar {\boldsymbol {\phi }}}^{i}$

(41)

Step 3 Compute the element shear angles ̄ϕ^e

${\bar {\boldsymbol {\phi }}}^{e}={\frac {1}{3}}\left({\bar {\boldsymbol {\phi }}}_{a}+{\bar {\boldsymbol {\phi }}}_{b}+{\bar {\boldsymbol {\phi }}}_{c}\right)$

(42)

where ${\textstyle {\bar {\boldsymbol {\phi }}}^{e}}$ are mean shear angles for element ${\textstyle e}$ for the ${\textstyle i}$th iteration and ${\textstyle a,b,c}$ are the global numbers of the three nodes of element ${\textstyle e}$.

Step 4 Compute the smoothed nodal shear angles ̃ϕₖ

The smoothed nodal values ${\textstyle {\tilde {\boldsymbol {\phi }}}_{k}^{i}}$ are computed as

${\tilde {\boldsymbol {\phi }}}_{k}^{i}={\frac {1}{n_{k}}}\sum \limits _{j=1}^{n_{k}}{\bar {\boldsymbol {\phi }}}^{j}\quad ,\quad k=1,N$

(43)

where ${\textstyle n_{k}}$ is the number of elements sharing the node with global number ${\textstyle k}$ and ${\textstyle N}$ is the total number of nodes in the mesh.

Step 5 Compute ̄wⁱ, i > 1

${\boldsymbol {K}}_{w}{\bar {\boldsymbol {w}}}^{i}={\boldsymbol {f}}_{w}-{\boldsymbol {K}}_{w\phi }{\tilde {\boldsymbol {\phi }}}^{i-1}\qquad \rightarrow {\bar {\boldsymbol {w}}}^{i}$

(44)

Return to step 2.

Convergence of the improved iterative scheme for the deflection field is quite fast (2–4 iterations), even for thick plates (see Section 6).

The accuracy and efficiency of the so called BPT+ triangle is shown in the examples presented in the paper.

4 BOUNDARY CONDITIONS

A BPT element with a side along a boundary edge has one of the triangles belonging to the patch missing (Figure 2). This is taken into account by ignoring the contribution of this element when performing the average of the deflection gradient in Eq.(30) [12,15,19,20].

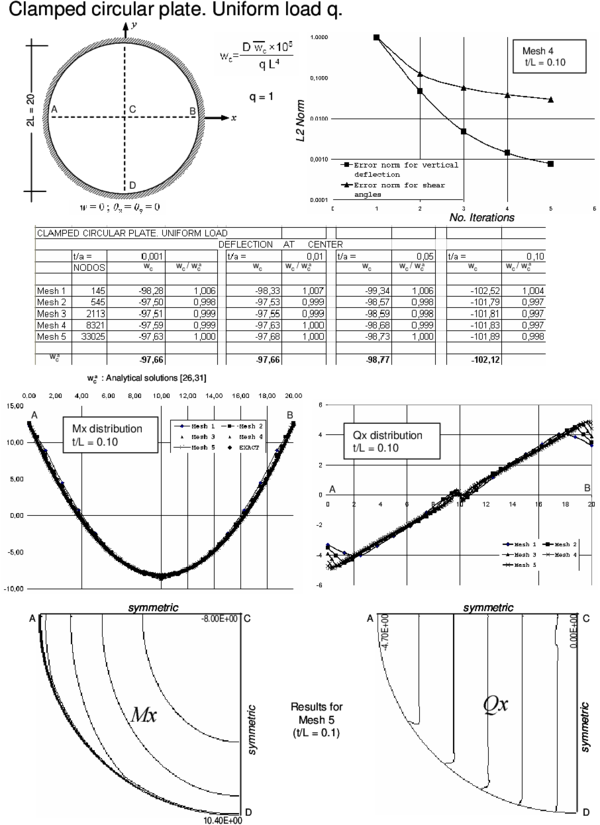
4.1 Clamped edge (w=0, θ=0)

The condition ${\textstyle w=0}$ is directly imposed at the edge nodes at the solution level when solving the system of equations for ${\textstyle {\bar {\boldsymbol {w}}}}$ in the standard manner.

The condition of zero rotations at a clamped edge introduces additional terms in the system of Eqs.(34).

In order to explain the process, let us consider for example a clamped edge corresponding to side 3 linking nodes 1 and 2 (with global numbers ${\textstyle i}$ and ${\textstyle j}$) in the boundary element of Figure 2b. At the clamped edge

${\boldsymbol {\theta }}\vert _{3}^{e}={\boldsymbol {\nabla }}w\vert _{3}^{e}+{\boldsymbol {\phi }}\vert _{3}^{e}=0\quad \to \quad {\boldsymbol {\nabla }}w\vert _{3}^{e}=-{\boldsymbol {\phi }}\vert _{3}^{e}$

(45)

where ${\textstyle {\boldsymbol {\theta }}\vert _{3}^{e}}$ are the rotations at the edge mid point.

The shear angles at the edge mid point are approximated by the average of the nodal values along the edge, i.e.

${\boldsymbol {\phi }}\vert _{3}^{e}={\frac {1}{2}}\left({\boldsymbol {\phi }}_{2}+{\boldsymbol {\phi }}_{3}\right)$

(46)

Introducing Eqs.(45) and (46) into the definition of matrix ${\textstyle {\boldsymbol {B}}_{w}}$ in Eq.(30) gives

${1 \over A^{e}}\int _{\Gamma ^{e}}\!\!{\boldsymbol {\nabla }}wd\Gamma \!\!=\!\!{1 \over A^{e}}\sum \limits _{j=1}^{2}{l_{j}^{e} \over 2}{\boldsymbol {T}}_{j}\left[\sum \limits _{i=1}^{3}{\boldsymbol {\nabla }}N_{i}^{e}w_{i}^{e}+\sum \limits _{i=1}^{3}{\boldsymbol {\nabla }}N_{i}^{p}w_{i}^{p}\right]_{j}-{1 \over A^{e}}{l_{3}^{e} \over 2}{\boldsymbol {T}}_{3}[{\boldsymbol {\phi }}_{2}+{\boldsymbol {\phi }}_{3}]$ $\!\!=\!\!{\boldsymbol {B}}_{w}{\bar {\boldsymbol {w}}}^{e}+\Delta {\boldsymbol {B}}_{\phi }{\bar {\boldsymbol {\phi }}}^{e}$

(47)

where ${\textstyle {\boldsymbol {B}}_{w}}$ is obtained by disregarding the contributions from the clamped side in the sum along the element sides in the expression of Box I and

$\Delta {\boldsymbol {B}}_{\phi }^{e}=-{l_{3}^{e} \over 2A^{e}}{\boldsymbol {T}}_{3}[{\boldsymbol {0}},{\boldsymbol {I}}_{2},{\boldsymbol {I}}_{2}]$

(48)

The bending strain field of Eq.(27) is now modified as

${\boldsymbol {\varepsilon }}_{b}^{e}={\boldsymbol {B}}_{w}{\bar {\boldsymbol {w}}}^{e}+({\boldsymbol {B}}_{\phi }+\Delta {\boldsymbol {B}}_{\phi }){\bar {\boldsymbol {\phi }}}^{e}={\boldsymbol {B}}_{w}{\bar {\boldsymbol {w}}}^{e}+{\bar {\boldsymbol {B}}}_{\phi }{\bar {\boldsymbol {\phi }}}^{e}$

(49)

where

${\bar {\boldsymbol {B}}}_{\phi }={\boldsymbol {B}}_{\phi }+\Delta {\boldsymbol {B}}_{\phi }$

(50)

The new matrix ${\textstyle {\bar {\boldsymbol {B}}}_{\phi }}$ substitutes matrix ${\textstyle {\boldsymbol {B}}_{\phi }}$ in the expression for ${\textstyle {\boldsymbol {K}}_{\phi }^{e}}$ of Eq.(35).

We recall that the above modifications are only needed for elements with a clamped edge.

The process is repeated twice if the element has two clamped edges.

4.2 Simply supported edge (w=0, θₛ=0)

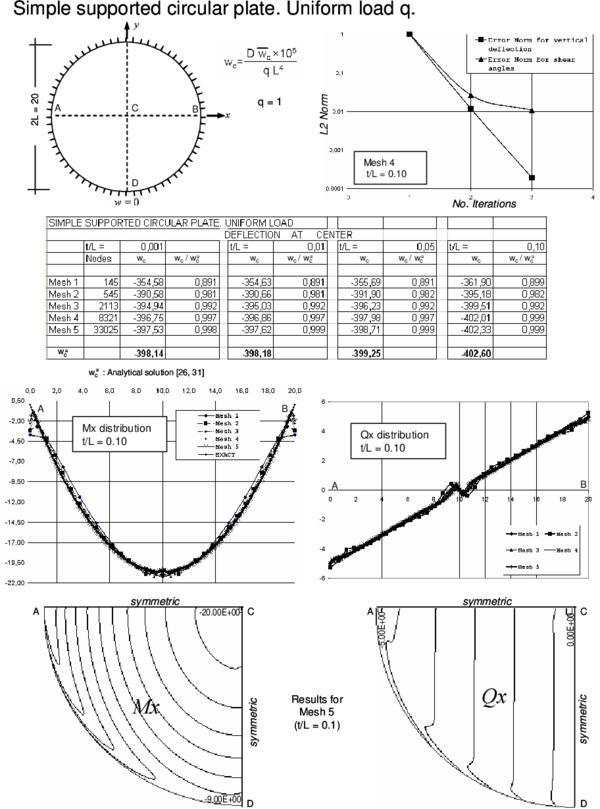
The condition ${\textstyle w=0}$ at the nodes laying on a simply supported (SS) edge is prescribed when solving the global system of equations as for the clamped case. Prescribing ${\textstyle w=0}$ at an edge node also automatically implies that ${\textstyle {\partial w \over \partial s}}$ is zero along the SS edge direction ${\textstyle s}$ and this is the option taken for the standard rotation-free thin BPT element. Note that this is equivalent to assuming a “soft” simply support condition in general plate theory (i.e. ${\textstyle w=M_{n}=M_{ns}=0}$ at the SS edge) [29,30].

The “hard” support condition requires prescribing the tangential rotation ${\textstyle \theta _{s}}$ to a zero value. This means

$\theta _{s}={\frac {\partial w}{\partial s}}+\phi _{s}=0\quad \rightarrow \quad \phi _{s}=-{\frac {\partial w}{\partial s}}$

(51)

Prescribing ${\textstyle w}$ at the SS nodes gives automatically ${\textstyle \left({\frac {\partial w}{\partial s}}\right)_{i}=0}$ and hence the nodal variable ${\textstyle {\bar {\phi }}_{s_{i}}}$ must be also prescribed to a zero value at these nodes. This condition can be imposed by transforming the cartesian shear strains to the boundary axes ${\textstyle s,n}$ and making ${\textstyle {\bar {\phi }}_{s_{i}}=0}$ at each simply supported boundary node.

Indeed, prescribing just ${\textstyle w_{i}=0}$ at the support nodes and letting ${\textstyle {\bar {\phi }}_{s_{i}}}$ free reproduces the soft support condition for Reissner-Mindlin theory. This is the approach chosen in the examples presented in the paper ( Figures 5, 6, 9, 10).

It is interesting that the BPT element does not suffer from the difficulties associated to prescribing the tangential rotation at SS nodes which occur in standard thin plate elements [29,32,33]. This is due to the fact that the rotations do not appear explicitly as variables in the BPT formulation and the SS condition is directly imposed by prescribing the deflection at the support nodes.

4.3 Symmetry edge (θₙ=0)

The condition of zero normal rotation (${\textstyle \theta _{n}=0}$) is imposed by neglecting the contributions from the normal rotation ${\textstyle {\frac {\partial w}{\partial n}}}$ at the symmetry edge when computing Eq.(30). The condition ${\textstyle \theta _{n}={\frac {\partial w}{\partial n}}+\phi _{n}=0}$ for the thick case introduces additional terms in the stiffness equations. The procedure is identical as explained for the clamped edge.

Remark 2 . The condition ${\textstyle {\bar {\phi }}_{n_{i}}=0}$ can also be imposed at free edge nodes. This however has not shown to be improve the quality of the solution or to lead to any computational advantage, other that the reduction in the number of DOFs, in those cases.

5 TWO-NODED ROTATION-FREE BEAM ELEMENT

A two-noded rotation-free beam element with shear deformation effects can be simply derived as a particular case of the formulation for the BPT element previously described. The resulting beam element is termed CCB+ as a reference to the cell-centered approach used to compute the curvature at the element center.

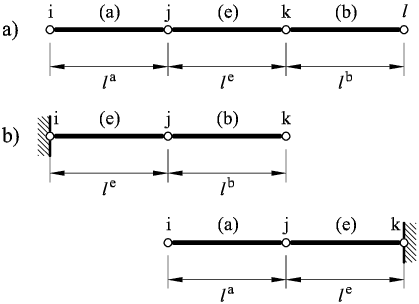
Figure 3 shows the patch of three beam elements needed for computing the constant curvature at the central element using a cell-centered finite-volume type scheme. The starting point in the formulation of the CCB+ element is the standard Timoshenko beam theory [29,30]. The relevant expressions are:

${\begin{array}{l}{\boldsymbol {Deflection}}:\,w\\[.2cm]{\boldsymbol {Rotation}}:\,\theta =\displaystyle {\frac {\partial w}{\partial x}}+\phi \\[.2cm]{\boldsymbol {Displacement~vector}}:\,{\boldsymbol {u}}=[w,\theta ]^{T}\\[.2cm]{\boldsymbol {Curvature}}:\,{\boldsymbol {\varepsilon }}_{b}=[{\kappa }]=\left[\displaystyle {\frac {\partial \theta }{\partial x}}\right]={\boldsymbol {L}}_{b}\theta \quad ,\quad {\boldsymbol {L}}_{b}=\left[\displaystyle {\frac {\partial }{\partial x}}\right]\\[.2cm]{\boldsymbol {Transverse~shear~deformation}}:\,{\boldsymbol {\sigma }}_{s}=[\gamma ]=\left[\displaystyle {\frac {\partial w}{\partial x}}-\theta \right]={\boldsymbol {L}}_{s}{\boldsymbol {u}}\quad ,\quad {\boldsymbol {L}}_{s}=\left[\displaystyle {\frac {\partial }{\partial x}},-1\right]\qquad \qquad \qquad \\\end{array}}$

(52)

${\boldsymbol {Constitutive~equations:}}$

${\begin{array}{lll}{\boldsymbol {\sigma }}_{b}=[M]={\boldsymbol {D}}_{b}{\boldsymbol {\varepsilon }}_{b}&,&{\boldsymbol {D}}_{b}=[EI]\\{\boldsymbol {\sigma }}_{s}=[Q]={\boldsymbol {D}}_{s}{\boldsymbol {\varepsilon }}_{s}&,&{\boldsymbol {D}}_{s}=[\alpha GA]\\\end{array}}$

(53)

where ${\textstyle I}$ and ${\textstyle A}$ are the inertia modulus and the area of the transverse cross section of the beam and the rest of the terms have been defined previously.

The Hu-Washizu functional for the beam has the same form as in Eq.(10) with ${\textstyle {\boldsymbol {m}}=[m]}$.

Similarly, the governing equations have identical expressions as for the plate problem Eqs.(11–13).

A linear interpolation is chosen for the deflection ${\textstyle w}$ and the shear angle ${\textstyle \phi }$ as

$w=\sum \limits _{i=1}^{2}N_{i}{\bar {w}}_{i}\quad ,\quad \phi =\sum \limits _{i=1}^{2}N_{i}{\bar {\phi }}_{i}$

(54)

Figure 3: (a) Patch of three rotation-free CCB+ elements. (b) Patch of element adjacents to a clamped boundary

${\begin{array}{l}\displaystyle \mathbf {B} _{w}={\frac {1}{2l^{a}l^{e}l^{b}}}\left[l^{b},-l^{b},-l^{a},l^{a}\right]\\[.3cm]\displaystyle \mathbf {B} _{\phi }={\frac {1}{l^{e}}}[1,-1]\end{array}}$

Box II. Matrices ${\boldsymbol {B}}_{w}^{e}$ and ${\boldsymbol {B}}_{\phi }^{e}$ for the 2-noded rotation-free CCB+ element

where ${\textstyle N_{i}=1/2(1+\xi \xi _{i})}$ with ${\textstyle \xi _{1}=-1}$ and ${\textstyle \xi _{2}=1}$ are the standard linear shape functions for the 2-noded Lagrange element [28,30].

Following an identical process as for the 3-noded BPT+ element, the same system of Eqs.(34) is found. The expressions for the stiffness matrices ${\textstyle {\boldsymbol {K}}_{w}^{e}}$, ${\textstyle {\boldsymbol {K}}_{\phi }^{e}}$ and ${\textstyle {\boldsymbol {K}}_{w_{\phi }}^{e}}$ coincide with those given in Eq.(35) simply by noting that the integrals change from area to line ones and substituting the area ${\textstyle A^{e}}$ by the element length ${\textstyle l^{e}}$. The form of matrices ${\textstyle {\boldsymbol {B}}_{w}}$ and ${\textstyle {\boldsymbol {B}}_{\phi }}$ is given in Box II.

The expressions for the equivalent force vector are similar to Eqs.(36)–(38), substituting the area integrals by integrals along the element length. For a uniform distribution of ${\textstyle q}$ and ${\textstyle m}$

${\begin{array}{l}f_{w_{i}}=\displaystyle {\frac {ql^{e}}{2}}+{\frac {2m}{l^{e}}}\xi _{i}\\[.2cm]f_{\phi _{i}}=\displaystyle {\frac {A^{e}}{2}}m\\\end{array}}$

(55)

where ${\textstyle \xi _{i}}$ is the value of the natural coordinate ${\textstyle \xi }$ at node ${\textstyle i}$.

The procedure for imposing the boundary conditions follows precisely the lines described for the BPT+ element in Section 4. The ${\textstyle \Delta {\boldsymbol {B}}_{\phi }}$ matrix for an element with a clamped node is (Eq.(48) and Figure 3b)

${\hbox{Left clamped node: }}\Delta {\boldsymbol {B}}_{\phi }={\frac {1}{l^{e}}}[1,0]$

(56)

${\hbox{Right clamped node: }}\Delta {\boldsymbol {B}}_{\phi }={\frac {1}{l^{e}}}[0,-1]$

(57)

A similar expression is obtained for an element with a node on the symmetry axis.

The CCB+ element is an extension of the 2-noded rotation-free CCB element based on Euler-Bernouilli beam theory. A description of the CCB element can be found in 11,30.

6 EXAMPLES

6.1 Square and circular plates

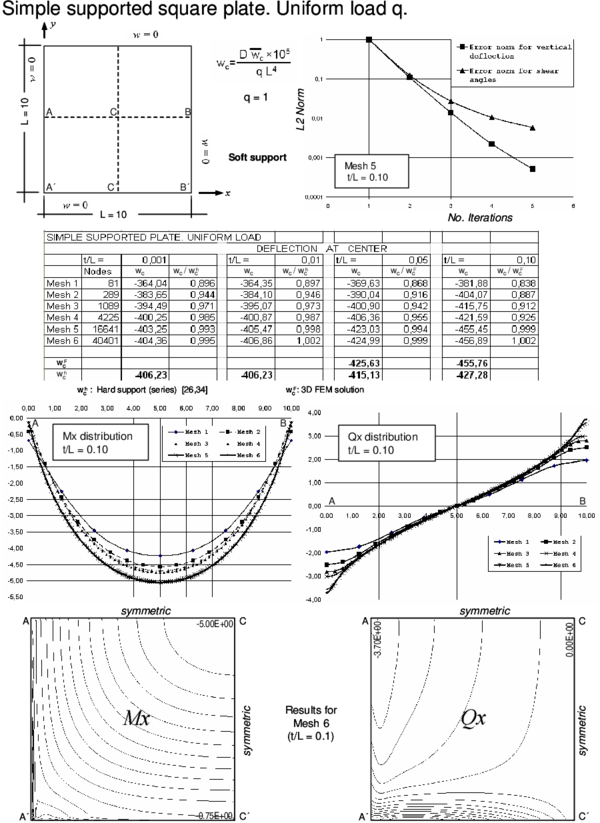
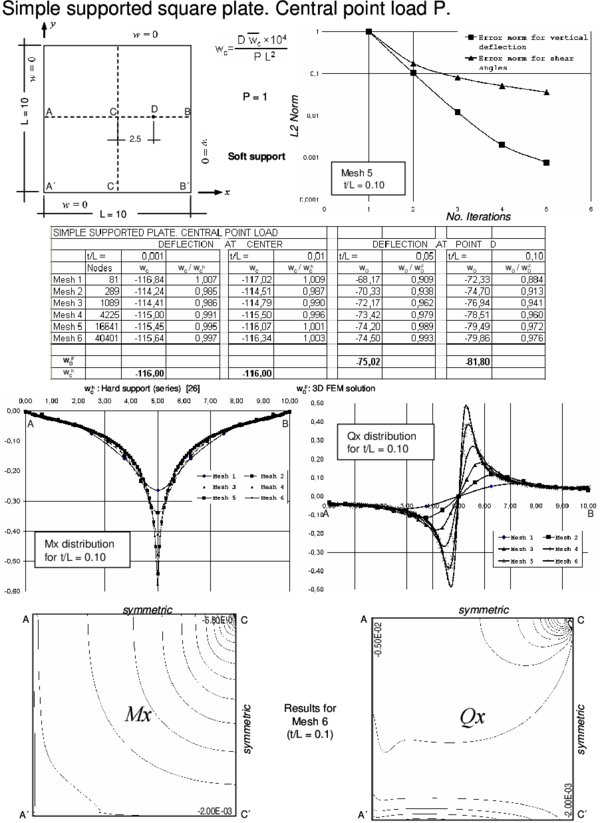
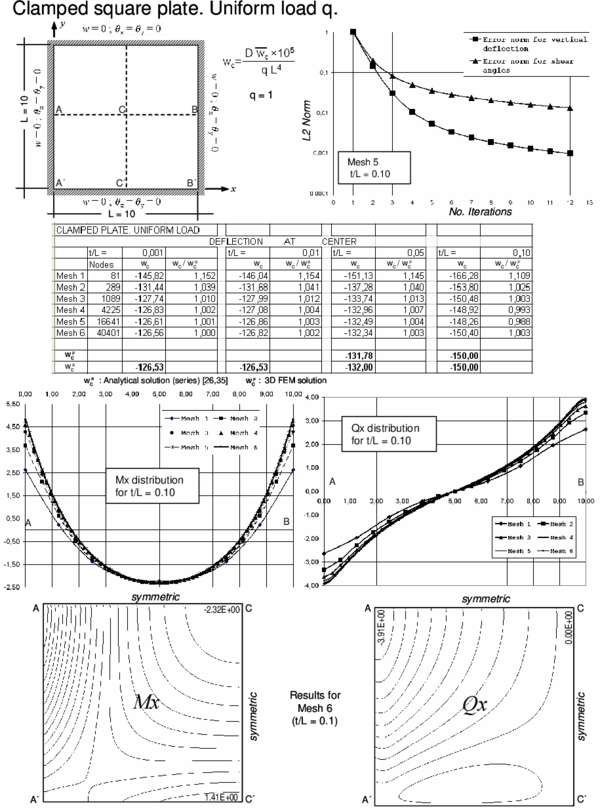
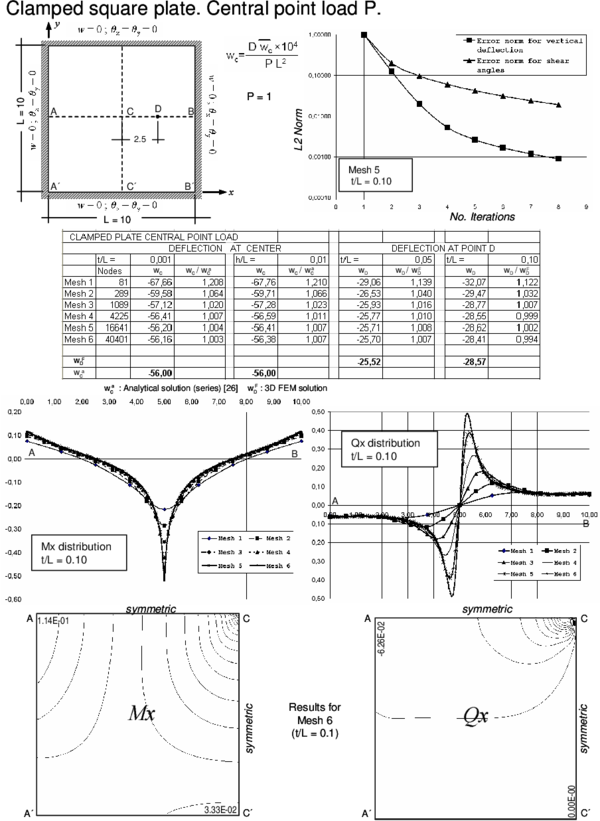
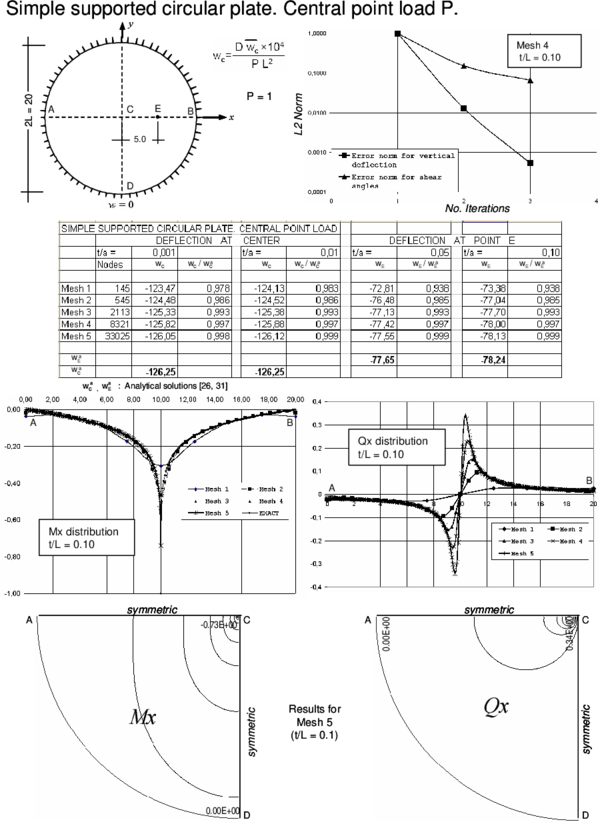
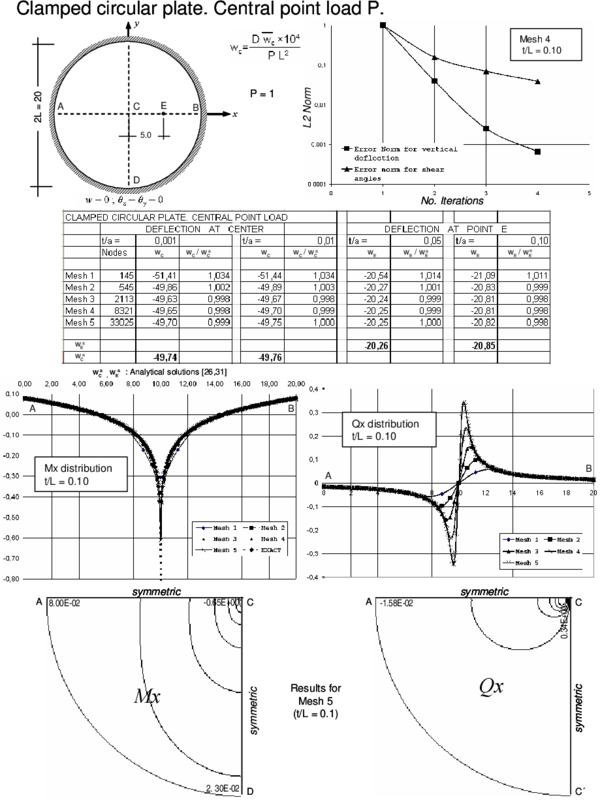
The efficiency and accuracy of the BPT+ element has been tested in the analysis of a number of square plates of side ${\textstyle L}$ and circular plates of diameter ${\textstyle 2L}$ under a uniformly distributed loading and a central point load for different thicknesses ranging from to ${\textstyle t/L=10^{-3}}$ (very thin plate) to ${\textstyle t/L=0.1}$ (thick plate). Simply supported and clamped boundary conditions have been considered. For rectangular plates the soft SS condition has been assumed. For circular plates ${\textstyle \phi _{s}}$ is automatically zero at the SS boundary for the problems studied due to symmetry and hence results correspond to the hard SS case. Figure 4 shows some of the different meshes used for the analysis.

Results for the cases studied using the enhanced iterative scheme of Section 3.4 are presented in Figures 5–12. Each figure shows:

• The convergence of the vertical deflection values and the shear angles with the number of iterations measured as

$L_{2}^{w}=\left[\sum \limits _{j=1}^{N}{\frac {({\bar {w}}_{j}^{i}-{\bar {w}}_{j}^{i-1})^{2}}{({\bar {w}}_{j}^{i})^{2}}}\right]^{1/2}$

(58)

$L_{2}^{\boldsymbol {\phi }}=\left[\sum \limits _{j=1}^{N}{\frac {[{\bar {\boldsymbol {\phi }}}_{j}^{i}-{\bar {\boldsymbol {\phi }}}_{j}^{i-1}]^{T}({\bar {\boldsymbol {\phi }}}_{j}^{i}-{\bar {\boldsymbol {\phi }}}_{j}^{i-1})}{[{\boldsymbol {\phi }}_{j}^{i}]^{T}{\boldsymbol {\phi }}_{j}^{i}}}\right]^{1/2}$

(59)

• where ${\textstyle N}$ is the number of nodes in the mesh and an upper index denotes the iteration number. A value of ${\textstyle {\bar {w}}_{j}^{0}=0}$ and ${\textstyle {\bar {\boldsymbol {\phi }}}_{j}^{0}=\mathbf {0} }$ has been taken. For the examples considered, the iterative scheme stops when ${\textstyle L_{2}^{w}<10^{-3}}$.

• The value of the normalized central deflection (${\textstyle w_{c}={\frac {D{\bar {w}}_{c}\cdot 10^{5}}{qL^{4}}}}$ for uniform load and ${\textstyle w_{c}={\frac {D{\bar {w}}_{c}\cdot 10^{4}}{PL^{2}}}}$ for point load with ${\textstyle D={\frac {Et^{3}}{12(1-\nu ^{2})}}}$) for the range of thickness ratios ${\textstyle 10^{-3}-10^{-1}}$ for each of the meshes considered. Results are compared with analytical and series values for the thin and thick cases [26,29,30,31] when available, or, alternatively, with FEM results obtained for the deflection at the center of the midle plane using a mesh of ${\textstyle 40\times 40\times 6}$ eight-noded hexahedra in a quarter of plate.

  For the point load case the analytical value for the deflection under the load given by thick plate theory is infinity. Hence, results for the deflection for thick plates are compared at the mid-point along a central line in this case.

• The distribution of the bending moment ${\textstyle M_{x}}$ and the shear force ${\textstyle Q_{x}}$ along the central line for the thick case (${\textstyle t/L=0.10}$) for each of the five meshes considered. The isovalues of ${\textstyle M_{x}}$ and ${\textstyle Q_{x}}$ over a quarter of the plate are also shown for the finer mesh.

The following conclusions are drawn from the examples:

Figure 4: Some of meshes of BPT+ elements used for analysis of square and circular plates

Figure 5: Simple supported square plate (soft support) under uniform load. Convergence of central deflection for different thicknesses. Upper curves show convergence of the vertical deflection and the shear angles for a thick plate with the number of iterations. Lower curves show the distribution of $M_{x}$ and $Q_{x}$ along the central line and their contours

Figure 6: Simple supported square plate (soft support) under central point load. Convergence of central deflection for different thicknesses. Upper curves show convergence of the vertical deflection and the shear angles for a thick plate with the number of iterations. Lower curves show the distribution of $M_{x}$ and $Q_{x}$ along the central line and their contours

Figure 7: Clampled square plate under uniform load. Convergence of central deflection for different thicknesses. Upper curves show convergence of the vertical deflection and the shear angles for a thick plate with the number of iterations. Lower curves show the distribution of $M_{x}$ and $Q_{x}$ along the central line and their contours

Figure 8: Clampled square plate under central point load. Convergence of central deflection for different thicknesses. Upper curves show convergence of the vertical deflection and the shear angles for a thick plate with the number of iterations. Lower curves show the distribution of $M_{x}$ and $Q_{x}$ along the central line and their contours

Figure 9: Simple supported circular plate under uniform load. Convergence of central deflection for different thicknesses. Upper curves show convergence of the vertical deflection and the shear angles for a thick plate with the number of iterations. Lower curves show the distribution of $M_{x}$ and $Q_{x}$ along the central line and their contours

Figure 10: Simple supported circular plate under central point load. Convergence of central deflection for different thicknesses. Upper curves show convergence of the vertical deflection and the shear angles for a thick plate with the number of iterations. Lower curves show the distribution of $M_{x}$ and $Q_{x}$ along the central line and their contours

Figure 11: Clampled circular plate under uniform load. Convergence of central deflection for different thicknesses. Upper curves show convergence of the vertical deflection and the shear angles for a thick plate with the number of iterations. Lower curves show the distribution of $M_{x}$ and $Q_{x}$ along the central line and their contours

Figure 12: Clampled circular plate under central point load. Convergence of central deflection for different thicknesses. Upper curves show convergence of the vertical deflection and the shear angles for a thick plate with the number of iterations. Lower curves show the distribution of $M_{x}$ and $Q_{x}$ along the central line and their contours

1. The BPT+ element reproduces accurately the expected results for the deflection field for thin and thick plates.
2. A converged solution of ${\textstyle L_{2}^{w}<10^{-2}}$ for the deflection field using the iterative algorithm of Section 3.4 was obtained in a maximum of four iterations for the thick case for all the meshes considered. The number of iterations reduced to two for thin plates, due to the less importance of shear effects in these cases.
3. The convergence of the shear angles is slightly slower than for the deflection field. However an error norm of ${\textstyle L_{2}^{\phi }<10^{-1}}$ obtained in 3-4 iterations was found to give accurate results for the shear strains and the shear forces distribution for the thick case.
4. The distribution of the bending moments and the shear forces (obtained directly from the shear angles by Eq.(23)) was good and in accordance with the expected results for the thick case.
5. For thin plates the distribution of bending moments is also very good. However the distribution of the shear forces deteriorates slightly if computed via Eq.(23). This is due to the fact that the shear angles tend to zero as the plate is thinner. It is more appropriate in theses cases to compute the shear forces from the bending moment distribution as in standard thin plate theory [29,30].
6. Similar good results were obtained for SS square plate problems solved with the “hard” SS condition obtained by prescribing ${\textstyle {\bar {\phi }}_{s_{i}}=0}$ at the support nodes (see Table 1).

Table. 1 Simply supported square thick plate (hard support) under uniform load. Normalized central deflection values for $t/L=0.10$ for the meshes of Figure 5

SS (hard) square thick plate. Uniform load, $t/L=0.10$
	Mesh 1	Mesh 2	Mesh 3	Mesh 4	Mesh 5	Mesh 6
$w_{c}$	-381,73	-404,59	-416,31	-421,98	-424,65	-425,59
$w_{c}/w_{c}^{a}$	0,893	0,947	0,974	0,988	0,994	0,996
$w_{c}^{a}$ (Series solution): -427.28 [29,30]
Convergence achieved in a maximum of 4 iterations for each mesh

Indeed for problems with a discontinuous shear force field (such as the case of internal point forces), the nodal continuity of the shear strains which is intrinsic to the element formulation is a drawback to accurately capturing shear force jumps. This can be overcome by computing the shear forces at the center of the elements adjacent to the point load and extrapolating the solution within each element so as to reproduce the shear force jump at the common node.

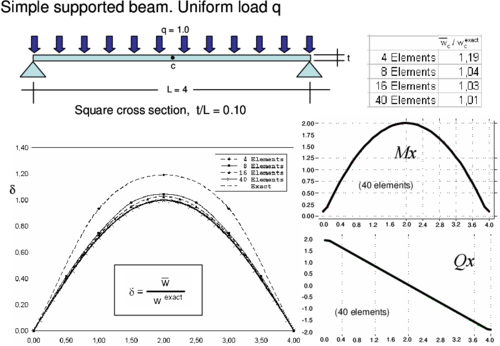
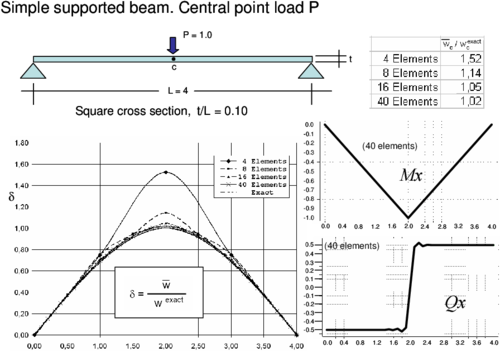
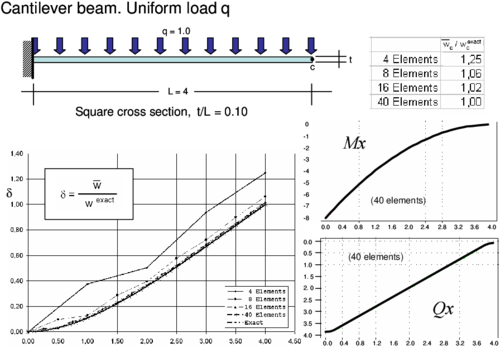
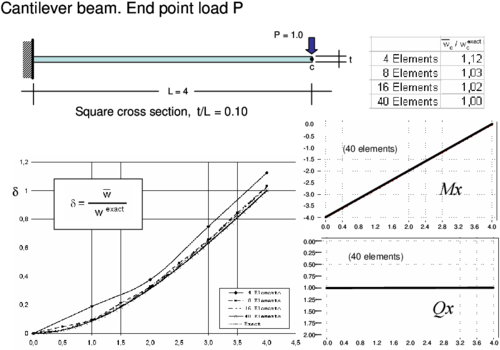
6.2 Simple supported and cantilever beams

The accuracy of the CCB+ beam element of Section 5 was tested in the analysis of simple supported and cantilever thick beams under distributed and point loads. Results of the study plotted in Figures 13–16 show the normalized distribution of the deflection along the beams and the normalized value of the central deflection (for the clamped beam) and the end deflection (for the cantilever beam) with the number of elements. Good results (error less than 10%) are obtained with a relatively coarse mesh (8 elements).

The distribution of the bending moment and the shear force along the beam is also plotted for the 40 element mesh. Results are practically coincident with the analytical values. Similar good behaviour was obtained for other thick and thin beam problems studied with the CCB+ element.

Figure 13: Simple supported thick beam under uniform load. Convergence of central deflection and distribution of the deflection for different meshes of CCB+ elements. Bending moment and shear force diagrams for 40 element mesh

Figure 14: Simple supported thick beam under central point load. Convergence of central deflection and distribution of the deflection for different meshes of CCB+ elements. Bending moment and shear force diagrams for 40 element mesh

Figure 15: Cantilever thick beam under uniform load. Convergence of end deflection and distribution of the deflection for different meshes of CCB+ elements. Bending moment and shear force diagrams for 40 element mesh

Figure 16: Cantilever thick beam under central point load. Convergence of end deflection and distribution of deflection for different meshes of CCB+ elements. Bending moment and shear force diagrams for 40 element mesh

7 CONCLUDING REMARKS

A methodology for extending the rotation-free plate and beam elements initially designed for thin/slender situations so as to account with shear deformation effects has been presented. The method allows one to introduce the effect of shear deformation in a progressive (iterative) manner starting from the initial thin solution.

The formulation is useful for analysis of plates and beams of a variety of thickness and materials. A particular interesting application of the new elements is the analysis of composite laminated plates and beams for which shear deformation effects are relevant.

The formulation is also suitable for implementing an adaptive solution scheme where the shear angles are introduced in structures (or zones of a structure) where the effect of shear deformation is relevant.

ACKNOWLEDGEMENTS

This research was partially supported by project SEDUREC of the Consolider Programme of the Ministerio de Educación y Ciencia of Spain.

REFERENCES

[1] Nay RA, Utku S. An alternative to the finite element method. Variational Methods Eng. 1972; Vol. 1:3/63–3/74.

[2] Chan ASL, Davies GAO Davies. A simplified finite element model for the impact of thin shell. In Bulson PS (ed.), Structures under Shock and Impact, Proc. 1st. Int. Conf., Cambridge, MA, USA, 365–380, 1989.

[3] Hampshire JK, Topping BHV, Chan HC. Three node triangular elements with one degree of freedom per node. Engng. Comput. 1992; 9:49–62.

[4] Phaal R, Calladine CR. A simple class of finite elements for plate and shell problems. I: Elements for beams and thin plates. Int. J. Num. Meth. Engng. 1992; 35:955–977.

[5] Phaal R, Calladine CR. A simple class of finite elements for plate and shell problems. II: An element for thin shells with only translational degrees of freedom. Int. J. Num. Meth. Engng. 1992; 35:979–996.

[6] Oñate E, Cervera M. Derivation of thin plate bending elements with one degree of freedom per node. Engineering Computations 1993; 10:553–561.

[7] Rio G, Tathi B, Laurent H. A new efficient finite element model of shell with only three degrees of freedom per node. Applications to industrial deep drawing test. in Recent Developments in Sheet Metal Forming Technology, MJM Barata Marques (ed), 18th IDDRG Biennial Congress, Lisbon, 1994.

[8] Sabourini F, Bounet M. Analysis of plates and shells with a simplified three noded triangular element. Thin Walled Structures 1995; 21:209–223.

[9] Rojek J, Oñate E. Sheet springback analysis using a simple shell triangle with translational degrees of freedom only. Int. J. of Forming Processes 1998; 1(3):275–296.

[10] Rojek J, Oñate E, Postek E. Application of explicit FE codes to simulation of sheet and bulk forming processes. J. of Materials Processing Technology 1998; 80-81:620–627.

[11] Jovicevic J, Oñate E. Analysis of beams and shells using a rotation-free finite element-finite volume formulation, Monograph 43, CIMNE, Barcelona, 1999.

[12] Oñate E, Zárate F. Rotation-free plate and shell triangles. Int. J. Num. Meth. Engng. 2000; 47:557–603.

[13] Cirak F, Ortiz M. Subdivision surfaces: A new paradigm for thin-shell finite element analysis. Int. J. Num. Meths in Engng 2000; 47:2039–2072.

[14] Cirak F, Ortiz M. Fully ${\textstyle C^{1}}$-conforming subdivision elements for finite deformations thin-shell analysis. Int. J. Num. Meths in Engng 2001; 51:813–833.

[15] Flores FG, Oñate E. A basic thin shell triangle with only translational DOFs for large strain plasticity. Int. J. Num. Meths in Engng 2001; 51:57–83.

[16] Guo YQ, Gatis W, Naceur H, Batoz JL. An efficient dkt rotation free shell element for spring simulations in sheet metal forming. Computers & Structures 2002; 80:2299–2312.

[17] Engel G, Garikipati K, Hughes TJR, Larson MG, Mazzei L, Taylor RL. Continuous/discontinuous finite element approximation of fourth-order elliptic problems in structural and continuum mechanics with applications to thin beams and plates, and strain gradient elasticity. Comput. Methods Appl. Mech. Engrg. 2002; 191:3669–3750.

[18] Oñate E, Cendoya P, Miquel J. Non linear explicit dynamic analysis of shells using the BST rotation-free triangle. Engineering Computations 2002; 19(6):662–706.

[19] Oñate E, Flores FG. Advances in the formulation of the rotation-free shell triangle. Comput. Meth. in Appl. Mech. Engng. 2005; 194:2406–2443.

[20] Flores FG, Oñate E. Improvements in the membrane behaviour of the three node rotation-free BST shell triangle using an assumed strain approach. Computer Methods in Applied Mechanics and Engineering 2005; 194:907–932.

[21] Brunet M, Sabourin F. Analysis of a rotation-free 4-node shell element. Int. J. Num. Meth. Engng. 2006; 66:1483–1510.

[22] Sabourini F, Brunet M. Detailed formulation of the rotation-free triangular element “S3” for general purpose shell analysis. Engrg. Comput. 2006; 23:469–502.

[23] Gärdsback M, Tibert G. A comparison of rotation-free triangular shell elements for unstructured meshes. Comput. Meth. Appl. Mech. Engng. 2007; 196:5001–5015.

[24] Oñate E, Flores FG, Neamtu L. Enhanced rotation-free basic shell triangle. Applications to sheet metal forming. E. Oñate and R. Owen (eds.), Computational Plasticity, 239–-265, 2007 Springer, The Netherlands.

[25] Bushnell D, Almroth BO. Finite difference energy method for non linear shell analysis. J. Computers and Structures 1971; 1:361.

[26] Timoshenko SP. Theory of Plates and Shells, McGraw Hill, New York, 1971.

[27] Ugural AC. Stresses in Plates and Shells, McGraw Hill, New York, 1981.

[28] Zienkiewicz OC, Taylor RL, Zhu JZ. The Finite Element Method. Its basis and fundamentals. 6th Edition, Elsevier, 2005.

[29] Zienkiewicz OC, Taylor RL. The Finite Element Method for Solid and Structural Mechanics. 6th Edition, Elsevier, 2005.

[30] Oñate E, Structural Analysis with the Finite Element Method. Linear Statics. Vol.2: Beams, Plates and Shells. CIMNE-Springer, 2009.

[31] Batoz, JL, Dhatt G. Modelisation des structures par élements finis. Vol. 2: Poutres et Plaques. Hermes, Paris, 1990.

[32] Hugues TJR. The finite element method. Linear static and dynamic finite element analysis. (p. 324), Prentice-Hall, 1987.

[33] Babuŝka I, Scapolla T. Benchmark computation and performance evaluation for a rhombic plate bending problem. International Journal for Numerical Methods in Engineering 1989; 28:155–180.

[34] Salerno VL, Golberg MA. Effect of shear deformation on the bending of rectangular plates. Journal Applied Mechanics 1960; 27: 54–58.

[35] Shrinivas S, Rao AK. Flexure of thick rectangular plates. Journal Applied Mechanics 1973; 298–299.