Published in Comput. Methods Appl. Mech. Engrg., Vol 193, 3087-3128, 2004
doi: 10.1016/j.cma.2003.12.056
Abstract
The paper presents combination of Discrete Element Method (DEM) and Finite Element Method (FEM) for dynamic analysis of geomechanics problems. Combined models can employ spherical (or cylindrical in 2D) rigid elements and finite elements in the discretization of different parts of the system. The DEM is a suitable tool to model soil/rock materials while the FEM in many cases can be a better choice to model other parts of the system considered. A typical example can be an idealization of rock cutting with a tool discretized with finite elements and rock or soil samples modelled with discrete elements. The FEM presented in the paper allows large elasto-plastic deformations in the solid regions. Such problems require the use of stabilized FEM to deal with the incompressibility constraint in order to eliminate the volumetric locking defect, especially when using triangular and tetrahedra elements with equal order interpolation for the displacement and the pressure variables. In the paper a stabilization based on the Finite Calculus (FIC) approach is used. Both theoretical algorithms of DEM and stabilized FEM are implemented in an explicit dynamic code. The paper presents some details of both formulations. A combined numerical algorithm is described finally. Selected numerical results illustrate the possibilities and performance of discrete/finite element analysis in geomechanics problems.
1 Introduction
The discrete element method (DEM) is nowadays acknowledged to be an effective procedure for analysis of granular and rock materials under static and dynamic loads. Typically in the DEM the soil/rock masses are modelled by a collection of spheres interacting with each other. The normal and tangential forces between spheres govern the motion of the discrete continuum. Modelling of discontinuities by the DEM is quite simple as they are produced by loss of adhesive contact between the spheres. Examples of application of the DEM to geomechanics and similar problems can be found in [1,2].
The coupling of the finite element method with the DEM is an effective approach for problems where standard continuum finite elements are adequate to model a part of the analysis domain, whereas the DEM is more adequate to treat other areas. Examples of such problems can be found in the interaction of solids and structures with granular media. The use of simple triangular and tetrahedra elements to model the “continuum” domain is very attractive due to the simplicity of their geometry in order to treat frictional contact conditions. Standard linear triangles and tetrahedra can suffer however from serious drawbacks in the presence of material nonlinearities inducing a near-incompressible behaviour as the numerical solution locks in these cases. The volumetric locking defect can be eliminated by using adequate mixed formulations with different interpolations for the displacement and pressure variables [3]. The use of an equal order interpolation for these variables is very attractive from the computational point of view and this is possible if an adequate stabilized formulation is chosen.
In this paper a stabilization method based on the finite calculus (FIC) approach [4,5] is used for deriving locking-free linear triangles and tetrahedra which can be effectively used in conjunction with the DEM.
One of the motivations of the present research is the simulation of the process of rock cutting, estimating at the same time the wear of the cutting tool. The main physical phenomenon considered is the interaction of the tool with a rock leading to failure of the rock and tool wear. The latter process is usually slower, although in some cases visible changes of the tool shape can be appreciated after a few minutes. The tool is assumed to be rigid in our numerical model. Two kinds of tool discretization have been used. The first one employs finite elements to represent the tool. In the second type of discretization the tool is also discretised with discrete elements. This allows to modify the shape of the tool easily by removing “worn” particles.
The formulation of the discrete element method has been extended for thermal and thermo-mechanical coupled problems in order to take into account temperature as one of the important factors influencing the tool wear process. Heat is generated during cutting due to friction dissipation. In the model friction between the tool and rock particles as well as friction between rock particles themselves is considered. Heat conduction through the tool and rock is analysed and the temperature distribution is obtained. Temperature of the tool surface lowers its hardness and increases wear.
The content of the paper is the following. In the next sections the main features of the DEM used are described. Details of different models derived to treat the frictional contact conditions are given.
In the second part of the paper the formulation of volumetric locking-free linear triangles and tetrahedra is presented using a FIC approach. Next an algorithm for dynamic analysis of geomechanics problems combining DEM and locking-free FEM is described. Examples of the applications of coupled DEM-FEM formulation to a number of geomechanics problems are presented.
2 DISCRETE ELEMENT METHOD FORMULATION
The numerical model of rock/soil media adopted in the present study is based on the spherical discrete element method (DEM) which is widely recognized as a suitable tool to model geomaterials [6,7,8,9]. Formulation of spherical discrete elements (called also distinct elements) following the main assumptions of Cundall [6,10] has been developed by Rojek et al. in [11] and implemented in an explicit dynamic formulation. Within the DEM, it is assumed that the solid material can be represented as a collection of rigid particles (spheres or balls in 3D and discs in 2D) interacting among themselves in the normal and tangential directions. Material deformation is assumed to be concentrated at the contact points. Appropriate contact laws allow us to obtain desired macroscopic material properties. The contact law used for rock modelling takes into account cohesive bonds between rigid particles. The contact law can be seen as the formulation of the material model at the microscopic level. Cohesive bonds can be broken, thus allowing to simulate fracture of material and its propagation.
2.1 Equations of motion
The translational and rotational motion of rigid spherical or cylindrical elements (particles) (Fig. 1) is described by means of the standard equations of rigid body dynamics. For the -th element we have
|
|
(1) |
|
|
(2) |
where is the element centroid displacement in a fixed (inertial) coordinate frame , – the angular velocity, – the element mass, – the moment of inertia, – the resultant force, and – the resultant moment about the central axes. Vectors and are sums of all forces and moments applied to the -th element due to external load, contact interactions with neighbouring spheres and other obstacles, as well as forces resulting from damping in the system. The form of the rotational equation (2) is valid for spheres and cylinders (in 2D) and is simplified with respect to a general form for an arbitrary rigid body with the rotational inertial properties represented by a second order tensor. In the general case it is more convenient to describe the rotational motion with respect to a co-rotational frame which is embedded at each element since in this frame the tensor of inertia is constant. The tensor of inertia for a sphere or cylinder (in 2D) does not change in the fixed global coordinate system , and hence the rotational motion can be easily described in this system.
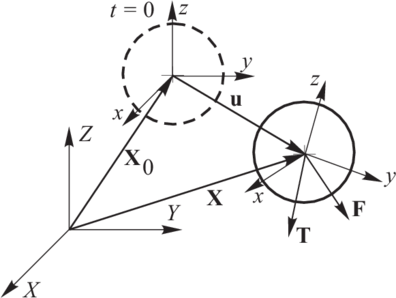
|
| Figure 1: Motion of a rigid particle |
Equations of motion (1) and (2) are integrated in time using a central difference scheme. The time integration operator for the translational motion at the -th time step is as follows:
|
|
(3) |
|
|
(4) |
|
|
(5) |
The first two steps in the integration scheme for the rotational motion are identical to those given by Eqs.(3) and (4):
|
|
(6) |
|
|
(7) |
The vector of incremental rotation is calculated as
|
|
(8) |
Knowledge of the incremental rotation suffices to update the tangential contact forces. It is also possible to track the rotational position of particles, if necessary [12]. Then the rotation matrices between the moving frames embedded in the particles and the fixed global frame must be updated incrementally using an adequate multiplicative scheme [11].
2.2 Contact search algorithm
Changing contact pairs of elements during the analysis process must be automatically detected. The simple approach to identify interaction pairs by checking every sphere against every other sphere would be very inefficient, as the computational time is proportional to , where is the number of elements. In our formulation the search is based on quad-tree and oct-tree structures. In this case the computation time of the contact search is proportional to , which allows to solve large frictional contact systems.
2.3 Evaluation of contact forces
2.3.1 Decomposition of the contact force
Once contact between a pair of elements has been detected, the forces occurring at the contact point are calculated. The interaction between the two interacting bodies can be represented by the contact forces and , which by the Newton's third law satisfy the following relation:
|
|
(9) |
We take and decompose into the normal and tangential components, and , respectively (Fig. 2)
|
|
where is the unit vector normal to the particle surface at the contact point (this implies that it lies along the line connecting the centers of the two particles) and directed outwards from the particle 1.
The contact forces and are obtained using a constitutive model formulated for the contact between two rigid spheres (or discs in 2D) (Fig. 3). The contact interface in our formulation is characterized by the normal and tangential stiffness and , respectively, the Coulomb friction coefficient , and the contact damping coefficient .
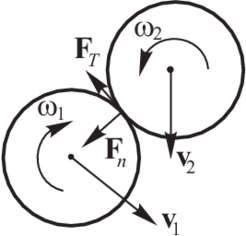
|
| Figure 2: Decomposition of the contact force into the normal and tangential components |
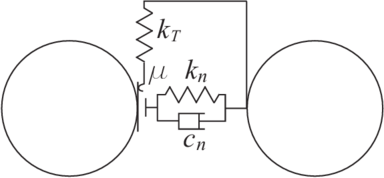
|
| Figure 3: Model of the contact interface |
2.3.2 Normal contact force
The normal contact force is decomposed into the elastic part and the damping contact force
|
|
(10) |
The damping part is used to decrease oscillations of the contact forces and to dissipate kinetic energy.
The elastic part of the normal contact force is proportional to the normal stiffness and to the penetration of the two particle surfaces , i.e.
|
|
(11) |
The penetration is calculated as
|
|
(12) |
where is the distance between the particle centres, and , their radiae. In the present study no cohesion is allowed, so no tensile normal contact forces are allowed and hence
|
|
(13) |
If , Eq. (11) holds, otherwise .
The contact damping force is assumed to be of viscous type and given by
|
|
(14) |
where is the normal relative velocity of the centres of the two particles in contact defined by
|
|
(15) |
The damping coefficient can be taken as a fraction of the critical damping for the system of two rigid bodies with masses and , connected with a spring of stiffness ([13]) with
|
|
(16) |
2.3.3 Tangential frictional contact
In the absence of cohesion (if the particles were not bonded at all or the initial cohesive bond has been broken) the tangential reaction appears by friction opposing the relative motion at the contact point. The relative tangential velocity at the contact point is calculated from the following relationship
|
|
(17) |
with
|
|
(18) |
where , , and , are the translational and rotational velocities of the particles, and and are the vectors connecting particle centres with contact points.
|
|
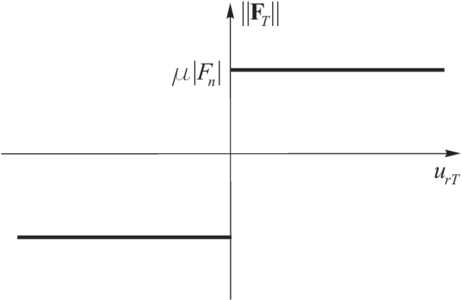
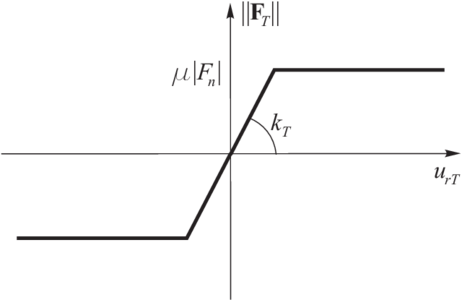
| Figure 4: Friction force vs. relative tangential displacement a) Coulomb law, b) regularized Coulomb law | |
The relationship between the friction force and the relative tangential displacement for the classical Coulomb model (for a constant normal force ) is shown in Fig. 4a. This relationship would produce non physical oscillations of the friction force in the numerical solution due to possible changes of the direction of sliding velocity. To prevent this, the Coulomb friction model must be regularized. The regularization procedure chosen involves decomposition of the tangential relative velocity into reversible and irreversible parts, and , respectively as:
|
|
(19) |
This is equivalent to formulating the frictional contact as a problem analogous to that of elastoplasticity, which can be seen clearly from the friction force-tangential displacement relationship in Fig. 4b. This analogy allows us to calculate the friction force employing the standard radial return algorithm []. First a trial state is calculated
|
|
(20) |
and then the slip condition is checked
|
|
(21) |
If , we have stick contact and the friction force is assigned the trial value
|
|
(22) |
otherwise (slip contact) a return mapping is performed giving
|
|
(23) |
2.4 Background damping
A quasi-static state of equilibrium for the assembly of particles can be achieved by application of adequate damping. The contact damping previously described is a function of the relative velocity of the contacting bodies. It is sometimes necessary to apply damping for non-contacting particles to dissipate their energy. We have considered two types of such damping of viscous and non-viscous type, referred here as background damping. In both cases damping terms and are added to equations of motion (1) and (2)
|
|
(24) |
|
|
(25) |
where
- for viscous damping
|
|
(26) |
|
|
(27) |
- for non-viscous damping
|
|
(28) |
|
|
(29) |
where , , and are damping constants. It can be seen from Eqs. (26)–(29) that both the non-viscous and viscous damping terms are opposite to the velocity and the difference lays in the evaluation of the damping force. Viscous damping is proportional to the magnitude of velocity, while non-viscous damping is proportional to the magnitude of the resultant force and the bending moment.
2.5 Numerical stability
Explicit integration in time yields high computational efficiency and it enables the solution of large models. The known disadvantage of the explicit integration scheme is its conditional numerical stability imposing the limitation on the time step , i.e.
|
|
(30) |
where is a critical time step determined by the highest natural frequency of the system
|
|
(31) |
If damping exists, the critical time increment is given by
|
|
(32) |
where is the fraction of the critical damping corresponding to the highest frequency . Exact calculation of the highest frequency would require solution of the eigenvalue problem defined for the whole system of connected rigid particles. In an approximate solution procedure, an eigenvalue problem can be defined separately for every rigid particle using the linearized equations of motion
|
|
(33) |
where
|
|
(34) |
and is the stiffness matrix accounting for the contributions from all the penalty constraints active for the -th particle. Equation (34) defines vectors and for a spherical particle in a 3D space. For a cylindrical particle in a 2D model the respective vectors are defined as
|
|
(35) |
Equation (33) leads to the eigenproblem
|
|
(36) |
whose eigenvalues ( in 3D case, and for 2D case) are the squared frequencies of the free vibration frequencies:
|
|
(37) |
In a 3D problem, three of six frequencies are translational, and the other three – rotational.
In the algorithm implemented, a further simplification is assumed. The maximum frequency is estimated as the maximum of natural frequencies of mass–spring systems defined for all the particles with one translational and one rotational degree of freedom. The translational and rotational free vibrations are governed by the following equations:
|
|
(38) |
|
|
(39) |
where it is assumed that the translational motion is due to the contact interaction along the normal direction (the spring stiffness represents the penalty stiffness in the normal direction) and the rotational stiffness is due to the contact stiffness (penalty) in the tangential direction. Given the tangential penalty , the rotational stiffness can be obtained as
|
|
(40) |
where is the length of the vector connecting the mass centre to the contact point.
The natural frequency of the translational vibrations is given by:
|
|
(41) |
while the rotational frequency can be obtained from
|
|
(42) |
where is the rotational inertia of a sphere
|
|
(43) |
and is given by Eq. (40). Substituting these expressions into Eq. (42) gives the rotational frequency as
|
|
(44) |
If , the rotational frequency is considerably higher than the translational frequency obtained from Eq. (41), which results in a smaller critical time increment (see Eq. (31)). To reduce the influence of the rotational frequencies in the value of the critical time step, the rotational inertia terms are scaled adequately. The concept of scaling rotational inertia terms is commonly used for shell elements [14].
3 MICROMECHANICAL CONSTITUTIVE MODELS
3.1 Elastic perfectly brittle model
The elastic perfectly brittle contact model is characterized by linear elastic behaviour when cohesive bonds are active. An instantaneous breakage of these bonds occurs when the interface strength is exceeded. When two particles are bonded the contact forces in both normal and tangential directions are calculated from the linear constitutive relationships:
|
where and are the normal and tangential contact force, respectively, and are the interface stiffness in the normal and tangential directions and and the normal and tangential relative displacements, respectively.
Cohesive bonds are broken instantaneously when the interface strength is exceeded in the tangential direction by the tangential contact force or in the normal direction by the tensile contact force. The failure (decohesion) criterion is written (for 2D) as:
|
where and are the interface strengths in the normal and tangential directions, respectively.
In the absence of cohesion the normal contact force can be compressive only, i.e.
|
|
(49) |
and the (positive) tangential contact force is given by
|
|
(50) |
if or zero otherwise. The friction force is given by Eq. (50) expressing the Coulomb friction law, with being the Coulomb friction coefficient.
|
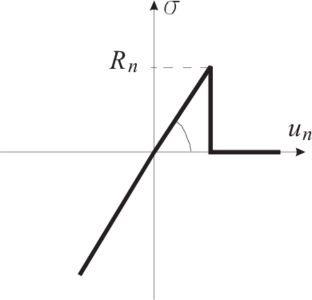
| Figure 5: Normal contact force in the elastic perfectly brittle model |
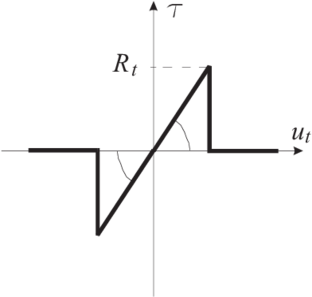
|
| Figure 6: Tangential contact force in the elastic perfectly brittle model (tensile normal contact force) |
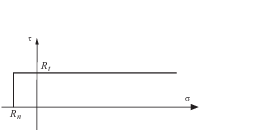
|
| Figure 7: Failure surface for the elastic perfectly brittle model |
Contact laws for the normal and tangential directions for the elastic perfectly brittle model are shown in Figs. 5 and 6, respectively. The failure surface for the elastic perfectly brittle model defined by conditions (47) and (48) is shown in Fig. 7.
3.2 Elasto-plastic contact model with linear softening
A contact law relates the contact force acting between two spheres to their relative displacement. The model developed is based on the analogous elasto-plastic relationships established for the normal and tangential directions:
|
|
(51) |
where is the normal or tangential contact force, the total relative displacement, the plastic component of the relative displacement, the elastic parameters which characterize the contact interface stiffness and the normal and tangential directions.
A general yield criterion has been assumed in the following form:
|
|
(52) |
where is the plastic softening modulus (assumed to be positive) and is the softening parameter represented by the plastic part of the relative displacement .
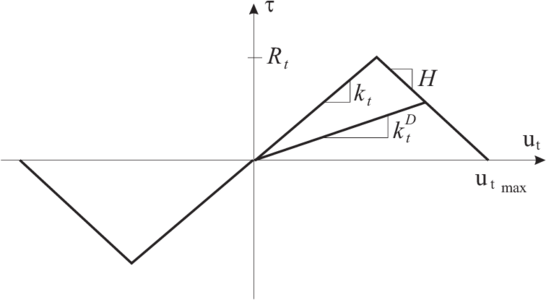
An elasto-plastic contact law with linear softening is assumed for the shear and normal tensile contact forces (Figs. 8 and 9). An elastic linear law is assumed for compression.
Dependence of the tangential force on the normal force is expressed by the application of the 2D failure criterion shown in Fig. 10. Yielding of contact bonds can occur under a combined tension and shear action (if the normal contact force is tensile) or due to shear only (if the normal contact force is compressive). After the contact bonds are broken due to yielding, standard frictional contact can occur between the spherical elements.
Flow rule
The plastic strain increments for both formulations (i.e. the normal and tangential motions) are calculated from the following flow rule:
|
|
(53) |
where is the absolute value of the slip rate (), the derivative of the plastic relative displacement (normal or tangential) and the contact force in the normal or tangential direction.
|
| Figure 8: Elasto-plastic contact law with softening for the normal direction |
|
| Figure 9: Elasto-plastic contact law with softening for the tangential direction |
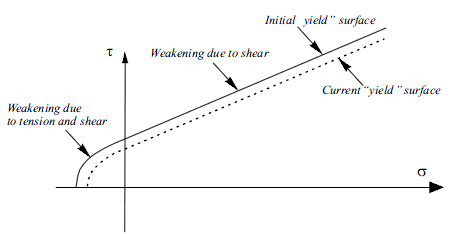
|
| Figure 10: Yield surface for elasto-plastic model |
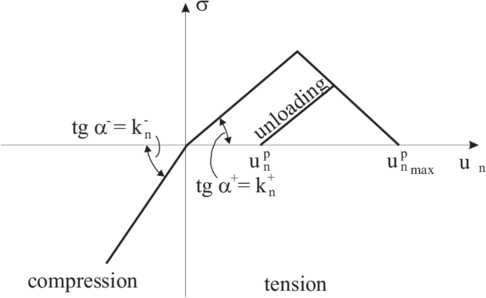
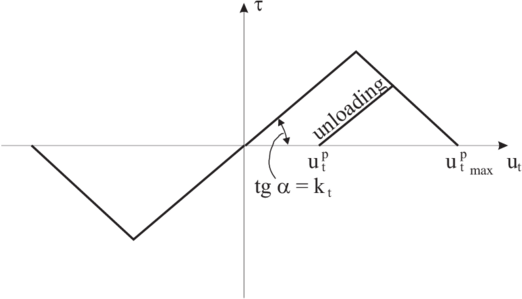
3.3 Contact model with elastic damage
The elastic perfectly brittle model can be easily extended to account for elastic damage by assuming a softening behaviour defined by a softening modulus introduced into the force-displacement relationship (Fig. 11).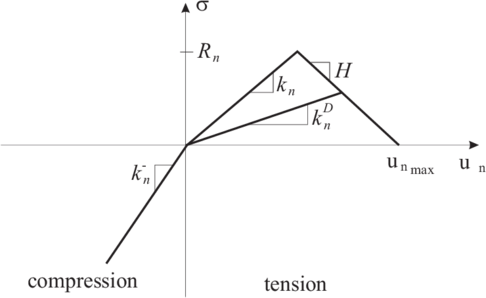
|
| Figure 11: Normal contact force in the contact model with elastic damage |
The constitutive relationship for 1D elastic damage is given by:
|
|
(54) |
where is the elastic damaged secant modulus and the scalar damage variable.
The scalar damage variable is a measure of material damage. For the undamaged state and for a damaged state . The scalar damage variable can be written in the following form:
|
|
(55) |
where is a function of total relative displacement. For linear strain softening is defined by
|
|
(56) |
where is the initial tensile strength and is the softening modulus (taken as positive).
A similar contact force–displacement law with damage (Fig. 12) can be introduced for the tangential direction. Then the bond decohesion can occur either due to tension or shear.
|
| Figure 12: Tangential contact force in the contact model with elastic damage |
An optional failure criterion has been implemented with a failure criterion based on the tensile contact force only. This criterion models better fracture of brittle materials, as the macroscopic failure is due to brittle rupture of atomic bonds in tension. This microscopic mechanism explains the macroscopic strain softening behaviour both under compression and tension states.
After the contact bonds are broken due to damage () standard frictional contact can occur between the spherical elements.
3.4 Contact model with friction, wear and heat generation
Frictional contact, wear and heat generation must be considered in order to accurately model tool-rock/soil interaction. Cohesion is not included into the formulation of this model. Hence, the normal contact forces can be compressive only. The normal contact force is calculated from the linear relationships:
|
|
(57) |
where is the normal relative displacement (penetration of one sphere against another). The frictional contact force is evaluated using the regularized Coulomb law
|
|
(58) |
where is the Coulomb friction coefficient. The frictional dissipation rate is calculated as
|
|
(59) |
where is the relative tangential velocity. The frictional dissipation is used to calculate the wear rate and the heat generated by friction . This is computed by
|
|
(60) |
where is the part of the friction work converted to heat (). Heat generation through frictional dissipation is assumed to be absorbed equally by the two particles in contact.
Wear rate is calculated using the Archard law [15], which assumes that the wear rate is proportional to the contact pressure and to the slip velocity
|
|
(61) |
with being the hardness of worn surface and being a dimensionless parameter. The Archard law was derived originally for adhesive wear, the same form of law, however, can be obtained for abrasive wear [16]. Values of adhesive and abrasive wear constants for different combinations of materials can be found in [16]. It is commonly accepted that wear is related to friction and thus friction coefficients are often introduced into Eq. (61). If the Coulomb friction law (58) holds, the Archard wear law can be written in the following equivalent form:
|
|
(62) |
in which the wear rate is related to frictional dissipation rate and .
Influence of temperature on wear can be taken into account by adaptation of the law of Archard given by Eq. (61). Thermal effects can be captured approximately by taking the hardness as a function of the temperature
|
|
(63) |
Then the Archard law (61) takes the following form:
|
|
(64) |
Computation of temperature can be performed by solving thermal conduction problem on the discrete domain [17].
4 FORMULATION OF QUASI-INCOMPRESSIBLE SOLID FINITE ELEMENTS
Many continuum finite elements exhibit so called “volumetric locking” in the analysis of incompressible or quasi-incompressible problems. Situations of this type are usual in the structural analysis of rubber materials, some geomechanical problems and most bulk metal forming processes. Volumetric locking is an undesirable effect leading to incorrect numerical results [3].
Volumetric locking is present in all low order solid elements based on the standard displacement formulation. The use of a mixed formulation or a selective integration technique eliminates the volumetric locking in many elements. These methods however, fail in some elements such as linear triangles and tetrahedra, due to lack of satisfaction of the Babuska-Brezzi conditions [3,18,19] or alternatively the mixed patch test [3,20,21] not being passed.
Considerable efforts have been made in recent years to develop linear triangles and tetrahedra producing correct (stable) results under incompressible situations. Brezzi and Pitkäranta [22] proposed to extend the equation for the volumetric strain rate constraint for Stokes flows by adding a laplacian of pressure term. A similar method was derived for quasi-incompressible solids by Zienkiewicz and Taylor [3]. Zienkiewicz et al. [23] have proposed a stabilization technique which eliminates volumetric locking in incompressible solids based on a mixed formulation and a Characteristic Based Split (CBS) algorithm initially developed for fluids [24,25,26] where a split of the pressure is introduced when solving the transient dynamic equations in time. Extensions of the CBS algorithm to solve bulk metal forming problems have been recently reported by Rojek et al. [24]. Other methods to overcome volumetric locking are based on mixed displacement (or velocity)-pressure formulations using the Galerkin-Least-Square (GLS) method [25], average nodal pressure and average nodal deformation [26,27] techniques, and Sub-Grid Scale (SGS) methods [28,29,30,31].
In this paper volumetric locking is avoided by using a finite calculus (FIC) formulation. The basis of the FIC method is the satisfaction of the equations of balance of momentum and the constitutive equation relating the pressure with the volumetric strain in a domain of finite size. The modified governing equations contain additional terms from standard infinitesimal theory. These terms introduce the necessary stability in the discretized equations to overcome the volumetric locking problem.
The FIC approach has been successfully used to derive stabilized finite element and meshless methods for a wide range of advective-diffusive and fluid flow problems [32,33,34,35,36,37,38,39]. The same ideas were applied in [4,5] to derive a stabilized formulation for quasi-incompressible and incompressible solids allowing the use of linear triangles and tetrahedra.
In the next section, the basis of the FIC method are given for static quasi-incompressible solid mechanics problems. The stabilized dynamic formulation for linear triangles and tetrahedra is presented and both semi-implicit and explicit monolithic solution schemes are described.
4.1 Equilibrium equations
The equilibrium equations for an elastic solid are written using the FIC technique as [32]
|
|
(65) |
where is the number of space dimensions of the problems (i.e. for 3D)
|
|
(66) |
In (65) and (66) and are the stresses and the body forces, respectively and are characteristic length distances of an arbitrary prismatic domain where equilibrium of forces is considered.
Equations (65) and (66) are completed with the boundary conditions on the displacements
|
|
(67) |
and the equilibrium of surface tractions
|
|
(68) |
In the above and are prescribed displacements and tractions over the boundaries and , respectively, are the components of the unit normal vector and are again the characteristic lengths.
The underlined terms in Eqs. (65) and (68) are a consequence of expressing the equilibrium of body forces and surface tractions in domains of finite size and retaining higher order terms than those usually accepted in the infinitesimal theory [32].
These terms are essential to derive a stabilized finite element formulation as described below.
4.1.1 Constitutive equations
The stresses are split into deviatoric and volumetric (pressure) parts
|
|
(69) |
where is the Kronnecker delta function. The linear elastic constitutive equations for the deviatoric stresses are written as
|
|
(70) |
where is the shear modulus,
|
|
(71) |
The constitutive equation for the pressure can be written for an arbitrary domain of finite size using the FIC formulation as [30]
|
|
(72) |
where is the bulk modulus of the material.
Note that for the standard relationship between the pressure and the volumetric strain of the infinitesimal theory is found.
For an incompressible material and Eq. (72) yields
|
|
(73) |
Eq. (73) expresses the limit incompressible behaviour of the solid. This equation is typical in incompressible fluid dynamic problems and there arises from the mass continuity conditions [32,33].
By combining Eqs. (65), (66), (69), (70) and (73) a mixed displacement–pressure formulation can be written as
|
|
(74) |
|
|
(75) |
Substituting Eq. (70) into (74) leads after some algebra to
|
|
(76) |
where is defined by Eq. (66) and
|
|
(77) |
Substituting Eq. (76) into (75) gives after some simplification
|
|
(78) |
|
|
(79) |
where
|
|
(80) |
The coefficients in Eq. (79) are also referred to as intrinsic time parameters per unit mass (their dimensions are where is the time).
4.2 Non linear transient dynamic analysis
The static formulation can be readily extended for the transient dynamic case accounting for geometrical and material non linear effects. Indeed in many situations of this kind, material quasi-incompressibility develops in specific zones of the solid due to the accumulation of plastic strains. It is well known that in these cases the use of equal order interpolations for displacements and pressure leads to locking solutions unless some precautions are taken.
The transient FIC equilibrium equations can be written in an identical form to eq. (65) (neglecting time stabilization terms [32,37,38]) with
|
|
(81) |
where is the density.
Eq. (81) is completed with the constitutive equations for the deviatoric stresses (eq. (70)) and the pressure (eq. (72)), as well with the boundary conditions (67) and (68) and the initial conditions for .
Following the arguments of the static case, the stabilized constitutive equation for the pressure can be expressed in terms of the residuals of the momentum equations by an expression identical to eq. (79). This equation is now written in an incremental form more suitable for non linear transient analysis.
We note that the stabilization terms are not larger needed in the numerical (FEM) solution equilibrium equations which can be asted in the standard form. This simply implies neglecting the terms involving in Eq. (74). The stabilized FIC form of the pressure constitutive equation (Eq. (79)) is however mandatory in order to avoid volumetric locking.
The set of stabilized equations to be solved are now:
Equilibrium
|
|
(82) |
Pressure constitutive equation
|
|
(83) |
where and are the increments of pressure and displacements, respectively. As usual denotes values at time .
In the derivation of Eq. (83) we have accepted that as the infinitesimal equilibrium equations are assumed to be satisfied at time (and hence ).
The weighted residual form of the FIC governing equations (82), (68) and (83) is
Equilibrium'
|
|
(84) |
Pressure constitutive equation
|
|
(85) |
where and are arbitrary test functions representing virtual displacements and virtual pressure fields, respectively.
Integrating by parts, the terms involving and in Eq. (84) and the term involving in Eq. (85) and neglecting the space derivatives of the intrinsic time parameters leads to
|
|
(86) |
|
|
(87) |
The residual is split now as
|
|
(88) |
where
|
|
(89) |
Note that is the part of not containing the pressure gradient and may be interpreted as the negative of a projection of the pressure gradient. In a discrete setting the terms can be considered belonging to a sub-scale space orthogonal to that of the pressure gradient terms.
In the infinitesimal limit and . This limit relationship between and can be weakly enforced by means of a weighted residual form.
The final set of integral equations is therefore
|
|
(90) |
|
|
(91) |
|
|
(92) |
where the coefficients are introduced in Eq. (92) for convenience.
We will choose continuous linear interpolations of the displacements, the pressure and the pressure gradient projection over three-node triangles (2D) and four-node tetrahedra (3D) [3]. The linear interpolations are written as
|
|
(93) |
where for 2D(3D) problems and denotes nodal variables. As usual are the linear shape functions [3]. The nodal variables are a function of the time . Substituting the approximations (93) into eqs. (90)–(92) gives the following system of discretized equations
|
|
(94) |
|
|
(95) |
|
|
(96) |
where is the nodal acceleration vector. The expression of the different matrices in vectors appearing in Eqs. (94)–(96) is presented in the Appendix.
A four steps semi-implicit time integration algorithm can be derived from eqs. (94)–(96) as follows
step
Step 1. Compute the nodal velocities
|
|
(97) |
Step 2. Compute the nodal displacements
|
|
(98) |
Step 3. Compute the nodal pressures
|
|
(99) |
Step 4. Compute the nodal projected pressure gradients
|
|
(100) |
In above, all matrices are evaluated at , and
|
|
(101) |
where the stresses are obtained by consistent integration of the adequate (non linear) constitutive law [33].
Note that steps 1, 2 and 4 are fully explicit as a diagonal form of matrices and has been chosen. The solution of step 3 with a diagonal form for still requires the inverse of a Laplacian matrix. This can be an inexpensive process using an iterative equation solution method (e.g. a preconditioned conjugate gradient method).
A three steps approach can be obtained by evaluating the projected pressure gradient variables at in a fully implicit form in Eq. (99). Eliminating then from the fourth step using Eq. (100) and substituting this expression into Eq. (99) leads to
|
|
(102) |
where
|
|
(103) |
Recall that for the full incompressible case and in all above equations.
The critical time step is taken as that of the standard explicit dynamic scheme [28].
Explicit algorithm
A fully explicit algorithm can be obtained by computing from step 3 in Eq. (99) as follows
|
|
(104) |
Obviously, solution of eq. (104) breaks down for as in this case. Therefore, the explicit algorithm is not applicable in the full incompressible limit. The explicit form can however be used with success in problems where quasi-incompressible regions exist adjacent to standard “compressible” zones.
5 DEM–FEM CONTACT ALGORITHM
Use of combined DEM/FEM models involves treatment of contact between spherical discrete elements and boundary of continuum subdomains discretized with finite elements as shown in Fig. 13. Similarly as in case of contact between two spheres (Fig. 2) the contact force between the sphere and external edge of a finite element is decomposed into normal and tangential components, and . In a general case the contact model between discrete elements and finite element edges can include cohesion, damping, friction, wear, heat generation and exchange.
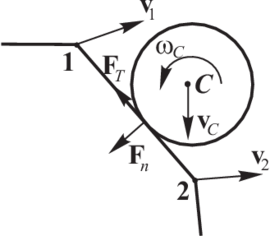
|
| Figure 13: Contact between a sphere and finite element edge |
Similarly to the relationship (10) the normal contact force is decomposed into the elastic part and the damping contact force
|
|
(105) |
The elastic part of the normal contact force is proportional to the normal stiffness and to the penetration of the two particle surfaces
|
|
(106) |
The penetration is calculated here as
|
|
(107) |
where is the distance of the particle centre and is the particle radius.
The contact damping force is assumed to be of viscous type
|
|
(108) |
where is the damping coefficient and is the normal component of the relative velocity at the contact point. The relative velocity at the contact point is calculated as
|
|
(109) |
where is the discrete element velocity at the contact point and is the velocity of the finite element edge at the contact point expressed in terms of the nodal velocities, and , and respective shape functions and . The relative velocity is decomposed into the normal and tangential velocity using the formulae (15) and (17).
The cohesive contact force is calculated using the elastic-perfectly brittle model described in Section 3.1. In the absence of cohesion the frictional contact reaction is calculated using the regularized Coulomb friction model described in section 2.3.3.
6 GENERAL DISCRETE ELEMENT-FINITE ELEMENT DYNAMIC FORMULATION
The general algorithm for the transient dynamic problem involving discrete elements and (stabilized) finite elements includes the following steps.
Step1. Compute the nodal velocities
Discrete elements
|
|
(110) |
with
|
|
(111) |
|
|
(112) |
with
|
|
(113) |
Finite elements
|
|
(114) |
Step2. Compute the nodal displacements
Discrete elements
|
|
(115) |
|
|
(116) |
Finite elements
|
|
(117) |
Step3. Compute the nodal pressures
Finite elements
|
|
(118) |
Step4. Update the nodal coordinates
Discrete and finite elements
|
|
(119) |
|
|
(120) |
Step 5. Check frictional contact forces
Step 6. Update residual force vector
Go to step 1
7 EXAMPLES
7.1 Uniaxial compression and tension tests of a rock material
Mechanical properties of rock materials are determined from laboratory tests such as compression, triaxial and tension tests. Figure 14 shows a cube specimen of a sandstone rock after unconfined compression test. The parameters of numerical discrete element model can be obtained carrying out simulations of basic laboratory tests. Such analyses allow us to determine microscopic constitutive parameters for a material sample modelled with discrete elements yielding required macroscopic properties. The most important macroscopic properties are Young modulus, Poisson ratio and compressive and tensile strengths. Microscopic parameters are in turn all the constitutive model parameters governing the frictional contact interaction between a pair of particles. Here elastic perfectly brittle constitutive model will be used with the contact stiffness in normal and tangential direction, interface tensile and shear strength and Coulomb friction coefficient being the microscopic parameters.

|
| Figure 14: Rock specimen after laboratory unconfined compression test |
Figure 15 presents the material sample prepared for testing. A material sample of mm is represented by an assembly of randomly compacted 2100 discs of radii 1–1.5 mm. It is shown in [40] that preparing a well-connected densely packed irregular assembly of particles is the key to successful simulation with discrete elements. Compaction of the particle assembly shown in Fig. 15 is characterized by a porosity of %.
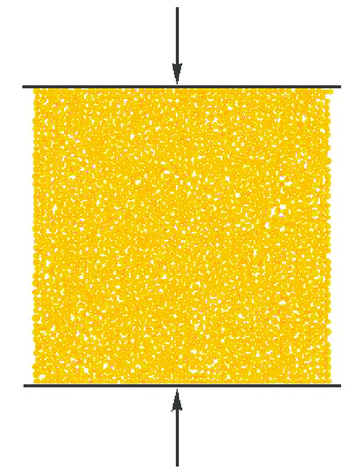
|
| Figure 15: Set-up of the numerical model of uncofined compression test |
The macroscopic response of a square material sample subjected to uniaxial compression has been studied. The loading has been introduced under kinematic control by prescribing the motion of rigid plates pressing on the top and bottom of the sample. The deformation in the direction was free. The velocity of the wall displacement was 1 mm/s which was found to be sufficiently low to obtain quasi-static loading.
The purpose of the present study was to determine the microscopic parameters for sandstone with the following macroscopic properties: Young modulus GPa, Poisson ratio and unconfined compressive strength MPa. The stress-strain relationship shown in Fig. 16 satisfying these requirements has been obtained with the following set of micromechanical parameters: contact stiffness in the normal and tangential directions GPa, Coulomb friction coefficient and cohesive bond strengths in the normal and tangential direction, MN/m and MN/m, respectively. The failure mode of the specimen obtained in the simulation is shown in Fig. 17. Particles with broken cohesive bonds are marked with different colour. Comparison of Figs. 14 and 17 show that numerical analysis yields a failure mode similar to that observed in experiments.
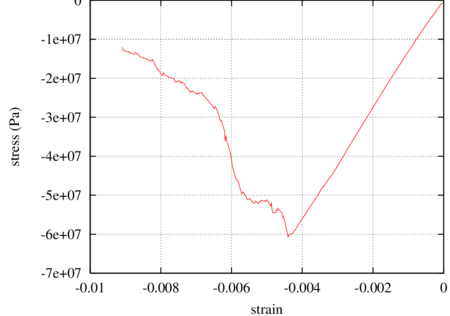
|
| Figure 16: Stress–strain relationship for uniaxial unconfined compression test |

|
| Figure 17: Failure mode obtained in the simulation of unconfined compression test |
Tensile strength of rocks is obtained experimentally from indirect tension (Brasilian) test. In the numerical procedure we checked the tensile strength of the particle assembly carrying out simulations of direct tension test. The stress–strain relationship obtained in this simulation is plotted in Fig. 18. The elastic modulus for tension and tensile strength obtained from the plots are the following: GPa, MPa. It can be noted that the curves both for compression and tension are typical for materials with brittle failure. The failure mode obtained in the analysis of a direct tension test is shown in Fig. 19.
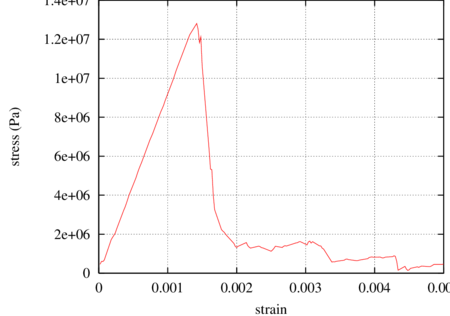
|
| Figure 18: Stress–strain relationship for uniaxial direct tension test |
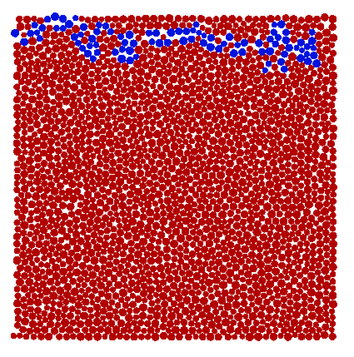
|
| Figure 19: Failure mode obtained in the simulation of direct tension test |
7.2 Simulation of rock cutting
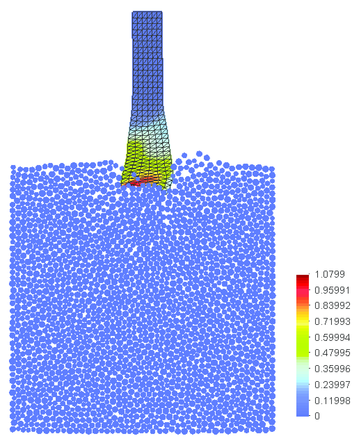
A material sample representing sandstone with parameters determined in the previous section has been used in the simulation of a rock cutting process. Two different solutions with the tool discretized with discrete and finite elements have been studied. The combined FEM/DEM model is shown in Fig. 20. The material sample mm is represented by an assembly of randomly compacted 2100 discs of radii 1–1.5 mm. Contact interface between particles representing the rock is characterized with the stiffness in the normal and tangential directions GPa, the cohesive bond strengths MN/m, MN/m, and the friction coefficient . The tool has been modelled with 6800 linear triangles. The following elasto-plastic parameters have been assumed for the tool material: Young modulus MPa, Poisson's ratio , yield stress MPa and hardening modulus MPa. The following parameters have been assumed for the tool-rock interface: contact stiffness modulus GPa, Coulomb friction coefficient .

|
| Figure 20: Rock cutting problem. 2100 discrete elements are used to model the rock whereas 6800 linear triangles are used to discretize the tool. |
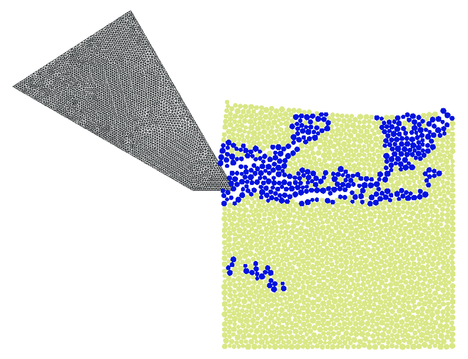
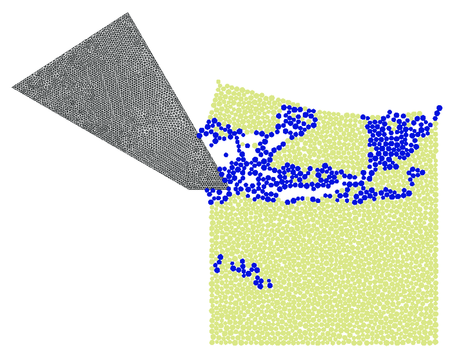
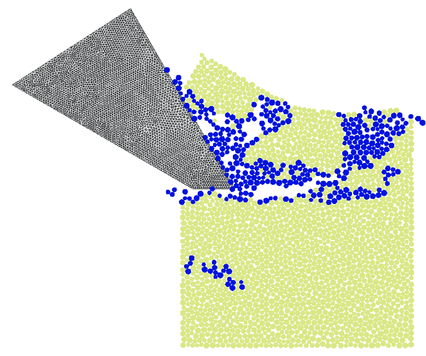
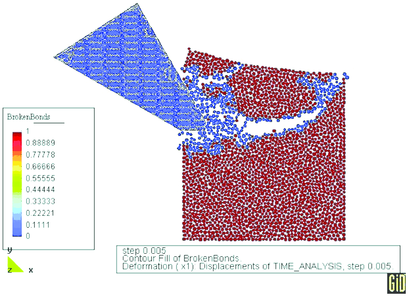
Cutting process has been carried out with prescribed horizontal velocity of the tool of 4 m/s. The cutting is shown in Fig. 21. In this figure we can also see the failure mode. Particles with broken bonds are coloured in blue. It can be clearly seen the formation of a chip during cutting which is typical for brittle materials.
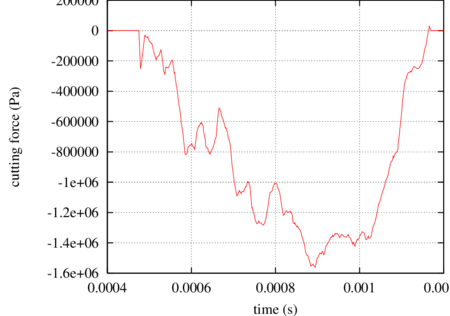
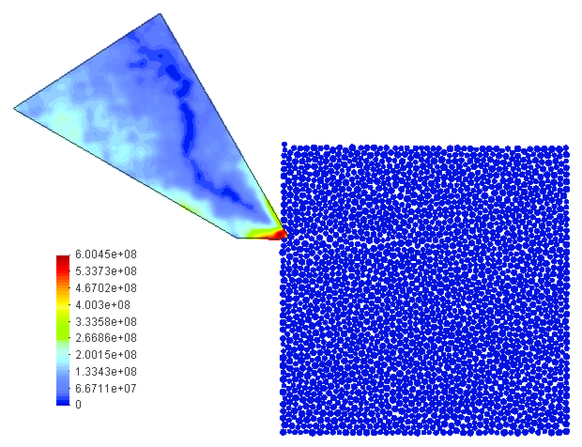
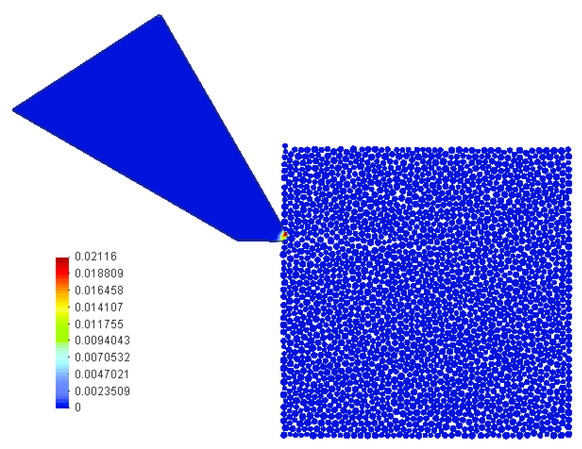
Variation of the cutting force in the initial phase of cutting is shown in Fig. 22. The Mises stress and efffective plastic strain distributions in the tool in the initial phase of cutting are shown in Figs. 23 and 24, respectively.
|
|
|

|
| Figure 21: Rock cutting process analysed using the FEM/DEM model. The failure mode | |
|
| Figure 22: Variation of the cutting force in the initial phase of cutting |
|
| Figure 23: Rock cutting process analysed using the FEM/DEM model. The Mises stresses in the tool in the initial phase of cutting |
|
| Figure 24: Rock cutting process analysed using the FEM/DEM model. The effective plastic strain in the tool in the initial phase of cutting |
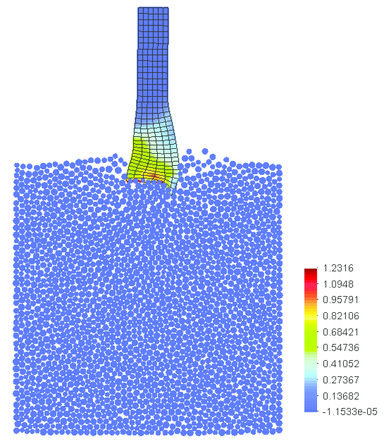
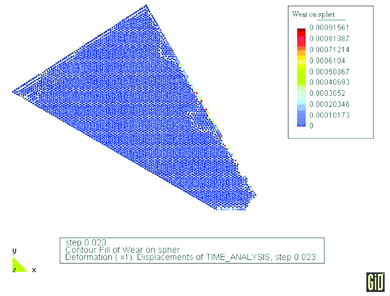
The model of rock cutting process presented above has been used to demonstrate the capabilities of the developed algorithm for wear estimation. Next the tool has been discretized with 4500 discrete elements (Fig. 25). This allows us to easily modify the shape of the tool. The tool shape is changed by eliminating particles if the accumulated wear exceeds the particle diameter. Particles are eliminated automatically and the analysis is continued with the modified shape of the tool.
|
| Figure 25: Rock cutting process analyzed with the tool discretized with 4500 discrete elements |
The required material constants and necessary for wear evaluation have been obtained in laboratory tests. The average Brinell hardness of 400 has been obtained for the tool steel and a value of the Archard wear constant has been taken in the wear simulation.
Evolution of the tool shape is obtained in a number of consecutive simulations of work cycles. The tool shape is modified continuously during the analysis. After finishing one work cycle the tool with a new shape is again used in the simulation of next work cycle. The whole procedure can be repeated as needed to reproduce the real working conditions of the tool. In this manner the evolution of change of tool shape in wear process during its whole service life can be obtained.
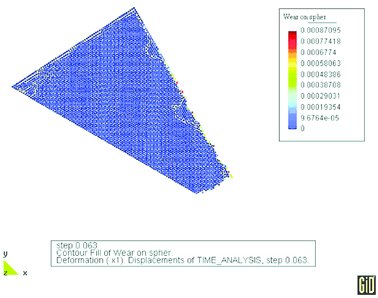
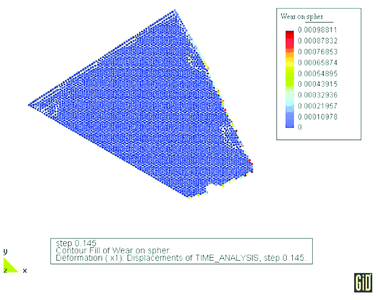
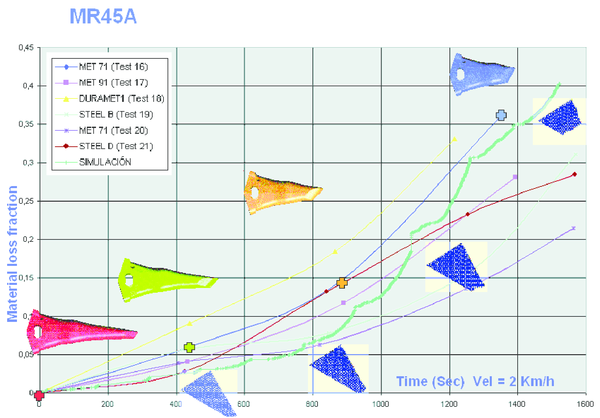
Tool shapes at different stages of wear are shown in Fig. 26. As much as 40% of the tool mass has been lost due to abrasive wear. Figure 27 presents the tool mass loss as a fraction of the initial tool mass versus analysis time. The wear curve obtained in the analysis agrees quite well with experimental curves obtained in field tests.

|
|
|
|
| Figure 26: Evolution of the cutting tool shape due to wear during the rock cutting process | |
|
| Figure 27: Mass loss fraction in the tool versus analysis time –- comparison of experimental and simulation wear curves |
7.3 Strip punch test
The strip punch test investigated experimentally by Dede [41] and studied numerically using a FE model by Klerck [42] is analysed here using the DEM model. Prismatic quartzite specimens of dimensions mm are crushed by a punch load applied in the strip 10 mm wide on the top side along the symmetry line as shown in Fig. 28. A confining pressure of 4.5 MPa was applied to the specimen sides.
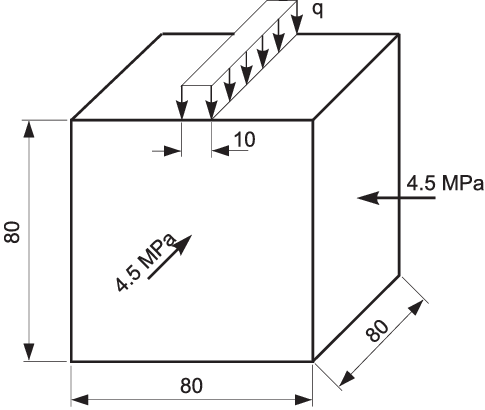
|
| Figure 28: Strip punch geometry and loading configuration |
 ] ]
|
| Figure 29: Experimental fracture pattern, after [41] |
 ] ]
|
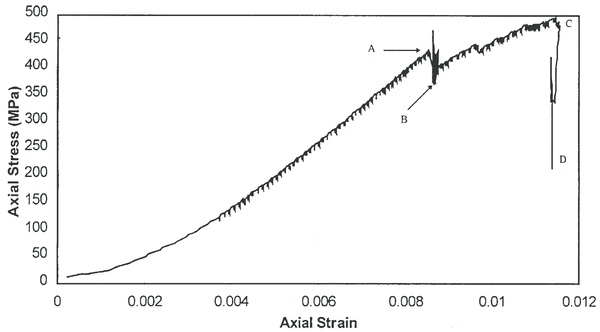
| Figure 30: Experimental axial stress vs. axial strain plot, after [41] |
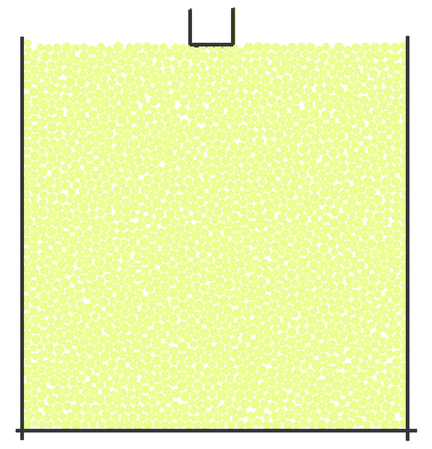
The 2D discrete element model used in our analysis is shown in Fig. 31. The square rock specimen mm is represented by an assembly of randomly compacted 2100 discs of radii 0.8–1.2 mm. Sliding conditions are prescribed at the bottom specimen side and confining pressure is introduced by means of rigid plates transmitting a confining load. Axial load is introduced by a rigid punch under a prescribed displacement.
|
| Figure 31: 2D discrete element model |
Required microscopic parameters for the DEM model corresponding to the macroscopic properties of quartzite rock given in [41] are: Young's modulus GPA, compressive strength MPa and tensile strength MPa. Those values have been obtained using the procedure presented in example 7.1 for the following microscopic parameters: the stiffness in the normal and tangential directions GPa, the cohesive bond strengths MN/m, MN/m, and the friction coefficient .
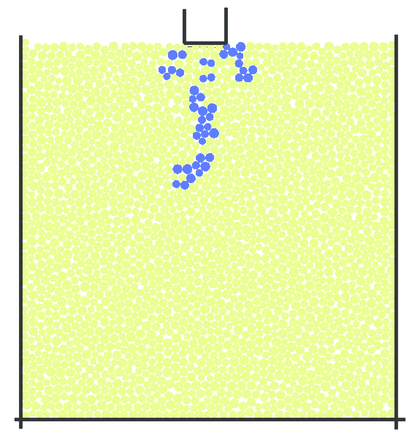
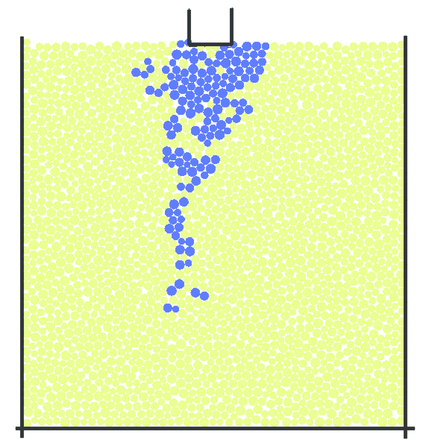
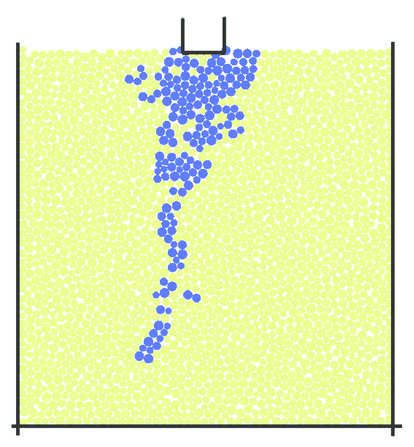
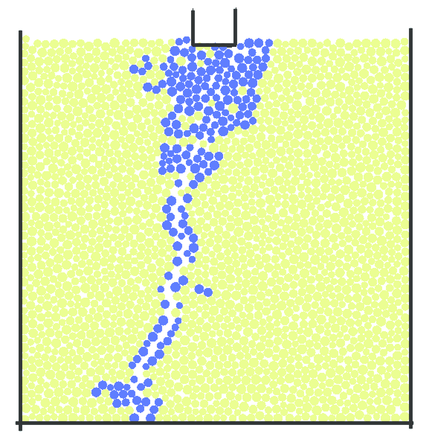
The numerical failure pattern is shown in Fig. 32. The cracking pattern obtained is similar to experimental results shown in Fig. 29. The triangular crushed zone below the punch and the axial cleavage crack are reproduced in the numerical simulation.
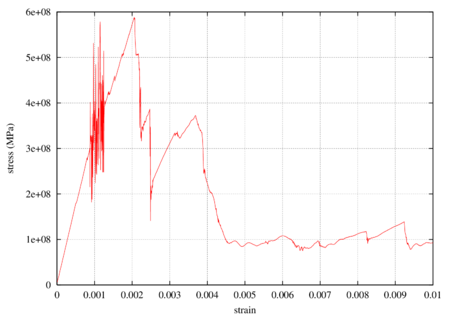
Quite a good agreement can also be observed between experimental (Fig. 30) and numerical (Fig. 33) critical values of axial stresses.
|
|
|
 ] ]
|
| Figure 32: Numerical failure pattern, after [41] | |
|
| Figure 33: Numerical axial stress vs. axial strain plot |
7.4 Impact of projectile against rock plate
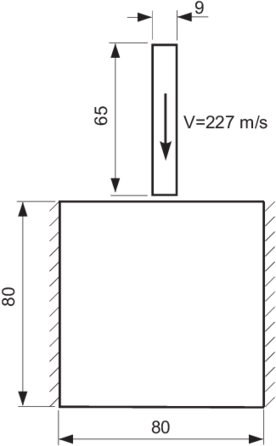
The impact of the projectile against a thick rock plate as defined in Fig. 34 has been studied in order to illustrate possibilities of combined FEM/DEM modelling for this kind of problems.
|
| Figure 34: Impact of projectile – definition of geometry |
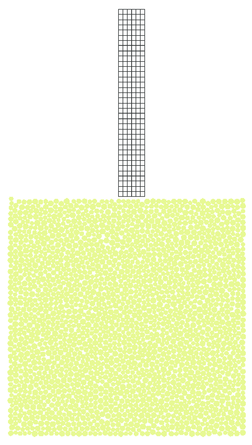
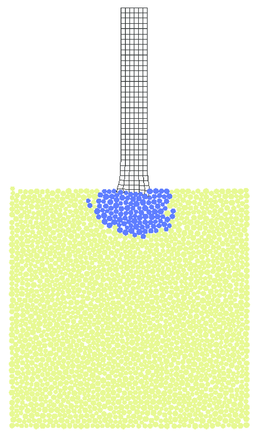
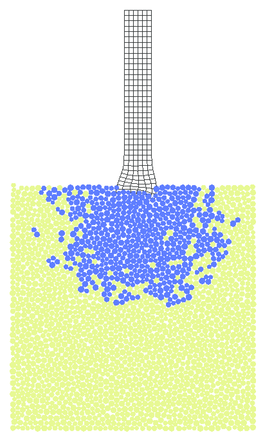
The projectile has been discretized with either equal order linear triangular elements using the FIC formulation previously described, and also with quadrilateral Q1/P0 elements based on a mixed formulation [3]. Projectile has been assumed to be made of steel with the following properties: Young's modulus MPa, Poisson's ratio , yield stress MPA and isotropic linear hardening modulus MPA. The macroscopic parameters of rock has been assumed the same as in the previous example (section 7.3). Again the same collection of discrete elements has been used.
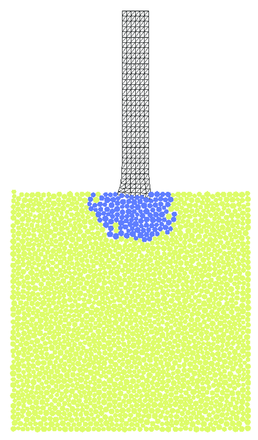
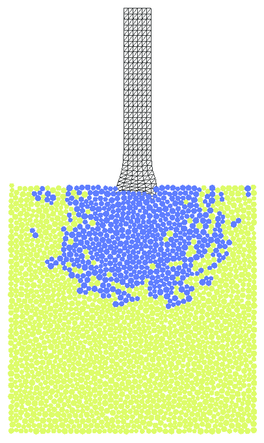
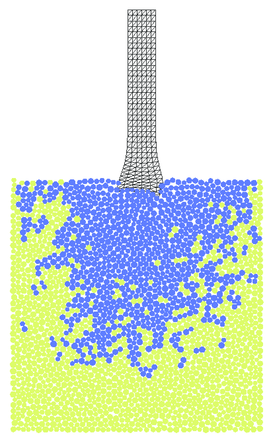
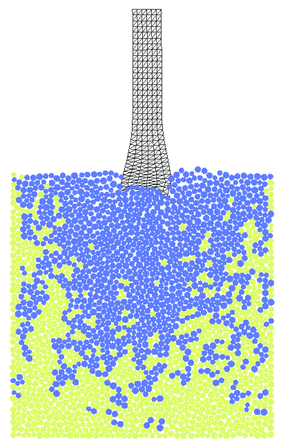
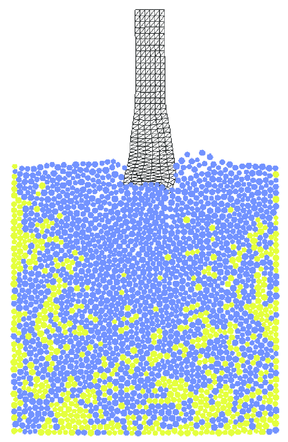
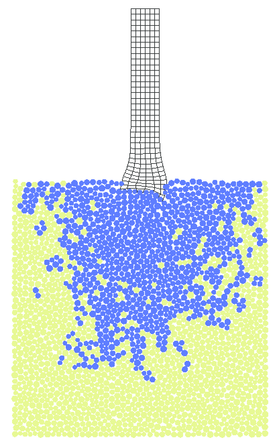
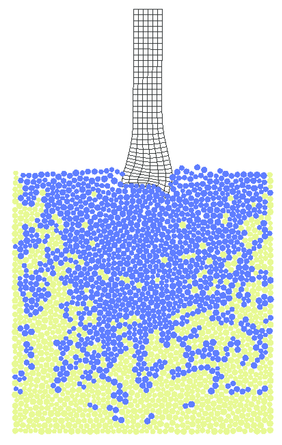
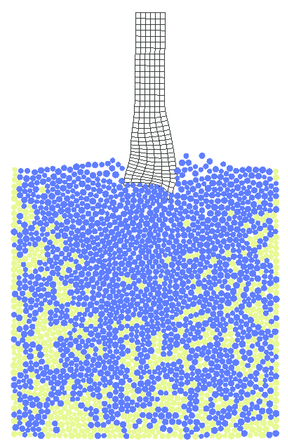
Fracturing of the plate under the impact as well as projectile deformation is shown in Figs. 35 and 36 for triangular and quadrilateral projectile discretizations, respectively. Results obtained with quadrilateral elements are considered as the reference ones for the solution obtained with the FIC formulation. The agreement observed between Figs. 35 and 36 confirms correctness of the FIC algorithm developed by the authors. Advantages of this algorithm can be observed especially in 3D models with more complicated geometry where meshing with tetrahedra is easier than with hexahedra. Effective plastic strains obtained with triangles and quadrilaterals also coincide as it can be seen in Fig. 37.
Non-symmetry observed in the deformation of the projectile can be attributed in the non-symmetry of the discrete elements in the zone of impact which initiates global buckling of the projectile.

|
|
|
|
|
|
| Figure 35: Impact of projectile – numerical results obtained using linear triangular elements based on FIC formulation | ||
|
|
|
|
|
|
| Figure 36: Impact of projectile – numerical results obtained using mixed bilinear Q1/P0 quadrilateral elements | ||
7.5 Study of pipe ovalization
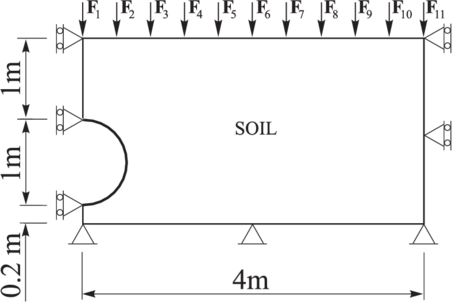
Interaction of soil and pipe leading to pipe ovalization has been studied. This example demonstrates another possibility of combined FEM/DEM modelling in geomechanics.
|
| Figure 38: Pipe ovalization – geometry definition |
The definition of the problem geometry is shown in Fig. 38. A pipe of 1m diameter and 1 cm thickness is buried 1 m under the surface of a soil. Due to symmetry only half of the geometry is modelled. The surface load increases linearly as
|
|
where is load factor and is the constant reference load defined by a set of uniformly distributed concentrated forces
|
|
The following values of reference forces have been assumed:
|
|
|
|
The load has been transmitted to soil by a kind of diaphragm with hinges in the places of force application.
The following material properties for the pipe have been assumed: Young's modulus MPa, Poisson's coefficient , density kg/m, yield stress MPa, isotropic hardening modulus MPa. The pipe has been discretized with 42 plane strain triangular elements based on the FIC formulation.
The soil specimen has been modelled by 15 000 cylindrical discrete elements of diameters in the range from 2 cm to 3 cm. The following microscopic parameters in the soil model have been used: density kg/m, the stiffness in the normal and tangential directions GPa, Coulomb friction coefficient .
The pipe–soil interface has been defined by the stiffness in the normal and tangential directions GPa, Coulomb friction coefficient .
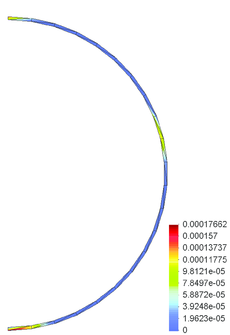
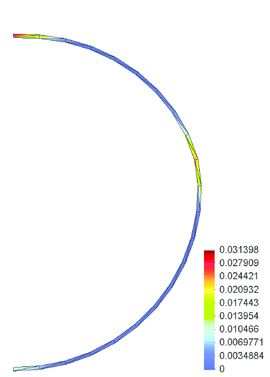
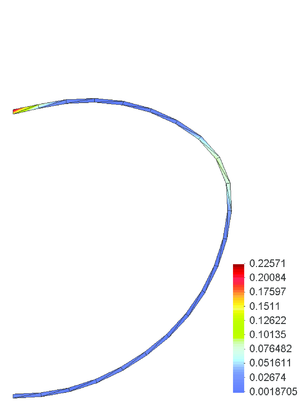
Numerical results for the deformed pipe shape are shown in Fig. 39. The increasing soil pressure leads to ovalization of the pipe. Due to large soil pressure the pipe instability is observed. Pipe material undergoes elasto-plastic deformation. Pipe cross-sections with effective plastic strain distribution at different load level are shown in Fig. 40.
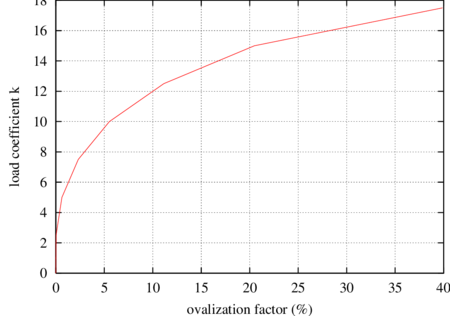
Pipe cross-sections deformation can be described using an ovalization factor parameter , defined in terms of the maximum and minimum pipe diameters, and , respectively as
|
|
Variation of the ovalization factor for different load levels is shown in Fig. 41. Numerical results agree with those given in [43].

|

|

|

|
| Figure 39: Pipe ovalization – deformed configuration at different load levels | |
|
|
|
|
| Figure 40: Pipe ovalization – deformed configuration | |
|
| Figure 41: Pipe ovalization factor |
Conclusions
The combination of spherical rigid elements and finite elements is a promising approach for simulation of geomechanical problems involving fracture, penetration and wear. The transient dynamic formulation presented allows to model the motion of discrete and finite elements using a unified algorithm. Frictional contact effects between the rigid spheres and between the spheres and finite elements can be simply accounted for. FIC stabilization procedure allows to use low order triangles and tetrahedra elements with equal order interpolation of the displacement and pressure variables free of the volumetric locking problem. This allows us to apply the presented formulation to problems where large plastic deformation occur in the continuum part of the domain. The discrete formulation can be used to model tools in rock cutting operations. This allows to reproduce tool wear simply by removing the worn particles from the tool surface, thus reproducing the material loss in a realistic manner. Further applications of this approach to the prediction of wear of rock cutting process can be found in [17,44].
References
[1] H. Konietzky, editor. Numerical Modeling in Micromechanics via Particle Methods. Balkema Publishers, 2002.
[2] B.K. Cook and R.P. Jensen, editors. Discrete Element Methods. Numerical Modeling of Discontinua. ASCE, 2002.
[3] O.C. Zienkiewicz and R.C. Taylor. The Finite Element Method. Butterworth-Heinemann, Oxford, V edition, 2000.
[4] E. Oñate, J. Rojek, R.L. Taylor, and O.C. Zienkiewicz. Linear triangles and tetrahedra for incompressible problem using a finite calculus formulation. In Proc. 2nd European Conference on Computational Mechanics ECCM-2001, Cracow, 26-29 June, 2001 (on CD ROM), 2001.
[5] E. Oñate, R.L. Taylor, O.C. Zienkiewicz, and J. Rojek. A residual correction method based on finite calculus. In FEMClass of 42 Meeting, 30–31 May, Ibiza (www.femclass42.com), 2002.
[6] P.A. Cundall and O.D.L. Strack. A discrete numerical method for granular assemblies. Geotechnique, 29:47–65, 1979.
[7] C.S. Campbell. Rapid granular flows. Annual Review of Fluid Mechanics, 2:57–92, 1990.
[8] Eng. Comput., 9(2), 1992. Special issue on Discrete Element Methods, Editor: G. Mustoe.
[9] J.R. Williams and R. O'Connor. Discrete Element Simulation and the Contact Problem. Archives Comp. Meth. Engng, 6(4):279–304, 1999.
[10] P.A. Cundall. Formulation of a Three Dimensional Distinct Element Model –- Part I. A Scheme to Detect and Represent Contacts in a System of Many Polyhedral Blocks. Int. J. Rock Mech., Min. Sci. & Geomech. Abstr., 25(3):107–116, 1988.
[11] J. Rojek, E. Oñate, F. Zarate, and J. Miquel. Modelling of rock, soil and granular materials using spherical elements. In 2nd European Conference on Computational Mechanics ECCM-2001, Cracow, 26-29 June, 2001.
[12] J. Argyris. An excursion into large rotations. Comput. Meth. Appl. Mech. Eng., 32:85–155, 1982.
[13] L.M. Taylor and D.S. Preece. Simulation of blasting induced rock motion. Eng. Comput., 9(2):243–252, 1992.
[14] T.J.R. Hughes. The Finite Element Method. Linear Static and Dynamic Analysis. Prentice-Hall, 1987.
[15] J.F. Archard. Contact and rubbing of flat surfaces. J. Appl. Phys., 24(8):981–988, 1953.
[16] E. Rabinowicz. Friction and wear of materials. 1995.
[17] J. Rojek, E. Oñate, F. Zarate, and J. Miquel. Thermomechanical discrete element formulation for wear analysis of rock cutting tools. (to be published).
[18] I. Babuska. The finite element method with lagrangian multipliers. Numer. Math., 20:179–192, 1973.
[19] F. Brezzi. On the existence, uniqueness and approximation of saddle-point problems arising from Lagrange multipliers. Rev. Francaise d'Automatique Inform. Rech. Opér., Ser. Rouge Anal. Numér., 8R-2:129–151, 1974.
[20] O.C. Zienkiewicz, S. Qu, R.L. Taylor, and S. Nakazawa. The patch test for mixed formulations. Int. J. Num. Meth. Eng., 23:1873–1883, 1986.
[21] O.C. Zienkiewicz and R.L. Taylor. The finite element patch test revisited: A computer test for convergence, validation and error estimates. Comput. Meth. Appl. Mech. Eng., 149:523–544, 1997.
[22] F. Brezzi and J. Pitkäranta. On the stabilization of finite element approximations of the Stokes problem. In W. Hackbusch, editor, Efficient Solution of Elliptic Problems, Notes on Numerical Fluid Mechanics. Vieweg, Wiesbaden, 1984.
[23] O.C. Zienkiewicz, J. Rojek, R.L. Taylor, and M. Pastor. Triangles and tetrahedra in explicit dynamic codes for solids. Int. J. Num. Meth. Eng., 43:565–583, 1998.
[24] J. Rojek, O.C. Zienkiewicz, E. Oñate, and R.L. Taylor. Simulation of metal forming using new formulation of triangular and tetrahedral elements. In Int. Conf. on Metal Forming 2000, Kraków, Poland, 2000. Balkema.
[25] T.J.R. Hughes, L.P. Franca, and G.M. Hulbert. A new finite element formulation for computational fluid dynamics: VIII. The galerkin/least-squares method for advective-diffusive equations. Comput. Meth. Appl. Mech. Eng., 73:173–189, 1989.
[26] J. Bonet, H. Marriot, and O. Hassan. Stability and comparison of different linear tetrahedral formulations for nearly incompressible explicit dynamic applications. Int. J. Num. Meth. Eng., 50:119–133, 2001.
[27] J. Bonet, H. Marriot, and O. Hassan. An average nodal deformation tetrahedron for large strain explicity dynamic applications. Commun. Num. Meth. in Engrg., 17:551–561, 2001.
[28] R. Codina and J. Blasco. Stabilized finite element method for transient Navier-Stokes equations based on pressure gradient projection. Comput. Meth. Appl. Mech. Eng., 182:287–300, 2000.
[29] R. Codina. Stabilization of incompressibility and convection through orthogonal sub-scales in finite element methods. Comput. Meth. Appl. Mech. Eng., 190:1579–1599, 2000.
[30] M. Chiumenti, Q. Valverde, C. Agelet de Saracibar, and M. Cervera. A stabilized formulation for incompressible elasticity using linear displacement and pressure interpolations. Comput. Meth. Appl. Mech. Eng., 2002.
[31] M. Chiumenti, Q. Valverde, C. Agelet de Saracibar, and M. Cervera. A stabilized formulation for incompressible plasticity using linear triangles and tetrahedra. Int. Journal of Plasticity, 2002.
[32] E. Oate. Derivation of stabilized equations for advective-diffusive transport and fluid flow problems. Comput. Meth. Appl. Mech. Eng., 151:233–267, 1998.
[33] E. Oate. A stabilized finite element method for incompressible flows using a finite increment calculus formulation. Comput. Meth. Appl. Mech. Eng., 182:355–370, 2000.
[34] E. Oate, J. García, and S. Idelhson. Computation of the stabilization parameter for the finite element solution of advective-diffusive problems. Int. J. Num. Meth. Fluids., 25:1385–1407, 1997.
[35] E. Oate, J. García, and S. Idelhson. An alpha-adaptive approach for stabilized finite element solution of advective-diffusive problems. In P. Ladeveze and J.T. Oden, editors, New Adv. in Adaptive Comp. Meth. in Mech. Elsevier, 1998.
[36] E. Oate and M. Manzan. A general procedure for deriving stabilized space-time finite element methods for advective-diffusive problems. Int. J. Num. Meth. Fluids., 31:203 – 221, 1999.
[37] E. Oate and J. García. A finite element method for fluid–structure interaction with surface waves using a finite calculus formulation. Comput. Meth. Appl. Mech. Eng., 191:635–660, 2001.
[38] J. García and E. Oate. An unstructured finite element solver for ship hydrodynamic problems. J. Appl. Mech., 2002.
[39] E. Oate, C. Sacco, and S. Idelhson. A finite point method for incompressible flow problems. Computing and Visualization in Science, 3:67–75, 2000.
[40] H. Huang. Discrete Element Modeling of Tool-Rock Interaction. PhD thesis, University of Minnesota, 1999.
[41] T. Dede. Fracture onset and propagation in layered media. M.Sc. Dissertation, University of the Witwaterstrand, Johannesburg, South Africa, 1997.
[42] P.A. Klerck. The Finite Element Modelling of Discrete Fracture in Quasi-brittle Materials. PhD thesis, University of Wales, Swansea, 2000.
[43] http://geosim.engr.mun.ca/pipesoil.htm.
[44] E. Oñate, C. Recarey, F. Zarate, J. Miquel, and J. Rojek. Characterization of micro-macro parameters in discrete element formulation. (to be published).
APPENDIX A
A.1 Matrices and vectors in FEM equations of motion using the FIC formulation
In FEM equations of motion using the FIC formulation (94)–(96) the following vectors and matrices have been used:
|
|
(A.1) |
is the mass matrix
|
|
(A.2) |
is the internal nodal force vector and the rest of matrices and vectors are
|
In above and ,
|
|
(A.4) |
is the standard infinitesimal strain matrix and is the deviatoric constitutive matrix [3]. Note that the expression of of eq. (A.2) is adequate for non linear structural analysis.
Document information
Published on 01/01/2004
DOI: 10.1016/j.cma.2003.12.056
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?