Published in Comput. Meth. Appl. Mech. Engng., Vol. 195, pp. 3926–3946, 2006
doi: 10.1016/j.cma.2005.07.020
Abstract
A stabilized finite element method (FEM) for the steady state advection-diffusion-absorption equation is presented. The stabilized formulation is based on the modified governing differential equations derived via the Finite Calculus (FIC) method. The basis of the method is detailed for the 1D problem. It is shown that the stabilization terms act as a non linear additional diffusion governed by a single stabilization parameter. A critical constant value of this parameter ensuring a stabilized solution using two node linear elements is given. More accurate numerical results can be obtained by using a simple expression of the non linear stabilization parameter depending on the signs of the numerical solution and of its derivatives. A straightforward two steps algorithm yielding a stable and accurate solution for all the range of physical parameters and boundary conditions is described. The extension to the multi-dimensional case is briefly described. Numerical results for 1D and 2D problems are presented showing the efficiency and accuracy of the new stabilized formulation.
1 INTRODUCTION
Considerable effort has been spent in recent years to derive finite element methods (FEM) [1] for the solution of the advection-diffusion-reaction equation. The physical behaviour of this equation is varied. In the propagation regime, originated by large values of the productive term (the Helmholtz equation), solutions are exponentially modulated sinusoidal functions. Typical problems found here in the numerical solution are those of phase, amplitude and pollution errors [2]. In the exponential regime, solutions are of the form of real exponential functions where absorptive (dissipative) or productive source terms are possible. Numerical schemes here find difficulties to approximate the sharp gradients appearing in the neighborhood of boundary and internal layers due to high Peclet and/or Damköhler numbers.
Stabilized methods to tackle above problems have been based on different kinds of streamline-upwind-Petrov-Galerkin (SUPG) [2-7], Galerkin Least Square [5-11], Subgrid Scale (SGS) [5,6,12,13] and Residual Free Bubbles [14] finite element methods. While a single stabilization parameter suffices to yield stabilized (and even nodally exact results) for the one-dimensional (1D) advection-diffusion and the diffusion-reaction equations (Vol. 3 in [1] and [8-15]), this is not the case for the diffusion-advection-reaction equation. Here, in general, two stabilization parameters are needed in order to ensure a stabilized solution for all range of physical parameters and boundary conditions [4,10,14]. As reported in [12,13] both SUPG, GLS and SGS methods with a single stabilization parameter (and indeed the standard Galerkin scheme) fail to obtain an stabilized solution for some specific boundary conditions in the exponential regime with negative (absorption) terms when there is a negative streamwise gradient of the solution.
Apart from the many practical applications of the advection-diffusion-reaction problem, the interest to derive stabilized numerical schemes for this equation extends to the solution of the transient advection-diffusion equation, as the discretized form of this equation in time can be interpreted as an analogous steady-state advection-diffusion-absorption problem. This analogy has been analyzed in [16,17].
In this paper we present a reliable and accurate stabilized formulation for the advection-diffusion-reaction equation in the exponential regime with absorption (destructive) reaction terms using a single stabilization parameter.
The stabilized formulation is based on the standard Galerkin FEM solution of the modified governing differential equations derived via the Finite Calculus (FIC) method [20]. The FIC equations are obtained by expressing the balance of fluxes in a domain of finite size. This introduces additional stabilizing terms in the differential equations of the infinitessimal theory which are a function of the balance domain dimensions. These dimensions are termed characteristic length parameters and play a key role in the stabilization process.
The modified governing equations lead to stabilized numerical schemes using whatever numerical method. It is interesting that many of the stabilized FEM can be recovered using the FIC formulation. The FIC method has been successfully applied to problems of convection-diffusion [18-24], diffusion-absorption [15], incompressible fluid flow [24-30] and standard and incompressible solid mechanics [31-33] using finite element and meshless procedures.
The Galerkin FEM-FIC formulation here proposed introduces naturally an additional non linear dissipation term into the discretized equations which is governed by a single stabilization parameter. In the absence of the absorption term the formulation simplifies to the standard Petrov-Galerkin approach for the advection-diffusion problem For the diffusion-absorption case the diffusion-type stabilization term is identical to that recently obtained by Felippa and Oñate using a variational FIC approach and modified equation methods [15]. The limit value of the stabilization parameter ensuring a stable numerical solution is derived. More accurate numerical results can be obtained using an expression of the stabilization parameter which is a function of the sign of the solution and that of its first and second derivatives. This introduces a non-linearity in the solution scheme and a simple iterative algorithm leading to stabilized and accurate results in just two iterations is presented. The merit of the new formulation is that it yields stabilized and accurate numerical solutions for the advection-diffusion-absorption equation for all range of the physical parameters and boundary conditions using a single stabilization parameter. As previously mentioned, this property was only attained by previous similar stabilized formulations using two stabilization parameters. We present a collection of 1D examples showing the efficiency and accuracy of the new FEM-FIC formulation for different values of the advective and absorptive terms.
In the last part of the paper the FIC formulation is extended to multi-dimensional advection-diffusion problems. The key ingredients of the formulation are given and some examples of the good performance of the new stabilized method for the solution of 2D problems are presented.
2 FIC FORMULATION OF THE 1D STATIONARY ADVECTION-DIFFUSION-ABSORPTION EQUATION
The governing equation for the 1D stationary advection-diffusion-absorption problem can be written in the FIC formulation as
|
|
(1) |
|
|
(2) |
|
|
(3) |
where
|
|
(4) |
In above equations is the state variable, is the problem domain, is the domain length, is the velocity field, is the diffusion, is the absorption, dissipation or destruction source parameter, is a constant source term, and are the prescribed values of the total flux and the unknown function at the Neumann and Dirichlet boundaries and , respectively and is a characteristic length which plays the role of a stabilization parameter. In the 1D problem and consist of four combinations at the end points of the problem domain.
Eqs.(1) and (2) are obtained by expressing the balance of fluxes in an arbitrary 1D domain of finite size within the problem domain and at the Neumann boundary, respectively. The variations of the transported variables within the balance domain are approximated by Taylor series expansions retaining one order higher terms than in the infinitessimal theory [20]. The underlined terms in Eqs.(1) and (2) emanate from these higher order expansions and they are essential to derive stabilized numerical schemes using whatever discretization method. Note that as the characteristic length parameter tends to zero the FIC differential equations gradually recover the standard infinitessimal form giving in the limit (for ) in and .
Similarly as in all stabilized methods, the stability and accuracy of the numerical solution depends on the values of the stabilization parameter, i.e. of the characteristic length . At the discrete level can be interpreted as a distance related to the (macroscopic) domain within which the space derivatives are computed. In the finite element practice it is usual to express as a proportion of a typical element dimension (i.e. the element length for 1D problems) [18].
Successful applications of the FIC method to a variety of problems in computational mechanics can be found in [18-31].
3 FINITE ELEMENT FORMULATION
We will construct a standard finite element discretization of the 1D analysis domain length with index ranging from 1 to the number of elements [1]. The state variable is approximated by over the analysis domain. The approximated variable is interpolated within each element with nodes in the standard manner, i.e.
|
|
(5a) |
with
|
|
(5b) |
where are the element shape functions and are nodal values of the approximate function . Substituting Eq.(5a) into Eqs.(1) and (2) gives
|
|
(6) |
|
|
(7) |
|
|
(8) |
where and and are the residuals of the approximate solution in the problem domain and on the Neumann and Dirichlet boundaries and , respectively.
The weighted residual form of Eqs.(6)–(8) is written as
|
|
(9a) |
where and are test functions satisfying on . In Eq.(9a) and in the following and denotes the value of at the boundary . Using Eqs.(6) and (7) into Eq.(9a) we have
|
|
(9b) |
Assuming smooth enough solutions and integrating by parts the term involving in the first integral gives for
|
|
(10) |
Note that the residual term has dissappeared from the boundary integral. This is due to the consistency of the FIC governing equations in the domain and on the Neumann boundary (Eqs.(1) and (2)).
The third term in Eq.(10) is computed as the sum of the integrals over the element interiors, therefore allowing for the space derivatives of to be discontinuous. Also in Eq.(10) has been assumed to be constant within each element, (i.e. within ).
The weak form is obtained by integrating by parts the advective and diffusive terms within in the first integral of Eq.(10). This gives
|
|
(11) |
Observation of the stabilization terms in the last integral of Eq.(11) shows that they introduce an additional diffusion (of value ) as well as an additional advection (of value ). The advective -type stabilization term is quite inconvenient for computational purposes as it leads to an antisymmetric stabilization matrix. In order to overcome this problem we will reformulate the stabilization terms in Eq.(11) with the aim of obtaining a single stabilizing term having the form of a diffusion.
With that purpose in mind we rewrite the integrand of the last term of Eq.(11) by splitting the constant source from the terms depending on in as
|
|
(12) |
We define now
|
|
(13) |
where is a stabilization parameter acting as a proportion of the actual physical diffusion .
Eqs. (12) and (13) allow to rewrite Eq.(11) as
|
|
(14) |
Wee see clearly that the last term of Eq.(14) introduces within each element an additional diffusion of value .
Substituting expression (5b) into (14) and choosing a Galerkin method with within each element gives the discrete system of FE equations written in the standard matrix form as
|
|
(15) |
where is the vector of nodal unknowns and the element contributions to matrix K and vector are
|
The amount of balancing diffusion in Eq.(16) clearly depends on the (non linear) stabilization parameter . The element and critical values of are deduced in the next section for linear two node elements.
We note that the integral of the term in Eq.(17) vanishes after asssembly when and are uniform over a patch of linear elements.
4 COMPUTATION OF THE STABILIZATION PARAMETER FOR LINEAR ELEMENTS
The matrix and the vector for two node linear elements are (for constant values of , and )
|
|
(18) |
|
|
(19) |
In Eqs.(18) and (19) index denotes element values.
4.1 Computation of the element stabilization parameter βe
Let us consider a mesh of just two elements 1 and 2 of equal size with nodes 1, 2 and 3.
For the particular case of the following difference equation is found from Eq.(18)
|
|
(20) |
where and are the element Peclet number and a velocity independent dimensionless element number, respectively. The Damköler number can be obtained as .
We will solve now for the value of for Dirichlet boundary conditions at nodes 1 and 3.
The two following cases are considered.
Case A. ϕ₁=0, ϕ₃= ϕ₃p
Application of the stencil of Eq.(20) gives the following value for
|
|
(21) |
A physically meaningful solution for any values of and must necessarily satisfy . Clearly this requires
|
|
(22) |
Case B. ϕ₁=ϕp₁, ϕ₃= 0
The stencil of Eq.(20) gives
|
|
(23) |
Now if
|
|
(24) |
From the results of above patch tests and the inspection of the modified governing equations assuming that the stabilization terms have the form of a diffusion, the following expression for the element stabilization parameter is proposed (see Appendix A):
|
|
(25) |
with
|
|
(26) |
and
|
|
(27) |
where denotes values computed at the element mid point.
It is clear from Eq.(26) that the computation of the stabilization parameter requires the knowledge of the sign of the numerical solution and that of the first and second derivatives of within each element. This necessarily leads to an iterative scheme. A simple algorithm which provides an stabilized and accurate solution in just two steps is presented in Section 4.3.
4.2 Critical stabilization parameter and unstability conditions
The following constant value of over the mesh yields a stabilized solution (for a uniform distribution of and )
|
|
(28) |
where is the critical stabilization parameter. The proof of Eq.(28) is given in the Appendix B.
The use of for all elements ensures a stabilized numerical solution for all ranges of and although it can yield slight overdiffusive results in some cases.
The use of is also an excellent choice to obtain a first stabilized solution in the iterative scheme described in the next section.
The following condition is an indicator of a unstable solution (see the Appendix B)
|
|
(29) |
4.3 Iterative solution scheme
The following two steps iterative scheme is proposed in order to obtain a stabilized and accurate solution.
step
Step 1. Compute a first stabilized solution using the critical value given by Eq.(28). This ensures a stabilized, although sometimes slightly overdiffusive solution.
Step 2.
Step 2.1. Compute the signs of the first and second derivatives of within each element. The second derivative field is obtained as follows
|
|
(30) |
where denotes averaged values of the first derivative at node of element . At the boundary nodes the constant value of the derivative of within the element is taken in Eq.(30); i.e. .
Step 2.2. Compute the enhanced stabilized solution using the element value of given by Eqs.(25) and (26).
In all the examples solved the above two steps have sufficied to obtain a converged stabilized solution. The reason of this is that the signs of the first and second derivative fields typically do not change any further after the second step over the relevant regions of the analysis domain (i.e. over regions adjacent to high gradient zones). We note that the stabilized solution is also remarkably accurate as shown in the examples presented in a next section.
4.4 Optimal value of the stabilization parameter
The optimal value of the stabilization parameter is defined as such that it guarantees a nodally exact solution. For 1D problems this parameter can be readily found making use of the exact analytical solution. For the zero source case this is written as
|
|
(31a) |
where
|
|
(31b) |
Constants and depend on the boundary conditions of the problem. For the Dirichlet problem ( at and at ) we obtain
|
|
(32) |
Let us now write the stencil of Eq.(20) for three arbitrary nodes , , and a uniform mesh with and as
|
|
(33) |
where is the nodal value of the stabilization parameter or the th node. Note that in Eq.(33) has assumed to be constant within the tributary domain of node .
The optimal nodal value of the stabilization parameter is found from Eq.(33) as
|
|
(34) |
where denotes the exact analytical value of as obtained from Eq.(31a) by
|
|
(35) |
Substituting the exact nodal values of Eq.(35) into Eq.(34) gives the analytical expression of as
|
|
(36) |
Eqs.(34) and (36) indicate that depends on the coordinate of node . The advective () and absorptive () limits of are given below.
In the examples presented in the next section we have found more convenient to compute by Eq.(34) with the numerical values of () computed from Eq.(35).
4.5 Advective limit (w=0)
If the absorption terms are zero, , and from Eq.(36)
|
|
(37) |
4.6 Absorptive limit (γ=0)
For , , , and Eq.(36) gives
|
|
(38) |
Note that both the advective and absorptive limits of are independent of the nodal coordinates.
Remark. The optimal stabilization parameter for the advective limit (Eq.(37)) coincides with the classical expression obtained by many authors (see Vol. 3 in [1]).
The expression of Eq.(38) coincides with that obtained by Felippa and Oñate [15] using the FIC variational approach and the modified equation method.
5 VALUE OF THE ELEMENT CHARACTERISTIC LENGTH PARAMETER
The expression of the element characteristic length parameter is deduced from Eq.(13) as
|
|
(39) |
where is defined in Eq.(25).
It can be readily deduced from Eq.(39) that vanishes in regions where is small. In high gradient zones for (advective limit), whereas for (absorptive limit). The sign of in the latter case depends on the sign of where and are defined in Eq.(27).
The expression of is needed in Eqs.(17) and (19) for the case of .
6 ADVANTAGES OF USING β VERSUS h AS THE STABILIZATION PARAMETER
The stabilized formulation described above can be derived using either or as the stabilization parameter. The choice of instead of has the advantage that is defined as a positive number (see Eq.(25)), whereas is a distance that can be either positive or negative, depending on the values of the absorptive parameter and of the sign ratio (see previous section). The change of sign of within the mesh introduces a difficulty in the iterative solution process. This difficulty is avoided by selecting as the stabilization parameter, which is the option chosen in this work.
Indeed, the characteristic length parameter is still needed in the expression of (see Eqs.(17) and (19)). This does not pose any problem as the value (and sign) of can be effectively computed in the second step from Eq.(39) using the stabilized solution obtained in the first step.
7 1D NUMERICAL EXAMPLES
The efficiency and accuracy of the iterative scheme described in the previous section is proved in a number of examples of application.
All examples presented in this section are solved in a 1D domain of discretized with eight two-node linear elements of unit size. The first set of examples is solved with the same Dirichlet conditions and and different values of and .
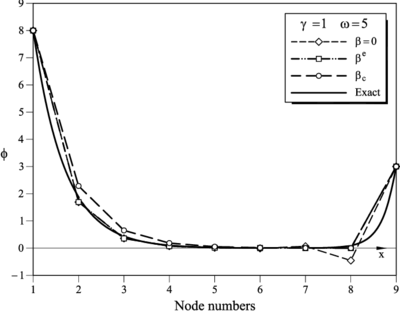
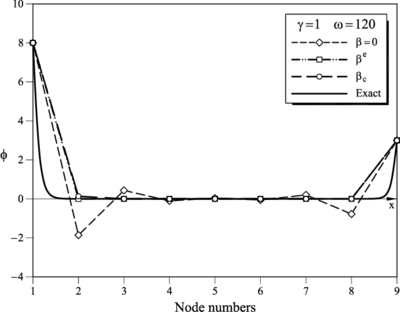
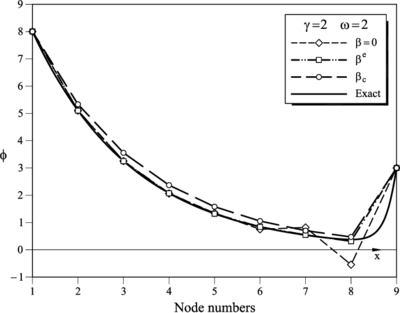
Tables 1–11 show the numerical results obtained at the nodes for the standard Galerkin method () and using the element () and critical () values of . Recall that the results for and correspond to those obtained respectively in the first and second step of the iterative algorithm described in Section 4.3. The exact analytical nodal solution is also presented as well as the optimal nodal value yielding nodaly exact results.
| , | |||||||
| ) | ) | ) | (exact) | ||||
| 1 | 8,00E+00 | 8,00E+00 | 8,00E+00 | 8,00E+00 | 2,233334 | 2,433334 | – |
| 2 | -1,19E+00 | 2,69E-10 | 7,92E-02 | 1,01E-01 | 2,233334 | 2,433334 | 2,49 |
| 3 | 1,78E-01 | 9,07E-21 | 7,84E-04 | 1,27E-03 | 2,233334 | 2,433334 | 2,49 |
| 4 | -2,69E-02 | 3,05E-31 | 7,76E-06 | 1,60E-05 | 2,233334 | 2,433334 | 2,49 |
| 5 | 6,06E-03 | 1,38E-41 | 7,69E-08 | 2,36E-07 | 2,433334 | 2,433334 | 2,51633 |
| 6 | -1,35E-02 | 1,08E-31 | 7,61E-10 | 3,30E-06 | 2,433334 | 2,433334 | 2,64614 |
| 7 | 7,93E-02 | 3,27E-21 | 7,54E-12 | 3,20E-04 | 2,433334 | 2,433334 | 2,64624 |
| 8 | -4,88E-01 | 9,90E-08 | 9,90E-08 | 3,10E-02 | 2,433334 | 2,433334 | 2,64624 |
| 9 | 3,00E+00 | 3,00E+00 | 3,00E+00 | 3,00E+00 | – | – | – |
| , | |||||||
| ) | ) | ) | (exact) | ||||
| 1 | 8,00E+00 | 8,00E+00 | 8,00E+00 | 8,00E+00 | 0 | 0,8333 | |
| 2 | 1,69E+00 | 1,69E+00 | 2,29E+00 | 1,88E+00 | 0 | 0,8333 | 0,2235 |
| 3 | 3,59E-01 | 3,59E-01 | 6,53E-01 | 4,41E-01 | 0 | 0,8333 | 0,2235 |
| 4 | 7,57E-02 | 7,59E-02 | 1,87E-01 | 1,03E-01 | 0 | 0,8333 | 0,2235 |
| 5 | 1,77E-02 | 1,61E-02 | 5,33E-02 | 2,43E-02 | 0 | 0,8333 | 0,2248 |
| 6 | -6,97E-03 | 3,42E-03 | 1,52E-02 | 5,79E-03 | 0 | 0,8333 | 0,3641 |
| 7 | 6,93E-02 | 6,46E-04 | 4,35E-03 | 4,36E-03 | 0,8333 | 0,8333 | 1,038 |
| 8 | -4,54E-01 | 1,85E-04 | 1,23E-03 | 9,56E-02 | 0,8333 | 0,8333 | 1,0681 |
| 9 | 3,00E+00 | 3,00E+00 | 3,00E+00 | 3,00E+00 | – | – | – |
| , | |||||||
| ) | ) | ) | (exact) | ||||
| 1 | 8,00E+00 | 8,00E+00 | 8,00E+00 | 8,00E+00 | 1,3333 | 3,3333 | – |
| 2 | -7,09E-01 | 2,96E-10 | 7,27E-01 | 2,22E-01 | 1,3333 | 3,3333 | 1,8645 |
| 3 | 6,32E-02 | 1,10E-20 | 6,61E-02 | 6,19E-03 | 1,3333 | 3,3333 | 1,8645 |
| 4 | -7,18E-03 | 4,08E-31 | 6,01E-03 | 1,72E-04 | 1,3333 | 3,3333 | 1,8645 |
| 5 | 7,74E-03 | 1,02E-32 | 5,46E-04 | 4,78E-06 | 1,3333 | 3,3333 | 1,866 |
| 6 | -3,27E-02 | 9,18E-32 | 4,97E-05 | 2,93E-07 | 3,3333 | 3,3333 | 3,2664 |
| 7 | 1,47E-01 | 2,75E-21 | 4,52E-06 | 4,25E-05 | 3,3333 | 3,3333 | 3,4167 |
| 8 | -6,65E-01 | 9,09E-11 | 1,32E-06 | 1,13E-02 | 3,3333 | 3,3333 | 3,4167 |
| 9 | 3,00E+00 | 3,00E+00 | 3,00E+00 | 3,00E+00 | – | – | – |
| , | |||||||
| ) | ) | ) | (exact) | ||||
| 1 | 8,00E+00 | 8,00E+00 | 8,00E+00 | 8,00E+00 | 18 | 20 | |
| 2 | -1,86E+00 | 0,00E+00 | 1,31E-01 | 3,66E-04 | 18 | 20 | 18,0054 |
| 3 | 4,34E-01 | 0,00E+00 | 2,15E-03 | 1,68E-08 | 18 | 20 | 18,0054 |
| 4 | -1,04E-01 | 0,00E+00 | 3,52E-05 | 7,66E-13 | 18 | 20 | 18,0054 |
| 5 | 3,69E-02 | 0,00E+00 | 5,78E-07 | 7,09E-17 | 18 | 20 | 18,0072 |
| 6 | -5,73E-02 | 0,00E+00 | 9,47E-09 | 6,97E-15 | 20 | 20 | 20,00075 |
| 7 | 2,02E-01 | 0,00E+00 | 1,55E-10 | 1,13E-09 | 20 | 20 | 20,00075 |
| 8 | -7,76E-01 | 0,00E+00 | 2,55E-12 | 1,84E-04 | 20 | 20 | 20,0075 |
| 9 | 3,00E+00 | 3,00E+00 | 3,00E+00 | 3,00E+00 | – | – | – |
| , | |||||||
| ) | ) | ) | (exact) | ||||
| 1 | 8,00E+00 | 8,00E+00 | 8,00E+00 | 8,00E+00 | 0,00E+00 | 1,02E+00 | |
| 2 | 7,81E+00 | 7,80E+00 | 7,80E+00 | 7,80E+00 | 0,00E+00 | 1,02E+00 | 5,17E-05 |
| 3 | 7,61E+00 | 7,61E+00 | 7,61E+00 | 7,61E+00 | 0,00E+00 | 1,02E+00 | 5,03E-05 |
| 4 | 7,44E+00 | 7,43E+00 | 7,43E+00 | 7,43E+00 | 0,00E+00 | 1,02E+00 | -3,15E-05 |
| 5 | 7,20E+00 | 7,24E+00 | 7,25E+00 | 7,24E+00 | 0,00E+00 | 1,02E+00 | -4,75E-03 |
| 6 | 7,20E+00 | 7,07E+00 | 7,07E+00 | 7,07E+00 | 0,00E+00 | 1,02E+00 | -3,66E-01 |
| 7 | 6,50E+00 | 6,89E+00 | 6,90E+00 | 6,89E+00 | 9,83E-01 | 1,02E+00 | 1,17E+00 |
| 8 | 7,91E+00 | 6,75E+00 | 6,73E+00 | 6,66E+00 | 9,83E-01 | 1,02E+00 | 1,09E+00 |
| 9 | 3,00E+00 | 3,00E+00 | 3,00E+00 | 3,00E+00 | – | – | – |
| , | |||||||
| ) | ) | ) | (exact) | ||||
| 1 | 8,00E+00 | 8,00E+00 | 8,00E+00 | 8,00E+00 | 0 | 0,01667 | – |
| 2 | 5,09855 | 5,099631 | 5,333333 | 5,10362871 | 0 | 1,33333333 | 0,01900914 |
| 3 | 3,253624 | 3,250922 | 3,555556 | 3,25587825 | 0 | 1,33333333 | 0,01900914 |
| 4 | 2,063041 | 2,071956 | 2,37037 | 2,07709922 | 0 | 1,33333333 | 0,0190093 |
| 5 | 1,349646 | 1,321954 | 1,580247 | 1,32509295 | 0 | 1,33333333 | 0,01903119 |
| 6 | 0,7519671 | 0,8390264 | 1,053498 | 0,84535221 | 0 | 1,33333333 | 0,02196073 |
| 7 | 0,819374 | 0,5463428 | 0,702332 | 0,53967226 | 0 | 1,33333333 | 0,32747624 |
| 8 | -0,5445008 | 0,3121959 | 0,4710313 | 0,3765327 | 0 | 1,33333333 | 1,36940125 |
| 9 | 3,00E+00 | 3,00E+00 | 3,00E+00 | 3,00E+00 | 1,33333333 | 1,33333333 | 1,36940125 |
| , | |||||||
| ) | ) | ) | (exact) | ||||
| 1 | 8,00E+00 | 8,00E+00 | 8,00E+00 | 8,00E+00 | 0 | 9,016667 | – |
| 2 | 1,05E+01 | 7,97E+00 | 7,96E+00 | 7,96E+00 | 0 | 9,016667 | 2,10E-06 |
| 3 | 7,34E+00 | 7,92E+00 | 7,92E+00 | 7,92E+00 | 0 | 9,016667 | 2,10E-06 |
| 4 | 1,11E+01 | 7,90E+00 | 7,88E+00 | 7,88E+00 | 0 | 9,016667 | 2,10E-06 |
| 5 | 6,39E+00 | 7,84E+00 | 7,84E+00 | 7,84E+00 | 0 | 9,016667 | 2,10E-06 |
| 6 | 1,21E+01 | 7,82E+00 | 7,80E+00 | 7,80E+00 | 0 | 9,016667 | 2,10E-06 |
| 7 | 5,01E+00 | 7,75E+00 | 7,76E+00 | 7,76E+00 | 8,983333 | 9,016667 | -4,44E-04 |
| 8 | 1,36E+01 | 7,72E+00 | 7,73E+00 | 7,72E+00 | 8,983333 | 9,016667 | 9,02E+00 |
| 9 | 3,00E+00 | 3,00E+00 | 3,00E+00 | 3,00E+00 | – | – | – |
| , | |||||||
| ) | ) | ) | (exact) | ||||
| 1 | 8,00E+00 | 8,00E+00 | 8,00E+00 | 8,00E+00 | 0 | 9,16667 | – |
| 2 | 8,65E+00 | 7,69E+00 | 7,62E+00 | 7,61E+00 | 0 | 9,16667 | 0,00022111 |
| 3 | 6,94E+00 | 7,22E+00 | 7,26E+00 | 7,24E+00 | 0 | 9,16667 | 0,00022111 |
| 4 | 8,20E+00 | 6,98E+00 | 6,91E+00 | 6,89E+00 | 0 | 9,16667 | 0,00022111 |
| 5 | 5,81E+00 | 6,50E+00 | 6,58E+00 | 6,55E+00 | 0 | 9,16667 | 0,00022111 |
| 6 | 8,00E+00 | 6,36E+00 | 6,27E+00 | 6,23E+00 | 0 | 9,16667 | 0,00022111 |
| 7 | 4,54E+00 | 5,83E+00 | 5,97E+00 | 5,93E+00 | 8,833333 | 9,16667 | 0,00021822 |
| 8 | 8,14E+00 | 5,59E+00 | 5,69E+00 | 5,64E+00 | 8,833333 | 9,16667 | 9,22133708 |
| 9 | 3,00E+00 | 3,00E+00 | 3,00E+00 | 3,00E+00 | – | – | – |
| , | |||||||
| ) | ) | ) | (exact) | ||||
| 1 | 8,00E+00 | 8,00E+00 | 8,00E+00 | 8,00E+00 | 0 | 9,16667 | – |
| 2 | 6,206664 | 6,510888 | 6,666698 | 6,562702696 | 0 | 9,666666667 | 0,004136478 |
| 3 | 5,555403 | 5,408537 | 5,555607 | 5,383633335 | 0 | 9,666666667 | 0,004136478 |
| 4 | 3,952791 | 4,348897 | 4,629694 | 4,416398125 | 0 | 9,666666667 | 0,004136478 |
| 5 | 4,030291 | 3,682072 | 3,858096 | 3,622938486 | 0 | 9,666666667 | 0,004136478 |
| 6 | 2,27974 | 2,871269 | 3,215095 | 2,972033521 | 0 | 9,666666667 | 0,004136478 |
| 7 | 3,207678 | 2,549878 | 2,679258 | 2,43807155 | 0 | 9,666666667 | 0,004136709 |
| 8 | 0,8884292 | 1,838311 | 2,232884 | 2,000042344 | 0 | 9,666666667 | 9,137861599 |
| 9 | 3,00E+00 | 3,00E+00 | 3,00E+00 | 3,00E+00 | 9,666666667 | – | – |
| , | |||||||
| ) | ) | ) | (exact) | ||||
| 1 | 8,00E+00 | 8,00E+00 | 8,00E+00 | 8,00E+00 | 0 | 12,333334 | |
| 2 | 2,94E+00 | 3,06E+00 | 4,00E+00 | 3,08E+00 | 0 | 12,333334 | 0,17281 |
| 3 | 1,32E+00 | 1,17E+00 | 2,00E+00 | 1,19E+00 | 0 | 12,333334 | 0,17281 |
| 4 | 1,80E-01 | 4,47E-01 | 1,00E+00 | 4,57E-01 | 0 | 12,333334 | 0,17281 |
| 5 | 5,99E-01 | 1,72E-01 | 5,00E-01 | 1,76E-01 | 0 | 12,333334 | 0,17281 |
| 6 | -6,33E-01 | 6,46E-02 | 2,50E-01 | 6,77E-02 | 0 | 12,333334 | 0,17281 |
| 7 | 1,16E+00 | 2,64E-02 | 1,25E-01 | 2,61E-02 | 0 | 12,333334 | 0,17281 |
| 8 | -1,83E+00 | 7,31E-03 | 6,25E-02 | 1,00E-02 | 12,333334 | 12,333334 | 12,2935 |
| 9 | 3,00E+00 | 3,00E+00 | 3,00E+00 | 3,00E+00 | – | – | – |
| , | |||||||
| ) | ) | ) | (exact) | ||||
| 1 | 8,00E+00 | 8,00E+00 | 8,00E+00 | 8,00E+00 | 9 | 29 | – |
| 2 | -9,18E-01 | 0,00E+00 | 1,14E+00 | 6,37E-02 | 9 | 29 | 9,8109 |
| 3 | 1,12E-01 | 0,00E+00 | 1,63E-01 | 5,08E-04 | 9 | 29 | 9,8109 |
| 4 | -3,24E-02 | 0,00E+00 | 2,33E-02 | 4,05E-06 | 9 | 29 | 9,8109 |
| 5 | 5,67E-02 | 0,00E+00 | 3,33E-03 | 3,22E-08 | 9 | 29 | 9,8109 |
| 6 | -1,50E-01 | 0,00E+00 | 4,76E-04 | 2,56E-10 | 9 | 29 | 9,8109 |
| 7 | 4,08E-01 | 0,00E+00 | 6,80E-05 | 9,14E-12 | 9 | 29 | 12,9409 |
| 8 | -1,11E+00 | 0,00E+00 | 9,71E-06 | 1,31E-12 | 29 | 29 | 29 |
| 9 | 3,00E+00 | 3,00E+00 | 3,00E+00 | 3,00E+00 | – | – | – |
We note that the numbers in the tables for the values of refer to element values for and and to nodal values for the case of .
Figures 1–6 show the distribution of along the domain for (Galerkin), and for some of the cases studied, as well as the exact solution.
|
| Figure 1: and . FIC results for a mesh of 8 linear elements obtained for (Galerkin), and . Comparison with the analytical solution (see Table 2) |
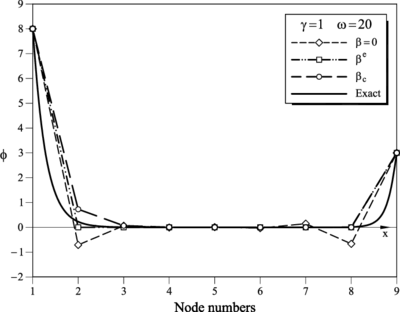
|
| Figure 2: and . FIC results for a mesh of 8 linear elements obtained for (Galerkin), and . Comparison with the analytical solution (see Table 3) |
|
| Figure 3: and . FIC results for a mesh of 8 linear elements obtained for (Galerkin), and . Comparison with the analytical solution (see Table 4) |
|
| Figure 4: and . FIC results for a mesh of 8 linear elements obtained for (Galerkin), and . Comparison with the analytical solution (see Table 6) |
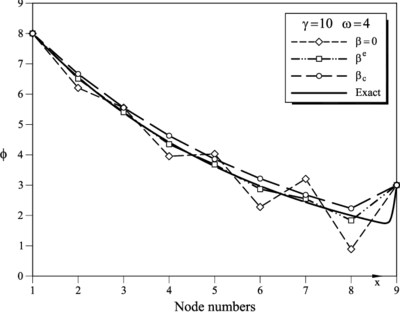
|
| Figure 5: and . FIC results for a mesh of 8 linear elements obtained for (Galerkin), and . Comparison with the analytical solution (see Table 9) |
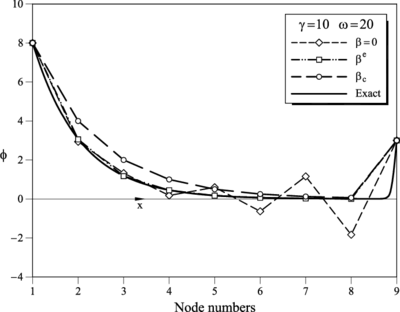
|
| Figure 6: and . FIC results for a mesh of 8 linear elements obtained for (Galerkin), and . Comparison with the analytical solution (see Table 10) |
We note that for the case (Table 9 and Figure 5) small oscillations around the exact distribution of are obtained for . This is due to the fact that in this case the stabilizing diffusion has been introduced in the last element of the mesh only. This suffices to stabilize the solution in the vecinity of the boundary layer at the right end of the domain. However it does not suffices to capture accurately the smooth distribution of in the rest of the domain (the errors osciallate between 9% for node 8 to a maximum of 4% for the rest of the nodes). The oscillations are very much reduced if an additional diffusion of similar value is introduced in the next element in the mesh.
The first set of examples is complemented by two similar problems with Dirichlet conditions and and and , respectively. Both cases are solved for and . The nodal results are shown in Tables 12 and 13, while the distributions of are plotted in Figures 7 and 8.
| , | |||||||
| ) | ) | ) | (exact) | ||||
| 1 | 1 | 1 | 1 | 1 | 22,3333333 | 42,3333333 | – |
| 2 | -0,1745558 | 3,7037E-11 | 0,09090909 | 0,00066183 | 22,3333333 | 42,3333333 | 22,4526286 |
| 3 | 0,03046973 | 1,3717E-21 | 0,00826446 | 4,3801E-07 | 22,3333333 | 42,3333333 | 22,4526286 |
| 4 | -0,00531866 | 5,0805E-32 | 0,00075131 | 2,8989E-10 | 22,3333333 | 42,3333333 | 22,4526286 |
| 5 | 0,00092839 | 1,8817E-42 | 6,8301E-05 | 1,9186E-13 | 22,3333333 | 42,3333333 | 22,4526286 |
| 6 | -0,00016203 | 6,9692E-53 | 6,2092E-06 | 1,2698E-16 | 22,3333333 | 42,3333333 | 22,4526286 |
| 7 | 2,8194E-05 | 2,5812E-63 | 5,6447E-07 | 8,4035E-20 | 22,3333333 | 42,3333333 | 22,4526286 |
| 8 | -4,6527E-06 | 9,5599E-74 | 5,1316E-08 | 5,5617E-23 | 22,3333333 | 42,3333333 | 22,4526199 |
| 9 | 0 | 0 | 0 | 0 | – | – | – |
| , | |||||||
| ) | ) | ) | (exact) | ||||
| 1 | 0 | 0 | 0 | 0 | 42,3333333 | 42,3333333 | – |
| 2 | -0,00040908 | 2,3464E-81 | 2,3464E-81 | 8,7898E-84 | 42,3333333 | 42,3333333 | 42,3333333 |
| 3 | 0,00130776 | 7,7431E-70 | 7,7431E-70 | 6,4435E-72 | 42,3333333 | 42,3333333 | 42,3333333 |
| 4 | -0,0039649 | 2,5552E-58 | 2,5552E-58 | 4,7236E-60 | 42,3333333 | 42,3333333 | 42,3333333 |
| 5 | 0,01198527 | 8,4323E-47 | 8,4323E-47 | 3,4627E-48 | 42,3333333 | 42,3333333 | 42,3333333 |
| 6 | -0,03622341 | 2,7826E-35 | 2,7826E-35 | 2,5384E-36 | 42,3333333 | 42,3333333 | 42,3333333 |
| 7 | 0,1094779 | 9,1827E-24 | 9,1827E-24 | 1,8608E-20 | 42,3333333 | 42,3333333 | 42,3333333 |
| 8 | -0,3308744 | 3,0303E-12 | 3,0303E-12 | 1,3641E-12 | 42,3333333 | 42,3333333 | 42,3333333 |
| 9 | 1 | 1 | 1 | 1 | – | – | – |
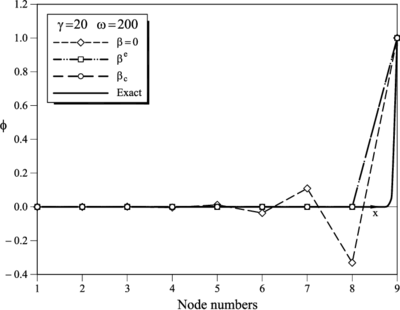
|
| Figure 7: and . FIC results for a mesh of 8 linear elements obtained for (Galerkin), and . Comparison with the analytical solution (see Table 12) |
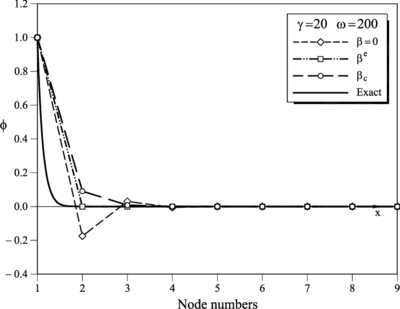
|
| Figure 8: and . FIC results for a mesh of 8 linear elements obtained for (Galerkin), and . Comparison with the analytical solution (see Table 13) |
In references [12,13] it was shown that the SUPG, GLS and SGS methods with a single stabilization parameter fail to provide a stabilized solution for the case , with and . The FIC results, however, are physically correct as shown in Table 13 and Figure 8.
The following conclusions are drawn from the results obtained for the 1D examples.
- The Galerkin solution () is unstable for the cases where the instability condition (Eq.(29)) is violated, as expected.
- The solution obtained with the critical value is always stable, although it yields slightly overdiffusive results in some cases (see Tables 2, 6, 9 and 10).
- The results obtained with are less diffusive than those obtained with and quite accurate for all ranges of and .
- The FIC algorithm provides a stabilized solution for Dirichlet problems when there is a negative streamwise gradient of the solution. This is an advantage versus SUPG, GLS and SGS methods using a single stabilization parameter which fail for these type of problems [12,13].
8 EXTENSION TO MULTI-DIMENSIONAL PROBLEMS
The stabilization procedure presented can be easily extended to multi-dimensional problems. Only the main ingredients of the formulation are presented here. For a more detailed description of the multi-dimensional formulation see [34].
Consider the general steady-state advection-diffusion-reaction equations written for the sourceless case as
|
|
(40) |
where for 2D problems
|
|
(41) |
are respectively the velocity vector, the gradient vector and the diffusivity matrix, respectively. For simplicity we have assumed an isotropic diffusion matrix.
The FIC form of Eq.(40) is written
|
|
(42) |
where is the original differential equation as defined in Eq.(40).
The Dirichlet and boundary conditions of the FIC formulation are
|
|
(43) |
|
|
(44) |
where is the normal vector to the boundary where the normal flux is prescribed. As usual index denotes the prescribed values.
In Eqs.(42) and (44) is the characteristic vector of the FIC formulation which components play the role of stabilization parameters. The underlined terms in Eqs.(42) and (44) introduce the necessary stability in the numerical solution.
As shown in [23] the components of the characteristic length h allow to obtain stabilized finite element solutions in the presence of strong gradients of near the boundaries (boundary layers) and within the analysis domain (internal layers). If vector h is taken to be parallel to the velocity u the standard SUPG method is recovered [20]. Keeping the more general form of h allows to reproduce the best features of the so called shock capturing or transverse dissipation schemes.
Oñate et al. [23] have recently shown that a general form of the characteristic lengths can be found by writting the FIC equations along the principal curvature directions of the solution denoted hereafter as and . The resulting FIC-FEM formulation is equivalent in this case (for linear elements) to adding a non linear stabilizing diffusion matrix to the standard infinitessimal equation. The stabilizing diffusion matrix depends on the velocities along the principal curvature directions of the solution which must be found iteratively. The iterative scheme can be simplified by assuming that the main principal curvature direction at each integration point within an element are coincident with the gradient vector direction at that point. For details see [23]. This technique is extended here accounting for the absorption term.
Following the ideas described in [23] the FIC equations can be written as
|
|
(45) |
where the stabilization matrix is given by
|
|
(46) |
|
|
(47) |
and
|
|
(48) |
where is the angle that the main principal curvature direction of the solution forms with the global axis. The different terms in Eq.(47–48) are
|
|
(49) |
|
|
where , are the velocity components along each of the principal curvature directions and and are the maximum values of the projection of the element sides along the principal directions and , respectively.
The values of and in Eq.(49) correspond to the critical stabilization parameters for the absorptive limit, as defined for the 1D problem. A non linear form of these parameters depending on the sign of the solution derivatives along the principal curvature directions can be obtained [23,34].
The derivation of the finite element equations follows the standard Galerkin procedure applied to Eq.(43–45). For details see [23,34].
The stabilized numerical results presented in the next section have been found by the following two steps algorithm.
Step 1. (Galerkin step). Solve the problem for with a zero value of the the stabilization matrix (i.e. ). Unstable results characterized by undershoots and overshoots in the numerical solution will be found for high values of the advective and the absorption terms.
Step 2. Compute the principal curvature directions of the solution at the element center. As mentioned above we have chosen the main principal direction to be parallel to the gradient vector for simplicity. The direction is chosen orthogonal to .
Compute , and from Eqs.(46–48). Solve for .
Excellent results are obtained with this simple two steps algorithm for problems with boundary layers orthogonal to the velocity vector as shown in the examples presented in the next section. A refined version of the algorithm applicable to problems with internal layers is described in [34].
8.1 2D Examples
The analysis domain in the first two 2D examples presented is a square of size 8 units. A relatively coarse mesh of four node bi-linear square elements is used in all cases.
The boundary conditions for the first and second examples are at the boundary and at and zero normal flux at and . This reproduces the condition of the 1D examples solved in previous sections. The first example is analized for , and giving , and which corresponds to the 1D example analyzed in Table 3. The correct solution for this absorptive dominant case is a boundary layer in the vecinity of the side at where is prescribed to a value of . The numerical results obtained with the standard (non stabilized) Galerkin solution (i.e. ) are oscillatory as expected. The stabilized FIC formulation elliminates the oscillations and yields the correct physical solution as shown in Figure 9. Note that the 2D solution coincides precisely with the 1D results of Table 3 and Figure 2 for .
The second example is similar to the first one with , and giving , and . This problem corresponds to the 1D case of Table 10. The Galerkin solution is again oscillatory, whrereas the FIC results are physically sound (see Figure 10). Once more the 2D FIC results coincide with the 1D values shown in Table 10 and Figure 6 for .
The boundary conditions for the third 2D example are at and and at and . The square domain has a side of 10 units in this case. A mesh of four node elements of unit length is used. The physical parameters are , and giving , and .
The correct solution for this absorption dominated problem has two boundary layers next to the boundaries at and . The Galerkin solution is oscillatory in these zones as expected (Figure 11) whereas the FIC results capture the boundary layer within the elements adjacent to the boundary.
The boundary conditions for the last example are at and and at and . The physical parameters are , and giving , and .
The correct solution has two boundary layers next to the boundaries at and . The Galerkin solution gives oscillatory results next to these boundaries and also next to the boundary at (Figure 12). All these oscillations disappear with the stabilized FIC formulation here proposed.
More accurate results for all these problems can be found by using the non linear form of the element absorptive stabilization parameter similarly as for the 1D case. Details of the iterative scheme and examples of applications are given in [34].
9 CONCLUSIONS
The FEM-FIC formulation presented allows to obtain a stabilized solution for the advection-diffusion-absorption equation. For the 1D problem the formulation is equivalent to adding a non-linear diffusion term to the standard discretized equations, together with a consistent modification of the constant source term for each element. The stabilizing diffusion term is governed by a single stabilization parameter. The use of the constant critical value of the stabilization parameter for all the elements in the mesh allows to obtain a stabilized numerical solution in a single step. A more accurate (less diffusive) solution can be obtained using the two-step iterative scheme proposed. This obviously increases the cost of the solution and for many practical cases the use of the critical stabilization parameter may be more attractive. The 1D examples presented demonstrate that the method provides stabilized and very accurate results for all range of the physical parameters and boundary conditions using a quite coarse mesh.
The equivalence of the FIC method with a stabilizing diffusion term extends naturally to multidimensional problems, where the advantages of the proposed approach should prove to be very advantageous as indicated by the excellent results obtained in the 2D examples solved.
ACKNOWLEDGEMENTS
The numerical solutions for the 2D problems were obtained by Dr. F. Zarate from CIMNE whose contribution is gratefully acknowledged.
The authors also thank Profs. C. Felippa and S.R. Idelsohn for many useful discussions.
This work has been sponsored by the Spanish Ministry of Educación y Ciencia (Plan Nacional, Project number: DPI2001-2193).
REFERENCES
[1] Zienkiewicz O.C. and Taylor R.L. The Finite Element Method. Volume 3. 5th Edition, Butterworth-Heinemann, 2001.
[2] Tezduyar T.E. and Park Y.J. Discontinuity-capturing finite element formulations for nonlinear convection-diffusion-reaction equations. Comput. Methods Appl. Mech. Engrg., 59, 307–325, 1986.
[3] Tezduyar T.E., Park Y.J. and Deans H.A. Finite element procedures for time-dependent convection-diffusion-reaction systems. Int. J. Num. Meth. Fluids, 7, 1013–1033, 1987.
[4] Idelsohn S., Nigro N. Storti M. and Buscaglia G. A Petrov-Galerkin formulation for advection-reaction-diffusion problems. Comput. Methods Appl. Mech. Engrg., 136, 27–46, 1996.
[5] Codina R. Comparison of some finite element methods for solving the diffusion-convection-reaction equation. Comput. Methods Appl. Mech. Engrg., 156, 186–210, 1998.
[6] Codina R. On stabilized finite element methods for linear systems of convection-diffusion-reaction equations. Comput. Meth. Appl. Mech. Engrg., 188, 61–82, 2000.
[7] Burman E. and Ern A. Nonlinear diffusion and discrete maxium principle for stabilized Galerkin approximations of the convection-diffusion-reaction equation. Comput. Meth. Appl. Mech. Engrg., 191, 3833–3855, 2002.
[8] Harari I. and Hughes T.J.R. Finite element methods for the Helmholtz equation in an exterior domain: model problems. Comput. Meth. Appl. Mech. Engrg., 87, 59–96, 1991.
[9] Harari I. and Hughes T.J.R. Galerkin/least squares finite element methods for the reduced wave equation with non-reflecting boundary conditions in unbounded domains. Comput. Meth. Appl. Mech. Engrg., 98, 411–454, 1992.
[10] Harari I. and Hughes T.J.R. Stabilized finite element method for steady advection-diffusion with production. Comput. Meth. Appl. Mech. Engrg., 115, 165–191, 1994.
[11] Harari I., Grosh K., Hughes T.J.R., Malhotra M., Pinsky P.M., Stewart J.R. and Thompson L.L. Recent development in finite element methods for structural acoustics. Archives of Computational Mechanics in Engineering, 3, 2-3, 131–309, 1996.
[12] Hauke G. and Garcia-Olivares A. Variational subgrid scale formulations for the advection-diffusion-reaction equation. Comput. Methods Appl. Mech. Engrg. 2000; 190:6847–6865.
[13] Hauke G. A simple subgrid scale stabilized method for the advection-diffusion reaction equation. Comput. Methods Appl. Mech. Engrg. 2002; 191:2925–2947.
[14] Brezzi F., Hauke G., Marin L.D. and Sangalli S. Link-cutting bubbles for the stabilization of convection-diffusion-reaction problems. Mathematical Models and Methods in Applied Sciences, World Scientific Publishing Company, 2002.
[15] Felippa C.A. and Oñate E. Nodally exact Ritz discretization of 1D diffusion-absorption and Helmholtz equations by variational FIC and modified equation methods. Research Report No. PI 237, CIMNE, Barcelona 2004. Submitted to Comput. Mechanics.
[16] Idelsohn S.R., Heinrich J.C. and Oñate E. Petrov-Galerkin methods for the transient advective-diffusive equation with sharp gradients. Int. J. Num. Meth. Engng., 39, 1455–1473, 1996.
[17] Harari I. Stability of semidiscrete advection-diffusion in transient computation. Proceedings of 6th World Congress on Computational Mechanics, Beijing, Sept. 2004, Z.H. Yao, M.W. Yuan and W.X. Zhong (Eds.), Tsinghua Univ. Press-Springer.
[18] Oñate E. Derivation of stabilized equations for advective-diffusive transport and fluid flow problems. Comput. Methods Appl. Mech. Engrg., 151 (1-2), 233–267, 1998.
[19] Oñate E. Possibilities of finite calculus in computational mechanics. Int. J. Num. Meth. Engng., 60, 255–281, 2004.
[20] Oñate E., García J. and Idelsohn S.R. Computation of the stabilization parameter for the finite element solution of advective-diffusive problems. Int. J. Num. Meth. Fluids, 25, 1385–1407, 1997.
[21] Oñate E., Manzan M. Stabilization techniques for finite element analysis of convection diffusion problems. In Comput. Anal. of Heat Transfer, WIT Press, G. Comini and B. Sunden (Eds.), 2000.
[22] Oñate E., Manzan M. A general procedure for deriving stabilized space-time finite element methods for advective-diffusive problems. Int. J. Num. Meth. Fluids, 31, 203–221, 1999.
[23] Oñate E., Zárate F. and Idelsohn S.R. Finite element formulation for convection-diffusion problems with sharp gradients using finite calculus. Comput. Meth. Appl. Mech. Engng. Submitted Nov. 2004.
[24] Oñate E., Idelsohn S.R., Zienkiewicz O.C. and Taylor R.L. A finite point method in computational mechanics. Applications to convective transport and fluid flow. Int. J. Num. Meth. Engng., 39, 3839–3866, 1996.
[25] Oñate E., Idelsohn S.R. and Sacco C. A finite point method for incompressible flow problems. Computing and Visualization in Science, 17, 127–154, 2000.
[26] Oñate E. A stabilized finite element method for incompressible viscous flows using a finite increment calculus formulation. Comput. Methods Appl. Mech. Engrg., 182, (1–2), 355–370, 2000.
[27] Oñate E., García J. A finite element method for fluid-structure interaction with surface waves using a finite calculus formulation. in Comput. Methods Appl. Mech. Engrg., 191 (6-7), 635-660, 2001.
[28] Idelsohn S.R., Oñate E. and Del Pin F. A Lagrangian meshless finite element method applied to fluid-structure interaction problems. Computers and Structures, 81, 655–671, 2003.
[29] Oñate E., Idelsohn S.R., Del Pin F. and Aubry R. The particle finite element method. An overview (PFEM). Int. J. Comput. Methods, 1 (2), 267–307, 2004.
[30] Oñate E., García J. and Idelsohn S.R. Ship Hydrodynamics. Encyclopedia of Computational Mechanics, T. Hughes, R. de Borst and E. Stein (Eds.), Vol. 3, Chapter 18, 579–607, J. Wiley, 2004.
[31] Oñate E., Perazzo F. and Miquel J. A finite point method for elasticity problems. Computers and Structures, 79, 22–25, 2151–2163, 2001.
[32] Oñate E., Taylor R.L., Zienkiewicz O.C. and Rojek J. A residual correction method based on finite calculus. Engineering Computations, 20 (5/6), 629–658, 2003.
[33] Oñate E., Rojek J., Taylor R.L. and Zienkiewicz O.C. Finite calculus formulation for analysis of incompressible solids using linear triangles and tetrahedra. Int. J. Num. Meth. Engng., 59 (11), 1473–1500, 2004.
[34] Oñate E., Miquel, J. and Zárate, F. Stabilized FIC/FEM formulation for multi-dimensional advection-diffusion-reaction problems. Research Report No. 269, CIMNE, Barcelona, May 2005.
APPENDIX A
Let us consider the modified form of the convection-diffusion reaction equation with the stabilization term having the form of a diffusion of value i.e.
|
|
(A.1) |
where is the stabilization parameter. For simplicity the source term has been taken equal to zero in Eq.(A.1).
From Eq.(A.1) we can obtain
|
|
(A.2) |
Let us estimate now the value of over a patch of finite elements. From the observation of the finite element matrices (Eq.(18)) we can write
|
|
(A.3) |
where is the maximum value of the approximate finite element function over a patch of elements of equal size and , and denote the signs of the solution and of its first and second derivatives, respectively.
Substitution of Eq.(A.3) into (A.2) gives the elemental value of the stabilization parameter as
|
|
(A.4) |
APPENDIX B. STABILITY ANALYSIS OF THE DISCRETIZED FIC ADVECTION-DIFFUSION-ABSORPTION EQUATION FOR LINEAR ELEMENTS
The discretized equation for the two linear element stencil of Eq.(20) can be written as
|
|
(B.1) |
The characteristic polinomial is
|
|
(B.2) |
and the characteristic roots are
|
|
(B.3) |
A non oscilatory (stable) numerical solution is found if . This is fulfilled if
|
|
(B.4) |
|
|
(B.5) |
The inequality (B.4) implies
|
|
(B.6) |
or
|
|
(B.7) |
The second inequality (B.5) implies
|
|
(B.8) |
or
|
|
(B.9) |
Hence the stability limit of is
|
|
(B.10) |
where is the critical stabilization parameter.
Indeed a stabilized solution will be obtained if .
The condition for the onset of instability for the original (non-stabilized) problem is obtained by making in Eq.(B.6) and (B.8) and reversing the sing of the inequalities, i.e. an oscilatory solution will be found if one of the two conditions is fullfiled
|
|
(B.11) |
Hence, the stability condition is found as
|
|
(B.12) |
Document information
Published on 01/01/2006
DOI: 10.1016/j.cma.2005.07.020
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?

![2D advection-conduction-absorption problem over a square domain of size equal to 8 units. ϕp=8 at x=0, ϕp=3 at x=8, qₙ=0 at y=0 and y=8. u = [2,0]T, k=1, s=20, w=20, γₓ=1 and γy=0. Galerkin and FIC solutions obtained with a mesh of 8 ×8 four node square elements.](/wd/images/thumb/b/bb/Draft_Samper_267560997_1174_fig9.png/600px-Draft_Samper_267560997_1174_fig9.png)
![2D advection-conduction-absorption problem over a square domain of size equal to 8 units. ϕp=8 at x=0, ϕp=3 at x=8, qₙ=0 at y=0 and y=8. u = [20,0]T, k=1, s=20, w=20, γₓ=10 and γy=0. Galerkin and FIC solutions obtained with a mesh of 8 ×8 four node square elements.](/wd/images/thumb/7/75/Draft_Samper_267560997_7137_Fig10.png/600px-Draft_Samper_267560997_7137_Fig10.png)
![2D advection-conduction-absorption problem over a square domain of size equal to 10 units. ϕp=8 at x=0, ϕp=3 at x=10, qₙ=0 at y=0 and y=10. u = [0,1×10⁻³]T, k=1, s=12, w=12, γₓ=0 and γy= 5×10⁻⁴. Galerkin and FIC solutions obtained with a mesh of 10 ×10 four node square elements.](/wd/images/thumb/f/fa/Draft_Samper_267560997_7278_Fig11.png/600px-Draft_Samper_267560997_7278_Fig11.png)
![2D advection-conduction-absorption problem over a square domain of size equal to 10 units. ϕp=8 at x=0, ϕp=3 at x=10, qₙ=0 at y=0 and y=10. u = [0,5]T, k=1, s=12, w=12, γₓ=0 and γy=2.5. Galerkin and FIC solutions obtained with a mesh of 10 ×10 four node square elements.](/wd/images/thumb/a/a1/Draft_Samper_267560997_4095_Fig12.png/600px-Draft_Samper_267560997_4095_Fig12.png)