Published in Finite Element Methods: 1970's and Beyond, Franca L.P., Tezduyar T.E. and Masud A. (Eds.),CIMNE, Barcelona, Spain, 2004
Abstract
The expression “finite calculus” refers to the derivation of the governing differential equations in mechanics by invoking balance of fluxes, forces, etc. in a space-time domain of finite size. The governing equations resulting from this approach are different from those of infinitesimal calculus theory and they incorporate new terms which depend on the dimensions of the balance domain. The new governing equations allow to derive naturally stabilized numerical schemes using any discretization procedure. The paper discusses the possibilities of the finite calculus method for the finite element solution of convection-diffusion problems with sharp gradients and incompressible fluid flow.
Keywords Stabilization, finite calculus, finite element method.
1 INTRODUCTION
It is well known that standard numerical methods such as the central finite difference (FD) method, the Galerkin finite element (FE) method and the finite volume (FV) method, among others, lead to unstable numerical solutions when applied to problems involving different scales, multiple constraints and/or high gradients. Examples of these situations are typical in the solution of convection-diffusion problems, incompressible problems in fluid and solid mechanics and strain or strain rate localization problems in solids and compressible fluids using the standard Galerkin FE method or central scheme in FD and FV methods [1,2]. Similar instabilities are found in the application of meshless methods to those problems [3-5].
The sources of the numerical instabilities in FE, FD and FV methods, for instance, have been sought in the apparent unability of the Galerkin FE method and the analogous central difference scheme in FD and FV methods, to provide a numerical procedure able to capture the different scales appearing in the solution for all ranges of the physical parameters. Typical examples are the spurious numerical oscillations in convection-diffusion problems for high values of the convective terms. The same type of oscillations are found in regions next to sharp internal layers appearing in high speed compressible flows (shocks) or in strain localization problems (shear bands) in solids. A similar problem of different nature emerges in the solution of incompressible problems in fluid and solid mechanics. Here the difficulties in satisfying the incompressibility constraint limit the choices of the approximation for the velocity (or displacement) variables and the pressure [1].
The solution of above problems has been attempted in a number of ways. The underdiffusive character of the central difference scheme for treating advective-diffusive problems has been corrected in an ad-hoc manner by adding the so called “artificial diffusion” terms to the standard governing equation [2]. The same idea has been successfully applied to derive stabilized FV and FE methods for convection-diffusion and fluid-flow problems [1,2]. Other stabilized FD schemes are based on the “upwind” computation of the first derivatives appearing in the convective operator [2]. The counterpart of upwind techniques in the FEM are the so called Petrov-Galerkin methods [1,6,7]. Among the many methods of this kind we can name the SUPG method [8-10], the Galerkin Least Square (GLS) method [11,12] the Characteristic Galerkin method [13-15] the Characteristic Based Split (CBS) method [16,17] and the Subgrid Scale (SS) method [18-21].
The Finite Calculus (FIC) is a different route to derive stabilized numerical methods. The starting point are the modified governing differential equations of the problem derived by expressing the balance of fluxes (or equilibrium of forces) in a space-time domain of finite size [22]. This introduces naturally new terms in the classical differential equations of the infinitesimal theory which are a function of the balance domain dimensions. The merit of the modified equations via the FIC approach is that they lead to stabilized schemes using any numerical method. In addition, the different stabilized FD, FE and FV methods typically used in practice can be recovered using the FIC equations [22,23]. Moreover, these equations are the basis for deriving a procedure for computing the stabilization parameters [24,25].
Most stabilized FEM schemes can be framed within an extended Galerkin approach where the standard Galerkin expression is modified by adding adequate residual-based terms as
|
|
(1) |
where [Galerkin] denotes the standard Galerkin expression, is a vector which terms depend on the shape functions (and the physical parameters of the problem), is the vector of residuals of the finite element equations and is a matrix of stabilization parameters.
The computation of the stabilization parameters is still an open problem and much effort has been devoted to this topic [1,2,7-21,36].
Different stabilized methods can be derived from Eq.(1) by chosing expressions for matrices and . In this paper we will focus in the stabilized finite element formulation using the FIC method. The equivalent form of Eq.(1) is written in the FIC formulation as [1-7]
|
|
(2) |
where is the number of residual equations, is the th residual equation and are characteristic length parameters which are typically of the order of the element dimensions.
The FIC formulation has been used in conjunction with the finite element formulation to solve a variety of problems in convection-diffusion [23-27] incompressible fluid dynamics involving free surfaces [28-32] and non linear solid mechanics problems allowing for large strains [28,41,42] using in all cases linear triangles and tetrahedra with equal interpolation for all variables.
The layout of the paper is the following. In the next section the main concepts of the FIC method are introduced. Applications of the FIC method to convection-diffusion problems with sharp gradients are detailed and some examples of application are given. Finally the possibilities of the FIC method in incompressible fluid mechanics are discussed and a finite element formulation is presented.
2 THE FINITE CALCULUS METHOD
We will consider a convection-diffusion problem in a 1D domain of length . The equation of balance of fluxes in a subdomain of size belonging to (Figure 1) is written as
|
|
(3) |
where and are the incoming and outgoing fluxes at points and , respectively. The flux includes both convective and diffusive terms; i.e. , where is the transported variable (i.e. the temperature in a thermal problem), is the velocity and is the diffusitivity of the material.
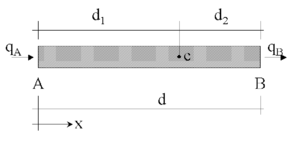
|
| Figure 1: Equilibrium of fluxes in a space balance domain of finite size |
Let us express now the fluxes and in terms of the flux at an arbitrary point within the balance domain (Figure 1). Expanding and in Taylor series around point up to second order terms gives
|
|
(4) |
Substituting Equation (2) into Equation (1) gives after simplification
|
|
(5) |
where and all the derivatives are computed at the arbitrary point .
Standard calculus theory assumes that the domain is of infinitesimal size and the resulting balance equation is simply . We will relax this assumption and allow the space balance domain to have a finite size. The new balance equation (3) incorporates now the underlined term which introduces the characteristic length . Obviously, accounting for higher order terms in Equation (2) would lead to new terms in Equation (3) involving higher powers of .
Distance in Equation (3) can be interpreted as a free parameter depending on the location of point within the balance domain. Note that and, hence, can take a negative value. At the discrete solution level the domain should be replaced by the balance domain around a node. This gives for an equal size discretization where is the element or cell dimension. The fact that Equation (3) is the exact balance equation (up to second order terms) for any 1D domain of finite size and that the position of point is arbitrary, can be used to derive numerical schemes with enhanced properties simply by computing the characteristic length parameter from an adequate “optimality” rule leading to an smaller error in the numerical solution [22-24].
Consider, for instance, Equation (3) applied to the 1D convection-diffusion problem. Neglecting third order derivatives of , Equation (3) can be rewritten in terms of as
|
|
(6) |
We see clearly that the FIC method introduces naturally an additional diffusion term in the standard convection-diffusion equation. This is the basis of the popular “artificial diffusion” procedure [1,2,6] where the characteristic length is typically expressed as a function of the cell or element dimension. The critical value of can be computed by introducing an optimality condition, such as obtaining a physically meaningful solution. An interpretation of the FIC equations as a modified residual method is presented in [28].
Equation (3) can be extended to account for source terms. The modified governing equation can then be written in compact form as
|
|
(7) |
with
|
|
(8) |
where is the external source.
The essential (Dirichlet) boundary condition for eqn. (7) is the standard one (i.e. on where is the boundary whete the prescribed value is imposed). For consistency a stabilized Neumann boundary condition must be obtained.
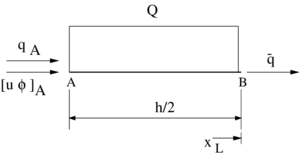
|
| Figure 2: Balance domain next to a Neumann boundary point B |
The length of the balance segment next to a Neumann boundary is taken as one half of the characteristic length for the interior domain (Figure 2). The balance equation, assuming a constant distribution for the source over , is
|
|
(9) |
where is the prescribed total flux at and .
Using a second order expansion for the advective and diffusive fluxes at point gives [22]
|
|
(10) |
where is given by eqn. (8).
Note that for the infinitesimal form of the 1D Neumann boundary condition is obtained.
The underlined terms in Equations (7) and (10) introduce the necessary stabilization in the discrete solution using whatever numerical scheme.
The time dimension can be simply accounted for the FIC method by considering the balance equation in a space-time slab domain. Application of the FIC method to the transient convection-diffusion equations and to fluid flow problems can be found in [23,26,29-33]. Quite generally the FIC equation can be written for any problem in mechanics as [22]
|
|
(11) |
where is the ith standard differential equation of the infinitesimal theory, are characteristic length parameters, is a time stabilization parameter and the time; and are respectively the number of balance equations and the number of space dimensions of the problem (i.e., for 2D problems, etc.). Indeed for the transient case the initial boundary conditions must be specified. The usual sum convention for repeated indexes is used in the text unless otherwise specified.
For example, in the case of the convection-diffusion problem and Equation (8) is particularized as
|
|
(12) |
with
|
|
(13) |
For a transient solid mechanics problems Equation (11) applies with and
|
|
(14) |
where are the displacements, are the stresses and the external body forces.
The modified Neumann boundary conditions in the FIC formulation can be written in the general case as [22]
|
|
(15) |
where are the generalized “fluxes” (such as the heat fluxes in a thermal problem or the stresses in solid or fluid mechanics), are the prescribed boundary fluxes and are the components of the outward normal to the Neumann boundary .
In above equations we have underlined once more the terms introduced by the FIC approach which are essential for deriving stabilized numerical formulations.
3 WHAT DO THE CHARACTERISTIC PARAMETERS MEAN?
The characteristic parameters in the space and time dimension ( and ) can be interpreted as free intrinsic parameters giving the “exact” expression of the balance equations (up to first order terms) in a space-time domain of finite size.
Let us consider now the discretized solution of the modified governing equations. For simplicity we will focuss here in the simplest scalar 1D problem. The variable is approximated as where denotes the approximated solution. The values of are now expressed in terms of a finite set of parameters using any discretization procedure (finite elements, finite diferences, etc.). The discretized FIC governing equation would read now
|
|
(16) |
where and is the residual of the discretized FIC equations.
The meaning of the characteristic parameters and in the discretized equation (16) changes (although the same simbols than in Eqs.(11) and (12) have been kept). The and parameters become now of the order of magnitude of the discrete domain where the balance laws are satisfied. In practice, this means that
|
|
(17) |
where is the grid dimension in the space discretization (i.e. the element size in the FEM or the cell size in the FDM) and is the time step used to solve the transient problem.
The values of the characteristic parameters can be found now in order to obtain an a correct numerical solution. The meaning of “correct solution” must be obviously properly defined. Ideally, this would be a solution giving “exact” values at a discrete number of points (i.e. the nodes in a FE mesh). This is infortunatelly impossible for practical problems (with the exception of very simple 1D and 2D cases) and, in practice, and are computed making use of some chosen optimality rule, such as ensuring that the error of the numerical solution diminishes for appropriate values of the characteristic parameters [22-27]. This suffices in practice to obtain physically sound (stable) numerical results for any range of the physical parameters of the problem, always within the limitation of the discretization method chosen.
It is quite usual to accept that the characteristic parameters are constant within each element. This assumption is not justificable “a priori” and, in general, we should regard those parameters as functions of the space and time dimension and of the solution at each point of the analysis domain.
4 FINITE ELEMENT DISCRETIZATION OF THE FIC EQUATIONS FOR ADVECTIVE-DIFFUSIVE PROBLEMS
Let us consider the FIC governing equations for the steady-state advective-diffusive problem defined in vector form for the multidimensional case as
|
|
(18) |
with
|
|
(20a) |
|
|
(20b) |
with
|
|
(21) |
In above equations is the characteristic length vector, is the gradient vector, is the diffusivity matrix, is the normal vector and is the velocity vector.
A finite element interpolation of the unknown can be written as
|
|
(22) |
where are the shape functions and are the nodal values of the approximate function [1].
Application of the Galerkin FE method to Equations (12)-(13) gives, after integrating by parts the term (and neglecting the space derivatives of )
|
|
(23) |
The last integral in Equation (23) has been expressed as the sum of the element contributions to allow for interelement discontinuities in the term , where is the residual of the FE solution of the infinitesimal equations.
Note that the residual terms have disappeared from the Neumann boundary . This is due to the consistency of the FIC terms in Equation (20b).
The last term in the third integral involving the derivatives of vanishes if is assumed to be constant wihtin each element.
4.1 Equivalence with SUPG form
The definition of vector is a crucial step as the quality of the stabilized solution depends on the module and direction of .
We could, for instance, assume that vector is parallel to the velocity , i.e. where is a characteristic length. Under these conditions, Equation (23) reads (for assumed to be constant within each element)
|
|
(24) |
Equation (24) coincides precisely with the so called Streamline-Upwind-Petrov-Galerkin (SUPG) method [1,6,7,10]. The ratio has dimensions of time and it is termed element intrinsic time parameter .
It is important to note that the SUPG expression is a particular case of the more general FIC formulation. This explains the limitations of the SUPG method to provide stabilized numerical results in the vicinity of sharp gradients of the solution transverse to the flow direction. In general, the adequate direction of is not coincident with that of and the components of introduce the necessary stabilization along the streamlines and the transverse directions to the flow. In this manner, the FIC method reproduces the best-features of the so-called stabilized discontinuity-capturing schemes [1,34,35].
5 INTERPRETATION OF THE DISCRETE SOLUTION OF THE FIC EQUATIONS
Let us consider the solution of a physical problem in a space domain , governed by a differential equation in with the corresponding boundary conditions. The “exact” (analytical) solution of the problem will be a function giving the sought distribution of for any value of the geometrical and physical parameters of the problem. Obviously, since the analytical solution is difficult to find (practically impossible for real situations), an approximate numerical solution is found by solving the problem , with , using a particular discretization method (such as the FEM). The distribution of in is now obtained for specific values of the geometrical and physical parameters. The accuracy of the numerical solution depends on the discretization parameters, such as the number of elements and the approximating functions chosen in the FEM. Figure 1 shows a schematic representation of the distribution of along a line for different discretizations where and are the coarser and finer meshes, respectively. Obviously for being sufficiently large a good approximation of will be obtained and for the numerical solution will coincide with the “exact” (and probably unreachable) analytical solution at all points. Indeed in some problems the solution can be found by a “clever” choice of the discretization parameters.
An unstable solution will occur when for some (typically coarse) discretizations, the numerical solution provides non physical or very unaccurate values of . A situation of this kind is represented by curves and of the left hand side of Figure 1. These unstabilities will disappear by an appropriate mesh refinement (curves in Figure 1) at the obvious increase of the computational cost.
In the FIC formulation the starting point are the modified differential equations of the problem as previously described. These equations are however not useful to find an analytical solution, , for the physical problem. Nevertheless, the numerical solution of the FIC equation can be readily found. Moreover, by adequately choosing the values of the characteristic length parameter , the numerical solution of the FIC equations will be always stable (physically sound) for any discretization level chosen.
This process is schematically represented in Figure 3 where it is shown that the numerical oscillations for the coarser discretizations and dissapear when using the FIC procedure.
We can conclude the FIC approach allows us to obtain a better numerical solution for a given discretization. Indeed, as in the standard infinitesimal case, the choice of will yield the (unreachable) exact analytical solution and this ensures the consistency of the method.
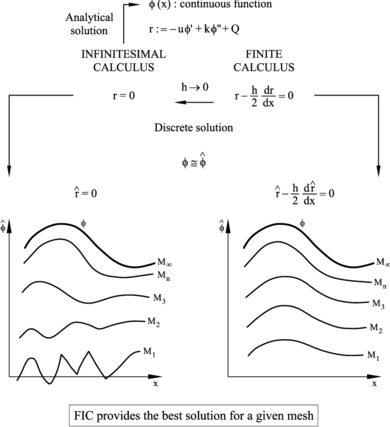
|
| Figure 3: Schematic representation of the numerical solution of a physical problem using standard infinitesimal calculus and finite calculus. |
6 COMPUTATION OF THE CHARACTERISTIC LENGTH VECTOR
The computation of the characteristic lengths is a crucial step as its value affect to the stability (and accuracy) of the numerical solution. This problem is common to all stabilized FE methods and different approaches to compute the stabilization parameters using typically extensions of the optimal values for simple 1D case (giving a nodally exact solution) have been proposed [1,2,6-21].
The computation the characteristic length values in 2D and 3D problems is of much higher complexity than in 1D problems. Indeed in 1D situations is an escalar (either positive or negative) while it becomes a vector 2D/3D problems. Moreover, numerical experiments indicate that in 2D/3D situations the direction of vector is crucial in order to obtain stabilized numerical solutions in problems where boundary layers and arbitrary internal sharp layers exist. It is well known that the SUPG assumption ( being parallel to ) generally does not suffice to give stable results in those cases [1,2,8,10,34,35]. Conversely, the numerical results in those cases are more insensitive to the module of which can be taken of the order of a typical element dimension.
Much effort has been spent by the author in the past in order to derive numerical schemes for computing vector in an iterative manner. The interested reader can find details on the different procedures in [22-30].
We present here a new approach for computing vector which is general and applicable to all FIC equations in mechanics.
The basis of the method is to assume that vector is a function of the gradient of the numerical solution. The simplest choice for convection-diffusion problems is
|
|
(25) |
where is a matrix which terms are a function of the element size and the inverse of the gradient vector components. The following simple expression of for 2D problems has found to give excellent numerical results in practice [43]
|
|
(26) |
where is a characteristic length parameter. As mentioned above the value of this length is not so relevant in practice. The rationale for choosing Eqs.(25) is explained in [43].
A simple expression for computing the length for each element is
|
|
(27) |
where are the element side vectors and is the number of sides for each element (i.e. for triangles, etc.).
Substituting Eqs.(25) into the weighted residual form Eqs.(23) gives
|
|
(28) |
where b.t. stands for the boundary integral terms.
Let us assume now that a linear interpolation is taken for in Eq.(22). This allows to neglect the second term of the second integral in (28). The new expression can be written as
|
|
(29) |
We see now clearly that the second integral has the form of a Laplacian matrix where the term takes the role of a diffusivity matrix.
Let us integrate now the diffusion term within the first integral of Eq.(29). This gives after small algebra
|
|
(30) |
where the diffusivity matrix is
|
|
(31) |
and is the unit matrix. In Eq.(29) the absolute value of is taken to ensure a positive value of the new diffusivity terms.
Eq.(30) yields the final system of discretized equations in the standard form
|
|
(32) |
where the stiffness matrix and the nodal vector are assembled from the element contributions
|
An iterative algorithm giving a stabilized solution can be implemented as follows
- Compute an initial solution solving Eq.(33) for an initial value of . Typically one can chose
(35) - Compute enhanced values of the gradient . This can be performed using a derivative recovery scheme [1,38].
- Compute updated element values of the characteristic length vector
(36) - Compute the element residuals using the enhanced derivative field by
(37) - Check for convergence of element residuals
(38) - Repeat steps 1–5 until convergence is satisfied using the updated value of
(39)
where denotes mean enhanced values for element for the th iteration.
where is a prescribed tolerance (typically ) and is the total number of elements in the mesh.
The term in the denominator in Eq.(38) is chosen so as to scale the residual error. For the denominator should be replaced by where is the maximum value of the velocity vector in the mesh, is the maximum prescribed value of at the Dirichlet boundary and for 2D/3D problems.
Numerical experimentals have shown that above process yields a converged stabilized solution in 2–3 iterations. Details and extensions of this scheme including numerical results can be found in [43].
7 GENERALIZATION OF THE FIC STABILIZATION PROCESS WITH GRADIENT ORIENTED CHARACTERISTIC LENGTH VECTORS
The FIC stabilization process described in previous section can be generalized by choosing vector h in the direction of the solution gradient as follows.
Let us consider a more general expression of the FIC equation (11) for a multidimensional problem where a different expression for is chosen for each balance equation (for simplicity we restrict onselves to steady state problems only)
|
|
(40) |
where and were defined in Eq.(11).
We choose the characteristic length vectors as
|
|
(41) |
where is an appropriate variable corresponding to the th balance equation. For instance in a fluid mechanics problem would be the velocity along the th axis.
The weak form of Eq.(40) is obtained after finite element discretization as
|
|
(42) |
We note that the stabilization term plays the role of a Laplacian which introduces a residual-type diffusion into the Galerkin equation.
The procedure is particularized next for the equations of an incompressible fluid.
8 FIC METHOD FOR INCOMPRESSIBLE FLUID MECHANICS
The FIC method can be applied to derive the modified equations of momentum, mass and energy conservation in fluid mechanics. The general form of these equations for a compressible fluid was presented in [22,29,32]. We will consider here the particular case of a viscous incompressible fluid. The FIC equations for the momentum and mass balance in this case can be written as (neglecting time stabilization terms)
Momentum
|
|
(43) |
Mass balance
|
|
(44) |
where
|
Above is the velocity along the ith global axis, is the (constant) density of the fluid, is the absolute pressure (defined positive in compression), are body forces and are the viscous deviatoric stresses related to the viscosity by the standard expression
|
|
(47) |
where is the Kronecker delta and the strain rates are
|
|
(48) |
The FIC boundary conditions are written as
|
|
(49) |
|
|
(50) |
and the initial condition for .
In Equation (45) are the total stresses, and are prescribed tractions and displacements on the boundaries and , respectively and are the components of the unit normal vector to the boundary. The sign in front the stabilization term in Equation (49) is positive due to the definition of in Eq.(45).
The and in above equations are characteristic lengths of the domain where balance of momentum and mass is enforced. In Equation (49) the lengths define the domain where equilibrium of boundary tractions is established [22].
Equations (43)–(50) are the starting point for deriving stabilized finite element methods for solving the incompressible Navier-Stokes equations using an equal order interpolation for the velocity and the pressure variables.
The weighted residual form of the momentum and mass balance equations can be written as
|
|
(51) |
|
|
(52) |
where and are arbitrary weighting functions representing virtual velocity and virtual pressure fields. Here and in the following no sum applies to the th superindex of .
Integrating by parts Eqs.(51) and (52) gives
|
|
(53) |
|
|
(54) |
In the derivation of Eqs.(53) and (54) the following assumptions have been made.
- at the Neumann boundary. This allows to elliminate the residual of the momentum equations at that boundary after the integration by parts.
- The volumetric strain rate vanishes at the boundary.
- The characteristic lengths and are constant within each element.
8.1 Gradient-form of the characteristic lengths
The following gradient-based expressions are taken for the characteristic lengths in the momentum and mass balance equations
|
|
(55a) |
|
|
(55b) |
The distances and are computed as
|
|
(56a) |
|
|
(56b) |
Substituting Eqs.(55) into (53) and (54) gives after integration by parts of the deviatoric stress and pressure term of in Eq.(53)
|
|
(57a) |
|
|
(57b) |
We see clearly that the stabilization terms in both equations take the form of a Laplacian matrix as it is desirable.
We introduce now a standard equal order linear finite element interpolation of the velocity and pressure fields as
|
|
(58) |
where are the linear shape functions, is the number of nodes per element and denotes nodal variables.
Substituting Eqs.(58) into (57) leads to the following system of equations
|
|
(59a) |
|
|
(59b) |
where for 2D problems
|
|
(60) |
It is interesting to analyze the steady-state form of Eqs.(59) for the Stokes flow case where the convective terms are neglected. Now the convective matrix and the stabilization matrix can be made equal to zero in the momentum equations and the resulting system can be written as
|
|
(61) |
The stability of the numerical solution is ensured by the presence of matrix guaranteeing a positive definitiveness of the equation system for any choice of the approximations for v and , thus overcoming the Babuska-Brezzi conditions [1].
The extension of above procedure to derive stabilized equations for incompressible solid mechanics problems is straight forward making use of the well known analogy between the Stokes equations for an incompressible flow and those of incompressible elasticity.
Applications of the FIC method here proposed to incompressible problems in fluid and solid mechanics can be found in [44,45].
9 CONCLUDING REMARKS
We have presented in this paper the possibilities of the finite calculus (FIC) method for deriving stabilized finite element formulations for a variety of problems in mechanics. In all cases the modified differential equations derived via the FIC method yield naturally a discretized system of equations with intrinsic stabilizations properties. These equations are more general than other standard stabilization methods (such as SUPG) and they allow to obtain correct numerical solutions for complex problems involving boundary layers and sharp internal layers. The key to the succes of the FIC method is the correct selection of the characteristic vector . We have presented a new gradient-based definition of which introduces naturally stabilization terms of laplacian-type in the equations for convective-diffusive transport and incompressible fluid flow problems.
Numerical examples with applications of the formulation here presented can be found in [43-45].
ACKNOWLEDGEMENTS
Thanks are given to Profs. J. García, S.R. Idelsohn, R.L. Taylor and O.C. Zienkiewicz for many useful discussions.
References
[1] Zienkiewicz OC, Taylor RL. The finite element method. 5th Edition, 3 Volumes, Butterworth–Heinemann, (2000).
[2] Hirsch C. Numerical computation of internal and external flow, J. Wiley, Vol. 1 1988, Vol. 2, 1990.
[3] Oñate E, Idelsohn SR, Zienkiewicz OC, Taylor RL. A finite point method in computational mechanics. Applications to convective transport and fluid flow. Int. J. Num. Meth. Engng., 39, 3839–3866, (1996).
[4] Oñate E, Idelsohn S. A mesh free finite point method for advective-diffusive transport and fluid flow problems. Comput. Mechanics, 21, 283–292, (1988).
[5] Oñate E, Sacco C, Idelsohn S. A finite point method for incompressible flow problems. Computing and Visualization in Science, 2, 67–75, (2000).
[6] Brooks A, Hughes TJR. Streamline upwind/Petrov-Galerkin formulation for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations. Comput. Methods Appl. Mech. Engrg., 32, 199–259, (1982).
[7] Codina R. Comparison of some finite element methods for solving the diffusion-convection-reaction equation. Comput. Methods Appl. Mech. Engrg., 156, 185–210, (1998).
[8] Hughes TJR, Mallet M. A new finite element formulations for computational fluid dynamics: III. The generalized streamline operator for multidimensional advective-diffusive systems. Comput Methods Appl. Mech. Engrg., 58, 305–328, (1986a).
[9] Hansbo P, Szepessy A. A velocity-pressure streamline diffusion finite element method for the incompressible Navier-Stokes equations. Comput. Methods Appl. Mech. Engrg., 84, 175–192, (1990).
[10] Cruchaga MA, Oñate E. A generalized streamline finite element approach for the analysis of incompressible flow problems including moving surfaces. Comput. Methods in Appl. Mech. Engrg., 173, 241–255, (1999).
[11] Hughes TJR, Franca LP, Hulbert GM. A new finite element formulation for computational fluid dynamics: VIII. The Galerkin/least-squares method for advective-diffusive equations. Comput. Methods Appl. Mech. Engrg., 73, 173–189, (1989).
[12] Tezduyar TE, Mittal S, Ray SE, Shih R. Incompressible flow computations with stabilized bilinear and linear equal order interpolation velocity–pressure elements. Comput. Methods Appl. Mech. Engrg., 95, 221–242, (1992).
[13] Douglas J, Russell TF. Numerical methods for convection dominated diffusion problems based on combining the method of characteristics with finite element or finite difference procedures. SIAM J. Numer. Anal., 19, 871, (1982).
[14] Pironneau O. On the transport-diffusion algorithm and its applications to the Navier-Stokes equations. Numer. Math., 38, 309, (1982)..
[15] Löhner R., Morgan K, Zienkiewicz OC. The solution of non-linear hyperbolic equation systems by the finite element method. Int. J. Num. Meth. in Fluids, 4, 1043, (1984).
[16] Zienkiewicz OC, Codina R. A general algorithm for compressible and incompressible flow. Part I: The split characteristic based scheme. Int. J. Num. Meth. in Fluids, 20, 869-85, (1995).
[17] Codina R, Vazquez M, Zienkiewicz OC. A general algorithm for compressible and incompressible flow - Part III. The semi-implicit form. Int. J. Num. Meth. in Fluids, 27, 13–32, (1998).
[18] Hughes TJR. Multiscale phenomena: Green functions, subgrid scale models, bubbles and the origins of stabilized methods. Comput. Methods Appl. Mech. Engrg, 127, 387–401, (1995).
[19] Brezzi F, Franca LP, Hughes TJR, Russo A. . Comput. Methods Appl. Mech. Engrg., 145, 329–339, (1997).
[20] Codina R. Stabilization of incompressibility and convection through orthogonal sub-scales in finite element method. Comput. Methods Appl. Mech. Engrg., 190, 1579–1599, (2000).
[21] Hauke G. A simple subgrid scale stabilized method for the advection-diffusion-reaction equation. Comput. Methods Appl. Mech. Engrg., 191, 2925–2948, (2002).
[22] Oñate E. Derivation of stabilized equations for advective-diffusive transport and fluid flow problems. Comput. Methods Appl. Mech. Engrg., 151:1-2, 233–267, (1998).
[23] Oñate E, Manzan M. Stabilization techniques for finite element analysis of convection diffusion problems. In Comput. Anal. of Heat Transfer, WIT Press, G. Comini and B. Sunden (Eds.), (2000).
[24] Oñate E, García J, Idelsohn SR. Computation of the stabilization parameter for the finite element solution of advective-diffusive problems. Int. J. Num. Meth. Fluids, 25, 1385–1407, (1997).
[25] Oñate E, García J, Idelsohn SR. An alpha-adaptive approach for stabilized finite element solution of advective-diffusive problems with sharp gradients. New Advances in Adaptive Comput. Methods in Mech., Elsevier, P. Ladeveze, J.T. Oden (Eds.), (1998).
[26] Oñate E, Manzan M. A general procedure for deriving stabilized space-time finite element methods for advective-diffusive problems. Int. J. Num. Meth. Fluids, 31, 203–221, (1999).
[27] Oñate E. Possibilities of finite calculus in computational mechanics. Int. J. Num. Meth. Engng., (2004).
[28] Oñate E, Taylor RL, Zienkiewicz OC, Rojek J. A residual correction method based on finite calculus. Engineering Computatlions, 20:5/6, 629–658, (2003).
[29] Oñate E. A stabilized finite element method for incompressible viscous flows using a finite increment calculus formulation. Comput. Methods Appl. Mech. Engrg., 182:1–2, 355–370, (2000).
[30] Oñate E, García J. A finite element method for fluid-structure interaction with surface waves using a finite calculus formulation. in Comput. Methods Appl. Mech. Engrg., 191:6-7, 635-660, (2001).
[31] García J, Oñate E. An unstructured finite element solver for ship hydrodynamics. J. Appl. Mechanics, 70, 18–26, (2003).
[32] Oñate E, García J, Bugeda G, Idelsohn SR. A general stabilized formulation for incompressible fluid flow using finite calculus and the FEM. In Towards a New Fluid Dynamics with its Challenges in Aeronautics, J. Periaux, D. Champion, O. Pironneau and Ph. Thomas (Eds.), CIMNE, Barcelona, (2002).
[33] Oñate E, García J, Idelsohn SR. Ship Hydrodynamics. Encyclopedia of Computational Mechanics, T. Hughes, R. de Borst and E. Stein (Eds.), J. Wiley, (2004) (to be published).
[34] Hughes TJR, Mallet M. A new finite element formulations for computational fluid dynamics: IV. A discontinuity capturing operator for multidimensional advective-diffusive system. Comput. Methods Appl. Mech. Engrg., 58, 329–336, (1986b).
[35] Codina R. A discontinuity-capturing crosswind dissipation for the finite element solution of the convection-diffusion equation. Comput. Methods Appl. Mech. Engrg., 110, 325–342, (1993).
[36] Tezduyar T. Stabilization parameters and local length scales in SUPG and PSPG formulations. Proceedings of the Fith World Congress on Computational Mechanics, (http://wccm.tuwien.ac.at), Vienna, Austria, July 7–12 (2002).
[37] Zienkiewicz OC, Zhu JZ. The Superconvergent patch recovery (SPR) and adaptive finite element refinement. Comput. Methods Appl. Mech. Engrg., 101, 207–224, (1992).
[38] Wiberg NW, Abdulwahab F, Li XD. (1997). Error estimation and adaptive procedures based on superconvergent patch recovery. Archives Comput. Meth. Engng., 4:3, 203–242, (1997).
[39] Ilinca F, Hétu JF, Pelletier D. On stabilized finite element formulation for incompressible advective-diffusive transport and fluid flow problems. Comp. Methods Appl. Mech. Engrg., 188, 235–257, (2000).
[40] Chetverushkin BN. Kinetic schemes and their application for simulation of viscous gas dynamics problems. European Congres on Computational Methods in Applied Sciences and Engineering (ECCOMAS 2000), Barcelona 11–14 September, E. Oñate et al. (Eds.), (2000).
[41] Oñate E, Rojek J, Taylor RL, Zienkiewicz OC. Linear triangles and tetrahedra for incompressible problems using a finite calculus formulation. In European Conference on Computational Mechanics (ECCM2001), Cracow, Poland, 26–29 June, (2001).
[42] Oñate E, Rojek J, Taylor RL, Zienkiewicz OC. Finite calculus formulation for analysis of incompressible solids using linear triangles and tetrahedra. To appear in Int. J. Num. Meth. Engng., (2004).
[43] Oñate E, Zarate F and Idelsohn SR. Stabilized FEM for convection-diffusion problems using a FIC approach with gradient-based stabilization parameters. Submitted to Comput. Meth. Appl. Mech. Eng., (2004).
[44] Oñate E and Flores F. Refined finite calculus method for finite element analysis of incompressible flows. Submitted to Comput. Meth. Appl. Mech. Eng., (2004).
[45] Oñate E and Rojek, J. FIC formulation for finite element analysis of incompressible solids. Submitted to Int. J. Num. Meth. Eng., (2004).
Document information
Published on 01/01/2004
Licence: CC BY-NC-SA license