Abstract
Spallart and Allmaras is a one-equation turbulence model developed for predicting complex aerodynamic flows [1]. It will be of great interest to extend its application to predict other kind of flows in presence of heat and mass transfer. Specifically we will demonstrate, by considering two applications, that this one equation model may replace the two equation models in several heat transfer applications such as HVAC, electronics cooling and fire propagation in buildings. This will reduce computing time and numerical stiffness in CFD calculations.
The first application is the 2D natural turbulent convection in a cavity differentially heated; which was considered as a benchmark case before applying CFD in any HVAC configuration. The exact configuration proposed by Ampofo [2], was then modeled and the radiation effect was studied.
The second application proposed by Riera [4] was the numerical prediction of a heat exchanger based on hybrid jet impingement/micro-channel; it was used for managing high heat-flux thermal of power electronics devices.
Those applications deal with low and high fluxes transfer respectively and allow demonstrating clearly the capacity of the one equation model to predict confined turbulent natural/ forced convection and jet-impingement heat transfer.
Keywords: Natural convection, conduction, radiation, cooling, microchannel, jet/impingement, CFD
1. Introduction
Natural turbulent convection in enclosure differentially heated find its application in multiple fields as for instance electronics cooling, HVAC (heating, ventilation and air-conditioning) systems, solar collectors and fire propagation in building… Such flow is considered as a HVAC benchmark case before studying any real case; then appears the importance to consider a one equation model instead of two equation models. In this work, the 2D natural convection, where the two vertical walls were differentially heated, and the horizontal walls were heat conductors, was considered. This application is a known problem that has been largely studied in the literature. Peng & Davidson [7] used large eddy simulation to investigate a buoyant flow in a cavity experimentally investigated by Ampofo [2]. This cavity was studied by Omri et al. [8] by considering two models. The same experiments of Ampofo [2] where used by the same authors, who indicated the success of the SST turbulence model in predicting this confined flow. They used four different grids (, , and ) to give an excellent analysis of the considered case. Essentially, they indicate that a reduced number of nodes () well positioned gives perfect results exactly like larger number (). The Rayleigh number was , indicating a low turbulence level in the cavity of Ampofo [2]. Thus, appeared the necessity of choosing the adapted turbulence models. In industrial applications, the two equations models were commonly employed in CFD codes. Nevertheless, by reference to the two equation models, the one-equation models should be more attractive from numerical point of view considering that they are more easy and robust. Menter [10] proposed an improved one-equation model using a constant ratio shear stress/turbulent kinetic energy as suggested by Bradshaw [11]. Baldawin [12] derived a one-equation model from the model with additional simplifying assumptions. This model was independent of algebraic length scale, making it attractive from numerical angle. However, this model was difficult for implementation in complexes geometries; moreover, several diffusive terms were neglected than its performance was different from the underlying model. As indicated by Deck [13], the Spalart & Allmaras model [1] was a compromise between two equation models and algebraic model. This model was, successfully used since its acceptable results in different aerodynamic flow problems and its numerical properties. Satisfactory results for transonic turbulent flow in industrial applications done by Gacherieu, Rogers, and Deck [14,15,16] and for slightly separated flow over expanded nozzles seen in Deck [13]. Nevertheless, its application to predict natural convection in simple and relatively complex geometries appeared of great importance; since its capacities to predict such flows will be evaluated, but also studying all physical phenomena characteristic of natural convection.
The success of the one equation model in predicting natural convection was not synonymous of success for predicting flows with heat transfer. It was important to extend its application for a wide range of those flows. We have deliberately chosen to apply it in a relatively complicated flow that combines a jet impingement with microchannel in the same device used for cooling. Jet impingement and microchannel are widely used in microelectronics cooling schemes of Lee [17]. They both allow extraction of high heat flux but still have some drawbacks. Microchannels could principally minimize the increasing temperature cooled object along the flow direction by increasing the water flow, but cannot eliminated this gradient of temperature. For jet impingements, obtaining a uniform temperature distribution went through considering a jets matrix; consequently the heat exchange coefficients was reduced but the flow structure became of high complexity as indicated by Brunschwiler [18].
The current authors [5] developed a jet-impingement/microchannels heat exchanger improving the uniformity of the temperature of the object supposed to be cooled. A design that used a jet impingement in the heat exchanger inlet followed by a stepwise varying width of microchannels. This microchannels disposition opposes the water-temperature increase since it increases the local heat transfer coefficient resulting in a relatively constant removal of heat flux. They used the SST model for predicting the flow and heat transfer in this device [4]. The results validated the proposed design, and showed that the cooled-object highest temperature was located just below the jet-impingement. In addition, the considered two-equation model gives reasonable results; thus, it will be convenient to consider the Spallart and Allmaras model to calculate the flow in this complex geometry.
O'Donovan [19] and Katti [20] studied the Reynolds number effect and the nozzle hydraulic diameter () to the nozzle to plate spacing () on the heat transfer distribution. Previous studies of Lin [21] and Choo [22] on slot jet impingement cooling configurations indicated the impact of nozzle to plate spacing on the stagnation point Nusselt number that depended on Reynolds number.
In this second section, the effect of nozzle to plate spacing () on the performance of heat exchange at stagnation point of jet impingement/microchannels cooling configuration will be studied experimentally. The nozzle to the plate effect on the device global performance was studied by analysing thermal resistance coefficient and uniformity of temperature. After this necessary experimental step, we consider the Spallart and Allmaras model to analyse the flow structure within this hybrid jet-impingement/microchannels heat exchanger. We will indicate the capacity of this model to predict a fine description of the flow.
2. Natural turbulent convection in a cavity
2.1. Experimental data
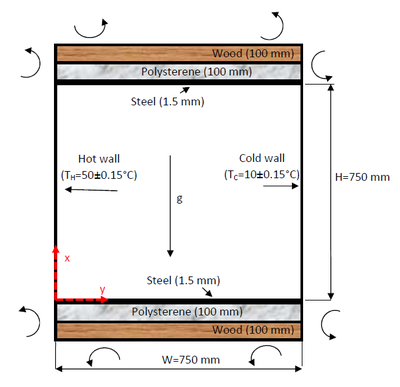
The natural convection cavity used here was experimentally investigated by Tian et al. [9] and also by Ampofo et al. [2] by considering an air-filled cavity. The dimensions and boundary conditions were indicated in Figure 1. The Rayleigh number was . The outside temperature was °C. In addition, the measurements were presented in the middle of the -direction (m) of the cavity, where Tian et al. [9] and Ampofo et al. [2] demonstrated that the flow fields were 2D.
|
| Figure 1. Schematic representation of the cavity |
2.2. Numerical model
The properties of the air as its specific heat and molecular transport were constant. The air effective viscosity and effective thermal conductivity depend respectively on local flow conditions. The air density was constant except in the gravity force, where it depends linearly on the temperature. Thus, mass, momentum and energy equations are:
|
|
(1) |
|
|
(2) |
|
|
(3) |
|
|
(4) |
where,
and are the velocity components in the and directions respectively,
is the temperature (°C, K);
is the reference temperature (°C, K);
is the thermal expansion coefficient ();
is the gravitational acceleration ();
is the effective eddy viscosity;
is the effective thermal conductivity;
is the specific heat capacity at constant pressure ();
is the turbulent dynamic viscosity;
is an empirical constant in turbulent viscosity;
the fluid density (kg/m);
the turbulent kinetic energy () and e Dissipation rate ().
The Spalart-Allmaras [1] one equation model resolves a transported equation of a variable similar to the turbulent kinematic viscosity.
|
|
(5) |
where
|
is the mean strain rate and is the mean rate of rotation. The constants: and as indicated in Spalart-Allmaras [1] were equal to 0.1355, 0.622, 0.667, 7.1, 3.2, 0.3, 2.0 and 0.4187 respectively, and were used with an energy Prandtl number equal to 0.85. The default model was referred to as SA model. The turbulent Prandtl number has also been modified from 0.667 to 0.75, which automatically modifies to 2.935 with a turbulent energy Prandtl number = 0.6. This modification was referred to as SAM model. When radiation was added to the SAM model, the model is referred to as SAMR model.
When adding radiation, the air as transparent medium was considered radiatively non-participating; surface to surface was used where all surfaces were considered gray and diffuse, consequently conduction equilibrated convection and radiation on each surface. To obtain net radiative heat fluxes over the walls, the number of zones of each surface was determined by the solving-used-mesh.
The solid horizontal were included in the calculation domain where only the heat conduction energy conservation was resolved. The thermal conductivities of the three solid layers indicated in Figure 1 were considered constant respectively.
The coupled elliptic partial differential equations (1) to (5) were discretized using second-order finite volume scheme. In the cavity, the rectangular grid was finer near the walls (boundary layer) and coarser in the central region of the cavity (Figure 1). Grid independence, as done by the same author [3], was tested by considering three non-uniform grids: , and . The SA model verified the same result, and the grid was used for all calculations of this cavity.
The following boundary conditions were applied:
- At the solid inside cavity walls , and All wall emissivities were zero.
- At the two vertical walls: °C and °C.
- At the two horizontal walls and respectively, the temperature and heat flux on the air side take the corresponding values in the solid walls.
- The convection coefficient of the outside air was and its temperature was constant (30°C).
2.3. Numerical results and discussion
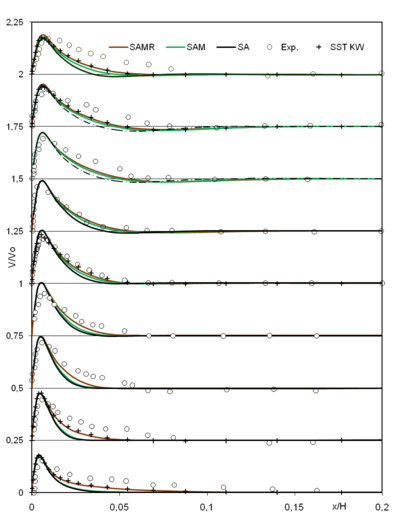
Figure 2 indicates the non-dimensional vertical velocity in the boundary layer close to the hot wall at the nine different heights presented in the experimental data. The calculations perfectly reproduce the whole core of the cavity (i.e. to ) where the flow in this zone is quiescent, explaining identical behavior of all models. The influence of constants modification and also the influence of the radiation are seen within the boundary layers (i.e and ). Model SA slightly underestimates the vertical velocity component; such behaviour is also noticed in the predictions of Peng and Davidson [7]. The constant modification suggested allows improving the velocity behaviour, i.e. a boundary layer thicker but the SAM model continue under estimating the experiment. The addition of radiation to SAM allows a better adjustment of the considered velocity component but not until reproducing quantitatively the experiment. Indicate that SAMR gives a satisfactory behaviour especially in the boundary layers located at and . The differences are appreciable especially while approaching the zones of inversion. Remember that these predictions are satisfactory with reference to other levels of modelling (SST by Omri [3] or LES by Peng [7]).
|
| Figure 2. Mean non-dimensional vertical velocity component at |
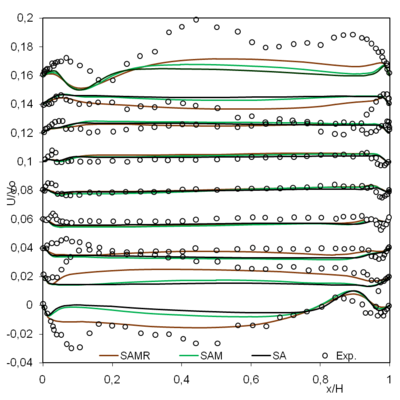
Figure 3 shows the second velocity component which represents the secondary flow, for example the maximum of at mid height () does not exceed the tenth of . Consequently, we are in the presence of low velocity values; however, the model qualitatively reproduces the experiment. The difference between the 3 models is better seen especially when approaching the horizontal boundary layers. The three model versions indicate certain symmetry of the profile speed (also checked by ). The radiation (SAMR model) tends indeed to align the model to the experiment and its contribution is clear in the regions near the horizontal boundary layers.
|
| Figure 3. Mean non-dimensional horizontal velocity component at and |
The air temperature profiles at the same nine different heights were indicated in Figure 4. Indicate that at the cavity mid-height () the numerical calculations are confused and also in the positions and . The differences are increasingly seen while tending towards the top or the bottom horizontal walls. Therefore, considering only the mid height cavity does not allow seeing the impact of some phenomenon (radiation, conducting horizontal walls and grid validation) is most likely not enough.
By comparing all heights, the differences between SA, SAM and SAMR are clearer; the correction of the Prandtl number seems to improve the agreement with experiment but it is insufficient especially for and . As an example for and the SA and SAM models deviate one and two degrees from the experiment respectively. Indeed, the radiation seems important at these locations; even though it is still difficult to estimate its exact contribution since predictions of the model without radiation is not exact. Therefore, radiation is relevant and as important in this cavity configuration as the conduction of the horizontal walls, especially in the top and bottom regions near the horizontal walls.
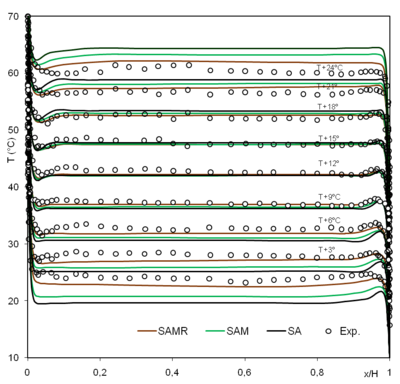
|
| Figure 4. Mean air temperature at and |
Lets consider the temperature at mid-section cavity in Figure 5, the prediction of SST model obtained by Omri [3] has also been added, which legitimates in a way the constant modification of the SA model. In the central zone () there are no differences between the various versions of SA model. These differences were accentuated while going towards the horizontal walls. The radiation was non-negligible, especially near the horizontal walls ( and ), where we can verify that for and radiation varies the SAM predictions by about 1.6°C.
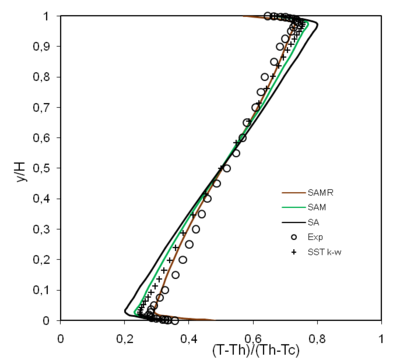
|
| Figure 5. Mean non-dimensional air temperature at |
Figure 6 shows the mean horizontal velocity component at the same place as in Figure 5 compared to Tian et al. [9] experimental data. The results of the considered turbulence model compare favorably with experimental data. In particular, at the central region where are similar. The maximum velocity values are under estimated, but the SAMR is closer to the experience peaks and valleys are better predicted and at the right vertical position . Moreover, it changes sign exactly like in the experiment indicating the importance of accounting for radiation in such a flow. It increases the maximum velocity of the SAM model by about 29%. Furthermore, this velocity component is essentially antisymmetric. They also show that horizontal boundary layer was thicker than the vertical one; it was approximately three times the ascending or descending flows boundary layer.
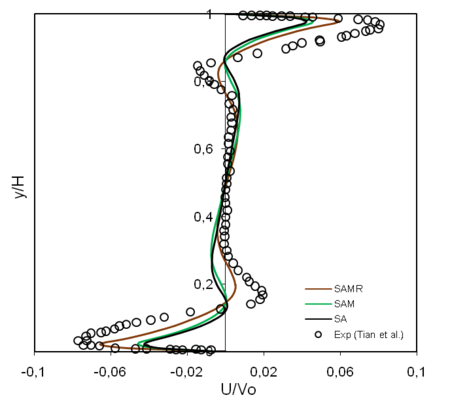
|
| Figure 6. Mean non-dimensional horizontal velocity component at |
The Nusselt Number along the four interior walls of the cavity is calculated in Figure 7. The calculation of this number strongly depends on the manner how derivative of temperature is calculated at the point near the wall. It should be noticed that Joubert et al. [23] showed that the difference in calculating the Nusselt number could reach 25% by using various computer codes. Over all, the Nusselt number is well reproduced by the three versions of the model.
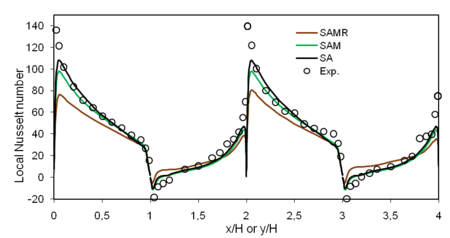
|
| Figure 7. Nusselt number along the four walls of the cavity |
3. Natural hybrid jet impingement/micro-channel cooling scheme
3.1. Test module and cooling system description
The schematic design of the experimental system used here indicated in Figure 8, where the test module was cooled with water from a thermostatic reservoir maintaining constant the temperature at inlet (TºC). The water circulated in the closed circuit by a peristaltic pump with variable speed (JP Selecta PERCOM N-M) delivering a constant flow rate (). After the pump the water is automatically filtered ( filter) entering then in the test module. The generation of constant heat flux () obtained with a ceramic heater (Watlow Ultramic 600) set to .

|
| Figure 8. Test module setup |
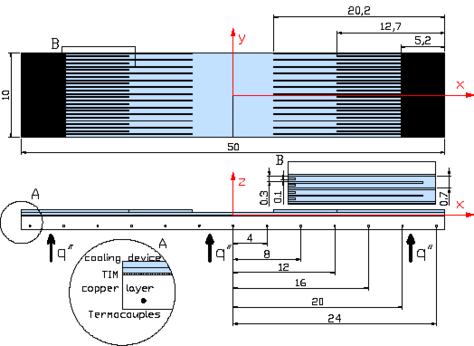
The combination of jet/impingement and microchannels has led to two distinct zones: One corresponded to jet impingement cooling followed by another zone using variable microchannels widths (Figure 9). The slot-width of the jet impingement ranged from 50 to m. The width of microchannels decreased from m to m increasing the flow speed resulting in increasing the convective heat transfer coefficient and then the heat exchange surface throughout the flow direction, compensating, thereby, the increase of the flow temperature. The microchannels was engraved in silicon using the process of lithography and DRIE creating a m constant depth microchannel arrangement. Figure 9 shows the heat exchanger microchannels configuration, that is similar to the one studied previously at millimeter scale [2].
|
| Figure 9. Microchannel heat exchanger scheme and experimental mount |
The microchannel heat exchanger was rooted on a copper layer using a thin Thermal Interface Material (TIM) layer of m, m and a thermal conductivity equal W/m·K.
From the inlet where the water was pumped (vertical to the microchannels disposition) the water passed through the microchannels and collected at the two outlets reaching then the reservoir. A thermocouples (Type-) was used to measure the inlet and outlet of microchannel water temperature. The temperature along the copper layer in the flow direction at different six positions () of the medium line (mm, mm) of microchannel was collected by data logger “Campbell CR23X” and then stored.
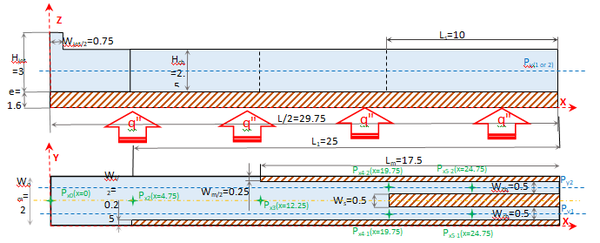
Below is a real picture of the heat exchanger as fabricated, it presents a symmetry with respect to y-axis and allow simplifications for numerical calculation domain (Figure 10). Additionally, the geometry (Figure 10a) has certain periodicity that allows more simplifications (Figures 10b and 10c).

|
|
| Figure 10. (a) Real heat exchanger. (b)-(c) Numerical calculation domain |
3.2. Results and discussion
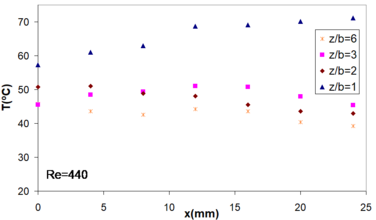
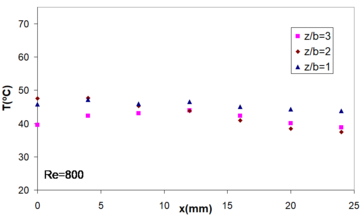
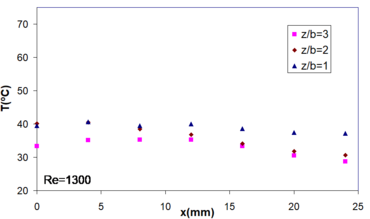
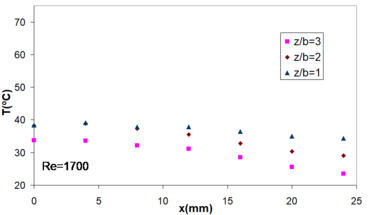
For a given Reynolds number, the temperature distribution depends on the nozzle to plate spacing (Figure 11).
|
|
| (a) | (b) |
|
|
| (c) | (d) |
| Figure 11. Temperature distribution at mm | |
The lower temperature at the stagnation point of the jet impingement was obtained for . We have also observed that temperature differences between several tests were higher for lowest value of Reynolds number (), indicating a higher impact of the nozzle to plate spacing on the performance of this device at low Reynolds numbers.
The results show variable temperature distributions as a function of and value. Consequently, obtaining specific temperature distributions depend on tailoring the nozzle according to plate spacing and flow regime.
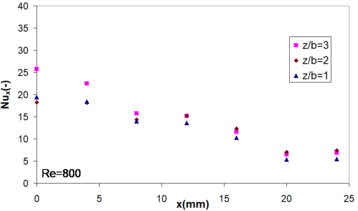
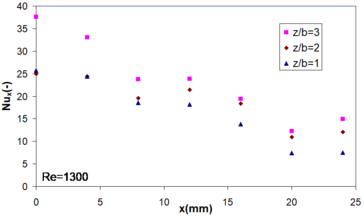
3.2.1 Distribution of local Nusselt number
The local Nusselt number compared cooling device performance to nozzle geometry configuration (Figure 12). It was defined as:
|
|
(6) |
where is the coolant thermal conductivity and the flow sections hydraulic diameter.
For all Reynolds numbers studied (440-1700), the distribution of local Nusselt number followed the tendency obtained by [5]. For a Reynolds number of 440, the local Nusselt number was multiplied by the number of microchannels in each section, resulting constant trend along the -axis (mm to mm). Consequently, the bottom wall heat sink temperature profile was uniform. This feature was obtained for some combinations of and (Figures 10a and 10b).
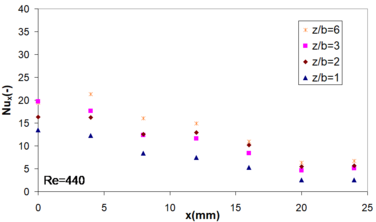
|
|
| (a) | (b) |
|

|
| (c) | (d) |
| Figure 12. Local Nusselt number distribution at mm | |
Large differences of stagnation point Nusselt number (at mm) were observed (Figures 12a-12d). This result is in conformity with the studies made by Choo et al. [22]. The Nusselt number stagnation point has significantly increased (: by factor 1.34 to factor 1.5 with respect to the worst result, as a function of ). The variation of nozzle to plate spacing was largely impacted on the whole distribution of local Nusselt number and temperature distribution. Consequently, the optimization of value was mandatory in order to obtain two main objectives of proposed design: high temperature uniformity and low thermal resistance coefficient.
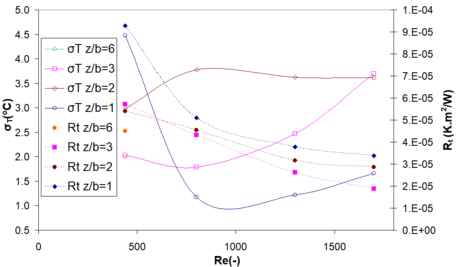
3.2.2 Temperature uniformity versus global thermal resistance coefficient
Figure 13 indicates the deviation of the temperature and global thermal resistance coefficient . It was defined as:
|
|
(7) |
where wasthe average temperature of the heat sink bottom.
|
| Figure 13. Standard deviation of the temperature and global thermal resistance coefficient |
Low thermal resistance coefficients (.K/W) were obtained at relatively low Reynolds numbers (<2000). The standard temperature deviation () varied between 1 and 5ºC.
On the one hand, the thermal resistance coefficient was decreased with Reynolds number for all studied spacing. For , the best heat exchange was obtained for . For , the lowest thermal resistance coefficient was obtained for . On the other hand, the standard deviation of temperatures, showing different trends as a function of .
All these results indicate that the jet impingement features, channel distribution and flow regime were coupled. Consequently, optimization of hybrid jet impingement/microchannel scheme, for decreasing thermal resistance coefficient and improving the temperature uniformity, should be coupled to take into account these aspects.
3.2.3 Numerical calculation and structure of the flow
3.2.3.1 Numerical calculation
The geometry considered was detailed in Figures 10(b) and (c) where the only variable to be changed are the inlet flow and the heat flux applied in the bottom of the heat exchanger, this corresponded to four cases as indicated in the Table 1.
| TEST 1 | TEST 2 | TEST 3 | TEST 4 | |
|---|---|---|---|---|
| Tin (°C) | 12.35 | 12.35 | 12.6 | 12.7 |
| Q(ml/min) | 1240 | 1240 | 790 | 505 |
| (W/cm) | 21.8 | 32 | 31 | 31 |
The solid was Aluminum with constant physical properties and all wall in contact with air were taken adiabatic. The description the equations of the SST model and all boundary conditions were indicated in [6] and they will be used with the SA model.
The mesh effects was tested before [6] using the SST model, where three different meshes were used 150000, 313000 and 620 000 nodes. The criteria was the temperature sensibility to mesh variation, it was decided that the medium mesh is convenient since the temperature variation by reference to the highest mesh do not exceed 3.5%. Other refinement were done to take into account the wall proximity effect.
3.2.3.2 Structure of the flow
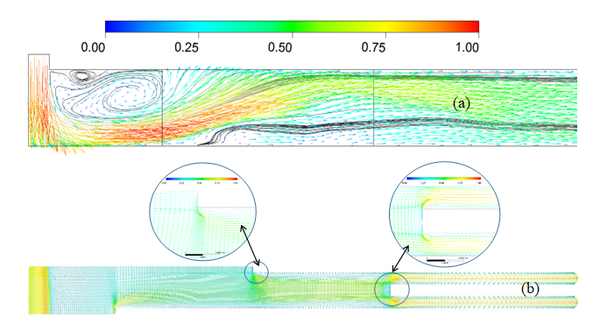
Let’s begin with a global description of the flow by choosing two perpendicular planes situated at the mid-height and the mid-width of the channel. The presence of jet impingement, several section changes and micro-channels make this study important as testing turbulence models. Accordingly, in this non-conventional geometry, one expects a presence of complex flow. As indicated in Figure 18, the jet impinged flat solid-surface resulting in more heat transfer. We were able to verify a local decrease of the temperature at the active wall at this level, where the jet-width became more than the double of its initial width at the inlet. As indicated in Figure 14a, the jet was detached from the bottom surface, becoming a flow parallel to the -axis. Two zones were identified, a recirculation zone at the top of impingement surface due to the jet impingement and change in direction, while the second was just after the jet detachment resulting of this detachment. The second zone, where the flow looked like quiescent have resulted in temperature increase. Figure 14b indicates velocity vectors in the mid-height of the channel. At the first obstacle (fins), the fluid was deviated towards central zone until the second obstacle, where the flow was piped until the last row of the channels where it was distributed uniformly between the micro-channels.
|
| Figure 14. Normalized velocity vectors in the mid-width and mid-height of the channel. (a) Plane (). (b) Plane () |
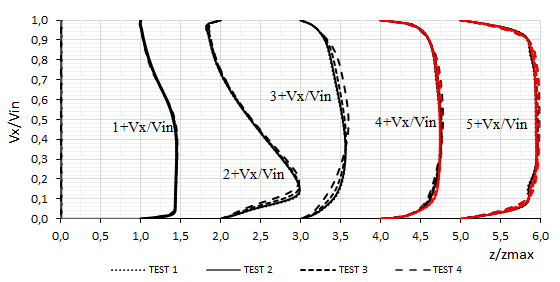
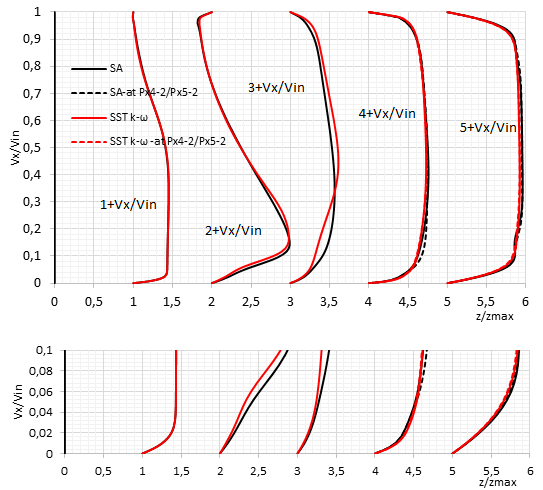
Figure 15 indicates vertical variations of velocity -component at different positions along -axis (, 4.75, 12.25, 19.75, 24.75) at mid-height and mid-width of the channel (Positions are as indicated in Figure 10). For the two last positions, they were in the medium of the two micro-channels.
|
| Figure 15. Normalized velocity profiles along the flow-path predicted by SA model at different positions (, , , , , as indicated in Figure 10) in the case of the fourth tests. The red color indicated the positions and |
At the origin of the -axis there was no -component of the velocity (), since this was the central region of the jet (along the -direction). However, for the position larger variation was seen, which was constantly indicating the expansion of the jet and detachment near the bottom wall. In the position the jet was totally detached along -direction. At positions and , the flow occupied the volume and developed in the micro-channels. The flows in the two micro-channels were slightly different due to non-uniform distribution of the fins.
|
| Figure 16. Velocity profiles along the flow-path predicted by SA model and SST model in different positions (, , , , , as indicated in Figure 10) |
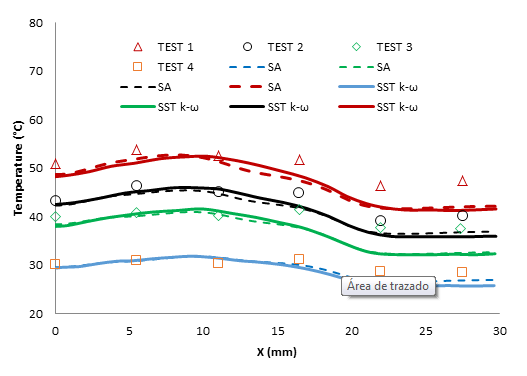
To compare the one equation to SST model TEST 2 dealing with maximum heat flux and also mass flow inlet (Figure 16(a)) was considered. Over all, the two models are comparable and the difference was declared at the position . In this region, the flow was affected by a fins- presence; we suspect that SST was more adapted for swirl. However, when the prediction of heat transfer convected by the fluid from the solid was considered, automatically the area of heat transfer was the proximity of the interface solid/fluid the boundary layer (Figure 16(b)); there is no difference between the two models and the result could be verified in the temperature profile indicated later (Figure 18).
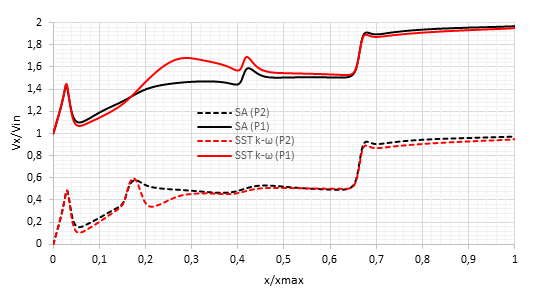
Figure 17 indicates the velocity variation along -axis at mid-height () of the channel at two -positions ( and ) which corresponded to the mid-width of the micro-channels. All velocity profiles increased along the flow path (-direction) constraining the naturally increasing-temperature profile to decrease; this represents a major advantage for this proposed design. In all those profiles, the first velocity pick () corresponded to the width of the jet at this position. The effect of first and second fins were seen at () and () relatively, where locally the SST behaves differently compared to SA model. In the entrance of the two micro-channels until the outflow, the two models were comparable. Moreover, they indicated that the flow was not developed, result verified by comparing the hydraulic diameter () to the microchannel length ().
|
| Figure 17. Velocity profiles along the flow-path predicted by SA model and SST model at the mid-height of the channel in two different places ( and as indicated in Figure 10) |
Figure 18 was the most important one since the existing experimental data allowing a common basis for comparison of both models. The impact of jet impingement was seen at and corresponded to minimum temperature, thereafter, the temperature increased reaching its maximum in the jet-detachment region. The temperature decreased after all along the flow path due to section change resulting in velocity decrease. The SA model reproduced the experimental data in the fourth cases as well as SST model in the region before the micro-channels (mm), the two models under estimated the temperature in the micro-channels with a slight advantage to SA model, this was verified by the velocities there (Figure 17 for ). This figure indicated that SA model behaved as well SST , and could be used in predicting heat transfer at the same level as the two-equation models.
4. Conclusion
Turbulent natural convection in air filled cavity was calculated numerically with the one equation model of Spallart and Allmaras [1] and a version modified by changing the values of the turbulent Prandtl number. The geometry was calculated considering convection, conduction and radiation. Conduction in horizontal walls has a significant effect on the temperature of air close to these walls. Comparisons were made at all experimental positions of the cavity showing the influence of radiation and conduction. The one equation model accurately predicts the flow in the cavity; also the modification of certain constants of the model improves its accuracy. Adding radiation results in an improvement of temperature profiles especially near horizontal walls. The one equation of Spallart and Allmaras could easily replace the two-equation models widely used in predicting turbulent natural convection flows.
The hybrid-cooling system, combining a jet and microchannels was studied. The flow was calculated numerically by comparing the one equation model with the SST model to the experimental data. The SA model was performant in predicting the hybrid cooling system as well as the SST model. In the case of the two models, the velocities along the path flow increased allowing heat extraction and improving the temperature uniformity. An under estimation of the temperature in the region of active wall adjacent to the micro-channels was seen by the two models, indicating a necessity to increase slightly the micro-channels width to reproduce the experimental data. In this region, the one equation performed slightly more than the SST model. The one equation model demonstrated its capability in predicting this relatively complex flow.
By considering the two flows, i.e. natural convection and flow impingement/microchannel cooling scheme, clearly the one equation model performed as well as the SST model and could be used in predicting confined turbulent natural and forced convection and also jet impingement heat transfer replacing the two-equation model.
Acknowledgments
This project was funded by the deanship of Scientific Research (DSR) at king Abdulaziz University, Jeddah, under Grant no: G-568-305-1436. The authors, therefore, acknowledge with thanks DSR for technical and financial support.
References
[1] Spalart P.R., Allmaras S.R. A one-equation turbulence model for aerodynamic flows. La recherché Aerospatiale 1:5-21, 1994.
[2] Ampofo F., Karayiannis T.G. Experimental benchmark data for turbulent natural convection in an air filled square cavity. International Journal of Heat and Mass Transfer, 46:3551-3572, 2003.
[3] Omri M., Galanis N. Numerical analysis of turbulent buoyant flows in enclosures: Influence of grid and boundary conditions. International Journal of Thermal Sciences, 46:727-738, 2007.
[4] Riera S., Barrau J., Rosell J.I., Omri M., Fréchette L.G. Experimental demonstration of a tailored-width microchannel heat exchanger configuration for uniform wall temperature. Journal of Physics: Conference Series, 476:1-5, 2013.
[5] Barrau J., Chemisana D., Rosell J., Tadrist L., Ibañez M. An experimental study of a new hybrid jet impingement/micro-channel cooling scheme. Applied Thermal Engineering, 30:2058-2066, 2010.
[6] Barrau J., Omri M., Chemisana D., Rosell J., Ibañez M., Tadrist L. Numerical study of a hybrid jet impingement/micro-channel cooling scheme. Applied Thermal Engineering, 33-34:237-245, 2012.
[7] Peng S.-H., Davidson L. Large eddy simulation for turbulent buoyant flow in a confined cavity. Int. J. Heat Fluid Flow, 22:323-331, 2001.
[8] Omri M., Galanis N. Numerical analysis of turbulent natural convection in a cavity. 13th Int. Heat Transfer Conf., Sydney Australia, 2006.
[9] Tian Y.S., Karayiannis T.G. Low turbulence natural convection in an air filled square cavity. Int. J. Heat Mass Transfer, Parts I & II, 43:849-884, 2000.
[10] Menter F.R. Eddy viscosity transport equations and their relation to the model. Journal Fluids Engineering, 119(4):876-884, 1997.
[11] Bradshaw P., Ferriss D.H., Atwell N.P. Calculation of boundary-layer development using the turbulent energy equation. J. Fluid Mech., 28(3):593-616, 1967.
[12] Baldawin B.S., Barth T.J. A one equation turbulence model for high Reynolds number wall bounded flows. NASA Tech. Memorandum, 102847, 1990.
[13] Deck S., Hallard R. Simulations numériques des écoulements décollés dans les tuyères. 37 ème Colloque d’Aérodynamique Appliquée, Aérodynamique et Propulsion des véhicules à grande vitesse. Arcachon, France, 103-111, 2001.
[14] Gacherieu C., Weber C. Assessment of algebraic and one equation turbulence models for transonic turbulent flow around a full aircraft configuration. 16th AIAA Applied Aerodynamics Conference, AIAA 98-32457, 1998.
[15] Rogers S.E., Both K., Nash S.M., Baker M.D., Slotnick J.P., Whitlock M., Cao H.V. Advances in overset CFD processes applied to subsonic high lift aircraft. 18th AIAA Applied Aerodynamics Conference, AIAA 2000-4126, 2000.
[16] Deck S., Duveau Ph., D’Espiney P., Guillen Ph. Development and application of Spalart-Allmaras one equation turbulence model to three-dimensional supersonic complex configurations. Aerospace Science and Technology, 6(3):171-183, 2002.
[17] Lee D., Vafai K. Comparative analysis of jet impingement and microchannel cooling for high heat flux applications. International Journal of Heat and Mass Transfer, 42:1555-1568, 1999.
[18] runschwiler T., Rothuizen H., Fabbri M., Kloter U., Michel B., Bezama R.J., Natarajan G., Direct liquid jet-impingement cooling with micronsized nozzle array and distributed return architecture. 20th ITHERM Conference, San Diego, 2006.
[19] O’Donovan T.S., Murray D.B. Jet impingement heat transfer – Part I: Mean and root-mean-square heat transfer and velocity distributions. International Journal of Heat and Mass Transfer, 50:3291–3301, 2007.
[20] Katti V., Prabhu S.V. Experimental study and theoretical analysis of local heat transfer distribution between smooth flat surface and impinging air jet from a circular straight pipe nozzle. International Journal of Heat and Mass Transfer, 51:4480–4495, 2008.
[21] Lin, ZH, Chou, Y.J., Hung Y.H. Heat transfer behaviours of a confined slot jet impingement. International Journal of Heat and Mass Transfer, 40:1095-1107, 1997.
[22] Choo K.S., Youn Y.J., Kim S.J., et al. Heat transfer characteristics of a micro-scale impinging slot jet. International Journal of Heat and Mass Transfer, 52:3169-3175, 2009.
[23] Joubert P., Le Quere P., Beghein C., Collignan B., Couturier S., Glock-ner S., Groleau D., Lubin P, Musy M., Sergent A., Vincent S. A numerical exercise for turbulent natural convection and pollutant diffusion in a two-dimensional partially partitioned cavity. Int. J. Thermal Sci., 44(4):311–322, 2005.
Document information
Published on 13/05/20
Accepted on 07/05/20
Submitted on 01/10/19
Volume 36, Issue 2, 2020
DOI: 10.23967/j.rimni.2020.05.001
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?