A hybrid finite element method applied to miscible displacements in heterogeneous porous media

Resumo

Estudamos o escoamento de fluidos miscíveis incompressíveis em meios porosos homogêneos com razão de mobilidade adversa com o objetivo de entender a influência desses parâmetros em processos de recuperação de reservatórios de petróleo. O problema é modelado matematicamente por um sistema acoplado de equações diferenciais parciais não-lineares. Através de um esquema de diferenças finitas atrasadas no tempo, um algoritmo sequencialmente implícito, que desacopla o sistema em cada iteração, é definido. Em seguida, um método misto híbrido dual estabilizado é utilizado no cálculo das aproximações dos campos de pressão e velocidade, a partir das leis de conservação de massa e de Darcy. Finalmente, o método Streamline Upwind Petrov-Galerkin (SUPG) é empregado para aproximar a equação da concentração da mistura. O bom desempenho da abordagem proposta é verificado via simulações numéricas onde é analisada a influência da permeabilidade e da mobilidade na recuperação de reservatórios de petróleo.

Abstract

We study incompressible miscible displacements in heterogeneous porous media with adverse mobility ratios in order to understand the influence of these parameters on the oil reservoir recovery processes. This problem is mathematically modeled by a coupled system of nonlinear partial differential equations. Through a backward finite difference scheme in time, a sequentially implicit time-stepping algorithm that uncouples the system at each time-step is defined. A Stabilized Dual Hybrid Mixed (SDHM) method is employed for computing velocity field and pressure approximations, involving the conservation of mass and Darcys law. Finally, the SUPG (Streamline Upwind Petrov-Galerkin) is used to approximate the concentration equation. The good performance of the proposed approach is verified via numerical simulations where it is analyzed the influence of the properties of porous media on the oil reservoir recovery.

Palavras-chave

Meios porosos ; Equação do transporte ; Lei de Darcy ; Métodos híbridos de elementos finitos ; Processos de recuperação de reservatórios

Keywords

Porous Media ; Transport Equation ; Darcys law Hybrid finite element methods ; Oil reservoir recovery processes

1. Introdução

Dentre as mais importantes aplicações na modelagem de escoamentos miscíveis em meios porosos destacamos os processos de recuperação terciária, em particular, as injeções de traçador e contínua. Os fluidos injetados provocam reações que alteram o comportamento do fluido residente, afetando diretamente a produção do reservatório. Na injeção de traçador ambos os fluidos possuem a mesma viscosidade e o principal objetivo é a caracterização do reservatório. Esse tema não será abordado aqui, contudo, contribuições dos autores em problemas relacionados encontram-se em [1] ; [2] ; [3] ; [4]  ;  [5] . Por outro lado, deslocamentos miscíveis advindos da injeção contínua com razão de mobilidade adversa frequentemente resultam em oscilações espúrias, sensibilidade à orientação da malha e surgimento de dedos viscosos (viscous fingers ). Quando um desses fingers atinge o poço produtor o fluido injetado passa a priorizar os caminhos percorridos, conhecidos como caminhos preferenciais e a extração do óleo fica comprometida, já que a mistura agora move-se rapidamente para o poço produtor através desses caminhos preferencias , não se propagando de forma adequada no reservatório, deixando assim grandes volumes de óleo nos locais onde o deslocamento não ocorreu [6]  ;  [7] .

Outra questão importante no estudo da recuperação de reservatórios decorre das características geológicas complexas do reservatório. As falhas geológicas, comuns nas formações porosas, podem gerar grandes descontinuidades em propriedades físicas de interesse, tais como a porosidade e a permeabilidade. Dentre os trabalhos que tratam da modelagem de campos de permeabilidade gerados aleatoriamente, com o intuito de simular meios porosos altamente heterogêneos, podemos citar [8]  ;  [9] , onde as permeabilidades são geradas a partir de uma função espacial randômica normalmente distribuída [10]  ;  [11] . Nesse caso o valor do campo de permeabilidades varia, em cada elemento, em torno de um valor fixado a partir da permeabilidade média do meio.

O transporte de fluidos miscíveis em meios porosos tem sido, em geral, representado matematicamente por um sistema de equações diferenciais parciais não-linear e acoplado, consistindo de um subsistema elíptico, envolvendo velocidade e pressão (subsistema de Darcy), e de uma equação do tipo convecção-difusão predominantemente convectiva expressando a conservação do fluido injetado (equação do transporte da concentração) [6] . Por fornecer informações sobre quanto da produção é influenciada pela injeção de um fluido, ou seja, quanto de óleo passa a ser recuperado a concentração é a variável de maior interesse na resolução do problema. Porém, especial atenção tem sido dada ao cálculo do campo de velocidades, visto que esse é o responsável pelo transporte da mistura, presente explicitamente na equação da concentração.

Neste trabalho o subsistema elíptico de Darcy é aproximado numericamente pela aplicação de um método de elementos finitos híbrido estabilizado denominado de método misto híbrido dual estabilizado (MHDE), introduzido em [5]  ;  [12] . O método MHDE é caracterizado pela continuidade entre os elementos via um multiplicador de Lagrange, identificado como traço da pressão, definido sobre as arestas dos elementos, combinado com a adição de termos de estabilização de resíduos de mínimos quadrados [13] e, nas arestas dos elementos, para o multiplicador. Na resolução da equação de transporte é empregado um algoritmo sequencialmente implícito no tempo combinado com o método SUPG no espaço [4] . A eficiência dessa metodologia é atestada via simulações numéricas para o problema do transporte miscível no domínio de 5 poços para cenários altamente heterogêneos, onde é analisada a influência da permeabilidade e da razão de mobilidade na recuperação do reservatório. Um estudo completo do método MHDE, considerando sua robustez em relação a outros métodos da literatura, pode ser encontrato em [12] .

O trabalho está organizado como segue. Na Seção 2 introduzimos o modelo matemático que descreve o processo físico do escoamento de um fluido em um meio poroso rígido para fluidos miscíveis incompressíveis. A seguir, na Seção 3 são apresentadas as aproximações para o campo de velocidades e a concentração. Simulações numéricas são exibidas na Seção 4 e, na Seção 5 , apresentam-se as conclusões.

2. Modelo matemático para o deslocamento miscível

Seja ${\textstyle \Omega \subset {\mathbb {R} }^{d}}$ (d  = 2 ou 3) um domínio aberto limitado de contorno regular ∂Ω, e T  > 0 um número real fixo. Assim, o escoamento de um fluido newtoniano incompressível em um meio poroso rígido é representado por uma equação do tipo convecção-difusão predominantemente convectiva para a concentração da mistura dos fluidos, denotada por c (x , t ), descrita pela equação do transporte

$\phi {\frac {\partial c}{\partial t}}+{\boldsymbol {\mbox{u}}}\cdot \nabla c-$$div\quad (D\nabla c)+{\overset {\mbox{ˆ}}{f}}c=g\quad em\quad \Omega \times (0,T),$

( 1)

com as seguintes condições iniciais e de contorno

$c({\boldsymbol {\mbox{x}}},0)={\mbox{   }}c_{0}({\boldsymbol {\mbox{x}}})\quad em\quad \Omega ,$

( 2)

$D\nabla c\cdot {\boldsymbol {\mbox{n}}}=0\quad sobre\quad \quad \quad \partial \Omega \times (0,T).$

( 3)

A velocidade de Darcy u  = u (x , t ) é dada pela solução do subsistema elíptico:

$div\quad {\boldsymbol {\mbox{u}}}={\mbox{   }}f\quad em\quad \Omega \times (0,T),$

( 4)

${\boldsymbol {\mbox{u}}}=-K({\boldsymbol {\mbox{x}}},c)\nabla p\quad em\quad \Omega \times (0,T),$

( 5)

${\boldsymbol {\mbox{u}}}\cdot {\boldsymbol {\mbox{n}}}=0\quad sobre\quad \Gamma =$$\partial \Omega \times (0,T),$

( 6)

composto pelas equações de conservação de massa (4) e de Darcy (5) . Aqui, p representa a pressão hidrostática e ϕ  = ϕ (x ) é a porosidade efetiva da rocha. Além disso, ${\textstyle K=K({\boldsymbol {\mbox{x}}},c)}$ é o tensor de condutividade hidráulica, dado por ${\textstyle K({\boldsymbol {\mbox{x}}},c):={\frac {K({\boldsymbol {\mbox{x}}})}{\mu (c)}},{\mbox{   }}\forall {\boldsymbol {\mbox{x}}}\in \Omega }$ onde ${\textstyle K({\boldsymbol {\mbox{x}}})}$ é o tensor de permeabilidade absoluta e μ (c   ) a viscosidade da mistura dos fluidos. As funções ${\textstyle {\mbox{   }}{\overset {\mbox{ˆ}}{f}},f,}$ e g r epresentam os termos de fonte e sumidouro e n  = (n₁ , n₂ ) denota a normal exterior à fronteira ∂Ω. Além disso, o tensor de dispersão-difusão ${\textstyle D(\cdot )}$ é definido por ${\textstyle D=D({\boldsymbol {\mbox{u}}})={\alpha }_{mol}I+\left|{\boldsymbol {\mbox{u}}}\right|\left\{{\alpha }_{l}E({\boldsymbol {\mbox{u}}})+\right.}$$\left.{\alpha }_{t}E^{\perp }({\boldsymbol {\mbox{u}}})\right\}$ com ${\textstyle E({\boldsymbol {\mbox{u}}})={\frac {1}{\left|{\boldsymbol {\mbox{u}}}\right|^{2}}}{\boldsymbol {\mbox{u}}}\otimes {\boldsymbol {\mbox{u}}},\quad \quad \quad \quad E^{\perp }({\boldsymbol {\mbox{u}}})=}$$I-E({\boldsymbol {\mbox{u}}}),$ onde a norma |u | é tal que ${\textstyle \vert {\boldsymbol {\mbox{u}}}\vert ^{2}=u_{1}^{2}+u_{2}^{2}+\ldots +}$$u_{d}^{2}$ , ⊗ é o produto tensorial e α_mol , α_l e α_t são os coeficientes de difusão molecular e de dispersão longitudinal e transversal, respectivamente. Em geral, a dispersão longitudinal (α_l ) é maior do que a transversal (α_t ) [6]  ;  [14] , onde supomos 0 < α_mol  ≤ α_l ; α_l  ≥ α_t  > 0; e 0 ≤ ϕ  ≤ 1. Adotamos ainda lei empírica [15]  ;  [16] para a viscosidade da mistura ${\textstyle \mu (c)={\mu }_{res}{\left[1-c+M^{\frac {1}{4}}c\right]}^{-4},\quad c\in [0,1]}$ , onde M denota a razão de mobilidade que, para escoamentos miscíveis, é definida como sendo a taxa entre as viscosidades do fluido residente, μ_res , e a do injetado, μ_inj , (M  = μ_res /μ_inj ). Quando M  >>1 (razão de mobilidade adversa) o fluido injetado é altamente viscoso, o problema estudado torna-se fortemente não-linear e acoplado exigindo métodos numéricos robustos que busquem de forma precisa e com baixo custo computacional resolver os complexos fenômenos físicos envolvidos.

3. Problema aproximado

Para introduzir as aproximações numéricas seguimos a metodologia de primeiro discretizar no espaço e depois no tempo (método de Rothe); portanto, sejam Δt  > 0, tal que N  = T /Δt   e ${\textstyle t^{\nu }=\nu \Delta t,{\mbox{   }}\nu \in R}$ e I_h  = {0 = t⁰  < t¹  < … < t^N  = T } uma partição do intervalo I  = [0, T ] e fazemos Δt  = max _n Δtⁿ , com Δtⁿ  = tⁿ  − t^{n −1} . O termo que envolve a derivada temporal da concentração, ${\textstyle {\frac {\partial c}{\partial t}}({\boldsymbol {\mbox{x}}},t)}$ , é aproximado usando diferenças finitas atrasadas, ou seja, ${\textstyle {\frac {\partial c}{\partial t}}({\boldsymbol {\mbox{x}}},t^{n})=}$${\frac {\partial c^{n}}{\partial t}}\cong {\frac {c^{n+1}-c^{n}}{\Delta t}}.$ Assim, para o problema modelo (1) -(6) , temos o seguinte algoritmo sequencialmente implícito de avanço no tempo: para n  = 0, 1, …, N  − 1 achar c^{n +1} satisfazendo

$\phi {\frac {c^{n+1}-c^{n}}{\Delta t}}+{\boldsymbol {\mbox{u}}}^{n}\cdot \nabla c^{n+1}-$$div\quad (D({\boldsymbol {\mbox{u}}}^{n})\nabla c^{n+1})+$${\overset {\mbox{ˆ}}{f}}^{n}c^{n+1}=g^{n+1}\quad \quad em\quad \Omega ,$

( 7)

$c^{0}({\boldsymbol {\mbox{x}}})=c_{0}({\boldsymbol {\mbox{x}}})\quad em\quad \Omega ,$

( 8)

$D({\boldsymbol {\mbox{u}}}^{n})\nabla c^{n+1}\cdot {\boldsymbol {\mbox{n}}}=$$0\quad sobre\quad \partial \Omega ,$

( 9)

onde uⁿ é dado por

${\boldsymbol {\mbox{u}}}^{n}=-(K({\boldsymbol {\mbox{x}}})/\mu (c^{n}))\nabla p^{n}\quad {\mbox{   }}em{\mbox{   }}{\mbox{   }}\Omega ,$

( 10)

$div\quad {\boldsymbol {\mbox{u}}}^{n}=f^{n}\quad {\mbox{   }}em{\mbox{   }}\Omega ,$

( 11)

${\boldsymbol {\mbox{u}}}^{n}\cdot {\boldsymbol {\mbox{n}}}=$${\mbox{   }}0\quad {\mbox{   }}sobre{\mbox{   }}\partial \Omega .$

( 12)

Em (7) , (8) , (9) , (10) , (11)  ;  (12) tem-se um método sequencialmente implícito que combina as vantagens de métodos explícitos e completamente implícitos [14]  ;  [17] ao tornar o sistema original parcialmente desacoplado e adicionar estabilidade por meio de uma aproximação implícita da concentração.

Visando calcular de forma eficiente a aproximação dos campos de velocidade e pressão, solução do problema semidiscreto (10) , (11)  ;  (12) foi introduzido o método MHDE em [5] . A seguir, apresentamos o Problema MHDE_h para a discretização espaço temporal do subsistema elíptico (10) , (11)  ;  (12) . Essa formulação consiste de um conjunto de problemas locais, definido no nível de cada elemento ${\textstyle K}$ da discretização de elementos finitos, acoplado a um sistema global, calculado somente sobre os multiplicadores de Lagrange, os quais são identificados como o traço da pressão na interface dos elementos (uma escolha natural no contexto estudado). Termos de estabilização são adicionados para gerar uma formulação adjunta consistente e simétrica, permitindo uma maior flexibilidade na escolha das funções bases dos espaços de aproximação.

Problema MHDE_h : achar ${\textstyle {\boldsymbol {\mbox{u}}}_{h}^{n}\in U_{h}^{m},\quad p_{h}^{n}\in Q_{h}^{l}}$ e o multiplicador de lagrange ${\textstyle {\lambda }_{h}^{n}\in M_{h}^{s}}$ tal que ${\textstyle \forall {\boldsymbol {\mbox{v}}}_{h}\in U_{h}^{m},{\mbox{   }}q_{h}\in Q_{h}^{l}e\quad {\mu }_{h}\in M_{h}^{s}}$

$\sum _{K\in T_{h}}\quad {\left(K^{-1}{\boldsymbol {\mbox{u}}}_{h}^{n},{\boldsymbol {\mbox{v}}}_{h}\right)}_{K}-$${\left(p_{h}^{n},div\quad {\boldsymbol {\mbox{v}}}_{h}\right)}_{K}+$${\int }_{\partial K}{\lambda }_{h}^{n}({\boldsymbol {\mbox{v}}}_{h}\cdot {\boldsymbol {\mbox{n}}}_{K})ds$ $+{\delta }_{1}{\left({\parallel K^{-1}\parallel }_{\infty }(div\quad {\boldsymbol {\mbox{u}}}_{h}^{n}-f),div\quad {\boldsymbol {\mbox{v}}}_{h}\right)}_{K}+$${\delta }_{2}(\parallel K{\parallel }_{\infty }{\left(K^{-1}{\boldsymbol {\mbox{u}}}_{h}^{n}+\nabla p_{h}^{n}),K^{-1}{\boldsymbol {\mbox{v}}}_{h}\right)}_{K}$ $+{\delta }_{3}({\parallel K\parallel }_{\infty }{\left(\nabla \times K^{-1}{\boldsymbol {\mbox{u}}}_{h}^{n}),\nabla \times K^{-1}{\boldsymbol {\mbox{v}}}_{h}\right)}_{K}=$$0,$

( 13)

$\sum _{K\in T_{h}}-{\left(div\quad {\boldsymbol {\mbox{u}}}_{h}^{n},q_{h}\right)}_{K}+$${\mbox{   }}{\left(f,q_{h}\right)}_{K}+{\delta }_{2}{\left(\parallel K{\parallel }_{\infty }(K^{-1}{\boldsymbol {\mbox{u}}}_{h}^{n}+\nabla p_{h}^{n}),\nabla q_{h}\right)}_{K}$ $+{\int }_{\partial K}\parallel K{\parallel }_{\infty }\beta (p_{h}^{n}-$${\lambda }_{h}^{n})q_{h}ds=0,$

( 14)

$\sum _{K\in T_{h}}\left[{\int }_{\partial K}{\mbox{   }}{\mu }_{h}({\boldsymbol {\mbox{u}}}_{h}^{n}\cdot {\boldsymbol {\mbox{n}}}_{K})ds+\right.$$\left.{\int }_{\partial K}\parallel K{\parallel }_{\infty }\beta ({\lambda }_{h}^{n}-\right.$$\left.p_{h}^{n}){\mu }_{h}ds\right]=0,$

( 15)

onde ${\textstyle U_{h}^{m}=\lbrace {\boldsymbol {\mbox{v}}}\in U_{\delta }:{\mbox{   }}{\boldsymbol {\mbox{v}}}\vert _{K}\in R^{m}\times R^{m}{\mbox{   }}{\mbox{   }}\forall K\in T_{h}\rbrace }$ , ${\textstyle Q_{h}^{l}=\lbrace q\in Q_{\delta }:{\mbox{   }}q\vert _{K}\in R^{l}{\mbox{   }}{\mbox{   }}\forall K\in T_{h}\rbrace }$ e ${\textstyle M_{h}^{s}=\lbrace \mu \in M:{\mbox{   }}\mu \vert _{e}\in P^{s}{\mbox{   }}{\mbox{   }}\forall e\in E_{h}^{0}\rbrace }$ são os espaços lagrangianos descontínuos de dimensão finita, ${\textstyle R^{r}}$ é o conjunto dos polinômios de grau menor ou igual a r   quando ${\textstyle K}$ é um triângulo, ou menor ou igual a r   em cada coordenada quando ${\textstyle K}$ é um quadrilátero (r  = l ou m   ), e ${\textstyle P^{s}}$ é o conjunto dos polinômios de grau menor ou igual a s sobre cada aresta e   . Aqui, ${\textstyle U_{\delta }=\prod _{K}(H^{1}(K)\times H^{1}(K))}$ , ${\textstyle Q_{\delta }=\prod _{K}H^{1}(K)}$ e ${\textstyle M_{\delta }=\lbrace \mu \in L^{2}(e),{\mbox{   }}\forall e\in E_{h}^{0}\rbrace }$ , onde ${\textstyle E_{h}^{0}}$ é o conjunto das arestas interiores, resultante da discretização do domínio.

O Problema MHDE_h é resolvido através de uma estratégia conhecida como técnica de condensação estática, que consiste em separar a resolução do problema em 2 etapas. Na primeira etapa, um sistema global para obtenção dos multiplicadores de Lagrange é montado e resolvido. Na segunda etapa, com o valor do multiplicador já conhecido nas interfaces, é possível calcular as variáveis de interesse (no nosso caso, velocidade e pressão), em cada subdomínio. Uma das vantagens dessa metodologia é a redução na dimensão do sistema global, envolvendo agora apenas os graus de liberdade associados com os multiplicadores, levando à diminuição do custo computacional [18] . Assim, o tempo necessário para resolver todos os problemas locais é desprezível em relação àquele empregado na resolução do sistema global. Seguindo as análises apresentadas em [12]  ;  [13] fazemos as seguintes escolhas para parâmetros de estabilização δ₁  = δ₃  = 0, 5, δ₂  = −0, 5 e β₀  = 0, sendo que para essa última, considerando-se ainda aproximações lagrangianas de igual ordem para todos os campos (r  = l  = m  = s ), demonstra-se a conservação local do método. Além disso, ressaltamos que o método MHDE é consistente e fornece taxas ótimas de convergência para as aproximações de todos os campos, i.e, pressão, velocidade e o multiplicador [12]  ;  [18] .

4. Resultados numéricos

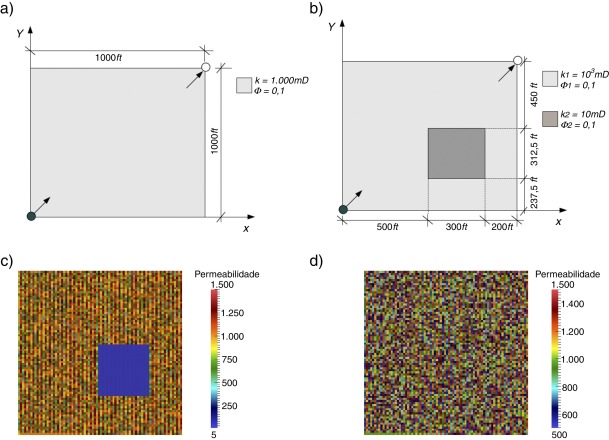
Analisamos aqui resultados das simulações numéricas referentes ao problema de injeção contínua em um meio poroso isotrópico (reservatório) com tensor de permeabilidade ${\textstyle K({\boldsymbol {\mbox{x}}})=kI}$ , onde ${\textstyle I}$ é o tensor identidade, representado pela configuração (arranjo) de 5 poços. Por razões de simetria o domínio é definido como um quadrado de lado L  = 1.000 ft , correspondendo a um quarto do arranjo, com um poço injetor e um poço produtor alinhados na diagonal principal [6] , como ilustrado na figura 1 (a), denotado por Cenário homogêneo , com permeabilidade constante k  = 10³mD e porosidade ϕ₁  = 0, 1. Além disso, consideramos um Cenário heterogêneo com 2 regiões de permeabilidades distintas, k₁  = 10³mD (cor clara) e k₂  = 10 mD (cor escura), ver figura 1 (b). A partir desses 2 cenários geramos os cenários 1 e 2 onde o campo de permeabilidades varia de elemento para elemento, de forma aleatória, de acordo com a seguinte equação:

Figura 1. Ilustrações dos meios porosos estudados: (a) cenário homogêneo, (b) cenário heterogêneo, (c) cenário 1 e (d) cenário 2.

$k_{e}=k(1+{\left(-1\right)}^{e}\ast rand(\cdot )\ast fator),\quad e=$$1,\ldots ,Nel$

( 16)

com rand (·) a função que retorna um valor aleatório entre 0 e 1, fator  ∈ [0, 1] e Nel o número de elementos. Para efeito de ilustração, são exibidos nas figuras 1 (c) e 1 (d), respectivamente, os cenários correspondentes a um fator de flutuação (fator ) igual a 0,5. Além desses, são também considerados nas simulações fator = 0,01; 0,1 e 0,2.

Nas definições dos espaços de aproximações do MHDE são empregadas funções de interpolação lagrangianas descontínuas de ordem igual a um, isto é, elementos quadrilaterais bilineares para a velocidade, pressão e concentração, e lineares para o multiplicador. Para o método SUPG tem-se ${\textstyle {\delta }_{K}\approx 0,92}$ (correspondente a um número de Péclet igual a 12, 5). Além disso, admite-se uma injeção contínua durante um total de 2.000 dias com Δt  = 2,5 dias, a uma taxa de 200 ft² /dia, com α_mol  = α_t  = 0,0 ft e α_l  = 1,0 ft .

Nas subseções seguintes são apresentadas simulações numéricas com o objetivo de entender a influência de 2 importantes parâmetros, a razão de mobilidade e a heterogeneidade do meio, para o transporte da concentração da mistura na recuperação de reservatórios considerando-se os cenários definidos anteriormente. Todas as simulações estão em t  = 1.500 dias após o início do processo, isto é, minutos após o breakthrough . Os resultados são mostrados na forma de mapas de concentração e curvas de isoconcentração da mistura para os valores 0,2 ; 0,4 ; 0,6 ; 0,8 e 1,0, com uma malha fixa de 80x80 elementos quadrilaterais bilineares.

4.1. Influência da razão de mobilidade

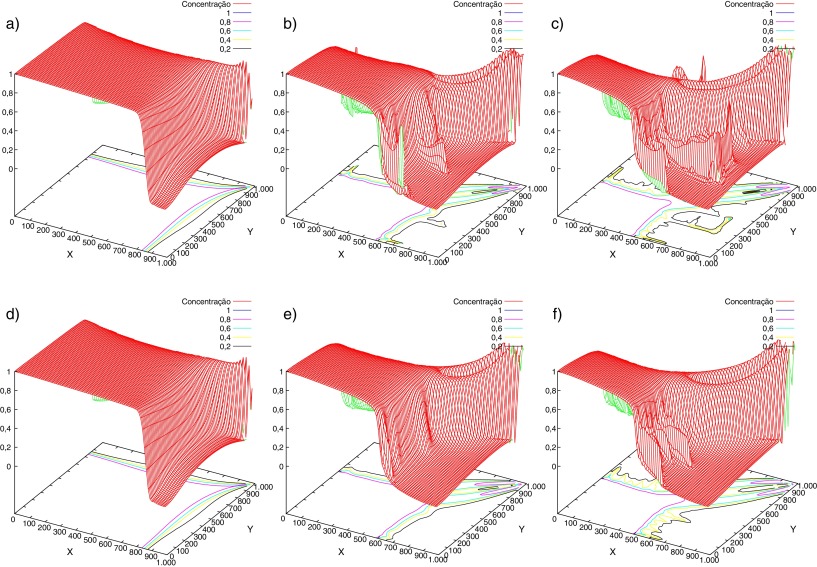
Na figura 2 são plotados os mapas de concentração para o cenário homogêneo, onde o campo de permeabilidade é uniforme e varia-se a razão de mobilidade, tornando, matematicamente, o problema altamente não linear e acoplado. Com o objetivo de ilustrar a robustez da metodologia proposta, na linha superior tem-se os campos de velocidade calculados via a aplicação do método de Galerkin usual, enquanto na linha inferior emprega-se o MHDE. Nota-se que para o caso mais singular, M  = 1.000, o MHDE produz uma solução mais estável do que aquela exibida pelo método de Galerkin (ver figuras 2 [c] e 2 [f]). Com o aumento do valor da mobilidade é esperado fisicamente o aparecimento dos fingers viscosos (como pode ser verificado nos resultados da figura 2 ), levando a novas trajetórias (caminhos) para o transporte da mistura entre os poços injetor e produtor e, consequentemente, a uma perda no processo de recuperação do reservatório. Desse modo, na figura 3 são apresentadas as curvas de recuperação para os cenários homogêneo e heterogêneo para M  = 1, 10, 20, 41 e M  = 300. Nota-se que para os mesmos valores da razão de mobilidade, a heterogeneidade do meio (região de menor permeabilidade, k₂  = 10mD ) leva a um pico de produção menor, ver figura 3 (b).

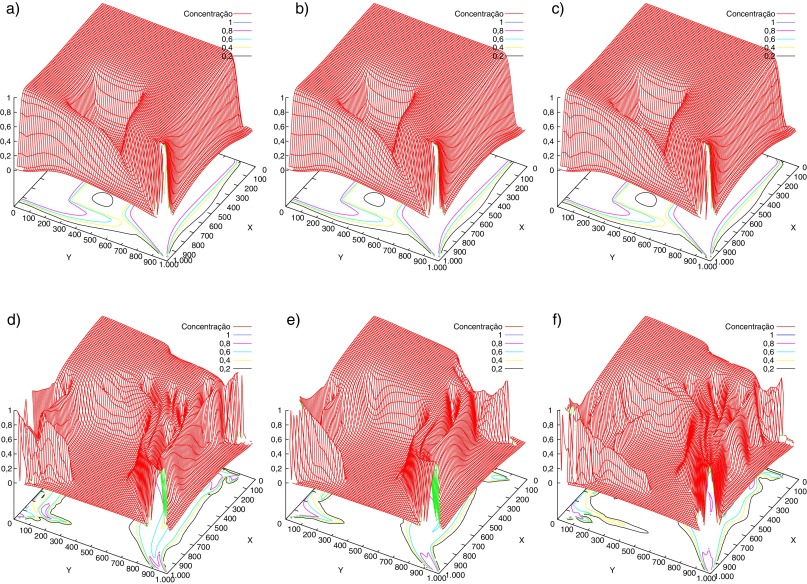
Figura 2. Mapas de concentração. Cenário homogêneo: método de Galerkin (linha superior) e MHDE (linha inferior) para M  = 1, 41 e 1.000, da esquerda para direita.

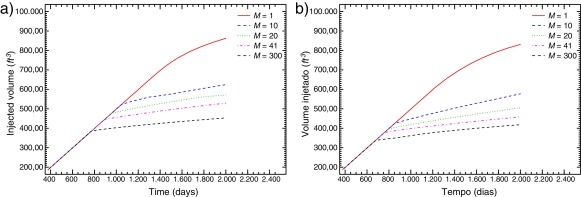
Figura 3. Curvas de produção variando a razão de mobilidade (M ). (a) Cenário homogêneo e (b) cenário heterogêneo.

4.2. Influência da permeabilidade

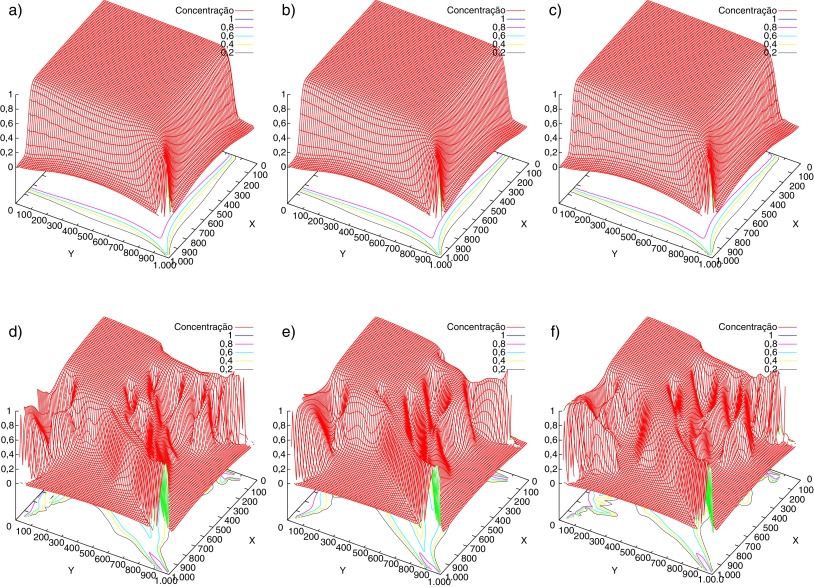
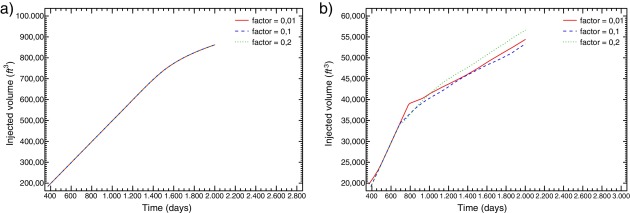
Finalmente, visando ilustrar o efeito da permeabilidade do meio na recuperação do reservatório são exibidos nas figuras 4 e 5 mapas da concentração para os cenários 1 e 2, tomando M  = 1 e M  = 41. Para M  = 1 (linhas superiores nos 2 cenários) a variação na permeabilidade leva a uma alteração imperceptível no transporte entre os 2 poços, como pode ser observado nas curvas de produção plotadas na figura 6 (a), referentes ao cenário 1. Porém, quando se considera uma razão de mobilidade adversa (M  = 41) a recuperação fica bastante afetada, como pode ser observado nos resultados exibidos (linhas inferiores nos 2 cenários) e, ainda mais evidente, através das curvas mostradas na figura 6 (b), onde, comparando-se com M  = 1, é possível observar a queda na recuperação do volume injetado.

Figura 4. Mapas de concentração. Cenário 1 com M  = 1 (linha superior) e M  = 41 (linha inferior), variando a permeabilidade do meio com fator = 0,01;0,1 e 0,2, da esquerda para a direita.

Figura 5. Mapas de concentração. Cenário 2 com M  = 1 (linha superior) e M  = 41 (linha inferior), variando a permeabilidade do meio com fator = 0,01;0,1 e 0,2, da esquerda para a direita.

Figura 6. Curvas de produção variando a permeabilidade do meio (fator ). Cenário 1 com (a) M  = 1 e (b) M  = 41.

5. Conclusões

Neste trabalho analisamos o deslocamento miscível incompressível considerando campos de permeabilidade gerados aleatoriamente e razões de mobilidade adversas no estudo de reservatórios de petróleo em meios porosos heterogêneos. Na aproximação numérica do problema modelo combinamos o método MHDE, o qual é caracterizado pela continuidade entre os elementos via um multiplicador de Lagrange, identificado como traço da pressão, definido sobre as arestas dos elementos, com um algoritmo sequencialmente implícito no tempo onde o método SUPG é utilizado na discretização espacial da equação do transporte.

Nas simulações numéricas apresentadas foi observada a eficiência do método proposto na captura dos efeitos das heterogeneidades do meio poroso na recuperação do reservatório (injeção contínua). De fato, constatou-se que o aumento das heterogeneidades leva ao aparecimento dos fingers viscosos e, consequentemente, à diminuição na produção da mistura. Ao captar o comportamento físico esperado, conclui-se que o método proposto é uma boa opção para a simulação computacional de problemas na área do transporte de escoamentos em meios com fortes singularidades.

Dentre os desenvolvimentos futuros dessa proposta pretende-se empregar malhas não estruturadas a fim de analisar uma possí vel influência da discretização espacial nos resultados obtidos.

Agradecimentos

Os autores agradecem à FACC, CAPES, CNPq e FAPERJ o apoio recebido para o desenvolvimento deste trabalho.

References

1. [1] J.N.C. Guerreiro, H.J.C. Barbosa, E.L.M. Garcia, A.F.D. Loula, S.M.C. Malta; Identification of reservoir heterogeneities using tracer breakthrough profiles; Anais do IV Latin American and Caribean Petroleum Engineer Conference, SPE 39066, Rio de Janeiro, RJ, Brazil (1997)
2. [2] M. R. Borges, Injeção de traçadores em reservatórios de petróleo: modelagem multi-escala e simulação numérica [acessado 25 Jun 2015], Ph.D. thesis, IPRJ, Universidade Estadual do Rio de Janeiro, Nova Friburgo, Brasil, http://www.bdtd.uerj.br/tde_busca/arquivo.php?codArquivo=626 (2006).
3. [3] M. C. Damiani, Determinação de padrões de fluxo em simulações de reservatórios de petróleo utilizando traçadores [acessado 25 Jun 2015], Masters thesis, COPPE, Universidade Federal do Rio de Janeiro, Rio de Janeiro, Brasil, http://www.cos.ufrj.br/index.php/component/docman/cat-view/1-mestrado/85-2007?start=45 (2007).
4. [4] S.M.C. Malta, A.F.D. Loula, E.L.M. Garcia; Numerical analysis of a stabilized finite element method for tracer injection simulations; Comput. Methods Appl. Mech. Engrg., 187 (2000), pp. 119–136
5. [5] Y.R. Núñez, C.O. Faria, A.F.D. Loula, S.M.C. Malta; A mixed-hybrid finite element method applied to tracer injection processes; International Journal of Modeling and Simulation for the Petroleum Industry, 6 (1) (2012), pp. 51–59
6. [6] D. Peaceman; Fundamental of Numerical Reservoir Simulation; Elsevier, Amsterdam (1977)
7. [7] J. Thomas; Fundamentos de Reservatórios de Petróleo; Interciência, Rio de Janeiro, RJ (2001)
8. [8] M.R. Borges, F. Furtado, F. Pereira, H.P.A. Souto; Scaling analysis for the tracer flow problem in self-similar permeability fields; Multiscale Modeling & Simulation, 7 (2008), pp. 1130–1147
9. [9] M.R. Borges, M.R. Correa; A semi-discrete central scheme for scalar hyperbolic conservation laws with heterogeneous storage coefficient and its application to porous media flow; International Journal for Numerical Methods in Fluids, 73 (3) (2013), pp. 205–224
10. [10] G. Dagan; Flow and Transport in Porous Formations; Springer-Verlag, New York (1989)
11. [11] L. Gelhar; Stochastic Subsurface Hydrology; Prentice-Hall, Englewood Cliffs (1993)
12. [12] Y. R. Núñez, Métodos de elementos finitos híbridos aplicados a escoamentos miscíveis em meios porosos heterogêneos [acessado 25 Jun 2015], Ph.D. thesis, Laboratório Nacional de Computação Científica, Petrópolis, Brasil, http://tede.lncc.br/handle/tede/203 (2014).
13. [13] M.R. Correa, A.F.D. Loula; Unconditionally stable mixed finite element methods for darcy flow; Computer Methods in Applied Mechanics and Engineering, 197 (2008), pp. 1525–1540
14. [14] R.E. Ewing, T.F. Russel; Efficient time-stepping methods for miscible displacement problems in porous media; SIAM J. Numer. Anal., 19 (1982), pp. 1–45
15. [15] A. Settari, H.S. Price, T. Dupont; Development and application of variational methods for simulation of miscible displacement in porous media; Soc. Pet. Eng. J. Trans. AIME, 263 (1977), pp. 228–246
16. [16] L.C. Young; A finite element method for reservoir simulation; Society of Petroleum Engineers Journal, 21 (1) (1981), pp. 115–128
17. [17] T.F. Russel, M.F. Wheeler, C. Chiang; Large-scale simulation of miscible displacement by mixed and characteristic finite element methods; Proceeding of SEG/SIAM/SPE Conference (1985), pp. 85–107
18. [18] I. H. A. da Igreja, Métodos de elementos finitos híbridos estabilizados para escoamentos de Stokes, Darcy e Stokes-Darcy acoplados [acessado 25 Jun 2015], Ph.D. thesis, Laboratório Nacional de Computação Científica, Petrópolis, Brasil, http://tede.lncc.br/handle/tede/225 (2015).