Numerical simulation for predicting concentration profiles of cohesive sediments in surf zone

Abstract

A hybrid numerical model is introduced for simulation of cohesive sediments concentration profiles in a surf zone. For this purpose, wave height reduction must be considered, due to muddy beds and wave breaking. Models, such as Sanford and Maa’s erosion model, Krone’s sedimentation model, Tajima’s wave breaking model and the visco-elastic–plastic rheological model, are used to investigate the interaction of wave and bed and to predict the concentration profile. A splitting algorithm has been used to split the three-dimensional advection–diffusion equation into a horizontal, two-dimensional equation, and a vertical, one-dimensional equation, due to different length scales. The one-dimensional equation is discretized over a non uniform grid, and, then solved implicitly using the QUICKEST scheme (third order in time and space). The two-dimensional equation is divided into two parts (advection and diffusion) and each part is separately solved at different time steps. A suitable mesh, regarding space and time intervals, is chosen for considering the stability of the present model. The computational domain extends from the shoreline to the deepwater zone. Finally, the results are analyzed and compared with experimental and field data and other models. Good agreement has been obtained with the data and other numerical models.

Keywords

Hybrid model ; Concentration ; Cohesive sediment ; Split method ; Surf zone

1. Introduction

Numerical simulation models have great potential for use in estimating the dredging effects in ports, and the maintenance of harbors and navigation channels in estuaries, etc. Cohesive sediment can also serve as a source or sink for pollutants introduced into the water column. Numerical modeling of concentration profiles for cohesive sediment in coastal zones should be carried out by considering the specific characteristics of the cohesive sediment, the interaction between wave and muddy bed, erosion and sedimentation. Muddy bed reaction on waves compared to sandy beds is quite different because, after occurrence of fluid mud in the bed, the energy depreciates and wave height is reduced. It was commonly proved that the friction coefficient of wave-induced bed shear stress for muddy bottoms is greater than for sandy bottoms  [1] .

In other words, soft mud interacts with waves, resulting in attenuation of wave height due to bottom friction, percolation losses and viscous damping within the sediment. These interactive modes are also manifested as changes in wave length, water particle motion, and the elevation of the interface between the fluid and bottom sediment  [1] . Wave breaking in near shore zones is the dominant phenomenon to cause long shore and on–off shore currents, which play a significant role in sediment transportation. Thus, prediction of the height and location of waves breaking on the shore is a very important issue.

The main objective of this paper is to predict the concentration profiles of cohesive sediment in a surf zone, considering Sanford and Maa’s erosion model  [2] , Krone’s sedimentation model  [3] , Tajima’s wave breaking model  [4] and the visco-elastic–plastic rheological model  [5] , [6]  and [7] for muddy beds. A splitting algorithm has been used to split the three-dimensional transport equation into a horizontal, two-dimensional equation and a vertical, one-dimensional equation, due to different length scales. The horizontal, two-dimensional equation is divided into two parts, including advection and diffusion, and each part is solved separately at different time steps  [8] .

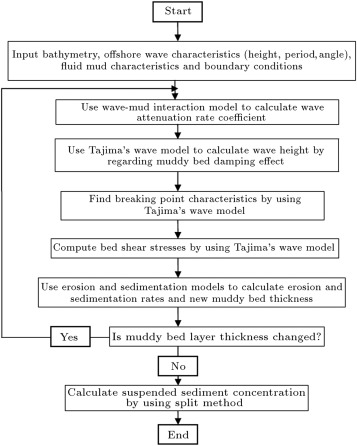
The flowchart of the present model is shown in Figure 1 . By defining input parameters, the wave–mud interaction model is used to calculate the wave attenuation rate coefficient. Wave height is calculated using Tajima’s wave model, and the breaking point is determined. Then, shear stresses are computed using Tajima’s wave model. These shear stresses are compared with critical erosion and sedimentation shear stress. Consequently, the amount of erosion and sedimentation are computed. The erosion and sedimentation rates are used in the advection–diffusion equation as sink and source terms. Suspended sediment concentration is calculated by solving the advection–diffusion equation using the standard split method. Finally, the results of modeling are analyzed and compared with experimental and field data and other models.

Figure 1. Flowchart of the present model.

2. Basic theory and equations

2.1. Rheological equations of mud and wave–mud interaction model

Rheology, defined as the science of fluid mud deformation, is an important field in the investigation of fluid mud behavior response to wave actions. The rheological property of the mud has been known to be rather complicated, which depends on many factors, such as mud density, mineral constituents, grain composition of mud, and type and concentration of ions in the water, etc. The visco-elastic–plastic model is a combination of linear visco-elastic and non linear plastic models, and is used for mud behavior modeling. In this model, fluid mud is assumed to be visco-elastic when stress is less than yield stress. The latter is considered to be visco-plastic when applied stress is greater than yield stress. The constitutive equation is expressed as [5]  and [6] :

$\sigma _{ij}=2\mu _{e}{\overset {\cdot }{e}}_{ij}$

( 1)

where ${\textstyle i}$ and ${\textstyle j}$ take the values 1 and 2, which correspond to ${\textstyle x}$ and ${\textstyle z}$ axis, respectively, ${\textstyle \omega }$ is the angular frequency of the wave, ${\textstyle \mu _{e}}$ is the apparent viscosity, ${\textstyle \sigma _{ij}}$ is the deviator part of the stress tensor, ${\textstyle {\overset {\cdot }{e}}_{ij}}$ is the deviator part of the strain rate tensor, ${\textstyle G}$ is the elastic modulus, ${\textstyle \mu _{1}}$ is the viscosity of mud in the viscoelastic state, ${\textstyle \mu _{2}}$ is the viscosity of mud in the viscoplastic state and ${\textstyle \tau _{y}}$ is the yield stress. ${\textstyle \vert \Pi _{e}\vert }$ is the objective of the deformation-rate tensor and is expressed as  [5] , [6]  and [7] :

$\vert \Pi _{e}\vert ={\frac {1}{2}}({\frac {\partial u}{\partial x}})^{2}+{\frac {1}{2}}({\frac {\partial w}{\partial z}})^{2}+{\frac {1}{4}}({\frac {\partial u}{\partial z}}+{\frac {\partial w}{\partial x}})^{2}{\mbox{,}}$

( 3)

where ${\textstyle x}$ and ${\textstyle z}$ are the horizontal and vertical coordinates, ${\textstyle u}$ and ${\textstyle w}$ are velocity components in ${\textstyle x}$ and ${\textstyle z}$ directions, respectively. The rheological parameters are evaluated from laboratory experiments  [5]  and [6] . The fluid system is divided into ${\textstyle N}$ layers, in which the water layer is represented by ${\textstyle N=1}$   [9] . For a small disturbance to this system, by neglecting convective accelerations, the momentum and continuity equations can be derived from the equation of motion for a Newtonian, laminar and incompressible fluid under wave action, as  [6]  and [10] :

${\frac {\partial u_{j}}{\partial t}}=-{\frac {1}{\rho _{j}}}{\frac {\partial p_{j}}{\partial x}}+\nu _{e,j}({\frac {\partial ^{2}u_{j}}{\partial x^{2}}}+{\frac {\partial ^{2}u_{j}}{\partial z^{2}}}){\mbox{,}}$

( 4)

where the subscripts, ${\textstyle j}$ , indicate the layers, and parameters ${\textstyle t}$ , ${\textstyle \rho }$ , ${\textstyle \nu _{e}}$ and ${\textstyle p}$ represent the time, density, kinematic viscosity of mud and dynamic pressure, respectively. The separated periodic solutions for ${\textstyle {\overset {\mbox{ˆ}}{u}}_{j}}$ , ${\textstyle {\overset {\mbox{ˆ}}{w}}_{j}}$ and ${\textstyle {\overset {\mbox{ˆ}}{p}}_{j}}$ are assumed as  [6]  and [10] :

${\overset {\mbox{ˆ}}{u}}_{j}(x,z;t)=u_{j}(z)exp[i(kx-\omega t)]{\mbox{,}}$

( 7)

where ${\textstyle \omega }$ is angular frequency and ${\textstyle k}$ is the unknown complex wave number, which can be expressed as:

$k=k_{r}+ik_{i}{\mbox{.}}$

( 10)

Displacements of water surface and interfaces, ${\textstyle \eta _{j}}$ , are represented as below:

$\eta _{j}=a_{j}exp[i(kx-\omega t)]{\mbox{,}}$

( 11)

where ${\textstyle a_{j}}$ is the amplitude of displacement of the ${\textstyle j}$ th layer and the water surface is expressed as ${\textstyle \eta _{1}}$ . Therefore, the real part of the wave number, ${\textstyle k_{r}}$ , gives the wave length ${\textstyle L=2\pi /k_{r}}$ and its imaginary part, ${\textstyle k_{i}}$ , is the wave attenuation rate, assuming the exponential wave height decay (Section  2.3 ). Finally, the fourth order differential equation for ${\textstyle w_{j}}$ is solved, with respect to the prevailing boundary conditions, and the solutions are obtained. The unknown constants and variables are determined from the boundary conditions at the water surface, the interfaces and the rigid bottom  [6]  and [10] . Finally, wave attenuation rate coefficient, ${\textstyle k_{i}}$ , is calculated by a wave–mud interaction model.

2.2. Tajima’s wave model

Tajima (2004)  [4] defined the equivalent linear wave with an energy flux equal to that of the actual nonlinear wave. The model uses linear wave theory to propagate waves until the waves reach breakpoint. After breaking, a broken wave dissipation term is introduced in the energy flux balance equation. The breaking criterion for a linear wave is defined as  [4] :

${\begin{array}{l}\displaystyle {\frac {k_{b}H_{b}}{tanh(k_{b}h_{b})}}=1.07-0.59exp(-8.6{\frac {h_{b}}{L_{0}}})+2.59tan\beta _{0}exp(-\\\displaystyle -15.1({\frac {h_{b}}{L_{0}}})^{1.5}){\mbox{,}}\end{array}}$

( 12)

where ${\textstyle \beta _{0}}$ is bed slope, ${\textstyle k_{b}=2\pi /L_{b}}$ is the wave number at breaking point, ${\textstyle H_{b}}$ is the wave height at breaking point, ${\textstyle L_{0}}$ is deepwater wave length and ${\textstyle h_{b}}$ is the wave depth at breaking point. Tajima’s formulation for broken wave energy dissipation is:

${\frac {\partial (EC_{g})}{\partial x}}=-K_{b}{\frac {C_{g}}{h}}(E-E_{r}){\mbox{,}}$

( 13)

where ${\textstyle C_{g}}$ is the group velocity, ${\textstyle x}$ is the horizontal direction, ${\textstyle h}$ is the water depth, ${\textstyle E_{r}=\rho gH_{r}^{2}/8}$ is the wave energy, based on the recovery wave height, and ${\textstyle K_{b}}$ is a dissipation factor. According to Tajima, ${\textstyle K_{b}}$ is dependent on the bed slope as:

$K_{b}={\frac {5}{2}}{\frac {\gamma _{s}^{2}tan\beta }{\gamma _{s}^{2}-\gamma _{r}^{2}}}{\mbox{,}}$

( 14)

where ${\textstyle \gamma _{s}=H/h}$ , and ${\textstyle tan\beta =\partial h/\partial x=\partial (h_{0}+{\bar {\eta }})/\partial x}$ is the slope of the mean water depth. Considering Tajima’s experimental data, which are detailed in Tajima (2004)  [4] , the values of ${\textstyle \gamma _{r}=0.3}$ and ${\textstyle \gamma _{s}=0.3+4tan\beta }$ are obtained. Surface roller energy, ${\textstyle E_{sr}}$ is calculated by:

$E_{sr}={\frac {\rho S_{sr}C^{2}/2}{L}}{\mbox{.}}$

( 15)

Also, energy dissipation rate is calculated by:

$\epsilon _{D}=K_{b}E_{sr}{\sqrt {\frac {g}{h}}}{\mbox{,}}$

( 16)

where ${\textstyle S_{sr}}$ is roller cross-sectional area, ${\textstyle C}$ is wave phase velocity and ${\textstyle L}$ is the wavelength. The volume flux due to the surface roller, which causes an increase in the return current, is:

${\overset {\rightarrow }{q}}_{sr}={\frac {S_{sr}}{T}}{\overset {\rightarrow }{n}}={\frac {2E_{sr}}{\rho C}}{\overset {\rightarrow }{n}}{\mbox{.}}$

( 17)

Tajima assumed the following equation to calculate the energy balance for the surface roller:

$\alpha \nabla (EC_{g}{\overset {\rightarrow }{n}})+\nabla (E_{sr}C{\overset {\rightarrow }{n}})=-{\frac {K_{sr}}{h}}E_{sr}C{\mbox{,}}$

( 18)

where ${\textstyle \alpha }$ is the fraction of the energy of broken wave energy that goes into the surface roller (Tajima assumes ${\textstyle \alpha =0.5}$ ), and ${\textstyle K_{sr}}$ is proportionality constant. Tajima takes ${\textstyle K_{sr}=K_{b}}$ , and the complete energy balance equation for the roller is expressed as  [4] :

$\nabla (E_{sr}C{\overset {\rightarrow }{n}})={\frac {K_{b}}{h}}(C_{g}{\frac {E-E_{r}}{2}}-CE_{sr}){\mbox{.}}$

( 19)

The near shore mean current velocity below the trough level is given by:

$\rho \nu _{t}{\frac {\partial {\overset {\rightarrow }{U}}}{\partial z}}={\overset {\rightarrow }{\tau }}_{c}\approx {\overset {\rightarrow }{\tau }}_{cb}+{\frac {{\overset {\rightarrow }{\tau }}_{cs}-{\overset {\rightarrow }{\tau }}_{cb}}{h_{tr}}}z{\mbox{.}}$

( 20)

In the above equation, the current shear stress is assumed to vary linearly in depth. Here, ${\textstyle \nu _{t}}$ is the turbulent eddy viscosity, ${\textstyle {\overset {\rightarrow }{\tau }}_{c}}$ is the mean current shear stress vector, ${\textstyle {\overset {\rightarrow }{\tau }}_{cb}}$ and ${\textstyle {\overset {\rightarrow }{\tau }}_{cs}}$ are the bottom and trough shear stress vectors, ${\textstyle h_{tr}=h_{0}+{\bar {\eta }}-H/2}$ is the trough water depth, and ${\textstyle z}$ is the elevation above the bottom. The surface roller acts as a source of wave energy dissipated by wave breaking. Only part of this energy is immediately transferred to turbulent energy, while the rest is temporarily stored in the surface roller. The surface roller introduces a new forcing term that accounts for the observed increase in return flow velocity. Close to the bottom, shear stress is considered constant, and the turbulent eddy viscosity is assumed to vary linearly with depth. Shear stress increases because of the effect of broken waves at the points away from the bottom. In this region, the rate of increase in turbulent eddy viscosity must be faster than the previous region. The turbulent eddy viscosity is defined as:

$\nu _{t}=\lbrace {\begin{array}{c}ku_{{_{\ast }}c}z\rightarrow {\mbox{  if  }}\rightarrow \delta \leq z\leq z_{m}\\ku_{{_{\ast }}s}z{\sqrt {\frac {z}{h_{tr}}}}\rightarrow {\mbox{  if  }}\rightarrow z_{m}<z\leq h_{tr}\end{array}}$

( 21)

where ${\textstyle \kappa =0.4}$ is Von Karman’s constant, ${\textstyle u_{{_{\ast }}c}}$ is the shear stress velocity at the bottom, ${\textstyle u_{{_{\ast }}s}}$ is the shear stress velocity at the surface, ${\textstyle z_{m}}$ is the depth where the two eddy viscosity profiles match in Eq. (21) , and ${\textstyle \delta }$ is the wave bottom boundary layer thickness, determined from Madsen’s model  [11] .

The mean current velocity at the outer edge of the boundary layer ${\textstyle z=\delta }$ is:

${\overset {\rightarrow }{U}}_{\delta }={\frac {{\overset {\rightarrow }{\tau }}_{cb}}{\kappa \rho u_{{_{\ast }}m}}}ln({\frac {\delta }{z_{0}}}){\mbox{,}}$

( 23)

where ${\textstyle z_{0}=k_{N}/30}$ , ${\textstyle k_{N}}$ is the equivalent Nikuradse roughness of the bottom. The maximum combined wave-current bottom shear velocity ${\textstyle u_{{_{\ast }}m}}$ is defined by  [4] :

$u_{{_{\ast }}m}^{2}={\frac {C_{\mu }\tau _{wm}}{\rho }}{\mbox{.}}$

( 24)

With:

$C_{\mu }={\sqrt {1+2\vert cos\phi _{cw}\vert {\frac {\vert {\overset {\rightarrow }{\tau }}_{cb}\vert }{\tau _{wm}}}+({\frac {\vert {\overset {\rightarrow }{\tau }}_{cb}\vert }{\tau _{wm}}})^{2}}}{\mbox{,}}$

( 25)

where ${\textstyle \phi _{cw}}$ is the angle between waves and currents. The boundary layer thickness, ${\textstyle \delta }$ , is given by:

$\delta =A{\frac {ku_{{_{\ast }}m}}{\omega }}{\mbox{,}}$

( 27)

where:

$A=exp[2.96({\frac {C_{\mu }A_{bm}}{k_{N}}})^{-0.071}-1.45]{\mbox{,}}$

( 28)

and ${\textstyle A_{bm}=u_{bm}/\omega }$ is the amplitude of the near-bottom wave orbital velocity, ${\textstyle u_{bm}}$ , whose value is provided by Tajima’s model. According to Madsen (1994)  [11] , wave friction factor, ${\textstyle f_{cw}}$ , can be approximate as a function of the dimensionless parameter, ${\textstyle X=C_{\mu }A_{bm}/k_{N}}$ as  [11] :

$f_{cw}=max\lbrace {\begin{array}{c}C_{\mu }exp(7.02X^{-0.078}-8.82)\rightarrow {\mbox{  if}}\rightarrow 0.2<X<10^{2}\\C_{\mu }exp(5.61X^{-0.109}-7.30)\rightarrow {\mbox{  if}}\rightarrow 10^{2}<X<10^{4}\\C_{\mu }exp(5.50X^{-0.120}-7.02)\rightarrow {\mbox{  if}}\rightarrow 10^{4}<X<10^{6}{\mbox{.}}\end{array}}$

( 29)

For the time-average over a wave period, the components of the wave volume flux above the trough level are:

$(q_{wx},q_{wy})=\int _{h-H/2}^{h+\eta }({\tilde {u}},{\tilde {v}})dz={\frac {E}{\rho C}}(cos\theta ,sin\theta ){\mbox{,}}$

( 30)

where ${\textstyle ({\tilde {u}},{\tilde {v}})}$ are the wave orbital velocity components in ${\textstyle x}$ and ${\textstyle y}$ directions, respectively, ${\textstyle E}$ is the wave energy density, and ${\textstyle \theta }$ is the angle of wave incidence. Wave radiation stresses, ${\textstyle S_{xx}}$ and ${\textstyle S_{xy}}$ , are given by:

$S_{xx}=\int _{0}^{h+\eta }(p+\rho {\tilde {u}}^{2})dz-{\frac {\rho g}{2}}h^{2}=E[{\frac {C_{g}}{C}}(1+cos^{2}\theta )-{\frac {1}{2}}]{\mbox{,}}$

( 31)

The volume fluxes in ${\textstyle x}$ and ${\textstyle y}$ directions due to the surface roller are:

$(q_{srx},q_{sry})={\frac {S_{sr}}{T}}(cos\theta ,sin\theta )={\frac {2E_{sr}}{\rho C}}(cos\theta ,sin\theta ){\mbox{,}}$

( 33)

where ${\textstyle S_{sr}}$ and ${\textstyle E_{sr}}$ are the surface area and energy of the roller, respectively. Averaged momentum fluxes due to the surface roller, ${\textstyle R_{xx}}$ and ${\textstyle R_{xy}}$ , are expressed as  [12] :

$R_{xx}={\frac {\rho S_{sr}C^{2}cos^{2}\theta }{L}}=2E_{sr}cos^{2}\theta {\mbox{,}}$

( 34)

According to the near shore current model, surface velocity is:

$U_{s}=C_{sb}\tau _{cbx}+C_{ss}\tau _{csx}{\mbox{,}}$

( 36)

where:

$C_{sb}={\frac {1}{\rho ku_{{_{\ast }}m}}}ln{\frac {\delta }{z_{0}}}+{\frac {1}{\rho ku_{{_{\ast }}c}}}ln{\frac {z_{m}}{\delta }}-{\frac {(z_{m}-\delta )}{\rho ku_{{_{\ast }}c}h_{tr}}}+{\frac {2}{\rho ku_{{_{\ast }}s}}}{\frac {({\sqrt {h_{tr}}}-{\sqrt {z_{m}}})^{2}}{\sqrt {z_{m}h_{tr}}}}{\mbox{,}}$

( 37)

where ${\textstyle u_{{_{\ast }}m}}$ is the maximum combined wave-current bottom shear velocity, ${\textstyle z_{0}=k_{N}/30}$ , ${\textstyle k_{N}}$ is the equivalent Nikuradse roughness of the bottom, and ${\textstyle {\overset {\mbox{ˆ}}{a}}}$ is the wave amplitude  [4] . Finally, the system of equations yields:

$\tau _{csx}={\frac {C_{sb}q_{cx}-C_{bb}U_{s}}{C_{bs}C_{sb}-C_{ss}C_{bb}}}{\mbox{,}}$

( 42)

Analogously, ${\textstyle \tau _{csy}}$ and ${\textstyle \tau _{cby}}$ are calculated  [4] :

$\tau _{csy}={\frac {C_{sb}q_{cy}-C_{bb}V_{s}}{C_{bs}C_{sb}-C_{ss}C_{bb}}}{\mbox{,}}$

( 44)

Briefly, the main variables that define the model are: wave set-up, ${\textstyle {\bar {\eta }}}$ , total flux due to currents, ${\textstyle (q_{cx},q_{cy})}$ , surface velocities, ${\textstyle (U_{s},V_{s})}$ , bottom shear stresses, ${\textstyle (\tau _{cbx},\tau _{cby})}$ , and trough shear stresses, ${\textstyle (\tau _{csx},\tau _{csy})}$ . Since there are five independent variables, it requires five boundary conditions at each of two boundaries: five at the offshore boundary and five at the onshore boundary  [4] .

2.3. Reduction of wave height due to muddy bed

The attenuation of wave height on a horizontal bed is usually approximated by an exponential function  [7] :

$H(x)=H_{0}e^{-k_{i}(x-x_{0})}{\mbox{,}}$

( 46)

where ${\textstyle H_{0}}$ is the incident wave height at ${\textstyle x=x_{0}}$ , and ${\textstyle k_{i}}$ is the wave attenuation coefficient. The wave attenuation coefficient depends on water depth, wave characteristics, the thickness of fluid mud layer and its rheological behavior. Applying the exponential wave height decay over a muddy and gentle bottom slope, the energy dissipation rate is expressed as:

$\epsilon _{Dm}=-{\frac {d}{dx}}(C_{g}E){\mbox{.}}$

( 47)

After simplifying, the above equation is:

${\begin{array}{l}\displaystyle \epsilon _{Dm}=-C_{g}(2\rho g{\frac {H}{8}}\times {\frac {dH}{dx}})=-C_{g}({\frac {2E}{H}}\times {\frac {dH}{dx}})=2EC_{g}(-{\frac {1}{H}}\times {\frac {dH}{dx}})=\\\displaystyle =2C_{g}k_{i}E{\mbox{,}}\end{array}}$

( 48)

where ${\textstyle E=\rho gH^{2}/8}$ is the wave energy per unit surface area, ${\textstyle \rho }$ is the water density and ${\textstyle C_{g}}$ is the group velocity.

2.4. Erosion model

Erosion is one of the major factors in sediment resuspension, sediment transport and beach deformation of cohesive shorelines. Erosion of cohesive sediments occurs when hydrodynamic erosive forces exceed gravitational, cohesive or frictional forces (surface erosion). The second condition occurs when flow-induced shear stress exceeds bed bulk shear stress, which is called mass erosion. The simple form of unlimited erosion linearly correlates as:

$E=M(\tau _{b}-\tau _{ce}){\mbox{.}}$

( 49)

Sanford and Maa (2001) chose the linear erosion rate formula as [2] :

$E(z,t)=M(z)[\tau _{b}(t)-\tau _{ce}(z)]{\mbox{,}}$

( 50)

where ${\textstyle E(z,t)}$ is erosion rate, which is a function of depth ${\textstyle (z)}$ and time ${\textstyle (t)}$ , ${\textstyle M}$ is erosion constant, ${\textstyle \tau _{b}}$ is the bed shear stress and ${\textstyle \tau _{ce}}$ is the critical bed shear stress of sediment erosion. The basic assumptions were as follows: (a) Erosion constant is proportional to sediment concentration at the water–mud interface; (b) Critical shear stress increases locally at a constant rate with depth. Therefore, erosion rate depends on both time and depth  [13] :

$M(z)=\rho _{s}\phi _{s}(z)\beta _{e}{\mbox{,}}$

( 51)

where ${\textstyle \rho _{s}}$ is the sediment density, ${\textstyle \phi _{s}(z)}$ is the volume fraction of sediment, ${\textstyle \beta _{e}}$ is a local constant, ${\textstyle E^{'}}$ is the erosion velocity and ${\textstyle \gamma =d\tau _{ce}/dz}$ is the rate of increase in resistance against erosion, with respect to depth, that is assumed to be locally constant. By assuming the homogeneous solution (${\textstyle d\tau _{b}/dt=0}$ ), the following solution is obtained:

$E^{'}=\beta _{e}(\tau _{b}-\tau _{ce0})exp[-\gamma \beta _{e}(t-t_{0})]{\mbox{,}}$

( 54)

where ${\textstyle \tau _{ce0}}$ is the critical shear stress when ${\textstyle \tau _{b}}$ is first applied at ${\textstyle t=t_{0}}$ . Mass erosion occurs with rapid increase in the fluid shear stress in the surf zone and where the wave breaks. The mass erosion rate per unit area ${\textstyle [ML^{-2}T^{-1}]}$ may be written as  [13] :

$S_{e0}^{m}={\frac {\rho _{dry}T_{L}}{\Delta t}}{\mbox{.}}$

( 55)

In the above equation, ${\textstyle \rho _{dry}}$ is the dry density and ${\textstyle T_{L}}$ is the thickness of the erodible layer. In this study, the values of critical shear stress for surface and mass erosion are considered 0.5 and 1.5 Pa  [2]  and [13] .

2.5. Sedimentation model

Cohesive sediments tend to agglomerate together. This process is called flocculation and the resulting particle is called floc. Floc size is different, which complicates prediction of settling velocity. Settling of mud floc is one of the most important parameters in evaluating the concentration profile in marine environments. Deposition rate ${\textstyle (D)}$ has the following formula  [3] :

$D=\lbrace {\begin{array}{c}(1-{\frac {\tau _{b}}{\tau _{cd}}})c_{b}w_{s}\rightarrow {\mbox{  for  }}\rightarrow \tau _{b}<\tau _{cd}\\0\rightarrow {\mbox{ for  }}\rightarrow \tau _{b}\geq \tau _{cd}\end{array}}{\mbox{,}}$

( 56)

where ${\textstyle \tau _{b}}$ is the bed shear stress, ${\textstyle \tau _{cd}}$ is the critical shear stress for the deposition, ${\textstyle c_{b}}$ is the near-bed particle concentration and ${\textstyle w_{s}}$ is the settling velocity. The near bottom concentration is dependent on depth-averaged sediment concentration, as described by Teeter (1986)  [14] . In this study, the value of critical shear stress for deposition is considered as 0.2 Pa  [3]  and [9] .

The settling velocity of cohesive sediment depends on concentration ${\textstyle (c)}$ and is usually divided into three regions  [9] :

(a) Free settling ${\textstyle (c<c_{1}=0.1-0.3g/l)}$

$w_{s}={\frac {(s-1)gD_{s}^{2}}{18\nu }}{\mbox{,}}$

( 57)

where ${\textstyle s}$ is the specific gravity of sediment, ${\textstyle D_{s}}$ is representative floc diameter and ${\textstyle \nu }$ is the fluid kinematic viscosity.

(b) Flocculation settling ${\textstyle (c_{1}<c<c_{2}=0.3-10g/l)}$

$w_{s}=k_{1}c^{4/3}{\mbox{,}}$

( 58)

where ${\textstyle k_{1}}$ is an empirical coefficient.

(c) Hindered settling ${\textstyle (c>c_{2})}$

$w_{s}=w_{s0}[1-k_{2}(c-c_{2})]^{4.66}{\mbox{,}}$

( 59)

where ${\textstyle w_{s0}}$ is the value of ${\textstyle w_{s}}$ at concentration ${\textstyle c_{2}}$ , ${\textstyle k_{2}}$ is the inverse of ${\textstyle (c_{s}-c_{2})}$ and ${\textstyle c_{s}}$ is the concentration at ${\textstyle w_{s}=0}$ . The Winterwerp’s equation can also be used  [15] :

$w_{s}=w_{0}{\frac {(1-\phi _{_{\ast }})(1-\phi _{p})}{1+2.5\phi }}{\mbox{,}}$

( 60)

where ${\textstyle \rho _{dry}}$ is the dry density of sediments, ${\textstyle c_{Total}}$ is the total concentration and ${\textstyle c_{gel}}$ is the gelling concentration of suspended sediments.

2.6. Suspended sediments concentration modeling

The partial differential equation describing three-dimensional advection–diffusion for suspended sediments can be written as  [8] :

${\begin{array}{l}\displaystyle {\frac {\partial c}{\partial t}}+{\frac {\partial (uc)}{\partial x}}+{\frac {\partial (vc)}{\partial y}}+{\frac {\partial (wc)}{\partial z}}-{\frac {\partial (w_{s}c)}{\partial z}}={\frac {\partial }{\partial x}}(k_{x}{\frac {\partial c}{\partial x}})+{\frac {\partial }{\partial y}}(k_{y}{\frac {\partial c}{\partial y}})+\\\displaystyle +{\frac {\partial }{\partial z}}(k_{z}{\frac {\partial c}{\partial z}})+S{\mbox{,}}\end{array}}$

( 64)

where ${\textstyle c}$ is suspended sediments concentration, ${\textstyle u}$ , ${\textstyle v}$ and ${\textstyle w}$ are velocity components in the ${\textstyle x}$ , ${\textstyle y}$ and ${\textstyle z}$ directions respectively; ${\textstyle w_{s}}$ is settling velocity of suspended sediments; ${\textstyle S}$ is the source or sink term; and ${\textstyle k_{x}}$ , ${\textstyle k_{y}}$ and ${\textstyle k_{z}}$ are diffusion coefficients in ${\textstyle x}$ , ${\textstyle y}$ and ${\textstyle z}$ directions, respectively. These coefficients are equal to eddy viscosities  [16] . In coastal waters, the horizontal length scale is generally much larger than the vertical scale. Therefore, Eq. (64) will split into a two-dimensional horizontal equation (Eq. (65) ) that is solved horizontally and, then, the one-dimensional vertical equation (Eq. (66) ) that is solved vertically  [17] .

${\frac {\partial c}{\partial t}}+{\frac {\partial (uc)}{\partial x}}+{\frac {\partial (vc)}{\partial y}}-{\frac {\partial }{\partial x}}(k_{x}{\frac {\partial c}{\partial x}})-{\frac {\partial }{\partial y}}(k_{y}{\frac {\partial c}{\partial y}})=S=E-D{\mbox{,}}$

( 65)

Also, the following boundary conditions for sediment are used  [17] :

• On free surface:

$(w-w_{s})c-k_{z}{\frac {\partial c}{\partial z}}=0{\mbox{.}}$

( 67)

• On bed:
• Deposition: ${\textstyle \tau _{b}\leq \tau _{cd}}$

$-w_{s}c-k_{z}{\frac {\partial c}{\partial z}}=D{\mbox{.}}$

( 68)

• Erosion: ${\textstyle \tau _{b}\geq \tau _{ce}}$

$-w_{s}c-k_{z}{\frac {\partial c}{\partial z}}=E{\mbox{.}}$

( 69)

• Equilibrium: ${\textstyle \tau _{cd}<\tau _{b}<\tau _{ce}}$

$-w_{s}c-k_{z}{\frac {\partial c}{\partial z}}=0{\mbox{,}}$

( 70)

where ${\textstyle \tau _{b}}$ is bed shear stress, ${\textstyle \tau _{cd}}$ is critical shear stress for deposition, ${\textstyle \tau _{ce}}$ is critical shear stress for erosion, and ${\textstyle E}$ and ${\textstyle D}$ are erosion and deposition rates (Sections  2.4  and 2.5 )

The horizontal two-dimensional equation (65) can be converted in a pure advection system by neglecting the diffusion part (Eq. (71) ) and in a pure diffusion system by neglecting the advection part (Eq. (72) ), and can be written as  [8] :

${\frac {\partial c}{\partial t}}+{\frac {\partial (uc)}{\partial x}}+{\frac {\partial (vc)}{\partial y}}=0{\mbox{,}}$

( 71)

By considering the layer-integrated hydrodynamic model, Eq. (65) was integrated over the layers to give the following two-dimensional layer-integrated equation:

${\frac {\partial hC}{\partial t}}+{\frac {\partial UhC}{\partial x}}+{\frac {\partial VhC}{\partial y}}={\frac {\partial }{\partial x}}[k_{x}h{\frac {\partial C}{\partial x}}]+{\frac {\partial }{\partial y}}[k_{y}h{\frac {\partial C}{\partial y}}]+(E_{k}-D_{k})h{\mbox{,}}$

( 73)

where ${\textstyle C}$ is depth averaged suspended sediment concentration, ${\textstyle U}$ and ${\textstyle V}$ are the depth averaged flow velocities in the ${\textstyle x}$ and ${\textstyle y}$ directions, respectively, ${\textstyle h(=\Delta z)}$ is water layer thickness, and ${\textstyle E_{k}}$ and ${\textstyle D_{k}}$ are erosion (source) and deposition (sink) terms in upward and downward directions, respectively. To solve Eq. (73) , a fractional step approach, also known as standard the split method, is used  [18] . In this approach, both advection and diffusion parts of the advection–diffusion equation are solved separately at each time step. The splitting approach is an accurate numerical method to solve advection and diffusion separately. A high resolution conservation algorithm for the advection part in incompressible flow was developed by Leveque (1996), who used a basic upwind method and proposed several correction terms to achieve better accuracy and stability  [19] . Also, to solve the diffusion part, a semi implicit finite difference scheme is employed, such that, it can easily be converted to a completely explicit or implicit scheme. Discretization of the concentration and velocity field in the solution domain is shown in Figure 2   [8] .

Figure 2. Discretization of concentration and velocity field in solution domain  [8] .

A conservative form of advection of scalar concentration or density function ${\textstyle C(x,t)}$ can be written, in general, as  [8] :

$C_{t}+\nabla .({\overset {\rightarrow }{U}}C)=0{\mbox{.}}$

( 74)

By assuming incompressible flow, a two-dimensional advection equation can be written as:

$C_{t}+(CU)_{x}+(CV)_{y}=0{\mbox{,}}$

( 75)

In discrete form and for every cell with an equal size of mesh in two directions, the following condition should satisfy:

$(U_{i+1,j}^{n+1}-U_{i,j}^{n+1})+(V_{i,j+1}^{n+1}-V_{i,j}^{n+1})=0{\mbox{,}}$

( 77)

where ${\textstyle n}$ is understood that all data is at time ${\textstyle t_{n}}$ . To solve this conservative form of the advection equation, the upwind method is used, which is based on flux calculation of the concentration at the cell interfaces. By assuming time steps, ${\textstyle \Delta t=k}$ , it can be written as:

$C_{i,j}^{n+1}=C_{i,j}^{n}-{\frac {k}{h}}[F_{i+1,j}-F_{i,j}+G_{i,j+1}-G_{i,j}]{\mbox{,}}$

( 78)

where ${\textstyle F_{i,j}}$ represents the flux at the left interface of cell ${\textstyle C_{i,j}}$ , and ${\textstyle F_{i+1,j}}$ represents the flux at the right interface of cell ${\textstyle C_{i,j}}$ . Similarly, ${\textstyle G_{i,j}}$ represents the flux at the bottom interface of cell ${\textstyle C_{i,j}}$ , and ${\textstyle G_{i+1,j}}$ represents the flux at the top interface of cell${\textstyle C_{i,j}}$ . These fluxes at the cell interfaces can be calculated as:

${\begin{array}{c}F_{i,j}=U_{i,j}^{n+1}C_{i-1,j}^{n}\\G_{i,j}=V_{i,j}^{n+1}C_{i,j-1}^{n}{\mbox{.}}\end{array}}$

( 79)

Therefore, Eq. (78) can be rewritten as:

${\begin{array}{l}\displaystyle C_{i,j}^{n+1}=C_{i,j}^{n}-{\frac {k}{h}}[U_{i+1,j}^{n+1}C_{i,j}^{n}-\\\displaystyle -U_{i,j}^{n+1}C_{i-1,j}^{n}+V_{i,j+1}^{n+1}C_{i,j}^{n}-\\\displaystyle -V_{i,j}^{n+1}C_{i,j-1}^{n}]{\mbox{.}}\end{array}}$

( 80)

The modifications can be incorporated in the flux calculation of ${\textstyle F}$ and ${\textstyle G}$ as follows:

${\begin{array}{c}(F_{i,j})^{new}=(F_{i,j})^{old}+U_{i,j}^{n+1}C_{i-1,j}^{n}\\(G_{i,j})^{new}=(G_{i,j})^{old}+V_{i,j}^{n+1}C_{i,j-1}^{n}\\(F_{i+1,j})^{new}=(F_{i+1,j})^{old}-\\\displaystyle -{\frac {1}{2}}{\frac {k}{h}}U_{i+1,j}^{n+1}V_{i+1,j}^{n+1}(C_{i,j}^{n}-C_{i,j-1}^{n})\\(G_{i,j+1})^{new}=(G_{i,j+1})^{old}-\\\displaystyle -{\frac {1}{2}}{\frac {k}{h}}U_{i,j+1}^{n+1}V_{i,j+1}^{n+1}(C_{i,j}^{n}-C_{i-1,j}^{n}){\mbox{.}}\end{array}}$

( 81)

To achieve a second order accurate algorithm, a second order Lax–Wendroff method is combined with the upgrade upwind method. The Lax–Wendroff method can be expressed as Eq. (82) . It can also be rearranged by considering the upwind method combined with a correction term, as Eq. (83) :

$F_{i-1,j}^{LW}={\frac {1}{2}}U_{i-1,j}(C_{i-1}+C_{i})-{\frac {k}{2h}}U_{i-1,j}^{2}(C_{i}-C_{i-1}){\mbox{,}}$

( 82)

Similarly, this method can be used at the interface between ${\textstyle C_{i,j}}$ and ${\textstyle C_{i-1,j}}$ by adding the following term to the interface flux. To avoid oscillation, a flux limiting factor is also introduced as  [8] :

${\begin{array}{l}\displaystyle (F_{i-1,j})^{new}=(F_{i-1,j})^{old}+{\frac {1}{2}}\vert U_{i-1,j}\vert (1-\\\displaystyle -{\frac {k}{h}}\vert U_{i-1,j}\vert )(C_{i}-C_{i-1})\Phi _{i}{\mbox{.}}\end{array}}$

( 84)

And, similarly, for the flux at the interface between ${\textstyle C_{i,j}}$ and ${\textstyle C_{i,j-1}}$ :

${\begin{array}{l}\displaystyle (G_{i-1,j})^{new}=(G_{i-1,j})^{old}+{\frac {1}{2}}\vert V_{i-1,j}\vert (1-\\\displaystyle -{\frac {k}{h}}\vert V_{i-1,j}\vert )(C_{i}-C_{i-1})\Phi _{i}{\mbox{.}}\end{array}}$

( 85)

The flux limiting term, ${\textstyle \phi _{i}}$ , is defined as:

$\Phi _{i}=\phi (\theta _{i}),\theta _{i}={\frac {q_{I}-q_{I-1}}{q_{i}-q_{i-1}}}\quad {\mbox{and}}\quad I=\lbrace {\begin{array}{c}i-1\rightarrow {\mbox{ if  }}\rightarrow u>0\\i+1\rightarrow {\mbox{ if  }}\rightarrow u\leq 0{\mbox{.}}\end{array}}$

( 86)

Some standard limiters are minmod, superbee, van Leer and monotonized centered, as Eqs. , ,  and  :

$\phi (\theta )=max(0,min(1,\theta )){\mbox{,}}$

( 87)

The superbee limiter provides the best results. The transverse motion of the correction wave at the interface between cells modifies the fluxes and can be calculated by the following expressions  [8] :

${\begin{array}{l}\displaystyle (G_{i-1,j+1})^{new}=(G_{i-1,j+1})^{old}-\\\displaystyle -{\frac {1}{2}}{\frac {k}{h}}\vert U_{i-1,j+1}\vert V_{i-1,j+1}(1-{\frac {k}{h}}\vert U_{i-1,j+1}\vert )(C_{i,j}-\\\displaystyle -C_{i-1,j})\Phi _{i}\end{array}}$

( 91)

Transverse motion between cells, ${\textstyle C_{i,j-1}}$ and ${\textstyle C_{i,j}}$ , modifies the fluxes, ${\textstyle F_{i+1,j-1}}$ and ${\textstyle F_{i+1,j}}$ , and can be calculated using the following expressions:

${\begin{array}{l}\displaystyle (F_{i+1,j-1})^{new}=(F_{i+1,j-1})^{old}-\\\displaystyle -{\frac {1}{2}}{\frac {k}{h}}\vert V_{i+1,j-1}\vert U_{i+1,j-1}(1-{\frac {k}{h}}\vert V_{i+1,j-1}\vert )(C_{i,j}-\\\displaystyle -C_{i,j-1})\Phi _{i}\end{array}}$

( 92)

Also, a finite difference representation for the diffusion part can be written as follows:

${\frac {\partial Ch}{\partial t}}={\frac {\partial }{\partial x}}(k_{x}h{\frac {\partial C}{\partial x}})+{\frac {\partial }{\partial y}}(k_{y}h{\frac {\partial C}{\partial y}})+(E-D){\mbox{.}}$

( 93)

The above equation is solved for time steps, ${\textstyle \Delta t=k}$ , using an explicit finite difference scheme. Introducing a new variable, ${\textstyle A}$ , Eq. (93) can be rewritten as:

${\frac {\partial Ch}{\partial t}}={\frac {\partial }{\partial x}}A_{x}+{\frac {\partial }{\partial y}}A_{y}+(E-D){\mbox{,}}$

( 94)

where:

$A_{x}=k_{x}h{\frac {\partial C}{\partial x}}\quad {\mbox{and}}\quad A_{y}=k_{y}h{\frac {\partial C}{\partial y}}{\mbox{.}}$

( 95)

Therefore, Eq. (94) is written as:

${\begin{array}{l}\displaystyle h(i,j){\frac {C^{n+1}(i,j)-C^{n}(i,j)}{\Delta t}}={\frac {A_{x}(i+1,j)-A_{x}(i,j)}{\Delta x}}+\\\displaystyle +{\frac {A_{y}(i,j+1)-A_{y}(i,j)}{\Delta y}}+(E(i,j)-D(i,j))\end{array}}$

( 96)

where ${\textstyle A_{x}(i,j)}$ and ${\textstyle A_{y}(i,j)}$ can be calculated as  [8] :

${\begin{array}{l}\displaystyle A_{x}(i,j)=k_{x}(i,j)h(i\\\displaystyle j)[\theta ({\frac {C^{n+1}(i,j)-C^{n+1}(i-1,j)}{\Delta x}})+\\\displaystyle +(1-\theta )({\frac {C^{n}(i,j)-C^{n}(i-1,j)}{\Delta x}})]{\mbox{,}}\end{array}}$

( 97)

The one-dimensional equation (66) was discretized over non uniform grid spacing in the vertical direction. It was solved implicitly using the QUICKEST (Quadratic Upstream Interpolation for Convective Kinematics with Estimated Streaming Terms) scheme and the backward or implicit Euler method. The coefficients at the resultant discretized equation are computed once and stored in arrays, and then they are used to update each constituent. The coefficients matrix has three diagonals with non-zero elements, and the values of concentrations are computed by inverting the resulting matrix and by using the Thomas tri-diagonal solver. The resultant discretization equation is  [17] :

$-a_{S}c_{k-1}^{n+1}+a_{P}c_{k}^{n+1}-a_{N}c_{k+1}^{n+1}=b{\mbox{,}}$

( 99)

where superscript ${\textstyle n+1}$ is an index for time and the subscript ${\textstyle k-1,k,k+1}$ denotes layer number at depth (at free surface, ${\textstyle k=1}$ ). Also, other parameters are defined as:

$a_{S}=K_{z}^{T}A(\vert Pe^{T}\vert )+[F^{T},0]{\mbox{,}}$

( 100)

where the symbol ${\textstyle [a,b]}$ is used to denote the greater value between ${\textstyle a}$ and ${\textstyle b}$ , superscripts ${\textstyle T}$ and ${\textstyle B}$ denote the control volume face (top and bottom), ${\textstyle Pe}$ is the grid Peclet number and ${\textstyle F}$ is the mass flow rate. The Peclet number is defined as the ratio of the rate of advection of a physical quantity by the flow to the rate of diffusion of the same quantity driven by an appropriate gradient. In the context of species or mass dispersion, the Peclet number is the product of the Reynolds number and the Schmidt number.

3. Study area and data

To model wave damping, the East Bay situated in Louisiana, USA was considered. The deposited sediments from the Mississippi River are very soft, with shear strength ranges from 1.57 kPa near the water-sediment interface to 2.36 kPa three meters into the sediment. The wave period was 7.75 s and the measured wave heights were 0.285 and 0.54 m at two stations, A and B (Figure 3 ). The wave height at B is set to be 0.54 m and the wave height transformations are calculated based on Tajima’s wave model. The bottom contours are shown in Figure 3   [6] .

Figure 3. Bathymetry and wave measurement stations in the East Bay, Louisiana  [6] .

Soltanpour’s experimental data are used for validation of the present model. The experiments were carried out in a wave flume at the Hydraulic Model Laboratory, Department of Civil Engineering, K. N. Toosi University of Technology. These laboratory experiments were performed in a wave flume; 17 m long, 0.6 m wide and 0.55 m deep. Water depth was kept constant at 35 cm in all experiments, wave period was 1.06 s, and the wave heights were varied during the tests. The mud was made using a mixture of kaolinite and water set on the bed  [5] . A concentration profile of cohesive sediments was modeled using two sets of field experiments along the Louisiana coast (US). One of these measurements was performed by Kemp (1986)  [20] at 30 km of coastline, southwest of Vermilion Bay, on the eastern Louisiana Chenier Plain. The sedimentation in the area is due to the Atchafalaya River. The bed material consists of about 50%–80% clay, 20%–50% silt and zero to 14% sand. Mud depth was found 0.18 m and mud density was taken 1270 kg/m³ . Measured water depth varied between 0.85 and 1.05 m and water density was considered 1030 kg/m³ in the region. The second data was collected using WAVCIS (Wave-Current-Surge Information System) in a 20 km length of south of Marsh Island along the Louisiana coast. These data are obtained by Sheremet and Stone (2003), Sheremet et al. (2005) and Sheremet (2006), and were reported by Sorourian (2007)  [13] . The study site is located along the 5-m isobaths, on a sloping shelf (<0.001). Bed material is inorganic fine sediment with a median grain size of 6.34 μm. The mean significant wave height was found to be 0.177 m and the mean significant wave period was 3.17 s  [13] . It is worthwhile to mention Jazayeri Shooshtari and Soltanpour’s model and experimental data, whose concentration profiles are used for validation. Experimental data were obtained by Van Rijn and Louisse (1987) and conducted on a kaolinite bed with ${\textstyle \rho _{dry}=640kg/m^{3}}$ under wave action. These experimental data were reported by Jazayeri Shooshtari and Soltanpour (2008)  [21] .

4. Results and discussion

Regarding the stability of the hybrid numerical model, space and time intervals must be chosen correctly. The bathymetry of the computational domain extends from shoreline to the deepwater zone. A suitable mesh was constructed for covering the study area. The spatial increments (${\textstyle \Delta x=\Delta y=1m}$ , ${\textstyle \Delta z=5cm}$ for concentration profile, time step=1 s) in the wave breaking zone and (${\textstyle \Delta x=\Delta y=10m}$ , ${\textstyle \Delta z=5cm}$ for concentration profile, time step=1 s) in the outer region were used to create a uniform mesh. In order to find the proper mesh size for discretization, a sensitive analysis was carried out for 600 m in a cross shore direction. The parameters, such as bed slope, deep water wave height, wave period, deep water wave angle, mud bed thickness and water content of mud, as 1%, 1.05 m, 7 s, 45°, 25 cm and 120%, respectively, were considered for sensitivity analysis. The Tajima’s wave model was run for 5 different mesh sizes. The wave heights at depth equal to 2.75 m were compared with the wave heights calculated from the exact solution (1.201 m), which is based on linear wave theory. The results are shown in Table 1 . The region in the surf zone is within 100–200 m of the shoreline, and out of this region is within 200–600 m of the shoreline.

Table 1. Sensitivity analysis for mesh sizes.

Case	Mesh size/surf zone (m)	Mesh size/out of surf zone (m)	Wave height at point with depth =  2.75 m	Relative error (%)	Wave height at breaking point (m)
1	1	10	1.203	0.17	1.403
2	5	15	1.257	4.66	1.464
3	10	20	1.291	7.49	1.502
4	15	25	1.397	16.32	1.624
5	20	30	1.504	25.23	1.772

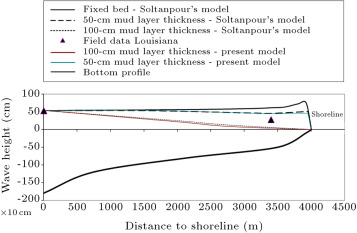
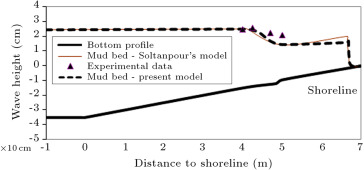
Figure 4  and Figure 5 show validation of present model by field data from Louisiana East Bay, Soltanpour’s model and its experimental data  [5] . The results of comparison show that there is good agreement. Figure 4 shows wave height distribution in Louisiana East Bay with different mud bed thicknesses for the present model, Soltanpour’s model and field data  [5] . As can be seen, the present model is matched well with Soltanpour’s model. For mud bed thickness equal to 50 cm, the difference in distance of the breaker line is about 5 m closer to the shoreline, and the wave height at breaking point is reduced about 4 cm relative to Soltanpour’s model. The results from field data and mentioned models show good agreement with mud bed thickness equal to 70 cm. Figure 5 shows wave height distribution in the experimental flume for the present model, Soltanpour’s model and experimental data (second case)  [5] . As can be seen, the present model is matched well with Soltanpour’s model. The result of the present model shows that the difference of breaker line in distance is about 4 cm closer to the shoreline, and wave height at breaking point is about 4 mm less than Soltanpour’s model.

Figure 4. Wave height distribution in Louisiana East bay with different mud bed thicknesses (present model, Soltanpour’s model and field data  [5] ).

Figure 5. Wave height distribution in experimental flume (present model, Soltanpour’s model and experimental data, second case  [5] ).

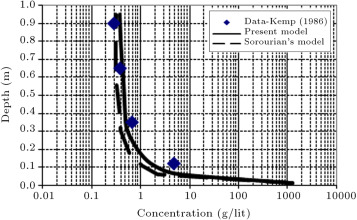
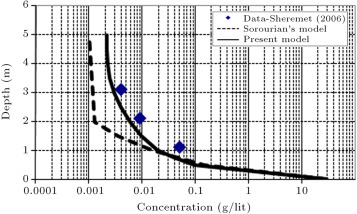
Another part of the validation for the suspended sediment concentration profile was to compare the results of the present model with Sorourian’s model and field data. The field data from the Louisiana coast are comprised of one set of data by Kemp (1986)  [20] and the second set of data by Sheremet (2006). Sorourian made the following assumptions in his model: (a) Linear wave theory; (b) One-dimensional and wave-averaged; and (c) Horizontal initial bed. He incorporated several theoretical concepts to enhance the accuracy of the suspended sediment concentration predictions, such as considering the electrochemical force between cohesive sediment particles, relating bed resistance to sediment characteristics, predicting bed shear stress by relating the wave friction factor to bed roughness and median grain diameter, and considering time-dependent erosion rate  [13] . Figure 6  and Figure 7 show the samples of comparison between concentration profiles of the present model with Sorourian’s model and field data. The results in these figures show that there is very good agreement with field data. The maximum suspended sediment concentration difference between the present model and field data is 3 g/l at depth 0.12 m (Figure 6 ) and 0.03 g/l at depth 1 m (Figure 7 ). As can be seen from these figures, the maximum difference in concentration with Sorourian’s model is 2.5 g/l at depth 0.06 m (Figure 6 ) and 0.006 g/l at depth 2 m (Figure 7 ). Due to assumptions made in Sorourian’s model, the present model predicts suspended sediment concentration more accurately.

Figure 6. Comparison of concentration profile between present model, Sorourian’s model (2007)  [13] and kemp field data (1986)  [20] for wave height equal to 0.117 m and wave period equal to 6.6 s after 90 min (total time=180 min, time step=1 s, mud thickness=18 cm).

Figure 7. Comparison of concentration profile between present model, Sorourian’s model (2007)  [13] and Sheremet field data (2006)  [13] for wave height equal to 0.177 m, wave period equal to 3.17 s and mud depth equal to 0.6 m (time: 12:59, 11/7/2003).

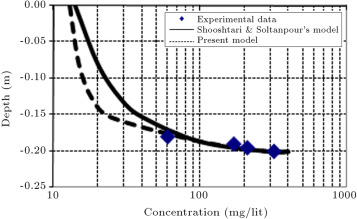
The results of the present model also are compared to Jazayeri Shooshtari and Soltanpour’s model and experimental data  [21] , which is shown in Figure 8 . Their model is a cross-shore numerical model that simulates a cohesive sediment profile under wave action. The partial differential equation of two-dimensional vertical advection–diffusion is solved. A dynamic mesh is employed, where the physical space in Cartesian coordinates is replaced by a computational ${\textstyle \sigma }$ -coordinate system. Both water level and bed surface are time dependent and the finite volume method is applied to solve the discredited equation  [21] . The results of the present model show that there is very good agreement with Jazayeri Shooshtari and Soltanpour’s model and experimental data at the zone near the bed. At the upper zone, the maximum suspended sediment concentration difference between the present model and Jazayeri Shooshtari and Soltanpour’s model is 16 mg/l at depth 0.15 m. As mentioned earlier, the splitting approach is a very accurate numerical method can be used to solve advection and diffusion parts, separately  [8] .

Figure 8. Comparison of concentration profile between present model, Jazayeri Shooshtari and soltanpour’s model and experimental data  [21] for wave height equal to 0.03 m and wave period equal to 1.5 s after 5 min (erosion threshold shear stress equal to 0.07 Pa and deposition threshold shear stress equal to 0.04 Pa).

Comparison of the results of the present model with Sorourian’s model (2007)  [13] , Jazayeri Shooshtari and Soltanpour’s model (2008)  [21] , and their reported experimental data and Louisiana coast field data, confirms the accuracy and validity of the present model. Based on the present results, the advection–diffusion equation is solved by the standard split method to obtain more accurate results in comparison to experimental and field data.

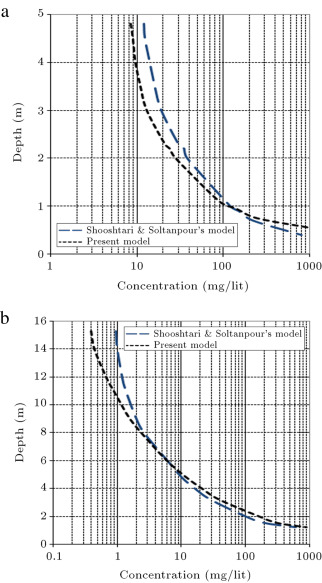
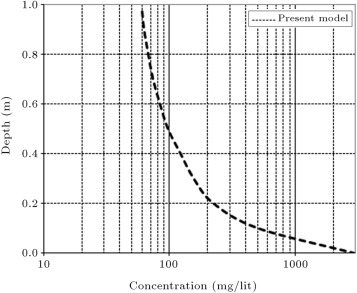
By assuming mud bed thickness equal to 80 cm, the present model has been run and concentration profiles are predicted at approximate depths equal to 5 and 16 m (out of the surf zone) after 60 min of entering the wave in Louisiana East Bay  [21] . The results are compared with Jazayeri Shooshtari and Soltanpour’s model results. As can be seen, the present model matches well with their model. Figure 9 (a) and (b) show the results of Jazayeri Shooshtari and Soltanpour’s model and the present model in predicting concentration profiles at these depths. To show the ability of the present model in prediction of the concentration profile within the surf zone, the model has been run for a depth equal to 1 m and mud thickness equal to 50 cm after 60 min. The result is shown in Figure 10 .

Figure 9. Comparison of concentration profile between present model with Jazayeri Shooshtari and Soltanpour’s model  [21] at approximate depth equal to (a) 5 m and (b) 16 m (out of surf zone), East Bay, Louisiana.

Figure 10. Concentration profile at depth equal to 1 m (within surf zone), East Bay, Louisiana.

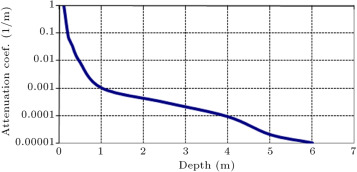
To introduce the application of the present model to calculating the wave attenuation coefficient, wave height, wave height to water depth ratio, bed shear stress and erosion rate, the model has been run by parameters, such as deep water wave height, wave period, deep water wave angle, water content of mud, and bed slope, as 1.05 m, 7 s, 45°, 120% and 0.01, respectively after 30 min. Variation of the wave attenuation coefficient as a function of water depth is shown in Figure 11 for a mud bed thickness equal to 70 cm. As can be observed, wave attenuation rate decreases as water depth increases. In other words, by increasing water depth, muddy bed effects are less, because deep water waves do not interact with the sea bed  [1] .

Figure 11. Variation of wave attenuation coefficient as a function of water depth.

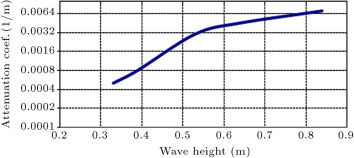
Variation of the wave attenuation coefficient as a function of wave height is shown in Figure 12 for a mud bed thickness equal to 70 cm, water depth equal to 1.2 m and different deepwater wave heights. As can be observed, wave attenuation rate increases as wave height increases. In other words, by increasing wave height, muddy bed effects are significant, because water waves have more interaction with the sea bed.

Figure 12. Variation of wave attenuation coefficient as a function of wave height.

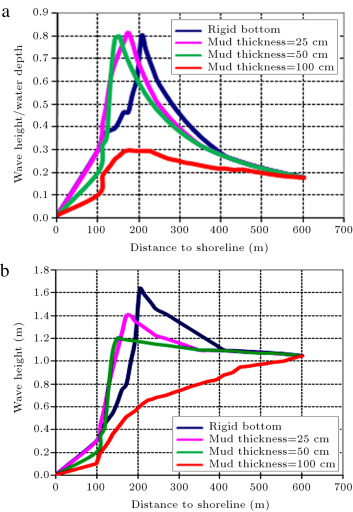
Figure 13 show the variation of (a) wave height to water depth ratio and (b) wave height versus distance to shoreline. Based on these figures, by increasing mud bed thickness, the wave breaker line is moved to the shoreline; on the other hand, if the mud bed is too thick, the water waves may not break, due to bottom friction, percolation losses and viscous damping within the sediment.

Figure 13. Variation of (a) wave height to water depth ratio (b) wave height for different values of mud bed thickness.

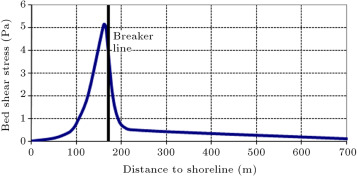
Bed shear stresses were also computed over the whole domain from the wave fields through Tajima’s wave model. Figure 14 shows the variation of bed shear stress versus distance to shoreline. Maximum bed shear stress occurs at a distance of about 168 m from the shoreline (breaker line is about 172 m from shoreline). As expected, maximum bed shear stress occurs near the breaker line.

Figure 14. Variation of bed shear stress versus distance to shoreline.

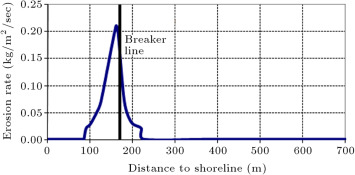
Figure 15 shows variation of the surface and mass erosion rate versus distance to shoreline. As mentioned formerly, the value of critical shear stress for mass erosion was considered 1.5 Pa, which corresponds to an erosion rate of 0.05 kg/m² /s. Maximum erosion rate occurs at a distance of about 168 m from the shoreline (breaker line is about 172 m from shoreline). Certainly, it is expected that maximum erosion rate will occur near the breaker line, because, if the wave breaks, much of the wave energy will be dissipated and lead to significant erosion in the bed  [12] .

Figure 15. Variation of erosion rate (less than 0.05 kg/m2 /s is surface erosion and more than 0.05 kg/m2 /s is mass erosion) versus distance to shoreline.

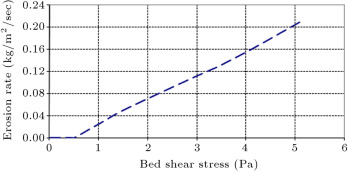
Figure 16 shows variation of the erosion rate versus bed shear stress. The low shear stress regime represents surface erosion, while the high shear stress regime corresponds to mass erosion. The top layer of loosely consolidated material overlies a layer of more consolidated material and can be easily disturbed and re-suspended into the water column. For shear stress less than 0.5 Pa, erosion rate is low, while above 0.5 Pa, erosion rate increases rapidly with higher shear stress.

Figure 16. Variation of erosion rate versus bed shear stress.

5. Conclusion

The purpose of the current research was a better estimation of wave height and suspended cohesive sediment concentration profiles by a newly hybrid numerical model, which has been realized. Reviewing various applications of the present numerical model, different levels of accuracy in the prediction of wave height and concentration profile for cohesive sediment were observed. The models, such as Sanford and Maa’s erosion model (2001)  [2] , Krone’s sedimentation model (1962)  [3] , Tajima’s wave breaking model (2004)  [4] , and the visco-elastic–plastic rheological model, were used to simulate interaction of the wave and muddy bed, and prediction of the concentration profile for cohesive sediment. The advection–diffusion equation was solved by the standard split method. Jazayeri Shooshtari and Soltanpour’s model and their reported experimental data, Sorourian’s model, Kemp’s field data and Sheremet’s field data were used for validation of the concentration profiles. Based on this research, the following specific conclusions can be drawn:

• The breaker line in the surf zone, using Tajima’s wave model, by considering a muddy bed, was predicted successfully. Considering Tajima’s wave model, moving the breaker line to the shoreline results in a reduction in wave height. It was also found that if the mud bed is too thick, wave breaking will not occur.
• The wave linear assumption reduces the accuracy of the wave height after breaking, but Tajima’s wave breaking model predicted a wave height reduction after breaking successfully.
• An increase in water depth caused the wave attenuation coefficient to decrease substantially, but the wave attenuation rate increased as wave height increased.
• It can be observed that by using the standard split method, the present model is capable of simulating the sediment concentration profile more accurately than the other models in comparison with experimental and field data.
• Maximum bed shear stress and erosion rate occur near the breaker line, as expected. For shear stress less than critical shear stress for surface erosion, the erosion rate is low and approximately constant, while, above it, the erosion rate increases rapidly with higher shear stress.

The generated effect by the presence of contaminants in the mud sediment is not included in the present model. A research on the combined behavior of fluid mud, transport and dissipation of contaminants is suggested as future study. In this study, cohesive sediments are used for concentration modeling, but it is recommended that a combination of fine and coarse aggregates is used for future studies.

References

1. [1] Jain, M. “Wave attenuation and mud entrainment in shallow waters”, Thesis with Degree of Doctor of Philosophy in the Graduate School of the University of Florida, USA (2007).
2. [2] L.P. Sanford, J.P. Maa; A unified erosion formulation for fine sediments; Marine Geology, 179 (2001), pp. 9–23
3. [3] Krone, R.B. “Flume study of transport of sediments in estuarial processes”, Final Report, H.E.L.S.E.R.L., University of California, Berkeley, California DA-04-203, CIVENG-59-2 (1962).
4. [4] Tajima, Y. “Waves, currents, and sediment transport in the surf zone along long and straight beaches”, Thesis with Degree of Doctor of Philosophy in the Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, USA (2004).
5. [5] Soltanpour, M. “Mathematical model of wave height distribution in cohesive profiles”, Third Iranian Hydraulic Conference, Tehran University, pp. 1–9 (2001).
6. [6] A. Oveisy, M. Soltanpour; 2D numerical modeling of wave transformation on soft muddy beds; Journal of Marine Engineering, 3 (4) (2006), pp. 15–27
7. [7] Oveisy, A. “A two-dimensional horizontal wave propagation and mud mass transport model on muddy coastal regions”, Thesis with Degree of Doctor of Philosophy in the Department of Civil Engineering, Queen’s University, Kingston, Ontario, Canada (2009).
8. [8] Singh, V. “Two dimensional sediment transport model using parallel computers”, Thesis with Degree of Master of Science in the Graduate Faculty in the Department of Civil and Environmental Engineering, Louisiana State University, USA (2005).
9. [9] A.J. Mehta; Hydraulic behavior of fine sediment, in coastal, estuarial and harbor; M.B. Abbott, W.A. Price (Eds.), Engineers’ Reference Book, E & FN Spon Ltd., London (1993), pp. 577–584
10. [10] Samsami, F., Soltanpour, M. and Haghshenas, A. “Experimental study of wave height reduction on the muddy beds”, Eighth International Conference on Coasts, Ports and Marine Structures , Ports and Shipping Organization, Tehran (2008).
11. [11] Madsen, O.S. “Spectral wave-current bottom boundary layer flows”, Proceedings of 24rd International Coastal Engineering Conference , ASCE, pp. 384–398 (1994).
12. [12] D. Reeve, A. Chadwick, C. Fleming; Coastal Engineering: Processes, Theory and Design Practice; Spon Press, Taylor and Francis Group, London and New York (2004)
13. [13] Sorourian, S. “Modeling of wave and current induced concentration of cohesive sediments”, Thesis with Degree of Master of Applied Science in the Department of Civil Engineering, University of Ottawa, Canada (2007).
14. [14] A.M. Teeter; Vertical transport in fine-grained suspension and newly deposited sediment; A.J. Mehta (Ed.), Estuarine Cohesive Sediment Dynamics, Springer-Verlag, Berlin, Heidelberg, New York, Tokyo (1986), pp. 170–191
15. [15] J. Winterwerp; On the flocculation and settling velocity of estuarine mud; Continental Shelf Research, 22 (2002), pp. 1339–1360
16. [16] J. Fredsoe, R. Deigaard; Mechanics of Coastal Sediment Transport, Advanced Series on Ocean Engineering, 3, , World Scientific Publishing, New Jersey (1992)
17. [17] Y. Wu, R.A. Falconer; A mass conservative 3-D numerical model for predicting solute fluxes in estuarine waters; Advances in Water Resources, 23 (2000), pp. 531–543
18. [18] R.J. Sobey; Fraction step algorithm for estuarine mass transport; International Journal of Numerical Methods in Fluids, 3 (1983), pp. 749–772
19. [19] J.R. Leveque; High resolution conservative algorithm for advection in incompressible flow; Journal of Numerical Analysis, 33 (2) (1996), pp. 627–665
20. [20] Kemp, G.P. “Mud deposition at the shore surface: wave and sediment dynamics in the Chenier plain of Louisiana”, Thesis with Degree of Doctor of Philosophy in the Department of Civil and Environmental Engineering, Louisiana State University, USA (1986).
21. [21] Jazayeri Shooshtari, M. and Soltanpour, M. “Two-dimensional modeling of suspended cohesive sediment transport”, Eighth International Conference on Coasts, Ports and Marine Structures , Ports and Shipping Organization, Tehran (2008).