On the use of Cartesian grid finite element code in structural optimization

Resumen

La optimización de forma estructural es un proceso iterativo constituido por un nivel superior que propone las geometrías a analizar, y un nivel inferior que evalúa numéricamente la respuesta estructural de estas, normalmente mediante el método de los elementos finitos (MEF). Estos procesos pueden reportar claros beneficios en entornos industriales pero su elevado coste computacional es un gran inconveniente. La eficiencia del proceso requiere eficiencia computacional en ambos niveles. Este trabajo se centra en la mejora del rendimiento del nivel inferior mediante una metodología que usa un código MEF para elasticidad 2D basado en mallas cartesianas independientes de la geometría, combinado con técnicas de reconstrucción de la solución a partir de la del MEF, adaptadas a este entorno. Estos mallados simplifican la generación de mallas y, con la estructura jerárquica adecuada reutilizan gran cantidad de cálculos. Las técnicas de reconstrucción juegan un doble papel: a ) su uso en estimadores de error del tipo Zienkiewicz-Zhu permite cuantificar la calidad de la solución MEF para poder guiar el proceso de refinamiento h -adaptativo conducente a minimizar el coste computacional para una precisión dada, y b ) proporcionan una solución, que puede ser utilizada en la práctica, más precisa que la del MEF. Los resultados numéricos, que incluyen una comparativa con un software comercial, muestran el efecto de la metodología propuesta sobre la mejora de la eficiencia de la optimización y de la calidad de la solución.

abstract

The structural shape optimization is an iterative process built up by a higher level, which proposes the geometries to analyze, and a lower level which is in charge of analyzing, numerically, their structural response, usually by means of the Finite Element Method (FEM). These techniques normally report notorious advantages in an industrial environment, but their high computational cost is the main drawback. The efficiency of the global process requires the efficiency of both levels. This work focuses on the improvement of the efficiency of the lower level by using a methodology that uses a 2D linear elasticity code based on geometry-independent Cartesian grids, combined with FEM solution and recovery techniques, adapted to this framework. This mesh type simplifies the mesh generation and, in combination with a hierarchical data structure, reuses a great calculus amount. The recovery technique plays a double role: a ) it is used in the Zienkiewicz-Zhu type error estimators allowing to quantify the FEM solution quality to guide the h -adaptive refinement process which minimizes the computational cost for a given accuracy; and b ) it provides a solution, more accurate than the FEM one, that can be used. The numerical results, which include a comparative with a commercial code, show the effect of the proposed methodology improving the efficiency in the optimization process and in the solution quality.

Palabras clave

Optimización de forma estructural ; Estimación de error ; Refinamiento adaptativo ; Algoritmos evolutivos ; Mallas cartesianas

Keywords

Structural shape optimization ; Error estimation ; Adaptive remeshing ; Evolutionary algorithms ; Cartesian grids

1. Introducción

El uso de técnicas de optimización de forma de componentes industriales conduce a la obtención de piezas de menor peso y mejores prestaciones. Desde el punto de vista industrial, la disminución del material utilizado en una pieza suele llevar asociada una reducción de costes que es muy importante en sectores donde se fabrican grandes series, como es el caso del sector automovilístico.

Los procesos de optimización están constituidos por un nivel superior, gobernado por el algoritmo de optimización utilizado, y un nivel inferior, gobernado por el método numérico utilizado para analizar cada una de las múltiples soluciones. En problemas relativos a optimización de forma de componentes mecánicos estructurales, en el nivel inferior, se ha de utilizar un método numérico como el de los elementos finitos (MEF) para determinar el valor de la función objetivo (peso, desplazamiento...) y el grado de cumplimiento de las restricciones (limitaciones sobre tensiones máximas...) con el nivel de precisión que garantice la convergencia adecuada del proceso de optimización. El desarrollo de procedimientos eficaces de optimización requiere mejorar el rendimiento mediante actuaciones sobre ambos niveles.

Para la correcta convergencia del problema de optimización estructural es necesario controlar el error de discretización de cada uno de los individuos que se analizan. Tal y como muestran Ródenas et al. [29]  and [30] , si no se garantiza una mínima calidad en los resultados del análisis de cada diseño, que son los que se utilizan para alimentar el algoritmo de optimización, no se puede asegurar un comportamiento correcto del proceso de optimización, ya que se puede empobrecer la velocidad de convergencia del proceso, converger a una solución no óptima o incluso producir una solución final no factible que incumpla las restricciones impuestas. Por tanto, resulta necesario utilizar procedimientos de análisis adaptativos que proporcionen soluciones de la precisión adecuada con el mínimo coste computacional posible. Indudablemente, la utilización de este tipo de procedimientos supone un elevado coste computacional en el proceso de optimización, lo que evidencia aún más la necesidad de desarrollar software de análisis computacionalmente eficiente.

Así, este trabajo trata fundamentalmente sobre la mejora del rendimiento del nivel inferior del proceso de optimización, centrándose específicamente en el desarrollo de metodologías eficientes de análisis mediante el MEF que utilicen refinamiento h -adaptativo a fin de garantizar la adecuada precisión de los análisis.

Los análisis mediante el MEF se pueden complicar debido a que numerosos problemas industriales son geométricamente complejos y requieren muchas horas de análisis para generar una malla de EF adecuada. Esta tarea se puede simplificar enormemente usando técnicas que permitan la utilización de mallas de fácil construcción que sean independientes de la geometría. Ejemplos de distintos nombres con los que se conoce este tipo de aproximaciones son los de Fictitious Domain[16] , [9] , [28] , [7]  and [26] , Implicit Meshing[3] , Immersed FEM[49] , Inmersed Boundary Method[48]  and [37] , Fixed Grid FEM[15]  and [8] , etc. Este tipo de técnicas se han descrito en [6] bajo el término inglés Finite elements in ambient space . Estas técnicas se han mostrado como una alternativa a la aproximación tradicional mediante el MEF, en que se crea una malla de elementos finitos explícita del dominio para realizar el análisis. Con estas técnicas se plantea mallar el dominio de cálculo Ω implícitamente embebiendo a este en un dominio ω_E geométricamente mucho más simple, cuyo mallado resulta trivial. En nuestro caso, el dominio Ω_E será un dominio rectangular, que contiene al dominio Ω, que será discretizado mediante una malla cartesiana . Para realizar el análisis primero se intersecta el dominio Ω_E con el contorno de Ω de manera que en la evaluación de integrales de elemento solo participe el dominio de interés Ω. Tras aplicar las condiciones de restricción mediante técnicas específicamente adaptadas a mallados no conformes con el contorno del componente que hay que analizar, se puede proceder a la resolución final del problema.

Este tipo de técnicas se han utilizado tanto en el contexto del método de los volúmenes finitos (MVF) como en el del MEF. La literatura sobre este tipo de técnicas se remonta, según [7] , a los años sesenta, en que V.K. Saul’ev publica, en ruso, el artículo Solution of certain boundary-value problems on high-speed computers by the fictitious-domain method (Sibirsk. Mat. Z. 4:912-925;1963). Posteriormente se han aplicado en diferentes campos. Entre otras referencias en cada disciplina, se pueden citar aplicaciones en: acústica [16] , [17]  and [12] , dinámica de fluidos e interacción fluido estructura [48]  and [18] , problemas biomédicos [27]  and [39] , convección-difusión [28] , optimización [9] , [19] , [22]  and [46] , etc. El presente trabajo se centrará en el contexto del MEF.

Por otro lado, durante los últimos años se han desarrollado formulaciones avanzadas del MEF, como el Extended Finite Element Method[24]  and [44] (XFEM), del grupo de T. Belytschko, o el Generalized Finite Element Method[42]  and [43] (GFEM), del grupo de I. Babu${\textstyle {\check {s}}}$ka, en las que uno de los objetivos es independizar la malla de la geometría. XFEM está principalmente desarrollado para modelar grietas o inclusiones usando modelos donde la malla es independiente de la geometría de la grieta. Tanto la técnica XFEM como la GFEM se basan en el uso del método de la partición de la unidad [23] (PUM) para introducir funciones de enriquecimiento de la solución. Estas funciones permiten representar la discontinuidad de desplazamientos en las caras de grieta y la solución singular conocida en el extremo de la misma. Además, permiten introducir una descripción geométrica de la grieta a través del Level Set Method[40] (LSM). Esto mejora notablemente la precisión del modelo y permite además independizar la malla de la geometría, lo que resulta de enorme interés al analizar procesos de crecimiento de grietas. En GFEM se sigue un planteamiento similar basado en el PUM para incorporar funciones de enriquecimiento que describan las características conocidas de la solución del problema. Una de las implementaciones de GFEM permite independizar la malla de la geometría utilizando técnicas que permiten intersectar una malla de elementos (por ejemplo cartesiana) independiente de la geometría del componente que se va a analizar.

La principal desventaja de estas técnicas es la falta de precisión del método en los elementos situados sobre el contorno [7] , [3] , [37]  and [15] . En el entorno del MEF se ha desarrollado el estimador del error de discretización de Zienkiewicz y Zhu [50] (ZZ), que requiere la evaluación de una solución reconstruida, recovered , σ^* en el caso de tensiones, de mayor calidad que la solución proporcionada directamente por el MEF σ^h . El estimador ZZ goza de gran popularidad por su robustez, precisión y facilidad de implementación pero también porque en el proceso de cálculo se crea σ^* , que puede ser utilizado como solución en vez de σ^h . De entre las técnicas de recovery destaca sin duda la técnica Superconvergent Patch Recovery[51] (SPR). A través de diversos trabajos [35] , [10] , [31]  and [33] , Ródenas y sus colaboradores han mostrado modificaciones de la técnica SPR que proporcionan un campo σ^* de gran precisión, dado que en su obtención se impone localmente el cumplimiento de las ecuaciones de equilibrio en el interior y en el contorno, así como la de compatibilidad. Esto ha permitido incluso crear los primeros procedimientos prácticos de obtención de cotas superiores del error de discretización basados en recovery[10]  and [33] , propiedad que anteriormente requería, casi necesariamente, la utilización de estimadores de error residuales [2] .

La referencia [3] indica: «Unfortunately, for an implicit mesh it would be very difficult to implement such a superconvergent recovery scheme of the stress field for elements that intersect the boundary» . Sin embargo, en el contexto del Extended Finite Element Method[24]  and [44] (XFEM), donde también la malla es independiente de la geometría, ya han sido propuestas, para mejorar la calidad de la solución, técnicas de tipo recovery basadas en la técnica Moving Least Squares[47] , [4] , [5]  and [11] (MLS), y la técnica basada en SPR anteriormente referenciada [34]  and [33] , que proporciona importantes mejoras de la solución, especialmente en el contorno del componente, incluso en elementos atravesados por la grieta.

En este trabajo se han adaptado las técnicas de recovery desarrolladas por Ródenas y sus colaboradores [35] , [10] , [34]  and [33] a fin de neutralizar los problemas de falta de precisión en contornos en los métodos con mallas independientes de la geometría, al tiempo que permiten la utilización del estimador ZZ para guiar el proceso h -adaptativo. Estas 2 características del código desarrollado de EF basado en mallados cartesianos proporciona, con un bajo coste computacional, resultados de alta precisión que permiten el correcto guiado del proceso de optimización.

Se puede tener en cuenta que en un proceso de optimización estructural pueden existir ciertas zonas del contorno que se van a mantener fijas a lo largo del proceso de optimización. La estructura de datos creada para implementar la metodología de análisis desarrollada permite aprovechar estas características, reutilizando la información previamente evaluada en los elementos situados sobre contornos fijos en geometrías anteriormente analizadas, aumentando más aún la eficacia del procedimiento de optimización.

La sección 2 de este trabajo planteará formalmente los problemas de optimización y de elasticidad. La sección 3 estará dedicada a presentar la metodología de análisis basada en el uso de mallados cartesianos, y en la sección 4 se describirán las características principales de la técnica de recovery . En la sección 5 se introducirá la técnica para la reutilización de resultados comunes a las distintas geometrías analizadas. Posteriormente, en la sección 6 se expondrán resultados numéricos que mostrarán la eficacia de la metodología desarrollada. Finalmente, la sección 7 presentará las conclusiones más importantes.

2. Planteamiento del problema

2.1. Optimización de componentes estructurales

El problema de optimización se puede considerar como un problema definido de la siguiente forma: dado un espacio de decisión (espacio de búsqueda) X , un espacio objetivo (valores objetivo) Y , una función objetivo f  : X  ⟶ Y y determinadas restricciones g_i :

$minf({\boldsymbol {\mbox{x}}})$ $donde\quad {\boldsymbol {\mbox{x}}}=\left\{x_{i}\right\}\quad i=$$1,2,...,n$ $sujeto\quad a\quad {\boldsymbol {\mbox{g}}}({\boldsymbol {\mbox{x}}})\leq \left\{g_{j}({\boldsymbol {\mbox{x}}})\right\}\quad j=$$1,2,...,m$ $a_{i}\leq x_{i}\leq b_{i}\quad i=1,2,...,n$

( 1)

En el caso de optimización de componentes estructurales, f es la función objetivo (FO) que suele ser, comúnmente, el peso del componente, x_i son las variables de diseño que definen cada configuración geométrica x , y g_j son restricciones en desigualdad que normalmente se expresan en función de tensiones y/o desplazamientos. Los valores a_i y b_i definen restricciones laterales.

En este trabajo se ha considerado la utilización de algoritmos evolutivos para resolver el problema de optimización. En concreto, se ha utilizado el algoritmo denominado Differential Evolution (DE), desarrollado por Storn y Price [41] , que es un algoritmo robusto que ha proporcionado buenos resultados en su aplicación a problemas de muy distinto tipo. De las 2 versiones diferentes propuestas por Storn y Price para este algoritmo, para este trabajo se ha escogido la DE1. El algoritmo de optimización será el encargado de proponer las distintas configuraciones geométricas que analizar, cada una de las cuales definirá un problema elástico, pero para este trabajo únicamente se ha considerado el caso bidimensional.

2.2. Definición del problema elástico

Considérese el problema de elasticidad lineal en 2D. Sea u el campo de desplazamientos solución del siguiente problema de contorno definido en ${\textstyle \Omega \subset R^{2}}$ :

$-\nabla \cdot {\boldsymbol {\sigma }}({\boldsymbol {\mbox{u}}})=$${\boldsymbol {\mbox{b}}}\quad en\quad \Omega$ ${\boldsymbol {\sigma }}({\boldsymbol {\mbox{u}}}){\boldsymbol {\mbox{n}}}=$${\boldsymbol {\mbox{t}}}\quad en\quad {\Gamma }_{N}$ ${\boldsymbol {\mbox{u}}}={\tilde {\boldsymbol {\mbox{u}}}}\quad en\quad {\Gamma }_{D}$

( 2)

donde Γ_N y Γ_D , con ${\textstyle \partial \Omega ={\overline {\Gamma }}_{N}\cup {\overline {\Gamma }}_{D}}$ y Γ_N  ∩ Γ_D  = 0 son las partes del contorno donde se aplican las restricciones de Neumann y Dirichlet. La forma débil del problema se enuncia así: encontrar un u  ∈ V tal que:

$a({\boldsymbol {\mbox{u}}},{\boldsymbol {\mbox{v}}})=l({\boldsymbol {\mbox{v}}})\quad \forall \quad {\boldsymbol {\mbox{v}}}\in V$

( 3)

donde V es el espacio de prueba estándar para el problema elástico y:

$a({\boldsymbol {\mbox{u}}},{\boldsymbol {\mbox{v}}}):={\int }_{\Omega }{\boldsymbol {\sigma }}{\left({\boldsymbol {\mbox{u}}}\right)}^{T}{\boldsymbol {\epsilon }}({\boldsymbol {\mbox{v}}})d\Omega =$${\int }_{\Omega }{\boldsymbol {\sigma }}{\left({\boldsymbol {\mbox{u}}}\right)}^{T}{\boldsymbol {\mbox{D}}}^{-1}{\boldsymbol {\sigma }}({\boldsymbol {\mbox{v}}})d\Omega$

( 4)

$l({\boldsymbol {\mbox{v}}}):={\int }_{\Omega }{\boldsymbol {\mbox{b}}}^{T}{\boldsymbol {\mbox{v}}}d\Omega +$${\int }_{{\Gamma }_{N}}{\boldsymbol {\mbox{t}}}^{T}{\boldsymbol {\mbox{v}}}d\Gamma$

( 5)

donde D es el tensor de Hooke, y σ y ϵ denotan los operadores de tensión y deformación, respectivamente.

El problema anteriormente planteado se va a resolver numéricamente mediante una implementación del método de los elementos finitos, con refinamiento h -adaptativo, que utiliza mallados cartesianos junto con una estructura de datos jerarquizada [36] para facilitar el manejo de la información y reducir el coste computacional.

3. Código MEF basado en mallados cartesianos

En esta sección se describirá la metodología de cálculo mediante mallados cartesianos independientes de la geometría del problema que se va a analizar.

3.1. Generación de la malla de cálculo

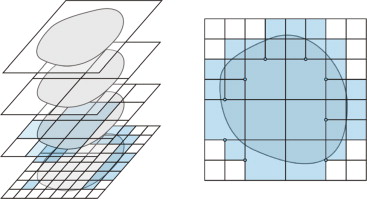
La metodología desarrollada se basa en la utilización de una secuencia de mallas cartesianas uniformemente refinadas, denominada batería de mallas ( fig. 1 a), que cubre el dominio que se va a analizar y que puede estar formada por elementos cuadriláteros bilineales o por cuadráticos serendípitos. El código desarrollado utiliza una adaptación de la estructura jerárquica de datos descrita en [36] . Esta estructura permite, por ejemplo, tener en cuenta que todos los términos involucrados en el cálculo de las matrices de rigidez de elementos geométricamente similares están relacionados por una constante que es función del factor de escala entre los mismos. De hecho, en el caso de elasticidad lineal en 2D, se puede demostrar que todas las matrices de rigidez de elementos geométricamente similares son exactamente iguales término a término. Dado que todos los elementos de la batería de mallas son geométricamente similares, la evaluación de los términos de la matriz de rigidez se realiza sobre un único elemento de referencia y es, inicialmente, compartida por todos los elementos de la batería de mallas . Por tanto, la estructura jerárquica, que determina las relaciones de jerarquía de la malla, permite el precálculo de gran cantidad de información de la malla y la reutilización de gran cantidad de cálculos, lo que aumenta notablemente la eficiencia computacional del algoritmo de cálculo.

Figura 1. Diferenciación entre la batería o estructura de mallas y la malla de cálculo.

En la implementación de la estructura de datos realizada se dispone de una serie de algoritmos que proporcionan las coordenadas de los nodos de la malla, la topología de los elementos, las distintas relaciones de jerarquía, de vecindad, etc., en el momento en que estos datos se necesitan. Esto permite el tratamiento virtual de toda la estructura de datos de la batería de mallas evitando su almacenamiento en memoria.

El primer paso del proceso de análisis consiste en determinar la malla de cálculo que se va a utilizar. Dado que se utiliza refinamiento h -adaptativo, inicialmente se han de determinar los elementos de cada nivel de la batería de mallas involucrados en el análisis ( fig. 1 a). La unión de los elementos seleccionados en cada nivel de la batería de mallas forma la malla de cálculo ( fig. 1 b). Puesto que la malla de cálculo está formada por elementos de distintos niveles (solamente se permite una diferencia máxima de un nivel de refinamiento entre elementos adyacentes), resulta necesario utilizar restricciones multipunto (MPCs) [1]  and [13] para garantizar continuidad C⁰ .

3.2. Intersección de la malla de cálculo. Integración

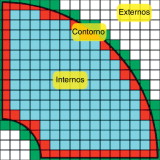
La malla de cálculo contiene 2 tipos de elementos (fig. 2 ).

• Elementos de contorno: situados a lo largo del contorno del dominio y solo parcialmente situados en el interior del dominio. La evaluación de las matrices de rigidez de elemento requiere evaluar la intersección de la malla con el dominio a fin de considerar adecuadamente el área de los elementos situada en el interior del dominio.
• Elementos internos: completamente situados en el interior del dominio. Estos elementos se tratan como elementos finitos estándar para los que su matriz de rigidez de elemento se ha evaluado sobre un único elemento de referencia.
• Elementos externos: que, al estar situados fuera del dominio de cálculo, no son considerados.

Figura 2. Tipos de elementos en relación con el contorno del problema. Elementos internos, externos y de contorno.

En la bibliografía existen múltiples procedimientos para realizar el proceso de intersección [15] , [8] , [18]  and [21] . El proceso utilizado en este trabajo es similar al usado en [8] . Este proceso tiene 3 pasos fundamentales:

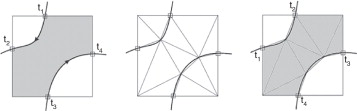
• Intersección del contorno con bordes de elemento: la figura 3 a muestra las intersecciones de las curvas que definen el contorno del dominio con los bordes de los elementos de la malla cartesiana. La zona coloreada representa el dominio del problema.

Figura 3. Proceso de intersección y generación de subdominios de integración de elementos de contorno.

• Adición de puntos intermedios: tal y como se muestra en la figura 3 b, se añaden puntos intermedios situados sobre el contorno. El número de puntos intermedios añadidos es creciente con la curvatura del contorno. A continuación se obtiene una triangulación de Delaunay a partir de los puntos de intersección calculados y con los nodos vértice de los elementos. Esta triangulación define subdominios de integración en el elemento.
• Selección de subdominios de integración internos: la figura 3 c representa los subdominios de integración seleccionados para evaluar la matriz de rigidez del elemento representado.

Este proceso genera, para cada elemento de contorno: a) una discretización del domino de cada elemento formada por un conjunto de subdominios de integración triangulares útiles para evaluar integrales de dominio y, al mismo tiempo, b) una discretización del contorno definida por los puntos del contorno utilizados para definir la triangulación, que será útil para evaluar integrales de contorno. Estas discretizaciones permitirán evaluar las integrales de elemento que se van a realizar. Así, las integrales de dominio en estos elementos se evaluarán considerando los subdominios de integración internos simplemente mediante:

${\int }_{{\Omega }^{e}\bigcap \Omega }f({\boldsymbol {\mbox{x}}})d\Omega =$$\sum _{i=1}^{{nst}_{e}}{\int }_{{\Omega }_{i}^{e}}f({\boldsymbol {\mbox{x}}})d\Omega$

( 6)

donde Ω_e es el dominio del elemento, nst_e es el número de subdominios de integración triangulares en el elemento e   , situados en el interior del dominio del problema, y ${\textstyle {\Omega }_{i}^{e}}$ es cada uno de estos subdominios de integración. Los dominios triangulares de integración pueden considerarse de tramos rectos si en la interpolación de desplazamientos se utilizan elementos lineales. Sin embargo, si se usan elementos cuadráticos es necesario tener al menos una aproximación cuadrática al contorno. Alternativamente, se pueden utilizar técnicas de mapping transfinito, habitualmente usadas en el contexto de refinamientos p -adaptativos [38]  and [45] , que permiten considerar la geometría exacta en el proceso de integración. La utilización del mapping transfinito para representar la geometría supone un aumento del coste computacional por subdominio de integración pero reduce al máximo el número total de subdominios. Los resultados presentados en este trabajo consideran una aproximación a la geometría del mismo orden que la interpolación de elementos finitos, dejando el uso del mapping transfinito para problemas que requieran una mayor precisión.

De manera similar, la evaluación de integrales de contorno se realizará considerando la discretización en nlc_e partes del contorno Γ dentro de cada elemento e   . Cabe señalar que en este caso, dado que se dispone de la definición paramétrica de la curva, cada tramo del contorno dentro del elemento ${\textstyle {\Gamma }_{i}^{e}}$ corresponde al contorno exacto del problema y no a una discretización en tramos rectos del mismo, como podría inferirse de la figura 3 c

${\int }_{{\Omega }^{e}\bigcap \Gamma }f({\boldsymbol {\mbox{x}}})d\Gamma =$$\sum _{i=1}^{{nlc}_{e}}{\int }_{{\Gamma }_{i}^{e}}f({\boldsymbol {\mbox{x}}})d\Gamma$

( 7)

3.3. Criterios de refinamiento

Existen 2 criterios de refinamiento implementados en el software: el primero de ellos está basado en criterios geométricos [20] ; el segundo, en la minimización del error en norma energética.

3.3.1. Refinamiento geométrico

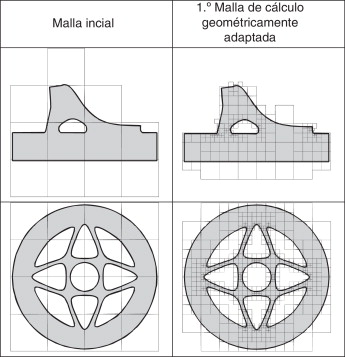
El proceso de análisis comienza adaptando las dimensiones de una malla cartesiana al dominio que se va a analizar, de manera que este quede embebido dentro de la malla. Esta malla cartesiana será una de las de la batería de mallas, del nivel especificado por el usuario. Posteriormente, la malla se interseca con el dominio del componente que se va a analizar. Para generar la primera malla de análisis se ejecuta un primer paso de refinamiento basado en la geometría del componente. En este paso se procede a refinar los elementos de contorno dentro de los cuales el indicador de curvatura del contorno, definido por la expresión (8) , sea excesivo. El proceso de refinamiento se continúa repitiendo hasta que en todos los elementos de contorno el indicador de curvatura relativa sea suficientemente bajo, generándose así la primera malla de cálculo, como se puede ver en los ejemplos de la tabla 1

Tabla 1. Comparación entre las mallas iniciales y la malla geométricamente adaptada mediante el criterio de curvatura

$k={\frac {\sum _{i=1}^{NinP}d_{i}}{NinP\cdot L}}$

( 8)

3.3.2. Refinamiento por minimización de error en norma energética

Particularizando la ecuación (9) al dominio de cada uno de los elementos de la malla se obtiene una estimación del error en norma energética a nivel de elemento. Con esta información, y usando el criterio de equidistribución del error en los elementos de la nueva malla [14] , se obtienen los nuevos tamaños de elemento en cada zona, lo que proporcionará las siguientes mallas de cálculo, tal y como se representa en la tabla 2

Tabla 2. Segunda y tercera malla de cálculo obtenidas a partir de la información del estimador en norma energética

${\left\|e_{es}\right\|}^{2}={\int }_{\Omega }{\left({\boldsymbol {\sigma }}^{\ast }-{\boldsymbol {\sigma }}^{h}\right)}^{T}{\boldsymbol {\mbox{D}}}^{-1}({\boldsymbol {\sigma }}^{\ast }-$${\boldsymbol {\sigma }}^{h})d\Omega$

( 9)

3.4. Reutilización de información de elemento

Las mallas cartesianas permiten reutilizar fácilmente información previamente calculada. En este apartado se expondrá, en particular, la reutilización de información asociada a la evaluación de la matriz de rigidez: a) de elementos del interior del dominio, y b) de elementos del contorno entre distintas geometrías.

3.4.1. Elementos del interior del dominio

En [36] se mostró que si 2 elementos son geométricamente semejantes, los términos involucrados en la evaluación de sus matrices de rigidez (matriz B de derivadas de funciones de forma y matriz jacobiana J de transformación de coordenadas) están relacionadas por una constante que es función del factor de escala que los relaciona. De hecho, en elasticidad lineal 2D (D constante), la matrices de rigidez serían exactamente iguales término a término. En el caso que nos ocupa, todos los elementos de la batería de mallas cartesianas son geométricamente semejantes, por lo que todos ellos, inicialmente, comparten el mismo objeto que almacena los distintos datos utilizados en la evaluación de la matriz de rigidez de un elemento de referencia, obteniéndose los valores de B y J para los elementos de los distintos niveles de la malla simplemente multiplicando los correspondientes valores evaluados para el elemento de referencia por una constante que es función del factor de escala (ver detalles en [36] ). Se obtiene así una importante mejora en la eficiencia del proceso de generación del sistema de ecuaciones, ya que todos los elementos interiores de las mallas de cálculo compartirán esta información.

3.4.2. Elementos del contorno entre distintas geometrías

Dado que todos los elementos del interior del dominio se crean de manera trivial y comparten información de sus matrices de rigidez, se puede decir que el coste computacional del procedimiento de generación del modelo de elementos finitos es el asociado exclusivamente al tratamiento de los elementos del contorno, es decir, a un problema (N-1)-dimensional.

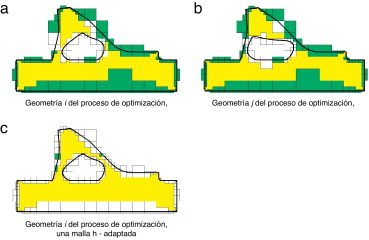
Cada uno de los elementos del contorno ha de tener un tratamiento individualizado, siguiendo el planteamiento expuesto en la sección 3.2 , puesto que cada uno de ellos estará, en general, cortado de manera distinta por el contorno. Evidentemente, el procedimiento desarrollado almacena información de manera que si un elemento del contorno se usa de nuevo en otra malla de la secuencia de análisis h -adaptativa, su información se reutiliza. Por lo tanto, en el análisis de cada una de las geometrías, el procedimiento permite reutilizar información para una geometría dada, es decir, de manera vertical . Como ejemplo, en la figura 4 se pueden observar dos mallas distintas para el mismo individuo i . En la figura 4 b se aprovecha la información evaluada de manera vertical en la figura 4 a de todos los elementos azules, y solo es necesario calcular de nuevo aquellos blancos.

Figura 4. Ejemplo de una geometría en su proceso de refinamiento: reutilización vertical . Los elementos azules son aquellos elementos de contorno que se reutilizan entre las dos mallas de la misma geometría. La zona amarilla corresponde a elementos internos. En la malla representada en la figura (b) solo se han evaluado los elementos sin colorear.

En el proceso de optimización, especialmente cuando se utilizan algoritmos evolutivos, se analizan gran cantidad de individuos, y cada uno de ellos corresponde a una geometría distinta. Con las técnicas tradicionales de mallado resulta casi imposible que, de manera automática, se reutilice información entre elementos de 2 geometrías distintas. Sin embargo, el procedimiento de análisis con mallados cartesianos desarrollado permite compartir información de manera horizontal entre algunos elementos del contorno de distintas geometrías. Para ello, de cara al proceso de optimización, los contornos se clasifican en 2 grupos:

• Contornos fijos: permanecen fijos durante todo el proceso de optimización.
• Contornos variables: se modifican durante el proceso de optimización por ser función de los parámetros que se van a optimizar que definen la geometría del problema.

En la figura 5 se observa el funcionamiento de reutilización horizontal de la información. En este caso, los elementos verdes de las figuras 5 a y 5 b se reutilizan en la figura 5 c.

Figura 5. Comparación de 2 geometrías distintas j  > i durante el proceso de optimización. Se observa que todos los elementos de color verde evaluados en individuos anteriores se reutilizan en los nuevos. Como se verá en la sección 5 , los contornos fijos de este problema son el contorno externo y el tramo recto inferior del contorno interno.

4. Recuperación del campo de tensiones

El uso de mallados cartesianos independientes de la geometría acelera el proceso de resolución del problema de elementos finitos. Sin embargo, como contrapartida, la calidad de los resultados en los elementos de contorno es baja [15]  and [3] . Loon et al. [21] proponen una alternativa a este problema consistente en modificar la geometría de los elementos del contorno para adaptarse al mismo, creando una malla conforme con el contorno. Sin embargo, nuestra propuesta se centra en mejorar la solución en tensiones utilizando técnicas de reconstrucción de la solución que garanticen un buen grado de calidad en el contorno. Al mismo tiempo, el campo reconstruido de tensiones se utilizará en la ecuación (9) para obtener una estimación del error de gran calidad, que permitirá guiar adecuadamente el proceso de refinamiento h -adaptativo de la malla. Para determinar el campo mejorado de tensiones se va a utilizar una técnica de reconstrucción de tipo Superconvergent Patch Recovery (SPR) desarrollada por Zienkiewicz y Zhu [51] , [52] , [54]  and [53] . La técnica propuesta se denomina SPR-C y fue expuesta inicialmente en [32] , adaptada posteriormente al Extended Finite Element Method[31]  and [33] y finalmente adaptada al caso de mallados cartesianos independientes de la geometría [25] . En esta técnica se propone un método de reconstrucción del campo de tensiones donde se fuerza, a nivel local dentro del patch formado por los elementos que rodean a cada nodo vértice, el cumplimiento de las ecuaciones de equilibrio interno, el equilibrio en el contorno y la compatibilidad, lo que garantiza un campo reconstruido de tensiones de gran calidad incluso en el contorno.

El método planteado se basa en la minimización, en patches de elementos conectados a cada nodo vértice, de la norma L₂ de la diferencia entre el campo reconstruido σ^* y el directamente extraído de EF σ^h según la ecuación (10) , donde ${\textstyle {\sigma }_{i}^{\ast }={\boldsymbol {\mbox{p}}}{\boldsymbol {\mbox{a}}}_{i}}$ , siendo ${\textstyle i=\left\{xx,yy,xy\right\}}$ , p la base polinómica y a_i los coeficientes incógnita que evaluar. Minimizando e integrando numéricamente la ecuación (10) y combinando las 3 componentes de tensiones, se obtiene el sistema de ecuaciones lineales de la expresión (11) , donde ${\textstyle \left|{\boldsymbol {\mbox{J}}}\right|}$ es el jacobiano de la transformación de coordenadas y P viene definido en (12) .

Las restricciones C de cumplimiento de las ecuaciones de equilibrio (interno y de contorno) y compatibilidad se imponen mediante multiplicadores de Lagrange, lo que da lugar al sistema de ecuaciones mostrado en (14) , que proporcionará los coeficientes incógnita que definirán cada una de las componentes de tensión que dan lugar a un campo estáticamente admisible en cada patch

$\Psi ={\int }_{{\Omega }_{i}}{\left({\boldsymbol {\sigma }}^{\ast }-{\boldsymbol {\sigma }}^{h}\right)}^{2}d\Omega$

( 10)

$\sum _{GP}{\boldsymbol {\mbox{P}}}^{T}{\boldsymbol {\mbox{P}}}\vert {\boldsymbol {\mbox{J}}}\vert \omega {\boldsymbol {\mbox{a}}}=$$\sum _{GP}{\boldsymbol {\mbox{P}}}^{T}{\boldsymbol {\sigma }}^{h}\vert {\boldsymbol {\mbox{J}}}\vert \omega$

( 11)

${\boldsymbol {\mbox{P}}}=\left[{\begin{array}{ccc}{\boldsymbol {\mbox{p}}}&0&0\\0&{\boldsymbol {\mbox{p}}}&0\\0&0&{\boldsymbol {\mbox{p}}}\\\end{array}}\right]$

( 12)

${\boldsymbol {\mbox{M}}}=\sum _{GP}{\boldsymbol {\mbox{P}}}^{T}{\boldsymbol {\mbox{P}}}\vert {\boldsymbol {\mbox{J}}}\vert \omega \quad {\boldsymbol {\mbox{G}}}=$$\sum _{GP}{\boldsymbol {\mbox{P}}}^{T}{\boldsymbol {\sigma }}^{h}\vert {\boldsymbol {\mbox{J}}}\vert \omega$

( 13)

$\left[{\begin{array}{cc}{\boldsymbol {\mbox{M}}}&{\boldsymbol {\mbox{C}}}^{T}\\{\boldsymbol {\mbox{C}}}&{\boldsymbol {0}}\end{array}}\right]\left\{{\begin{array}{c}{\boldsymbol {\mbox{a}}}\\{\boldsymbol {\lambda }}\end{array}}\right\}=\left\{{\begin{array}{c}{\boldsymbol {\mbox{G}}}\\{\boldsymbol {\theta }}\end{array}}\right\}\quad \Rightarrow \quad {\boldsymbol {{\mbox{QA}}={\mbox{f}}}}$

( 14)

4.1. Eficiencia del proceso de reconstrucción del campo de tensiones

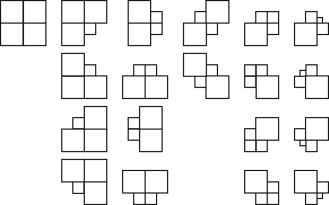
En el proceso de refinamiento h -adaptativo de la malla, entre 2 elementos adyacentes se permite una diferencia máxima de un nivel de refinamiento. Teniendo esto en cuenta, junto con las características topológicas de las mallas, es fácil comprobar que aparecerá un número reducido de configuraciones de patches internos. En la figura 6 se muestran las 19 posibles configuraciones de patches internos para un problema de 2 dimensiones.

Figura 6. Posibles formas de patches internos en 2D.

La evaluación de los coeficientes de los polinomios a que describen el campo recuperado según la ecuación (14) se realiza en un espacio normalizado de coordenadas. Así, la matriz de coeficientes en esta ecuación será la misma para todos los patches internos de la malla de cada una de las configuraciones mostradas en la figura 6 , que son los que contienen, exclusivamente, elementos internos. Por tanto, para acelerar el proceso de recuperación de tensiones se procede, en primer lugar, a codificar y clasificar cada uno de los patches internos de la malla, agrupándolos en hasta 19 conjuntos de patches . Para cada uno de estos conjuntos se evalúa una única vez la inversa de la matriz del sistema Q⁻¹ de (14) , para posteriormente evaluar el vector de incógnitas en cada patch como A = Q⁻¹ f . Este procedimiento reduce considerablemente el tiempo computacional asociado a la recuperación del campo de tensiones y lo hace depender, en la práctica, del número de patches en el contorno, lo que corresponde, nuevamente, a un espacio (N -1)-dimensional.

5. Resultados numéricos

El objetivo de esta sección es el de verificar la robustez y la eficiencia del nivel inferior (algoritmo de resolución CG-FEM) y su efecto sobre el rendimiento computacional del algoritmo de optimización. Para comprobar el funcionamiento del nivel inferior se analiza el comportamiento del algoritmo de resolución utilizando, en primer lugar, un problema de optimización para el que se conoce la solución exacta, considerándose posteriormente problemas sin solución exacta. Para todos los análisis se ha utilizado elementos cuadriláteros cuadráticos de 8 nodos. Los parámetros de configuración del algoritmo evolutivo (individuos por generación, número de generaciones...) se han basado en experiencias anteriores [29] . La selección de dichos parámetros tiene influencia sobre el comportamiento del algoritmo evolutivo, influencia que ya se ha evaluado en bibliografía relevante [41] . No obstante, la selección del dichos parámetros no afecta al propósito del artículo.

En los análisis se ha utilizado un PC DELL PE1950 con 2 procesadores Intel Xeon E5430 y con 32Gb de memoria. El sistema operativo es Windows Server 2003 Enterprise x64 SP2.

El parámetro para estimar el error de discretización utilizado en los análisis es el error relativo estimado en norma energética γ definido por la expresión (15) donde la norma energética ${\textstyle \left\|{\boldsymbol {\mbox{u}}}^{h}\right\|}$ viene definida por la expresión (16)

${\gamma }^{2}={\frac {{\left\|{\boldsymbol {\mbox{e}}}_{es}\right\|}^{2}}{{\left\|{\boldsymbol {\mbox{u}}}^{h}\right\|}^{2}+{\left\|{\boldsymbol {\mbox{e}}}_{es}\right\|}^{2}}}$

( 15)

${\left\|{\boldsymbol {\mbox{u}}}^{h}\right\|}^{2}={\int }_{\Omega }{\left({\boldsymbol {\sigma }}^{h}\right)}^{T}{\boldsymbol {\mbox{D}}}^{-1}{\boldsymbol {\sigma }}^{h}d\Omega$

( 16)

Para definir la precisión del estimador de error, en el problema con solución analítica se utilizará el índice de efectividad θ   dado por la siguiente expresión, donde ${\textstyle \left\|{\boldsymbol {e_{es}}}\right\|}$ y ${\textstyle \left\|{\boldsymbol {e}}\right\|}$ son el error estimado y exacto en norma energética, respectivamente:

$\theta ={\frac {\left\|{\boldsymbol {\mbox{e}}}_{es}\right\|}{\left\|{\boldsymbol {\mbox{e}}}\right\|}}$

( 17)

5.1. Optimización de sección sometida a presión en superficie circular interna

Para comprobar el funcionamiento de la aplicación combinada entre el software de optimización y el de resolución de elementos finitos se ha resuelto un problema con solución óptima analítica conocida. En el problema se pretende minimizar el área de una sección transversal sometida a presión en su superficie circular interna manteniendo las tensiones de Von Mises por debajo del límite de fluencia del material S_y .

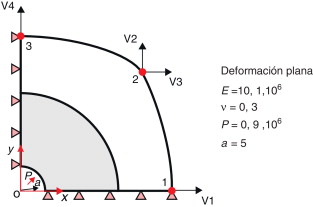
La superficie externa de la sección está dada por un spline cúbico definido por 3 puntos. Sobre la superficie circular interna se aplica una presión P . Como se muestra en la figura 7 , se han considerado 2 condiciones de simetría para definir el modelo.

Figura 7. Sección transversal con presión en superficie circular interna. Variables de diseño y geometría óptima (área sombreada).

La solución óptima tendrá una superficie externa circular, es decir, la geometría óptima corresponderá a la de un cilindro sometido a presión interna, configuración cuya solución exacta en desplazamientos y tensiones es:

$u_{r}={\frac {P(1+\nu )}{E(k^{2}-1)}}\left[(1-2\nu )r+{\frac {R_{0}^{2}}{r}}\right];k=$${\frac {R_{0}}{a}}$

( 18)

${\sigma }_{r}={\frac {P}{k^{2}-1}}\left(1-{\frac {R_{0}^{2}}{r^{2}}}\right)$ ${\sigma }_{\theta }={\frac {P}{k^{2}-1}}\left(1+{\frac {R_{0}^{2}}{r^{2}}}\right)$

( 19)

Estas expresiones permiten determinar el radio externo mínimo para S_y  = 2 ·10⁶ . El radio resultante es R₀  = 10,67033824461, que corresponde a un área óptima A_opt  = 69,787307715081.

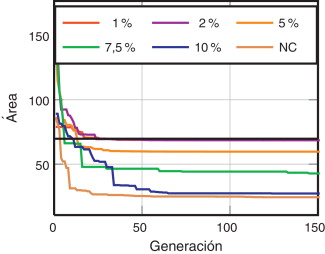
Las variables de diseño corresponden a las coordenadas de los puntos 1, 2 y 3 de la figura 7 . El algoritmo evolutivo ha considerado un total de 150 generaciones con 30 individuos por generación. Se han realizado optimizaciones para varios niveles de error admisibles prescritos: γ ≤ (1, 2, 5, 7,5, 10, NC)% para comprobar la influencia del error de discretización sobre el error en el área obtenida, donde NC utiliza solamente el refinamiento geométrico inicial.

En la figura 8 se muestra la evolución del área con el número de generaciones para los diversos análisis, siendo la línea negra el valor óptimo analítico. En la figura se observa que el área obtenida de los análisis tiende al área óptima a medida que se imponen valores más pequeños de γ .

Figura 8. Evolución del área del cilindro con el número de generaciones para distintos valores de γ .

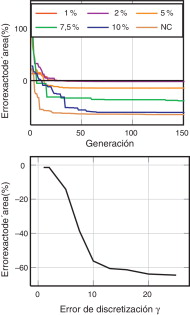
El la figura 9 a se muestra la evolución del error relativo entre el área obtenida y el área óptima analítica. En la figura 9 b se muestra el error relativo en área con respecto a la solución analítica, evaluado en función del error prescrito γ . Se observa que para valores γ ≤ 10 % el error de discretización prescrito influye notablemente en el error en área obtenido al final del proceso de optimización. A partir de γ  = 10% las variaciones de γ prácticamente no tienen influencia sobre el resultado final, dado que el refinamiento geométrico proporciona ya soluciones con aproximadamente un error del 10%, independientemente del nivel de error prescrito. Resultados similares a los aquí presentados, que muestran la necesidad de garantizar que los análisis de EF se realizan con un nivel de precisión adecuado, pueden encontrarse en [29]  and [30] . Aparentemente, en la figura 9 pasar de γ  = 1% a γ  = 2% no supone mejora alguna. Sin embargo, a la hora de analizar estos resultados hay que tener en cuenta que en la definición del contorno externo se ha utilizado un spline definido por 3 puntos, que no puede representar exactamente una circunferencia. Dado que la parametrización utilizada no puede representar la geometría óptima analítica, el proceso converge en función de γ a una solución cercana, pero no igual a la óptima.

Figura 9. Relación entre el error en el área óptima y el error de discretización γ para el problema del cilindro sometido a presión interna.

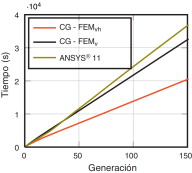
La figura 10 compara los tiempos de cálculo en función del número de generación obtenidos en 3 situaciones: a) usando CG-FEM , compartiendo información de intersecciones en contornos de manera vertical (entre las distintas mallas del análisis adaptativo de cada individuo); b) usando CG-FEM , compartiendo información de intersecciones en contornos de manera horizontal (también entre los distintos individuos del proceso de optimización), y c) utilizando el código comercial ANSYS^® 11 como solver , utilizando la instrucción ADAPT para realizar los análisis h -adaptativos, basados en el uso del mallador libre 2D de ANSYS^® 11 con elementos cuadráticos. Esta figura muestra claramente que el rendimiento del código basado en el uso de mallas cartesianas supera notablemente al del código comercial (compilado), pese a que el código del primero está completamente desarrollado en Matlab^® 2009b, no habiéndose compilado ninguna de las subrutinas creadas. Se observa también claramente que el hecho de poder compartir información de manera horizontal entre distintas geometrías reduce notablemente el tiempo total del proceso de optimización. El ahorro en tiempo computacional aumenta a medida que disminuye la relación entre la longitud del perímetro y el área del dominio analizado. Hay que tener en cuenta que este problema no resulta especialmente favorable a la técnica de reutilización horizontal de información (entre distintas geometrías), dado que el único contorno fijo es el del arco de circunferencia que define el interior de la sección.

Figura 10. Comparación de tiempos de cálculo del proceso de optimización utilizando: ANSYS® 11, código de CG-FEM compartiendo verticalmente   la información de intersecciones (curva ${\textstyle {CG-FEM}_{v}}$ ) y compartiendo también horizontalmente esta información (curva CG  − FEMvh ).

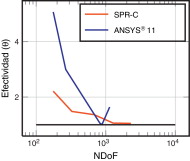
La figura 11 muestra la evolución del índice de efectividad θ del estimador de error con el número de grados de libertad para la geometría correspondiente a la solución óptima analítica. Se muestra la evolución de θ tanto para los resultados de campo de tensiones reconstruido mediante el promediado directo en nodos usado en ANSYS^® 11 y mediante la técnica de reconstrucción cuyo uso se propone en este artículo. Los valores de θ cercanos a la unidad indican buena precisión del estimador de error. La buena precisión del estimador de error tiene varias repercusiones. En primer lugar, el adecuado comportamiento del análisis h -adaptativo requiere una adecuada estimación del error de discretización a nivel local, algo que no puede obtenerse si no hay buena estimación a nivel global. Por otro lado, valores de θ cercanos a la unidad son el producto de campos σ^* de gran precisión. Esto resulta muy importante dado que σ^* será utilizado en la evaluación de las tensiones que guiarán el procedimiento de optimización, ya que son más precisas que las de EF. Finalmente, una estimación precisa del error de discretización permitirá detener el proceso de refinamiento h -adaptativo de la malla en momento adecuado. La figura muestra claramente que la estimación de error obtenida con la técnica propuesta en este artículo, que proporciona efectividades θ  ≈ 1, mejora notablemente la obtenida mediante el procedimiento utilizado por ANSYS^® 11.

Figura 11. Cilindro sometido a presión interna. Q8. Evolución de la efectividad global del estimador del error (θ ) con el número de grados de libertad para el solver ANSYS® 11 y para la técnica SPR-C. La línea negra indica la unidad.

5.2. Presa de gravedad

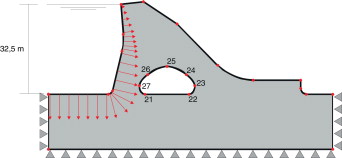
En este problema se desea maximizar el área del hueco interno de la sección de la presa de gravedad cuyo modelo se muestra en la figura 12 o, equivalentemente, minimizar la sección de material, manteniendo las tensiones máximas de Von Mises por debajo de S_y . En el modelo se ha considerado que el lado inferior y los laterales tienen impedido su desplazamiento en dirección perpendicular al contorno. Se han considerado tanto la presión ejercida por el agua como las cargas gravitatorias.

Figura 12. Optimización de una presa de gravedad. Modelo del problema por resolver y geometría inicial.

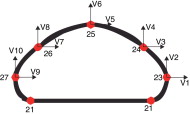
Para el proceso de optimización se han utilizado 100 generaciones y 30 individuos por generación. Las variables de diseño corresponden a las coordenadas (x , y ) de los puntos 23 al 27 del agujero interno ( fig. 13 ). Para el hormigón se ha considerado un módulo de Young ${\textstyle E=13,1\cdot {10}^{10}{\frac {N}{m^{2}}}}$ , un coeficiente de Poisson μ  = 0,25 y un límite de fluencia ${\textstyle S_{y}=27,5\cdot {10}^{6}{\frac {N}{m^{2}}}}$ . La densidad del agua se ha tomado de ${\textstyle 1.000{\frac {kg}{m^{3}}}}$ y la del hormigón de ${\textstyle 2.300{\frac {kg}{m^{3}}}}$ .

Figura 13. Optimización de una presa de gravedad. Detalle del agujero interno y variables de diseño.

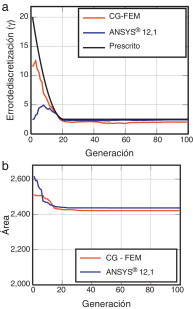
Este problema se ha resuelto utilizando tanto ANSYS^® 12.1 como el código CG-FEM propuesto en este artículo, con un error de discretización prescrito (γ ) variable, desde un valor inicial de 20% hasta un valor de 2,5% en 20 iteraciones, tal y como muestra la figura 14 a, a fin de reducir el coste computacional en las primeras etapas de la optimización tal como se describe, por ejemplo, en [29] . Se observa que en la figura ambos solvers son capaces de conseguir un error global menor que el prescrito.

Figura 14. Optimización de una presa de gravedad. Evolución del error prescrito, estimado y del área de la sección transversal de la presa para una evolución del error prescrito variable. Se han utilizado como solvers CG-FEM y ANSYS® 12.1.

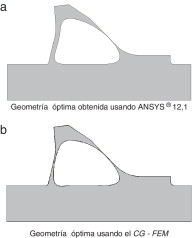
En la figura 15 se muestran las geometrías óptimas obtenidas en ambos procesos de optimización. Se obtienen unas áreas de 2.420, 92 m² con ANSYS^® 12.1 y 2.447,0 m² con el solver CG-FEM .

Figura 15. Optimización de una presa de gravedad. Geometrías óptimas obtenidas después del proceso de optimización estructural.

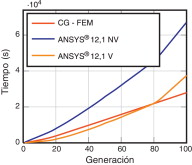
La figura 16 muestra que el tiempo que requiere ANSYS^® 12.1 (azul) para resolver el problema de optimización es muy superior al requerido por el programa CG-FEM (rojo). Esto ocurre, en primer lugar, porque el número de individuos que analizar por ANSYS^® 12.1 es mayor, ya que el programa considera que muchas de las geometrías por analizar no son válidas, puesto que es incapaz de mallarlas. El porcentaje de individuos considerados como defectuosos por ANSYS^® 12.1 es del 50,11%. Cuando se lanza la aplicación de optimización con el solver CG-FEM , el porcentaje de individuos defectuosos es del 4,13%. La aleatoriedad implícita en el proceso de optimización justificaría cierto grado de diferencia en el porcentaje de individuos defectuos, pero no llegaría a justificar las diferencias obtenidas. Este análisis muestra la robustez de la metodología de análisis mediante CG-FEM . Este comportamiento del nivel inferior no es el que se espera, ya que añade restricciones extras no deseadas al problema de optimización limitando el espacio de soluciones.

Figura 16. Comparación de tiempos de cálculo entre ANSYS® 12.1 (considerando todas las geometrías propuestas por el solver , incluyendo el tiempo dedicado a geometrías no válidas, curva ANSYS® 12.1 NV, o solamente considerando las geometrías válidas, curva ANSYS® 12.1 V) y la metodología propuesta, curva CG-FEM .

La figura 16 muestra el tiempo acumulado total de cálculo cuando en el nivel inferior se utiliza ANSYS^® 12.1 teniendo en cuenta (curva ANSYS^® 12.1 NV) el procesamiento que requieren tanto las geometrías consideradas válidas como las no válidas, y lo compara con el caso en que solo se muestra el tiempo dedicado al análisis de geometrías válidas conseguido con ANSYS^® 12.1 y con la metodología propuesta (curvas ANSYS^® 12.1 V y CG-FEM , respectivamente). En estas curvas se puede observar que la curva CG-FEM evoluciona linealmente a partir de la generación 20, una vez alcanzado el error mínimo prescrito, mientras que en las obtenidas con ANSYS^® 12.1 hay un aumento más pronunciado de tiempo en las últimas generaciones, probablemente debido a que al final del proceso se generan configuraciones geométricas extremas (la figura 15 muestra las geometrías óptimas obtenidas al final del proceso), que aparentemente conducen a mayores tiempos de mallado al utilizar ANSYS^® 12.1.

En este caso, los tiempos de cálculo representados en la figura 15 por las curvas ANSYS^® 12.1 NV y CG-FEM muestran que con cada una de las técnicas, el tiempo de proceso por cada configuración geométrica es prácticamente el mismo, pese a que CG-FEM está íntegramente programado en Matlab^® 2009b y que tiene una proporción de elementos de contorno muy elevada, lo que reduce la eficacia computacional de la metodología propuesta.

6. Conclusiones

En este artículo se ha propuesto la utilización de un procedimiento de cálculo de componentes estructurales 2D mediante el MEF, que ha sido implementado con un software denominado CG-FEM , como módulo de cálculo en programas de optimización estructural. Las características principales de CG-FEM son:

• Está basado en el uso de mallados cartesianos independientes de la geometría.
• Utiliza una estructura de datos jerárquica.
• Utiliza procedimientos muy precisos de reconstrucción de la solución.

Estas características han permitido que CG-FEM sea un código de EF computacionalmente eficaz que proporciona resultados de gran precisión. Centrándonos en el nivel inferior de los algoritmos de optimización estructural, la eficacia de estos últimos requiere que los análisis numéricos se realicen con el mínimo coste computacional posible para aumentar su rendimiento, así como con gran precisión, con el fin de guiar adecuadamente el proceso de optimización hacia la solución óptima. En este sentido, el uso de los procedimientos de cálculo sobre los que se basa CG-FEM se puede considerar de gran relevancia en programas de optimización de forma estructural.

Pese a que en este artículo se ha utilizado CG-FEM como nivel inferior de un algoritmo de optimización basado en un algoritmo evolutivo, también se podría utilizar en combinación con otro tipo de algoritmos. De hecho, en estos momentos se está desarrollando un procedimiento de cálculo de sensibilidades que permitirá su utilización con algoritmos basados en el gradiente de la solución. De la misma manera, también se están iniciando desarrollos encaminados a aumentar el rendimiento de CG-FEM a través del uso de procedimientos de cálculo en paralelo, para los que resultan especialmente adecuados los mallados cartesianos, junto con la estructura de datos jerárquica.

Agradecimientos

Los autores agradecen el apoyo financiero recibido del proyecto de investigación DPI2010-20542 del Ministerio de Economía y Competitividad y del programa FPU (AP2008-01086), de la Universitat Politècnica de València y de la Generalitat Valenciana (PROMETEO/2012/023). Los autores también agradecen el apoyo ofrecido por el proyecto europeo INSIST (FP7-PEOPLE-2011-ITN).

Los autores también agradecen el uso de las figuras 2-7 tomadas de la publicación: E. Nadal, J. J. Ródenas, J. Albelda, M. Tur, J. E. Tarancón, F. J. Fuenmayor, Efficient Finite Element Methodology Based on Cartesian Grids: Application to Structural Shape Optimization. Abstract and Applied Analysis, vol. 2013, Article ID 953786, 19 páginas, 2013. doi:10.1155/2013/953786.

References

1. [1] J.F. Abel, M.S. Shepard; An algorithm for multipoint constraints in finite element analysis; Int. J. Numer. Methods Eng., 14 (1979), pp. 464–467
2. [2] M. Ainsworth, J. Tinsley Oden; A posteriori Error Estimation in Finite Element Analysis; John Wiley & Sons, Chichester (2000)
3. [3] J. Bishop; Rapid stress analysis of geometrically complex domains using implicit meshing; Comput. Mech., 30 (2003), pp. 460–478
4. [4] S.P.A. Bordas, M. Duflot; Derivative recovery and a posteriori error estimate for extended finite elements; Comput. Meth. Appl. Mech. Eng., 196 (35-36) (2007), pp. 3381–3399
5. [5] S.P.A. Bordas, M. Duflot, P. Le; A simple error estimator for extended finite elements; Commun. Numer. Methods Eng., 24 (11) (2008), pp. 961–971
6. [6] S.P.A. Bordas, T. Rabczuk, N.-X. Hung, V.P. Nguyen, S. Natarajan, T. Bog, et al.; Strain smoothing in FEM and XFEM; Comput. Struct., 88 (23-24) (2010), pp. 1419–1443
7. [7] E. Burman, P. Hansbo; Fictitious domain finite element methods using cut elements: I. A stabilized Lagrange multiplier method. Department of Mathematical Sciences; Chalmers University of Technology. Göteborg Sweden, 43 (2009)
8. [8] F. Daneshmand, M.J. Kazemzadeh-Parsi; Static and dynamic analysis of 2D and 3D elastic solids using the modified FGFEM; Elem. Anal. Des., 228 (2009), pp. 3891–3910
9. [9] G.C.A. DeRose Jr., A.R. Díaz; Solving three-dimensional layout optimization problems using fixed scale wavelets; Comput. Mech., 25 (2000), pp. 274–285
10. [10] P. Díez, J.J. Ródenas, O.C. Zienkiewicz; Equilibrated patch recovery error estimates: simple and accurate upper bounds of the error; Int. J. Numer. Methods Eng., 69 (10) (2007), pp. 2075–2098
11. [11] M. Duflot, S.P.A. Bordas; A posteriori error estimation for extended finite elements by an extended global recovery; Int. J. Numer. Methods Eng., 76 (2008), pp. 1123–1138
12. [12] C. Farhat, U. Hetmaniuk; A fictitious domain decomposition method for the solution of partially axisymmetric acoustic scattering problems. Part I: Dirichlet boundary conditions.; Int. J. Numer. Methods Eng., 54 (2002), pp. 1309–1332
13. [13] C. Farhat, C. Lacour, D. Rixen; Incorporation of linear multipoint constraints in substructured based iterative solvers. Part 1: A numerically scalable algorithm.; Int. J. Numer. Methods Eng., 43 (1998), pp. 997–1016
14. [14] F.J. Fuenmayor, J.L. Oliver; Criteria to achieve nearly optimal meshes in the h-adaptive finite element method; Int. J. Numer. Methods Eng., 39 (23) (1996 December), pp. 4039–4061
15. [15] M.J. García-Ruíz, G.P. Steven; Fixed grid finite elements in elasticity problems; Eng. Computation., 16 (2) (1999), pp. 145–164
16. [16] E. Heikkola, Y.A. Kuznetsov, K.N. Lipnikov; Fictitious domain methods for the numerical solution of three-dimensional acoustic scattering problems; J. Comput. Acoust., 7 (3) (1999), pp. 161–193
17. [17] U. Hetmaniuk, C. Farhat; A finite element-based fictitious domain decomposition method for the fast solution of partially axisymmetric sound-hard acoustic scattering problems; Finite Elem. Anal. Des., 39 (2003), pp. 707–725
18. [18] A. Jahangirian, Y. Shoraka; Adaptive unstructured grid generation for engineering computation of aerodynamic flows; Math. Comput. Simul., 78 (2008), pp. 627–644
19. [19] G.W. Jang, Y.Y. Kim, K.K. Choy; Remesh-free shape optimization using the wavelet-Galerkin method; Int. J. Solids Struct., 41 (2004), pp. 6465–6483
20. [20] R. Löhner, J. Cebral, M. Castro, J.D. Baum, H. Luo, E. Mestreau, et al.; Adaptive Embedded Unstructured Grid Methods.; ,in: G. Buscaglia, E. Dari, O. Zamonsky (Eds.), Mecánica Computacional, XXIII, Bariloche (2004)
21. [21] R.v. Loon, P.D. Anderson, J.d. Hart, F.P.T. Baaijens; A combined fictitious domain/adaptive meshing method for fluid-structure interaction in heart valves; Int. J. Numer. Methods Fluids, 46 (5) (2004), pp. 244–533
22. [22] RA.E. Mäkinen, R. Rossi, J. Toivanen; A moving mesh fictitious domain approach for shape optimization problems; ESAIM-MATH MODEL NUM, 34 (1) (2000), pp. 31–45
23. [23] J.M. Melenk, Babuška. Ivo; The partition of unity finite element method: Basic theory and applications; Comput. Meth. Appl. Mech. Eng., 139 (1-4) (1996), pp. 289–314
24. [24] N. Moës, J. Dolbow, T. Belytschko; A finite element method for crack growth without remeshing; Int. J. Numer. Methods Eng., 46 (1) (1999), pp. 131–150
25. [25] E. Nadal, S. Bordas, J.J. Ródenas, J.E. Tarancón, M. Tur; Accurate Stress Recovery for the Two-Dimensional Fixed Grid Finite Element Method; Procedings of the Tenth International Conference on Computational Structures Technology (2010), pp. 1–20
26. [26] L. Parussini, V. Pedirola; Fictitious Domain approach with hp-finite element approximation for incompressible fluid flow; J. Comput. Phys., 228 (2009), pp. 3891–3910
27. [27] T. Preusser, M. Rumpf, L.O. Schwen; Finite Element Simulation of Bone Microstructures; In 14th FE Workshop (2007)
28. [28] I. Ramière, P. Angot, M. Belliard; Fictitious domain methods to solve convection-diffusion problems with general boundary conditions; Proc. in the 17th Computational Fluid Dynamics Conference AIAA (2005)
29. [29] J.J. Ródenas, G. Bugeda, J. Albelda, E. Oñate; On the need for the use of error-controlled finite element analyses in structural shape optimization processes; Int. J. Numer. Methods Eng., 87 (2011), pp. 1105–1126
30. [30] J.J. Ródenas, G. Bugeda, J. Albelda, E. Oñate, E. Nadal; Sobre la necesidad de controlar el error de discretizaci’on de elementos finitos en optimización de forma estructural con algoritmos evolutivos; Rev. Int. Metodos Numer. Calc. Diseño Ing, 28 (1) (2012), pp. 1–11
31. [31] J.J. Ródenas, E. Giner, F.J. Fuenmayor, O.A. González-Estrada; Accurate recovery-type error estimation for linear elastic fracture mechanics in FEM and X-FEM based on a singular+smooth field splitting; International Conference on Adaptive Modeling and Simulation. ADMOS 2007, pages 202-205. International Center for Numerical Methods in Engineering (CIMNE) (2007)
32. [32] J.J. Ródenas, O.A. González-Estrada, P. Díez, F.J. Fuenmayor; Upper bounds of the error in the extended finite element method by using an equilibrated-stress patch recovery technique; International Conference on Adaptive Modeling and Simulation. ADMOS 2007, pages 210-213. International Center for Numerical Methods in Engineering (CIMNE) (2007)
33. [33] J.J. Ródenas, O.A. González-Estrada, P. Díez, F.J. Fuenmayor; Accurate recovery-based upper error bounds for the extended finite element framework; Comput. Meth. Appl. Mech. Eng., 199 (37-40) (2010), pp. 2607–2621
34. [34] J.J. Ródenas, O.A. González-Estrada, J.E. Tarancón, F.J. Fuenmayor; A recovery-type error estimator for the extended finite element method based on singular+smooth stress field splitting; Int. J. Numer. Methods Eng., 76 (4) (2008), pp. 545–571
35. [35] J.J. Ródenas, M. Tur, F.J. Fuenmayor, A. Vercher; Improvement of the superconvergent patch recovery technique by the use of constraint equations: the SPR-C technique; Int. J. Numer. Methods Eng., 70 (6) (2007), pp. 705–727
36. [36] J.J. Ródenas, JE Tarancón, J. Albelda, A Roda, and F J Fuenmayor;1; Hierarchical properties in elements obtained by subdivision: A hierarquical h-adaptivity program. In P. Díez and N.-E. Wiberg, editors, Adaptive Modeling and Simulation 2005, 2005.
37. [37] A.M. Roma, C.S. Peskin, M.J. Bergery; An Adaptive Version of the Immersed Boundary Method; J. Comput. Phys., 153 (1999), pp. 509–534
38. [38] R. Sevilla and S. Fernández-Méndez.;1; NURBS-enhanced finite element method (NEFEM). Online, (February):56-83, 2008.
39. [39] C.M. Silva Santos, D.M. Greaves; Using hierarchical Cartesian grids with multigrid acceleration; Int. J. Numer. Methods Eng., 69 (2007), pp. 1755–1774
40. [40] M. Stolarska, D.L. Chopp, N. Moës, T. Belytschko; Modelling crack growth by level sets in the extended finite element method; Int. J. Numer. Methods Eng., 51 (8) (2001), pp. 943–960
41. [41] R. Storn, K. Price; Differential evolution–a simple and efficient adaptive scheme for global optimisation over continuous spaces; Technical report (1995)
42. [42] T. Strouboulis, K. Copps, I. Babuška; The generalized finite element method; Comput. Meth. Appl. Mech. Eng., 190 (32-33) (2001 May), pp. 4081–4193
43. [43] T. Strouboulis, L. Zhang, I. Babuscaronka; Assessment of the cost and accuracy of the generalized FEM; Int. J. Numer. Methods Eng., 69 (2) (2007), pp. 250–283
44. [44] N. Sukumar; Modeling quasi-static crack growth with the extended finite element method. Part I: Computer implementation; Int. J. Solids Struct., 40 (26) (2003), pp. 7513–7537
45. [45] B.A. Szabó, I. Babuška; Finite Element Analysis; John Wiley & Sons, New York (1991)
46. [46] M. Victoria, O.M. Querin, P. Martí; Topology design for multiple loading conditions of continuum structures using isolines and isosurfaces; Finite Elem. Anal. Des., 46 (3) (2010), pp. 229–237
47. [47] Q.Z. Xiao, B.L. Karihaloo; Improving the accuracy of XFEM crack tip fields using higher order quadrature and statically admissible stress recovery; Int. J. Numer. Methods Eng., 66 (9) (2006), pp. 1378–1410
48. [48] T. Ye, R. Mittal, H.S. Udaykumar, W. Shyyy; Accurate Cartesian Grid Method for Viscous Incompressible Flows with Complex Immersed Boundaries; J. Comput. Phys., 156 (1999), pp. 209–240
49. [49] L. Zhang, A. Gerstenberger, X. Wang, W.K. Liu; Immersed finite element method; Comput. Meth. Appl. Mech. Eng., 193 (2004), pp. 2051–2067
50. [50] O.C. Zienkiewicz, J.Z. Zhu; A simple error estimator and adaptive procedure for practical engineering analysis; Int. J. Numer. Methods Eng., 24 (2) (1987), pp. 337–357
51. [51] O.C. Zienkiewicz, J.Z. Zhu; The superconvergent patch recovery and a posteriori error estimates. Part 1: The recovery technique; Int. J. Numer. Methods Eng., 33 (7) (1992), pp. 1331–1364
52. [52] O.C. Zienkiewicz, J.Z. Zhu; The superconvergent patch recovery and a posteriori error estimates. Part 2: Error estimates and adaptivity; Int. J. Numer. Methods Eng., 33 (7) (1992), pp. 1365–1382
53. [53] O.C. Zienkiewicz, J.Z. Zhu; Superconvergence and the superconvergent patch recovery; Finite Elem. Anal. Des., 19 (1-2) (1995), pp. 11–23
54. [54] O.C. Zienkiewicz, J.-Z. Zhu, J. Wu; Superconvergent patch recovery techniques - some further tests; Commun. Numer. Methods Eng., 9 (3) (1993), pp. 251–258