Analysis of laminated beams using the natural neighbour radial point interpolation method

Resumo

Neste trabalho aplica‐se o método sem malha natural neighbour radial point interpolation method (NNRPIM) à análise unidimensional de vigas laminadas, considerando a teoria de Timoshenko.

O NNRPIM combina o conceito matemático dos vizinhos naturais com a interpolação radial pontual. Os diagramas de Voronoï permitem impor a conectividade nodal e construir a malha de fundo para efeitos de integração, por intermédio das células de influência. É apresentada a construção das funções de interpolação NNRPIM, sendo, para estas, usada a função de base radial multiquadrática. As funções de interpolação geradas possuem continuidade infinita e a propriedade de delta Kronecker, o que facilita a imposição das condições de fronteira, uma vez que estas podem ser impostas com o método da imposição direta, tal como no método dos elementos finitos (FEM).

De modo a obter o campo de deslocamentos e de deformações, a teoria de deformação de Timoshenko para vigas sujeitas a esforços transversos é considerada. Vários exemplos numéricos de vigas isotrópicas e vigas laminadas são apresentados de modo a demonstrar a convergência e a exatidão da aplicação proposta. Os resultados obtidos são comparados com soluções analíticas disponíveis na literatura.

Abstract

In this work, a meshless method, “natural neighbour radial point interpolation method” (NNRPIM), is applied to the one‐dimensional analysis of laminated beams, considering the theory of Timoshenko.

The NNRPIM combines the mathematical concept of natural neighbours with the radial point interpolation. Voronoï diagrams allows to impose the nodal connectivity and the construction of a background mesh for integration purposes, via influence cells. The construction of the NNRPIM interpolation functions is shown, and, for this, it is used the multiquadratic radial basis function. The generated interpolation functions possess infinite continuity and the delta Kronecker property, which facilitates the enforcement of boundary conditions, since these can be directly imposed, as in the finite element method (FEM).

In order to obtain the displacements and the deformation fields, it is considered the Timoshenko theory for beams under transverse efforts. Several numerical examples of isotropic beams and laminated beams are presented in order to demonstrate the convergence and accuracy of the proposed application. The results obtained are compared with analytical solutions available in the literature.

Palavras‐chave

Método sem malha ; Viga de Timoshenko ; Laminados ; Função de base radial

Keywords

Meshless ; Timoshenko beam ; Laminated ; Radial basis function

1. Introdução

Recentemente, os métodos sem malha [1] têm‐se afirmado como alternativa numérica ao método dos elementos finitos (MEF)[2] , permitindo a resolução de problemas com geometrias muito complexas, apresentando um menor tempo de processamento [1]  and [3] . Distinto do MEF, onde o domínio é discretizado numa malha de elementos, nos métodos sem malha o domínio do problema é discretizado numa malha de nós e a conectividade nodal é obtida por domínios de influência. Estes domínios, ao contrário dos elementos no MEF, podem e devem sobrepor‐se. É esta sobreposição e a escolha de domínios de influência convenientes que permitem aos métodos sem malha, mesmo perante malhas nodais muito irregulares, obter bons resultados.

Numa primeira fase foram desenvolvidos vários métodos sem malha com recurso a funções aproximadoras –como o element free galerkin method (EFGM) [1] ou o meshless local Petrov‐Galerkin method[4] – no entanto, apesar destes terem sido aplicados com sucesso à mecânica computacional, alguns problemas ficaram por resolver, tal como a imposição das condições de fronteira, devido à falta da propriedade de delta Kronecker. Esta é uma das consequências diretas do uso de funções aproximadoras em vez de funções interpoladoras. Assim, de forma a dar resposta a esta limitação, novos métodos sem malha foram desenvolvidos na última década, entre os quais o point interpolation method (PIM) [5]  and [6] , o natural neighbour finite element method (NNFEM) [7]  and [8] e o meshless finite element method (MFEM) [9] , fazendo uso de funções interpoladoras.

O PIM é um método bastante atrativo pelo uso de funções interpoladoras, gerando assim funções de forma com a propriedade de delta Kronecker. A construção destas funções de forma, tal como as suas derivadas parciais, é um processo simples, quando comparado com o EFGM. Entretanto o PIM evoluiu e em vez de utilizar funções de base polinomiais foi proposto, e aplicado com sucesso, o uso de funções de base radial [10]  and [11] , sendo criado o radial point interpolation method (RPIM). Nos primeiros trabalhos sobre o RPIM as funções de base radial utilizadas foram a multiquadrática e a gaussiana [10]  and [11] . Este utiliza o conceito de «domínio local de influência» em vez de «domínio global de influência», gerando assim matrizes de rigidez esparsas e em banda, mais ajustadas a problemas de geometrias complexas.

O natural element method (NEM) é atualmente um dos métodos sem malha mais populares, isto porque as funções de forma são construídas com base nos vizinhos naturais, através de funções interpoladoras. A construção destas funções interpoladoras baseia‐se em conceitos matemáticos, como são o caso dos diagramas de Voronoï [12] .

A necessidade de uma malha de fundo para efeitos de integração é também um tema de grande discussão nos métodos sem malha. O método apresentado neste trabalho dá uma resposta original e eficiente a essa necessidade.

Neste trabalho o natural neighbour radial point interpolation method (NNRPIM) [13] é aplicado à resolução de problemas de vigas, considerando a teoria da deformação de Timoshenko (teoria de deformação de corte de primeira ordem). Recorrendo às células de Voronoï, um conjunto de células de influência é criado a partir de uma discretização nodal. Para efeitos de integração é criada uma malha de fundo com pontos de quadratura distribuídos segundo a regra gaussiana.

O NNRPIM utiliza funções de base radial (RBF) para construir as funções de interpolação. Na literatura é possível encontrar vários trabalhos sobre a obtenção dos parâmetros de forma ótimos das RBF [14] , [15]  and [16] que conduzem à melhor solução. Relativamente ao NNRPIM, é possível encontrar na literatura estudos sobre os parâmetros de forma ótimos para o problema da mecânica dos sólidos bidimensional e tridimensional [13] , assim como para a formulação de Reissner‐Mindlin para placas e laminados [17] . Os parâmetros de forma obtidos no trabalho de Dinis et al. [13,17] diferem dos valores obtidos no trabalho de Wang and Liu [11], no entanto, os parâmetros de forma obtidos por Dinis et al. [13,17] conduzem a soluções mais próximas da solução considerada como exata.

É notório, após consultar a literatura disponível, o interesse contínuo por parte da comunidade académica no sentido de desenvolver modelos matemáticos eficientes na previsão da resposta estática e dinâmica deste tipo de estruturas unidimensionais. É possível consultar em [18] uma revisão detalhada sobre algumas das teorias de deformação de vigas e placas usadas na análise estática e dinâmica. O problema de vigas espessas encontra‐se bem estudado no campo dos elementos finitos [19]  and [20] . No entanto, no domínio dos métodos sem malha este é ainda um tema pouco explorado [21] , [22] , [23]  and [24] .

2. Vizinhos naturais

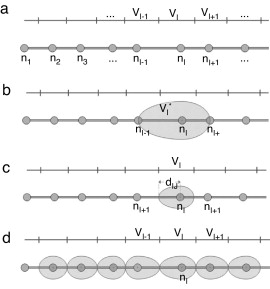
Surgido em 1980, por Sibson [25] , o conceito de vizinhos naturais permite impor uma conectividade nodal celular [26] , traduzindo‐se no conjunto de nós mais próximos do nó em análise que, no caso unidimensional representado na figura 1 (a), serão o nó mais à esquerda e o nó mais à direita.

Figura 1. Esquematização da construção do diagrama de Voronoï. a) Identificação dos nós; b) célula contendo os nós vizinhos; c) célula de Voronoï; d) diagrama de Voronoï.

Os vizinhos naturais são determinados recorrendo ao diagrama de Voronoï, sendo que este é constituído por um conjunto de células de Voronoï. A cada uma dessas células está associado apenas um nó, para além do conjunto de todos os pontos que estão mais próximos desse nó do que de qualquer outro.

Na figura 1 são exemplificadas as diferentes etapas para a determinação do diagrama de Voronoï. Assim, numa primeira fase, o domínio do problema é discretizado numa malha nodal com N nós, N  = {n₁ , n₂ , n₃ , ..., n_N }.

Posteriormente, é construída uma célula provisória, V_I^* , que contem os nós mais próximos do nó em estudo (n_I ), ou seja, que contém os seus nós vizinhos (n_I‐1 e n_I+1 ), figura 1 (b).

De seguida, é determinada a célula de Voronoï, figura 1 (c). Esta tem por base a célula provisória V_I^* , no entanto, a distância entre os seus limites e n_I será obtida por ${\textstyle {\frac {\epsilon ({\boldsymbol {x}}_{J},{\boldsymbol {x}}_{I})}{2}}=}$$d_{IJ}={\frac {\sqrt {{\left(x_{I}-x_{J}\right)}^{2}}}{2}}$ , sendo ɛ a norma euclidiana de x_J e x_I , com J  ≠ I , onde J é um nó vizinho de I .

No final, obtém‐se o diagrama de Voronoï do domínio nodal [13]  and [27] , figura 1 (d).

O diagrama de Voronoï permite impor a conectividade nodal e construir a malha de fundo para efeitos de integração [27] .

2.1. Células de influência e conectividade nodal

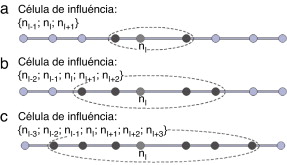
No caso do NNRPIM as células de influência servem para impor a conectividade nodal e permitem a criação da malha de integração, sendo constituídas por um conjunto de nós na vizinhança do ponto de interesse [13] , [26]  and [27] . Três tipos distintos de células de influência são seguidamente apresentados na figura 2 para o nó I (n_I ).

Figura 2. (a) Célula de influência de primeiro grau; (b) célula de influência de segundo grau; (c) célula de influência de terceiro grau.

Como é visível, as células de influência de terceiro grau, figura 2 (c), apresentam uma maior conectividade nodal. Espera‐se, assim, com as células de influência de terceiro grau, obter resultados mais próximos da solução analítica.

2.2. Integração Numérica no natural neighbour radial point interpolation method

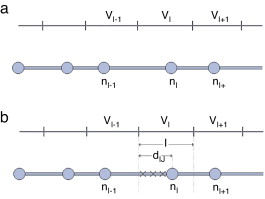
O esquema de integração usado no NNRPIM 1D consiste, numa primeira fase, em definir as células de Voronoï, figura 3 (a). Posteriormente, são distribuídos na partição celular definida pela distância d_IJ o número pretendido de pontos de quadratura, figura 3 (b), que permitirão a integração numérica das funções NNRPIM. Essa distribuição é feita segundo a regra de Gauss, onde cada ponto de integração tem um peso associado.

Figura 3. Passos para a integração numérica no NNRPIM. (a) Determinação das células de Voronoï; (b) distribuição dos pontos de quadratura (3 pontos de quadratura).

No caso da integração nodal, os pontos de integração são os próprios nós, pelo que essa apresentará um aspeto semelhante à figura 3 (a). Nesse caso, o peso correspondente ao ponto de integração é a distância l .

Na secção 5 é apresentado um estudo onde é obtido o número de pontos de integração por partição celular, necessários e suficientes para integrar numericamente o problema da viga de Timoshenko.

3. Funções de forma natural neighbour radial point interpolation method

Neste trabalho foram usadas funções interpolantes, do tipo pontual radial – RPI [10] . Considere‐se uma função u (x ) , definida num domínio Ω e discretizada por um conjunto de N nós, onde se assume que apenas os nós pertencentes à célula de influência afetam a função u (x ) , e que esta passa por todos os nós, usando uma função de base radial. Assim, e considerando o valor da função num ponto de interesse x_I , tem‐se que

${\boldsymbol {u}}\left({\boldsymbol {x}}_{I}\right)=\sum _{i=1}^{n}R_{i}\left({\boldsymbol {x}}_{I}\right)a_{i}\left({\boldsymbol {x}}_{I}\right)+$$\sum _{j=1}^{m}p_{j}\left({\boldsymbol {x}}_{I}\right)b_{j}\left({\boldsymbol {x}}_{I}\right)=$$\left\{{\boldsymbol {R}}^{T}\left({\boldsymbol {x}}_{I}\right),{\boldsymbol {p}}^{T}\left({\boldsymbol {x}}_{I}\right)\right\}\left\{{\begin{array}{c}{\boldsymbol {\mbox{a}}}\\{\boldsymbol {\mbox{b}}}\end{array}}\right\}$

( 1)

Sendo que ${\textstyle R_{i}\left(x_{I}\right)}$ é a função de base radial (RBF), n é o número de nós no interior da célula de influência de x_I , e a_i (x_I ) e b_j (x_I ) são coeficientes não constantes de ${\textstyle R_{i}\left({\boldsymbol {x}}_{I}\right)}$ e ${\textstyle p_{j}\left({\boldsymbol {x}}_{I}\right)}$ , respetivamente. O monómio j   da base polinomial é definido por ${\textstyle p_{j}\left({\boldsymbol {x}}_{I}\right)}$ e m é o número de monómios da base. Os vetores da equação (1) definem‐se por,

${\begin{array}{l}{\boldsymbol {R}}^{T}({\boldsymbol {x}}_{I})=\lbrace R_{1}({\boldsymbol {x}}_{I}),R_{2}({\boldsymbol {x}}_{I}),...,R_{n}({\boldsymbol {x}}_{I})\rbrace \\{\boldsymbol {p}}^{T}({\boldsymbol {x}}_{I})=\lbrace p_{1}({\boldsymbol {x}}_{I}),p_{2}({\boldsymbol {x}}_{I}),...,p_{m}({\boldsymbol {x}}_{I})\rbrace \\{\boldsymbol {a}}^{T}({\boldsymbol {x}}_{I})=\lbrace a_{1}({\boldsymbol {x}}_{I}),a_{2}({\boldsymbol {x}}_{I}),...,a_{n}({\boldsymbol {x}}_{I})\rbrace \\{\boldsymbol {b}}^{T}({\boldsymbol {x}}_{I})=\lbrace b_{1}({\boldsymbol {x}}_{I}),b_{2}({\boldsymbol {x}}_{I}),...,b_{m}({\boldsymbol {x}}_{I})\rbrace \end{array}}$

( 2)

Nas funções de base radial (RBF) a variável é a norma euclidiana (r_ij ) entre o ponto de interesse x_I e o nó vizinho, ${\textstyle r_{ij}={\sqrt {{\left(x_{I}-x_{i}\right)}^{2}}}}$ .

Neste trabalho é usada a função de base radial multiquadrática, ${\textstyle R(r_{ij})={\left({r_{ij}}^{2}+c^{2}\right)}^{p}}$ .

Esta foi proposta por Hardy [27]  and [28] , e os parâmetros c e p são os parâmetros de forma que carecem de otimização, de modo a maximizar a performance do método. Na secção 5 é apresentado um estudo da otimização dos parâmetros c e p .

Por forma a garantir que a matriz de interpolação das funções de base radial é invertível, as bases polinomiais usadas têm de ser completas [13] . Assim, neste trabalho serão usadas as seguintes bases polinomiais 1D:

${\mbox{Base}}{\mbox{ }}{\mbox{nula}}-{\boldsymbol {x}}^{T}=$$\lbrace x\rbrace ;{\mbox{ }}{\boldsymbol {p}}^{T}({\boldsymbol {x}})=$$\lbrace 0\rbrace ;{\mbox{ }}m=0{\mbox{,}}$

( 3)

${\mbox{Base}}{\mbox{ }}{\mbox{constante}}-{\boldsymbol {x}}^{T}=$$\lbrace x\rbrace ;{\mbox{ }}{\boldsymbol {p}}^{T}({\boldsymbol {x}})=$$\lbrace 1\rbrace ;{\mbox{ }}m=1{\mbox{,}}$

( 4)

${\mbox{Base}}{\mbox{ }}{\mbox{linear}}-{\boldsymbol {x}}^{T}=$$\lbrace x\rbrace ;{\mbox{ }}{\boldsymbol {p}}^{T}({\boldsymbol {x}})=$$\lbrace 1,x\rbrace ;{\mbox{ }}m=2{\mbox{,}}$

( 5)

${\mbox{Base}}{\mbox{ }}{\mbox{quadrática}}-{\boldsymbol {x}}^{T}=$$\lbrace x\rbrace ;{\mbox{ }}{\boldsymbol {p}}^{T}({\boldsymbol {x}})=$$\lbrace 1,x,x^{2}\rbrace ;{\mbox{ }}m=3{\mbox{.}}$

( 6)

Para que a solução obtida seja única, a base polinomial tem ainda de satisfazer os requerimentos extra, [13]  and [27]

$\sum _{i=1}^{n}p_{j}({\boldsymbol {x}}_{i})a_{i}({\boldsymbol {x}}_{i})=$$0,{\mbox{ }}j=1,2,\ldots ,m$

( 7)

Assim, uma nova equação matricial pode ser escrita

$\left\{{\begin{array}{c}{\boldsymbol {u}}_{s}\\0\end{array}}\right\}={\boldsymbol {G}}\left\{{\begin{array}{c}{\boldsymbol {a}}\\{\boldsymbol {b}}\end{array}}\right\}$

( 8)

e desenvolvida,

$\left\{{\begin{array}{c}{\boldsymbol {a}}\\{\boldsymbol {b}}\end{array}}\right\}={\boldsymbol {G}}^{-1}\left\{{\begin{array}{c}{\boldsymbol {u}}_{s}\\0\end{array}}\right\}$

( 9)

As funções teste são obtidas substituindo a equação (9) na equação (1),

${\boldsymbol {u}}(x_{I})=\lbrace {\boldsymbol {R}}^{T}({\boldsymbol {x}}_{I}),{\boldsymbol {p}}^{T}({\boldsymbol {x}}_{I})\rbrace {\boldsymbol {G}}^{-1}\left\{{\begin{array}{c}{\boldsymbol {u}}_{s}\\0\end{array}}\right\}=\varphi ({\boldsymbol {x}}_{I}){\boldsymbol {u}}_{s}$

( 10)

Sendo φ (x ) a função de interpolação definida por

$\varphi ({\boldsymbol {x}}_{I})=\lbrace {\boldsymbol {R}}^{T}({\boldsymbol {x}}_{I}),{\boldsymbol {p}}^{T}({\boldsymbol {x}}_{I})\rbrace {\boldsymbol {G}}^{-1}=$$\lbrace {\varphi }_{1}({\boldsymbol {x}}_{I}),{\varphi }_{2}({\boldsymbol {x}}_{I}),\ldots ,{\varphi }_{n}({\boldsymbol {x}}_{I})\rbrace$

( 11)

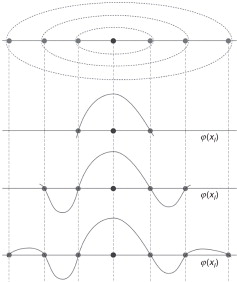
A figura 4 mostra esquematicamente as funções de interpolação para uma célula de influência de primeiro, segundo e terceiro grau, respetivamente.

Figura 4. Representação esquemática das funções de interpolação de células de influência de primeiro, segundo e terceiro grau.

De notar que as funções de interpolação apresentam valor máximo para o nó em estudo e que passam obrigatoriamente por todos os restantes nós pertencentes à célula de influência.

4. Equações de equilíbrio

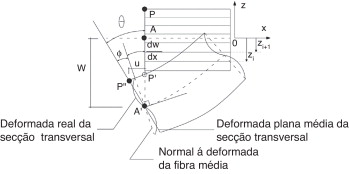
Neste trabalho, a teoria de deformação de primeira ordem é aplicada a vigas (fig. 5 ). A teoria de Timoshenko, teoria em que este trabalho se baseia, assenta em 3 hipóteses, que são:

• Os deslocamentos segundo z de todos os pontos da secção transversal da viga são pequenos e iguais aos deslocamentos do eixo da viga;
• A deformação segundo y é nula;
• As secções transversais retas normais ao eixo antes da deformação da viga permanecem planas após a deformação, mas não necessariamente normais ao eixo da viga.

Figura 5. Aplicação das hipóteses da teoria de Timoshenko a uma viga laminada30 .

Os resultados obtidos por estas hipóteses são, no entanto, uma melhor aproximação quando se tratam de vigas com uma maior relação espessura/vão, uma vez que esta teoria de deformação permite considerar a deformação de corte.

O campo de deslocamentos pode ser obtido a partir da figura 5 . Assim,

${\begin{array}{l}u(x,t)=u_{0}(x,t)+z\cdot \theta (x,t)\\w(x,t)=w_{0}(x,t)\end{array}}$

( 12)

No caso da teoria de Timoshenko, o vetor das deformações reduz‐se a:

${\begin{array}{l}{\epsilon }_{xx}={\frac {\partial u}{\partial x}}\\{\gamma }_{zx}={\frac {\partial w}{\partial x}}+{\frac {\partial u}{\partial z}}\end{array}}$

( 13)

Assim,

$\left\{{\begin{array}{l}{\epsilon }_{xx}\\{\gamma }_{zx}\end{array}}\right\}={\boldsymbol {\epsilon }}=\left\{{\begin{array}{l}{\frac {\partial u}{\partial x}}\\{\frac {\partial u}{\partial z}}+{\frac {\partial w}{\partial x}}\end{array}}\right\}=\left\{{\begin{array}{l}{\frac {\partial (u_{0}(x,t)+z\cdot \theta (x,t))}{\partial x}}\\{\frac {\partial (u_{0}(x,t)+z\cdot \theta (x,t))}{\partial z}}+{\frac {\partial (w_{0}(x,t))}{\partial x}}\end{array}}\right\}$

( 14)

O que simplificando,

$\left\{{\begin{array}{l}{\epsilon }_{xx}\\{\gamma }_{zx}\end{array}}\right\}={\boldsymbol {\epsilon }}=\left\{{\begin{array}{l}{\frac {\partial u_{0}(x,t)}{\partial x}}+z\cdot {\frac {\partial \theta (x,t))}{\partial x}}\\\theta (x,t)+{\frac {\partial w_{0}(x,t)}{\partial x}}\end{array}}\right\}$

( 15)

As deformações podem ainda ser representadas como,

${\boldsymbol {\epsilon }}={\boldsymbol {L}}\cdot {\boldsymbol {u}}$

( 16)

Onde L é um operador diferencial e u é o vetor campo de deslocamentos. Assim,

${\boldsymbol {\epsilon }}={\boldsymbol {L}}\cdot {\boldsymbol {u}}=$$\left[{\begin{array}{lll}{\frac {\partial }{\partial x}}&0&z{\frac {\partial }{\partial x}}\\0&{\frac {\partial }{\partial x}}&1\end{array}}\right]\left[{\begin{array}{c}u_{0}\\w_{0}\\\theta \end{array}}\right]$

( 17)

O valor da tensão na camada i é obtido por aplicação da lei de Hooke,

${\boldsymbol {\sigma }}_{i}={\boldsymbol {c}}_{i}\cdot {\boldsymbol {\epsilon }}$

( 18)

Onde c_i é a matriz constitutiva do material da camada i , definida por,

${\boldsymbol {c}}_{i}=\left[{\begin{array}{cc}E_{i}&0\\0&{\frac {kE_{i}}{2+2{\nu }_{i}}}\end{array}}\right]$

( 19)

Sendo E_i o módulo de Young da camada i e ν_i o valor do coeficiente de Poisson respetivo, k é o fator de correção ao corte de valor igual a 5/6. Considere o sólido de domínio Ω e fronteira Г. As equações de equilíbrio são expressas por

$\nabla {\boldsymbol {\sigma }}+{\boldsymbol {b}}=0{\mbox{ }}em{\mbox{ }}\Omega$

( 20)

Sendo ∇ o gradiente, σ a tensão e b o conjunto das forças externas aplicadas no corpo. Aplicando a forma fraca de Galerkin,

$\psi =\int _{\Omega }\delta {\boldsymbol {\epsilon }}^{T}{\boldsymbol {\sigma }}d\Omega -$$\int _{\Omega }\delta {\boldsymbol {u}}^{T}{\boldsymbol {q}}d\Omega -$$\int _{\Gamma }\delta {\boldsymbol {u}}^{T}{\boldsymbol {t}}d\Gamma$

( 21)

Sendo q a força de corpo, e t a força externa aplicada na fronteira natural Γ .

Substituindo a equação (16) no primeiro termo da equação (21) obtém‐se,

$\int _{\Omega }\delta {\boldsymbol {\epsilon }}^{T}{\boldsymbol {\sigma }}d\Omega =$$\int _{\Omega }\delta {\left({\boldsymbol {Lu}}\right)}^{T}{\boldsymbol {c}}_{i}({\boldsymbol {Lu}})d\Omega$

( 22)

Considerando a equação (10),

$\int _{\Omega }\delta {\boldsymbol {\epsilon }}^{T}{\boldsymbol {\sigma }}d\Omega =$$\int _{\Omega }\delta {\left({\boldsymbol {L}}{\varphi }_{I}\left({\boldsymbol {x}}\right){\boldsymbol {u}}_{I}\right)}^{T}{\boldsymbol {c}}_{i}\left({\boldsymbol {L}}{\varphi }_{I}\left({\boldsymbol {x}}\right){\boldsymbol {u}}_{I}\right)d\Omega =$$\int _{\Omega }\delta {\left({\boldsymbol {B}}{\boldsymbol {u}}_{I}\right)}^{T}{\boldsymbol {c}}_{i}\left({\boldsymbol {B}}{\boldsymbol {u}}_{I}\right)d\Omega =$$\delta {{\boldsymbol {u}}_{I}}^{T}\left[\int _{\Omega }\delta {\boldsymbol {B}}^{T}{\boldsymbol {c}}_{i}{\boldsymbol {B}}d\Omega \right]{\boldsymbol {u}}_{I}$

( 23)

Sendo B a matriz de deformabilidade, a qual pode ser decomposta,

${\boldsymbol {B}}=z.{\boldsymbol {B}}^{f}+{\boldsymbol {B}}^{A}+$${\boldsymbol {B}}^{C}=z\left[{\begin{array}{ccc}0&0&{\frac {\partial \varphi \left({\boldsymbol {x}}_{I}\right)}{\partial x}}\\0&0&0\end{array}}\right]+\left[{\begin{array}{ccc}{\frac {\partial \varphi \left({\boldsymbol {x}}_{I}\right)}{\partial x}}&0&0\\0&0&0\end{array}}\right]+\left[{\begin{array}{ccc}0&0&0\\0&{\frac {\partial \varphi \left({\boldsymbol {x}}_{I}\right)}{\partial x}}&1\end{array}}\right]$

( 24)

Onde B^f , B^A e B^C são as componentes de B correspondentes à flexão, ao esforço axial e ao corte, respetivamente.

No problema em estudo as matrizes de deformabilidade correspondentes ao esforço axial e ao corte podem ser agrupadas,

${\boldsymbol {B}}={\boldsymbol {B}}^{A}{\mbox{+}}{\boldsymbol {B}}^{C}=$$\left[{\begin{array}{ccc}{\frac {\partial \varphi \left({\boldsymbol {x}}_{I}\right)}{\partial x}}&0&0\\0&{\frac {\partial \varphi \left({\boldsymbol {x}}_{I}\right)}{\partial x}}&1\end{array}}\right]$

( 25)

Assim, a matriz de rigidez K do problema da viga de Timoshenko pode ser obtido a partir de,

${\boldsymbol {K}}=\int _{\Omega }{\left(z{\boldsymbol {B}}^{f}+{\boldsymbol {B}}^{AC}\right)}^{T}{\boldsymbol {c}}_{i}(z{\boldsymbol {B}}^{f}+$${\boldsymbol {B}}^{AC})d\Omega$

( 26)

Sabendo que dΩ  = dA  · dz e dA  = b  · dx , uma vez que a largura da viga é constante, a equação (26) pode ser reescrita da seguinte forma,

${\boldsymbol {K}}=\int _{\Omega }{\left(z{\boldsymbol {B}}^{f}{\boldsymbol {+}}{\boldsymbol {B}}^{AC}\right)}^{T}{\boldsymbol {c}}_{i}(z{\boldsymbol {B}}^{f}{\boldsymbol {+}}{\boldsymbol {B}}^{AC})d\Omega =$$\int _{0}^{L}\int _{-h/2}^{h/2}bz^{2}\left[{\left({\boldsymbol {B}}^{f}\right)}^{T}{\boldsymbol {c}}_{i}\left({\boldsymbol {B}}^{f}\right)\right]dzdx+$$\int _{0}^{L}\int _{-h/2}^{h/2}bz\left[{\left({\boldsymbol {B}}^{f}\right)}^{T}{\boldsymbol {c}}_{i}\left({\boldsymbol {B}}^{AC}\right)\right]dzdx+$$\int _{0}^{L}\int _{-h/2}^{h/2}bz\left[{\left({\boldsymbol {B}}^{AC}\right)}^{T}{\boldsymbol {c}}_{i}\left({\boldsymbol {B}}^{f}\right)\right]dzdx+$$\int _{0}^{L}\int _{-h/2}^{h/2}b\left[{\left({\boldsymbol {B}}^{AC}\right)}^{T}{\boldsymbol {c}}_{i}\left({\boldsymbol {B}}^{AC}\right)\right]dzdx$

( 27)

Considerando a propriedade distributiva e a largura da viga unitária (b  = 1),

${\boldsymbol {K}}=\int _{0}^{L}{\left({\boldsymbol {B}}^{f}\right)}^{T}\left[\sum _{i}^{k}\left({\frac {z_{i+1}^{3}-z_{i}^{3}}{3}}\right){\boldsymbol {c}}_{i}\right]\left({\boldsymbol {B}}^{f}\right)dx+$$\int _{0}^{L}{\left({\boldsymbol {B}}^{f}\right)}^{T}\left[\sum _{i}^{k}\left({\frac {z_{i+1}^{2}-z_{i}^{2}}{2}}\right){\boldsymbol {c}}_{i}\right]\left({\boldsymbol {B}}^{AC}\right)dx+$$\int _{0}^{L}{\left({\boldsymbol {B}}^{AC}\right)}^{T}\left[\sum _{i}^{k}\left({\frac {z_{i+1}^{2}-z_{i}^{2}}{2}}\right){\boldsymbol {c}}_{i}\right]\left({\boldsymbol {B}}^{f}\right)dx+$$\int _{0}^{L}{\left({\boldsymbol {B}}^{AC}\right)}^{T}\left[\sum _{i}^{k}\left(z_{i+1}-\right.\right.$$\left.\left.z_{i}\right){\boldsymbol {c}}_{i}\right]\left({\boldsymbol {B}}^{AC}\right)dx$

( 28)

Sendo k o número de camadas do laminado e z_i e z_i + 1 respetivamente as coordenadas das faces inferior e superior da camada i , figura 5 .

O segundo termo da equação (21) pode ser desenvolvido considerando a equação (10),

$\int _{\Omega }\delta {\boldsymbol {u}}^{T}{\boldsymbol {q}}d\Omega =$$\delta {\boldsymbol {u}}^{T}\int _{\Omega }{\boldsymbol {Hq}}d\Omega$

( 29)

sendo a matriz H definida por,

${\boldsymbol {H}}=\left[{\begin{array}{ccc}\varphi \left({\boldsymbol {x}}_{I}\right)&0&0\\0&\varphi \left({\boldsymbol {x}}_{I}\right)&0\\0&0&\varphi \left({\boldsymbol {x}}_{I}\right)\end{array}}\right]$

( 30)

e q por,

$q=\left[{\begin{array}{l}N\\V\\M\end{array}}\right]$

( 31)

onde N é o esforço axial, V o esforço de corte e M o momento fletor.

Raciocínio idêntico pode ser seguido para o terceiro termo da equação (21),

$\int _{\Gamma }\delta {\boldsymbol {u}}^{T}{\boldsymbol {t}}d\Gamma =$$\delta {\boldsymbol {u}}^{T}\int _{\Gamma }{\boldsymbol {Ht}}d\Gamma$

( 32)

sendo F_q  = ∫Hq''dΩ e Ft  = ∫Ht''dΓ . A equação (21) pode então ser apresentada na forma matricial,

$\psi =\delta {\boldsymbol {U}}^{T}\left[{\boldsymbol {KU}}-\right.$$\left.{\boldsymbol {F}}\right]=0$

( 33)

sendo K   a matriz de rigidez global, ${\textstyle {\boldsymbol {F}}=\left({\boldsymbol {F}}_{q}+\right.}$$\left.{\boldsymbol {F}}_{t}\right)$ o vetor global dos momentos e das forças externas aplicadas e U o campo de deslocamentos. Assim, o sistema linear de equações pode ser apresentado na forma matricial, KU  = F .

As condições de fronteira são impostas diretamente na matriz de rigidez K , assim como no MEF, uma vez que as funções de interpolação radiais pontuais possuem a propriedade de delta Kronecker [17] .

5. Otimização dos parâmetros de forma da Radial Basis Function

Nesta secção são determinados os parâmetros de forma p e c ótimos, e o número de pontos de quadratura suficientes para integrar o problema de vigas, para cada um dos tipos de células de influência apresentados na secção 2.1.

Foi analisada uma viga isotrópica (E = 1.000 Pa, ν = 0,3) de dimensões L = 10 m e h = 1 m (L/h = 10) simplesmente apoiada em ambas as extremidades e sujeita a uma carga uniformemente distribuída q = q₀ , sendo q₀  = 1 N/m. Nesta análise a viga foi discretizada em 33 nós, distribuídos numa malha regular e numa outra irregular.

O erro médio do deslocamento transversal é obtido através de,

${\epsilon }_{w}={\frac {1}{N}}\sum _{i=1}^{N}{\frac {\left|{\delta }_{w{\mbox{ }}NNRPIM}^{i}-{\delta }_{w{\mbox{ }}{\mbox{Analítica}}}^{i}\right|}{{\delta }_{w{\mbox{ }}{\mbox{Analítica}}}^{i}}}$

( 34)

onde ${\textstyle {\delta }_{w{\mbox{ }}NNRPIM}^{i}}$ e ${\textstyle {\delta }_{w{\mbox{ }}{\mbox{Analítica}}}^{i}}$ são os deslocamentos transversais obtidos no nó i pelo NNRPIM e pela equação analítica para vigas finas, respetivamente, e N é o número total de nós que discretiza o domínio do problema.

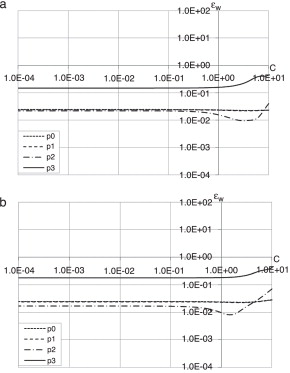
Fez‐se variar os valores do parâmetro c   entre 0,0001 e 10,0001 e estudou‐se a variação do erro médio do deslocamento vertical (${\textstyle {\epsilon }_{w}}$ ) para a viga em questão (malha regular e malha irregular), considerando diferentes bases polinomiais – ausência de base polinomial (p₀ ), base polinomial constante (p₁ ), linear (p₂ ) e quadrática (p₃ ).

Na figura 6 apresentam‐se os resultados obtidos para células de influência de segundo grau, ${\textstyle v_{2}}$ . Resultados semelhantes são obtidos quando células de influência de primeiro grau, ${\textstyle v_{1}}$ , e de terceiro grau, ${\textstyle v_{3}}$ , são consideradas.

Figura 6. Erro do valor do deslocamento para a malha regular (a) e irregular (b), com a variação do parâmetro c, para células de influência de segundo grau.

Na tabela 1 encontra‐se um quadro resumo dos parâmetros c ótimos obtidos para cada uma das formulações.

Tabela 1. Valores do parâmetro c ótimo para as várias formulações

c	p0	p1	p2	p3
v1	0,0001	0,0001	0,0001	‐
v2	0,0001	0,0001	0,0001	0,0001
v3	0,0001	0,0001	0,0001	0,0001

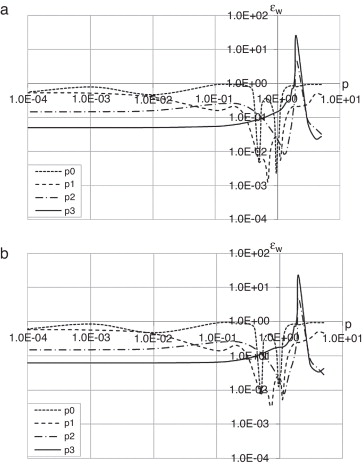
Considerando os parâmetros c da tabela 1 , procedeu‐se a uma nova análise do problema para a mesma viga (L/h = 10), fazendo‐se variar o parâmetro p entre 0,0001 e 5,0001. Na figura 7 apresentam‐se os resultados, novamente, para células de influência de segundo grau.

Figura 7. Erro do valor do deslocamento para a malha regular (a) e irregular (b), com a variação do parâmetro p, para células de influência segundo grau.

Na tabela 2 são apresentados os parâmetros p ótimos obtidos para cada uma das formulações.

Tabela 2. Valores do parâmetro p ótimo para as várias formulações

P	p0	p1	p2	p3
v1	0,5001	0,9999	5,0001	‐
v2	0,9999	0,9999	1,2501	5,0001
v3	0,9999	0,9999	0,6500	5,0001

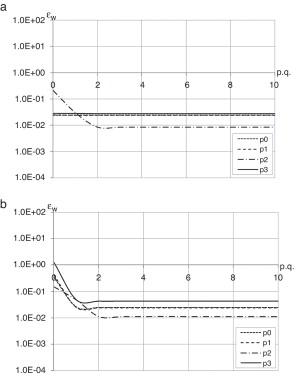
Considerando, para cada formulação, os parâmetros c e p da Tabela 1  and Tabela 2 , respetivamente, procedeu‐se a uma nova análise do problema para a mesma viga, fazendo‐se variar o número de pontos de quadratura entre 0‐10 em cada partição celular. Na figura 8 são apresentados os resultados para células de influência de segundo grau.

Figura 8. Erro do valor do deslocamento para a malha regular (a) e irregular (b), com a variação do número de pontos de quadratura, para células de influência de segundo grau.

Na tabela 3 são apresentados os valores do número de pontos de quadratura suficientes para as diferentes formulações.

Tabela 3. Valores do número de pontos de quadratura suficientes para as várias formulações

p.q.	p0	p1	p2	p3
v1	2	2	2	‐
v2	2	2	2	2
v3	2	2	2	2

Pela análise das tabelas anteriores (Tabela 1 , Tabela 2  and Tabela 3 ) é ainda possível observar que não se obtiveram resultados para a formulação v1p3, pois o uso de uma base polinomial quadrática, para o caso do problema unidimensional, exige no mínimo 3 nós no interior de cada célula de influência. Para valores inferiores o problema torna‐se indeterminado, sendo a matriz geométrica G não‐invertível.

Quanto ao valor do parâmetro ótimo c , ficou claro que este deverá tomar o valor 0,0001, independentemente da formulação usada. O mesmo se sucedeu para o número ótimo de pontos de integração, sendo que neste caso o seu valor ótimo será 2.

O valor do parâmetro p ótimo, no entanto, não parece ser tão geral e sofre algumas variações nas diferentes formulações.

Após a análise dos resultados obtidos, verifica‐se que a formulação que apresenta melhores resultados é a formulação v2p0, uma vez que é a que aparenta ser mais estável e ter um menor erro. Assim, daqui em diante esta será a formulação usada para os diferentes problemas de vigas que serão considerados.

6. Exemplos numéricos

6.1. Estudo de vigas

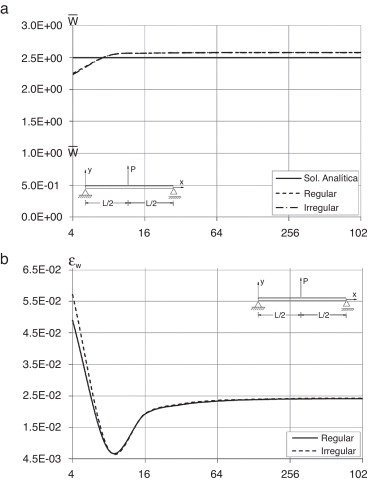
Nesta secção procede‐se ao estudo da convergência de 4 vigas simplesmente apoiadas, com diferentes tipos de cargas aplicadas, utilizando o NNRPIM. São obtidos os resultados do deslocamento transversal no centro da viga para malhas regulares e irregulares, em função do número de divisões da viga (número de nós = número de divisões + 1). As soluções NNRPIM são comparadas com as soluções analíticas. São também obtidos, para cada tipo de viga, com a respetiva carga, o erro médio do deslocamento transversal através da equação (34). Os resultados do estudo de convergência são apresentados nas Figura 10 , Figura 11 , Figura 12  and Figura 13 .

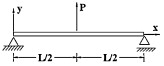
Figura 10. Carga concentrada a meio vão. (a) Estudo de convergência do deslocamento transversal da malha regular e irregular; (b) erro do deslocamento transversal da malha regular e irregular para diferentes números de divisões da viga.

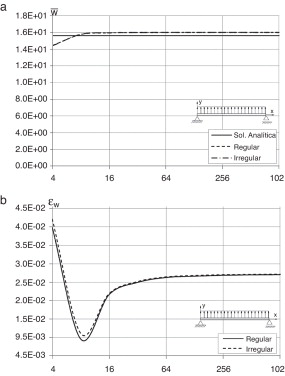
Figura 11. Carga uniformemente distribuída. (a) Estudo de convergência do deslocamento transversal da malha regular e irregular; (b) erro do deslocamento transversal da malha regular e irregular para diferentes números de divisões da viga.

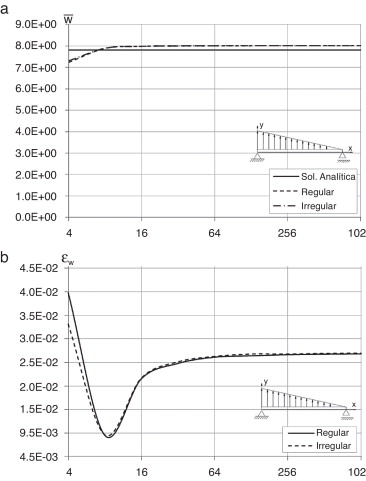
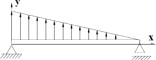
Figura 12. Carga triangularmente distribuída: a) estudo de Convergência do deslocamento transversal da malha regular e irregular; b) Erro do deslocamento transversal da malha regular e irregular para diferentes números de divisões da viga.

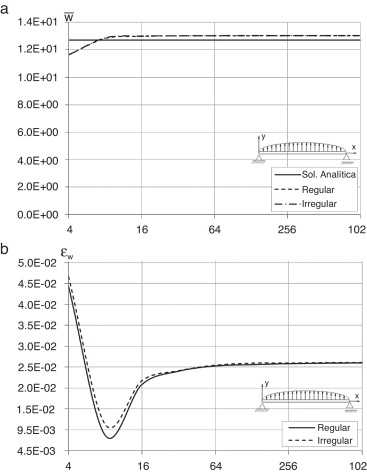
Figura 13. Carga parabolicamente distribuída: a) estudo de Convergência do deslocamento transversal da malha regular e irregular; b) erro do deslocamento transversal da malha regular e irregular para diferentes números de divisões da viga.

O estudo foi efetuado para vigas com as dimensões L = 10 m e h = 1 m, sendo as propriedades materiais E = 1.000 Pa e ν = 0,3.

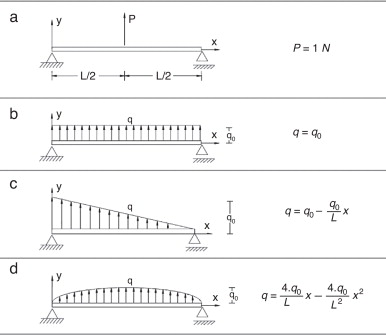
Os 4 tipos de carregamentos usados estão representados na figura 9 , sendo q₀  = 1N /m .

Figura 9. Tipos de carregamentos usados. (a) Carga concentrada a meio vão; (b) carga uniformemente distribuída; (c) carga triangularmente distribuída; (d) carga parabolicamente distribuída.

Os resultados apresentados nas Figura 10 , Figura 11 , Figura 12  and Figura 13 e tabela 4 encontram‐se sob a forma de deslocamentos transversais normalizados. Sendo essa normalização efetuada por,

${\overline {w}}=w_{max}\left({\frac {Eh^{3}}{L^{4}q_{0}}}\right)$

( 35)

Tabela 4. Valores dos deslocamentos normalizados para diferentes relações L/h

	Deslocamentos normalizados
		L/h = 5	L/h = 10	L/h = 20	L/h = 50	L/h = 100
	v2p0 regular	2,812	2,578	2,519	2,503	2,499
	v2p0 irregular	2,812	2,578	2,520	2,502	2,496
	Analítica	2,500	2,500	2,500	2,500	2,500
	v2p0 regular	17,185	16,015	15,722	15,638	15,618
	v2p0 irregular	17,188	16,017	15,724	15,635	15,601
	Analítica	15,625	15,625	15,625	15,625	15,625
	v2p0 regular	8,593	8,008	7,861	7,819	7,809
	v2p0 irregular	8,594	8,008	7,862	7,818	7,800
	Analítica	7,813	7,813	7,813	7,813	7,813
	v2p0 regular	14,008	13,033	12,789	12,719	12,702
	v2p0 irregular	14,011	13,035	12,790	12,717	12,708
	Analítica	12,708	12,708	12,708	12,708	12,708

Na tabela 4 são apresentados os valores dos deslocamentos transversais no centro da viga obtidos considerando diferentes relações L/h e uma malha única de 1.025 nós.

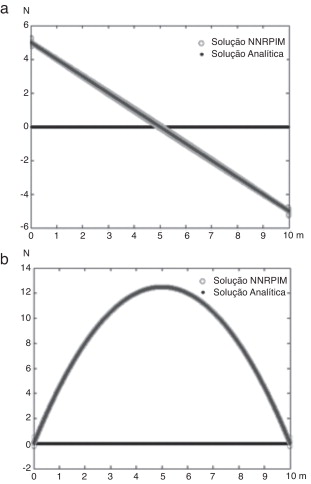
Apresentam‐se de seguida os diagramas de esforços transversos e momentos fletores para as vigas estudadas com dimensões L = 10 m e h = 1 m (fig. 9 ). Foi usada uma malha regular com 1025 nós.

Da análise das Figura 14 , Figura 15 , Figura 16  and Figura 17 constata‐se que a distribuição do campo de momentos e esforços transversos é suave ao longo de toda a viga.

Figura 14. Diagrama de: a) esforços Transversos; b) momentos flectores; para a viga com carga concentrada a meio vão.

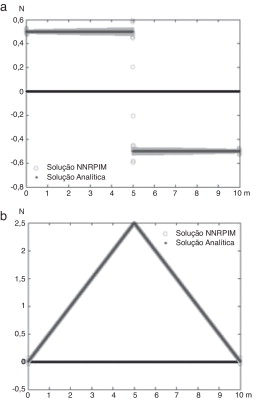
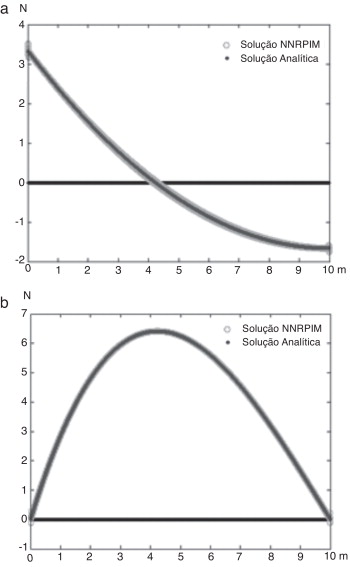
Figura 15. Diagrama de: a) esforços Transversos – N versus m; (b) momentos flectores – N.m versus m; para a viga com carga uniformemente distribuída.

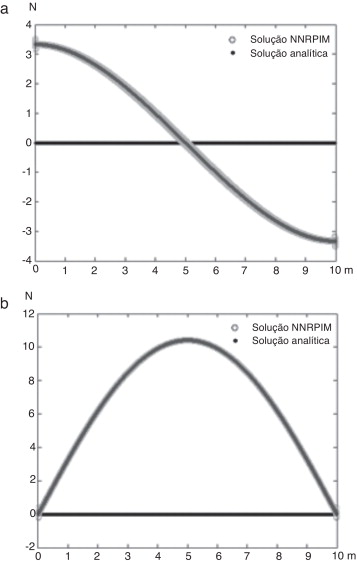
Figura 16. Diagrama de: (a) esforços transversos, (b) momentos fletores; para a viga com carga triangularmente distribuída.

Figura 17. Diagrama de: (a) esforços transversos, (b) momentos fletores; para a viga com carga parabolicamente distribuída.

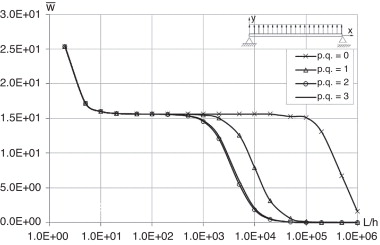
De modo a estudar o comportamento do NNRPIM em situações de ocorrência do fenómeno de retenção ao corte, fez‐se variar a altura da viga h entre h  = 0,0001 e h  = 5 m, mantendo‐se o comprimento constante, L  = 10.

Assim, na figura 18 são apresentados os resultados obtidos considerando as condições de fronteira essenciais e naturais indicadas.

Figura 18. Deslocamento transversal normalizado obtido no centro da viga fazendo variar a relação L/h.

Analisou‐se o problema recorrendo a 2 esquemas de integração distintos, a integração nodal, p  . q  . =0, e a integração utilizando pontos de quadratura de Gauss (secção 2.2), p  . q  . = k , sendo k o número de pontos de quadratura por partição de célula de integração.

6.2. Estudo de laminados

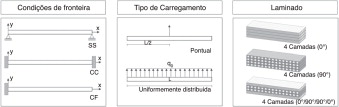
Nesta secção procede‐se ao estudo do problema de vigas laminadas. Analisam‐se vigas com condições de fronteira distintas, sujeitas a 2 tipos de carregamentos, considerando diferentes tipos de laminados (fig. 19 ).

Figura 19. Tipo de vigas laminadas estudadas.

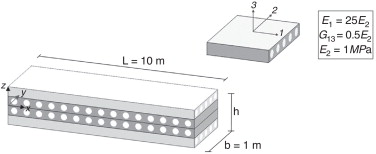
Na figura 20 são apresentadas genericamente as propriedades geométricas e materiais das vigas laminadas em estudo. Sendo E_i o módulo de elasticidade na direção material i e G_ij o módulo de distorção entre as direções materiais i e j .

Figura 20. Dimensões da viga e propriedades usadas para os laminados.

O deslocamento transversal no centro da viga laminada obtido com o NNRPIM, ${\textstyle w_{max}{\mbox{,}}}$ é normalizado com base na expressão,

${\overline {w}}=w_{max}\times {\frac {E_{2}h^{3}}{q_{o}L^{4}}}\times 100$

( 36)

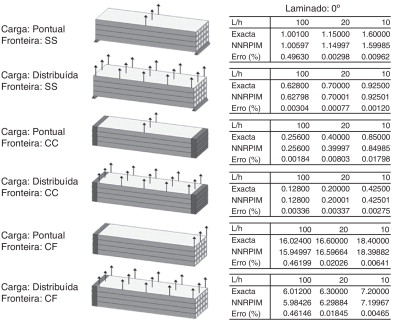
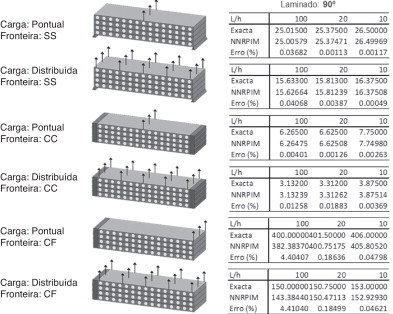
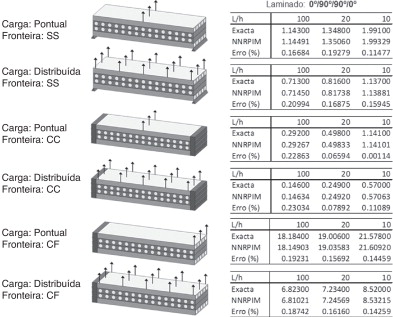
onde q₀  = 1N /m . Para o caso da carga uniformemente distribuída q  = q₀ , já para a carga pontual Q  = q₀  · L . Os resultados normalizados obtidos pelo NNRPIM são comparados com a solução analítica [29] . Os resultados obtidos encontram‐se nas Figura 21 , Figura 22  and Figura 23 para as vigas laminadas a 0°, 90° e 0°/90°/90°/0°, respetivamente. Na tabela 5 é apresentada uma comparação entre algumas das soluções obtidas com o NNRPIM e soluções disponíveis na literatura obtidas por outros autores.

Figura 21. Resultados do deslocamento transversal no centro da viga laminada a 0°.

Figura 22. Resultados do deslocamento transversal no centro da viga laminada a 90°.

Figura 23. Resultados do deslocamento transversal no centro da viga laminada a 0°/90°/90°/0°.

Tabela 5. Comparação dos resultados obtidos com o NNRPIM com os resultados de outros autores

Laminado	SS		SS
L/h	100	10	100	10
[0]n Reddy29	0,628	0,925	0,128	0,425
[0]n Ferreria et al.14	0,628	0,925	0,128	0,425
[0]n NNRPIM	0,628	0,925	0,128	0,425
[90]n Reddy29	15,633	16,375	3,132	3,875
[90]n Ferreira et al.14	15,624	16,375	3,132	3,875
[90]n NNRPIM	15,627	16,375	3,132	3,875

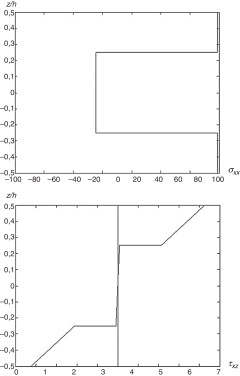
Na figura 24 é possível observar os diagramas para a tensão normal e de corte da viga laminada a 0°/90°/90°/0°.

Figura 24. Diagramas para a viga laminada 0°/90°/90°/0°, encastrada nas 2 extremidades e com carga pontual aplicada, para L/h = 10: a) Tensão normal, b) tensão de corte.

Fez‐se agora variar a espessura da viga h entre h  = 0,10 e h  = 5 mantendo‐se o comprimento L  = 10.

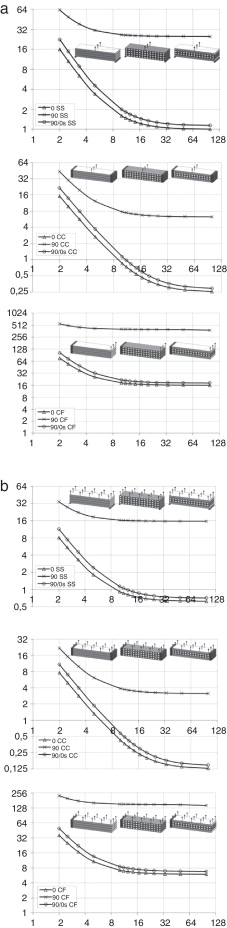
Na figura 25 são apresentados os deslocamentos transversais normalizados obtidos para as diferentes vigas laminadas consideradas, em função das suas condições de fronteira e tipo de carregamento.

Figura 25. Estudo de convergência para os diferentes laminados: a) cargas pontuais; b) cargas distribuídas.

7. Conclusões

Neste trabalho foi estendido à análise de vigas laminadas um método sem malha, o NNRPIM. Por forma a obter a conectividade nodal é construído o diagrama de Voronoï da malha nodal que discretiza o domínio do problema. Com base nas células de Voronoï obtidas é construída a malha de integração.

Distintas formulações NNRPIM foram estudadas, considerando células de influência de diferentes graus e utilizando várias bases polinomiais. Para cada uma das formulações NNRPIM foi determinado o esquema de integração mais eficiente. Também os parâmetros de forma c e p da função de base radial multiquadrática foram analisados e otimizados.

As conclusões mais relevantes deste trabalho podem ser resumidas como:

• A formulação que apresenta resultados mais estáveis e precisos é a formulação NNRPIM v2p0.
• Para a formulação NNRPIM v2p0, os parâmetros de forma da função de base radial multiquadrática óptimos são c = 0,0001 e p = 0,9999.
• Determinou‐se que a eficiência da análise é maximizada se forem utilizados 2 pontos de integração em cada partição celular.
• Independentemente do tipo de problema em estudo, o NNRPIM apresenta consistentemente uma elevada taxa de convergência e uma elevada precisão. A solução final convergida é sempre muito próxima da solução analítica do problema considerado.
• O arranjo nodal não perturba significativamente a precisão ou a convergência do NNRPIM.
• A distribuição do campo de momentos e esforços transversos é suave ao longo de toda a viga. As perturbações nas fronteiras essenciais da viga devem‐se à menor conectividade nodal dos nós periféricos.

O NNRPIM provou ser um método alternativo válido para a análise de vigas laminadas.

Agradecimentos

Os autores agradecem o financiamento disponibilizado pelo Ministério da Ciência, Tecnologia e Ensino Superior – Fundação para a Ciência e Tecnologia (Portugal), através da bolsa SFRH/BPD/75072/2010 e pelo FEDER/FSE, através da bolsa PTDC/EME‐TME/098050/2008.

Bibliografia

1. [1] T. Belytschko, Y. Krongauz, D. Organ, M. Fleming, P. Krysl; Meshless Methods: An overview and recent developments; Computer Methods in Applied Mechanics and Engineering, 139 (1996), pp. 3–47
2. [2] B. Nayroles, G. Touzot, P. Villon; Generalizing the Finite Element Method: Diffuse Approximation and Diffuse Elements; Computational Mechanics, 10 (1992), pp. 307–318
3. [3] Y.T. Gu; Meshfree methods and their comparisons; International Journal of Computational Methods, 2 (4) (2005), pp. 477–515
4. [4] Z.T. Atluri; SN, A new meshless local Petrov–Galerkin (MLPG) approach in computational mechanics; Computational Mechanics, 22 (2) (1998), pp. 117–127
5. [5] G.R. Liu, Y.T. Gu; A Point Interpolation Method for Two‐Dimensional Solids; International Journal for Numeric Methods in Engineering, 50 (2001), pp. 937–951
6. [6] J.G. Wang, G.R. Liu, Y.G. Wu; A Point Interpolation Method for Simulating Dissipation Process of Consolidation; Computational Methods in Applied Mechanics and Engineering, 190 (2001), pp. 5907–5922
7. [7] N. Sukumar, B. Moran, A. Yu Semenov, V.V. Belikov; Natural neighbour Galerkin methods; International Journal for Numeric Methods in Engineering, 50 (2001), pp. 1–27
8. [8] J. Braun, M. Sambridge; A numerical method for solving partial differential equations on highly irregular evolving grids; Nature, 376 (1995), pp. 655–660
9. [9] R. Sergio, S. Idelsohn, E. Oñate, N. Calvo, F. del Pin; The Meshless Finite Element Method; International Journal for Numeric Methods in Engineering, 58 (2003), pp. 893–912
10. [10] J.G. Wang, G.R. Liu; A Point Interpolation Meshless Method based on Radial Basis Functions; International Journal for Numeric Methods in Engineering, 54 (2002), pp. 1623–1648
11. [11] J.G. Wang, G.R. Liu; On the Optimal Shape Parameters of Radial Basis Functions used for 2‐D Meshless Methods; Computational Methods in Applied Mechanics and Engineering, 191 (2002), pp. 2611–2630
12. [12] G.M. Voronoi; Nouvelles applications des paramètres continus à la théorie des formes quadratiques, Deuxième Mémoire: Recherches sur les parallélloèdres primitifs; J. Reine Angew. Math., 134 (1908), pp. 198–287
13. [13] L.M.J.S. Dinis, R.M. Natal Jorge, J. Belinha; Analysis of 3D solids using the natural neighbour radial point interpolation method; Computer Methods in Applied Mechanics and Engineering, 196 (2007), pp. 2009–2028
14. [14] A.J.M. Ferreira, C.M.C. Roque, P.A.L.S. Martins; Radial basis functions and higher‐order shear deformation theories; Composite Structures, 66 (2004), pp. 287–293
15. [15] V. Bayona, M. Moscovo, M. Kindelan; Optimal constant shape parameter for multiquadic based RBF‐FD method; Journal of Computacional Physics, 230 (2011), pp. 7384–7399
16. [16] V. Bayona, M. Moscovo, M. Kindelan; Optimal variable shape parameter for multiquadric based RBF‐FD method; Journal of Computacional Physics, 230 (2012), pp. 2466–2481
17. [17] L.M.J.S. Dinis, R.M. Natal Jorge, J. Belinha; Analysis of plates and laminates using the natural neighbour radial point interpolation method; Engineering Analysis with Boundary Elements, 32 (2008), pp. 267–279
18. [18] R.K. Kapania, S. Raciti; Recent Advances in Analysis of Laminated Beams and Plates, Part I: Shear Effects and Buckling; American Institute of Aeronautics and Astronautics Journal, 27 (1989), pp. 923–934
19. [19] R.P. Shimpi, A.V. Ainapure; A beam finite element based on layerwise trigonometric shear deformation theory; Composite Structures, 53 (2001), pp. 153–162
20. [20] R. Kadoli, K. Akhtar, N. Ganesan; Static analysis of functionally graded beams using higher order shear deformation theory; Applied Mathematical Modelling, 32 (2008), pp. 2509–2525
21. [21] C.J.Y. Atluri SN, H.G. Kim; Analysis of thin beams, using the meshless local Petrov±Galerkin method, with generalized moving least squares interpolations; Computational Mechanics, 24 (1999), pp. 334–347
22. [22] J.Y. Cho, S.N. Atluri; Analysis of shear flexible beams, using the meshless local Petrov‐Galerkin method, based on a locking‐free formulation,; Engineering Computations, 18 (2001), pp. 215–240
23. [23] J.R. Xiao, M.A. McCarthy; Meshless analysis of Timoshenko beams based on a locking‐free formulation and variational approaches; Computational Methods in Applied Mechanics and Engineering, 192 (2003), pp. 4403–4424
24. [24] M.R. Moosavi, F. Delfanian, A. Khelil; The orthogonal meshless finite volume method for solving Euler–Bernoulli beam and thin plate problems; Thin‐Walled Structures, 49 (2011), pp. 923–932
25. [25] R. Sibson; A vector identity for the Dirichlet tessellation; Mathematical Proceedings of the Cambridge Philosophical Society, 87 (1980), pp. 151–155
26. [26] L.M.J.S. Dinis, R.M. Natal Jorge, J. Belinha; A natural neighbour meshless method with a 3D shell‐like approach in the dynamic analysis of thin 3D structures; Thin‐Walled Structures, 49 (2011), pp. 185–196
27. [27] L.M.J.S. Dinis, R.M. Natal Jorge, J. Belinha; Extensão do “Natural Neighbour Radial Point Interpolation Method” à análise de laminados compósitos; Presented at the CMNE/CILAMCE 2007, Porto (2007)
28. [28] L.M.J.S. Dinis, R.M. Natal Jorge, J. Belinha; The dynamic analysis of plates using a radial interpolation meshless method with a shell‐like formulation; Presented at the 3rd International Conference on Integrity, Reliability and Failure, Porto/Portugal (2009)
29. [29] J.N. Reddy; Mechanics of Laminated Composite Plates and Shells: Theory and Analysis; CRC Press (2004)
30. [30] J. A. Belinha, “Análise Elasto‐Plástica Considerando o Método Livre de Elementos de Galerkin. Problemas Bidimensionais, Placas e Laminados.,” Grau de Mestre em Estruturas de Engenharia Civil, Faculdade de Engenharia da Universidade do Porto, Universidade do Porto, Porto, 2004.