Visco-plastic Chaboche model for nickel-based alloys under anisothermal cyclic loading

VISCO-PLASTIC CHABOCHE MODEL FOR NICKEL-BASED ALLOYS UNDER ANISOTHERMAL CYCLIC LOADING

HÉLÈNE MORCH*, LAURENT DUCHÊNE* AND ANNE-MARIE HABRAKEN*†

* Dpt ArGEnCo, MS²F-MSM

University of Liège

Allée de la Découverte 9, 4000 Liège, Belgium

e-mail: helene.morch@ulg.ac.be; l.duchene@ulg.ac.be; anne.habraken@ulg.ac.be

http://www.uee.ulg.ac.be/cms/c_2672632/fr/mecanique-des-solides-et-des-materiaux-msm

^† Fund for Scientific Research (FRS-FNRS)

www.fnrs.be

Key words: Constitutive modeling, Nickel-based superalloys, Cyclic plasticity, Thermo-mechanical modeling

Summary: The mechanical behavior of visco-plastic materials such as nickel-based alloys is highly dependent on temperature. Some characteristics such as viscosity, hardening, static recovery, dynamic recovery have more or less influence on the overall behavior depending on the considered temperature. The unified constitutive model developed by Chaboche [1] is very efficient in representing this complexity as it is very adaptable and can contain many features. A basic Chaboche model contains a viscosity law and one or several hardening equations. Within these hardening equations, it is possible to add several features that will represent the complex behavior of the material.

The aim of this study is to understand the role of the different parameters and the influence of the different features in an advanced Chaboche model adapted to cyclic anisothermal loading. This specific model was also developed in [2],[3]. However, part of this study is based on particular cases where different features of the model are analyzed [4]–[6].

1 INTRODUCTION

The use of nickel-based superalloys at high temperature requires advanced visco-plastic models to accurately represent the material behavior. The Chaboche model is very efficient for representing complex behavior as it can include various features such as isotropic hardening, kinematic hardening, static recovery, or thermo-mechanical behavior. The drawback of this type of model is the number of parameters. Indeed, a high level of accuracy of the model requires a high number of parameters. As a consequence, the determination of these parameters can be an arduous task. To facilitate this important step in the completion of the model, a sensitivity study can provide valuable information. The sensitivity analysis reveals which tests are more relevant for the determination of each parameter, but also how the parameters can impact the model and what physical meaning they have.

2 VISCO-PLASTIC MODELING

The visco-plastic model used in this study is a Chaboche-type constitutive model as developed in Ahmed, 2013 [2] for superalloy Haynes 230 at high temperture. This model, described hereafter, was implemented in the 3D finite element code Lagamine [7] developed at the University of Liège. For simplification, the model is described here as a 1D model, since only uniaxial tests are used in this study.

2.1 Visco-plasticity

The mechanical strain can be decomposed in an elastic contribution and a visco-plastic contribution:

$\epsilon ={\epsilon }^{e}+{\epsilon }^{vp}$

(1)

The elastic strain and the stress are related through Hooke's law, where E is the Young's modulus:

$\sigma =E{\epsilon }^{e}$

(2)

The yield locus is defined by the von-Mises criterion, with ${\textstyle X}$ the back-stress, ${\textstyle {\sigma }_{0}}$the initial yield strength, and ${\textstyle R}$ the isotropic hardening variable:

$f=\left|\sigma -X\right|-{\sigma }_{0}-R$

(3)

The viscosity is modeled through Norton's equation (equation (4)), with viscous parameters ${\textstyle n}$ and ${\textstyle K}$.

${\overset {\cdot }{p}}=\left|{\overset {\cdot }{\epsilon }}^{vp}\right|={\left\langle {\frac {f}{K}}\right\rangle }^{n}$ $where\,\left\langle x\right\rangle =\left\{{\begin{matrix}x\,if\,x\geq 0\\0\,if\,x<0\end{matrix}}\right.$

(4)

2.2 Hardening equations

The evolution of the isotropic variable ${\textstyle R}$, described by equation (5) depends on the plastic strain rate ${\textstyle {\overset {\cdot }{p}}}$ and on two parameters ${\textstyle b}$ and ${\textstyle Q}$. ${\textstyle b}$ can be understood as the rate at which variable ${\textstyle R}$ will reach its saturation value ${\textstyle Q}$.

${\overset {\cdot }{R}}=b\left(Q-R\right){\overset {\cdot }{p}}$

(5)

The back-stress ${\textstyle X}$ is composed of one or several back stresses ${\textstyle {X}_{i}}$. Each of these ${\textstyle {X}_{i}}$ obeys a non linear kinematic hardening rule defined through an Armstrong-Frederick equation [8]. Following the work of Yaguchi et al., 2002 [4], [5] a state variable ${\textstyle {Y}_{i}}$ can be added in the equation in order to model the evolution of the mean stress and a temperature-dependency term is used for anisothermal modeling. The variable ${\textstyle {Y}_{i}}$ is controlled by parameters ${\textstyle {\alpha }_{b,i}}$and ${\textstyle {Y}_{st,i}}$, both positive. The equation of a back stress ${\textstyle {X}_{i}}$ therefore consists of 4 terms:

• strain hardening, controlled by parameter ${\textstyle {C}_{i}}$;

• dynamic recovery, controlled by parameter ${\textstyle {\gamma }_{i}}$;

• static recovery, controlled by parameters ${\textstyle {b}_{i}}$ and ${\textstyle {r}_{i}}$;

• temperature rate, with the influence of parameter ${\textstyle {C}_{i}}$.

$X=\sum _{i=1}^{n}{X}_{i}$ ${\overset {\cdot }{X}}_{i}={C}_{i}{\overset {\cdot }{\epsilon }}^{vp}-{\gamma }_{i}\left({X}_{i}-\right.$$\left.{Y}_{i}\right){\overset {\cdot }{p}}-{b}_{i}\,{\left|{X}_{i}\right|}^{{r}_{i}}{X}_{i}+$${\frac {1}{{C}_{i}}}{\frac {\partial {C}_{i}}{\partial T}}{\overset {\cdot }{T}}{X}_{i}$ $with\,{\overset {\cdot }{Y}}_{i}=-{\alpha }_{b,i}\left({Y}_{st,i}{\frac {{X}_{i}}{\left|{X}_{i}\right|}}+\right.$$\left.{Y}_{i}\right){\left|{X}_{i}\right|}^{{r}_{i}}$

(6)

Cyclic hardening is represented by the evolution of the dynamic recovery parameter ${\textstyle {\gamma }_{i}}$. The rate of evolution of this parameter is controlled by the plastic strain rate ${\textstyle {\overset {\cdot }{p}}}$ and a parameter ${\textstyle {D}_{{\gamma }_{i}}}$. The parameter ${\textstyle {\gamma }_{i}}$evolves towards a saturation value ${\textstyle {\gamma }_{i}^{0}}$ which depends on the radius of the strain memory surface ${\textstyle q}$. The strain memory surface ${\textstyle {g}_{M}}$ is defined by equation (8), where ${\textstyle H(x)}$ is the Heaviside step function.

	${\overset {\cdot }{\gamma }}_{i}={D}_{{\gamma }_{i}}\left({\gamma }_{i}^{0}-{\gamma }_{i}\right){\overset {\cdot }{p}}$ $with\,\,{\gamma }_{i}^{0}={a}_{{\gamma }_{i}}+{b}_{{\gamma }_{i}}{e}^{-{c}_{{\gamma }_{i}}q}$	(7)
	${g}_{M}\left({\epsilon }^{vp}-\zeta \right)=\left|{\epsilon }^{vp}-\zeta \right|-$$q$ ${\overset {\cdot }{\zeta }}=\left(1-\eta \right)H\left({g}_{M}\right){\overset {\cdot }{p}}$ ${\overset {\cdot }{q}}=\eta ~H\left({g}_{M}\right){\overset {\cdot }{p}}$	(8)

2.3 Influence of the maximum temperature

In the case of anisothermal cyclic loading on Haynes 230, experiments show that the maximum temperature of the cycle has an influence on the overall behavior of the material [2]. This is modeled by a variation of the Young's modulus, expressed as a weighted average of the initial Young's modulus at temperature ${\textstyle T}$ and the Young's modulus at maximum temperature ${\textstyle {T}_{max}}$:

$E={f}_{E}E+\left(1-{f}_{E}\right){E}_{{T}_{max}}$ ${\overset {\cdot }{f}}_{E}={b}_{E}\left({f}_{E}^{S}-{f}_{E}\right){\overset {\cdot }{p}}$

(9)

The weighted average factor ${\textstyle {f}_{E}}$ represents the weight of the initial Young's modulus. A small value of ${\textstyle {f}_{E}}$ corresponds to a significant influence of the maximum temperature. ${\textstyle {f}_{E}}$ evolves at a rate ${\textstyle {b}_{E}}$ towards a saturated value ${\textstyle {f}_{E}^{S}}$.

3 METHOD

The sensitivity study was conducted using reference sets of parameters available in the literature. These sets of parameters came from models that did not contain as many features as the model hereinbefore presented. However, using different sub-models allowed to study the sensitivity of the model to each of the parameters.

3.1 Numerical tests

The sensitivity study was conducted numerically on each parameter by performing a cyclic test and modifying one parameter at a time. Different sets of reference parameters were used to perform the simulations. Table 1 summarizes the reference articles used depending on the tested parameters.

Table 1 : Reference articles used to obtain parameters

Parameter studied	Set of reference parameters used
$K,n,\,b,\,Q,\,{C}_{1},\,{C}_{2},\,{\gamma }_{1},{\gamma }_{2}$	Zhan and Tong, 2007 [6]
${b}_{1},\,{r}_{1},{\alpha }_{b,1},\,{Y}_{st,1},{D}_{{\gamma }_{1}},{a}_{{\gamma }_{1}},{b}_{{\gamma }_{1}},{c}_{{\gamma }_{1}},\eta$	Yaguchi et al., 2002a [4]
${b}_{E},\,{f}_{E}^{s}$	Yaguchi et al., 2002b [5]

The first model used [6] is an isothermal model describing the behavior of Alloy X at 650°C with two back-stresses for kinematic hardening, where no static recovery effect is taken into account. To study the influence of static recovery, variable Y, and cyclic hardening, a different model was used [4]. The latter describes the behavior of IN738LC at 850°C. Kinematic hardening is modeled using only one back-stress, with an internal variable Y. The influence of parameters ${\textstyle {b}_{E}}$ and ${\textstyle {f}_{E}^{s}}$ was tested on an anisothermal model [5] identical to [4].

It is to be noted that no reference was available for parameters ${\textstyle {D}_{{\gamma }_{1}},{a}_{{\gamma }_{1}},{b}_{{\gamma }_{1}},{c}_{{\gamma }_{1}},\eta ,\,{b}_{E}}$ and ${\textstyle {f}_{E}^{s}}$, therefore, a reference value was determined for each of these parameters through trial and error, to obtain results that seemed coherent with the experimental data available (although the parameters were not determined to fit experimental curves). These reference values are summarized in Table 2.

Table 2 : Reference parameters

${D}_{{\gamma }_{1}}$	${a}_{{\gamma }_{1}}$	${b}_{{\gamma }_{1}}$	${c}_{{\gamma }_{1}}$	$\eta$	${b}_{E}$	${f}_{E}^{s}$
10	300	100	10	0.2	1000	0.2

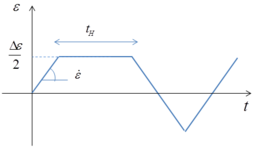
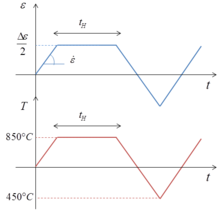
The sensitivity of the model on the different parameters was tested on two strain-controlled cyclic tests. A schematic representation of one period of the cyclic tests is given in Figure 1 (a). Anisothermal tests (Figure 1 (b)) were used to evaluate the sensitivity of the model to parameters ${\textstyle {b}_{E}}$ and ${\textstyle {f}_{E}^{s}}$. For both Test 1 and Test 2, the strain amplitude is ${\textstyle \Delta \epsilon =}$$2\%$. The strain rates ${\textstyle {\overset {\cdot }{\epsilon }}}$ and hold times ${\textstyle {t}_{H}}$ of Test 1 and 2 are respectively {0.1%/s, 20s} and {0.001%/s, 1000s}. Each of these tests were performed for 50 cycles, which is enough for the stress-strain hysteresis loop to reach its saturation value using the reference parameters.

(a)

(b)

Figure 1: (a) Strain-controlled isothermal test; (b) Strain-controlled anisothermal test

3.2 Sensitivity criteria

Different criteria ${\textstyle {F}_{i}}$ were used to determine the sensitivity of the model to the different parameters:

• ${\textstyle {F}_{1}:}$ The tensile stress before the first hold time (equivalent to the stress at the end of a tensile test);

• ${\textstyle {F}_{2}:}$ The amount of stress relaxation during the first hold time (equivalent to a relaxation test);

• ${\textstyle {F}_{3}:}$ The stress amplitude ${\textstyle {\sigma }_{amp}=}$${\frac {{\sigma }_{max}-{\sigma }_{min}}{2}}$ at the 50^th cycle;

• ${\textstyle {F}_{4}:}$ The mean stress ${\textstyle {\sigma }_{mean}=}$${\frac {{\sigma }_{max}+{\sigma }_{min}}{2}}$ at the 50^th cycle.

The mean stress and the stress amplitude were also used as criteria to study the sensitivity over the cycles.

For each criterion ${\textstyle {F}_{i}}$, the sensitivity to a parameter ${\textstyle P}$ is expressed as ${\textstyle {\frac {\partial {F}_{i}}{\partial P}}}$. The criterion ${\textstyle {F}_{i}}$ is computed for three values of the parameter ${\textstyle P}$ and the sensitivity ${\textstyle {\frac {\partial {F}_{i}}{\partial P}}}$ is calculated as the slope of the ${\textstyle {F}_{i}(P)}$ line obtained from a linear regression.

4 RESULTS

4.1 Viscous parameters ${\textstyle {\mathit {\boldsymbol {K,n}}}}$4.1 Viscous parameters K , n {\textstyle {\mathit {\boldsymbol {K,n}}}}

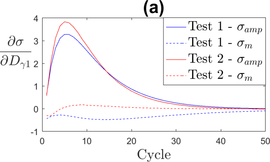
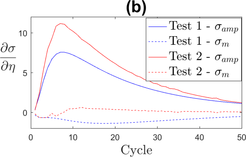
The viscous parameters ${\textstyle K}$ and ${\textstyle n}$ represent the relation between the stress and the strain rate. Figure 2 shows the sensitivity of criteria ${\textstyle {F}_{1},\,{F}_{2},\,{F}_{3}}$ and ${\textstyle {F}_{4}}$. Both parameters have an influence on the tensile stress ( ${\textstyle {F}_{1}}$) and on the stabilized stress amplitude ( ${\textstyle {F}_{3}}$). The stress relaxation is also influenced by these viscous parameters but to a smaller extent.

Figure 2: (a) Sensitivity to the drag stress ${\textstyle {\mathit {K}}}$; (b) Sensitivity to the viscous exponent ${\textstyle {\mathit {\,n}}}$

4.2 Isotropic hardening parameters ${\textstyle {\mathit {\boldsymbol {b,Q}}}}$4.2 Isotropic hardening parameters b , Q {\textstyle {\mathit {\boldsymbol {b,Q}}}}

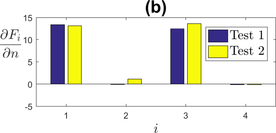
The isotropic hardening parameters ${\textstyle b}$ and ${\textstyle Q}$ control the growth of the yield surface. Knowing this, it is predictable that these parameters will influence mostly the tensile stress and the stress amplitude. Figure 3 shows that these parameters influence mainly the stress amplitude over the cycles, with ${\textstyle b}$ reaching a peak around the 10th cycle, where the stress amplitude starts to stabilize. The small sensitivity of the tensile stress to these isotropic hardening parameters is due to the test itself, which only reaches a 1% strain, therefore not allowing isotropic hardening to fully develop. In practise, a tensile test to rupture would show as much sensitivity to isotropic hardening as the cyclic tests that were performed here.

Figure 3 - (a) Sensitivity to parameter ${\textstyle {\mathit {b}}}$; (b) Stress amplitude and mean stress sensitivity to ${\textstyle {\mathit {b}}}$ over cycles; (c) Sensitivity to parameter ${\textstyle {\mathit {Q}}}$

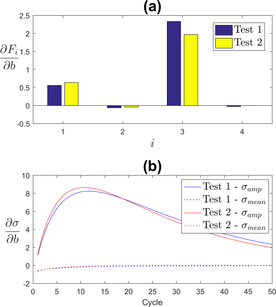
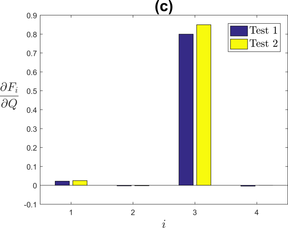
4.3 Kinematic hardening parameters ${\textstyle {\mathit {\boldsymbol {C}}}_{\mathit {\boldsymbol {i}}}}$4.3 Kinematic hardening parameters C i {\textstyle {\mathit {\boldsymbol {C}}} {\mathit {\boldsymbol {i}}}}

Kinematic hardening is characterized by a change in the position of the yield surface. As for isotropic hardening, the parameters controlling kinematic hardening influence the tensile stress and the stress amplitude, as seen in Figure 4. As shown in Tong et al. [9], the use of two parameters ${\textstyle {C}_{1}}$ and ${\textstyle {C}_{2}}$ allows the description of a transient region with a fast growing back-stress ${\textstyle {X}_{1}}$ and a steady-state behaviour once ${\textstyle {X}_{1}}$ has reached its stabilized value, with back-stress ${\textstyle {X}_{2}}$ growing at a quasi-steady pace. The parameters ${\textstyle {C}_{1}}$ and ${\textstyle {C}_{2}}$ also have an influence on the shape of the hysteresis loop, and more particularly on its curvature in the visco-platic domain.

Figure 4 - (a) Sensitivity to parameter ${\textstyle {\mathit {C}}_{\mathit {1}}}$; (b) Sensitivity to parameter ${\textstyle {\mathit {C}}_{\mathit {2}}}$

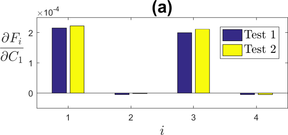
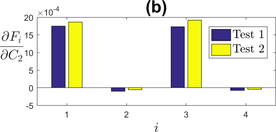
4.4 Dynamic recovery parameters ${\textstyle {\mathit {\boldsymbol {\gamma }}}_{\mathit {\boldsymbol {i}}}}$4.4 Dynamic recovery parameters γ i {\textstyle {\mathit {\boldsymbol {\gamma }}} {\mathit {\boldsymbol {i}}}}

The dynamic recovery parameters ${\textstyle {\gamma }_{1}}$ and ${\textstyle {\gamma }_{2}}$ have the opposite effect of ${\textstyle {C}_{1}}$ and ${\textstyle {C}_{2}}$. Figure 5 shows that ${\textstyle {F}_{1}}$ and ${\textstyle {F}_{3}}$ show a negative sensitivity to both ${\textstyle {\gamma }_{1}}$ and ${\textstyle {\gamma }_{2}}$, which means an increase in ${\textstyle {\gamma }_{i}}$ will lead to a decrease in ${\textstyle {F}_{j}}$. Similarly to the kinematic hardening parameters, ${\textstyle {\gamma }_{1}}$ and ${\textstyle {\gamma }_{2}}$ also have an effect on the curvature of the hysteresis loop.

Figure 5 - (a) Sensitivity to parameter ${\textstyle {\mathit {\gamma }}_{\mathit {1}}}$; (b) Sensitivity to parameter ${\textstyle {\mathit {\gamma }}_{\mathit {2}}}$

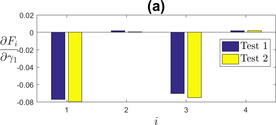
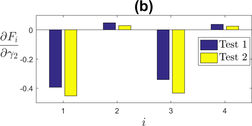
4.5 Static recovery parameters ${\textstyle {\mathit {\boldsymbol {b}}}_{\mathit {\boldsymbol {i}}}{\mathit {\boldsymbol {,\,\,}}}{\mathit {\boldsymbol {r}}}_{\mathit {\boldsymbol {i}}}}$4.5 Static recovery parameters b i , r i {\textstyle {\mathit {\boldsymbol {b}}} {\mathit {\boldsymbol {i}}}{\mathit {\boldsymbol {,\,\,}}}{\mathit {\boldsymbol {r}}} {\mathit {\boldsymbol {i}}}}

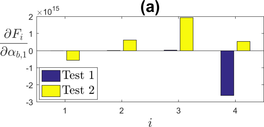
To study the influence of the static recovery parameters, the internal variable ${\textstyle Y}$ was not taken into account. Indeed, parameter ${\textstyle {r}_{i}}$ is used both in the static recovery term of the back-stress evolution and in the evolution of internal variable ${\textstyle Y}$ - equation (6). Figure 6 shows the sensitivity to static recovery parameters ${\textstyle {b}_{1},\,\,{r}_{1}}$ without considering the effect of ${\textstyle {r}_{1}}$ on ${\textstyle Y}$. It is apparent that Test 2, which is slower and has longer hold times than Test 1, is much more impacted by the variation of these parameters. This is an expected result considering static recovery is a phenomenon that takes place at a constant strain. The influence is maximal on the stress relaxation (criterion ${\textstyle {F}_{2}}$), but also appears on the other criteria. This can be explained by equation (6): a higher value of ${\textstyle {b}_{1}}$ or ${\textstyle {r}_{1}}$ will lead to a greater decrease in the back-stress ${\textstyle {X}_{1}}$, therefore lowering the tensile stress and stress amplitude.

Figure 6 - (a) Sensitivity to ${\textstyle {\mathit {b}}_{\mathit {1}}}$; (b) Sensitivity to ${\textstyle {\mathit {r}}_{\mathit {1}}}$ (without considering the internal variable Y)

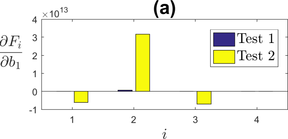
4.6 Mean stress evolution parameters ${\textstyle {\mathit {\boldsymbol {\alpha }}}_{\mathit {\boldsymbol {b,i\,}}}{\mathit {\boldsymbol {,\,}}}{\mathit {\boldsymbol {Y}}}_{\mathit {\boldsymbol {st,i}}}{\mathit {\boldsymbol {,\,}}}{\mathit {\boldsymbol {r}}}_{\mathit {\boldsymbol {i}}}}$4.6 Mean stress evolution parameters α b , i , Y s t , i , r i {\textstyle {\mathit {\boldsymbol {\alpha }}} {\mathit {\boldsymbol {b,i\,}}}{\mathit {\boldsymbol {,\,}}}{\mathit {\boldsymbol {Y}}} {\mathit {\boldsymbol {st,i}}}{\mathit {\boldsymbol {,\,}}}{\mathit {\boldsymbol {r}}} {\mathit {\boldsymbol {i}}}}

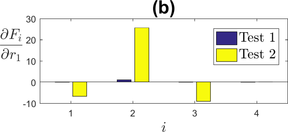
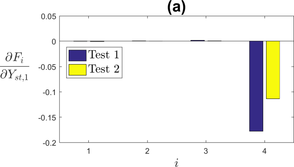
The internal variable ${\textstyle {Y}_{1}}$ that controls the evolution of the mean stress over cycles is calculated using three parameters ${\textstyle {\alpha }_{b,1\,},\,{Y}_{st,1},\,{r}_{1}}$. Figure 7 (a) represents the sensitivity to parameter ${\textstyle {\alpha }_{b,1}}$.

Figure 7 - (a) Sensitivity to ${\textstyle {\mathit {\boldsymbol {\alpha }}}_{{\mathit {b}}{\mathit {,1}}}}$; (b) Sensitivity to modified ${\textstyle {\mathit {\alpha }}_{{\mathit {b}}{\mathit {,1}}}}$

The sensitivity computed with Test 1 seems coherent: the parameter influences only the mean stress. However, sensitivities computed with Test 2 give rather unexpected results, and show a bigger influence on the stress amplitude than on the mean stress. The reason for this can be found by considering the evolution of variable ${\textstyle {Y}_{1}}$ over time, described by equation (6). The variable ${\textstyle {Y}_{1}}$ varies within ${\textstyle -}$${Y}_{st,1}$ and ${\textstyle +{Y}_{st,1}}$. Therefore, according to (6), ${\textstyle {\overset {\cdot }{Y}}_{1}}$ is positive when ${\textstyle {X}_{1}>0}$ and negative when ${\textstyle {X}_{1}<0}$ unless ${\textstyle {Y}_{1}}$ has reached its upper bound or lower bound. During a cycle, if ${\textstyle {\alpha }_{b,1}}$ is small enough, ${\textstyle {Y}_{1}}$ decreases slowly while ${\textstyle {X}_{1}>0}$ (tensile deformation), and then increases when ${\textstyle {X}_{1}<0}$ (compressive deformation). The time spent in compressive deformation is much smaller than in tension, therefore, the variable ${\textstyle {Y}_{1}}$ globally decreases over cycles. However, if ${\textstyle {\alpha }_{b,1}}$ is too big compared to the frequency of the test, the variable ${\textstyle {Y}_{1}}$ reaches its upper and lower bound during the first cycle. This is an unwanted effect because ${\textstyle {Y}_{1}}$ will assume positive values, meaning the mean stress can increase over cycles, which is physically incoherent.

As a result, in order to represent the mean stress evolution properly, ${\textstyle {\alpha }_{b,1}}$ should be chosen accordingly to the frequency of the cyclic test. Particularly, the value of ${\textstyle {\alpha }_{b,1}}$ should be bigger for bigger frequencies. Figure 7 (b) shows the sensitivity to ${\textstyle {\alpha }_{b,1}}$, using ${\textstyle {\alpha }_{b,1}=}$$0.01\ast {\alpha }_{b,1}$ for Test 2. It appears clearly that ${\textstyle {\alpha }_{b,1}}$ then only influences the mean stress.

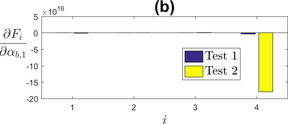
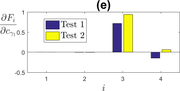
The influence of parameters ${\textstyle {Y}_{st,1}}$ and ${\textstyle {r}_{1}}$ is tested using the modified value of ${\textstyle {\alpha }_{b,1}}$ for Test 2. The results are shown in Figure 8. ${\textstyle {Y}_{st,1}}$ has an influence on the mean stress, as expected. ${\textstyle {r}_{1}}$ has an influence on both stress relaxation and mean stress since this parameter is used both for the variable ${\textstyle {Y}_{1}}$ and for the static recovery term in the equation of the back-stress.

Figure 8 - (a) Sensitivity to ${\textstyle {\mathit {Y}}_{\mathit {st,1}}}$; (b) Sensitivity to ${\textstyle {\mathit {r}}_{\mathit {1}}}$

4.7 Cyclic hardening parameters ${\textstyle {\mathit {\boldsymbol {D}}}_{{\mathit {\boldsymbol {\gamma }}}_{\mathit {\boldsymbol {i}}}}{\boldsymbol {,\,}}{\mathit {\boldsymbol {a}}}_{{\mathit {\boldsymbol {\gamma }}}_{\mathit {\boldsymbol {i}}}}{\boldsymbol {,\,}}{\mathit {\boldsymbol {b}}}_{{\mathit {\boldsymbol {\gamma }}}_{\mathit {\boldsymbol {i}}}}{\boldsymbol {,}}{\mathit {\boldsymbol {c}}}_{{\mathit {\boldsymbol {\gamma }}}_{\mathit {\boldsymbol {i}}}}{\boldsymbol {,\,}}{\mathit {\boldsymbol {\eta }}}}$4.7 Cyclic hardening parameters D γ i , a γ i , b γ i , c γ i , η {\textstyle {\mathit {\boldsymbol {D}}} {{\mathit {\boldsymbol {\gamma }}} {\mathit {\boldsymbol {i}}}}{\boldsymbol {,\,}}{\mathit {\boldsymbol {a}}} {{\mathit {\boldsymbol {\gamma }}} {\mathit {\boldsymbol {i}}}}{\boldsymbol {,\,}}{\mathit {\boldsymbol {b}}} {{\mathit {\boldsymbol {\gamma }}} {\mathit {\boldsymbol {i}}}}{\boldsymbol {,}}{\mathit {\boldsymbol {c}}} {{\mathit {\boldsymbol {\gamma }}} {\mathit {\boldsymbol {i}}}}{\boldsymbol {,\,}}{\mathit {\boldsymbol {\eta }}}}

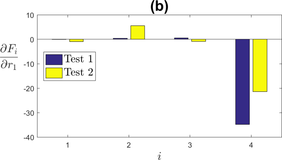
Cyclic hardening is described using five parameters that impact the value of parameter ${\textstyle {\gamma }_{i}}$ over the cycles. Parameters ${\textstyle {D}_{{\gamma }_{i}}}$ and ${\textstyle \eta }$ control respectively the rate of cyclic hardening and the rate of growth of the plastic strain memorization surface. Figure 9 (a) and (b) show the sensitivity of the stress amplitude and mean stress to ${\textstyle {D}_{{\gamma }_{1}}}$ and ${\textstyle \eta }$ . In both cases, the sensitivity grows to a peak value, and then decreases towards 0 as the values of ${\textstyle {\gamma }_{1}}$ (for ${\textstyle {D}_{{\gamma }_{1}}}$) and ${\textstyle q}$ (for ${\textstyle \eta }$ ) stabilize. ${\textstyle {a}_{{\gamma }_{i}},\,{b}_{{\gamma }_{i}}}$ and ${\textstyle {c}_{{\gamma }_{i}}}$ control the stabilized value of ${\textstyle {\gamma }_{i}}$. Therefore, it is expected that these parameters only influence the stabilized value of the stress amplitude, as seen in Figure 9. Parameters ${\textstyle {a}_{{\gamma }_{i}}}$ and ${\textstyle {b}_{{\gamma }_{i}}}$ have a negative influence while ${\textstyle {c}_{{\gamma }_{i}}}$ has a positive influence on the stress amplitude. These parameters also have a small influence on the mean stress, which can be explained by the fact that the evolution law of ${\textstyle {Y}_{1}}$ depends on the back-stress ${\textstyle {X}_{1}}$, which is itself dependent on ${\textstyle {\gamma }_{1}}$. The sensitivity observed for Test 2 on the mean stress should however not be taken into account, as it is the result of the inadequacy of ${\textstyle {\alpha }_{b,1\,}}$ mentioned in the previous paragraph.

Figure 9 - (a) Cyclic sensitivity to ${\textstyle {\mathit {D}}_{{\mathit {\gamma }}_{\mathit {1}}}}$; (b) Cyclic sensitivity to ${\textstyle {\mathit {\eta }}}$; (c) Sensitivity to ${\textstyle {\mathit {a}}_{{\mathit {\gamma }}_{\mathit {1}}}}$; (d) Sensitivity to ${\textstyle {\mathit {b}}_{{\mathit {\gamma }}_{\mathit {1}}}}$; (e) Sensitivity to ${\textstyle {\mathit {c}}_{{\mathit {\gamma }}_{\mathit {1}}}}$

4.8 Maximum temperature parameters ${\textstyle {\mathit {\boldsymbol {b}}}_{\mathit {\boldsymbol {E}}}{\mathit {\boldsymbol {,\,}}}{\mathit {\boldsymbol {f}}}_{\mathit {\boldsymbol {E}}}^{\mathit {\boldsymbol {S}}}}$4.8 Maximum temperature parameters b E , f E S {\textstyle {\mathit {\boldsymbol {b}}} {\mathit {\boldsymbol {E}}}{\mathit {\boldsymbol {,\,}}}{\mathit {\boldsymbol {f}}} {\mathit {\boldsymbol {E}}}^{\mathit {\boldsymbol {S}}}}

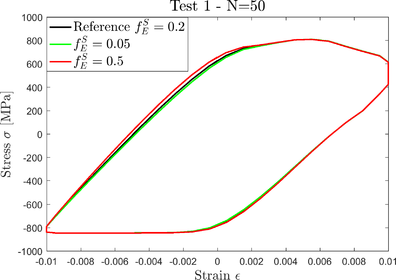
Parameters ${\textstyle {b}_{E}}$ and ${\textstyle {f}_{E}^{S}}$, that represent the influence of the maximum temperature, do not have a visible and clear influence on the criteria used previously. Figure 10 shows the stabilized hysteresis loop of Test 1 for three values of ${\textstyle {f}_{E}^{S}}$. Small values of ${\textstyle {f}_{E}^{S}}$ - i.e. substantial influence of the maximum temperature - lead to a decrease in the slope of the stress-strain curve in the small temperature domain (corresponding to compression strain). This is an expected result considering that the Young's modulus, which partly controls the slope of the stress-strain curve, decreases with temperature.

Figure 10 - Influence of parameter ${\textstyle {\mathit {f}}_{\mathit {E}}^{\mathit {S}}}$ on the stabilized hysteresis loop

The influence of ${\textstyle {b}_{E}}$ is difficult to show, as ${\textstyle {b}_{E}}$ represents the rate at which the slope decreases over time. Ahmed, 2013 [2] suggests that ${\textstyle {b}_{E}}$ should be chosen to make ${\textstyle {f}_{E}}$ evolve at a quick rate, so that the saturation value ${\textstyle {f}_{E}^{S}}$ is reached for a cumulative plastic strain ${\textstyle p}$ of approximately 0.2% for Haynes 230.

5 CONCLUSION

Based on numerical tests, the sensitivity of the model to each of its parameters was determined based on various criteria. The results of this sensitivity study were analyzed to narrow down the number and type of tests necessary for the determination of each parameter. The study shows that tensile tests, relaxation tests, and cyclic tests are necessary for the determination of the parameters of this model. A special attention should be given to parameter ${\textstyle {\alpha }_{b,1}}$ for the representation of the mean stress evolution. Indeed, the sensitivity study revealed that this parameter must be chosen with consideration to the frequency of the test simulated. Particularly, low-frequency cyclic tests should be modeled with a small value of ${\textstyle {\alpha }_{b,1}}$.

Further work needs to be made to determine a dependency law between ${\textstyle {\alpha }_{b,1}}$ and the test frequency, based on experimental tests. The sensitivity study can also serve as a basis to establish a method for the determination of the parameters.

ACKNOWLEDGEMENTS

The authors acknowledge Cockerill Maintenance & Ingénierie (CMI) and the Interuniversity Attraction Poles Program - Belgian State - Belgian Science Policy (P6-24). A.M. Habraken and L. Duchêne acknowledge the Belgian Fund for Scientific Research FRS-FNRS for its support.

REFERENCES

[1] J. L. Chaboche, “A review of some plasticity and viscoplasticity constitutive theories,” Int. J. Plast., vol. 24, no. 10, pp. 1642–1693, 2008.

[2] R. Ahmed, “Constitutive Modeling for Very High Temperature Thermo-Mechanical Fatigue Responses,” North Carolina State University, 2013.

[3] R. Ahmed, M. Menon, and T. Hassan, “Constitutive Model Development for Thermo-Mechanical Fatigue Response Simulation of Haynes 230,” in Proceedings of the ASME 2012 Pressure Vessels & Piping Conference, 2012, pp. 171–179.

[4] M. Yaguchi, M. Yamamoto, and T. Ogata, “A viscoplastic constitutive model for nickel-base superalloy, part 1: Kinematic hardening rule of anisotropic dynamic recovery,” Int. J. Plast., vol. 18, no. 8, pp. 1083–1109, 2002.

[5] M. Yaguchi, M. Yamamoto, and T. Ogata, “A viscoplastic constitutive model for nickel-base superalloy, part 2: Modeling under anisothermal conditions,” Int. J. Plast., vol. 18, no. 8, pp. 1111–1131, 2002.

[6] Z. L. Zhan and J. Tong, “A study of cyclic plasticity and viscoplasticity in a new nickel-based superalloy using unified constitutive equations. Part II: Simulation of cyclic stress relaxation,” Mech. Mater., vol. 39, no. 1, pp. 73–80, 2007.

[7] “Lagamine code, http://www.uee.ulg.ac.be/cms/c_2383455/en/lagamine.” .

[8] P. J. Armstrong and C. O. Frederick, “A Mathematical Representation of the Multi Axial Bauschinger Effect,” CEGB Report RD/B/N 731,Central Electricity Generating Board, 1966.

[9] J. Tong, Z. L. Zhan, and B. Vermeulen, “Modelling of cyclic plasticity and viscoplasticity of a nickel-based alloy using Chaboche constitutive equations,” Int. J. Fatigue, vol. 26, no. 8, pp. 829–837, 2004.