The concept hyperbeam as generalization of 1-dimensional models in rod elastostatics

Resumen

Este artículo trata de la formulación general de los problemas lineales de estática de piezas alargadas, y de la identificación de características formales y estructurales comunes a todos ellos, válidas para cualquier hipótesis cinemática de partida. Por medio de una factorización apropiada de la densidad de energía potencial complementaria en la pieza alargada, se introducen de modo natural y consistente las variables generalizadas (esfuerzos y deformaciones) que definen el modelo de viga, para cualquier hipótesis cinemática expresable como combinación lineal de desplazamientos generalizados. La identificación de esta función de energía complementaria con el funcional de Hamilton empleado en mecánica analítica permite una construcción sistemática de las ecuaciones que rigen esta clase de problemas. Dentro de este marco, se ha marcado como objetivo el establecer las condiciones generales necesarias para que las ecuaciones de equilibrio de la pieza se puedan plantear sin que en su escritura intervengan los desplazamientos del modelo. La conclusión fundamental es que ello es posible siempre que la cinemática de la sección transversal responda a un movimiento de sólido rígido. Como consecuencia, se introduce el concepto de hiperviga que define aquellos modelos cuyo modo de deformación no cumple la condición anterior; en ellos, los esfuerzos y los desplazamientos generalizados están acoplados en las ecuaciones de equilibrio. Esta circunstancia está relacionada con la idea de hiperestatismo local y justifica la denominación empleada.

Abstract

This paper is concerned with the general formulation of linear problems in rod elastostatics, and with the identification of their common formal and structural features, valid for every kinematical hypothesis. The generalized variables (section forces and generalized deformations) defining the 1-dimensional model are introduced in a consistent and natural way, through a convenient factorization of the density of complementary potential energy, for every kinematical constraint which can be expressed as a linear combination of the generalized displacements. The identification of this complementary energy function with the Hamiltonian functional of analytical mechanics allows a systematic procedure to construct the equations which rule this class of problems. In this frame, the main target is to establish the required conditions to write the rod equilibrium equations in a purely statical form (with no interplay of kinematical variables). We primarily conclude that this is possible when the kinematics of the cross-sections is constrained to a rigid body movement. As a consequence, the concept of hyperbeam is proposed in order to define those models with deformation modes beyond rigid body movements of the cross section: in them, section forces and generalized displacements are coupled in the equilibrium equations. This is related to the idea of local static indeterminacy (hyperstaticity ) and justifies the new name.

Palabras clave

Modelos de vigas ; Estatica de vigas ; Formulación variacional ; Matriz de equilibrio ; Matriz de acoplamiento ; Desacoplamiento de las ecuaciones de equilibrio ; Modelo hiperviga

Keywords

Beam models ; Beam elastostatics ; Variational formulation ; Equilibrium matrix ; Coupling matrix ; Uncoupled equilibrium equations ; Hyperbeam model

1. Introducción

Los problemas de mecánica de sólidos relativos a piezas alargadas (vigas rectas o curvas) han sido abordados tradicionalmente mediante modelos basados en distintas teorías que trataban de explicar un determinado fenómeno o modo de solicitación de la pieza. Así, entre los primeros problemas resueltos analíticamente se encuentra el problema de flexión plana de piezas alargadas planteado por Bernoulli y resuelto por Euler en 1744 o el problema de la torsión de alambres de sección circular abordado por Coulomb en 1784 [14] . El desarrollo de la teoría de la elasticidad a lo largo del siglo xix permitió establecer una relación directa entre la mecánica de sólidos y las teorías de flexión y torsión, reflejada en los trabajos publicados por Navier y Saint–Venant [13] , entre otros. Ya en el siglo xx se desarrollaron modelos particulares más elaborados para estudiar problemas específicos, como el de la torsión alabeada de piezas de pared delgada [15] , la flexión anticlástica [12] o la distorsión de vigas de sección abierta o cerrada [8] . En este contexto, aparecen dos puntos de vista complementarios en el desarrollo e interpretación de las teorías de piezas alargadas y también de placas y láminas (véase por ejemplo la introducción de la referencia de Antman [1] ): (a) como teorías directas que gobiernan el comportamiento de cuerpos ideales uni- (o bi-) dimensionales (continuos de Cosserat), o (b) como teorías que describen el comportamiento de cuerpos tridimensionales con restricciones cinemáticas intrínsecas. Esta última aproximación, que es la empleada en el artículo, ha resultado más atractiva desde el punto de vista de las aplicaciones en ingeniería, ya que permite relacionar las variables del modelo de pieza alargada (esfuerzos y desplazamientos generalizados) con las magnitudes asociadas a los puntos materiales del sólido (tensiones y deformaciones).

En la mencionada referencia [1] , y en su obra recopilatoria más reciente [2] , Antman desarrolla un marco general para las teorías no lineales de piezas alargadas, empleando el procedimiento usado por Euler para la obtención de la elástica: la deducción de las ecuaciones diferenciales del problema mediante el cálculo de variaciones. Esta técnica ha sido ampliamente usada en la construcción de soluciones numéricas a los problemas de mecánica de sólidos, pero solo se ha aplicado de forma parcial en el desarrollo de las teorías lineales de vigas con aplicación en el ámbito de la ingeniería.

El planteamiento variacional o analítico, marco idóneo para la obtención de las ecuaciones en sistemas mecánicos con restricciones internas (el más simple y económico , Lanczos [6, p. xxiv] ), es la herramienta con la que el primer autor ha desarrollado la formulación unificada de vigas y láminas – [9] , [10] y [11] – y permite identificar los elementos comunes a cualquier modelo de piezas alargadas en función de las restricciones cinemáticas que lo definen. En efecto, limitándonos a la estática de vigas elásticas, se puede definir la función lagrangiana del problema ${\textstyle L(s,{\boldsymbol {u}},{\boldsymbol {u}}^{'})}$ (densidad lineal de energía potencial), en la que u (s ) representa los desplazamientos generalizados adoptados y s el parámetro longitud de arco de la curva directriz de la pieza. Entonces, las ecuaciones de Euler-Lagrange

${\frac {\partial L}{\partial {\boldsymbol {u}}}}-{\frac {d}{ds}}\left({\frac {\partial L}{\partial {\boldsymbol {u}}^{'}}}\right)=$$0$

( 1)

conforman las ecuaciones diferenciales de segundo orden en los desplazamientos generalizados que rigen el problema. La formulación unificada expresa mediante una notación compacta las variables y operadores que organizan las ecuaciones del problema, y proporciona un modo sistemático de construirlas.

En el marco de la formulación unificada, este trabajo profundiza en el empleo de la herramienta variacional para el análisis: el formalismo de Hamilton permite introducir de forma natural las deformaciones generalizadas y los esfuerzos, así como identificar dos componentes fundamentales en las ecuaciones del problema: la matriz de equilibrio y la matriz de acoplamiento locales. El objetivo final consiste en establecer la condiciones mediante las que el problema de equilibrio se puede plantear de forma independiente al de la determinación de los desplazamientos generalizados. En síntesis, el desacoplamiento del problema de equilibrio se dará cuando la cinemática adoptada en el modelo sea un movimiento de sólido rígido de la sección transversal. Esta conclusión permite definir el concepto de hiperviga como modelo de pieza alargada cuya cinemática incluye movimientos adicionales a los de sólido rígido (como alabeo o distorsión).

El artículo se organiza del siguiente modo: la sección 2 constituye una síntesis de la formulación unificada presentada en las referencias citadas; en ella se repasan los principales ingredientes que permiten la construcción sistemática de las ecuaciones de equilibrio: la hipótesis cinemática, las matrices de deformación, las rigideces locales, los esfuerzos y el operador diferencial que define las ecuaciones de campo. Toda esta presentación de conceptos se lleva a cabo desde una perspectiva lagrangiana: las ecuaciones de Euler-Lagrange constituyen el hilo conductor de la exposición. En la sección 3 se introduce el punto de vista dual o hamiltoniano, que se apoya en una transformación similar a la de Legendre y permite construir sistemáticamente las ecuaciones del problema en su forma canónica a partir de la densidad de energía complementaria. Para ello se introduce de modo natural las deformaciones generalizadas como variables complementarias en la formulación; la forma de Hamilton da pie a la aparición de dos nuevos ingredientes de la formulación que serán claves para el desarrollo subsiguiente: la matriz de equilibrio local y la matriz de acoplamiento local. En la sección 4 se determinan las matrices de deformación en el caso general de una viga de directriz curva no plana, así como la versión particular de las mismas correspondiente al caso particular de sección transversal indeformable. Estos resultados serán necesarios para obtener expresiones compactas de las matrices que componen las ecuaciones diferenciales de lo que denominamos viga estándar o viga de Timoshenko, que se caracteriza por el desacoplamiento de las ecuaciones de equilibrio, objeto de la sección 5. Precisamente, el estudio de las condiciones bajo las que se produce el desacoplamiento, y la introducción del concepto de hiperviga como modelo general en el que no hay desacoplamiento son objeto de la sección 6; estas condiciones se formulan como proposiciones que relacionan las características geométricas de la hipótesis cinemática con la estructura de las ecuaciones de equilibrio, y constituyen el colofón del trabajo.

Comentarios sobre la notación. Las variables en cursiva (mayúsculas o minúsculas), como θ o Q hacen referencia a vectores o conjuntos de variables agrupadas en forma de vector. Las variables en letra recta, como h o ${\textstyle {\overset {\mbox{ˆ}}{\boldsymbol {\mbox{D}}}}_{00}}$ , se refieren a matrices. Por regla general, todas aquellas variables con asterisco, como d * están asociadas a los puntos materiales del sólido tridimensional. Los objetos sin asterisco se refieren al modelo, aunque este criterio no se sigue de forma estricta para evitar una complicación innecesaria en las expresiones.

2. Revisión de la formulación unificada de la estática de piezas alargadas

El ámbito de estudio se limita a problemas lineales de equilibrio en piezas alargadas sin restricciones de forma (salvo la condición de esbeltez inherente a las piezas alargadas) y su aplicación al caso particular de elementos con sección transversal, curvatura y torsión constantes a lo largo de la directriz, aunque bajo determinadas condiciones las técnicas y razonamientos seguidos en este trabajo pueden aplicarse a otros casos de naturaleza distinta (viga columna por ejemplo [4] ).

La formulación unificada del problema de equilibrio proporciona una vía elegante y directa para definir conceptos tan importantes como las cargas y esfuerzos propios del modelo, su matriz de rigidez o el análisis del acoplamiento entre respuestas elementales (torsión-flexión-distorsión...) necesario para validar cada solución. En las siguientes líneas repasaremos de forma breve los distintos conceptos que vertebran la presentación unificada.

2.1. Hipótesis fundamental

La hipótesis fundamental materializa el paso del sólido 3D al modelo 1D. Si d *(s , y , z ) es el vector de desplazamientos de un punto material de la viga y u (s ) es el vector de desplazamientos generalizados del modelo, la hipótesis establece una relación entre ambos mediante la matriz h (y , z ):

${\boldsymbol {d}}^{\ast }(s,y,z)={\boldsymbol {\mbox{h}}}(y,z)\quad {\boldsymbol {u}}(s)$

( 2)

2.2. Matrices de deformación

Las deformaciones de los puntos materiales e *(s , y , z ) se determinan  [9, ecs. 13 y 14] mediante la fórmula:

${\boldsymbol {e}}^{\ast }(s,y,z)={\boldsymbol {\mbox{B}}}_{0}(s,y,z)\quad {\boldsymbol {u}}(s)+$${\boldsymbol {\mbox{B}}}_{1}(s,y,z)\quad {\boldsymbol {u}}^{'}(s)$

( 3a)

con los operadores E₀ a E₃ definidos en [11, ec. 3.3] para una pieza de directriz curva plana (τ  = 0).

2.3. Cargas y esfuerzos generalizados

Las cargas generalizadas propias del problema son:

${\boldsymbol {Q}}(s)={\int }_{A}{\boldsymbol {\mbox{h}}}^{T}(y,z)\quad {\rho }^{\ast }{\boldsymbol {g}}(s,y,z)\quad \mu dA+$${\int }_{\partial A}{\boldsymbol {\mbox{h}}}^{T}({\overline {s}})\quad {\overline {\boldsymbol {q}}}(s,{\overline {s}})\quad {\overline {\mu }}d{\overline {s}}$

( 4)

ρ *g define las fuerzas másicas por unidad de volumen (ρ   * es la densidad del material estructural) mientras que ${\textstyle {\overline {\boldsymbol {q}}}(s,{\overline {s}})}$ define la fuerza por unidad de superficie aplicada en cada punto del contorno lateral de la pieza. La función μ  = 1 − χy proporciona el diferencial de volumen de la pieza alargada (dV  = μdAds ) con χ (s ) igual a la curvatura de su directriz.

Por otra parte los esfuerzos generalizados f (s ) tienen la siguiente definición estática  [9, ec. 31] :

${\boldsymbol {f}}(s)={\int }_{A}{\boldsymbol {\mbox{h}}}^{T}\quad {\boldsymbol {t}}^{\ast }\quad dA$

( 5)

siendo ${\textstyle {\boldsymbol {t}}^{\ast }=\lbrace {\sigma }_{s}^{\ast }\quad {\tau }_{sy}^{\ast }\quad {\tau }_{sz}^{\ast }\rbrace ^{T}}$ el vector tensión en los puntos de la sección transversal.

2.4. Densidad lineal de energía potencial

La energía potencial V   almacenada en la viga se puede expresar como integral a lo largo de la directriz de la densidad lineal de energía potencial ${\textstyle L}$ . A su vez, suponiendo que la relación entre tensiones y deformaciones es lineal, ésta puede escribirse en función de los desplazamientos generalizados y sus derivadas:

$L(s,{\boldsymbol {u}},{\boldsymbol {u}}^{'})={\frac {1}{2}}\left({\boldsymbol {u}}^{T}{\boldsymbol {\mbox{D}}}_{00}{\boldsymbol {u}}\quad +\right.$$\left.\quad {\boldsymbol {u}}^{T}{\boldsymbol {\mbox{D}}}_{01}{\boldsymbol {u}}^{'}\quad +\right.$$\left.\quad {\boldsymbol {u}}^{{'}T}{\boldsymbol {\mbox{D}}}_{10}{\boldsymbol {u}}+\right.$$\left.{\boldsymbol {u}}^{{'}T}{\boldsymbol {\mbox{D}}}_{11}{\boldsymbol {u}}^{'}\right)-$${\boldsymbol {u}}^{T}{\boldsymbol {Q}}$

( 6)

En esta expresión las matrices D_rs son las rigideces locales, que dependen de la matriz constitutiva C y tienen esta expresión [9, ec. 34]

${\boldsymbol {\mbox{D}}}_{rs}={\int }_{A}{\boldsymbol {\mbox{B}}}_{r}^{T}{\boldsymbol {\mbox{C}}}{\boldsymbol {\mbox{B}}}_{s}\quad \mu dA\quad r=$$0,1\quad s=0,1$

( 7)

2.5. Ecuaciones diferenciales del problema

Desde un punto de vista puramente lagrangiano, las ecuaciones diferenciales del problema se obtienen desarrollando las ecuaciones de Euler-Lagrange, de modo que

${\frac {\partial L}{\partial {\boldsymbol {u}}}}={\boldsymbol {\mbox{D}}}_{00}{\boldsymbol {u}}+$${\boldsymbol {\mbox{D}}}_{01}{\boldsymbol {u}}^{'}-{\boldsymbol {Q}}$

( 8a)

Sustituyendo en (1) ,

${\boldsymbol {\mbox{D}}}_{00}{\boldsymbol {u}}+{\boldsymbol {\mbox{D}}}_{01}{\boldsymbol {u}}^{'}-$${\frac {d}{ds}}\left({\boldsymbol {\mbox{D}}}_{10}{\boldsymbol {u}}+\right.$$\left.{\boldsymbol {\mbox{D}}}_{11}{\boldsymbol {u}}^{'}\right)=$${\boldsymbol {Q}}$

( 9)

se obtiene el sistema lagrangiano de n ecuaciones diferenciales de segundo orden en los n desplazamientos generalizados u (s ) de la viga.

Aunque el planteamiento clásico de la teoría de vigas introduce los esfuerzos sobre la sección mediante su definición estática, en la deducción lagrangiana de las ecuaciones de campo éstos no aparecen de forma directa. No obstante, es posible desarrollar la definición estática de los esfuerzos (5) empleando las matrices de deformación [9, ecs. 31 a 35] :

${\boldsymbol {f}}={\boldsymbol {\mbox{D}}}_{10}{\boldsymbol {u}}+$${\boldsymbol {\mbox{D}}}_{11}{\boldsymbol {u}}^{'}={\frac {\partial L}{\partial {\boldsymbol {u}}^{'}}}$

( 10)

obteniendo así dos definiciones alternativas (constitutiva y energética, respectivamente) de los esfuerzos generalizados.

De este modo, empleando ahora la definición energética de los esfuerzos generalizados (10) , las ecuaciones de Euler-Lagrange (1) pueden reorganizarse para proporcionar un sistema de 2n ecuaciones diferenciales ordinarias en los n desplazamientos u (s ) y los n esfuerzos f (s ):

${\frac {\partial L}{\partial {\boldsymbol {u}}}}-{\boldsymbol {f}}^{'}=$$0$

( 11a)

Utilizando la forma explícita del funcional ${\textstyle L(s,{\boldsymbol {u}},{\boldsymbol {u}}^{'})}$ el sistema de ecuaciones diferenciales que rige el problema puede entonces escribirse en la forma canónica siguiente:

${\frac {d}{ds}}{\boldsymbol {E}}(s)={\boldsymbol {\mbox{W}}}(s){\boldsymbol {E}}(s)-$${\boldsymbol {F}}(s)$

( 12)

E (s ) es el vector estado que agrupa todas las variables del problema, desplazamientos y esfuerzos generalizados:

${\boldsymbol {E}}(s)=\left\{{\begin{array}{c}{\boldsymbol {u}}(s)\\{\boldsymbol {f}}(s)\end{array}}\right\}$

( 13)

y F (s ) el término independiente o de carga:

${\boldsymbol {F}}(s)=\left\{{\begin{array}{c}{\boldsymbol {0}}\\{\boldsymbol {Q}}(s)\end{array}}\right\}$

( 14)

En cuanto al operador W , tiene la composición siguiente:

${\boldsymbol {\mbox{W}}}=\left[{\begin{array}{ccc}-{\boldsymbol {\mbox{D}}}_{11}^{-1}{\boldsymbol {\mbox{D}}}_{10}&\quad \quad &{\boldsymbol {\mbox{D}}}_{11}^{-1}\\{\boldsymbol {\mbox{D}}}_{00}-{\boldsymbol {\mbox{D}}}_{01}{\boldsymbol {\mbox{D}}}_{11}^{-1}{\boldsymbol {\mbox{D}}}_{10}&\quad \quad &{\boldsymbol {\mbox{D}}}_{01}{\boldsymbol {\mbox{D}}}_{11}^{-1}\end{array}}\right]$

( 15)

La naturaleza del sistema de ecuaciones depende de la geometría de la pieza. Si ésta es de curvatura, torsión y sección transversal constantes, entonces W es una matriz constante y sus autovalores K , definidos por la ecuación característica

$\vert {\boldsymbol {\mbox{W}}}-K{\boldsymbol {I}}\vert =$$0$

( 16)

articulan la construcción de la solución del problema de equilibrio.

3. Forma hamiltoniana de las ecuaciones

En el ámbito de la Mecánica Clásica, la transformación de Legendre [3, secs. 14 y 15] proporciona el método para transformar un sistema lagrangiano de ecuaciones diferenciales de segundo orden, en su forma de primer orden (canónica o hamiltoniana). El empleo de la transformada en la construcción de las ecuaciones de la estática de vigas con grandes rotaciones se ha mostrado en [7, sec. 5.2] . En el caso que nos ocupa, la transformación pura de Legendre de la función lagrangiana (la densidad lineal de energía potencial), considerada como función de u ′, se lleva a cabo introduciendo las variables estáticas ${\textstyle {\boldsymbol {f}}=\partial L/\partial {\boldsymbol {u}}^{'}}$ y definiendo así la función de Hamilton: ${\textstyle H(s,{\boldsymbol {u}},{\boldsymbol {f}})=}$${\boldsymbol {f}}\quad {\boldsymbol {u}}^{'}-L(s,{\boldsymbol {u}},{\boldsymbol {u}}^{'})$ . Si bien esta transformación permite construir directamente las ecuaciones canónicas del problema de equilibrio, proponemos una transformación alternativa mediante la que el funcional dual ${\textstyle H}$ admite una interpretación física elegante. Para ello introducimos como variable en la formulación un nuevo vector de funciones e (s ), las deformaciones generalizadas , y factorizamos la densidad lineal de energía potencial de modo que desaparezcan los términos híbridos en el funcional:

$L(s,{\boldsymbol {u}},{\boldsymbol {e}})={\frac {1}{2}}\left({\boldsymbol {e}}^{T}{\boldsymbol {\mbox{D}}}_{11}{\boldsymbol {e}}+\right.$$\left.{\boldsymbol {u}}^{T}{\overset {\mbox{ˆ}}{\boldsymbol {\mbox{D}}}}_{00}{\boldsymbol {u}}\right)-$${\boldsymbol {u}}^{T}{\boldsymbol {Q}}$

( 17)

En esta factorización el vector

${\boldsymbol {e}}={\boldsymbol {\mbox{D}}}_{11}^{-1}{\boldsymbol {\mbox{D}}}_{10}\quad {\boldsymbol {u}}+$${\boldsymbol {u}}^{'}={\boldsymbol {\mbox{H}}}^{T}{\boldsymbol {u}}+$${\boldsymbol {u}}^{'}$

( 18)

es función de los desplazamientos generalizados y sus derivadas, y representa como veremos las deformaciones generalizadas del modelo. En las expresiones anteriores se ha introducido por conveniencia dos nuevas matrices:

${\boldsymbol {\mbox{H}}}={\boldsymbol {\mbox{D}}}_{01}{\boldsymbol {\mbox{D}}}_{11}^{-1}$

( 19a)

La nueva transformación requiere definir las variables estáticas como derivadas del funcional de Lagrange respecto de las funciones e :

${\boldsymbol {f}}={\frac {\partial L}{\partial {\boldsymbol {e}}}}=$${\boldsymbol {\mbox{D}}}_{11}{\boldsymbol {e}}$

( 20)

Sustituyendo e por su expresión (18) se observa que el resultado coincide exactamente con la definición previa (10) de los esfuerzos. Por ello queda plenamente justificada la definición de e como vector de deformaciones generalizadas a la vista de su relación lineal con los esfuerzos. Consecuentemente, las expresiones  (20) son las ecuaciones constitutivas del modelo.

El nuevo funcional de Hamilton se define, por tanto, del siguiente modo:

$H(s,{\boldsymbol {u}},{\boldsymbol {f}})={\boldsymbol {f}}^{T}{\boldsymbol {e}}-$$L(s,{\boldsymbol {u}},{\boldsymbol {e}})$

( 21)

y se interpreta directamente como la densidad lineal de energía complementaria   . Su expresión en función de los esfuerzos y desplazamientos generalizados se construye eliminando las deformaciones generalizadas en el lado derecho de la igualdad. Puesto que ${\textstyle {\boldsymbol {e}}={\boldsymbol {\mbox{D}}}_{11}^{-1}{\boldsymbol {f}}}$ ,

$H(s,{\boldsymbol {u}},{\boldsymbol {f}})={\frac {1}{2}}\left({\boldsymbol {f}}^{T}{\boldsymbol {\mbox{D}}}_{11}^{-1}{\boldsymbol {f}}-\right.$$\left.{\boldsymbol {u}}^{T}{\overset {\mbox{ˆ}}{\boldsymbol {\mbox{D}}}}_{00}{\boldsymbol {u}}\right)+$${\boldsymbol {u}}^{T}{\boldsymbol {Q}}$

( 22)

Para obtener las ecuaciones de Hamilton correspondientes a la transformación se opera sobre (21) :

${\frac {\partial H}{\partial {\boldsymbol {f}}}}={\boldsymbol {e}}=$${\boldsymbol {\mbox{H}}}^{T}{\boldsymbol {u}}+{\boldsymbol {u}}^{'}$

( 23a)

Despejando las derivadas de los desplazamientos generalizados y los esfuerzos, y operando a partir de (22) , las ecuaciones del problema se transforman en:

${\boldsymbol {u}}^{'}={\frac {\partial H}{\partial {\boldsymbol {f}}}}-$${\boldsymbol {\mbox{H}}}^{T}{\boldsymbol {u}}={\boldsymbol {\mbox{D}}}_{11}^{-1}{\boldsymbol {f}}-$${\boldsymbol {\mbox{H}}}^{T}{\boldsymbol {u}}$

( 24a)

Ordenadas en forma matricial:

$\left\{{\begin{array}{c}{\boldsymbol {u}}^{'}\\{\boldsymbol {f}}^{'}\end{array}}\right\}=\left[{\begin{array}{ccc}-{\boldsymbol {\mbox{H}}}^{T}&\quad \quad &{\boldsymbol {\mbox{D}}}_{11}^{-1}\\{\overset {\mbox{ˆ}}{\boldsymbol {\mbox{D}}}}_{00}&\quad \quad &{\boldsymbol {\mbox{H}}}\end{array}}\right]\left\{{\begin{array}{c}{\boldsymbol {u}}\\{\boldsymbol {f}}\end{array}}\right\}-\left\{{\begin{array}{c}{\boldsymbol {0}}\\{\boldsymbol {Q}}\end{array}}\right\}$

( 25)

Teniendo en cuenta las definiciones (3 ) es inmediato comprobar que la matriz del sistema coincide con el operador W definido en (15) . Por lo tanto a partir del funcional ${\textstyle H(s,{\boldsymbol {u}},{\boldsymbol {f}})}$ se obtiene directamente la forma canónica de las ecuaciones del problema de equilibrio. La tabla es una síntesis de las estructuras duales asociadas a la transformación propuesta.

Tabla. Resumen de la transformación propuesta

	Sistema original	Nuevo sistema
Función	Lagrangiana ${\textstyle L(s,{\boldsymbol {u}},{\boldsymbol {e}})}$	Hamiltoniana ${\textstyle H(s,{\boldsymbol {u}},{\boldsymbol {f}})}$
	densidad lineal de energía potencial	densidad lineal de energía complementaria
Variables	Deformaciones generalizadas e (s )	Esfuerzos generalizados f (s )
Dualidad	${\textstyle {\frac {\partial L}{\partial {\boldsymbol {e}}}}=}$${\boldsymbol {f}}$	${\textstyle {\frac {\partial H}{\partial {\boldsymbol {f}}}}=}$${\boldsymbol {e}}$
	${\textstyle H={\boldsymbol {f}}^{T}{\boldsymbol {e}}-}$$L$	${\textstyle L={\boldsymbol {f}}^{T}{\boldsymbol {e}}-}$$H$
	${\textstyle L={\frac {1}{2}}\left({\boldsymbol {e}}^{T}{\boldsymbol {\mbox{D}}}_{11}{\boldsymbol {e}}+\right.}$$\left.{\boldsymbol {u}}^{T}{\overset {\mbox{ˆ}}{\boldsymbol {\mbox{D}}}}_{00}{\boldsymbol {u}}\right)-$${\boldsymbol {u}}^{T}{\boldsymbol {Q}}$	${\textstyle H={\frac {1}{2}}\left({\boldsymbol {f}}^{T}{\boldsymbol {\mbox{D}}}_{11}^{-1}{\boldsymbol {f}}-\right.}$$\left.{\boldsymbol {u}}^{T}{\overset {\mbox{ˆ}}{\boldsymbol {\mbox{D}}}}_{00}{\boldsymbol {u}}\right)+$${\boldsymbol {u}}^{T}{\boldsymbol {Q}}$
Ecuaciones de equilibrio	${\textstyle {\frac {\partial L}{\partial {\boldsymbol {u}}}}=}$${\boldsymbol {f}}^{'}$	${\textstyle {\frac {\partial H}{\partial {\boldsymbol {u}}}}=}$${\boldsymbol {\mbox{H}}}{\boldsymbol {f}}-{\boldsymbol {f}}^{'}$

Las deformaciones generalizadas e (s ) proporcionan la mejor medida de las deformaciones del modelo: no solo permiten introducir la densidad lineal de energía complementaria, sino que también simplifican la expresión de las ecuaciones constitutivas del modelo, pues únicamente es necesaria la matriz D₁₁ para definirlas. Además, las expresiones de las funciones lagrangiana y hamiltoniana resultan muy compactas (ver tabla ) y permiten identificar el papel de la matriz ${\textstyle {\overset {\mbox{ˆ}}{\boldsymbol {\mbox{D}}}}_{00}}$ que adquiere especial relevancia en las próximas secciones.

Por otra parte, retornando al bloque de ecuaciones (24b) , ${\textstyle {\boldsymbol {f}}^{'}={\overset {\mbox{ˆ}}{\boldsymbol {\mbox{D}}}}_{00}{\boldsymbol {u}}+}$${\boldsymbol {\mbox{H}}}{\boldsymbol {f}}-{\boldsymbol {Q}}$ , éste relaciona los esfuerzos en cada sección con sus derivadas, por lo que queda justificada la naturaleza de matriz de equilibrio local de H .

4. Determinación de las componentes de los operadores característicos de la formulación

En esta sección se deducen las expresiones de las matrices de deformación para el caso de la pieza alargada con directriz curva (sin restricciones sobre su torsión geométrica). Los resultados presentados constituyen la generalización de los obtenidos en [11, cap. 3] . En particular se buscan expresiones adecuadas al caso particular de sección transversal indeformable. La clave de la formulación estriba (a) en referir los desplazamientos del sólido al sistema de referencia formado por el triedro de Frênet en cada sección y (b) en utilizar como medidas de la deformación las componentes físicas de la fracción lineal de la diferencia de métricas.

4.1. Geometría de la pieza alargada

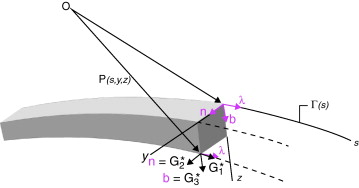
La pieza alargada se define como el conjunto de puntos materiales B  : {A (y , z ) × Γ (s ), s  ∈ [0, L ]} donde Γ es la curva directriz de la pieza, de tangente unitaria λ , y A su sección transversal, contenida en el plano definido por los vectores n y b , normal y binormal de Γ respectivamente. Este volumen se parametriza en las coordenadas curvilíneas (s , y , z ) longitud de arco de la directriz y posición dentro de la sección transversal respectivamente. Con ello el vector posición de los puntos de B puede darse como:

${\boldsymbol {\mbox{P}}}(s,y,z)={\boldsymbol {R}}(s)+y{\boldsymbol {n}}(s)+$$z{\boldsymbol {b}}(s)$

( 26)

En todo lo anterior L es la longitud sobre la cual Γ intersecta a B , o simplemente longitud de la pieza, mientras que A puede variar a lo largo de la misma. Resumimos la condición de pieza alargada mediante la expresión:

$h/L<\epsilon ,h={\sqrt {(y_{max}-y_{min})^{2}+(z_{max}-z_{min})^{2}}}$

En ella h es la dimensión máxima de la sección transversal mientras que ϵ  < 1. Los vectores naturales del sistema curvilíneo así definido son:

${\boldsymbol {G}}_{1}^{\ast }={\frac {\partial {\boldsymbol {\mbox{P}}}}{\partial s}}=$$\mu {\boldsymbol {\lambda }}-\tau (z{\boldsymbol {n}}-y{\boldsymbol {b}})$

( 27a)

con μ  = 1 − χy , siendo χ la curvatura y τ la torsión de la curva directriz Γ (s ). Las componentes del tensor métrico en el sistema s , y , z valen entonces:

$G_{11}^{\ast }={\boldsymbol {G}}_{1}^{\ast }\cdot {\boldsymbol {G}}_{1}^{\ast }=$${\mu }^{2}+{\tau }^{2}(y^{2}+z^{2})$

( 28a)

El determinante de este tensor vale G * = μ² , por lo que el diferencial de volumen del sólido referido a este sistema coordenado es dV  = μ  ds  dy  dz ( fig. 1 )

Figura 1. Definición gráfica de las líneas y superficies coordenadas del sistema (s , y , z ).

4.2. Configuración deformada

La posición de los puntos materiales de B en la nueva configuración del sólido será:

${\boldsymbol {p}}(s,y,z)={\boldsymbol {\mbox{P}}}(s,y,z)+$${\boldsymbol {d}}^{\ast }(s,y,z)$

( 29)

El vector d *(s , y , z ) define el desplazamiento de los puntos P (s , y , z ) de B debido al cambio de configuración. Para desarrollar toda la formulación que sigue es conveniente expresar d * por medio de sus componentes físicas ${\textstyle u^{\ast },v^{\ast },w^{\ast }}$referidas al triedro de Frênet–Serret :

${\boldsymbol {d}}^{\ast }(s,y,z)=u^{\ast }{\boldsymbol {\lambda }}+$$v^{\ast }{\boldsymbol {n}}+w^{\ast }{\boldsymbol {b}}$

( 30)

Los vectores naturales en la configuración deformada se obtienen son, por tanto,

${\boldsymbol {g}}_{1}^{\ast }={\frac {\partial {\boldsymbol {p}}}{\partial s}}=$${\boldsymbol {G}}_{1}^{\ast }+{\frac {\partial {\boldsymbol {d}}^{\ast }}{\partial s}}+$${\boldsymbol {\Omega }}_{0}^{T}{\boldsymbol {d}}^{\ast }$

( 31a)

En esta expresión el término ∂d */∂ s   debe interpretarse como ${\textstyle {\frac {\partial u^{\ast }}{\partial s}}{\boldsymbol {\lambda }}+}$${\frac {\partial v^{\ast }}{\partial s}}{\boldsymbol {n}}+$${\frac {\partial w^{\ast }}{\partial s}}{\boldsymbol {b}}$ . Lo mismo sucede con las derivadas respecto de y y z . El último término del primer vector es el resultado de operar las derivadas de los vectores del triedro:

${\frac {d}{ds}}\left\{{\begin{array}{c}{\boldsymbol {\lambda }}\\{\boldsymbol {n}}\\{\boldsymbol {b}}\end{array}}\right\}={\boldsymbol {\Omega }}_{0}\left\{{\begin{array}{c}{\boldsymbol {\lambda }}\\{\boldsymbol {n}}\\{\boldsymbol {b}}\end{array}}\right\}=\left[{\begin{array}{ccc}0&\chi &0\\-\chi &0&\tau \\0&-\tau &0\end{array}}\right]\left\{{\begin{array}{c}{\boldsymbol {\lambda }}\\{\boldsymbol {n}}\\{\boldsymbol {b}}\end{array}}\right\}$

( 32)

La matriz Ω₀ caracteriza el cambio de orientación del triedro de Frênet a lo largo de la directriz.

4.3. Componentes físicas de la deformación

Para evaluar las deformaciones de la pieza alargada partimos del tensor de deformaciones de Green [5, ec. 2.1.22] , ${\textstyle {\frac {1}{2}}(g_{ij}^{\ast }-G_{ij}^{\ast })}$ . Las expresiones (4.2 ) de los vectores de la base en la configuración deformada ${\textstyle {\boldsymbol {g}}_{i}^{\ast }}$ permiten evaluar la fracción lineal del tensor de deformaciones. Aprovechando la antisimetría de Ω₀ y agrupando en O (ɛ² ) todos los términos de segundo orden en las componentes de d * se obtiene:

$g_{11}^{\ast }-G_{11}^{\ast }=2{\boldsymbol {G}}_{1}^{\ast }\cdot \left({\frac {\partial {\boldsymbol {d}}^{\ast }}{\partial s}}-\right.$$\left.{\boldsymbol {\Omega }}_{0}{\boldsymbol {d}}^{\ast }\right)+$$O({\varepsilon }^{2})$ $g_{22}^{\ast }-G_{22}^{\ast }=2{\boldsymbol {n}}\cdot {\frac {\partial {\boldsymbol {d}}^{\ast }}{\partial y}}+$$O({\varepsilon }^{2})$ $g_{33}^{\ast }-G_{33}^{\ast }=2{\boldsymbol {b}}\cdot {\frac {\partial {\boldsymbol {d}}^{\ast }}{\partial z}}+$$O({\varepsilon }^{2})$ $g_{12}^{\ast }-G_{12}^{\ast }={\boldsymbol {G}}_{1}^{\ast }\cdot {\frac {\partial {\boldsymbol {d}}^{\ast }}{\partial y}}+$${\boldsymbol {n}}\cdot \left({\frac {\partial {\boldsymbol {d}}^{\ast }}{\partial s}}-\right.$$\left.{\boldsymbol {\Omega }}_{0}{\boldsymbol {d}}^{\ast }\right)+$$O({\varepsilon }^{2})$ $g_{13}^{\ast }-G_{13}^{\ast }={\boldsymbol {G}}_{1}^{\ast }\cdot {\frac {\partial {\boldsymbol {d}}^{\ast }}{\partial z}}+$${\boldsymbol {b}}\cdot \left({\frac {\partial {\boldsymbol {d}}^{\ast }}{\partial s}}-\right.$$\left.{\boldsymbol {\Omega }}_{0}{\boldsymbol {d}}^{\ast }\right)+$$O({\varepsilon }^{2})$ $g_{23}^{\ast }-G_{23}^{\ast }={\boldsymbol {n}}\cdot {\frac {\partial {\boldsymbol {d}}^{\ast }}{\partial z}}+$${\boldsymbol {b}}\cdot {\frac {\partial {\boldsymbol {d}}^{\ast }}{\partial y}}+$$O({\varepsilon }^{2})$

( 33)

Las componentes físicas de las expresiones anteriores definen las deformaciones infinitesimales en los puntos materiales del sólido:

${\epsilon }_{s}^{\ast }={\frac {g_{11}^{\ast }-G_{11}^{\ast }}{2G_{11}^{\ast }}}{\gamma }_{sy}^{\ast }=$${\frac {g_{12}^{\ast }-G_{12}^{\ast }}{\sqrt {G_{11}^{\ast }G_{22}^{\ast }}}}$ ${\epsilon }_{y}^{\ast }={\frac {g_{22}^{\ast }-G_{22}^{\ast }}{2G_{22}^{\ast }}}{\gamma }_{sz}^{\ast }=$${\frac {g_{13}^{\ast }-G_{13}^{\ast }}{\sqrt {G_{11}^{\ast }G_{33}^{\ast }}}}$ ${\epsilon }_{z}^{\ast }={\frac {g_{33}^{\ast }-G_{33}^{\ast }}{2G_{33}^{\ast }}}{\gamma }_{yz}^{\ast }=$${\frac {g_{23}^{\ast }-G_{23}^{\ast }}{\sqrt {G_{22}^{\ast }G_{33}^{\ast }}}}$

( 34)

Operando resulta:

${\epsilon }_{s}^{\ast }={\frac {1}{{\mu }^{2}{\gamma }^{\ast }}}\left({\boldsymbol {G}}_{1}^{\ast T}{\frac {\partial }{\partial s}}-\right.$$\left.{\boldsymbol {G}}_{1}^{\ast T}{\boldsymbol {\Omega }}_{0}\right){\boldsymbol {d}}^{\ast }$

( 35a)

con ${\textstyle {\gamma }^{\ast }=1+{\left({\frac {\tau }{\mu }}\right)}^{2}(y^{2}+}$$z^{2})$ y

${\boldsymbol {G}}_{1}^{\ast T}=\mu \lbrace 1\quad \quad \quad {\frac {\tau }{\mu }}z\quad \quad \quad {\frac {\tau }{\mu }}y\rbrace$ ${\boldsymbol {n}}^{T}=\lbrace 0\quad \quad 1\quad \quad 0\rbrace$ ${\boldsymbol {b}}^{T}=\lbrace 0\quad \quad 0\quad \quad 1\rbrace$

( 36)

Agrupando resultados se obtiene

${\boldsymbol {e}}^{\ast }=\lbrace {\epsilon }_{s}^{\ast }\quad \quad {\epsilon }_{y}^{\ast }\quad \quad {\epsilon }_{z}^{\ast }\quad \quad {\gamma }_{sy}^{\ast }\quad \quad {\gamma }_{sz}^{\ast }\quad \quad {\gamma }_{yz}^{\ast }\rbrace ^{T}$ $=\left({\boldsymbol {\mbox{E}}}_{1}{\frac {\partial }{\partial s}}+\right.$$\left.{\boldsymbol {\mbox{E}}}_{2}{\frac {\partial }{\partial y}}+\right.$$\left.{\boldsymbol {\mbox{E}}}_{3}{\frac {\partial }{\partial z}}-\right.$$\left.{\boldsymbol {\mbox{E}}}_{1}{\boldsymbol {\Omega }}_{0}\right){\boldsymbol {d}}^{\ast }$

( 37)

donde

${\boldsymbol {\mbox{E}}}_{1}={\frac {1}{\mu {\sqrt {{\gamma }^{\ast }}}}}{\left[{\frac {1}{\mu {\sqrt {{\gamma }^{\ast }}}}}{\boldsymbol {G}}_{1}^{\ast }\quad \quad \quad {\boldsymbol {0}}\quad \quad \quad {\boldsymbol {0}}\quad \quad \quad {\boldsymbol {n}}\quad \quad \quad {\boldsymbol {b}}\quad \quad \quad {\boldsymbol {0}}\right]}^{T}$

( 38a)

${\boldsymbol {\mbox{E}}}_{2}={\left[{\boldsymbol {0}}\quad \quad \quad {\boldsymbol {n}}\quad \quad \quad {\boldsymbol {0}}\quad \quad \quad {\frac {1}{\mu {\sqrt {{\gamma }^{\ast }}}}}{\boldsymbol {G}}_{1}^{\ast }\quad \quad \quad {\boldsymbol {0}}\quad \quad \quad {\boldsymbol {b}}\right]}^{T}$

( 38b)

${\boldsymbol {\mbox{E}}}_{3}={\left[{\boldsymbol {0}}\quad \quad \quad {\boldsymbol {0}}\quad \quad \quad {\boldsymbol {b}}\quad \quad \quad {\boldsymbol {0}}\quad \quad \quad {\frac {1}{\mu {\sqrt {{\gamma }^{\ast }}}}}{\boldsymbol {G}}_{1}^{\ast }\quad \quad \quad {\boldsymbol {n}}\right]}^{T}$

( 38c)

Desarrollando estas ecuaciones se obtienen las expresiones explícitas de las componentes físicas de las deformaciones para la pieza alargada de directriz curva genérica:

${\epsilon }_{s}^{\ast }={\frac {1}{\mu {\gamma }^{\ast }}}\left({\frac {\partial u^{\ast }}{\partial s}}-\right.$$\left.\chi v^{\ast }+{\frac {\tau }{\mu }}\left(y{\frac {\partial w^{\ast }}{\partial s}}-\right.\right.$$\left.\left.z\left({\frac {\partial v^{\ast }}{\partial s}}+\right.\right.\right.$$\left.\left.\left.\chi u^{\ast }\right)+\tau (yv^{\ast }+\right.\right.$$\left.\left.zw^{\ast })\right)\right)$ ${\epsilon }_{y}^{\ast }={\frac {\partial v^{\ast }}{\partial y}}$ ${\epsilon }_{z}^{\ast }={\frac {\partial w^{\ast }}{\partial z}}$ ${\gamma }_{sy}^{\ast }={\frac {1}{\sqrt {{\gamma }^{\ast }}}}\left({\frac {\partial u^{\ast }}{\partial y}}+\right.$$\left.{\frac {1}{\mu }}\left({\frac {\partial v^{\ast }}{\partial s}}+\right.\right.$$\left.\left.\chi u^{\ast }\right)-{\frac {\tau }{\mu }}\left(w^{\ast }+\right.\right.$$\left.\left.z{\frac {\partial v^{\ast }}{\partial y}}-\right.\right.$$\left.\left.y{\frac {\partial w^{\ast }}{\partial y}}\right)\right)$ ${\gamma }_{sz}^{\ast }={\frac {1}{\sqrt {{\gamma }^{\ast }}}}\left({\frac {\partial u^{\ast }}{\partial z}}+\right.$$\left.{\frac {1}{\mu }}{\frac {\partial w^{\ast }}{\partial s}}+\right.$$\left.{\frac {\tau }{\mu }}\left(v^{\ast }-z{\frac {\partial v^{\ast }}{\partial z}}+\right.\right.$$\left.\left.y{\frac {\partial w^{\ast }}{\partial z}}\right)\right)$ ${\gamma }_{yz}^{\ast }={\frac {\partial v^{\ast }}{\partial z}}+$${\frac {\partial w^{\ast }}{\partial y}}$

Si se introduce ahora la hipótesis fundamental genérica d *(s , y , z ) = h (y , z ) u (s ), ésta permite expresar las deformaciones en función de los desplazamientos generalizados, y las ecuaciones ( 2.2 ) se transforman en:

${\boldsymbol {e}}^{\ast }={\boldsymbol {\mbox{B}}}_{0}{\boldsymbol {u}}+$${\boldsymbol {\mbox{B}}}_{1}{\boldsymbol {u}}^{'}$

( 39a)

4.4. Definición estática de los esfuerzos

Teniendo en cuenta que la tracción total actuante sobre un elemento de área definido por los incrementos infinitesimales dθ^jdθ^k es [5, ecs. 2.2.14 y 2.2.15] :

${\boldsymbol {T}}^{\ast i}d{\theta }^{j}d{\theta }^{k},{\boldsymbol {T}}^{\ast i}=$${\sqrt {g^{\ast }}}\quad T^{\ast ij}{\boldsymbol {g}}_{j}^{\ast }$

siendo i  ≠ j  ≠ k y T^*ij el tensor de tensiones de Cauchy, en el caso lineal de la pieza alargada tendremos en cada punto de su sección transversal una tracción t *(s , y , z ) igual a:

${\boldsymbol {t}}^{\ast }dy\quad dz={\boldsymbol {T}}^{\ast 1}dy\quad dz$ $={\sqrt {G^{\ast }}}\quad \left(T^{\ast 11}{\boldsymbol {G}}_{1}^{\ast }+\right.$$\left.T^{\ast 12}{\boldsymbol {G}}_{2}^{\ast }+T^{\ast 13}{\boldsymbol {G}}_{3}^{\ast }\right)dy\quad dz$

( 40)

luego en componentes físicas,

${\boldsymbol {t}}^{\ast }dy\quad dz$ $={\sqrt {G^{\ast }}}\quad dy\quad dz\sum _{i}{\frac {T_{<1i>}^{\ast }}{\sqrt {G_{11}^{\ast }G_{ii}^{\ast }}}}{\boldsymbol {G}}_{i}^{\ast }$ $={\frac {1}{\mu {\sqrt {{\gamma }^{\ast }}}}}\left(T_{<11>}^{\ast }{\frac {{\boldsymbol {G}}_{1}^{\ast }}{\mu {\sqrt {{\gamma }^{\ast }}}}}+\right.$$\left.T_{<12>}^{\ast }{\boldsymbol {n}}+T_{<13>}^{\ast }{\boldsymbol {b}}\right)\quad \mu \quad dy\quad dz$

( 41)

Recurriendo a la definición (4.3 ) del operador E₁ se llega entonces a la siguiente ecuación:

${\boldsymbol {t}}^{\ast }dA={\boldsymbol {\mbox{E}}}_{1}^{T}{\boldsymbol {s}}^{\ast }\mu dA$

( 42)

En ella ${\textstyle {\boldsymbol {s}}^{\ast }=\lbrace {\sigma }_{s}^{\ast }\quad {\sigma }_{y}^{\ast }\quad {\sigma }_{z}^{\ast }\quad {\tau }_{sy}^{\ast }\quad {\tau }_{sz}^{\ast }\quad {\tau }_{yz}^{\ast }\rbrace ^{T}}$ es el vector que agrupa las seis componentes físicas de las tensiones ordenadas de forma consistente con el vector e *. Premultiplicando por la matriz de la hipótesis h^T (y , z ) e integrando sobre la sección transversal de la pieza resulta:

${\int }_{A}{\boldsymbol {\mbox{h}}}^{T}{\boldsymbol {t}}^{\ast }dA=$${\int }_{A}{\boldsymbol {\mbox{h}}}^{T}{\boldsymbol {\mbox{E}}}_{1}^{T}{\boldsymbol {s}}^{\ast }\mu dA=$${\int }_{A}{\boldsymbol {\mbox{B}}}_{1}^{T}{\boldsymbol {s}}^{\ast }\mu dA$

( 43)

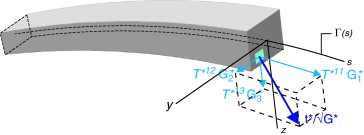
Este resultado constituye la definición estática de los esfuerzos generalizados f (s ) en la pieza de directriz curva genérica ( fig. 2 ).

Figura 2. Definición gráfica del vector tensión en el problema lineal.

4.5. Factorización alternativa para el caso de sección transversal indeformable

Como alternativa a la expresión genérica (37) se propone la siguiente factorización en la que únicamente intervienen tres componentes de la deformación:

${\boldsymbol {e}}^{\ast }=\lbrace {\epsilon }_{s}^{\ast }\quad \quad {\gamma }_{sy}^{\ast }\quad \quad {\gamma }_{sz}^{\ast }\rbrace ^{T}$ $=\left({\boldsymbol {\mbox{E}}}_{1}{\frac {\partial }{\partial s}}+\right.$$\left.{\boldsymbol {\mbox{E}}}_{2}{\frac {\partial }{\partial y}}+\right.$$\left.{\boldsymbol {\mbox{E}}}_{3}{\frac {\partial }{\partial z}}-\right.$$\left.{\boldsymbol {\mbox{E}}}_{1}{\boldsymbol {\Omega }}_{0}\right){\boldsymbol {d}}^{\ast }$

( 44)

con

${\boldsymbol {\mbox{E}}}_{1}={\frac {1}{\mu {\sqrt {{\gamma }^{\ast }}}}}{\left[{\frac {{\boldsymbol {G}}_{1}^{\ast }}{\mu {\sqrt {{\gamma }^{\ast }}}}}\quad \quad \quad {\boldsymbol {n}}\quad \quad \quad {\boldsymbol {b}}\right]}^{T}$

( 45a)

Es decir,

${\boldsymbol {\mbox{E}}}_{1}={\frac {1}{\mu {\sqrt {{\gamma }^{\ast }}}}}\left[{\begin{array}{ccc}{\frac {1}{\sqrt {{\gamma }^{\ast }}}}&-{\frac {\tau z}{\mu {\sqrt {{\gamma }^{\ast }}}}}&{\frac {\tau y}{\mu {\sqrt {{\gamma }^{\ast }}}}}\\0&1&0\\0&0&1\end{array}}\right]$

( 46a)

En este caso, E₁ es una matriz cuadrada no singular y la correspondiente fracción de B₀ puede entonces expresarse como:

${\boldsymbol {\mbox{B}}}_{0}={\boldsymbol {\mbox{E}}}_{1}\left({\overline {\boldsymbol {\mbox{h}}}}_{0}-\right.$$\left.{\boldsymbol {\Omega }}_{0}{\boldsymbol {\mbox{h}}}\right)$

( 47)

con

${\overline {\boldsymbol {\mbox{h}}}}_{0}={\boldsymbol {\mbox{E}}}_{1}^{-1}\left({\boldsymbol {\mbox{E}}}_{2}{\frac {\partial {\boldsymbol {\mbox{h}}}}{\partial y}}+\right.$$\left.{\boldsymbol {\mbox{E}}}_{3}{\frac {\partial {\boldsymbol {\mbox{h}}}}{\partial z}}\right)$

( 48)

Además, para las restantes componentes de la deformación tendremos:

${\boldsymbol {\overset {\mbox{ˆ}}{e}}}^{\ast }=\lbrace {\epsilon }_{y}^{\ast }\quad \quad {\epsilon }_{z}^{\ast }\quad \quad {\gamma }_{yz}^{\ast }\rbrace ^{T}=$$\left({\overset {\mbox{ˆ}}{\boldsymbol {\mbox{E}}}}_{2}{\frac {\partial }{\partial y}}+\right.$$\left.{\overset {\mbox{ˆ}}{\boldsymbol {\mbox{E}}}}_{3}{\frac {\partial }{\partial z}}\right){\boldsymbol {d}}^{\ast }$

( 49)

con

${\overset {\mbox{ˆ}}{\boldsymbol {\mbox{E}}}}_{2}=\left[{\begin{array}{c}{\boldsymbol {n}}^{T}\\{\boldsymbol {0}}\\{\boldsymbol {b}}^{T}\end{array}}\right]=\left[{\begin{array}{ccc}0\quad &1\quad &0\quad \\0\quad &0\quad &0\quad \\0\quad &0\quad &1\quad \end{array}}\right],{\overset {\mbox{ˆ}}{\boldsymbol {\mbox{E}}}}_{3}=$$\left[{\begin{array}{c}{\boldsymbol {0}}\\{\boldsymbol {b}}^{T}\\{\boldsymbol {n}}^{T}\end{array}}\right]=\left[{\begin{array}{ccc}0\quad &0\quad &0\quad \\0\quad &0\quad &1\quad \\0\quad &1\quad &0\quad \end{array}}\right]$

( 50)

Las matrices de deformación asociadas serán:

${\overset {\mbox{ˆ}}{\boldsymbol {\mbox{B}}}}_{0}={\overset {\mbox{ˆ}}{\boldsymbol {\mbox{E}}}}_{2}{\frac {\partial {\boldsymbol {\mbox{h}}}}{\partial y}}+$${\overset {\mbox{ˆ}}{\boldsymbol {\mbox{E}}}}_{3}{\frac {\partial {\boldsymbol {\mbox{h}}}}{\partial z}}$

( 51a)

Esta factorización es especialmente útil en modelos con sección transversal indeformable, para los cuales se cumple por hipótesis ${\textstyle {\boldsymbol {\overset {\mbox{ˆ}}{e}}}^{\ast }=}$${\boldsymbol {0}}$ , y conviene trabajar únicamente con las componentes no nulas de la deformación.

5. Un paso previo al concepto de hiperviga: el modelo «viga estándar»

Denominamos modelo viga estándar al modelo que reproduce el problema lineal de flexión y extensión de una viga en la que la sección transversal permanece plana e indeformable (aunque no necesariamente sigue siendo normal a la tangente). Este modelo también se conoce como viga de Timoshenko . En esta sección se va a particularizar las expresiones de las principales variables y operadores que intervienen en la formulación unificada.

La hipótesis fundamental corresponde a un movimiento de sólido rígido infinitesimal de la sección transversal:

$\left\{{\begin{array}{c}u^{\ast }\\v^{\ast }\\w^{\ast }\end{array}}\right\}=\left[{\begin{array}{cccccc}1\quad &0\quad &0\quad &0&z&-y\\0\quad &1\quad &0\quad &-z&0&0\\0\quad &0\quad &1\quad &y&0&0\end{array}}\right]\left\{{\begin{array}{c}u\\v\\w\\{\theta }_{s}\\{\theta }_{y}\\{\theta }_{z}\end{array}}\right\}$

( 52)

${\textstyle {\boldsymbol {d}}=\lbrace u\quad v\quad w\rbrace ^{T}}$ define la traslación de la sección y θ  = {θ_sθ_yθ_z }^T sus rotaciones infinitesimales respecto a los ejes coordenados, luego:

${\boldsymbol {d}}^{\ast }(s,y,z)=\left[{\begin{array}{cc}{\boldsymbol {1}}&{\boldsymbol {\Lambda }}\end{array}}\right]\left\{{\begin{array}{c}{\boldsymbol {d}}\\{\boldsymbol {\theta }}\end{array}}\right\}$

( 53)

y la matriz de la hipótesis fundamental se compone de un bloque identidad y otro bloque que representa la rotación infinitesimal:

${\boldsymbol {\mbox{h}}}=\left[{\begin{array}{cc}{\boldsymbol {1}}&{\boldsymbol {\Lambda }}\end{array}}\right],con\quad {\boldsymbol {\Lambda }}=$$\left[{\begin{array}{ccc}0&z&-y\\-z&0&0\\y&0&0\end{array}}\right]$

( 54)

Puesto que la sección transversal se considera indeformable, el modelo estándar debe cumplir ${\textstyle {\boldsymbol {\overset {\mbox{ˆ}}{e}}}^{\ast }=}$${\boldsymbol {0}}$(49) . En efecto, si denominamos Λ₂ y Λ₃ a las derivadas de de la rotación infinitesimal respecto de y y z :

${\boldsymbol {\Lambda }}_{2}={\frac {\partial {\boldsymbol {\Lambda }}}{\partial y}}=$$\left[{\begin{array}{ccc}0\quad &0\quad &-1\quad \\0\quad &0\quad &0\quad \\1\quad &0\quad &0\quad \end{array}}\right],\quad \quad {\boldsymbol {\Lambda }}_{3}=$${\frac {\partial {\boldsymbol {\Lambda }}}{\partial z}}=$$\left[{\begin{array}{ccc}0\quad &1\quad &0\quad \\-1\quad &0\quad &0\quad \\0\quad &0\quad &0\quad \end{array}}\right]$

entonces

${\boldsymbol {\overset {\mbox{ˆ}}{e}}}^{\ast }=\left[{\begin{array}{cc}{\boldsymbol {0}}\quad &{\overset {\mbox{ˆ}}{\boldsymbol {\mbox{E}}}}_{2}{\boldsymbol {\Lambda }}_{2}+{\overset {\mbox{ˆ}}{\boldsymbol {\mbox{E}}}}_{3}{\boldsymbol {\Lambda }}_{3}\end{array}}\right]\left\{{\begin{array}{c}{\boldsymbol {d}}\\{\boldsymbol {\theta }}\end{array}}\right\}={\boldsymbol {0}}$

como corresponde al modelo en estudio. De este modo podemos apoyarnos en lo que sigue en la factorización desarrollada en el último apartado de la sección anterior.

Para obtener los bloques del operador diferencial que define las ecuaciones del problema necesitamos evaluar las rigideces locales de la sección mediante las matrices de deformación. Por tanto, en la expresión (47) , ${\textstyle {\boldsymbol {\mbox{B}}}_{0}={\boldsymbol {\mbox{E}}}_{1}\left({\overline {\boldsymbol {\mbox{h}}}}_{0}-\right.}$$\left.{\boldsymbol {\Omega }}_{0}{\boldsymbol {\mbox{h}}}\right)$ , para la cinemática considerada se tiene:

${\overline {\boldsymbol {\mbox{h}}}}_{0}=\left[{\begin{array}{cc}{\boldsymbol {0}}&{\overline {\boldsymbol {\Lambda }}}_{0}\end{array}}\right]$

( 55a)

Utilizando este resultado, B₀ admite la siguiente expresión alternativa:

${\boldsymbol {\mbox{B}}}_{0}={\boldsymbol {\mbox{E}}}_{1}\left({\boldsymbol {\mbox{h}}}_{0}-\right.$$\left.{\boldsymbol {\mbox{h}}}\quad {\overset {\mbox{ˆ}}{\boldsymbol {\Omega }}}_{0}\right)$

( 56)

con

${\boldsymbol {\mbox{h}}}_{0}=\left[{\begin{array}{cc}{\boldsymbol {0}}&{\boldsymbol {\Lambda }}_{0}\end{array}}\right],{\overset {\mbox{ˆ}}{\boldsymbol {\Omega }}}_{0}=$$\left[{\begin{array}{cc}{\boldsymbol {\Omega }}_{0}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {\Omega }}_{0}\end{array}}\right]$

( 57)

y

${\boldsymbol {\Lambda }}_{0}={\overline {\boldsymbol {\Lambda }}}_{0}-$$\left({\boldsymbol {\Omega }}_{0}{\boldsymbol {\Lambda }}-\right.$$\left.{\boldsymbol {\Lambda }}{\boldsymbol {\Omega }}_{0}\right)=$$\left[{\begin{array}{ccc}0\quad &0\quad &0\quad \\0\quad &0\quad &-1\quad \\0\quad &1\quad &0\quad \end{array}}\right]$

( 58)

La expresión de las rigideces locales (7) se particulariza del siguiente modo:

${\boldsymbol {\mbox{D}}}_{00}={\boldsymbol {\mbox{h}}}_{0}^{T}{\boldsymbol {\mbox{C}}}_{00}{\boldsymbol {\mbox{h}}}_{0}-$$\left({\boldsymbol {\mbox{h}}}_{0}^{T}{\boldsymbol {\mbox{C}}}_{01}{\overset {\mbox{ˆ}}{\boldsymbol {\Omega }}}_{0}+\right.$$\left.{\overset {\mbox{ˆ}}{\boldsymbol {\Omega }}}_{0}^{T}{\boldsymbol {\mbox{C}}}_{10}{\boldsymbol {\mbox{h}}}_{0}\right)+$${\overset {\mbox{ˆ}}{\boldsymbol {\Omega }}}_{0}^{T}{\boldsymbol {\mbox{D}}}_{11}{\overset {\mbox{ˆ}}{\boldsymbol {\Omega }}}_{0}$

( 59a)

con las matrices auxiliares

${\boldsymbol {\mbox{C}}}_{00}={\int }_{A}{\boldsymbol {\mbox{E}}}_{1}^{T}{\boldsymbol {\mbox{C}}}{\boldsymbol {\mbox{E}}}_{1}\quad \mu \quad dA$

( 60a)

A partir de estos resultados es mecánico comprobar que para la viga estándar, con independencia de la forma inicial de su directriz, se cumple:

${\overset {\mbox{ˆ}}{\boldsymbol {\mbox{D}}}}_{00}=$${\boldsymbol {\mbox{D}}}_{00}-{\boldsymbol {\mbox{D}}}_{01}{\boldsymbol {\mbox{D}}}_{11}^{-1}{\boldsymbol {\mbox{D}}}_{10}=$${\boldsymbol {0}}$

( 61)

La demostración de esta propiedad se incluye en el Anexo.

Por otra parte, dado que ${\textstyle {\boldsymbol {\mbox{D}}}_{01}=}$${\boldsymbol {\mbox{h}}}_{0}^{T}{\boldsymbol {\mbox{C}}}_{01}-$${\overset {\mbox{ˆ}}{\boldsymbol {\Omega }}}_{0}^{T}{\boldsymbol {\mbox{D}}}_{11}$ , la matriz de equilibrio local vale:

${\boldsymbol {\mbox{H}}}={\boldsymbol {\mbox{D}}}_{01}{\boldsymbol {\mbox{D}}}_{11}^{-1}=$${\boldsymbol {\mbox{h}}}_{0}^{T}{\boldsymbol {\mbox{C}}}_{01}{\boldsymbol {\mbox{D}}}_{11}^{-1}+$${\overset {\mbox{ˆ}}{\boldsymbol {\Omega }}}_{0}$ $=\left[{\begin{array}{c}{\boldsymbol {0}}\\{\boldsymbol {\Lambda }}_{0}^{T}\end{array}}\right]\left[{\begin{array}{cc}{\boldsymbol {1}}&{\boldsymbol {0}}\end{array}}\right]+\left[{\begin{array}{cc}{\boldsymbol {\Omega }}_{0}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {\Omega }}_{0}\end{array}}\right]$

( 62)

resultando

${\boldsymbol {\mbox{H}}}=\left[{\begin{array}{cc}{\boldsymbol {\Omega }}_{0}&{\boldsymbol {0}}\\{\boldsymbol {\Lambda }}_{0}^{T}&{\boldsymbol {\Omega }}_{0}\end{array}}\right]=\left[{\begin{array}{cccccc}0&\chi &0&0&0&0\\-\chi &0&\tau &0&0&0\\0&-\tau &0&0&0&0\\0&0&0&0&\chi &0\\0&0&1&-\chi &0&\tau \\0&-1&0&0&-\tau &0\end{array}}\right]$

( 63)

En cuanto a las deformaciones generalizadas, éstas son:

${\boldsymbol {e}}={\boldsymbol {\mbox{H}}}^{T}{\boldsymbol {u}}+$${\boldsymbol {u}}^{'}=\left\{{\begin{array}{c}{\boldsymbol {d}}^{'}-{\boldsymbol {\Omega }}_{0}{\boldsymbol {d}}+{\boldsymbol {\Lambda }}_{0}{\boldsymbol {\theta }}\\{\boldsymbol {\theta }}^{'}-{\boldsymbol {\Omega }}_{0}{\boldsymbol {\theta }}\end{array}}\right\}=\left\{{\begin{array}{c}{\epsilon }_{s}\\{\gamma }_{sy}\\{\gamma }_{sz}\\{\kappa }_{s}\\{\kappa }_{y}\\{\kappa }_{z}\end{array}}\right\}$

( 64)

En componentes:

${\epsilon }_{s}={\frac {du}{ds}}-\chi v{\kappa }_{s}={\frac {d{\theta }_{s}}{ds}}-$$\chi {\theta }_{y}$ ${\gamma }_{sy}={\frac {dv}{ds}}+\chi u-\tau w-{\theta }_{z}{\kappa }_{y}=$${\frac {d{\theta }_{y}}{ds}}+\chi {\theta }_{s}-\tau {\theta }_{z}$ ${\gamma }_{sz}={\frac {dw}{ds}}+\tau v+{\theta }_{y}{\kappa }_{z}=$${\frac {d{\theta }_{z}}{ds}}+\tau {\theta }_{y}$

6. Desacoplamiento del problema estático y concepto de hiperviga

La estructura triangular de W resultante para la viga estándar (consecuencia de la nulidad de ${\textstyle {\overset {\mbox{ˆ}}{\boldsymbol {\mbox{D}}}}_{00}}$ ) conduce al desacoplamiento del bloque de ecuaciones de equilibrio, lo que permite integrar directamente los esfuerzos. En forma explícita:

${\boldsymbol {u}}^{'}=-{\boldsymbol {\mbox{H}}}^{T}{\boldsymbol {u}}+$${\boldsymbol {\mbox{D}}}_{11}^{-1}{\boldsymbol {f}}$

( 65)

En el caso de que la geometría de la sección transversal de la pieza así como la curvatura y torsión de su directriz Γ (s ) sean constantes, W es un operador constante y la solución de los esfuerzos se puede obtener sistemáticamente mediante las siguientes expresiones:

${\boldsymbol {f}}(s)=exp\left(s{\boldsymbol {\mbox{H}}}\right)\quad {\boldsymbol {f}}_{0}-$${\int }_{t=0}^{s}exp\left((s-t){\boldsymbol {\mbox{H}}}\right)\quad {\boldsymbol {Q}}(t)\quad dt$

( 67)

con f₀ igual al valor inicial (en el origen) de los esfuerzos generalizados f (s ): f₀  = f (0). En cuanto a los desplazamientos generalizados, estos valen:

${\boldsymbol {u}}(s)=exp\left(-s{\boldsymbol {\mbox{H}}}\right)\quad {\boldsymbol {u}}_{0}-$${\int }_{t=0}^{s}exp\left(-(s-t){\boldsymbol {\mbox{H}}}\right)\quad {\boldsymbol {U}}(t)\quad dt$

( 68)

con

${\boldsymbol {U}}(s)={\boldsymbol {\mbox{D}}}_{11}^{-1}\left(exp\left(s{\boldsymbol {\mbox{H}}}\right)-\right.$$\left.{\int }_{t=0}^{s}exp\left((s-t){\boldsymbol {\mbox{H}}}\right)\quad {\boldsymbol {Q}}(t)\quad dt\right)$

( 69)

En definitiva, en el caso de que las ecuaciones de equilibrio estén desacopladas, el procedimiento de integración solo exige manipular un sistema de dimensión n caracterizado por la matriz de equilibrio H , en lugar de un sistema de 2n  × 2n caracterizado por W , como sucede en la solución general:

${\boldsymbol {\mbox{E}}}(s)=exp\left(s{\boldsymbol {\mbox{W}}}\right)\quad {\boldsymbol {f}}_{0}-$${\int }_{t=0}^{s}exp\left((s-t){\boldsymbol {\mbox{W}}}\right)\quad {\boldsymbol {F}}(t)\quad dt$

( 70)

Proposición 6.1

Para que las ecuaciones de equilibrio del modelo 1D adopten una expresión exclusivamente estática (desacoplamiento del equilibrio), es decir, que estas se puedan expresar como combinación lineal del vector f (s   ) y su derivada, es necesario que las matrices de deformación satisfagan una relación de la forma ${\textstyle {\overset {\mbox{ˆ}}{\boldsymbol {\mbox{D}}}}_{00}=}$${\boldsymbol {\mbox{D}}}_{00}-{\boldsymbol {\mbox{D}}}_{01}{\boldsymbol {\mbox{D}}}_{11}^{-1}{\boldsymbol {\mbox{D}}}_{10}=$${\boldsymbol {0}}$ .

Demostración

Utilizando la densidad lineal de energía complementaria y la ecuación (23b) se cumple:

${\frac {\partial H}{\partial {\boldsymbol {u}}}}={\boldsymbol {\mbox{H}}}{\boldsymbol {f}}-$${\boldsymbol {f}}^{'}={\boldsymbol {Q}}-{\overset {\mbox{ˆ}}{\boldsymbol {\mbox{D}}}}_{00}{\boldsymbol {u}}$

Por lo tanto, esta ecuación solo adoptará una expresión estática pura si ${\textstyle {\overset {\mbox{ˆ}}{\boldsymbol {\mbox{D}}}}_{00}=}$${\boldsymbol {0}}$ .

Por otra parte, la versión lagrangiana de las ecuaciones equilibrio es (tabla y ecuación (8b) ):

${\frac {\partial L}{\partial {\boldsymbol {u}}}}={\boldsymbol {f}}^{'}=$${\boldsymbol {\mbox{D}}}_{00}{\boldsymbol {u}}+{\boldsymbol {\mbox{D}}}_{01}{\boldsymbol {u}}^{'}-$${\boldsymbol {Q}}$

luego

${\boldsymbol {\mbox{D}}}_{00}{\boldsymbol {u}}+{\boldsymbol {\mbox{D}}}_{01}{\boldsymbol {u}}^{'}-$$({\boldsymbol {f}}^{'}+{\boldsymbol {Q}})={\boldsymbol {0}}$

Ahora tratamos de expresar la ecuación de equilibrio como combinación lineal de los esfuerzos, sus derivadas y las cargas, y hacemos uso de la ecuación (10) :

${\boldsymbol {\mbox{A}}}{\boldsymbol {f}}+{\boldsymbol {\mbox{B}}}{\boldsymbol {f}}^{'}+$${\boldsymbol {\mbox{C}}}{\boldsymbol {Q}}={\boldsymbol {\mbox{A}}}\left({\boldsymbol {\mbox{D}}}_{10}{\boldsymbol {u}}+\right.$$\left.{\boldsymbol {\mbox{D}}}_{11}{\boldsymbol {u}}^{'}\right)+$${\boldsymbol {\mbox{B}}}{\boldsymbol {f}}^{'}+{\boldsymbol {\mbox{C}}}{\boldsymbol {Q}}$

Igualando término a término las expresiones anteriores se deduce B  = C  = − 1 y

${\boldsymbol {\mbox{D}}}_{00}={\boldsymbol {\mbox{A}}}{\boldsymbol {\mbox{D}}}_{10}$ ${\boldsymbol {\mbox{D}}}_{01}={\boldsymbol {\mbox{A}}}{\boldsymbol {\mbox{D}}}_{11}$

Luego ${\textstyle {\boldsymbol {\mbox{A}}}={\boldsymbol {\mbox{D}}}_{01}{\boldsymbol {\mbox{D}}}_{11}^{-1}\equiv {\boldsymbol {\mbox{H}}}}$ , y ${\textstyle {\boldsymbol {\mbox{D}}}_{00}=}$${\boldsymbol {\mbox{D}}}_{01}{\boldsymbol {\mbox{D}}}_{11}^{-1}{\boldsymbol {\mbox{D}}}_{10}$ . La primera condición introduce la matriz de equilibrio local H , de n  × n , mientras que la segunda conduce a la relación deseada. Además, bajo estos supuestos también se cumplirá D₀₀  = HD₁₁H^T .

Proposición 6.2

Para que las ecuaciones de equilibrio del modelo 1D adopten una expresión exclusivamente estática (desacoplamiento del equilibrio), es decir, que estas se puedan expresar como combinación lineal del vector f (s ) y su derivada, es suficiente que la hipótesis fundamental se reduzca a un movimiento de sólido rígido de la sección transversal de la pieza.

Demostración

La sección anterior proporciona una prueba completa de esta proposición en el marco estricto de la formulación unificada y por ello vamos a presentar una demostración alternativa, de carácter exclusivamente estático. Basándonos en la hipótesis fundamental planteada, la composición del vector de esfuerzos generalizados es directamente:

${\boldsymbol {f}}(s)={\int }_{A}{\boldsymbol {\mbox{h}}}^{T}{\boldsymbol {t}}^{\ast }\quad dA=$${\int }_{A}\left[{\begin{array}{c}{\boldsymbol {1}}\\{\boldsymbol {\Lambda }}^{T}\end{array}}\right]{\boldsymbol {t}}^{\ast }\quad dA=\left\{{\begin{array}{c}{\boldsymbol {N}}\\{\boldsymbol {M}}\end{array}}\right\}$

( 71)

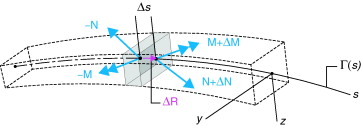
con los vectores N  = ∫ _At * dA , M  = ∫ _AΛ^Tt * dA , cuyas tres componentes se identifican con las definiciones habituales de esfuerzos: axil y cortantes, torsor y momentos flectores respectivamente. Denominando Q_N y Q_M a las densidades lineales de fuerzas y momentos aplicadas al modelo, el equilibrio vectorial linealizado de la pieza exige que se cumpla las siguientes ecuaciones de equilibrio (fig. 3 ):

$-{\boldsymbol {N}}+\left({\boldsymbol {N}}+\Delta {\boldsymbol {N}}\right)+$${\boldsymbol {Q}}_{N}\Delta s={\boldsymbol {0}}$ $-{\boldsymbol {M}}+\left({\boldsymbol {M}}+\Delta {\boldsymbol {M}}+\right.$$\left.\Delta {\boldsymbol {R}}\times {\boldsymbol {N}}\right)+$${\boldsymbol {Q}}_{M}\Delta s={\boldsymbol {0}}$

Figura 3. Esfuerzos implicados en el equilibrio vectorial de la viga.

Teniendo en cuenta (32) se tiene:

$\Delta {\boldsymbol {f}}=\left({\frac {d{\boldsymbol {f}}}{ds}}+\right.$$\left.{\overset {\mbox{ˆ}}{\boldsymbol {\Omega }}}_{0}^{T}{\boldsymbol {f}}\right)\Delta s,\quad \quad \Delta {\boldsymbol {R}}=$${\boldsymbol {\lambda }}\Delta s$

Y las ecuaciones de equilibrio se transforman en:

${\boldsymbol {N}}^{'}-{\boldsymbol {\Omega }}_{0}{\boldsymbol {N}}+$${\boldsymbol {Q}}_{N}={\boldsymbol {0}}$

( 72a)

Pero como λ  × N  ≡ Λ₀N , se obtiene finalmente

${\boldsymbol {f}}^{'}-{\boldsymbol {\mbox{H}}}{\boldsymbol {f}}+$${\boldsymbol {Q}}={\boldsymbol {0}}$

Para determinar el equilibrio disponemos por lo tanto de seis ecuaciones en las seis componentes de los esfuerzos generalizados f (s ) exclusivamente, consistentes estas con la hipótesis fundamental adoptada: un movimiento de sólido rígido infinitesimal para las secciones transversales de la pieza.

Definición 6.1 En el marco del análisis 1D de piezas alargadas nos referiremos al modelo hiperviga cuando se cumplan las siguientes condiciones:

• Condición necesaria . La hipótesis fundamental incluye alguna componente de desplazamiento distinta del movimiento de sólido rígido infinitesimal para las secciones transversales.
• Condición suficiente . Las ecuaciones de equilibrio acoplan esfuerzos y desplazamientos, luego
• En el caso general (problemas no lineales) ello exige:

${\frac {{\partial }^{2}H}{\partial {\boldsymbol {u}}\partial {\boldsymbol {u}}}}\not =$${\boldsymbol {0}}$

• En el caso lineal basta que se cumpla:

${\overset {\mbox{ˆ}}{\boldsymbol {\mbox{D}}}}_{00}=$${\boldsymbol {\mbox{D}}}_{00}-{\boldsymbol {\mbox{H}}}{\boldsymbol {\mbox{D}}}_{11}{\boldsymbol {\mbox{H}}}^{T}\not =$${\boldsymbol {0}}$

Hablaremos de una hiperviga cuando al formular la hipótesis fundamental del modelo 1D consideremos para los desplazamientos generalizados u (s   ) componentes más allá de las estrictamente requeridas por el modelo estándar. La segunda condición introduce el acoplamiento entre esfuerzos y desplazamientos en las ecuaciones de equilibrio como factor discriminatorio entre vigas e hipervigas. Este aspecto ha sido analizado en la sección anterior, deduciendo que en el caso lineal el acoplamiento se materializa o no en función del valor del operador ${\textstyle {\overset {\mbox{ˆ}}{\boldsymbol {\mbox{D}}}}_{00}}$ , que denominamos matriz de acoplamiento local. La condición equivalente para el caso general se deduce de la tabla .

Volviendo ahora a las ecuaciones de equilibrio de la viga estándar f ′ = Hf  − Q y teniendo en cuenta que son directamente integrables, se puede afirmar que este modelo es localmente isostático. Por el contrario las hipervigas resultan entonces localmente indeterminadas, o localmente hiperestáticas, y por lo tanto el término ${\textstyle {\overset {\mbox{ˆ}}{\boldsymbol {\mbox{D}}}}_{00}{\boldsymbol {u}}}$ debe interpretarse como un vector de esfuerzos generalizados estáticamente indeterminados o hiperestáticos.

7. Conclusiones

• Este trabajo profundiza en el análisis de las características formales y las relaciones entre las variables que intervienen en la formulación general de los problemas lineales de estática de vigas, válidas para cualquier hipótesis de partida que defina la cinemática del modelo.
• Se ha empleado, como en trabajos anteriores del primer autor, las herramientas de la mecánica analítica, aportando ahora como novedad el punto de vista hamiltoniano. Se ha mostrado que una factorización adecuada de la densidad lineal de energía de deformación permite introducir de modo natural y consistente los esfuerzos del modelo (20) y las deformaciones generalizadas (18) . Empleando estas variables duales, se ha propuesto una versión alternativa de la transformada de Legendre para definir el funcional hamiltoniano (22) que se identifica directamente con la densidad lineal de energía potencial complementaria.
• El formalismo de Hamilton aplicado al funcional anterior proporciona directamente las ecuaciones que rigen el problema en su forma canónica (25) . En la expresión del operador interviene la matriz de equilibrio local H , y la matriz de acoplamiento local ${\textstyle {\overset {\mbox{ˆ}}{\boldsymbol {\mbox{D}}}}_{00}}$ . Estas dos estructuras son piezas clave para alcanzar la conclusión principal del artículo.
• Se ha estudiado el caso particular del modelo de viga de Timoshenko (o viga estándar) sin restricción alguna sobre su geometría inicial (curva espacial), concluyendo que en él, la matriz de acoplamiento local se anula.
• El resultado anterior da lugar a dos proposiciones en las que se demuestra: (a) que la nulidad de la matriz de acoplamiento local es condición necesaria para que las ecuaciones de equilibrio tengan una forma estática pura, y (b) que para que esto suceda, es suficiente que la cinemática de las secciones transversales esté restringida a un movimiento de sólido rígido.
• El concepto de hiperviga constituye la generalización de los modelos clásicos de vigas a cinemáticas que incluyen movimientos que no son de sólido rígido. Su denominación se justifica en la observación de que el acoplamiento de esfuerzos y desplazamientos generalizados en las ecuaciones de equilibrio constituye una forma de hiperestatismo local en las ecuaciones.
• Por último, subrayamos que la formulación del equilibrio por la vía vectorial (newtoniana) conecta únicamente con un movimiento de sólido rígido para los puntos materiales de la sección. Cualquier otro modo de desplazamiento requiere la imposición de restricciones internas adicionales a la de sólido rígido y dificulta la interpretación de las variables estáticas. En este caso la formulación variacional mediante el formalismo de Hamilton permite ampliar las opciones cinemáticas más allá de aquellas que solo contemplan la traslación y rotación de las secciones, y constituye un procedimiento sistemático para la generación de variables estáticas consistentes y de las ecuaciones del problema.

Anexo

Para calcular el término ${\textstyle {\overset {\mbox{ˆ}}{\boldsymbol {\mbox{D}}}}_{00}}$ se evalúa en primer lugar el bloque ${\textstyle {\boldsymbol {\mbox{D}}}_{01}{\boldsymbol {\mbox{D}}}_{11}^{-1}{\boldsymbol {\mbox{D}}}_{10}}$ :

${\boldsymbol {\mbox{D}}}_{01}{\boldsymbol {\mbox{D}}}_{11}^{-1}{\boldsymbol {\mbox{D}}}_{10}$ $={\boldsymbol {\mbox{h}}}_{0}^{T}{\boldsymbol {\mbox{C}}}_{01}{\boldsymbol {\mbox{D}}}_{11}^{-1}\left({\boldsymbol {\mbox{C}}}_{10}{\boldsymbol {\mbox{h}}}_{0}-\right.$$\left.{\boldsymbol {\mbox{D}}}_{11}{\overset {\mbox{ˆ}}{\boldsymbol {\Omega }}}_{0}\right)-$${\overset {\mbox{ˆ}}{\boldsymbol {\Omega }}}_{0}^{T}\left({\boldsymbol {\mbox{C}}}_{10}{\boldsymbol {\mbox{h}}}_{0}-\right.$$\left.{\boldsymbol {\mbox{D}}}_{11}{\overset {\mbox{ˆ}}{\boldsymbol {\Omega }}}_{0}\right)$ $={\boldsymbol {\mbox{h}}}_{0}^{T}{\boldsymbol {\mbox{C}}}_{01}{\boldsymbol {\mbox{D}}}_{11}^{-1}{\boldsymbol {\mbox{C}}}_{10}{\boldsymbol {\mbox{h}}}_{0}-$$\left({\boldsymbol {\mbox{h}}}_{0}^{T}{\boldsymbol {\mbox{C}}}_{01}{\overset {\mbox{ˆ}}{\boldsymbol {\Omega }}}_{0}+\right.$$\left.{\overset {\mbox{ˆ}}{\boldsymbol {\Omega }}}_{0}^{T}{\boldsymbol {\mbox{C}}}_{10}{\boldsymbol {\mbox{h}}}_{0}\right)+$${\overset {\mbox{ˆ}}{\boldsymbol {\Omega }}}_{0}^{T}{\boldsymbol {\mbox{D}}}_{11}{\overset {\mbox{ˆ}}{\boldsymbol {\Omega }}}_{0}$

Considerando ahora la composición particular del operador h (y , z ) para el modelo adoptado e introduciendo las matrices auxiliares:

${\boldsymbol {\Lambda }}_{01}={\int }_{A}{\boldsymbol {\mbox{E}}}_{1}^{T}{\boldsymbol {\mbox{C}}}{\boldsymbol {\mbox{E}}}_{1}{\boldsymbol {\Lambda }}\quad \mu \quad dA,{\boldsymbol {\Lambda }}_{11}=$${\int }_{A}{\boldsymbol {\Lambda }}^{T}{\boldsymbol {\mbox{E}}}_{1}^{T}{\boldsymbol {\mbox{C}}}{\boldsymbol {\mbox{E}}}_{1}{\boldsymbol {\Lambda }}\quad \mu \quad dA$

tendremos

${\boldsymbol {\mbox{C}}}_{01}=\left[{\begin{array}{cc}{\boldsymbol {\mbox{C}}}_{00}&{\boldsymbol {\Lambda }}_{01}\end{array}}\right],{\boldsymbol {\mbox{D}}}_{11}=\left[{\begin{array}{cc}{\boldsymbol {\mbox{C}}}_{00}&{\boldsymbol {\Lambda }}_{01}\\{\boldsymbol {\Lambda }}_{01}^{T}&{\boldsymbol {\Lambda }}_{11}\end{array}}\right]$

Sea

${\boldsymbol {\mbox{D}}}_{11}^{-1}=\left[{\begin{array}{cc}{\overline {\boldsymbol {\mbox{C}}}}_{00}&{\overline {\boldsymbol {\Lambda }}}_{01}\\{\overline {\boldsymbol {\Lambda }}}_{01}^{T}&{\overline {\boldsymbol {\Lambda }}}_{11}\end{array}}\right]$

Entonces

${\boldsymbol {\mbox{C}}}_{01}{\boldsymbol {\mbox{D}}}_{11}^{-1}{\boldsymbol {\mbox{C}}}_{10}=$$\left[{\begin{array}{cc}{\boldsymbol {\mbox{C}}}_{00}&{\boldsymbol {\Lambda }}_{01}\end{array}}\right]\left[{\begin{array}{cc}{\overline {\boldsymbol {\mbox{C}}}}_{00}&{\overline {\boldsymbol {\Lambda }}}_{01}\\{\overline {\boldsymbol {\Lambda }}}_{01}^{T}&{\overline {\boldsymbol {\Lambda }}}_{11}\end{array}}\right]\left[{\begin{array}{c}{\boldsymbol {\mbox{C}}}_{00}\\{\boldsymbol {\Lambda }}_{01}^{T}\end{array}}\right]$ $=\left({\boldsymbol {\mbox{C}}}_{00}{\overline {\boldsymbol {\mbox{C}}}}_{00}+\right.$$\left.{\boldsymbol {\Lambda }}_{01}{\overline {\boldsymbol {\Lambda }}}_{01}^{T}\right){\boldsymbol {\mbox{C}}}_{00}+$$\left({\boldsymbol {\mbox{C}}}_{00}{\overline {\boldsymbol {\Lambda }}}_{01}+\right.$$\left.{\boldsymbol {\Lambda }}_{01}{\overline {\boldsymbol {\Lambda }}}_{11}\right){\boldsymbol {\Lambda }}_{01}^{T}$

Desarrollando el producto ${\textstyle {\boldsymbol {\mbox{D}}}_{11}{\boldsymbol {\mbox{D}}}_{11}^{-1}}$ se comprueba directamente que los términos entre paréntesis valen respectivamente 1 y 0 , por lo que ${\textstyle {\boldsymbol {\mbox{C}}}_{01}{\boldsymbol {\mbox{D}}}_{11}^{-1}{\boldsymbol {\mbox{C}}}_{10}=}$${\boldsymbol {\mbox{C}}}_{00}$ . Este resultado permite afirmar que el modelo viga estándar posee la propiedad característica siguiente:

${\overset {\mbox{ˆ}}{\boldsymbol {\mbox{D}}}}_{00}=$${\boldsymbol {\mbox{D}}}_{00}+{\boldsymbol {\mbox{D}}}_{01}{\boldsymbol {\mbox{D}}}_{11}^{-1}{\boldsymbol {\mbox{D}}}_{10}=$${\boldsymbol {0}}$

References

1. [1] S.S. Antman; Ordinary differential equations of non-linear elasticity I: Foundations of the theories of non-linearly elastic rods and shells; Arch. Rational Mech. Anal., 61 (1976), pp. 307–351
2. [2] S.S. Antman, Nonlinear problems of elasticity, Appl. Math. Sci., 107 (1995), Springer-Verlag, Berlín y Nueva York.
3. [3] V.I. Arnold; Mathematical Methods of Classical Mechanics 2.^a ed., Springer (1989)
4. [4] D.O. Brush, B.O. Almroth; Buckling of bars, plates and shells, McGraw-Hill (1975)
5. [5] A.E. Green, W. Zerna; Theoretical Elasticity. 2.^a ed., Oxford at the Clarendon Press (1968)
6. [6] C. Lanczos; The Variational Principles of Mechanics. 4.^a ed., University of Toronto Press (1970)
7. [7] C. Lázaro, Formulación material y espacial del modelo goemétricamente exacto de piezas alargadas. Tesis doctoral. Universidad Politécnica de Valencia, Valencia, (2005).
8. [8] J. Manterola, La sección abierta y cerrada bajo solicitación excéntrica. Puentes II. Monografía n.^o 15 de la A.F.C.E. (1976).
9. [9] S. Monleón; Tópicos del análisis unidimensional de estructuras; Parte 1. Vigas y arcos. Rev. Internac. Mét. Num. Cálc. Dis. Ing., 9 (1993), pp. 161–179
10. [10] S. Monleón; Tópicos del análisis unidimensional de estructuras; Parte 2. Placas y láminas. Rev. Internac. Mét. Num. Cálc. Dis. Ing., 11 (1995), pp. 37–59
11. [11] S. Monleón, Análisis de vigas, arcos, placas y láminas: una presentación unificada. 2.^a ed., Editorial de la Uiversidad Politécnica de Valencia, 2001.
12. [12] J.T. Oden, E.A. Ripperger; Mechanics of Elastic Structures. 2.^a ed., McGraw-Hill (1981)
13. [13] B. Saint-Venant; De la Torsion des Prismes, Tome XIV de l’Académie des Sciences, París (1855)
14. [14] S.P. Timoshenko; History of Strength of Materials, McGraw-Hill. Reeditado por Dover en (1953) 1983
15. [15] B.Z. Vlassov, Análisis de vigas, arcos, placas y láminas: una presentación unificada. 2.^a ed., Pièces Longues en Voiles Minces. 2.^a ed., Éditions Eyrolles, París, 1962.