Resumen
El refuerzo de estructuras de hormigón armado con laminados de fibras de carbono CFRP (Carbon Fiber Reinforced Polymer) se inició en los años ochenta. Actualmente, es una de las tecnologías más prometedoras por las buenas características mecánicas de los laminados y su facilidad de manipulación. Los laminados se adhieren al hormigón mediante resinas de tipo epoxídico. La capacidad del refuerzo está directamente ligada a la capacidad de anclaje en la interfaz laminado-hormigón. En la medida que el hormigón es capaz de transferir las tensiones al laminado, este entra en carga y colabora en el mecanismo resistente del elemento estructural. Conocer el comportamiento en la interfaz es fundamental para garantizar la seguridad de los refuerzos. En este trabajo se han realizado un ensayo de corte puro y una simulación tridimensional para comprender mejor el comportamiento en la interfaz entre el laminado y el hormigón.
Abstract
The strengthening of concrete structures with laminates of carbon fibers CFRP (Carbon Fibers Reinforced Polymer) began in the 1980s. Nowdays, this technology is one of the most promising one because of the good mechanical properties of laminates and their easy hand-work. Laminates are bonded to the concrete structure by means of epoxy resins. The load-carrying capacity of the strengthening depends directly on the proper behavior of the interface laminate-concrete. While the concrete is capable of transferring stresses to the laminate, this one becomes in charge and collaborates to the strength mechanism of the structure. The safety factor of the reinforcement can be guaranteed if we can predict the behavior at the interface between both materials. In this work we present a pure shear test and a simulation three-dimensional to characterize the behavior of the interface between the laminate and the concrete.
Palabras clave
Fibras de carbono ; Hormigón ; Refuerzo ; Teoría de mezclas ; Longitud de anclaje
Keywords
Carbon fibers ; Concrete ; Strengthening ; Mixing theory ; Anchor length
1. Introducción
Frente al incremento del uso de los materiales compuestos conformados por polímeros reforzados con fibras largas (FRP) como una alternativa de refuerzo de las estructuras, es importante buscar nuevas herramientas que permitan estudiar su comportamiento para optimizar su diseño y utilización tanto en la reparación de los elementos estructurales con cierto nivel de daño, como en la rehabilitación de los elementos que requieren tener un mejor comportamiento dentro de la estructura. En las edificaciones, los polímeros reforzados más utilizados como refuerzo son los compuestos con fibras de vidrio (GFRP), con fibras de carbono (CFRP) y con fibras de aramida (AFRP).
Los laminados de fibras con carbono CFRP están compuestos por carbono (fibras) y epoxi (matriz) que en conjunto permiten el adecuado comportamiento en una, dos y tres direcciones en función de la orientación de las fibras. En los ensayos realizados se han usado laminados unidireccionales. Cuando estos se utilizan como refuerzo para estructuras de hormigón armado, reúnen todos los requisitos para resistir los esfuerzos de tracción y permiten su colocación exterior adhiriéndose por medio de un epóxico.
La comparación entre la experimentación y la simulación numérica con elementos finitos representan una estrategia eficiente para estudiar el comportamiento de las estructuras reforzadas con materiales compuestos. Dado que la simulación numérica de los materiales compuestos es un campo que está en desarrollo, y que su uso en obras civiles es relativamente reciente, aún hay aspectos de los FRP que, por su complejidad, no han sido suficientemente estudiados para su utilización como refuerzo en estructuras de hormigón armado. Entre estos aspectos, se destaca la pérdida de adherencia entre el FRP y el hormigón.
Entre los resultados experimentales existentes se ha encontrado que los mecanismos de fallo de la adherencia del FRP son factores críticos para el comportamiento de los elementos reforzados solicitados a cortante o flexión. Además, dejan claro que existe la necesidad de nuevas herramientas que permitan predecir de una forma más precisa la pérdida de adherencia por el deslizamiento entre el FRP y el hormigón o por la delaminación del FRP [1] .
En este artículo se ha diseñado un experimento para estudiar la adherencia entre el laminado y el hormigón. Dado que en el ensayo no es posible medir el estado de tensiones en las interfaces, se ha utilizado la simulación numérica como instrumento para evaluar la distribución de tensiones en el área de contacto de los tres materiales.
2. Diseño y ejecución del experimento
2.1. Descripción del ensayo de doble corte
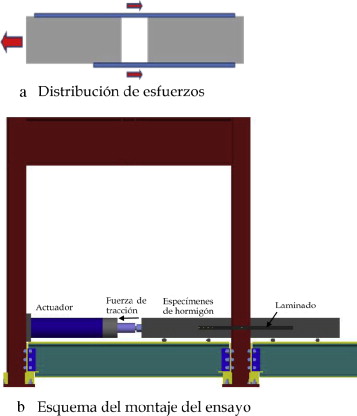
Para estudiar la transmisión de tensiones entre las capas hormigón-epoxi-laminado CFRP, se ha diseñado un ensayo de doble corte. El objetivo era poner en tracción un laminado y trasmitir el esfuerzo axial como rasante en la zona reforzada sin que aparecieran efectos indeseables por flexión. Para ello se han construido dos bloques de hormigón de 0,250 × 0,250 × 1,000 m y se han unido de forma casi-simétrica mediante dos laminados de CFRP.
Cuando uno de los bloques sufre un estiramiento, los laminados de CFRP entran en tracción y transmiten un esfuerzo axil simétrico y paralelo sobre el otro bloque (fig. 1a). Los bloques de hormigón se han colocado en el interior de un marco de carga y alineados con un actuador MTS de 100 kN como puede observarse en la figura 1 b. El bloque se conecta con el actuador mediante un par de redondos embebidos en el centro de las piezas. Los laminados de CFRP se pegan a ambos lados de los bloques con una longitud de adherencia menor en uno de ellos para asegurar el fallo en dicha zona. Debajo de los bloques se colocan delgadas láminas de teflón para reducir las fuerzas de fricción entre los bloques y el marco. Antes de proceder al ensayo se comprueba que dichas fuerzas son casi despreciables frente a la carga de rotura del sistema. El control del actuador se realiza con control de carga mediante el sistema Flex-Test de MTS. Todas las mediciones de desplazamientos, cargas y deformaciones se capturan de forma continua mediante un adquisidor de datos MGCPlus-HBM.
|
|
|
Figura 1. Ensayo de doble corte. |
La geometría del ensayo se indica en la figura 2 , donde se ve que las bandas de CFRP adheridas tienen una longitud de contacto diferente 0,21 m y 0,50 m. Una de las láminas tiene menor longitud con el propósito de inducir el fallo en ese sector y que, de esta forma, se garantice que la rotura se produce en dicho laminado súbitamente. Las bandas de CFRP tienen un ancho de 0,05 m y un espesor de 0,0012 m.
|
|
|
Figura 2. Geometría de la probeta del ensayo de doble corte [16] . |
2.2. Materiales utilizados en el ensayo
- Laminado de CFRP: Está conformado por fibra de carbono embebida en matriz epoxi. Presenta una orientación de fibras unidireccional con bajo módulo elástico; la fibra de carbono utilizada (sistema MBRACE de BASF) tiene una curva tensión – deformación completamente lineal hasta la rotura.
- Epoxi: El sistema de adhesivo epoxi para la adhesión de laminados está compuesto por dos productos, una capa de imprimación MBRACE Primer y la capa adhesiva MBRACE Adhesive.
- Hormigón: Hormigón «in situ» recogido en una obra en las inmediaciones de Terrassa. Se realizaron ensayos según el control de calidad estándar que señala la EHE y se hicieron mediciones complementarias sobre los bloques mediante ensayos no destructivos con esclerómetro. Acorde con los resultados el hormigón corresponde a un H-50.
2.3. Preparación de los ensayos
2.3.1. Preparación de la superficie del elemento de hormigón armado
La preparación de la superficie de hormigón se realizó con un martillo vibrador para dar una ligera rugosidad en la zona sobre la que se fijan los laminados. Este ligero decapado mostrado en la figura 3 también permite eliminar zonas del hormigón que tengan defectos puntuales como lechadas, carbonatación o pequeñas coqueras.
|
|
|
Figura 3. Zona central del bloque decapada. |
El proceso de preparación de la superficie se inició definiendo la zona sobre la cual se colocarán los laminados. En esta zona se realizó la eliminación mecánica de la capa superficial (< 1 mm) del elemento de hormigón, debido a que con una leve rugosidad en la superficie se garantiza una adecuada adherencia del epoxi que une el laminado con el hormigón.
2.3.2. Imprimación
Se distribuyó el producto MBRACE Primer de forma uniforme sobre toda la superficie, con la ayuda de una brocha, garantizando una impregnación completa de la porosidad y las oquedades del soporte (fig. 4 ).
|
|
|
Figura 4. Capa de imprimación. |
2.3.3. Aplicación del adhesivo
El adhesivo que es el producto MBRACE Adhesive se aplicó sobre las superficies del hormigón decapado y del laminado, como se muestra en la figura 5 . Por medio de una espátula se aplicó una capa de contacto de aproximadamente 1 mm de espesor, cubriéndose las pequeñas irregularidades que existían en la zona a ser reforzada. En el caso en que existan grandes oquedades deben tratarse, previamente, mediante morteros de reparación estructural.
|
|
|
Figura 5. Capa de adhesivo. |
2.3.4. Colocación del laminado
Finalmente se colocó el laminado sobre la capa de adhesivo (fig. 6 ); fue conveniente presionar el laminado para eliminar burbujas y mejorar el contacto entre las superficies.
|
|
|
Figura 6. Laminados adheridos. |
2.3.5. Colocación de la instrumentación
El laminado corto, como se indica en la figura 7 , se instrumentó con galgas extensométricas cada 0,05 m a lo largo de los 0,210 m de la superficie reforzada. En la figura 7 a se observa que las galgas señaladas del 1 al 5 están en la zona de adherencia, y que las denominadas A/B corresponden a las galgas colocadas para corroborar la simetría en el comportamiento de los laminados durante el proceso de carga. También se midió el desplazamiento relativo de los bloques con el captador, como se muestra en la figura 7 b.
|
|
|
Figura 7. Instrumentación en el ensayo. |
2.3.6. Montaje del ensayo
Durante el montaje, como se ve en la figura 8 , fue necesario alinear el bloque de hormigón y el actuador. Esta alineación se hizo para garantizar la distribución simétrica de esfuerzos entre los dos laminados y evitar que se produzcan por excentricidades, efectos de flexión que pueden distorsionar los resultados del ensayo.
|
|
|
Figura 8. Alineación entre el bloque y el actuador. |
2.3.7. Ejecución del ensayo
El ensayo de doble corte se hizo por control de carga, en la figura 9 se observa que la carga se aplica a uno de los bloques. El bloque conectado con el actuador se traccionó con una velocidad de carga muy baja 500 N/min, hasta que se produjo el desprendimiento de los laminados. El fallo ocurrió de forma súbita; primero colapsó el laminado más corto, y casi de forma instantánea, se desprendió el otro laminado.
|
|
|
Figura 9. Conexión del actuador al bloque de hormigón. |
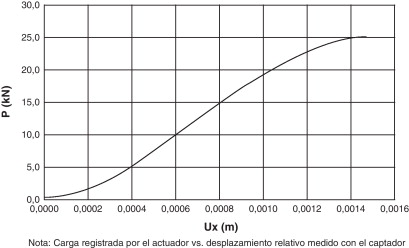
En la figura 10 se presenta la gráfica carga-desplazamiento, donde se aprecia un comportamiento no lineal al inicio del ensayo, el cual corresponde a la reacomodación del montaje del ensayo; luego se presenta un comportamiento lineal hasta una carga aproximada a 15 kN, donde comienza la reducción de la rigidez del sistema debido a la pérdida de adherencia en la interfaz hormigón-epoxi-FRP.
|
|
|
Figura 10. Curva carga (P)-desplazamiento (Ux) en el ensayo de doble corte. |
3. Estado del conocimiento sobre la simulación numérica de la interfaz hormigón-epoxi-refuerzo con FRP
La eficiencia del refuerzo para las estructuras de hormigón armado depende tanto de la apropiada selección de la configuración del refuerzo, como de la adherencia entre el FRP y el hormigón [2] .
Los estudios experimentales realizados demuestran que uno de los parámetros críticos para definir la resistencia del hormigón armado reforzado con FRP es la adherencia entre el hormigón y el FRP [3] , de la que depende el mecanismo de transmisión de tensiones y por tanto del comportamiento del compuesto. Consecuentemente, el comportamiento de la interfaz hormigón-epoxi-laminado en FRP es uno de los aspectos que necesitan más estudio.
Frente a la complejidad del comportamiento de la interfaz hormigón-epoxi-FRP es evidente que, además de la experimentación, se debe utilizar la simulación numérica para evaluar el comportamiento estructural de los elementos reforzados, para optimizar los diseños y para garantizar la eficiencia del FRP como refuerzo [4] .
En la década pasada, gran parte de las simulaciones se realizaron en vigas reforzadas, sin embargo, solo algunas capturaron los modos de fallo de la interfaz por deslizamiento, debido al gran coste computacional que implica el simular un fenómeno de este grado de complejidad [5] and [6] . En los primeros estudios, se realizaron grandes simplificaciones; por ejemplo, no se consideró el daño en el hormigón y se supuso la adherencia perfecta entre el hormigón y el FRP durante todo el proceso de carga; además, en algunos casos no se modeló la capa del adhesivo o se consideró como un material lineal y elástico. Por tanto, la precisión de los resultados obtenidos mediante estas simulaciones es limitada, pero dieron las bases para establecer la distribución de las tensiones normales y tangenciales en la zona interfacial hormigón-FRP. Posteriormente, los estudios han puesto énfasis en el análisis no lineal con elementos finitos de la interfaz, con el objetivo de simular el proceso de deslizamiento entre el FRP y el hormigón [7] .
El avance del uso de los elementos finitos en el análisis del comportamiento de la interfaz hormigón-epoxi-FRP ha sido relacionado con la simulación de la propagación de las fisuras en el hormigón y en la zona interfacial. En ese sentido se desarrollaron dos tipos de aproximación en la simulación de fisuras:
- Modelos de fisura discreta. En esta formulación se utiliza la mecánica de fractura elástica y se predeterminan la dirección y posición de las fisuras en el mallado donde, por cada incremento de carga, se requiere que la malla de elementos finitos se modifique de acuerdo con la propagación de cada una de las fisuras. Asegura una buena precisión de la simulación del proceso de formación y propagación de fisuras, pero tiene un elevado coste computacional por el remallado. Este modelo ha sido utilizado, entre otros, por Yang et al. [6] , Niu y Wu [8] and [9] y Niu et al. [10] , quienes se han enfocado sus modelos hacia el comportamiento de la interfaz en vigas reforzadas con FRP.
- Modelos de fisura distribuida. La malla de elementos finitos no se modifica y el proceso de fisuración se determina a través de la mecánica de medios continuos mediante ecuaciones constitutivas no lineales. Las fisuras son simuladas como discontinuidades locales que son distribuidas dentro del sólido aplicando la teoría de la mecánica del continuo. Entre los estudios que han utilizado este tipo de modelos para el análisis de la interfaz hormigón-epoxi-FRP están Wu y Yin [11] , Lu et al. [7] and [12] , y Ebead y Neale [13] .
Los investigadores que utilizan los modelos de fisuración han estudiado el deslizamiento entre el FRP y el hormigón considerando que el fallo ocurre por el modo de fractura de deslizamiento y/o de apertura en el hormigón. Es por ello que simulan el comportamiento de la interfaz a través de una ley constitutiva, que se asigna a elementos de interfaz con espesor nulo [6] , [8] , [9] and [10] , o, con dimensiones específicas [11] and [13] . Otra alternativa es simular el deslizamiento mediante los modelos de fisuración asignados a los elementos del hormigón adyacentes al laminado [7] and [12] , requiriendo un mallado fino en la zona con refuerzo, sin modelizar elementos de interfaz.
Recientemente, se han aplicado modelos constitutivos de daño y de plasticidad a la simulación no lineal para el estudio del proceso de degradación de la interfaz hormigón-FRP, entre este grupo están Perera et al. [5] , y, Coronado y López [14] . Esta estrategia está en desarrollo y tiene un campo de aplicación bastante amplio para el estudio del deslizamiento del refuerzo en estructuras de hormigón.
A pesar que, desde el año 2002, Ueda et al. [15] recomendaron estudiar con mayor detalle el deterioro de las propiedades de la interfaz de las zonas cercanas a las fisuras en el hormigón, en las simulaciones recientes solo se ha considerado el daño en el hormigón y en pocos estudios se ha modelizado el adhesivo. Además, tampoco se ha tenido en cuenta que el epoxi puede tener un comportamiento no lineal en respuesta al daño del hormigón o presentar daño y/o plasticidad ante las concentraciones de tensiones en las zonas afectadas.
Es importante que el FRP y el hormigón armado se puedan modelizar considerando el estado de cada uno de los materiales que lo componen; una potente herramienta para ello es la teoría de mezclas de serie/paralelo [16] . Asimismo, es necesario que en las simulaciones se considere el daño, tanto en el hormigón como en el adhesivo y en la matriz polimérica del FRP, bajo el principio de que el daño en los materiales produce la reducción de las propiedades mecánicas de la interfaz, lo cual afecta la adherencia.
4. Teoría de mezclas serie/paralelo para materiales compuestos
La teoría de mezclas, como gestor del uso de los modelos constitutivos que describen el comportamiento de los materiales simples que componen los materiales compuestos, constituye una herramienta que puede ser utilizada dentro de una técnica de elementos finitos para simular apropiadamente el comportamiento de dichos materiales. No obstante, es necesario el desarrollo de nuevas herramientas que mejoren la simulación numérica a nivel global y local, de manera que se represente de una forma más precisa el comportamiento real de los compuestos, con la finalidad de obtener información que no se puede medir en los ensayos de los elementos reforzados con FRP. Una excelente alternativa para la simulación numérica es la teoría de mezclas serie/paralelo [17] and [18] , recientemente validada a través de diferentes pruebas experimentales. Esta teoría se fundamenta en la teoría de mezclas clásica, propuesta por Trusdell y Topin (1960), la cual considera que el comportamiento de cada componente define el comportamiento global del compuesto.
La teoría de mezclas clásica surgió como una solución a la limitación que inicialmente presentaban los modelos constitutivos en el estudio de los materiales compuestos, por tratarlos desde un punto de vista macroscópico como un material homogéneo, sin tener en cuenta la contribución de sus materiales componentes [19] . Esta teoría utiliza en la mecánica del continuo bajo el principio de interacción de las sustancias que componen el material, suponiendo que en el volumen infinitesimal del compuesto participan en paralelo todos sus componentes; asimismo, se considera que cada uno de ellos contribuye al comportamiento del compuesto en la misma proporción que su participación volumétrica [20] . La teoría de mezclas clásica presenta una restricción para su uso en los diferentes tipos de materiales compuestos, ya que parte de la hipótesis de que los componentes que coexisten en un punto están en paralelo y tienen la misma deformación; por lo tanto, se puede utilizar en el campo lineal, y con algunas adaptaciones se puede aplicar en casos no lineales, siempre que no se consideren significativos los movimientos relativos entre los componentes del compuesto [21] .
Debido a las diferencias en el comportamiento de los componentes, a su interacción y a la forma en que están distribuidos en el compuesto, los materiales compuestos tienen una elevada anisotropía y un comportamiento no lineal incluso para bajas tensiones, lo que hace que su modelación numérica sea compleja. No obstante, a través de la teoría de mezclas serie/paralelo complementada con los modelos constitutivos y el modelo de mapeo de espacios [22] , se obtiene la no linealidad y la anisotropía del compuesto como resultado de la interacción de cada uno de los componentes con su correspondiente ecuación constitutiva.
4.1. Fundamentos de la teoría serie/paralelo
En la teoría serie/paralelo [17] se considera que en una dirección particular los componentes se comportan en paralelo y en las otras direcciones en serie. Se utilizan las siguientes hipótesis:
- En cada volumen infinitesimal del compuesto participan en conjunto todos sus componentes, es decir, la distribución de los componentes es homogénea.
- Los componentes tienen la misma deformación en la dirección en paralelo (condición de isodeformación) y la misma tensión en la dirección en serie (condición de isotensión).
- La adherencia entre los componentes es perfecta.
- La contribución de los componentes en la respuesta del compuesto es proporcional a la participación volumétrica de cada material componente.
4.1.1. Definición de los tensores de deformación y de tensión [23]
El tensor deformación ɛ se descompone una parte en serie ɛS y otra en paralelo ɛP por medio de los tensores de proyección de cuarto orden ( ) en paralelo y en serie, respectivamente
|
|
( 1) |
|
|
El tensor de tensiones σ también se separa en sus componentes en serie σS y en paralelo σP
|
|
( 2) |
|
|
donde los tensores de proyección de cuarto orden se hallan a través del tensor de proyección paralelo de segundo orden NP y del tensor identidad de cuarto orden
|
|
( 3) |
siendo e1 el vector unidad que indica la dirección del comportamiento en paralelo, es decir, la dirección de la fibra.
4.1.2. Ecuación de compatibilidad de deformaciones en el compuesto
Con el fin de minimizar el costo computacional, la implementación numérica de la teoría fue desarrollada para descomponer el compuesto c en un determinado número de capas ncap , tal que cada capa j sea conformada por una matriz m y una fibra f[24] . En lo que respecta a la ecuación de compatibilidad de deformaciones en el compuesto, existe una condición de iso-deformación entre las capas y el compuesto. Se parte de la hipótesis que las capas que coexisten en un punto están en paralelo y tienen la misma deformación; por tanto, el tensor de deformación total del compuesto cɛ es equivalente a los tensores de deformación total de las capas que lo componen
|
|
( 4) |
4.1.3. Ecuaciones de equilibrio y de compatibilidad en las capas del compuesto [25]
La participación de los componentes en el comportamiento de la capa j se considera a través de los coeficientes de participación volumétrica de la matriz y de la fibra . Consecuentemente, con las hipótesis enunciadas de la teoría serie/paralelo, en cada capa del compuesto j se plantean las siguientes ecuaciones de equilibrio y de compatibilidad de deformaciones:
- Comportamiento en paralelo
|
|
( 5) |
- Comportamiento en serie
|
|
( 6) |
4.1.4. Ecuación constitutiva de los materiales que componen las capas del compuesto
Como la implementación de la teoría serie/paralelo se realiza a nivel constitutivo a partir del estado de deformación en un punto de Gauss, una vez que se obtiene la deformación del compuesto cɛ , se calcula el estado tenso-deformacional de cada componente cumpliendo con las ecuaciones de equilibrio y de compatibilidad, para luego hallar el estado de tensiones y de deformaciones del compuesto. Dicho estado se determina mediante la ecuación constitutiva que rige el comportamiento de cada componente, por ejemplo, en el caso de un componente elasto-plástico la ecuación correspondería a:
|
|
( 7) |
de tal forma que es el tensor constitutivo de la matriz m o de la fibra f de la capa j , , , son los tensores de deformación total, elástico y plástico.
4.1.5. Ecuación de equilibrio en el compuesto
La ecuación de equilibrio de tensiones (6) se verifica calculando la tensión residual de la capa jΔσS y revisando que esta sea menor que una tolerancia Toler , tal como se muestra en la ecuación (8). Cuando la tensión residual es mayor, la predicción de la deformación de la matriz se corrige en forma iterativa. Una vez se obtiene una tensión residual menor que la tolerancia, se hace la recomposición de los tensores de tensión y de deformación de la capa j.
|
|
( 8) |
Luego de realizar el análisis de cada capa, el tensor de tensión del compuesto cσ se determina a través de la suma de los tensores de tensión de las capas del compuesto ncap de acuerdo con el porcentaje de participación volumétrica de cada capa jk[16] .
|
|
( 9) |
5. Generalidades del modelo constitutivo de daño isótropo
En la simulación realizada para el ensayo de doble corte definido anteriormente, se propone utilizar el modelo de daño isótropo para estudiar la pérdida de adherencia en la interfaz hormigón-epoxi –CFRP, aplicando este modelo constitutivo en el hormigón, el epoxi y la matriz polimérica del compuesto. El modelo de daño isótropo desarrollado por Oliver et al. [26] se fundamenta en la teoría de daño continuo presentada inicialmente por Kachanov [27] . Bajo el contexto de la mecánica del continuo, este modelo de daño isótropo simula el proceso de degradación de las propiedades de un material debido a la fisuración [28] . El modelo de daño isótropo es una particularización del modelo de daño anisótropo, en el que la degradación del material se desarrolla en todas las direcciones por igual y depende de una variable escalar interna de daño d . [29] La variable de daño d transforma el tensor de tensiones σ del material con daño en un tensor de tensiones efectivas de un material ficticio sin daño, tal que:
|
|
( 10) |
donde la variable de daño d es una medida de la pérdida de rigidez del material; su rango de valores es 0 ≤ d ≤ 1, donde 0 corresponde al material sin daño y 1 equivale al material completamente dañado.
Con el modelo de daño isótropo se define el valor de la tensión en que se inicia el daño y la evolución del parámetro de daño para describir el comportamiento de un determinado material. El criterio de daño isótropo esta dado como [30]
|
|
( 11) |
Fσ es la función continua de tensiones que determina la superficie de daño, que se divide en una función que depende del tensor de tensiones y en una función κ (d ) que establece la posición del umbral de daño. Esta formulación constitutiva permite que el modelo de daño isótropo se utilice bajo cualquier función de fluencia propuesta en la literatura, como Von Misses, Mohr Coulomb o Drucker-Prager [28] .
La variación del parámetro del daño es obtenida a través del parámetro de consistencia del daño y de la condición de Kuhn-Tucker [29] , haciendo posible la integración explícita de la variable de interna de daño, tal que
|
|
( 12) |
κo es el valor inicial del umbral de daño que corresponde a una propiedad del material y está relacionado con la resistencia a compresión o a tracción, de acuerdo con la función de umbral de daño con la que se realice el análisis. La función escalar G [χ ] que establece la evolución del ablandamiento del material es invertible y positiva, y su derivada es positiva y monótona creciente [29] . Específicamente, para este artículo se utilizó una función de ablandamiento lineal, definida como
|
|
( 13) |
siendo A un parámetro que depende de la energía de fractura del material. Para este caso, en el que la función de ablandamiento es lineal, A viene dada por
|
|
( 14) |
donde es el valor que se obtiene del criterio de daño expresado en (11) para el primer umbral de degradación, gf es la energía máxima específica, Gf es la energía de fractura del material y lf es la longitud de fractura. La longitud de fractura está relacionada con las dimensiones del elemento finito en el que se aplica el criterio de daño; este parámetro permite que el proceso de degradación resultante sea independiente del mallado, con lo cual se garantiza la objetividad y exactitud de la solución del análisis numérico realizado.
6. Resultados de las mediciones experimentales en la interfaz hormigón-epoxi-CFRP
Para el ensayo de control de carga se colocaron 5 galgas sobre el laminado, en la zona de anclaje. Asimismo, se colocaron dos galgas de control a ambos lados del espécimen A/B (SGA/B) con el fin de verificar que no existiera diferencia de deformaciones entre ambos lados del espécimen, y de esta forma garantizar que la carga se distribuyera sin excentricidades sobre los dos laminados. Los resultados conseguidos en las mediciones se muestran en la figura 11 .
|
|
|
Figura 11. Distribución de deformaciones en el laminado. |
Cuando la carga alcanzó los 25 kN el laminado despegó, y las galgas muestran cómo se va transfiriendo la carga conforme se va reduciendo la zona adherida del laminado. Se puede observar que el nivel de carga y la magnitud de las deformaciones están muy por debajo del límite elástico del laminado, incluso cuando ocurre el desprendimiento total del laminado. Por lo tanto, en todo momento durante el ensayo, el laminado tiene un comportamiento elástico y solo está sometido a tracción pura (esfuerzo axial). En la figura 11 se observa que primero se presenta un estado de carga no lineal en el SG4, después en el SG3, luego en el SG2 y, finalmente, en el SG1, hasta que se produce el desprendimiento de la lámina. Las galgas de control A/B mostraron que no hubo diferencia de deformaciones entre las dos bandas como se señala con la curva SGA/B, además se observa que las láminas fuera de la zona de adherencia permanecen con un comportamiento lineal.
En la figura 12 se presenta el estado de deformaciones a lo largo de la lámina, medido con las galgas (SG) para diferentes niveles de carga.
|
|
|
Figura 12. Interpolación de las deformaciones medidas con las galgas (SG) para iso-cargas. |
7. Simulación numérica de la interfaz hormigón-epoxi-CFRP
Son pocas las investigaciones que consideran los modelos tridimensionales, en el estudio del comportamiento de la interfaz hormigón-epoxi- FRP, pero en ellos realizan simplificaciones que no consideran el comportamiento no lineal la zona interfacial. Entre las más recientes se encuentran: Un modelo tridimensional de un ensayo de doble corte con placas de GFRP [31] , en el que el hormigón y el GFRP fueron representados con elementos sólidos suponiendo un comportamiento elástico y lineal, mientras que la interfaz se simuló como dos sistemas de resortes de rigidez constante. Una simulación tridimensional de un ensayo de corte simple [32] , en la que se evidencia que la distribución de tensiones es diferente a la obtenida cuando se considera un estado plano de tensiones, aunque se consideró el comportamiento elástico lineal en el hormigón, el epoxi y el FRP. Dicha diferencia que se debe tanto a la incidencia de la relación entre el ancho del FRP y el del bloque de hormigón (bFRP /bh ), como a la influencia los coeficientes de Poisson de cada uno de los materiales que conforma la interfaz.
En este artículo se realiza una simulación numérica del test de doble corte en tres dimensiones, mediante el programa de elementos finitos PLCD [33] , y se analiza el comportamiento no lineal de la zona interfacial, aprovechando las ventajas que ofrece la teoría serie/paralelo en determinar el comportamiento tanto de los componentes, como del compuesto.
7.1. Características del modelo de simulación de la probeta
Solo se modelizó el bloque conectado con el actuador y al que se le aplica la fuerza de tracción, con una malla compuesto por hexaedros de 8 nodos. El modelo tiene cinco materiales simples y sus propiedades se muestran en la tabla 1 , donde Ex, Ey y Ez son los módulos de elasticidad en las direcciones «x», «y» y «z» , ν es el módulo de Poisson, σc y σt son las tensiones máximas resistentes de compresión y de tracción, Gc y Gt son las energías de aplastamiento y de fractura. Las propiedades mecánicas de los materiales fueron obtenidas de ensayos realizados por el fabricante.
| Material | Criterio de límite | Ex=Ey=Ez MPa | ν | σc MPa | σt MPa | Gc kPa·m | Gt kPa·m |
|---|---|---|---|---|---|---|---|
| Hormigón | Mohr-Coulomb | 3,65·104 | 0,25 | 52,0 | 3,0 | 55,0 | 0,5 |
| Acero | Von Mises | 2,00·105 | 0,00 | 270,0 | 270,0 | 2.000,0 | 2.000,0 |
| Epoxi | Mohr-Coulomb | 1,25·104 | 0,20 | 80,2 | 22,9 | 36,0 | 3,0 |
| Matriz polimérica | Mohr-Coulomb | 1,20·104 | 0,20 | 87,5 | 29,2 | 36,0 | 3,0 |
| Fibra de carbono | Von Mises | 2,26·105 | 0,00 | 2.200,0 | 2.200,0 | 14.500,0 | 14.500,0 |
De acuerdo con la teoría serie/paralelo, en el hormigón armado y en el CFRP, las matrices de estos compuestos son el hormigón y la matriz polimérica, respectivamente, mientras que el acero y las fibras de carbono constituyen el refuerzo. Además, para considerar su correspondiente anisotropía, se tiene en cuenta que las barras de acero y las fibras de carbono están orientadas a 0 grados de la dirección en que se aplica la carga. En la figura 13 se indican los cuatro materiales compuestos asignados al modelo y en la tabla 2 se muestran los porcentajes volumétricos en los que participan los componentes en cada material compuesto.
|
|
|
Figura 13. Configuración de los materiales compuestos [16] . |
| Material compuesto | Matriz de hormigón | Acero a 0° | Matriz de resina | Matriz polimérica | Fibra de carbono a 0° |
|---|---|---|---|---|---|
| 1 | 100 | ||||
| 2 | 49,8 | 50,2 | |||
| 3 | 100 | ||||
| 4 | 0,32 | 0,68 |
En las recientes investigaciones de la interfaz hormigón-epoxi-FRP, en las que se han modelizado ensayos de adherencia, se han considerado diferentes criterios de daño para el hormigón. Sin embargo, se observa que no se ha tenido en cuenta el daño en el adhesivo o en la matriz del FRP, efectos que evidentemente, reducen las propiedades mecánicas de los materiales que componen la interfaz y, por ende, afectan la adherencia [16] . Por ello, en este artículo para analizar el comportamiento de la interfaz de una forma integral, se aplicó el modelo de daño de isótropo en el hormigón, el epoxi y la matriz polimérica del compuesto, considerando la hipótesis que no hay daño inicial, para el acero se consideró un modelo elasto-plástico y para la fibra de carbono se utilizó como un modelo elástico. Además se supuso un estado inicial de adherencia perfecta en las interfaces hormigón-epoxi, epoxi-CFRP y hormigón-acero.
7.2. Daño en las interfaces
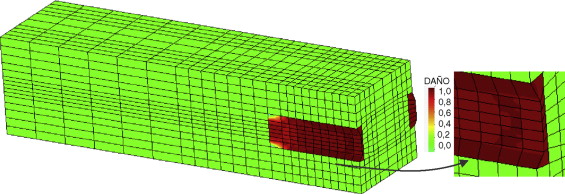
En la prueba experimental la carga máxima obtenida sobre el laminado de control fue de 25 kN y, en la simulación, fue de 25,1 kN. En los dos casos la probeta tuvo una baja ductilidad durante el fallo, el cual se produjo deslizándose el laminado y desprendiéndose una sección del extremo del bloque de hormigón, tal como se aprecia en la figura 14 .
|
|
|
Figura 14. Daño en el bloque de hormigón y en el adhesivo con la carga máxima de 25 kN. |
Una de las ventajas del uso de la teoría serie/paralelo consiste en que, al asignar un modelo constitutivo a cada componente de los compuestos, se puede observar la evolución de las variables internas acorde con el modelo utilizado. Por ello, en la simulación del test de doble corte se puede estudiar la evolución del daño en el hormigón y en el epoxi como se observa respectivamente en las Figura 15 and Figura 16 , lo que permite analizar el mecanismo de fallo de las interfaces de una forma integral. Al comparar la figura 14 con la figura 15 , se observa que la parte desprendida del hormigón en el bloque tiene una forma similar a la sección que se deforma en el modelo numérico y que presenta el mayor daño.
|
|
|
Figura 15. Distribución del daño en el bloque de hormigón con la carga máxima de 25,1 kN. |
|
|
|
Figura 16. Distribución del daño en el adhesivo con la carga máxima de 25,1 kN. |
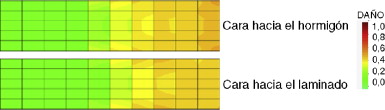
El mayor daño en el hormigón se produce hacia los bordes superior e inferior de la zona con refuerzo, con un máximo del 75% hacia donde termina el FRP, como se puede ver en la figura 16 . Este daño se extiende hasta 0,28 m desde el extremo del bloque, es decir, a 0,07 m más allá del laminado. Asimismo, en la figura 16 se ve que el epoxi tiene mayor nivel de daño en el extremo donde se desprende el hormigón y se va reduciendo hacia el centro de la zona con refuerzo. Además, en la interfaz con el hormigón el máximo daño es del 22%, mientras que en la interfaz con el laminado es del 45%.
Como la zona reforzada con mayor daño es la de los bordes superior e inferior, en la figura 17 se muestra la evolución del daño en el hormigón y en la figura 18 en el epoxi, a lo largo del borde superior. En lo referente al daño en el hormigón, en la figura 17 se observa que hay una distribución de daño uniforme con un 67% y que el máximo daño ocurre en el extremo donde termina el laminado dentro del bloque, con un 75% correspondiente al momento del fallo.
|
|
|
Figura 17. Daño en el hormigón. |
|
|
|
Figura 18. Daño en el epoxi. |
En lo que respecta al daño en el epoxi mostrado en la figura 18 para una longitud de anclaje de 0,21 m la distribución de daño no es uniforme; asimismo, el máximo daño en el epoxi ocurre en el extremo del bloque donde se adhiere el refuerzo. La poca uniformidad de la distribución de daño en el adhesivo y su concentración en el extremo se debe a que, por la corta longitud del laminado, hay una mayor concentración de tensiones.
Con lo visto en la prueba y en la simulación se ve la importancia de tener en cuenta el daño en el epoxi, lo que muestra que su comportamiento no es elástico ni es lineal como se ha supuesto en algunas investigaciones [5] , [6] , [7] and [32] . Sin embargo, es evidente la necesidad de comprobar en un futuro si, al utilizar un modelo constitutivo de daño más sofisticado para el epoxi en lugar del modelo de daño isótropo, los modos de rotura cambian o si el modelo constitutivo de daño que se asigne al adhesivo no influye de forma perceptible en la respuesta global del refuerzo.
7.3. Deformaciones
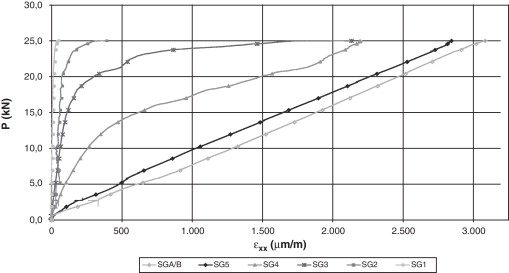
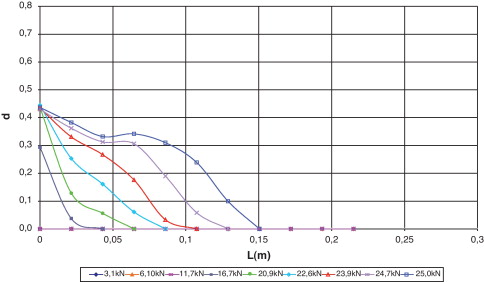
En la figura 19 se presentan las deformaciones en el compuesto de acuerdo con la ubicación de las galgas en la probeta. Se observa la similitud que existe entre la evolución de las deformaciones medidas en el ensayo y la obtenida en la simulación a 0,05 m (SG4), 0,10 m (SG3), 0,15 m (SG2) y 0,20 m (SG1) del extremo donde se adhiere el refuerzo. No obstante para 0,0 m (SG5), con la galga se obtuvo una respuesta lineal diferente a lo calculado mediante el modelo numérico, pero la pendiente es parecida. Esto probablemente se debe al hecho de que la galga se encuentra en la frontera de la zona de adherencia del laminado, mientras que el punto de Gauss analizado está dentro del laminado adherido al hormigón. En este caso, en general, se puede decir que en la simulación y en la prueba experimental, el compuesto tiene una relación de carga deformación similar.
|
|
|
Figura 19. Evolución de las deformaciones ɛxx en el compuesto [16] . |
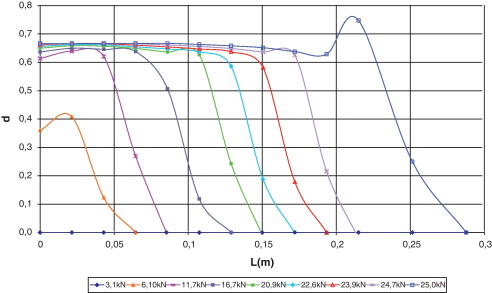
En la figura 20 se muestra la distribución de deformaciones obtenida mediante la simulación numérica y el ensayo de laboratorio a lo largo del centro del laminado para los diferentes niveles de carga. Se observa que hasta la carga de 23,9 kN el comportamiento es similar; a partir de este valor, el modelo no simula el aumento excesivo de deformación que ocurre a 0,10 m del extremo. Dicho incremento experimentalmente indica la flexión local del laminado a causa de una fisuración localizada. Sin embargo, esta pequeña discrepancia no es relevante frente a todas las ventajas que tiene el uso de la teoría serie/paralelo en el análisis de materiales compuestos.
|
|
|
Figura 20. Distribución de las deformaciones en el compuesto ɛxx [16] . |
7.4. Distribución de tensiones en las interfaces
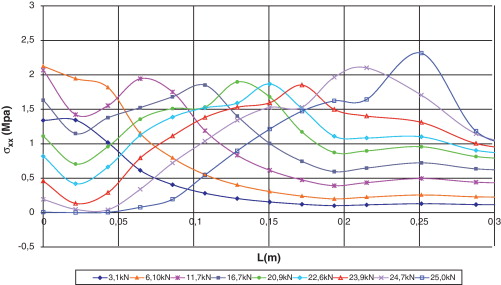
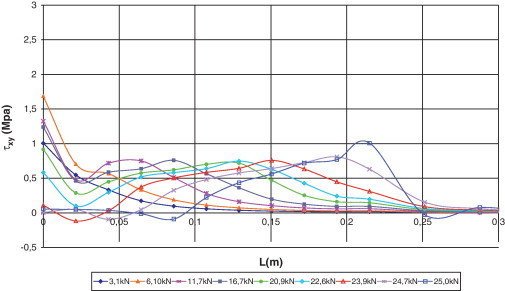
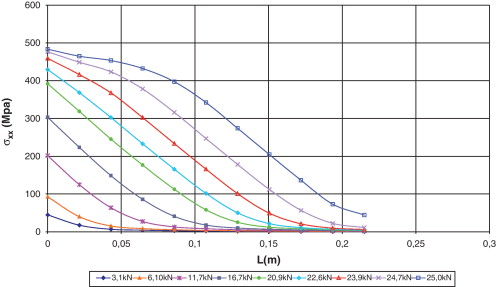
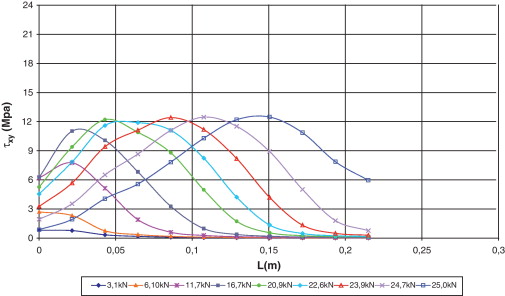
Otra de las ventajas que tiene la teoría serie/paralelo es que durante todo el proceso de carga permite identificar el estado de tensiones y de deformaciones, tanto en el compuesto, como en sus componentes. Debido a que el fallo se produce en la zona reforzada con el laminado corto, en este sector se analiza el comportamiento de las tensiones axiales y tangenciales del hormigón, del epoxi y del FRP en el borde superior de la zona reforzada, es decir, a una altura de 0,15 m de la base del bloque.
En la figura 21 se muestran las tensiones axiales, y en la figura 22 las tensiones tangenciales en el hormigón. En lo que respecta a las tensiones axiales, en la figura 21 se observa que, hasta una carga aplicada de 6,1 kN, la mayor tensión se presenta en el extremo donde se adhiere el CFRP.
|
|
|
Figura 21. Distribución de tensiones axiales en el hormigón. |
|
|
|
Figura 22. Distribución de tensiones tangenciales en el hormigón. |
Luego, como señal del deslizamiento, para los otros niveles de carga, la máxima tensión, con valores entre 1,85 y 2,0 MPa, se produce a lo largo de la zona reforzada hacia el extremo donde termina el FRP. Finalmente para la carga de fallo, hay una tensión de 2,31 MPa a 0,04 m del refuerzo, lo que muestra la pérdida de capacidad de la zona reforzada.
Referente a las tensiones tangenciales indicadas en la figura 22 , se observa que para los diferentes niveles de carga hasta 20,9 kN, las mayores tensiones ocurren en el extremo donde se adhiere el FRP, donde se alcanza la máxima tensión de 1,68 MPa con una carga de 6,1 kN. Luego, para niveles de carga superiores a 20,9 kN, las mayores tensiones están entre 0,75 y 0,80 MPa, y se producen a lo largo de la zona con refuerzo hacia el otro extremo laminado. Finalmente, con la carga última, donde finaliza el refuerzo, la tensión se incrementa a 1,0 MPa.
Al analizar las gráficas de las Figura 21 and Figura 22 se deduce que el comportamiento del hormigón en la interfaz corresponde a la acción conjunta de las tensiones tangenciales y axiales. Para los primeros niveles de carga (hasta 16,6 kN), las tensiones tangenciales alcanzan valores entre un 67 y un 89% de las tensiones axiales y luego, para los otros niveles, equivalen entre un 38 y un 48%. Además, se aprecia que las tensiones tangenciales tienen mayor incidencia en el daño que ocurre en el extremo del bloque de hormigón que en el lado donde termina el CFRP.
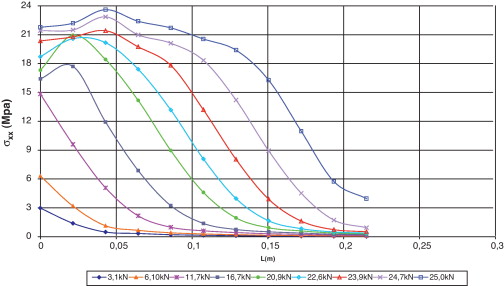
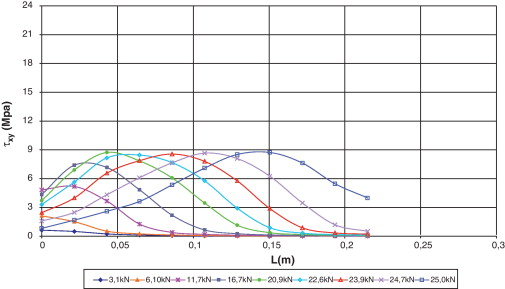
En la figura 23 se pueden observar las tensiones axiales, y en la figura 24 las tensiones tangenciales en el epoxi. Las tensiones axiales mostradas en la figura 23 señalan que al incrementarse el nivel de carga en el epoxi, se amplía el área de desarrollo de las tensiones axiales. También se aprecia que hasta una carga de 11,7 kN, la mayor tensión se presenta en el extremo donde se adhiere el CFRP. Luego, hasta una carga de 20,9 kN, las mayores tensiones se presentan a 0,02 m del extremo inicial, y para los otros niveles de carga, las mayores tensiones se dan a 0,04, con valores entre 21 y 24 MPa.
|
|
|
Figura 23. Distribución de tensiones axiales en el epoxi. |
|
|
|
Figura 24. Distribución de tensiones tangenciales en el epoxi. |
La evolución de las tensiones tangenciales en el epoxi es aproximadamente parabólica, tal y como puede verse en la figura 24 . Inicialmente hasta una carga de 11,4 kN, las mayores tensiones se presentan en el extremo del bloque. Luego, a medida que se incrementa la carga, el sector en el que se desarrollan las mayores tensiones (entre 8,50 y 8,80 MPa) va cambiando hacia el otro extremo donde termina el laminado.
Las tensiones tangenciales alcanzan valores entre un 34 y un 42% de las tensiones axiales, por lo que el comportamiento del epoxi depende de la acción conjunta de las tensiones tangenciales y axiales. Sin embargo, el porcentaje de participación de las tensiones tangenciales en el epoxi es menor que en el hormigón. Al comparar la evolución de las tensiones con el daño en el epoxi, se observa que la longitud de adherencia de 0,21 m es insuficiente para que se desarrolle toda la capacidad del CFRP, ya que el daño se concentra en el inicio de la zona.
En la figura 25 se muestran las tensiones axiales y en la figura 26 las tensiones tangenciales en el CFRP. Las tensiones axiales en el laminado observadas en la figura 25 tienen una tendencia casi lineal hasta una fuerza de 22,6 kN y, después tienen una distribución semi-parabólica. Para los diferentes niveles de carga, la mayor tensión ocurre en el extremo donde se adhiere el laminado y la menor se produce donde finaliza el refuerzo.
|
|
|
Figura 25. Distribución de tensiones axiales en el CFRP. |
|
|
|
Figura 26. Distribución de tensiones tangenciales en el CFRP. |
Las tensiones tangenciales en el laminado tienen una distribución de tensiones parabólica, tal y como se muestra en la figura 26 . Para cargas menores o iguales a 6,1 kN, la mayor tensión se presenta en el extremo donde se adhiere el laminado; luego ocurre a 0,05 m hasta una carga de 16,6 kN. Para los otros niveles, el sector con la mayor tensión cambia y la longitud de distribución aumenta, manteniendo un valor de máxima tensión tangencial entre 12,0 y 12,5 MPa.
Al comparar las dos gráficas de las Figura 25 and Figura 26 se puede ver como en la zona donde termina el laminado, las tensiones axiales y tangenciales son bajas en el CFRP incluso para la carga de fallo, lo que indica que no se alcanza a desarrollar la capacidad del FRP. Por otra parte, ya que las tensiones tangenciales son desde un 2 hasta un 4% de las tensiones axiales, se evidencia que el CFRP está solicitado básicamente por acciones axiles.
Al comparar la distribución de tensiones y su magnitud, se observa que las tensiones tangenciales máximas en el hormigón para cargas mayores a 16,6 kN están entre un 6 y un 8% de las tensiones en el laminado, mientras que con respecto a las tensiones axiales la relación es menor a un 0,1%. Por lo tanto, el epoxi, al no ser tan resistente como el laminado y al tener mayor resistencia que el hormigón, debe tener la capacidad suficiente para garantizar que las tensiones se transmitan y distribuyan en forma adecuada desde el laminado al hormigón.
Coincidiendo con lo encontrado por Chen y Pan [32] , en la simulación realizada en este artículo, al observar el comportamiento del hormigón, del adhesivo y del FRP, se concluye que en la simulación tridimensional, la contribución de las tensiones axiales y tangenciales es diferente a lo indicado en los estudios en los que se ha considerado el estado plano de tensiones. En lo que respecta al comportamiento de la interfaz, en el hormigón y en el epoxi, tanto las tensiones tangenciales como las tensiones axiales tienen un porcentaje de participación significativo, mientras que en el FRP predominan las tensiones axiales.
8. Conclusiones
Los ensayos de laboratorio de doble corte permiten evaluar el comportamiento en los extremos de un laminado adherido al hormigón, incluyendo el proceso del desprendimiento del refuerzo. Esto permite estudiar la zona efectiva de distribución de esfuerzos en los extremos del laminado y sus deformaciones bajo un estado de cortante puro. No obstante, se requieren de otras herramientas de análisis complementarias, como la simulación numérica, para detallar el comportamiento de las interfaces hormigón-epoxi-FRP en la zona de adherencia.
El FRP no se está aprovechando eficientemente como refuerzo en elementos de hormigón, en este estudio se evidencia que el deslizamiento entre el FRP y el hormigón se produce al sobrepasarse la resistencia de la interfaz o del hormigón y, que en ningún caso, se supera la resistencia del laminado. Dado que el estado de tensiones de las interfaces es de difícil medición, es necesario utilizar la simulación numérica como una herramienta complementaria a la experimentación. Para comprender mejor el proceso de transferencia de los esfuerzos entre el hormigón, el epoxi y el FRP, y para darle al proyectista estructural un instrumento que le permita mejorar el cálculo de los elementos de hormigón armado reforzados con FRP.
En este trabajo a través de la teoría serie/paralelo se estudia el comportamiento de la interfaz hormigón-epoxi-CFRP y se comparan los resultados con los obtenidos en un ensayo. Igualmente, se modeliza el adhesivo que es susceptible al daño y se considera su comportamiento no lineal. Además, se muestra la importancia de utilizar modelos tridimensionales, ya que permiten calcular el proceso de fallo de una forma integral. No obstante, se requiere de una formulación que permita simular de una forma más adecuada el deslizamiento localizado que puede existir en algunos sectores de la interfaz.
La teoría serie/paralelo es una herramienta versátil para analizar el comportamiento de materiales compuestos y de sus componentes dentro de una estructura. Por una parte permite que cada componente del compuesto se analice mediante la ecuación constitutiva que sea más conveniente para predecir su comportamiento (elasticidad, plasticidad, daño etc.), y por otra, al calcular el comportamiento del material compuesto en cada punto de Gauss, lo acopla al resto del mallado, definiendo a su vez, el comportamiento global de la estructura. Por tanto, esta herramienta numérica conlleva a un mejor análisis de estructuras con materiales compuestos sin ocasionar excesivos costos computacionales, ya que permite el uso de diferentes tipos de no linealidades y utiliza un único mallado para el análisis de la estructura, de los materiales compuestos y de sus componentes.
Agradecimientos
Este trabajo ha sido apoyado por el Ministerio de Ciencia e Innovación de España a través de los proyectos «RECOMP», Ref. BIA2005-06952, «DECOMAR», Ref. MAT2003-08700-C03-02 y «DELCOM», Ref. MAT2008-02232/MAT; por el Ministerio de Fomento de España a través del proyecto «Reparación y Refuerzo de Estructuras de Hormigón Armado con Materiales Compuestos»; por Agencia Española de Cooperación Internacional para el Desarrollo (AECID), Ref. A/012257/07 y Ref. C/016189/08, por el programa Alβan, Programa de Becas de Alto Nivel de la Unión Europea para América Latina, beca n.° E06D101053CO; por la Secretaría de Educación Pública de México, Subsecretaría de Educación superior, Programa para el Mejoramiento del Profesorado PROMEP, beca folio UACHIS-160; por el proyecto VALTEC Ref. 08-2-0022 del CIDEM; por el Centro Internacional para los Métodos Numéricos en Ingeniería (CIMNE), España y por el laboratorio CER-LITEM del Departamento de Resistencia de Materiales de la Universidad Politécnica de Catalunya, Terrassa, España.
Bibliografía
- [1] A. Nanni; North American design guidelines for concrete reinforcement and strengthening using FRP: Principles, aplications and unresolved issues; Construction and Building Materials, 17 (2003), pp. 439–446
- [2] L.C. Hollaway; The evolution of and the way forward for advanced polymer composites in the civil infrastructure; Construction and Building Materials, 17 (2003), pp. 365–378
- [3] S.S. Pendhari, T. Kant, M.Y. Desai; Aplication of polymer composites in civil construction: A general review; Composite Structures, 84 (2007), pp. 114–124
- [4] V.M. Karbhari; Materials considerations in FRP rehabilitation of concrete structures, Journal of Materials in Civil Engineering; ASCE, 13 (2001), pp. 90–97
- [5] R. Perera, A. Recuero, A.D. Diego, C. López; Adherence analysis of fiber reinforced polymer strengthened RC beams; Computers and Structures, 82 (2004), pp. 1865–1873
- [6] Z.J. Yang, J.F. Chen, D. Proverbs; Finite element modelling of concrete cover separation failure in FRP plated RC beams; Construction and Building Materials, 17 (2003), pp. 3–13
- [7] X.Z. Lu, L.P. Ye, J.G. Teng, J.J. Jiang; Meso-scale finite element model for FRP sheets/plates bonded to concrete; Engineering Structures, 27 (2005), pp. 564–575
- [8] H. Niu, Z. Wu; Numerical analysis of debonding mechanisms in FRP–strengthened RC beams; Computer-Aided Civil and Infrastructure Engineering, 20 (2005), pp. 354–368
- [9] H. Niu, Z. Wu; Effects of FRP-concrete interface bond properties on the performance of RC beams strengthened in flexure with externally bonded FRP sheets; Journal of Materials in Civil Engineering. ASCE, 18 (2006), pp. 723–731
- [10] H. Niu, V.M. Karbhari, Z. Wu; Diagonal macro-crack induced debonding mechanisms in FRP rehabilitated concrete; Composites Part B: Engineering, 35 (2006), pp. 627–641
- [11] Z. Wu, J. Yin; Fracturing behaviors of FRP-strengthened concrete structures; Engineering Fracture Mechanics, 70 (2003), pp. 1339–1355
- [12] X.Z. Lu, J.J. Jiang, J.G. Teng, L.P. Ye; Finite element simulation of debonding in FRP-to-concrete bonded joints; Construction and Building Materials, 20 (2006), pp. 412–424
- [13] U.A. Ebead, K.W. Neale; Mechanics of fibre-reinforced polymer-concrete interfaces; Canadian Journal of Civil Engineering, 34 (2007), pp. 367–377
- [14] C.A. Coronado, M.M. López; Damage aproach for the prediction of debonding failure on concrete elements strengthened with FRP; Journal of Composites for Construction ASCE, 11 (2007), pp. 391–400
- [15] T. Ueda, R. Yamaguchi, K. Shoji, Y. Sato; Study on behaviour in tension of reinforced concrete members strengthened by carbon fiber sheet; Journal of Composites for Construction ASCE, 6 (2002), pp. 168–174
- [16] M. Molina, Estudio numérico de la adherencia de los materiales compuestos como refuerzo en estructuras de hormigón armado, Master en Métodos Numéricos para Cálculo y Diseño en Ingeniería, Universidad Politécnica de Cataluña, Barcelona, España, 2009.
- [17] F. Rastellini, Modelación numérica de la no-linealidad constitutiva de laminados compuestos, Ph.D. thesis, Universidad Politécnica de Cataluña, Barcelona, España, 2006.
- [18] X. Martínez, Micro-mechanical simulation of composite materials using the serial/parallel mixing theory, Ph.D. thesis, Universidad Politécnica de Cataluña, Barcelona, España, 2008.
- [19] S. Oller, Simulación Numérica del Comportamiento Mecánico de los Materiales Compuestos, Centro Internacional de Métodos Numéricos en la Ingeniería-CIMNE, Barcelona, España, 2003.
- [20] E. Car, F. Zalamea, S. Oller, J. Miquel, E. Oñate; Numerical simulation of fiber reinforced composites-Two procedures; International Journal of Solids and Structures, 39 (2002), pp. 1967–1986
- [21] E. Car, S. Oller, E. Oñate, Tratamiento Numérico de Materiales Compuestos, Monografía N.° 57, Centro Internacional de Métodos Numéricos en la Ingeniería (CIMNE), Barcelona, España, 2000.
- [22] S. Oller, S. Botello, J. Miquel, E. Oñate; An anisotropic elastoplastic model based on an isotropic formulation; Engineering Computations, 12 (1995), pp. 245–262
- [23] F. Rastellini, S. Oller, O. Salomon, E. Oñate; Composite materials non-linear modelling for long fibre-reinforced laminates: Continuum basis, computational aspects and validations; International Journal of Computers & Structures, 86 (2008), pp. 879–896
- [24] M. Molina, S. Oller, A.H. Barbat, X. Martínez; Análisis numérico de estructuras de hormigón reforzadas con FRP por medio de la teoría de mezclas serie/paralelo; Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 26 (2010), pp. 135–155
- [25] X. Martínez, S. Oller, F. Rastellini, A. Barbat; A numerical procedure simulating RC structures reinforced with FRP using the serial/parallel mixing theory; Computers and Structures, 86 (2008), pp. 1604–1618
- [26] J. Oliver, M. Cervera, S. Oller, J. Lubliner. Isotropic damage models and smeared crack analysis of concrete, en: N. Bicáníc, H. Mang (Eds.), Second International Conference on Computer Aided Analysis and Design of Concrete Structures, Vol 2. Zell Am See, Austria, 1990, pp. 945-958.
- [27] L.M. Kachanov; Time of rupture process under creep conditions. Izvestia Akaademii Nauk; USSR Otd. Tekh Nauk, 8 (1958), pp. 26–31
- [28] X. Martínez, F. Rastellini, S. Oller, F. Flores, E. Oñate; Computationally optimized formulation for the simulation of composite materials and delamination failures; Composites Part B: Engineering, 42 (2011), pp. 134–144
- [29] S. Oller, Fractura mecánica. Un enfoque global, Centro Internacional de Métodos Numéricos en la Ingeniería-CIMNE, Barcelona, España, 2001.
- [30] J. Lubliner, J. Oliver, S. Oller, E. Oñate; A plastic-damage model for concrete; International Journal of Solids and Structures, 25 (1989), pp. 299–326
- [31] M. Nehdi, A.E. Damatty, R. Rahimi; Investigation on lap-joint behaviour of GFRP plates bonded to silica fume and rice husk ash concrete; International Journal of Adhesion & Adhesives, 23 (2003), pp. 323–333
- [32] J.F. Chen, W. Pan; Three dimensional stress distribution in FRP-to-concrete bond test specimens; Construction and Building Materials, 20 (2006), pp. 46–58
- [33] CIMNE, PLCD Manual: Código termomecánico nolineal de elementos finitos dirigido a estudiantes de Ph.D., Universidad Politécnica de Cataluña, Barcelona, España (1991-2011).
Document information
Published on 01/06/12
Accepted on 27/05/11
Submitted on 03/03/11
Volume 28, Issue 2, 2012
DOI: 10.1016/j.rimni.2011.11.007
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?
![Geometría de la probeta del ensayo de doble corte [16].](/wd/images/5/54/Draft_Content_643215200-1-s2.0-S0213131511000411-gr2.jpg)








![Configuración de los materiales compuestos [16].](/wd/images/d/d3/Draft_Content_643215200-1-s2.0-S0213131511000411-gr13.jpg)

![Evolución de las deformaciones ɛxx en el compuesto [16].](/wd/images/8/89/Draft_Content_643215200-1-s2.0-S0213131511000411-gr19.jpg)
![Distribución de las deformaciones en el compuesto ɛxx [16].](/wd/images/c/c1/Draft_Content_643215200-1-s2.0-S0213131511000411-gr20.jpg)