LBM simulation of natural convection in an inclined triangular cavity filled with water

Abstract

This paper presents a numerical study of natural convection in a triangular cavity filled with water. The horizontal wall is hot, the vertical wall is cold and the inclined wall is insulated. Lattice Boltzmann method (LBM) is applied to solve the coupled equations of flow and temperature fields. This study has been carried out for the pertinent parameters in the following ranges: Rayleigh number varied from Ra = 10³ to 10⁶ and the inclination angle between ${\textstyle \Phi =0{\mbox{°}}}$ and ${\textstyle 315{\mbox{°}}}$. The effects of Rayleigh numbers and inclination angle on the streamlines, isotherms, Nusselt number are investigated. Results show that the heat transfer rate increases with the increase of Rayleigh number. In addition it is observed that the lower heat transfer rate is obtained for ${\textstyle \Phi =135{\mbox{°}}}$; however, the highest heat transfer is achieved at ${\textstyle \Phi =0{\mbox{°}}}$. The inclination angle greatly influences the heat transfer rate depending on the Rayleigh number.

Keywords

Inclination angle; Lattice Boltzmann method; Natural convection; Water

Nomenclature

c- lattice speed

c_s- speed of sound

c_i- discrete particle speeds

c_p- specific heat at constant pressure

F- external forces

f- density distribution functions

f^eq- equilibrium density distribution functions

g- internal energy distribution functions

g^eq- equilibrium internal energy distribution functions

${\textstyle {\overset {\rightarrow }{\quad {\mbox{g}}}}_{r}}$- gravity vector

Ma- Mach number

Nu- local Nusselt number

Pr- Prandtl number

Ra- Rayleigh number

T- temperature

${\textstyle u(u{\mbox{,}}v)}$- velocities

${\textstyle x(x{\mbox{,}}y)}$- lattice coordinates

Greek symbols

Δx- lattice spacing

Δt- time increment

τ_α- relaxation time for temperature

τ_ν- relaxation time for flow

${\textstyle \nu }$- kinematic viscosity

α- thermal diffusivity

${\textstyle \rho }$- fluid density

ψ- non-dimensional stream function

${\textstyle \Phi }$- inclination angle

Subscripts

c- cold

h- hot

m- mean

1. Introduction

Laminar natural convection on cavities has attracted many researchers, due to its practical engineering applications, such as heat removal from electrical and electronic equipments, solar collectors and nuclear reactor design [1], [2], [3] and [4]. Koca et al. [5] analyzed natural convection in a triangular enclosure for different Prandtl numbers. The governing equations are formulated based on a stream function–vorticity approach and solved with the finite-difference method. It is observed that both flow and temperature distributions are affected with the variation of Prandtl number. Omri et al. [6] studied numerically natural convection in a triangular cavity using the Control Volume Finite Element Method (CVFEM). The found results show that the flow structure is sensitive to the cover tilt angle. Ching et al. [7] investigated numerically mixed convection in a right triangular enclosure. The found results show that the increase of the buoyancy ratio enhances the heat transfer rate. Also, the direction of the sliding wall motion can be a good control parameter for the flow and temperature distributions. Oztop et al. [8] studied experimentally and numerically the effect of Rayleigh number and the inclination angle on natural convection in a triangular cavity filled with air. The bottom wall of the cavity is hot, the inclined wall is cold and the vertical wall is adiabatic. Results show that the heat transfer increases with the increase of Rayleigh number. Ghasemi and Aminossadati [9] investigated numerically mixed convection in a lid-driven triangular enclosure filled with a water-Al₂O₃ nanofluid. A comparison study between two different scenarios of upward and downward left sliding walls is presented. The effects of parameters such as Richardson number, solid volume fraction and direction of the sliding wall motion on the heat transfer rate are examined. The found results show that the addition of Al₂O₃ nanoparticles enhances the heat transfer rate for all values of Richardson number and for each direction of the sliding wall motion. Mejri and Mahmoudi [10] studied natural convection in an open cavity with a sinusoidal thermal boundary condition. The cavity is filled with a water–Al₂O₃ nanofluid and subjected to a magnetic field. Lattice Boltzmann method (LBM) is applied to solve the coupled equations of flow and temperature fields. The found results show that the heat transfer rate decreases with the increase of Hartmann number and increases with the rise of Rayleigh number. Also, for all phase deviations the addition of nanoparticles increases heat transfer rate. Mejri et al. [11], [12], [13] and [14] studied the laminar natural convection and entropy generation in a square enclosure, with sinusoidal temperature distribution, filled with a water-Al₂O₃ nanofluid and subjected to a magnetic field. Mahmoudi et al. [15], [16] and [17] studied the effect of magnetic field and its direction on water-Al₂O₃ nanofluid filled cavity with a linear boundary condition, and the results show that the magnetic field direction controls the flow and heat transfer rates in the cavity. Mahmoudi et al. [18] studied MHD natural convection in a square cavity filled with nanofluid in the presence of uniform heat generation/absorption. The results show that adding nanoparticle reduces the entropy generation. Mahmoudi et al. [19] applied the double-population Lattice Boltzmann Method to solve natural convection problem in an inclined triangular cavity filled with air. The found results show that the inclination angle can be used as a relevant parameter to control heat transfer. Mahmoudi et al. [20] studied natural convection cooling of water-Al₂O₃ nanofluid by two heat sinks vertically attached to the horizontal walls of a cavity subjected to a magnetic field. Results show that the heat sinks positions greatly influence the heat transfer rate depending on the Hartmann number, Rayleigh number and nanoparticle solid volume fraction.

The aim of the present study was to investigate numerically natural convection in a triangular cavity filled with water. Furthermore, Lattice Boltzmann method (LBM) is applied to solve the coupled equations of flow and temperature fields. The results of LBM are validated with previous published results and the effects of the main parameters (Rayleigh number and inclination angle) on flow and thermal fields are researched.

2. Mathematical formulation

2.1. Problem statement

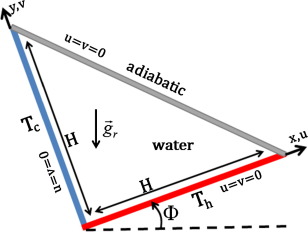
A triangular inclined cavity is considered for the present study with the physical dimensions as shown in Fig. 1. The temperatures T_h and T_c < T_h are uniformly imposed respectively along the horizontal and vertical walls (the horizontal wall is the source of heat). The inclined wall is assumed to be adiabatic. The cavity is filled with water. The fluid is Newtonian and incompressible. The flow is considered to be study two dimensional and laminar and the radiation effects are negligible. The density variation in the fluid is approximated by the standard Boussinesq model.

Figure 1. Geometry of the present study.

2.2. Lattice Boltzmann method

For the incompressible non isothermal problems, Lattice Boltzmann Method (LBM) utilizes two distribution functions, f and g, for the flow and temperature fields respectively.

For the flow field:

$f_{i}(x+c_{i}\Delta t{\mbox{,}}t+\Delta t)=f_{i}(x{\mbox{,}}t)-$${\frac {1}{{\tau }_{\nu }}}(f_{i}(x{\mbox{,}}t)-f_{i}^{\mbox{eq}}(x{\mbox{,}}t))+$$\Delta {tF}_{i}$

(1)

For the temperature field:

$g_{i}(x+c_{i}\Delta t{\mbox{,}}t+\Delta t)=g_{i}(x{\mbox{,}}t)-$${\frac {1}{{\tau }_{\alpha }}}(g_{i}(x{\mbox{,}}t)-g_{i}^{\mbox{eq}}(x{\mbox{,}}t))$

(2)

where the discrete particle velocity vectors defined by c_i, ${\textstyle \Delta t}$ denote lattice time step which is set to unity. ${\textstyle {\tau }_{\nu }}$ and ${\textstyle {\tau }_{\alpha }}$ are the relaxation time for the flow and temperature fields, respectively. ${\textstyle f_{i}^{\mbox{eq}}}$ and ${\textstyle {\mbox{g}}_{i}^{\mbox{eq}}}$ are the local equilibrium distribution functions that have an appropriately prescribed functional dependence on the local hydrodynamic properties which are calculated with Eqs. (1) and (2) for flow and temperature fields respectively.

$f_{i}^{\mbox{eq}}={\omega }_{i}\rho \left[1+{\frac {3(c_{i}.u)}{c^{2}}}+\right.$$\left.{\frac {9{\left(c_{i}.u\right)}^{2}}{2c^{4}}}-{\frac {3u^{2}}{2c^{2}}}\right]$

(3)

$g_{i}^{\mbox{eq}}={\omega }_{i}^{'}T\left[1+3{\frac {c_{i}.u}{c^{2}}}\right]$

(4)

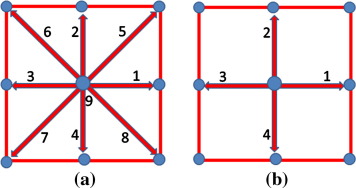
u and ${\textstyle \rho }$ are the macroscopic velocity and density, respectively. c   is the lattice speed which is equal to ${\textstyle \Delta x/\Delta t}$ where ${\textstyle \Delta x}$ is the lattice space similar to the lattice time step ${\textstyle \Delta t}$ which is equal to unity, ${\textstyle {\omega }_{i}}$ is the weighting factor for flow, and ${\textstyle {\omega }_{i}^{'}}$ is the weighting factor for temperature. D2Q9 model for flow and D2Q4 model for temperature are used in this work so that the weighting factors and the discrete particle velocity vectors are different for these two models and they are calculated with Eqs (5), (6) and (7) as follows:

For D2Q9:

${\omega }_{0}={\frac {4}{9}}{\mbox{,}}{\omega }_{i}={\frac {1}{9}}\quad {\mbox{for}}\quad i=$$1{\mbox{,}}2{\mbox{,}}3{\mbox{,}}4\quad {\mbox{and}}\quad {\omega }_{i}=$${\frac {1}{36}}\quad {\mbox{for}}\quad i=5{\mbox{,}}6{\mbox{,}}7{\mbox{,}}8$

(5)

The discrete velocities for the D2Q9 (Fig. 2a) are defined as follows:

$c_{i}={\begin{array}{cc}0&i=0\\(cos[(i-1)\pi /2]{\mbox{,}}sin[(i-1)\pi /2])c&i=1{\mbox{,}}2{\mbox{,}}3{\mbox{,}}4\\{\sqrt {2}}(cos[(i-5)\pi /2+\pi /4]{\mbox{,}}sin[(i-5)\pi /2+\pi /4])c&i=5{\mbox{,}}6{\mbox{,}}7{\mbox{,}}8\end{array}}$

(6)

For D2Q4:

Figure 2. Discrete velocity vectors for (a) D2Q9 and (b) D2Q4.

The temperature weighting factor for each direction is equal to ${\textstyle {\omega }_{i}^{'}=1/4}$.

The discrete velocities for the D2Q4 (Fig. 2b) are defined as follows:

$c_{i}=(cos[(i-1)\pi /2]{\mbox{,}}sin[(i-1)\pi /2])c\quad i=$$1{\mbox{,}}2{\mbox{,}}3{\mbox{,}}4$

(7)

The kinematic viscosity ν   and the thermal diffusivity ${\textstyle \alpha }$ are then related to the relaxation time by Eq. (8):

$\nu =\left[{\tau }_{\nu }-{\frac {1}{2}}\right]c_{s}^{2}\Delta t\quad \alpha =$$\left[{\tau }_{\alpha }-{\frac {1}{2}}\right]c_{s}^{2}\Delta t$

(8)

where c_s   is the lattice speed of sound which is equal to ${\textstyle c_{s}=c/{\sqrt {3}}}$. In the simulation of natural convection, the external force term F corresponding to the buoyancy force appearing in Eq. (1) is given by Eq. (9):

$F_{i}={\frac {{\omega }_{i}}{c_{s}^{2}}}F\cdot c_{i}$

(9)

$F=\rho \beta g_{r}(T-T_{m})$

(10)

where β   is the thermal expansion coefficient and ${\textstyle T_{m}}$ is the mean temperature. The macroscopic quantities ρ, u and T can be calculated by the mentioned variables, with Eqs. (11), (12) and (13):

$\rho =\sum _{i}f_{i}$

(11)

$\rho u=\sum _{i}f_{i}c_{i}$

(12)

$T=\sum _{i}{\mbox{g}}_{i}$

(13)

2.3. Boundary conditions

The implementation of boundary conditions is very important for the simulation. The distribution functions out of the domain are known from the streaming process. The unknown distribution functions are those toward the domain.

2.3.1. Flow

Bounce-back boundary conditions were applied on all solid boundaries, which mean that incoming boundary populations are equal to out-going populations after the collision.

2.3.2. Temperature

The bounce back boundary condition is used on the adiabatic wall. Temperature at the isothermal wall is known. Since we are using D2Q4, the unknown internal energy distribution functions are evaluated respectively as follows:

${\mbox{Horizontal wall:}}\quad g_{2}=T_{h}-g_{1}-g_{3}-g_{4}$

(14)

${\mbox{Vertical wall:}}\quad g_{1}=T_{c}-g_{2}-g_{3}-g_{4}$

(15)

2.4. Non-dimensional parameters

By fixing Rayleigh number, Prandtl number and Mach number, the viscosity and thermal diffusivity are calculated from the definition of these non dimensional parameters.

$\nu =N\cdot Ma\cdot c_{s}{\sqrt {\frac {Pr}{Ra}}}$

(16)

where N is number of lattices in y  -direction. Rayleigh and Prandtl numbers are defined as ${\textstyle Ra={\frac {g\beta H^{3}(T_{h}-T_{c})}{\nu \alpha }}}$ and ${\textstyle Pr={\frac {\nu }{\alpha }}{\mbox{,}}}$ respectively. Mach number should be less than ${\textstyle Ma=0.3}$ to insure an incompressible flow. Therefore, in the present study, Mach number was fixed at ${\textstyle Ma=0.1}$. Nusselt number is one of the most important dimensionless parameters in the description of the convective heat transport. The local Nusselt number Nux and the average value Nu at the hot wall are calculated as follows:

${\mbox{Nux}}=-{\frac {H}{T_{h}-T_{c}}}{\frac {\partial T}{\partial y}}_{y=0}$

(17)

${\mbox{Nu}}={\frac {1}{H}}{\int }_{0}^{H}{\mbox{Nuxdx}}$

(18)

3. Validation of the numerical code

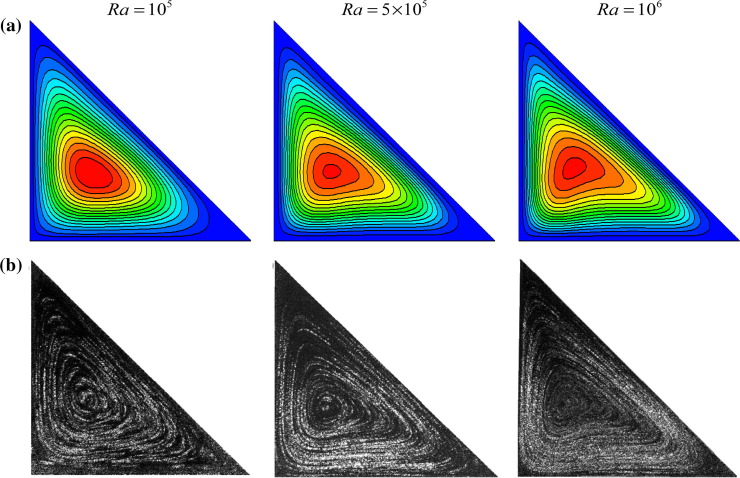
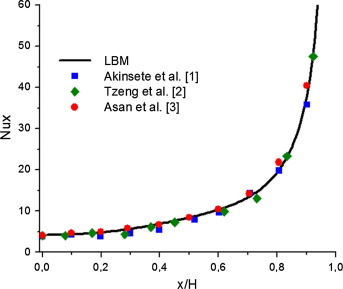
Lattice Boltzmann Method scheme was utilized to obtain the numerical simulations in an inclined triangular cavity filled with water. In order to check on the accuracy of the numerical technique employed for the solution of the considered problem, the present numerical code was validated with the published study of Gurkan and Orhan [4] for the same cavity filled with water for ${\textstyle \Phi =0{\mbox{°}}{\mbox{.}}}$ The results are presented in Fig. 3; the streamlines have a good agreement between both compared results. Another validation with the results by Akinsete et al. [1], Tzeng et al. [1] and Asan al. [2] for natural convection in a triangular cavity filled with air for Ra = 2772 is presented in Fig. 4, and excellent agreement is also found.

Figure 3. Comparison of the streamlines between (a) the present result and (b) experimental results by Gurkan et al. [4].

Figure 4. Comparison of the local Nusselt number between the present results and published results.

4. Results and discussion

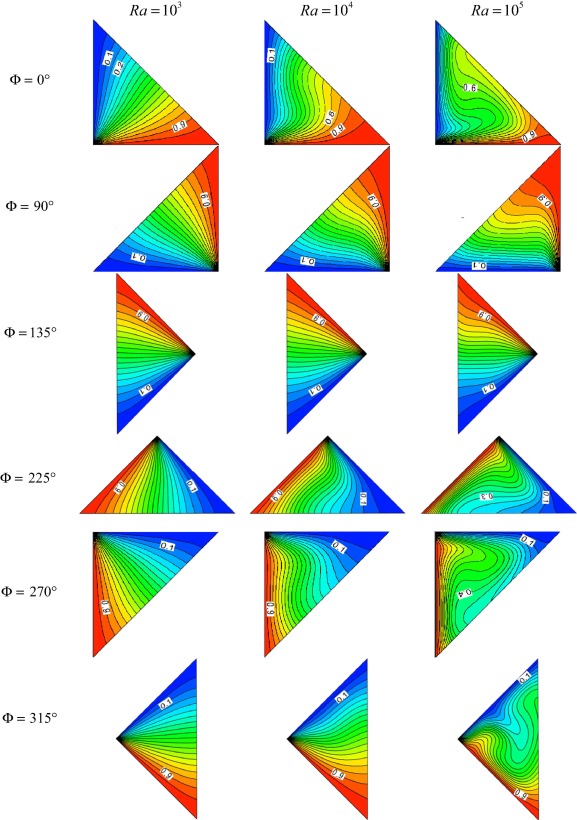
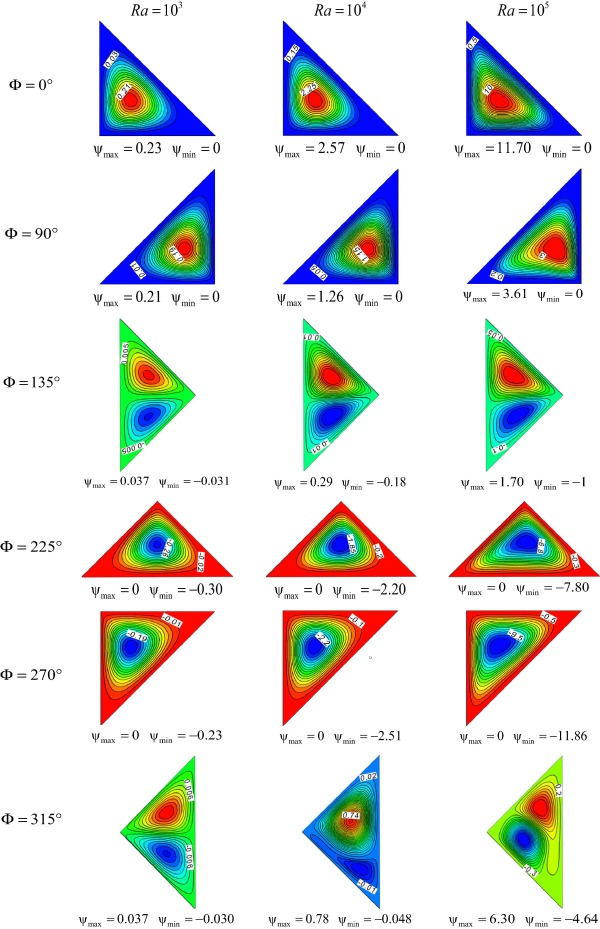
Figure 5 and Figure 6 illustrate the effect of the inclination angle and the Rayleigh number, on the isotherms and the streamlines. For low Rayleigh number ${\textstyle Ra={10}^{3}}$, the conduction regime is dominant, and weak cell circulation in the cavity is found. For all inclination angles, the rise of Rayleigh number has the tendency to increase the fluid flow intensity in the enclosure and establish the convective regime. For ${\textstyle \Phi =0{\mbox{°}}}$, a big cell in clockwise rotation is formed inside the cavity. The increase of Rayleigh number increases the intensity of these cells and decreases the boundary layer thickness near the hot wall indicating the presence of an intense temperature gradient and a strong heat transfer rate in this region. For ${\textstyle \Phi =90{\mbox{°}}}$, a big cell in clockwise rotation is formed inside the cavity. The intensity of these cells does not increase significantly with the increase of Rayleigh number, and on the other hand the isotherms are parallel lines; the heat transfer is mainly by conduction even for high Rayleigh numbers. The lower horizontal wall is cold; the fluid is stratified at the bottom of the cavity. For ${\textstyle \Phi =135{\mbox{°}}}$, two asymmetrical weak cells of opposite flow direction are formed inside the cavity. The large top cell flows in anticlockwise direction near the hot wall whereas the lower cell flows in clockwise direction near the cold wall. The isotherms are parallel lines, the flow intensity is weak even for large Rayleigh numbers, the heat transfer is mainly by conduction. For ${\textstyle \Phi =225{\mbox{°}}}$ and ${\textstyle 270{\mbox{°}}}$, and a big cell in anticlockwise rotation is formed inside the cavity. The intensity of these cells becomes significantly stronger with the increase of Rayleigh number; the convection mode is dominant. On the other hand, for high Rayleigh numbers, the isothermal lines are closer near the hot wall; therefore, the temperature gradient and the heat transfer are higher in this region. For ${\textstyle \Phi =315{\mbox{°}}}$, two asymmetrical cells of opposite flow direction are formed inside the cavity. The top cell flows in clockwise direction near the cold wall whereas the lower cell flows in anticlockwise direction near the hot wall. For high Rayleigh numbers, the flow intensity becomes significantly stronger. Also, the isotherms are more closed near the hot and cold walls indicating that the heat transfer is dominated by convection inside the cavity.

Figure 5. Isotherms for different Rayleigh numbers and inclination angles.

Figure 6. Streamlines for different Rayleigh numbers and inclination angles.

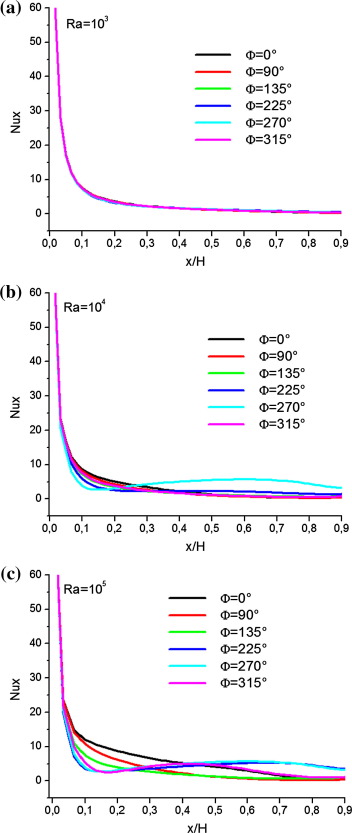
Fig. 7a–c shows the local Nusselt number along the hot wall for different inclination angles and for ${\textstyle Ra={10}^{3}{\mbox{,}}}$${\textstyle Ra={10}^{4}}$ and ${\textstyle Ra={10}^{5}{\mbox{.}}}$ For low Rayleigh number ${\textstyle Ra={10}^{3}-{10}^{4}{\mbox{,}}}$ the inclination angle effect on the local Nusselt number is practically non-existent. The inclination angle effect on the heat transfer rate increases with the increase of Rayleigh number. The heat transfer occurs mainly at left side of the hot wall (near the cold wall) and then it decreases highly along the wall until reaching a zero value, indicating that the fluid temperature in cavity is the same as the wall. At high Rayleigh number (${\textstyle Ra={10}^{5}}$), for ${\textstyle \Phi =0{\mbox{°}}}$ respectively ${\textstyle 90{\mbox{°}}}$ and ${\textstyle 135{\mbox{°}}}$ the local Nusselt number highly decreases for x/H < 0.1 and then it slightly decreases along the wall until reaching a zero value at x/H = 0.8 respectively x/H = 0.4. For ${\textstyle \Phi =225{\mbox{°}}}$ and ${\textstyle 270{\mbox{°}}}$ the local Nusselt number highly decreases until reaching a minimum value at x/H = 0.15 and then it slightly increases along the wall. For ${\textstyle \Phi =315{\mbox{°}}}$ the local Nusselt number has the same behavior as ${\textstyle \Phi =225{\mbox{°}}}$ and ${\textstyle 270{\mbox{°}}}$ for x/H < 0.45 respectively as ${\textstyle \Phi =0{\mbox{°}}}$ for x/H > 0.45. Fig. 7 shows that the local Nusselt number is affected by the inclination angle according to Rayleigh number.

Figure 7. Variation of the local Nusselt number for (a) Ra = 103 (b) Ra = 104 and (c) Ra = 105.

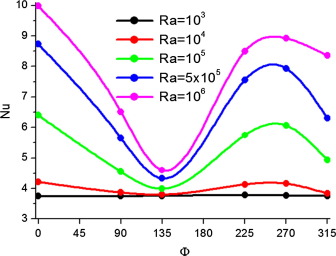
Fig. 8 shows the effect of the inclination angle and the Rayleigh number on the average Nusselt number. Results show that for all inclination angles, the increase of Rayleigh number increases the heat transfer rate. The lower effect of Rayleigh number is obtained for ${\textstyle \Phi =135{\mbox{°}}}$, whereas the intense effect of Rayleigh number is obtained for ${\textstyle \Phi =0{\mbox{°}}}$. For low Rayleigh number ${\textstyle Ra={10}^{3}}$, the average Nusselt number is constant; the inclination angle effect is non-existent, and the heat transfer occurs mainly by conduction. Also, results show that the inclination angle effect on heat transfer rate increases with the increase of Rayleigh number. For all Rayleigh number, the increase of the inclination angle decreases heat transfer rate for ${\textstyle 0{\mbox{°}}\leqslant \Phi \leqslant 135{\mbox{°}}}$ and increases heat transfer rate for ${\textstyle 135{\mbox{°}}\leqslant \Phi \leqslant 270{\mbox{°}}}$. The lower heat transfer rate is obtained for ${\textstyle \Phi =135{\mbox{°}}}$; however, the highest heat transfer is achieved at ${\textstyle \Phi =0{\mbox{°}}}$. The inclination angle of the cavity is a factor to control the heat transfer rate.

Figure 8. Variation of the average Nusselt number with the inclination angle and Rayleigh number.

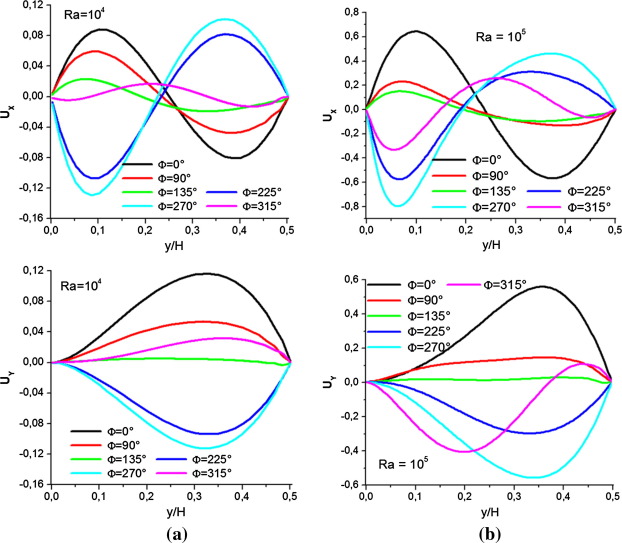
Fig. 9a and b shows the horizontal and the vertical velocities profiles in the middle of the cavity (along the y-axis) at x/H = 0.5 for different inclination angles and both Rayleigh numbers ${\textstyle Ra={10}^{4}-{10}^{5}{\mbox{.}}}$ Results show that for ${\textstyle \Phi \not =135{\mbox{°}}}$ the maximum magnitude of horizontal and vertical velocities increases significantly with the rise of Rayleigh number, more the fluid velocity increases more the convection is advantaged. For ${\textstyle \Phi =135{\mbox{°}}}$, fluid velocity is very weak for both Rayleigh numbers ${\textstyle Ra={10}^{4}-{10}^{5}}$; the conduction mode is dominant. Moreover, results show that the horizontal and the vertical velocities profiles depend strongly on the inclination angle. The inclination angle is a factor to control the flow intensity inside the cavity.

Figure 9. Vertical and horizontal velocities distributions in the middle of the cavity at x/H = 0.5 for (a) Ra = 104 and (b) Ra = 105.

Fig. 10a–c shows the dimensionless temperature profiles along the y-axis at x/H = 0.5 for different inclination angles and Rayleigh numbers. For low Rayleigh number ${\textstyle Ra={10}^{3}}$, the conduction mode is dominant; the temperature distribution inside the cavity is almost the same for all inclination angles. The inclination angle effect is practically non-existent. The inclination angle effect on the temperature distribution inside the cavity increases with the increase of Rayleigh number. For ${\textstyle \Phi =90{\mbox{°}}}$ the increases of Rayleigh number stabilize the temperature in the middle of the cavity. For ${\textstyle \Phi =135{\mbox{°}}{\mbox{,}}}$ the temperature profile varies linearly along the y  -axis; the heat transfer is dominated by conduction inside the cavity. For ${\textstyle \Phi =0{\mbox{°}}}$ and ${\textstyle 315{\mbox{°}}}$, the low temperature variation along the y  -axis at ${\textstyle Ra={10}^{4}}$ indicates the existence of a homogeneous temperature in the middle of the cavity. The increases of Rayleigh number decrease the temperature inside the cavity. The temperature profile is the same for ${\textstyle \Phi =225{\mbox{°}}}$ and ${\textstyle 270{\mbox{°}}}$; the temperature decreases along the y-axis, and the lowest temperature is obtained near the adiabatic wall.

Figure 10. Dimensionless temperature in the middle of the cavity at x/H = 0.5 for (a) Ra = 103 (b) Ra = 104 and (c) Ra = 105.

5. Conclusions

In this paper the effects of the inclination angle and Rayleigh number have been analyzed with Lattice Boltzmann Method. This study has been carried out for the pertinent parameters in the following ranges: Rayleigh number Ra = 10³–10⁵ and the inclination angle between ${\textstyle \Phi =0{\mbox{°}}}$ and ${\textstyle 315{\mbox{°}}}$. This investigation was performed for various mentioned parameters and some conclusions are summarized as follows:

• A good agreement valid with previous published results demonstrates that Lattice Boltzmann Method is an appropriate method for different applicable problems.
• The heat transfer rate increases with the increase of Rayleigh number.
• For low Rayleigh number, the inclination angle effect is practically non-existent.
• The inclination angle effect on heat transfer rate increases with the increase of Rayleigh number.
• The lower heat transfer rate is obtained for ${\textstyle \Phi =135{\mbox{°}}}$ and the highest heat transfer is achieved at ${\textstyle \Phi =0{\mbox{°}}}$.

References

1. [1] V. Akinsete, T.A. Coleman; Heat transfer by steady laminar free convection in triangular enclosures; Int. J. Heat Mass Transf., 25 (1982), pp. 991–998
2. [2] S.C. Tzeng, J.H. Liou, R.Y. Jou; Numerical simulation-aided parametric analysis of natural convection in a roof of triangular enclosures; Heat Transf. Eng., 26 (2005), pp. 69–79
3. [3] H. Asan, L. Namli; Numerical simulation of buoyant flow in a roof of triangular cross section under winter day boundary conditions; Energy Build., 33 (2001), pp. 753–757
4. [4] Y. Gurkan, A. Orhan; Laminar natural convection in right-angled triangular enclosures heated and cooled on adjacent walls; Int. J. Heat Mass Transf., 60 (2013), pp. 365–374
5. [5] A. Koca, H.F. Oztop, Y. Varol; The effects of Prandtl number on natural convection in triangular enclosures with localized heating from below; Int. Commun. Heat Mass Transf., 34 (2007), pp. 511–519
6. [6] A. Omri; Numerical investigation on optimization of a solar distiller dimensions; Desalination, 206 (2007), pp. 373–379
7. [7] Y.C. Ching, H.F. Oztop, M.M. Rahman, M.R. Islam, A. Ahsan; Finite element simulation of mixed convection heat and mass transfer in a right triangular enclosure; Int. Commun. Heat Mass Transf., 39 (2012), pp. 689–696
8. [8] H.F. Oztop, Y. Varol, A. Koca, M. Firat; Experimental and numerical analysis of buoyancy-induced flow in inclined triangular enclosures; Int. Commun. Heat Mass Transf., 39 (2012), pp. 1237–1244
9. [9] B. Ghasemi, S.M. Aminossadati; Mixed convection in a lid-driven triangular enclosure filled with nanofluids; Int. Commun. Heat Mass Transf., 37 (2010), pp. 1142–1148
10. [10] I. Mejri, A. Mahmoudi; MHD natural convection in a nanofluid-filled open enclosure with a sinusoidal boundary condition; Chem. Eng. Res. Des., 98 (2015), pp. 1–16
11. [11] I. Mejri, A. Mahmoudi, M.A. Abbassi, A. Omri; Magnetic field effect on entropy generation in a nanofluid-filled enclosure with sinusoidal heating on both side walls; Powder Technol., 266 (2014), pp. 340–353
12. [12] I. Mejri, A. Mahmoudi, M.A. Abbassi, A. Omri; MHD natural convection in a nanofluid-filled enclosure with non-uniform heating on both side walls; Fluid Dyn. Mater. Process., 10 (2014), pp. 83–114
13. [13] I. Mejri, A. Mahmoudi, M.A. Abbassi, A. Omri; Magnetic field effect on natural convection in a nanofluid filled enclosure with non-uniform heating on both side walls; Int. J. Heat Technol., 32 (2014), pp. 127–133
14. [14] I. Mejri, A. Mahmoudi, M.A. Abbassi, A. Omri; Lattice Boltzmann simulation of MHD natural convection in a nanofluidfilled enclosure with non-uniform heating on both side walls; IEEE Xplore, Composite Materials & Renewable Energy Applications (ICCMREA), 2014 International Conference (2014) http://dx.doi.org/10.1109/ICCMREA.2014.6843797
15. [15] A. Mahmoudi, I. Mejri, M.A. Abbassi, A. Omri; Lattice Boltzmann simulation of MHD natural convection in a nanofluid-filled cavity with linear temperature distribution; Powder Technol., 256 (2014), pp. 257–271
16. [16] A. Mahmoudi, I. Mejri, M.A. Abbassi, A. Omri; Lattice Boltzmann simulation of magnetic field direction effect on natural convection of nanofluid-filled cavity; Int. J. Heat Technol., 32 (2014), pp. 9–14
17. [17] A. Mahmoudi, I. Mejri, M.A. Abbassi, A. Omri; Lattice Boltzmann simulation of MHD natural convection in a nanofluid-filled cavity with linear temperature distribution; IEEE Xplore, Composite Materials & Renewable Energy Applications (ICCMREA), 2014 International Conference (2014) http://dx.doi.org/10.1109/ICCMREA.2014.6843796
18. [18] A. Mahmoudi, I. Mejri, M.A. Abbassi, A. Omri; Analysis of the entropy generation in a nanofluid-filled cavity in the presence of magnetic field and uniform heat generation/absorption; J. Mol. Liq., 198 (2014), pp. 63–77
19. [19] A. Mahmoudi, I. Mejri, M.A. Abbassi, A. Omri; Numerical study of natural convection in an inclined triangular cavity for different thermal boundary conditions: application of the lattice Boltzmann method; Fluid Dyn. Mater. Process., 9 (2013), pp. 353–388
20. [20] A. Mahmoudi, I. Mejri, A. Omri; Study of natural convection cooling of a nanofluid subjected to a magnetic field; Phys. A, 451 (2016), pp. 333–348