Abstract
The shapes of trees are complex and fractal-like, and they have a set of physical, mechanical and biological functions. The relation between them always draws attention of human beings throughout history and, focusing on the relation between shape and structural strength, architects have designed a number of treelike structures, referred as dendriforms. The replication and adoption of the treelike patterns for constructing architectural structures have been varied in different time periods based on the existing and advanced knowledge and available technologies. This paper, by briefly discussing the biological functions and the mechanical properties of trees with regard to their shapes, overviews and investigates the chronological evolution and advancements of dendriform and arboreal structures in architecture referring to some important historical as well as contemporary examples.
Keywords
Architecture ; Tree ; Dendriforms ; Fractal geometry ; Branching structures ; Technology
1. Introduction
The world of natural phenomena draws our attention as a source and inspiration. Although learning from nature is not a new concept, but with the development of technological advancement, it is a re-emerging approach within a wide range of disciplines. The concept of Biomimicry, considered as the science and philosophy of learning from nature (Benyusis, 2002 ), is a source of architectural design inspiration with different approaches undertaken by architects and engineers that refer nature. Often, nature as inspiration is combined with mathematics in order to move beyond the superficial inspiration and realize structurally rational designs. Mathematics offer rules which guide architects and engineers to understand the complexity of natural shapes. The irregular non-Euclidean geometry of natural trees have been now possible to explain through mathematics by the concept of complex, non-linear and fractal geometries (Casti, 1989 ). ‘Fractal׳, coined by Benoit Mandelbrot in the 1970s, can theoretically define the geometry of many natural objects (Mandelbrot, 1982 ). According to Mandelbrot (1982)
‘Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line ’.
There is an age-old connection between trees and architecture. From the prehistoric age to the contemporary periods, trees and plants had been mainly used for the decorative purpose in architecture. In the Classical and Roman periods (500 BC to 400 AD), vegetal and floral shapes, that were designed with small details, focusing on the esthetic proportions of design for enriching the architectural decorations, became the prominent features in architecture. Special emphasizes were given to the design perfections even for the tiniest details, and only few selected geniuses had that ability. Architects fascination towards the tree shape, however, has not been limited to decorative purposes. Since far past, architects and constructors attempted to mimic one of the most relevant aspects of treelike shapes, i.e. their structural and mechanical features, by frequently applying and developing specific mathematical concepts.
Dendriforms were constructed during medieval age in the framework of arches and vaults masonry construction, which was an advanced and fundamental technique available at that time. In the 19th century, during the period of Art Nouveau, the fascination towards vegetal and floral forms had reached to its apex, especially when architects developed the skills of using cast iron in construction, allowed designers to execute a wide variety of vegetal features, possessing some structural characters, too. In the same century, the development of ‘graphic statics’ as a theoretical approach, helping to understand the association between structural forms and equilibrium of forces, allowed 19th century architects to build several unique style dendriform structures. During the modern period of early and mid-20th century, architects abstracted the form of tree׳s complex configuration as a simple Euclidean and hyperbolic geometries, and built dendriform structures like a mushroom or umbrella shape by using a newly developed reinforced concrete technology and a cantilever technique.
Nowadays, the imitation of the complex and almost inexpressible appearances of vegetal shapes has become possible, in new effortless ways, within a short time, by using digitally advanced computational processes and simple mathematical algorithms. The mathematical revolution of the fractal theory and the development of computer technology made architects and engineers able to connect architecture and trees fractal-like complex appearance in much more structurally rational and optimal ways. Rapid prototyping tools and 3D printers have made possible to actualize the intricate digital designs to physical forms easily and quickly.
This paper starts the discussion by exploring the underlying geometric characteristics of tree shapes by discussing the notion of fractal geometry that possess a fundamental property of self-similarity, and then studying their biological, structural and mechanical functions with reference to their fractal-like configurations. Afterwards, it discusses and overviews some important dendriform examples which are divided into two parts. The first part deals with the historical examples of treelike structures starting from the prehistoric age to the 20th century modern period until the 1970s; and the second part deals with the examples of dendriforms of contemporary period starting from the 1980s to the recent times. In the second part, in the frame of contemporary examples, this paper includes some relevant examples of dendriforms that have been proposed and experimented in academia as a part of research and exploration on treelike structures.
2. Fractal geometry, tree׳s self-similarity and its efficiencies
2.1. Fractal geometry and nature׳s forms
Fractal geometry, a branch of mathematics developed in the 1970s studies abstract configurations characterized by self-similarity patterns and recursive growth (Mandelbrot, 1982 ). Although, from the mathematical point of view, fractal objects are sets that have fractional dimension so that they are intermediate objects between one and two dimensional shapes or two and three dimensional forms (Falconer, 2003 ), but in the general sense fractal objects show the properties of being exactly or nearly the same at every progressive scale. However, in mathematical definition, no natural object is purely a fractal, instead it can be called as an ‘approximate fractal’ or ‘statistical fractal’ that display ‘self-similarity’ and ‘self-affinity’ over extended but finite scale of ranges (Bovill, 1996 ). In this paper ‘fractal’ term is frequently used to refer natural fractal, means ‘approximate fractal’ or ‘fractal-like’.
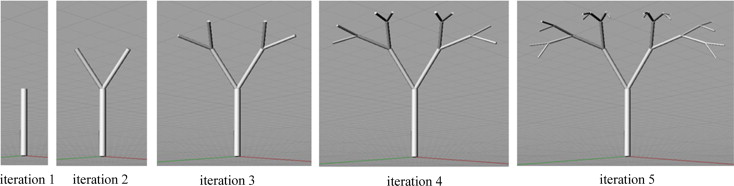
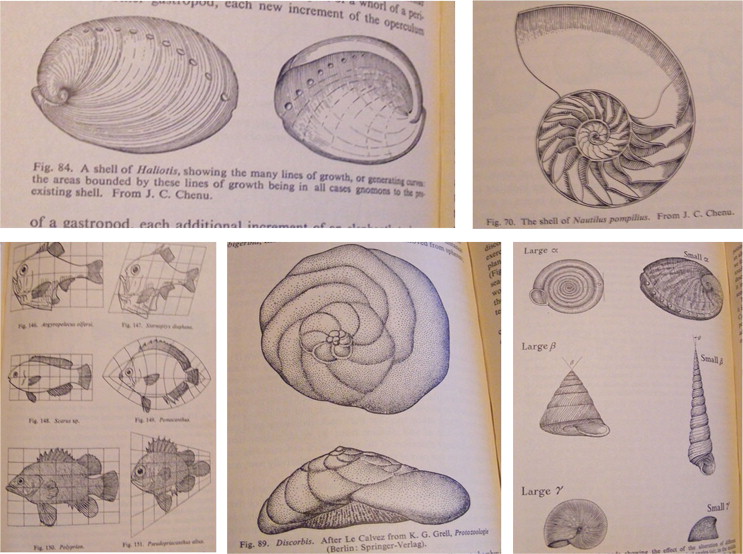
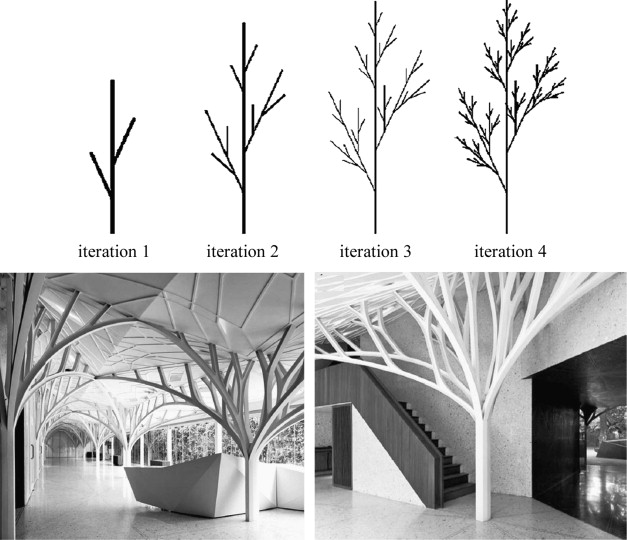
Mathematical property for generating fractals is known as iteration, recursion, and subdivisions through the automated process of Iterated Function System (IFS) (Figure 1 ), Lindenmayer System (L-System) and Shape Grammar. In a very wide range of phenomena, the geometry of nature displays fractal-like properties (Mandelbrot, 1982 ). Any form, shape and pattern of a natural object are its phenomenological outcomes and therefore, it is understood that there is a strong correlation between biological forms and mechanical properties (Figure 2 ) (Thompson, 1992 ). Accordingly, fractal geometry of nature, possibly has a connection with nature׳s structural and mechanical behavior. However, there is a recent debate about the fractal geometry and its definition to explain the form and pattern of nature. Bejan (2000) critically argues in his ‘constructal law’ that it is the ‘laws of thermodynamics’ which govern the geometry and form of the natural objects, and there is no functional connection between nature׳s forms and fractal geometry.
|
|
|
Figure 1. Fractal tree generation by using Iterated Function System (IFS) as an algorithmic code in the computer. |
|
|
|
Figure 2. Some sketches of biological forms according to their functions and necessities illustrated by D׳Arcy Thompson׳ in his seminal book On Growth and Form ( Thompson, 1992 ). |
For many centuries, a variety of nature׳s forms, which in many cases present fractal geometry in their structural appearance, such as trees, cells, crystals, etc., have been creatively used by architects and engineers in projects like shells, light-weight structures, arcs, tents and bridges. In the past, several technical ways were exercised to connect fractal concepts with architecture by the method based on physical modeling process. But, nowadays, a procedural generative approach based on a composition of mathematical functions can be practiced by using the advantages of contemporary computer technology for connecting the fractal concept with architecture (Huylebrouck and Hammer, 2006 ).
2.2. Tree׳s fractal-like branches and their functions
Trees with their branches are one of the finest examples of nature׳s approximate fractals that are self-similar in pattern and highly irregular. There are different explanations about the tree׳s fractal-like branching appearance from different angles of disciplines such as biological, structural and mechanical. However, the basic explanation is functional needs. Tree׳s leaves which are essential helpers for making food, need ample amount of sunlight for photosynthesis and that is the reason they are spread and exposed to as much sunlight as possible. The majority of trees also morphs its outer shape, i.e., crown like a concave oval shape so that leaves can be exposed to sunlight throughout all the hours of daytime with the changing of sun path from morning to evening. But, at the same time, for basic biological needs, all leaves spread over large surface area need fluids and water. Branching arrangement is the optimized network for transporting the fluids to leaves, flowers and fruits. In addition, because of branching pattern, the new leaves grow at top such a way that they avoid shading the older leaves from sunlight. Biologist Leopold (1971) has attempted to give a more scientific explanation, although hypothetical, about the motive of tree׳s branching pattern. According to him, by analogy, it seems possible that the branching patterns of trees are governed by opposing tendencies which are analogous to minimum energy expenditure and uniform energy utilization. In the case of trees, it can be supposed that the minimum energy expenditure involves minimizing the total length of all branches and stems, while the uniform energy utilization might concern providing a photosynthetic surface which tends to attain the most efficient use of sunlight under certain constraints. Nevertheless, from a structural point of view, there are different explanations of the tree׳s branching pattern regarding the mechanical aspect of the tree׳s structure.
3. Mechanical properties of a tree and the efficiency of branching pattern
‘Trees are organisms that stand by themselves, so their shape has an inherent structural rationality’.
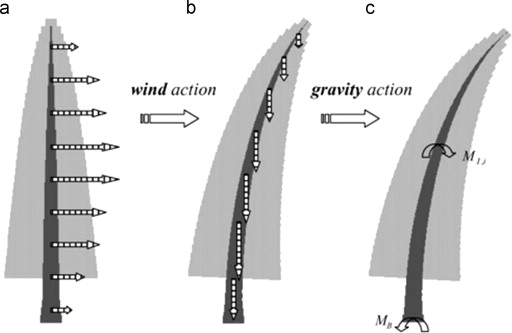
Trees are exposed to different types of external and internal loads. Wind is one of the main external loads against which tree manages to configure its own shape so that it can withstand against strong wind force and tackle resultant bending moments. Axial compression due to its own weight is another load that is carried by tree stems and trunk. In bending condition, when the tree is exposed to wind, the stresses change from tensile at the convex side to compressive at the concave side of a component (Figure 3 ). On the other hand, internal shear stresses prevent component parts from slipping on shear-loaded interfaces. Structurally, for a good performance, these internal stresses must be homogeneous for distributing the loads evenly. Trees optimize their shape to follow this structural demand (Mattheck, 1991 ). Tree׳s fractal-like branches have great contribution to tackle the wind loads. The sway of a tree is not harmonic under the heavy wind load, but is very complex due to the dynamic interaction of branches. Under the wind loading forces, the group of complex patterned branches as a mass contributes a dynamic damping, known as mass damping, which acts to reduce dangerous harmonic sway motion of the trunk and so minimizes loads and increases the mechanical stability of the tree (James et al., 2006 ). The fractal skeleton of a tree diverges the heavy wind to lower the impact on its tree-body (Eloy, 2011 ). Besides, higher fractal dimension of branches helps to increase the drag forces and frictions in trees, thus lessens the wind velocity on its path especially during storms (Kang et al., 2011 ).
|
|
|
Figure 3. (a) Schematic wind forces acting on the initial shape of the tree; (b) schematic gravity forces acting on a deformed shape; (c) basal and internal bending moments in each element (Ancelin et al., 2004 ). |
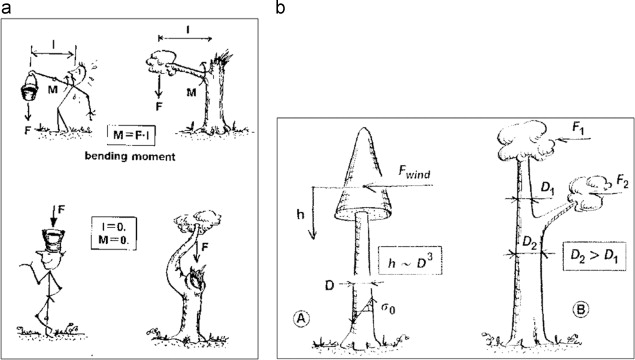
According to the biomechanics of tree׳s shape, trees make compromises. Longer a branch, the more likely it is to break under the pull of gravitation. Therefore, the tree has to compromise its shape that can expose as many leaves as possible, but by limiting the growth of a branch to a manageable length (Thomas, 2001 ). Mattheck (1991) explains the compromising of branch length and its angle under the gravitational pull by the principle of minimum lever arm illustrated in ‘Figure 4 a (left)’. It shows a man holding a filled water bucket with his arm outstretched, but after increasing fatigue, he decides to carry the bucket on his head, and in doing so he reduces the moment arm associated with the bucket by aligning the force of the bucket load over his center of mass. Similar behavior is seen in trees, which is illustrated by ‘Figure 4 a (right)’. After the loss of a tree׳s leading shoot or branch, the lateral succeeding branch turns itself to take the place of its predecessor by aligning its self-weight over the trunk׳s center of mass. This phenomenon of needing a main central stem that leads other side stems or branches is known as Apical Dominance. Negative gravitropism describes it as self-correcting and countergravity growth phenomenon (Mattheck, 1991 ). As it will be shown after, the concept of a branch aligning itself with the centroid of mass offers a useful idea for the derivation of a dendriform structure by using graphic statics. Another phenomenon trees show is the changing of branching angles with ages. Younger branches at the top of the tree are the most upright, while the increasingly older branches further down tend to become more horizontal. The older branches are required to take the load of new branches and get heavier causing sagging and resulting in larger branching angle (Thomas, 2001 ). Although these older large-angled branches become structurally weaker, but functionally it gets the advantage by offering an oval shape canopy of large surface of leaves that is very good for maximum exposing to changing sun angles.
|
|
|
Figure 4. (a) Principle of minimum lever arm; (b) tapering of tree to achieve constant stress distribution (Mattheck and Kubler, 1997 ). |
However, Metzger (1893) proposed another mechanical concept of trees that can be observed in the examples of some dendriform structure. According to his finding, tapering of trees can ensure a uniform distribution of the surface bending stress if the stem diameter (D ) has a cubic relation (h −D3 ) to the distance (h ) from the effective point of wind load ( Figure 4 b). Besides, the sudden change in diameters of branching stems at the area of branch joints illustrates the overall load distribution, and therefore, stresses of equal intensity occurs in the above and below of branch joints (Mattheck and Kubler, 1997 ).
4. Dendriforms in the past: prehistoric age – 1970 AD
4.1. Origin and ancient examples; dendriforms as decorations: prehistoric age – 500 AD
Dendriform, as mentioned before, is an imitation of the form and shape of a tree or plants. Treelike branching structure is also known as ‘dendritic structure’ (Schulz and Hilgenfeldt, 1994 ). ‘Dendron’ (δενδρον) is the Greek word for ‘tree’, and therefore, the term ‘dendritic structure’ uses this natural entity for describing a mesh-free ramified system or branching structure (Kull and Herbig, 1994 ). Another similar expression of ‘treelike’ is ‘arboreal’ which means ‘relating to or resembling a tree’.
The origin of dendriforms in architecture is unknown. A number of very ancient cave arts and paintings have been found, showing the figures of trees and plants, and hence confirming the human fascination towards the shapes of trees and plants since the prehistoric ages. Vegetal shapes can be seen as one of the significant decorative elements in the earliest examples of architecture, notably in the decorations of Egyptian palaces and pyramids, even in the Hieroglyphs of the ancient period of Egypt (3000 BC to 600 BC). Constructed during this ancient civilized period, the graceful papyrus-cluster columns of Luxor Temple (1400 BC) built with sandstone were one of the oldest examples of dendriform columns having the capitals that imitate the umbels of papyrus plant in bud (Figure 5 a). During this period we find many other such Egyptian columns that have the common features like stone shafts carved to resemble tree trunks or bundled reeds or plant stems and the capitals with lily, lotus, palm or papyrus plant motifs. The ancient Egyptian architect Imhotep, who lived 27th century BC, is credited with carving columns to resemble bundled reeds and other plant forms used for constructing the houses for common peoples, by placing the columns close together so they could carry the weight of the heavy stone roof and beams (Shaw, 2000 ). In the same ancient era, we find other examples of column structures having vegetal and mainly floral shaped capitals with treelike columns in India. Inspired by religiously sacred plants and flowers such as lotus and amalaka, we find many vegetal and floral decorations in the columns and capitals in the rock-cut architectures of Ajanta caves constructed during Satavahana and Vãkãtaka Periods (200 BC to 500 AD) when Buddhism was at its high peak in India (Figure 5 b).
|
|
|
Figure 5. (a) Ancient Egyptian columns inspired by a bundle of papyrus plants in Luxor Temples, Egypt, built in 1400 BC; (b) ancient rock-cut columns with lotus capitals in Ajanata caves in India built in 200 BC. |
The use of trees and plants as a prominent ornamental features is also seen in the Greek and Roman columns in Classical and Roman periods (500BC to 400 AD). Acanthus plants appeared widely in the capitals of the Corinthian and Composite order columns and also appeared in friezes, dentils and other decorated areas in the ancient Greek and Roman architectures (Figure 6 ). During this period, the focus had been given for designing complicated and intricate shapes of trees and plants for enriching the architectural decorations. It was very difficult and time-taking to design and craft the complex, elaborated and detailed figures of plants and flowers on stone; only some selected master artisans and craftsmen were skillful to design and craft those floral and geometric features in architecture. They used to be perfectionists with the brilliant sense of esthetic proportions for making decorative details. Legendary Greek architect and sculptor Callimachus was one of such great craftsmen, who was known for his penchant for elaborately detailed sculptures or drapery, is credited for inventing the famous Corinthian capital. According to Vitruvius (c. 75 BC to c. 15 BC), Callimachus was inspired by the natural composition of acanthus plant grown through the woven votive basket that had been left on the grave of a young girl, by mixing its spiny, deeply cut leaves with the weave of the basket (Pollio, 2004 ). In the later periods, i.e., in post-Roman periods, we find many other examples of mimicking trees and plants as esthetic and decorative features, especially in the Baroque and Rococo periods. These were the high times when complicated and richly decorated floral ornamentations were designed using stone, masonry and stucco. Outstanding use of floral and plant decorations with much more geometric complexity and sophistications is also extensively seen in the Islamic architectures of pre-medieval periods.
|
|
|
Figure 6. (a) Acanthus plants; (b) Corinthian column head in Pantheon, Rome built in 126 AD; (c) floral decorations in the column capitals and friezes of Maison Carrée built in 16 BC. |
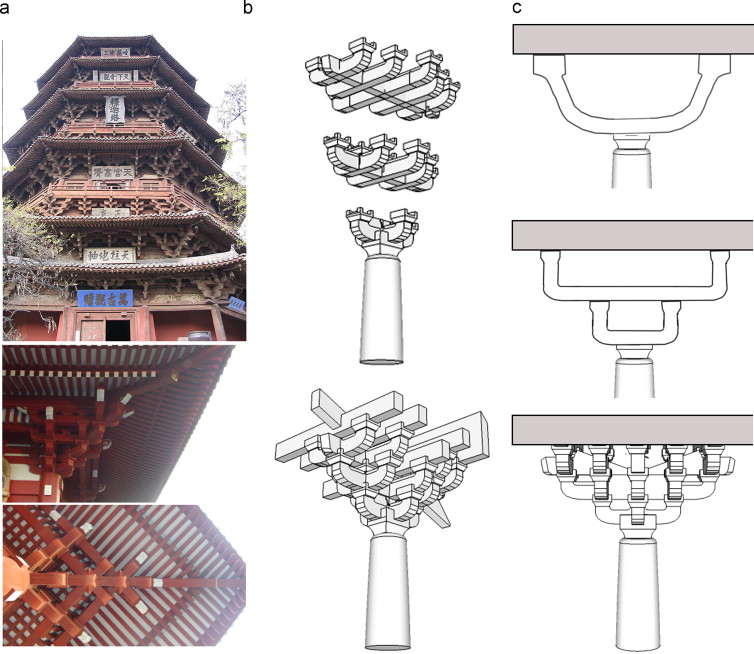
4.2. Traditional Chinese Dougong Brackets; structural dendriforms: 771 BC to 476 BC
One of the first examples of a true wooden dendriforms are the Chinese Dougong Brackets, dating back more than two thousand years, mainly found in Chinese temples and palaces (Figure 7 a). Dougong is basically a unique wooden bracketing system. ‘Dou’ means wooden block or piece and ‘gong’ means wooden bracket. The typical construction of dougong is basically an interlocking assemblage of some ‘gongs’, i.e., bow-shaped brackets. Inspired by the organization of tree branches as a sequence of cantilevers, the dougong is an assemblage of structural cantilevers placed in between the column top and the beam, that carries the load of the beam and the overhang roof into the column. Dougong ׳s lowest bracket takes the load of its immediate upper bracket which is longer (almost double) than the lower one. This new bracket is projected outward as a cantilever. Later, another bracket is placed on the second and so on. Generally, each bracket is oriented perpendicular to the lower. This process of arrangement, is continued iteratively until it gets a reasonable height and projection ( Figure 7 b).
|
|
|
Figure 7. (a) Dougong brackets from China (The Sakyamuni Pagoda of Fogong Temple, 1056 AD) and Japan (Sensoji temple, 628 AD); (b) typical assemblage of Dougong brackets, can be referred to the Iterated Function System (IFS); (c) schematic diagram of the abstract form of larger bracket as column capital replaced by interlocking self-similar smaller brackets to increase the stiffness as well as to transfer the roof and beam load sequentially to the column. |
By its structural strategy, one large bracket could transfer the roof and beam loads to the columns the same way through capital as in the case of the stone-made capitals of ancient Egyptian, Indian, Greek or Roman columns. But, in the case of huge timber construction, the large size timber bracket was not stiff enough and due to the weather effect the upper part of it could become bent after a few years. To avoid this structural problem, Chinese genius constructors intelligently replaced one large bracket (acting as a column capital) by a number of such smaller brackets. They repeated this strategy for each new smaller bracket until they got enough stiffness. This geometric operation can be explained by the Iterated Function System (IFS) method of fractal generation (Figure 7 c) Larger the number of smaller brackets, the stiffer is the dragon . This unique fractal-like geometric operation was meant for transferring the load sequentially from the uppermost bracket to the lowermost bracket. Besides, from the point of view of structural mechanics, the dougong structure is highly resistant to earthquakes because of its tight interlocking arrangement even without glue, nails and any other fasteners ( Yan et al., 2008 ). Dougong had been widely practiced in the Spring and Autumn period (771 BC to 476 BC). It got its high popularity during the Medieval period, especially in the period of Song dynasty (960 AD to 1279 AD), and later it became an essential and an idiosyncratic ornamental feature when used in palatial structures and religious temples.
4.3. Medieval period: masonry vaults as dendriforms: 12th century AD to 16th century AD
Until the medieval period, no other significant examples of dendriforms can be found that were directly inspired by the tree׳s structural properties except few examples. The Basilica Cistern in Istanbul constructed in the 6th century of Byzantine period is such an example of pre-medieval dendriform structures. This under water huge reservoir was constructed by more than 9 m high and 300 marble columns, imitating a dense forest (Figure 8 a). This unique column forest was designed for supporting the massive area of vault structures composed by semi-circular arches, referring a typical style of Byzantine architecture.
|
|
|
Figure 8. (a) Column forest in the Basilica Cistern in Istanbul constructed during the Byzantine period; (b) early Gothic style fan vault in Sainte-Chapelle in Paris. |
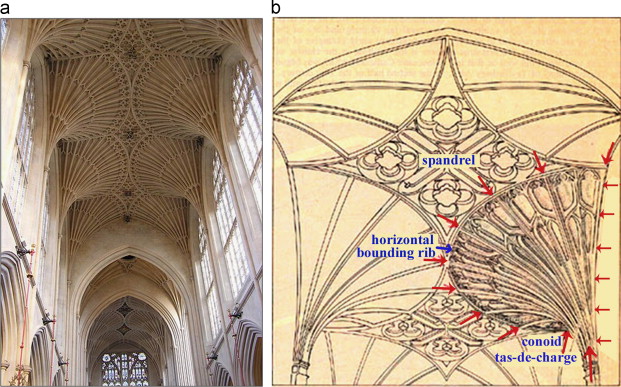
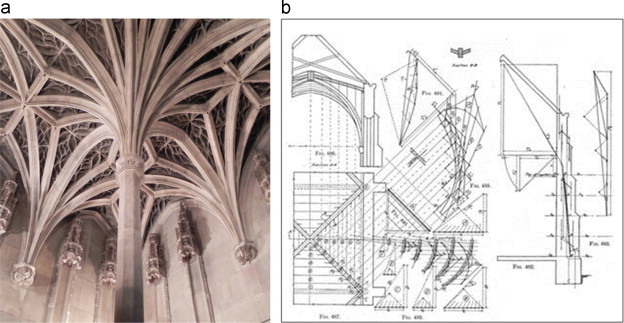
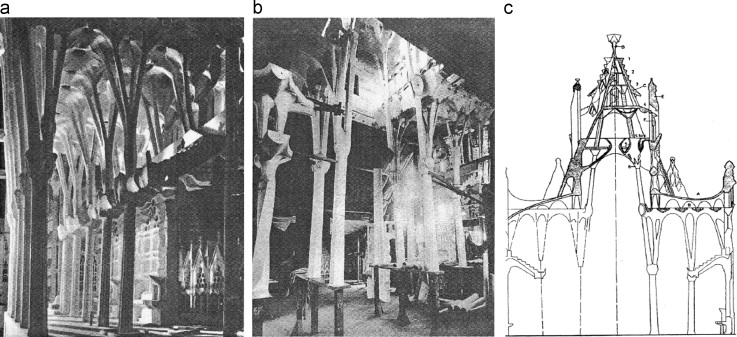
However, after a long gap, in the beginning of the medieval period in the 12th century AD, with the development of cathedrals construction, an important kind of dendriform structure appeared in architecture – the fan vaults. Ornamented fan vaults were the abstract imitation of tree׳s form. One of the earliest examples of fan vaults is seen in the interior of the Sainte-Chapelle in Paris constructed during 1242 AD to 1248 AD. The typical Gothic style in characteristics, these vaults, enclosed by stained glass, is supported by the columns, each of which is a bundle of thin columns that become ribs on the upper side and make a complex ribs network for carrying the vaults (Figure 8 b). This Gothic bundle column might be inspired by the ancient Egyptian columns which were imitated by the bundle of papyrus plants used in ancient Egyptian vernacular houses for making strong supports. Another early example of fan vault can be seen in the cloisters of Gloucester Cathedral constructed in 1351 AD designed by Thomas of Cambridge. During this period different styles of vault structure were widely practiced. Most vaults were constructed by extruding the arch, which was a basic structural element. But, in the Gothic period, there was a new structural approach for constructing vault known as a fan vault where the pointed arch was used. By its construction, this type of vault was produced by ribs which were equal in curvature and rotated at equal distances around a central (vertical) axis, forming the conoid shape. Flat central spandrels as keystones filled the spaces in between the sequences of conoids. Spandrels has an important role in providing compressive forces along the entire upper edge of conoid to keep the conoid in stress equilibrium which is important for a fan vault conoid in terms of structural strength (Figure 9 b) (Walter and Leedy, 1978 ).
|
|
|
Figure 9. (a) Fan vault in the Chapel of King׳s College, Cambridge; (b) schematic diagram of stresses in fan vaulting. |
Accordingly, it can be understandable that the conoid shaped columns of fan vaults were inspired by the structural appearance of a tree where a single trunk supports a large surface of crown. A series of fan vaults were designed during that period to replicate the forest from inside. One very good example of such man-made replication of forest-like vault can be sensed in the chapel of King׳s College in Cambridge (Figure 9 a). In this period, a number of fan vaults and ribbed vaults, giving the sense of the forest, were constructed by following the similar structure and conceptual approaches as applied in the construction of the chapel of King׳s College (Figure 10 ).
|
|
|
Figure 10. (a) Gothic ribbed vault; (b) the web of the vault is cut into strips which are analyzed as 2D arches (Wolfe, 1921 ). |
While in the medieval periods we find the imitation of trees in architecture as the major structural elements, in the late medieval periods, mainly during the Baroque and Rococo periods, we surprisingly notice the reappearance of vegetal and floral shapes in architecture as heavy decorations without any structural means. While the Baroque period is noticed for the perfect symmetric decorations, Rococo is famous for the asymmetric ornamentations.
4.4. The Art Nouveau: 1890 AD to 1920 AD
In the late 19th century till the beginning of the 20th century, during the period of Art Nouveau that gained high popularity for three decades from 1890 AD to 1920 AD, trees and plant shapes had become the leading features as decorative arts in architecture, can be considered as the ‘golden age’ of vegetal shapes in art and architecture. This new art movement was inspired by the natural forms and structures, mainly flowers and plants, including the flowing geometric curves and spirals, intending to harmonize the man-made structures with the natural environment. In architecture, this period has a historical importance, marked as an inventive approach at that time, by using cast iron that allowed architects and artisans to obtain complicated compositions of vegetal forms as heavily detailed decorations made in metals and as self-sustained freestanding design elements as well. In the Art Nouveau architecture, cast iron, meant for casting metallic decorations as esthetic elements, was also used as structural members, enthused by the structural strength of trees and plants. We find one of such fine examples in the Grand Palais in Paris, considered as a masterpiece of Art Nouveau architecture, constructed in 1900. The exterior of this massive palace combines an imposing Classical stone façade with a sharp contrast of Art Nouveau ironwork of treelike structures (Figure 11 a). In the same year, one of the famous examples of such ornamented iron dendriforms was constructed at the entrance gates of Paris subway metro stations, designed by Hector Guimard, was inspired by the curvilinear forms of vines and flowers (Figure 11 b).
|
|
|
Figure 11. (a) Grand Palais in Paris built in 1900. (b) Entrance gate of Paris Metro designed by Hector Guimard in 1900. |
4.5. Gaudi׳s equilibrium approach for treelike columns: 1880 AD to 1920 AD
In the same time period, a unique style of structural dendriforms can be found in the works of Antonio Gaudi, who was a pioneer in his ability to fuse architectural form with structural rationality inspired by nature. His design approach of embedding the forms and structures of trees and plants, including zoological features in architecture was completely different and unique. His quest for finding his own architectural language was heavily inspired by the structural characters of natural forms. His lifelong study of the organic structural system from nature has translated into his use of ruled geometrical forms such as cone, helicoid, hyperboloid and hyperbolic paraboloid to design the vaults, and the entire structural system of the Chappels and Cathedral, like tree trunks with branches. He often said ‘There is no better structure than the trunk of a tree or a human skeleton ’ ( Barrallo and Sánchez-Beitia, 2011 ).
The branching pattern of tree has a structural mechanism to hold the large tree crown, and this structural concept was adopted by Gaudi, especially in his later works, most famously in the Sagrada Familia Cathedral in Barcelona, construction began in 1982. Gaudí imagined this church as if it were the structure of a forest, with a set of treelike columns divided into different branches to support a structure of intertwined hyperboloid vaults. In this particular work, he not only adopted the tree׳s structural concept of supporting crown load, but also imitated the exact structural appearance of tree branches and morphed it gently (Park, 2005 ); even, he imagined this church as if it were the structure of a forest, with a set of treelike columns divided into different branches to support a structure of intertwined hyperboloid vaults (Orman, 2013 ). He applied the concept of branching column for holding the canopy in a systematic way with the close study of structural forces and stresses (Saudi, 2002 ). He inclined the columns so they could put up better with the perpendicular pressures on their section by providing them a double turn helicoid shape (right turn and left turn), as seen in the branches and trunks of trees, thus creating a structure that is nowadays known as fractals (Gómez, 2002 ). Together with a modulation of the space which divides it into small, independent and self-supporting units, it creates a structure that perfectly supports the mechanical traction forces, thus fuses the constructional innovation with the esthetic originality. In this context, Gaudi once clarified, ‘my structural and aesthetic ideas have an ‘indisputable’ logic ’ ( Martinell, 1951 ).
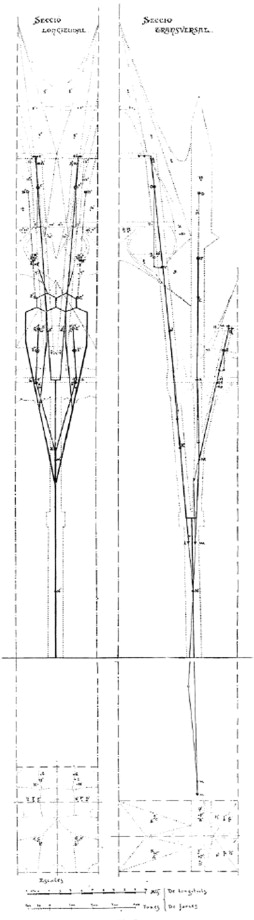
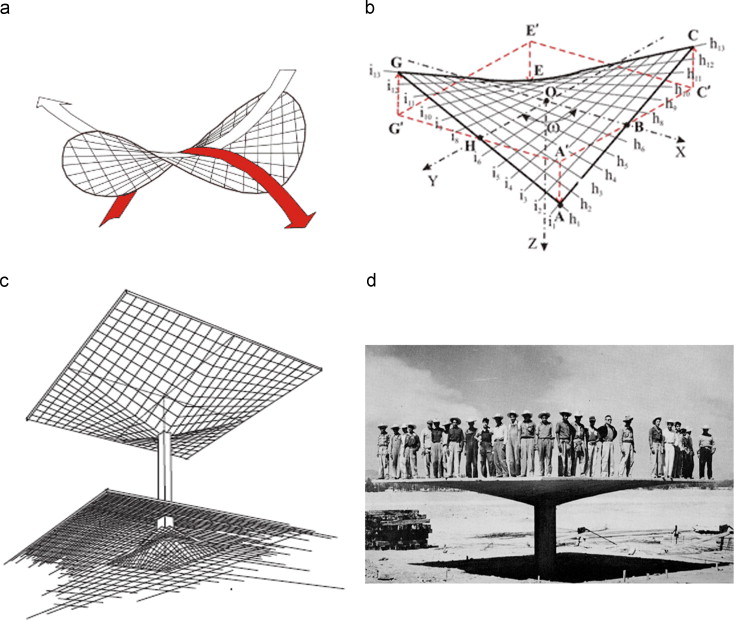
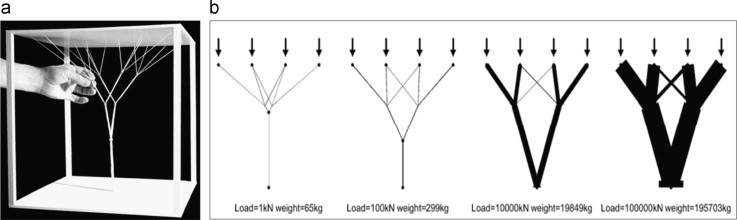
The principal idea behind Gaudi׳s use of the fractal-like tree column can be referred to as the center of force method that can be analyzed by ‘graphic statics’. During his time, ‘graphic statics’ was an advanced tool that allowed the designers to take forms and forces into account simultaneously. Antonio Gaudi, famously known for the physical scale modeling method for structural calculations, also used ‘graphic statics’ as a form-finding tool for visualizing the stress equilibrium in designing some of his signature style structures in the late 19th century. In designing treelike column in Sagrada Familia Cathedral, the weights and centers of gravity of the main parts were fixed and the base of the column was also fixed. Gaudi used a graphical equilibrium analysis method to design the treelike structure that would collect the roof weights and take the loading forces to the bases of the columns (Figure 12 ). By using the graphic static method, Gaudi calculated the total weight and center of force for each roof segment to attain equilibrium between various segments of a roof mass (Huerta, 2006 ). Afterward, he fixed the position of a base column, which diverges into multiple branches directed towards the center of gravity of all roof segments. In doing so, each particular branch is assigned to each roof segment, and the weight load of each segment is transferred axially all the way to the ground. Finding an equilibrium solution was the main but the fundamental basis for each single analysis and design method used by Antonio Gaudi for the construction of treelike column (Huerta, 2006 ). Gaudi intentionally maintained the acute angle of branching so that the branches can transfer the load towards the center of gravity more efficiently and quickly by following minimal paths principle. He made a series of different scales of physical models to understand the actual stress behavior and to confirm his assumptions and calculations (Figure 13 a and b). Gaudi׳s structural dendriforms are one of the earliest and finest examples of making treelike concrete-made branching structures inspired by nature. When in early 20th century the trend of structural minimalism was becoming popular, Gaudi׳s treelike sculpted structural supports, in contrast, were stunningly appealing and uniquely special in the field of architecture.
|
|
|
Figure 12. Graphical equilibrium analysis of the main nave of the Sagrada Familia (Sugraries, 1923 ). |
|
|
|
Figure 13. (a) View of the interior of a plaster model of interior of the Sagrada Familia. (b) Big model in Gaudi׳s workshop. (c) Gaudi placed ‘hidden’ flying buttresses to absorb some of the horizontal thrusts of the roof (Puig Boada, 1929 ). |
4.6. Mushroom and umbrella structures in 20th century: 1930 AD to 1970 AD
In the first half of the 20th century, many architects and structural engineers adopted structural functionality of trees in a minimalist way, during the trend of ‘structural minimalism’ with the limited but relatively sophisticated techniques and knowledge. They took the abstract form of a tree׳s overall shape like a mushroom or umbrella shape. The booming of reinforced concrete technology in the beginning of the 20th century had offered architects and engineers easy and numerous structural solutions to achieve free-form, sculpted and abstract structural forms.
In the past, reinforced concrete was used masterfully by builders in ancient Rome mainly as the material for supporting columns. At that time it was reinforced with iron, but the knowledge of the medium was lost during the Middle Ages. After centuries gap, experimentation of using reinforced concrete began again in 19th century France. In the 1880s engineers used reinforced concrete in bridge abutments as well as in other non-architectural applications. In the beginning of the 1990s, steel became widely available and it replaced the weaker iron for making reinforced concrete. In 1908, C.A.P. Turner in Chicago and Robert Maillart in Switzerland independently pioneered for using first time steel-reinforced concrete for the building constructions (Lipman and Wright, 1986). Concrete posts were designed to support cast-concrete floor slabs in such a way that the posts flared outward at the top to reduce shearing stresses that would otherwise tend to cause them to punch through the slabs. Later, this type of columns came to be known as ‘mushroom’ columns or ‘umbrella’ structures because they looked like mushrooms or umbrellas.
4.6.1. Early examples of reinforced concrete mushroom and umbrella structures: 1930s
One of the earliest known examples of reinforced concrete mushroom structure, meant for making the shapes like ‘mushroom’ or ‘umbrella’, is the Skovshoved Petrol Station, situated in Skovshoved in Denmark, which was designed by Arne Jacobsen in 1936 (Figure 14 a), considered as an example of the functionalist style typical of the time. Two years later, Italian engineer Giorgio Baroni independently designed inverted mushroom umbrella structures, known as ‘Baroni׳s tree’ in 1938 (Figure 14 b), that can also be considered as the first known inverted reinforced concrete umbrella structures (Greco, 2001 ), and were unusual by the shape of a structure in that time. During the same period, a notable Argentine architect Amancio Williams, who developed, starting in 1939, and with the collaboration of the Italian engineer Giulio Pizzetti, the project of an umbrella shell roof of minimal thickness. The shape Amancio Williams proposed was derived from the cone ended with a unique appearance of wavy edges of the canopy that was completely different from the regular hypars (Figure 15 a). The study of the optimal shape and of the optimal reinforcement configuration yielded to a thickness of about 5 cm, incredibly unusual at that time period for a cantilevered structure. Williams applied his umbrella for designing the monument to commemorate the famous Argentine composer Alberto Williams on the centenary of his birth. But, unfortunately, it was not built in real structures, except the construction of its small scale prototype model (Figure 15 a). In 1966, Williams adapted and built a similar solution for constructing the pavilion for the Bunge and Born Exhibition in Palermo, and used his umbrellas for the first time as the real structures, but reduced their base and thickness. It was almost entirely built in reinforced concrete, but the pavilion was demolished after two months, despite Williams׳s efforts to avoid this happening. However, three decades later in 1999, his son Claudio Williams collaborating with architect Claudio Vekstein had constructed two giant umbrellas, the highest known concrete umbrella till date, meant for designing the monument Alberto Williams, at Vicente López in Buenos Aires, Argentina, as a tribute for the excellence of Amanico Williams in the occasion of the “End of the Millennium” (Figure 15 b). Amancio׳s attempt of deriving the shape from structural optimization concepts make his work of great importance in the development of a morphogenetic approach to shell design (Chiorino and Sassone, 2010 ).
|
|
|
Figure 14. (a) Umbrella structure of Skovshoved Petrol Station, situated in Skovshoved in Denmark, designed by Arne Jacobsen in 1936. (b) Mushroom umbrella structures, known as ‘Baroni׳s tree’, designed by Giorgio Baroni in 1938. |
|
|
|
Figure 15. (a) Amancio Williams with the study model of his umbrella structure; (b) small prototype model of Williams׳ umbrella; (c) the monument of Alberto Williams, at Vicente López in Buenos Aires, originally designed by Amancio Williams, later constructed in larger scale by Claudio Williams and Claudio Vekstein in the occasion of the ‘End of the Millennium’ (Chiorino and Sassone, 2010 ). |
4.6.2. Wright׳s tubular mushroom column: 1930s
In the same decade of 1930s, the developments and sophistications of mushroom columns quickly reached their apex in the Johnson Wax Administration Building, designed by F.L. Wright and constructed in 1939, became a landmark example of concrete mushroom structures. In the 1930s, in one of his early conversations with Herbert Johnson, the owner of the Johnson Wax factory, Wright had promised him to give a beautiful building in which a person could ‘feel as though he were among pine trees breathing fresh air and sunlight’ (Lipman and Wright, 1986 ). According to Lipman and Wright (2003) description,
‘In Administration Building , Wright created a private, air-conditioned working area nestled within a man-made forest, and though he screened out the surrounding environment, one element in the universe outside entered his forest-light which poured in, bathing every surface and silhouetting the columns above .’
Undoubtedly, Wright׳s use of the unique style tubular mushroom column, both technically and spatially, was a major innovation in the 20th century architectures. Wright named the columns ‘dendriform’, i.e., tree-shaped. Lipman and Wright (2003) believes that Wright׳s mushroom columns created for the Administration Building are structurally more efficient than their predecessors. For evaluating the exact load capacity of his columns, he constructed a real scale prototype mushroom column and placed tons of cement bags and later heavy pug iron top onto the column. In this real scale manual test, it was found that Wright׳s creation could carry an unbelievable high load of 60 t, five times the load required by the state (Figure 16 ). Wright׳s mushroom columns, inspired by natural tree׳s structural strength, remain one of the most remarkable structural designs in the 20th century architecture. In their unprecedented structural and esthetic achievement they were the ultimate example of Wright׳s dictum, ‘Form does not follow function. Rather, form and function are one ’ ( Lipman and Wright, 1986 ).
|
|
|
Figure 16. (a) Load testing on tubular mushroom column by F.L. Wright in 1938; (b) tubular mushroom columns supporting a glass ceiling, Johnson׳s Wax Building, 1939, by F.L. Wright (Lipman and Wright, 1986 ). |
4.6.3. Candela׳s umbrella column shell: 1950–1960s
In the period of 1950–1960s, one of the most pioneer designers of thin shell structures Spanish structural engineer and architect Felix Candela designed a number of umbrella column shells which can be considered as the successors of Wright׳s mushroom columns. Advanced in technique and sophisticated in design, Candela׳s tree-inspired column acts not only as a structural support but also as a shell structure like umbrella which covers a large span of the area, considered to be a highly advanced and extraordinary structural innovation at that time period. After the Mexican Revolution and during the nation׳s reconstruction phase in the 1950s, massive demand of the construction of new market spaces and warehouses, structures of this type provided an opportunity for Candela to build large covered spaces. Within just a few years, he had constructed a series of concrete umbrellas in the new industrial zones of Mexico. It begun with the construction of his first experimental umbrella structure in 1952. Candela derived the idea of his umbrella structure from a sketch displayed in an article by a Frenchman named F. Aimond. On the site of another project at Valejjo in Mexico, Candela constructed a second experimental umbrella in 1953 (Figure 17 d), and he referred to this experiment ‘as a lesson to find the optimum rise, which depends on the area covered by the umbrellas. On this simple proportion depends the success in the design of these structures, since the necessary calculations are elementary ’ ( Gralock and Billington, 2008 ).
|
|
|
Figure 17. Felix Candela׳s hypars and umbrella column shell; (a) hyperbolic paraboloid with curved edges, (b) hyperbolic paraboloid with straight edges, (c) prototypical ‘umbrella’ structure showing foundation, which is also an umbrella form, and (d) second experimental umbrella, Valejjo, Mexico D.F., 1953 (Garlock and Billington, 2008 ). |
After successful experiments he constructed a series of umbrella structures for markets and warehouses in 1950. Later, he further modified the common form of umbrella structure; he used folded hypars (hyperbolic paraboloid) as an efficient alternative of the common umbrella, because they can also cover large areas and the folds can break up the expanse of the roof visually appealing ways (Figure 17 b); and he also used umbrella shape for the construction of its foundation (Figure 17 c). The first such cantilever was used for creating a fan shape structure by placing three folded hypars together for constructing the entrance lobby of the Lederle Laboratories in Mexico City in 1956. Later, he developed a new form of rectangular umbrella by arranging folded hypars. This type of unique umbrella structure was first constructed in the subway station roof of La Candelaria in Mexico City in 1968. The evolution of Candela׳s umbrella column shells inspired by natural trees and shells shows the sophistication of dendriform structures with the advancement of knowledge, technical innovation and esthetic creativity.
4.6.4. Nervi׳s umbrella structure with complex columns: 1960s
In following years, the notable Italian architect and engineer Pier Luigi Nervi also designed and constructed several such reinforced umbrella structures with a new construction approach where sometimes he used steel cantilevers as principal radial branches instead of monolithic concrete structure. Palazzo del Lavoro in Turin is one of such fine examples constructed in 1961 (Figure 18 ). The columns of Palazzo del Lavoro were cast in steel framework lined with narrow timber boards clearly readable in the finishes (Figure 18 b) (Cement and Concrete Association, 1960 ). These columns are cantilevered supports and their graceful splayed geometries bring structural efficiency by varying capacity with the bending moment distribution (Figure 18 c). However, the most innovative approach, inspired by Gaudi׳s hypar (hyperbolic paraboloid) structure of Portico of Colonia Guell Crypt, Barcelona, built in 1915, Nervi designed the trunks of the umbrella columns with complex formal gestures, such as recurring use of ruled surfaces, seen in his many projects. In Palazzo del Lavoro, the column starts sprouting from the basic shape of ‘cross’ or ‘+’, and then it merges into a circle at the top (Figure 18 a). At that time there were no digital technologies, therefore, to perfectly draw and then erect this complex shape of the column was without a doubt a masterly engineering work which followed not only the geometrically formal logic but also structural sense. Therefore, Nervi׳s design tactic of geometric manipulation could be defined as rational complexity (Perguni and Andreani, 2013 ). In recent studies, Nervi׳s depiction of himself as an Architect–Engineer, relying on his intuition as well as on his technical skills, has been placed in a richer historical context (Sassone and Piccoli, 2013 ).
|
|
|
Figure 18. Palazzo del Lavoro in 1961, by Pier Luigi Nervi. (a) Geometric articulation of column, (b) steel frame-work, and (c) completed construction (Perguni and Andreani, 2013 ). |
From the 1950–1960s, apart from Nervi׳s umbrella structures, we find a number of other dendriform structures that differ in design and originality in construction techniques. Umbrellas and mushroom structures in Hunter College Library and Administrative Building in New York designed by Parcel Breuer and Associates (1958–1960), gas station in Ljubljana by Milan Mihelič (1968), and another gas station in Ljubljana by Edvard Ravnikar (1969) are less known but important such examples. Umbrella and mushroom structures did not lose their appeal even in more recent times, and therefore, it is worth knowing to follow their evolution after the ‘golden age’ of concrete shell construction.
5. Contemporary dendriform architecture: 1970 AD to present)
In recent times, the complexity became a design trend in many creative fields – from art and industrial design to interior design and architecture. During this phase, architects and engineers, who were fascinated by the tree׳s shape and structure, started designing dendriforms with complex and fractal-like branching configurations. In the late 20th century, apart from the improvement of concrete technology and high quality timbers and plywoods, the advancement of lightweight but very strong steel as a material offered architects and designers numerous opportunity to explore complex designs in architecture. One of the initial creators of exploring branching structures using steel was German architect Frei Otto.
5.1. Otto׳s experiments with ‘branching’ structure: 1970s
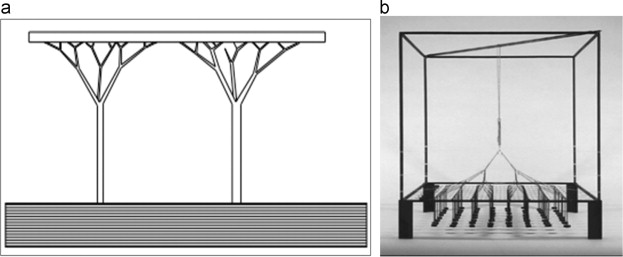
Fractal-like branching structure has its own mechanical advantage in terms of structural strength with the functional needs of carrying wide-span tree crown. The structural significance of the tree׳s branching pattern was still not much addressed in the construction of structural dendriforms until the experimental works of 20th century׳s pioneer German architect Frei Otto, who carried out methodical research on lightweight and adaptable construction by considering the fundamental aspects of the relationship between architecture and nature. Apart from his remarkable works that include suspended construction, dome shells and grid shells, Otto systematically researched and worked on the model of treelike branching structures (Figure 19 ) (Nerdinger, 2005 ).
|
|
|
Figure 19. (a) Design sketches by Frei Otto (Schulz and Hilgenfeldt, 1994 ). (b) Frei Otto׳s hanging models of branching systems (Nerdinger, 2005 ). |
Branching structures in construction, both in their overall appearance and in the nature of the structure itself, exhibit a particularly close relationship between the course of the forces and their shape. This relationship is a functional combination between the roof construction and supporting structures. One of the main structural advantages of the treelike branching system is to have short distances from the loading points to the supports. Based on his model studies of treelike columns and branching structure, Otto designed support pillars of a six-angle grid shell in the King׳s Office, Council of Ministers in Riyadh in 1979.
5.2. Branching structures for large-span architecture: 1990s
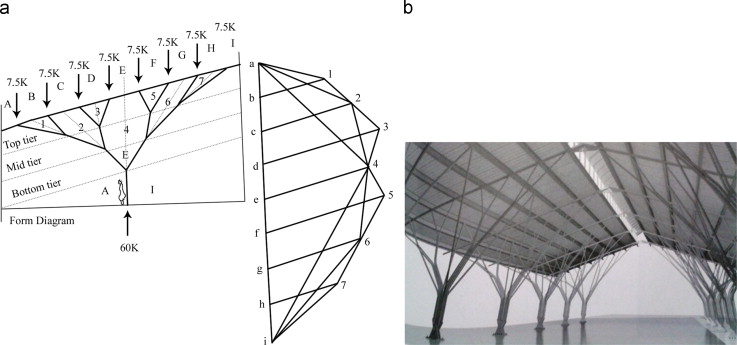
After Otto׳s work, the architectural articulation of tree-column occurs in several buildings and masterpieces that have lightweight structures (Charlson, 2005 ). Over the past thirty years, there was a great improvement in designing dendritic and branching structures. In the last decade, the same approach of the treelike column with branching structure has been done in more logical and advanced way by using optimization methods with the application of computational and simulation techniques in computer. In the late 20th century, Zalewski and Allen (1998) have reintroduced the wider potency of graphic statics method in their book Shaping Structures : Statics . Later, as the consultants of Boston Structure Group, they applied computer supported ‘graphic statics’ for finding the optimized form for steel-made dendriform compressive structures and for achieving the maximum force equilibrium in designing a long-span market roof (Figure 20 ) (Allen and Zalewski, 2009 ).
|
|
|
Figure 20. (a) Computer-supported ‘graphic static’ method for finding the form for compressive dendriform structures for market roof supports. (b) Final outcome of the market roof by Boston Structure Group (Zalewski and Allen, 1998). |
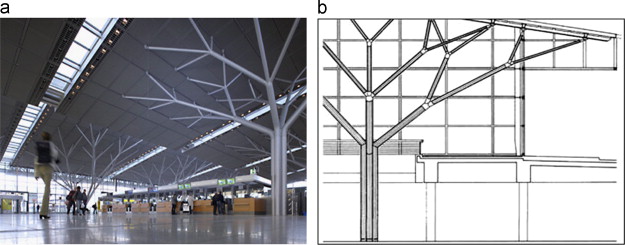
Besides, one of the finest examples of three-dimensional dendriform structure using computational methods for form finding and optimization is seen in the interior of Stuttgart Airport Terminal building built in 1992 (Figure 21 ). In this dendriform structure, instead of ‘graphic statics’, search algorithm was used for form finding and in the optimization process (Charlson, 2005 ). Another such example can be seen in the main entrance of Palaice de Justice, Melun in France built in the 1990s. In the case of Stuttgart Terminal, four separate steel members sprout from the base as a trunk and then each member turn into a separate stem, and finally each branching stem further splits into another four branches, following the fractal characters of self-similarity and iteration like tree branching (Figure 22 ). The cross-sectional diameter of the column trunk and each branching element are incrementally decreased upwards to achieve nearly constant stress throughout this dendriform structure. This structural strategy reminds Metzger׳s (1893) finding of tree׳s mechanical property, explaining the tapering feature of trees that can ensure a uniform distribution of the surface bending stress if the stem diameter (D ) has a cubic relation (h–D3 ) to the distance (h ) from the effective point of wind load. However, while in the case of Palaice de Justice, at Melun in France, a thick single monolithic steel member as a trunk grows up and splits into four branches, and each branch made of a single monolithic steel member again splits into four different branches of four different single steel members. Each single member tapers at the end, thus mimicking the structural concept of natural tree where the radius of the lower part of a tree trunk is more than the diameter of the upper part of the trunk ( Figure 4 b). That is how, the lower part of the column of Palaice de Justice reduces its self-weight on top and supports the upper load of the glass roof and its branches more efficiently.
|
|
|
Figure 21. (a) Structural ‘trees’ in Stuttgart Airport Terminal, Stuttgart, by Von Gerkan, Marg+Partner, 1991; (b) schematic form diagram of Stuttgart Airport dendriforms. |
|
|
|
Figure 22. A ‘tree’-supported canopy at the main entrance. Palaice de Justice, Melun, France, Jourda and Perraudin Architects, 1992 (Charlson, 2005 ). |
Dendritic columns at the Oriente Station, Lisbon, constructed in 1998 designed by Santiago Calatrava is unique compared to the columns of the Stuttgart Airport Terminal and Palaice de Justice, Melun. Unlike the linear branches of the previous two examples, the branches of the treelike structure of Oriente station are elegantly curved sprouting from the trunk (Figure 23 a). In its unique approach, recalling the pointed Gothic arches of Oxford University Museum׳s courtyard structure, the steel ribbed dendriform of Oriente station not only acts as a structural support, but also forms a roof canopy. In this case, the steel ribbed canopy bears a strong resemble to a grove of palm trees, an association reinforced by its detailing (Figure 23 b). Apart from its square fabricated-steel column-bases, branching and ribbed members of the roof canopy comprise I-sections. The main arch members representing main branches are made not only curve, but also taper to reduce the self-weight on top. In this dendriform example, the hunched and rounded rib-to-arch connections and thin sections mimic similar properties of palm thongs, thus strengthen the botanical analogy by its appearance too (Calatrava, 2003 ).
|
|
|
Figure 23. Oriente Station, Lisbon. Santiago Caltrava, 1996. (a) A view along the canopy structure. (b) Palm tree thong-like ribs connect to a primary arch. |
5.3. Computer-aided form finding and optimal design of branching structures: 21st century
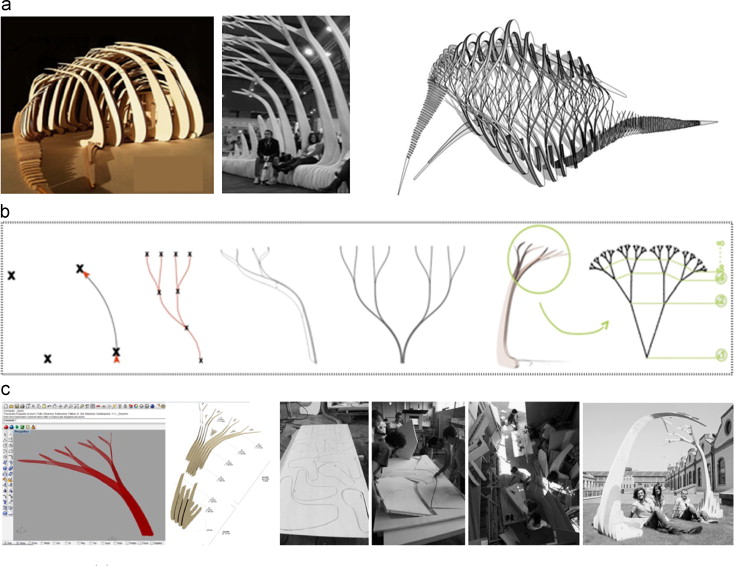
In the beginning of the 21st century, the computer-supported algorithmic and parametric technique has advanced the design and construction of dendritic structures. Branching numbers, angles, lengths and other associated parameters can be parametricized and optimized by using different search algorithms. Using the genetic algorithm, including a physical model study, Buelow (2007) experimented to generate branching structures for minimal path under compression (Figure 24 ) and separately under tension, thus developed a form-finding scheme for using less material but getting maximum strength.
|
|
|
Figure 24. Exploring branching structures by genetic algorithms for minimal paths. (a) Thread model with adjustable nodes used to study geometry. (b) Branching columns loaded from above in compression using four levels of loading (Buelow, 2007 ). |
The computer has also helped enormously to recreate the branching forms similar to natural trees. Apart from IFS, as we mentioned before, L-System is an another algorithmic digital generator which is based on the parallel rewriting system, a type of formal grammar, that can potentially produce natural fractals. Developed by a Hungarian biologist Aristid Lindenmayer in 1968, L-systems can reproduce the dynamic of plant growth (Figure 25 a), offering architects to apply this system of form generation in architectural designs. An interesting example of using the L-system for the development of architectural form is the Tote Restaurant in Mumbai, designed by Serie Architects and constructed in 2009 (Figure 25 b). As an analogy to the green areas surrounding the building, the architects proposed a continuation of tree-shaped branching structures inside of the restaurant. The arboreal and asymmetric structures support the roof while intersecting with each other, and designed as a steel truss using I-beam and pipe profiles. Accordingly, this building can be considered as an example of how algorithmic techniques and digital tools may be used for modeling fractal forms for architectural designs, with special emphasis on the morphogenesis process (Gawell, 2013 ).
|
|
|
Figure 25. Above – fractal generation (plant growth) using L-System; below – the Tote Restaurant, Mumbai, designed by the Serie Architects, UK (Gawell, 2013 ). |
Structural column of the entrance porch of the Qatar National Convention Centre in Doha is one of such very significant built examples where an extended evolutionary algorithm was used for finding a form that can support a maximum length of the roof (Figure 26 a). Constructed in 2011, designed by Japanese architect Arata Isozaki and RHWL architects, its dendritic steel-made hollow tube structure spanning 250 m in the shape of the native sidra tree grows up to support the overhanging roof structure ( Figure 26 c). In designing a pair of a structural column, an initial shape and design parameters were taken as a starting point, and modified during the design process. So, as design parameters, the initial conditions in terms of height, volume, loads, support points or functional requirements were established. Then, using shape analysis methods, the initial system evolved into multiple directions with the purpose of optimizing its structural behavior. The design parameters were modified during this phase, and the optimal structure with the most interesting shape was chosen from the population of all final shapes of optimal structures (Figure 26 b). In this project, the purpose was not to establish the optimal structure for a particular or all problems, but to apply computer analysis based on the efficiency of the structural behavior as a design tool in the exploration of new architectural forms (Sasaki, 2007 ).
|
|
|
Figure 26. Qatar National Convention Centre (2011). (a) Form-finding by suing extended evolutionary optimization algorithm, (b) final shape after optimization, and (c) final construction in Doha (Sasaki, 2007 ). |
Therefore, form-finding computational techniques not only take the designing and construction process of dendritic structures a step ahead, but also encourage architects to connect their design ideas with the nature (trees) more methodically with deeper understandings of the optimization and efficiency of nature׳s structures. Nevertheless, Mutsuro Sasaki worries, ‘Nowadays the definition of new forms is freer than ever of any geometrical, structural or constructive restraint, and there is therefore a risk of incongruity between the architectural shape and its structural support, that might have unfortunate architectural consequences ’ ( Larena, 2009 ). In this context, it is sensible to reconsider structural efficiency as a valid design device, with the purpose of relating form, force and structure within a rational mechanical basis.
6. Recent researches on dendriforms design
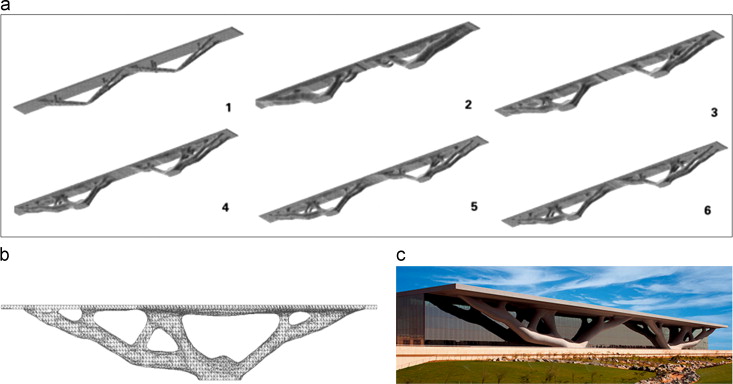
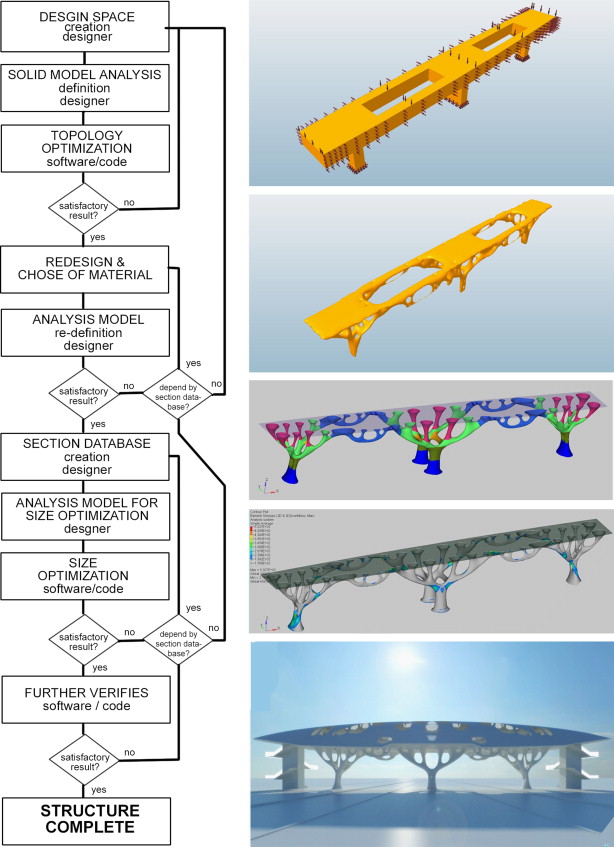
In current years, in academia and research institutes, a number of highly advanced researches are carried out and still continued for designing structurally extra efficient, technologically very innovative and esthetically more creative dendriform structures. One of such innovative, sophisticated, and structurally as well as esthetically rational approaches has been carried out very recently by L. Frattari, J.P. Dagg and G. Leoni in 2013, in their experimental approach in which they have explored the structural optimization potentials applied in architecture. They have proposed conceptual design tool based on ‘Topology Optimization’ and ‘Size Optimization’ for form finding process computationally, and applied to the case study of a bridge of 50 m long and its shelter. In this attempt, inspired by the organic form of a tree structure, they obtained the most efficient branching supports for the bridge structure with the compromise of their esthetic appearance. The optimization process and its strategy are illustrated in ‘Figure 27 ’ (Frattari et al., 2013).
|
|
|
Figure 27. Topology optimization and size optimization for form finding of a 50 m long bridge and its shelter, inspired by the tree׳s organic form (Frattari et al., 2013). |
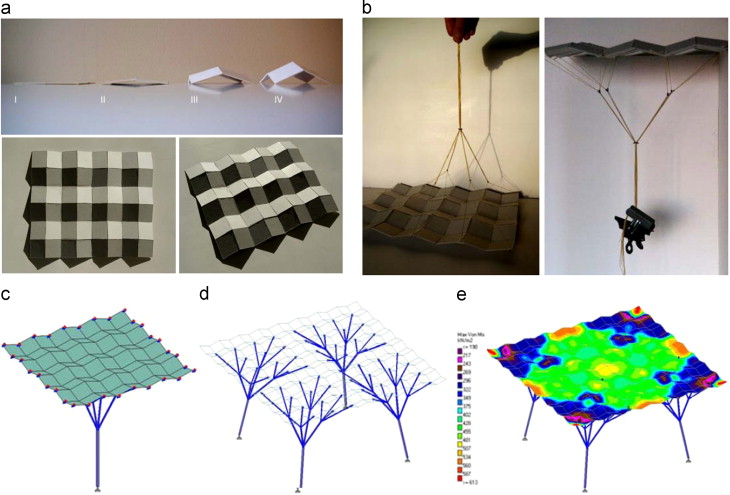
Falk and Buelow (2009) had developed a different but interesting design approach as exploration and optimization for finding new shapes of plate-based roof structures braced by branching columns and tensile members by using evolutionary computation and genetic algorithm methods. In their interesting approach, they optimized the geometric relationships between the roof and branching columns for least weight by exploring the parameters of roof geometry and the related branching column geometry including their topologies. Made completely by the cross-laminated timber, the combination of faceted plate assembly of roof and the branching column support system showed the combined action of structural efficiency and stiffness, confirming the new scope of structural and architectural applications designed for rational construction (Figure 28 ) (Falk and Buelow, 2009).
|
|
|
Figure 28. (a) Above – transformation from flat to pitched unit assembly, below – cardboard model of a rhombic based plate assembly, in plan and in perspective. (b) Thread model photos of the assembly and its column structure. (c) Isometric and elevation of STAAD FEA model. (d) Pavilion geometry with four branching columns. (e) Internal stress assessed by FEA (Falk and Buellow, 2009). |
Apart from exploring the innovative designs of dendriforms in academia that mainly possess the structural interests, students and researchers from WoodLab in Politecnico di Torino has paid principal attention to esthetic interests in designing a fractal-like natural forest in the workshop project of ‘Monalisa Pavilion’ through the algorithmic arrangement of a series of timber-made curved branching structures composed of layered poplar plywood (Figure 29 ). In this design approach, the team had specifically used Iterated Function System (IFS) as an algorithmic code to produce fractal branches (Figure 29 b) (Callegari et al., 2013 ). This team has paid additional but a significant attention to deal with the mechanical properties of the poplar plywood in bending the timber branches, connected by metal screws at the joints, for achieving more organic and natural appearance, (Figure 29 b) thus understanding the stress behavior of wood fibers of curved branches.
|
|
|
Figure 29. Monalisa pavilion inspired by and to recreate tree forest. (a) Conceptual model, real scale pavilion, top view of conceptual drawing. (b) Fractal branching generation using IFS. (c) Production progress of real scale ‘tree’ unit in the university workshop (Callegari et al., 2013 ). |
Nevertheless, in recent years, while complex geometry and parametric designs are getting liberty to create free-form futuristic architectures with the advancement of computer-aided digital technologies, some researchers look back to the history and restudy the geometrical complexity, structural solidity and longevity of old decorated masonry buildings. Using sophisticated computational techniques, Block Research Group from ETH Zurich has recreated the modern version of a masonry fan vault resembling with nature׳s forested canopy. They developed and applied ‘three dimensional thrust network analysis’ for assessing the mechanical and structural behavior of branching structures computationally, then used three dimensional computational method for obtaining lower-bound solutions of masonry vaults with complex geometries (Block and Ochsendorf, 2008 ). Later, they applied algorithms for optimizing the structure, and finally generated a new kind of treelike ribbed masonry vault (Figure 30 a). In this context, it is worth mentioning the project of the Chinese Pavilion constructed in Shanghai Expo in 2011 (Figure 31 a). In this interesting project, the basic structural concept of the typical interlocking systems of brackets, famously known as the traditional dougong brackets, was reincarnated in a contemporary way where the abstract form of dougong was represented as a main building structure like a big tree with a large canopy, instead of a smaller part or element of the structure. Another such example of wooden dendriform is Metropol Parsol in Spain, world׳s largest wooden structure, which was built by interlocking system using the algorithmic and parametric technique as a form-finding process ( Figure 31 b). This massive wooden treelike structure, designed by Jürgen Mayer-Hermann built in 2011, is popularly known as Las Setas de la Encarnación (in Spanish language) which means Incarnación׳s mushrooms. Architect Mayer expresses that the form of the building which consists of six parasols in the form of giant mushrooms (‘Las setas’ in Spanish language), is inspired by the vaults of the Cathedral of Seville and the ficus trees in nearby Plaza de Cristo de Burgos ( Moore, 2012 ). This huge structure is a complex assemblage of large wooden pieces of birch trees.
|
|
|
Figure 30. (a) Computational model of a treelike branching ribbed masonry vault (). (b) ‘Fibrous Structures’, AA Workshop, Istanbul (Pasquero et al., 2007 ). Source : Block Research Group, ETH Zurich. 2011 |
|
|
|
Figure 31. (a) The China Pavilion at Expo 2010 in Shanghai, inspired by traditional Chinese Dougong brackets (). (b) Metropol Parasol at Seville in Spain, an algorithmic design of huge wooden dendriforms, popularly known as Las Setas de la Encarnación (in Spanish, which means ‘Incarnación׳s mushrooms’). Source : internet |
In the frame of the researches on dendriform structures, some researchers have attempted to explore the efficiency of tree׳s fractal-like branching structures with completely different angles. In a research-oriented ‘Fibrous Structures’ workshop hosted by the Istanbul Technical University in Istanbul in 2007, a group of students not only developed a concrete prototype of branching structure on top part to support a roof, but also constructed another but inverted branching structure at the bottom part as a network of foundation to distribute the load evenly to the ground, thus mimicked the concept of structural efficiencies of tree׳s branching stems on top and simultaneously its branching roots at ground for uniform load distribution (Figure 30 b). In this workshop, students made a physical model based on the digital model of branching structure, and then after getting the structural feedback from physical model they modified the digital model for getting a final form; thus the interaction between the digital and physical modeling worked as a new approach of form finding process that had produced the most efficient and feasible structure at the end (Pasquero et al., 2007 )
7. Conclusion
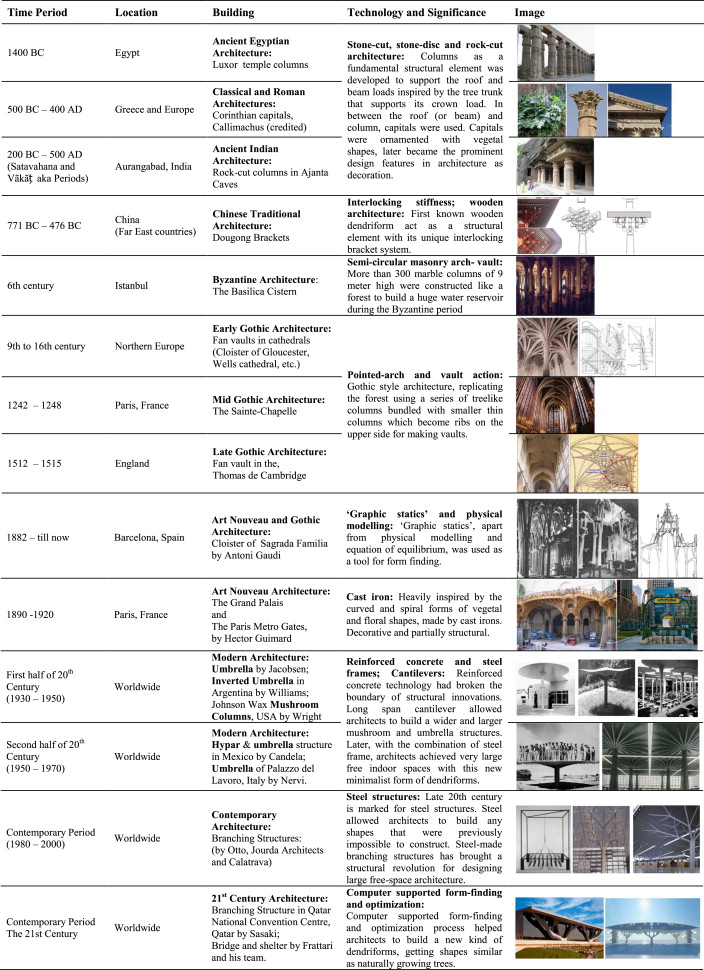
In this paper we have discussed how the underlying geometry of trees, possible to be explained by the concepts of fractals and non-Euclidean geometry, was used as an inspiration source by architects and constructors who employed the powerful properties of self-similarity as a way to improve and optimize their structural and architectural solutions. From the analysis of a set of dendriforms from historical to contemporary times, we have attempted to narrate the evolution of dendriforms design as a logical consequence of the understanding of intrinsic relations between forms and structures in trees and plants, and as an effect of the advancements in constructional, theoretical, graphical, technological and computational knowledges in different time periods (Table 1 ).
|
|
|
Table 1. Chronological evolution and development of dendriform structures. |
It is important to emphasize that terms as ‘dendriform’, ‘treelike column’ or ‘branching structure’ are used among the architectural and engineering community, mainly focusing on the appearance and on the formal similarity between architectural structures and natural shapes. However, the most inspiring feature of a natural tree undoubtedly is its capacity of carrying a large surface supported by a narrow element (trunk) through fractal-like branching configuration. Such an idea has been teaching and guiding architects to improve the efficiency of their design realizations, by understanding nature׳s complex forms.
Although treelike structural system in architecture is taken from the trees׳ shapes and geometry, they frequently show different mechanical behaviors. While, in the case of naturally growing trees, the branches mainly carry bending moments, in man-made structures bending is systematically replaced by axial forces, in order to reduce the internal stresses. The reason relies on the fact that the roofing system, that in manmade structures substitutes the crown, can have structural elements inside of it, linking the ends of branches.
In recent times, research on the properties of trees and plants, including fractals and other underlying geometric and mechanical features, have opened a new vista for the innovations of forms and structures in architecture, thanks to the rapid advancement of science and technology. A deeper understanding of fractal-like form and its associated structural behavior can unfold more unknown facts and mechanisms of trees׳ forms and functions. Thus, by using the emerging technologies, researchers can offer architecturally and structurally more innovative, better optimized and highly efficient dendriform structures, that can not only solve both the structural and spatial problems in architecture, but also gift esthetically innovative designs.
Acknowledgment
This work was supported by the Politecnico di Torino Ph.D. research grant, XXVII cycle (University Research Scholarship).
References
- Allen and Zalewski, 2009 E. Allen, W. Zalewski; Form and Forces: Designing Efficient, Expressive Structures, John Wiley & Sons, New York (2009)
- Ancelin et al., 2004 P. Ancelin, B. Courbaud, T. Fourcaud; Development of an individual tree-based mechanical model to predict wind damage within forest stands; For. Ecol. Manag., 203 (1) (2004), pp. 101–121
- Barrallo and Sánchez-Beitia, 2011 J. Barrallo, S. Sánchez-Beitia; The geometry of organic architecture: the works of Eduardo Torroja, Felix Candela and Miguel Fisac; Bridges 2011: Mathematics, Music, Art, Architecture, Culture, Tessellations Publishing (2011), pp. 65–72 The University of Melbourne, Melbourne
- Bejan, 2000 A. Bejan; Shape and Structure, from Engineering to Nature, Cambridge University Press, Cambridge (2000)
- Benyusis, 2002 J.M. Benyusis; Biomimicry: Innovation Inspired by Nature (revised ed.), Prennial, New York (2002)
- Block and Ochsendorf, 2008 Block, P., Ochsendorf, J., 2008. Lower-bound analysis of masonry vaults. In: Proceedings of the 6th International Conference on Structural Analysis of Historical Construction. Bath, UK.
- Bovill, 1996 C. Bovill; Fractal Geometry in Architecture and Design, Birkhauser, Boston (1996)
- Buelow, 2007 Buelow, P., 2007. A Geometric Comparison of Branching Structures in Tension and in Compression versus Minimal Paths. URL: 〈http://deepblue.lib.umich.edu/bitstream/2027.42/58599/1/pvb_IASS07.pdf〉 .
- Calatrava, 2003 S. Calatrava; Orient Station, 1997–98, University of Manitoba, Manitoba (2003)
- Callegari and Iasef, 2013 Callegari, G., Iasef, M.R., et al., 2013. Monalisa wood pavillon: optimization and parametric design by using poplar engineered components. In: Proceedings of the ISCHP2013. Florence, Italy
- Casti, 1989 J.L. Casti; Alternate Realities: Mathematical Models of Nature and Man, John Wiley & Sons, New York (1989)
- Cement and Concrete Association, 1960 Cement and Concrete Association; The Palzzo del Lavoro: Pier Luigi Nervi; Concr. Q., 47 (1960), pp. 17–20
- Charlson, 2005 A.W. Charlson; Structure as Architecture, Elsevier and Architectural Press, Oxford (2005)
- Chiorino and Sassone, 2010 Chiorino M.A., Sassone, M., 2010. The morphogenesis of shell structures: a conceptual, computational and constructional challenge. In: Proceedings of the TAAE International Conference on Structures and Architecture, Invited Key-note.
- Eloy, 2011 C. Eloy; Leonardo׳s rule, self-similarity, and wind-induced stresses in trees; Phys. Rev. Lett., 107 (25) (2011), p. 258101
- Falconer, 2003 K. Falconer; Fractal Geometry, Mathematical Foundations and Applications (2nd ed.), Wiley, London (2003)
- Falk and Buelow (2009) Falk, A., Buelow, P.V., 2009. Combined timber plate and branching column systems–variations and development of system interaction. In: Proceedings of the International Association for Shell and Spatial Structures (IASS) Symposium, Valencia.
- Garlock and Billington, 2008 M.E.M. Garlock, D.P. Billington; Félix Candela: Engineer, Builder, Structural Artist, Princeton University Art Museum Monographs, Yale University Press, Yale. (2008)
- Gawell, 2013 E. Gawell; Non-Euclidean geometry in the modeling of contemporary architectural forms; J. Pol. Soc. Geom. Eng. Graph., 24 (2013), pp. 35–43
- Gómez, 2002 Gómez, C.A.J., 2002. Gaudí: Geometria, Estructura i Construcció, en Gaudí 2002. Misceŀlània, pp. 144.
- Greco, 2001 C. Greco; Giorgio Baroni, coperture sottili in cemento armato in forma di paraboloide iperbolico; Area, 57 (XII) (2001), pp. 24–31 (Italian)
- Huerta, 2006 S. Huerta; Structural design in the work of Gaudi; Archit. Sci. Rev., 49 (4) (2006), pp. 324–339
- Huylebrouck and Hammer, 2006 D. Huylebrouck, J. Hammer; From fractal geometry to fractured architecture: the federation square of Melbourne; Math. Intell., 28 (4) (2006), pp. 44–48
- James et al., 2006 K.R. James, N. Haritos, P.K. Ades; Mechanical stability of trees under dynamic loads; Am. J. Bot., 93 (10) (2006), pp. 1522–1530
- Kang et al., 2011 H.S. Kang, D. Dennis, C. Meneveau; Flow over fractals: drag forces and near wakes; Fractals, 19 (04) (2011), pp. 387–399
- Kull and Herbig, 1994 U. Kull, A. Herbig; Leaf venation patterns and principles of evolution; Stuttg.: Mitt. SFB, 230 (1994), pp. 167–175
- Larena, 2009 Larena, A.B., 2009. Shape design methods based on the optimisation of the structure. Historical background and application to contemporary architecture. In: Proceedings of the Third International Congress on Construction History, Cottbus.
- Leopold, 1971 L.B. Leopold; Trees and streams: the efficiency of branching patterns; J. Theor. Biol., 31 (2) (1971), pp. 339–354
- Lipman and Wright (2003) Lipman, J., Wright, F. L., 2003. Frank Lloyd Wright and the Johnson Wax Buildings. Courier Dover Publications
- Lipman and Wright, 1986 J. Lipman, F.L. Wright; Frank Lloyd Wright and the Johnson Wax Buildings, Courier Dover Publiction, New York (1986)
- Mandelbrot, 1982 B.B. Mandelbrot; The Fractal Geometry of Nature, W. H. Freeman and Co., New York (1982)
- Martinell, 1951 Martinell, C. (1951, Gaudi I la Sagrada Familia Comentada per all Mateix,Ayma, S.L. (Ed.), S. L. Editores; Barcelona.
- Mattheck, 1991 C. Mattheck; Trees: The Mechanical Design, Springer-Verlag; Berlin, Heidelberg, New York (1991)
- Mattheck and Kubler, 1997 C. Mattheck, H. Kubler; Wood – The Internal Optimization of Trees, Springer-Verlag, Berlin, Heidelberg, New York (1997)
- Metzger, 1893 K. Metzger; Der Wind als maûgebender Faktor fur das Wachstum der WaldbaÈume; MuÈndender Forstl. Hefte, 3 (1893), pp. 35–86
- Moore, 2012 Moore, R., 2012. Metropol Parasol, Seville by Jürgen Mayer H – Review. Art and Design. The Observer. Guardian.
- Nerdinger, 2005 W. Nerdinger; Frei Otto Complete Works: Lightweight Construction Natural Design, Birkhäuser, Basel; Boston; Berlin (2005)
- Orman, 2013 B. Orman; Art Nouveau & Gaudí: The way of nature; JCCC Honor. J., 4 (1) (2013), p. 2
- Park, 2005 J.H. Park; Early shape morphing: the metamorphosis of polygons in Antoni Gaudi׳s Sagrada Familia Cathedral and Le Corbusier׳s Firminy Chapel; J. Asian Archit. Build. Eng., 4 (1) (2005), pp. 25–30
- Pasquero et al., 2007 Pasquero, C., Poletto, M., and Kozikoğ lu, N., 2007. Fibrous Structures Workshop Evaluation Report. URL: 〈http://workshop.arkitera.com/fibrous/wp-content/uploads/2007/08/fibrous-report-lafarge-2705-ec.pdf〉 .
- Perguni and Andreani, 2013 P. Perguni, S. Andreani; Pier Luigi Nervi׳s columns: flow of lines and forces; J. Int. Assoc. Shell Spat. Struct., 54 (176–177) (2013), pp. 137–148
- Pollock, 2005 N. Pollack; Toyo Ito fuses structure and wrapper in a network of concrete trees at the new Tod׳s Omotesando Building in Tokyo; Archit. Rec., 193 (2005), pp. 78–85
- Pollio, 2004 Vitruvius Pollio; Ten books on architecture, Digireads.com Publishing; New York (2004)
- Puig Boada, 1929 I. Puig Boada; El Temple de la Sagrada Familin, Editorial Barcino, Barcelona (1929)
- Sasaki, 2007 M. Sasaki; Morphogenesis of Flux Structure, AA Publications, London (2007)
- Sassone and Piccoli, 2013 M. Sassone, E. Piccoli; The grid structures of Nervi׳s First Hangars in Orvieto: innovation in context; J. Int. Assoc. Shell Spat. Struct., 54 (3) (2013), pp. 159–168
- Saudi, 2002 Saudi, A., 2002. Gaudí i els seus coŀlaboradors: artistes i industrials a l׳entorn del 1900. In: Casanova, Rossend. Gaudí 2002. Misceŀlània. Planeta, Barcelona (in Catalan).
- Schulz and Hilgenfeldt, 1994 H.C. Schulz, S. Hilgenfeldt; Experimente zum Chaos; Spektrum Wiss., 1 (1994), pp. 72–81
- Shaw, 2000 I. Shaw; The Oxford History of Ancient Egypt, Oxford University Press, Oxford (2000)
- Sugraries, 1923 Sugraries Gras, D., 1923. Disposicio Esthtica del Temple de la Sagrada Familia. Anuario de In Asociacidn de Arquitectos de Cataluria. pp. 17–36.
- Thomas, 2001 P. Thomas; The shapes of trees: a matter of compromise; Arnoldia, 61 (1) (2001), pp. 14–21
- Thompson, 1992 D.W. Thompson; On Growth and Form (2nd ed. (1st ed., 1917)) (1992) (Dover reprint of 1942); Dover Publications, New York
- Walter and Leedy, 1978 C. Walter, Leedy Jr.; The origin of fan vaulting; Art Bull., 60 (2) (1978), pp. 207–213
- Wolfe, 1921 W.S. Wolfe; Graphical Analysis: A Text Book on Graphic Statics, McGraw-Hill book company, Inc., New York (1921)
- Yan et al., 2010 S. Yan, Hongtie Zhao, X. Jianyang; Experimental study on lateral stiffness of Dougong layer in Chinese historic buildings; Engi. Mech., 27 (3) (2010), pp. 74–78
- Zalewski and Allen, 1998 W. Zalewski, E. Allen; Shaping Structures: Statics, Wiley, New York (1998)
Document information
Published on 12/05/17
Submitted on 12/05/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?