Diseño de aliviaderos de bloques en forma de cuña

El agua es la fuerza motriz de la naturaleza
Leonardo Da Vinci

RESUMEN

Los aliviaderos de bloques en forma de cuña son una tipología innovadora que permite el sobrevertido sobre el cuerpo de presas de materiales sueltos de una manera segura, con la consiguiente ventaja económica que presenta frente a las soluciones habituales de aliviaderos exentos de hormigón. Sin embargo apenas se ha aplicado esta solución de aliviadero por algunas incertidumbres que plantea, fundamentalmente en cuanto al desarrollo de presiones intersticiales en la capa granular de apoyo de los bloques y sus efectos sobre la estabilidad de los mismos, así como por la ausencia de procedimientos técnicos de diseño.

En esta tesis doctoral se ha propuesto un procedimiento completo para el diseño de aliviaderos con bloques en forma de cuña, el cual se ha automatizado mediante el desarrollo de un código informático propio.

Como base para el desarrollo del procedimiento de diseño se han desarrollado varias campañas de modelación numérica, respaldadas por ensayos de validación en modelo físico. De tal forma que se caracterizó el comportamiento de la capa de drenaje y sus condiciones de saturación, se desarrolló un método para el ajuste numérico-experimental de leyes de pérdida de carga parabólica en medios porosos, así como una formulación para el cálculo del coeficiente de seguridad a deslizamiento de una capa de drenaje parcialmente saturada. También se calibró y validó un método numérico para reproducir el fenómeno de infiltración entre bloques. Finalmente se caracterizó la estabilidad de los bloques en forma de cuña ante acciones de vandalismo y frente a solicitaciones hidráulicas debidas al sobrevertido.

Según los resultados obtenidos en las campañas de modelación se propone un procedimiento de cálculo que permite definir la geometría apropiada de aliviadero, garantizando la estabilidad del cuerpo de presa, de la capa de drenaje y de los propios bloques, evitando la subpresión en el apoyo granular de los mismos con las incertidumbres que ello acarrea.

ABSTRACT

Wedge-shaped block spillways are an innovative typology that allows overflowing over the body of earth and rockfill dams in a safe and economic way, in front of the usual solutions of side concrete spillways. However, this solution has hardly been applied due to some uncertainties, related with the saturation process of the granular support layer and the stability effects induced on the blocks, as well as the lack of technical design procedures.

In this thesis a complete procedure has been proposed to design wedge-shaped block spillways. The procedure has been automated through the development of a computer code.

The development of the design procedure was based on several numerical campaigns, supported by physical validation tests. In such way the behavior of the drainage layer and its saturation conditions were characterized, a method for numerical-experimental fitting of parabolic head loss laws in porous media was developed, as well as a formulation to obtain a safety factor against mass sliding for partially saturated drainage layers. A specific numerical method was also calibrated and validated in order to reproduce the infiltration between blocks. Finally, the stability of wedge-shaped blocks was characterized against vandalism and hydraulic actions.

According to these results a specific procedure was proposed to define the appropriate spillway geometry, to ensure the stability of the dam body, the drainage layer and the blocks.

SIMBOLOGÍA

A sección transversal del drenaje.

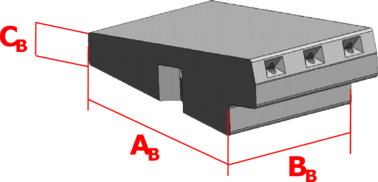
A_B es la dimensión longitudinal del apoyo del bloque testado para obtener el caudal de infiltración.

B_B es la dimensión transversal del apoyo del bloque testado para obtener el caudal de infiltración.

C_B es el espesor del bloque testado para obtener el caudal de infiltración.

a,b coeficientes dependientes del material poroso para ecuación parabólica.

B es el ancho del aliviadero.

B_v es el ancho de fondo de valle.

C es el número de Cauchy.

c,m coeficientes dependientes del material poroso para ecuación exponencial.

c cohesión del talud.

d profundidad de la superficie de rotura.

d₆₀ d₅₀ d₁₀ Tamaño de la abertura del tamiz que deja pasar en %.

d_s el diámetro equivalente de la piedra.

d_rr es el diámetro medio del rip-rap.

E factor de forma de piedras

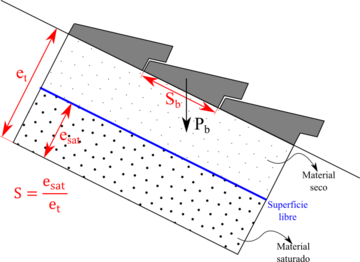
e_t espesor total de la capa de drenaje.

e_sat es el espesor saturado de la capa de drenaje.

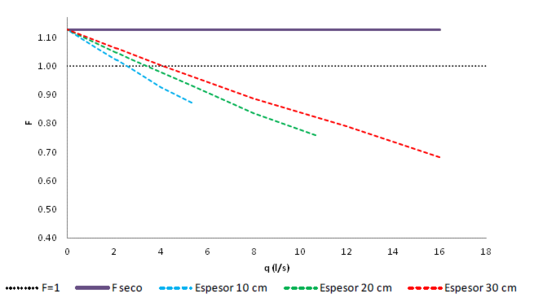
F coeficiente de seguridad frente al deslizamiento en masa.

F_d es el coeficiente de seguridad a deslizamiento del drenaje fijado por el usuario.

F_r coeficiente de seguridad a deslizamiento del repié fijado por el usuario.

g aceleración de la gravedad.

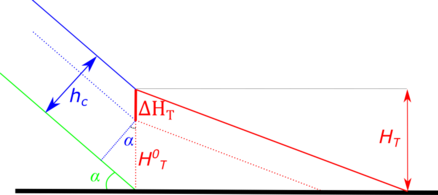
H es la altura del labio del aliviadero.

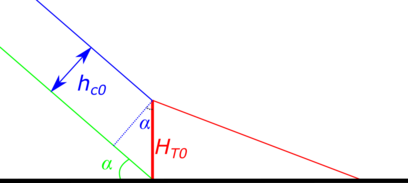
H_t0 es la altura del repié inicial.

H_t es la altura del repié.

h_c es la altura de los cajeros.

h_c0 es la altura inicial de los cajeros con factor de seguridad.

i gradiente hidráulico.

GS es el grado de saturación máximo fijado por el usuario.

Gs peso unitario de la partícula.

K permeabilidad intrínseca del medio.

k_l la permeabilidad en régimen laminar.

k_t la permeabilidad en régimen turbulento.

M es la masa del bloque definido por el usuario para diseñar el aliviadero.

M_B es la masa del bloque testado para obtener el caudal de infiltración.

N talud de aguas abajo del espaldón (H:V).

n porosidad.

P_i presión hidrostática.

P_B es el peso del bloque.

P₀ es presión absoluta.

P_v es la presión de vapor del agua a una cierta temperatura.

q caudal unitario.

q_i es el caudal unitario de infiltrado.

Q caudal absoluto circulante.

Re el número de Reynolds.

R_w es el número de filas de bloques.

S es el grado de saturación del drenaje en tanto por uno.

S₀ el talud de presa.

S_B es la superficie de apoyo del bloque.

T_c es el talud del cajero en grados.

v la velocidad media del agua en el medio poroso.

v_c velocidad crítica de erosión.

V₀ es la velocidad del agua sobre la pseudosolera del escalonado.

W es el número de bloques del aliviadero.

y calado.

y_d calado en el drenaje.

Z cota de la línea de corriente.

α es la pendiente de la presa en grados.

α_r es el talud del repié en grados.

β coeficiente de subpresión.

β₀ coeficiente de forma para movimiento turbulento.

γ_e,sat es el peso específico saturado del material.

γ_e,dry es el peso específico seco del material.

γ_s peso específico de la piedra aislada.

γ_w es el peso específico del agua.

φ ángulo de rozamiento interno del material.

λ factor de homotecia.

ρ_w densidad del agua.

σ factor de aireación definido como la relación entre el peso específico de la mezcla de agua y aire y el peso específico del agua.

σ_w coeficiente de subpresión.

V viscosidad dinámica del agua.

1. INTRODUCCIÓN

1.1. Motivación

Los aliviaderos de bloques en forma de cuña son una tipología innovadora que permite el sobrevertido sobre el cuerpo de presa, de una manera segura, en presas y balsas de materiales sueltos, con la consiguiente ventaja económica que presenta frente a las soluciones de aliviaderos exentos de hormigón, que son los que se proyectan de manera más habitual para las presas de materiales sueltos en la actualidad.

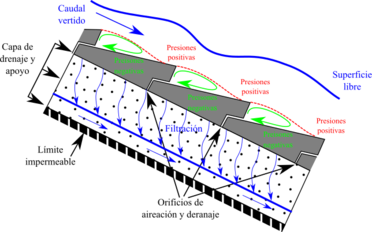
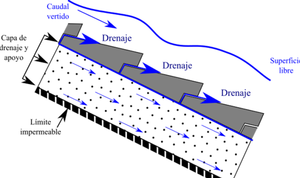
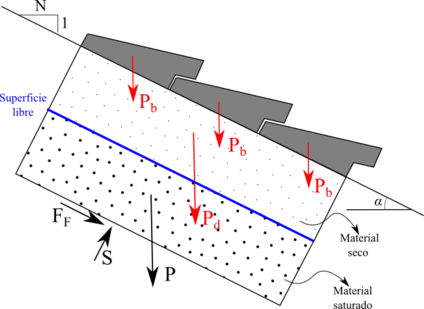
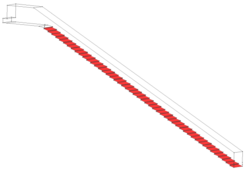
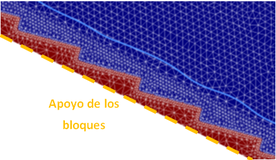
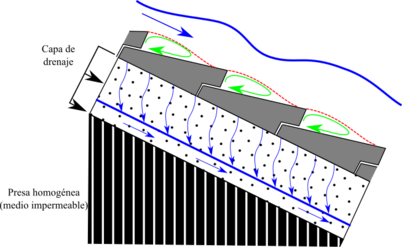
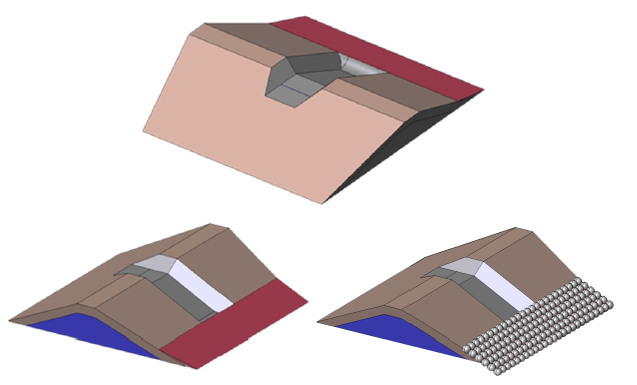
Los aliviaderos de bloques en forma de cuña están constituidos por bloques independientes de hormigón prefabricado, dispuestos uno junto al otro, sin ningún tipo de mortero que los una, y apoyados sobre una capa granular que actúa como capa de apoyo y drenaje para los bloques. A su vez esta capa granular se apoya sobre el espaldón de aguas abajo de la propia presa.

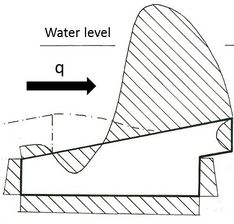
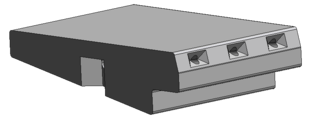
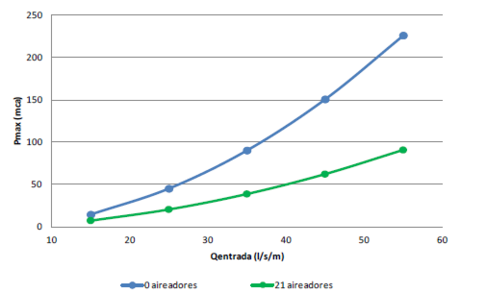
La forma de los bloques en forma de cuña genera un perfil escalonado (Figura 1) donde se desarrollan, cuando el agua circula sobre los bloques, zonas de presiones negativas inmediatamente aguas abajo de la contrahuella de cada escalón. Estas presiones negativas se transmiten, mediante unos aireadores, al contacto entre el bloque y la capa granular de apoyo, originando una succión estabilizadora entre ambos, lo que confiere una estabilidad adicional frente a diseños de bloques planos.

Figura 1. Esquema del funcionamiento hidráulico de un aliviadero de bloques en forma de cuña.

Esta tipología de aliviadero resulta de interés por el previsible ahorro de costes que implicaría en el proyecto de presas y balsas de materiales sueltos al no ser necesario construir un aliviadero exento (Figura 2).

Figura 2. Ejemplos de presas de materiales sueltos con aliviadero exento (Izquierda, presa Shuibuya, China) y con aliviadero de bloques en forma de cuña (derecha, presa de Barriga, España).

Sin embargo apenas se ha aplicado esta solución de aliviadero por algunas incertidumbres que plantea, fundamentalmente en cuanto al desarrollo de presiones intersticiales en la capa granular de apoyo y sus efectos sobre la estabilidad de los bloques, para distintos caudales de sobrevertido. En consecuencia, los pocos aliviaderos existentes de esta tipología se han diseñado apoyándose en ensayos físicos con modelos a una escala similar a la del propio aliviadero a proyectar y con caudales unitarios similares, para así disipar las mencionadas incertidumbres. Por ello el desarrollo de esta tipología de aliviadero se encuentra limitada en la actualidad a presas de altura y caudal de avenida moderados que permitan su ensayo físico a gran escala.

Para intentar profundizar en el conocimiento de este tipo de aliviaderos y optimizar su funcionamiento y diseño el Grupo de Investigación en Seguridad de Presas y Embalses (SERPA) de la Escuela Técnica Superior de Ingenieros de Caminos, Canales y Puertos de la UPM, junto con el Centro Internacional de Métodos Numéricos en Ingeniería (CIMNE) y la empresa de construcciones prefabricadas PREHORQUISA han llevado a cabo los proyectos de investigación ACUÑA (IPT20110997020000) y DIABLO, DESARROLLO DE UN CÓDIGO DE DISEÑO ÓPTIMO DE ALIVIADEROS FORMADOS POR BLOQUES EN FORMA DE CUÑA del Programa Estatal de Investigación, Desarrollo e Innovación Orientada a los Retos de la Sociedad 2014 (RTC201450815), obteniendo como resultados un nuevo prototipo de bloque forma de cuña “ACUÑA” que mejora el funcionamiento de diseños anteriores y un procedimiento automatizado para diseñar aliviaderos de bloques en forma de cuña. Esta tesis doctoral se ha desarrollado en el marco de estos dos proyectos de investigación.

1.2. Objetivos

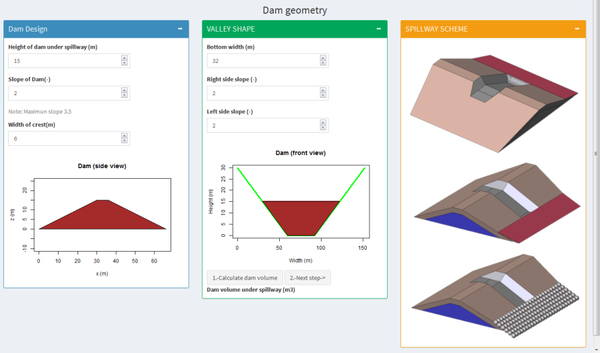
El objetivo fundamental de la tesis doctoral será la elaboración de un procedimiento que permita el diseño de aliviaderos con bloques en forma de cuña, y que sea susceptible de automatizarse mediante un programa informático. El procedimiento deberá a partir de los datos básicos de altura de presa, talud del espaldón, permeabilidad de los materiales y caudal de avenida de proyecto entre otros, para ofrecer como resultado: las características geométricas básicas del aliviadero, en lo relativo a la anchura del canal de descarga, la altura de los cajeros laterales y el tamaño y número de bloques necesarios para construir el aliviadero. Así como definir las características y espesores del material de la capa de apoyo y drenaje de los bloques para que no desarrolle presiones intersticiales cuando el aliviadero se encuentre en funcionamiento.

Para poder desarrollar el procedimiento planteado se deberán alcanzar los siguientes objetivos parciales.

• Caracterizar el comportamiento de la capa de drenaje para varios materiales porosos.

• Caracterizar y cuantificar los caudales de agua que alcanzan la capa de drenaje ante distintos escenarios de sobrevertido y taludes de espaldón.

• Determinación de las condiciones de estabilidad de los bloques en forma de cuña.

• Desarrollo de un algoritmo de diseño

Para alcanzar dichos objetivos se han desarrollado varias campañas de modelación numérica, respaldadas por ensayos de validación en modelo físico.

1.3. Estructura de la tesis

Esta tesis comienza con un resumen del estado del arte (capítulo 2) en conceptos relacionados con los aliviaderos de bloques en forma de cuña, tratando como aspectos fundamentales: las presas de materiales sueltos como elemento a proteger y las aplicaciones hasta la fecha de la tecnología aliviaderos de bloques y sus fundamentos.

En el capítulo 3 se define la metodología seguida para desarrollar las campañas de modelación de la investigación. Este capítulo se ha estructurado en tres subapartados que describen el método seguido para caracterizar la capacidad hidráulica de capas de drenaje, caracterizar caudales de infiltración entre bloques y determinar condiciones de estabilidad de los mismos.

En el capítulo 4 se muestran los resultados obtenidos en las campañas de modelación y se realiza la discusión de los mismos.

En base a los resultados y conclusiones obtenidas en los capítulos previos se desarrolla un procedimiento completo de diseño de aliviaderos de bloques en forma de cuña, recogido en el capítulo 5.

Finalmente, en el capítulo 6 se recoge un resumen de las conclusiones generales de esta tesis, las aportaciones originales realizadas y las posibles líneas de investigación futura.

2. ESTADO DEL ARTE

El estado del arte de esta tesis se ha dividido en dos apartados, que agrupan los principales antecedentes en relación a su campo de investigación. La división por apartados es la siguiente:

• Las presas de materiales sueltos.

• Los aliviaderos de bloques en forma de cuña.

Cada uno de estos apartados cuenta con una sección específica relativa a la aplicación de modelos numéricos de simulación en ese campo.

2.1. Las presas de materiales sueltos

2.1.1. Introducción

El término presas de materiales sueltos engloba una gran variedad de subtipologías de presas, como las presas de núcleo y escollera, presas de pantalla o presas homogéneas entre otras. Todas ellas tienen en común el estar constituidas por materiales granulares, bien sean cohesivos o no cohesivos. Las presas de materiales sueltos, en general, presentan una ventaja económica en la construcción del cuerpo de presa frente a otras tipologías, por la eficiencia de los medios de puesta en obra. Sin embargo no son capaces en términos generales de desaguar sobre ellas un tiempo prolongado caudales importantes sin sufrir daños estructurales. Por tanto es necesario en la mayoría de los casos construir órganos de desagüe exentos al cuerpo de presa que encarecen la obra y hacen que la ventaja económica frente a otras tipologías de presa se reduzca o incluso desaparezca.

A continuación se expone el estado del arte sobre las presas de materiales sueltos en sus aspectos más relevantes, relativos a las características mecánicas de los materiales porosos no cohesivos, la caracterización de su capacidad hidráulica, sus procesos de rotura y posibles protecciones.

2.1.2. Características mecánicas

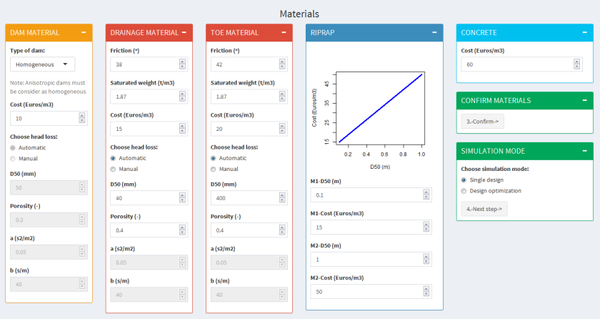
Los materiales porosos no cohesivos empleados en las presas de materiales sueltos (fundamentalmente en sus espaldones) pueden ser de características muy diferentes, desde materiales tipo grava o zahorra hasta tipo escollera con piedras de gran tamaño. Estos materiales se caracterizan principalmente por su ángulo de rozamiento interno y por su alta permeabilidad, siendo estos parámetros los que condicionan la resistencia mecánica del espaldón y la formación de la red de filtración en su interior. La función primordial de estos materiales es estabilizar el elemento impermeable.

La definición del ángulo de rozamiento interno de un material presenta ciertas incertidumbres por lo que se han llevado a cabo diversas investigaciones en esta línea.

Trollope [1] calculó teóricamente el ángulo de rozamiento interno de partículas subredondeadas, y Parkin [2] concluyó que el ángulo de rozamiento interno para materiales con partículas pequeñas (arenas) se parece al ángulo teórico, sin embargo conforme crece el tamaño de las partículas del material, y su forma se aleja de la redondeada, observa que el ángulo real se aleja del teórico previsto por Trollope.

En esta línea Yu et al. [3] concluyeron que al aumentar el tamaño máximo de las partículas, a igualdad del resto de parámetros, el ángulo de rozamiento interno del material aumenta.

De Cea y Olalla [4] realizaron un estudio del rozamiento interno de los materiales de distintas presas de materiales sueltos españolas, observando que existe una gran heterogeneidad según la presa y que la diferencia entre el ángulo de rozamiento interno de un material no cohesivo seco o saturado es escasa.

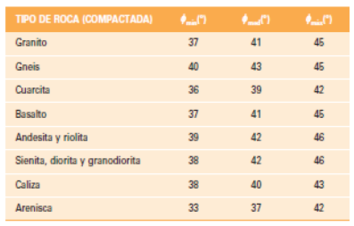
Por último indicar que la Guía para el proyecto y la ejecución de muros de escollera en obras de carretera [5], publicada por el Ministerio de Fomento dentro de su serie normativa, ofrece una serie de tablas donde indica los valores habituales del ángulo de rozamiento interno según tipo de material y forma de puesta en obra, basando sus resultados para la escollera compactada (Figura 3) en el estudio de presas de materiales sueltos españolas.

Figura 3. Valores de referencia para el ángulo de rozamiento interno de escollera compactada para distintos materiales. Fuente: Guía para el proyecto y la ejecución de muros de escollera en obras de carretera [5].

2.1.3. Capacidad hidráulica

Toledo [6] definió el proceso de saturación del espaldón de una presa de materiales sueltos según el siguiente proceso:

1) Infiltración (qi).

Fase inicial, formación un nivel de agua en el cimiento (supuesto impermeable) y sin salida de agua por el espaldón.

2) Infiltración (qi) y circulación interna (qci).

El caudal infiltrado circula por el espaldón saliendo posteriormente por el pie del talud.

3) Infiltración (qi), circulación interna (qci) y circulación externa (qce) al espaldón.

Parte del caudal se infiltra, parte circula por el espaldón saliendo por el pie y parte circula por el exterior en la dirección del talud.

d) La última fase desemboca en la saturación completa del espaldón.

Para caracterizar detalladamente el grado de saturación de un material poroso no cohesivo es preciso conocer la ley de pérdida de carga de ese material.

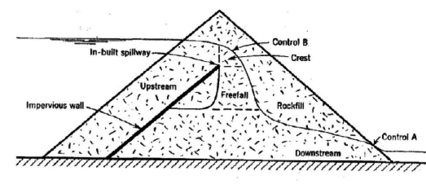
En esta línea los trabajos de Parkin et al. [7],[8], compararon las redes de filtración obtenidas con fórmulas de pérdida de carga lineal y exponencial, observando distintas alturas de saturación, aunque en la zona del pie se observaron resultados similares. También los autores obtuvieron conclusiones sobre el control hidráulico a lo largo del dominio de filtración según las condiciones de funcionamiento, observando dos controles hidráulicos, como se aprecia en la Figura 4. Este aspecto del control hidráulico resulta determinante para la simulación numérica de la línea de saturación con simplificaciones unidimensionales.

Figura 4. Controles hidráulicos en medio poroso. Fuente: Parkin et al. [7],[8].

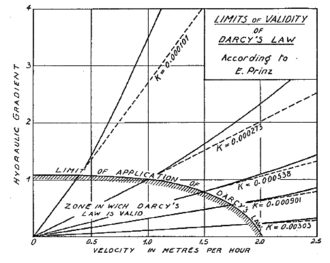
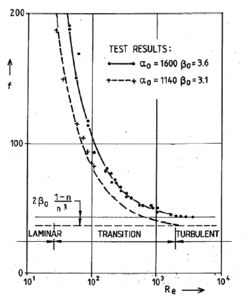
Leliavsky [9] destacó la importancia del material fino en la definición de la permeabilidad de un material granular, y analizó los límites de aplicación de la fórmula de pérdida de carga lineal en función del la velocidad de filtración y del gradiente hidráulico obteniendo el gráfico de la Figura 5.

Figura 5. Limites de aplicación de la fórmula de pérdida de carga lineal. Fuente: Leliavsky [9].

Posteriormente Solvik [10] clasifica la filtración en materiales porosos mediante tres tipos de leyes en función del predominio del régimen hidráulico:

1) Laminar:

$v={k}_{l}\cdot i$

(1)

Siendo:

${k}_{l}={\frac {1}{{\alpha }_{0}}}\cdot {\frac {{n}^{2}}{{(1-n)}^{3}}}\cdot {\frac {g\cdot {d}_{l}^{2}}{\nu }}$	(2)
${d}_{l}={d}_{10}$	(3)

2) Turbulento:

${v}^{2}={k}_{t}\cdot i$

(4)

Siendo:

$Re={\frac {v\cdot {d}_{t}}{\nu }}>600$	(5)
${d}_{t}=1.7\cdot {d}_{10}$	(6)
${k}_{t}={\frac {1}{{\beta }_{0}}}\cdot {\frac {{n}^{3}}{1-n}}\cdot g\cdot {d}_{t}$	(7)

β₀ coeficiente de forma para movimiento turbulento.

Re el número de Reynolds.

3) Transición:

$i={\frac {v}{{k}_{l}}}+{\frac {{v}^{2}}{{k}_{t}}}$

(8)

Siendo:

k_l la permeabilidad en régimen laminar.

k_t la permeabilidad en régimen turbulento.

El autor compara (Figura 6) la curva teórica obtenida según su formulación con resultados de ensayos físicos.

Figura 6. Comparación entre resultados teóricos de emplear la formulación de Solvik y ensayos físicos. Fuente: Solvik [10].

En esta misma línea Toledo [6] realizó el estudio de la ley de resistencia aplicable a medios porosos con alta permeabilidad, típicos en los espaldones de las presas de materiales sueltos. Concluyendo que una ley lineal, no es aplicable a la filtración en materiales granulares gruesos al no contemplar su régimen turbulento. En consecuencia concluyó que la ley aplicable es del tipo:

$i=c\cdot {v}^{m}$

(9)

Siendo:

c, m coeficientes dependientes del material.

v la velocidad media del agua en el medio poroso.

La ley exponencial que utilizó Toledo es equivalente a la siguiente ley parabólica, más extendida en la literatura técnica:

$i=a\cdot v+b\cdot {v}^{2}$

(10)

Siendo:

a,b coeficientes dependientes del material.

v la velocidad media del agua en el medio poroso.

Para la determinación de los valores de los coeficientes a, b dependientes del material existen diversas formulaciones, entre las que destacan entre otras:

Ergun [11]:

$i=150\cdot {\frac {{(1-n)}^{2}}{{n}^{3}}}\cdot {\frac {V}{g\cdot {d}_{50}}}\cdot v+$$1.75\cdot {\frac {(1-n)}{{n}^{3}}}\cdot {\frac {{\rho }_{w}}{{d}_{50}}}\cdot {v}^{2}$

(11)

Siendo:

i gradiente hidráulico.

n porosidad.

g aceleración de la gravedad.

v la velocidad media del agua en el medio poroso.

V viscosidad dinámica del agua.

d₅₀ diámetro medio de las partículas.

ρρ_w densidad del agua.

Ward [12]:

$i={\frac {V}{g\cdot K}}v+0.55\cdot {\frac {1}{g{\sqrt {K}}}}\cdot {v}^{2}$

(12)

Siendo:

i gradiente hidráulico.

g aceleración de la gravedad.

v la velocidad media del agua en el medio poroso.

V viscosidad dinámica del agua.

K permeabilidad intrínseca del medio.

Se debe tener en cuenta que estas leyes no tienen en cuenta la posible anisotropía del medio poroso generado por los procesos de compactación y puesta en obra. En esta línea Cruz et al. [13] señalan que considerar un medio isótropo cuando realmente puede contener estratos anisótropos queda del lado de la inseguridad, al aumentar la saturación del medio.

Por último dentro de este apartado cabe destacar que Zeigler [14], mediante ensayos físicos en el USBR, estudió el flujo en un canal relleno de arena de talud inclinado, concluyendo que la posición de la superficie libre del agua es paralela a la solera del mismo en todo su recorrido (Figura 7). Es equivale a decir que el calado se mantiene constante a lo largo un canal inclinado con medio poroso, así como su velocidad.

Figura 7. Ensayos de filtración en canal de arena de Zeigler. Izquierda: imagen de la instalación. Derecha: esquema del flujo observado. Fuente: Zeigler [14].

2.1.4. Procesos de rotura

Sparks [15] identificó hace más de 50 años los dos mecanismos de rotura de espaldones de presa de material granular no cohesivo, el de erosión y el deslizamiento en masa. Ambos mecanismos pueden actuar de manera separada o conjunta en función del caudal, el talud de la presa y el material de su espaldón, como indicó Morán [16].

En cuanto al mecanismo de erosión ya a finales de los años 70 del pasado siglo Stephenson [17] indicó que la estabilidad a deslizamiento por arrastre es más crítica que la estabilidad al vuelco en partículas aisladas sometidas a un caudal de agua en un talud.

Posteriormente Hartung y Scheuerlain [19] describieron aspectos asociados al mecanismo de erosión, como son la aparición de presiones intersticiales, la migración de partículas del cuerpo de presa, y la erosión de la superficie del espaldón por las altas velocidades del agua superficial, el cual es altamente turbulento y aireado.

Los autores desarrollaron una formulación para determinar la velocidad crítica de arrastre de piedras. Esta formulación permite definir el tamaño de piedra para evitar su erosión:

${V}_{c}=1.2\cdot {\sqrt {\frac {2\cdot g\cdot ({\gamma }_{s}-{\gamma }_{w})}{\sigma \cdot {\gamma }_{w}}}}\cdot {\sqrt {{d}_{s}\cdot cos\alpha }}$

(13)

Siendo:

v_cvelocidad crítica a la que la piedra empieza a moverse.

γ_s peso específico de la piedra.

γ_w peso específico del agua.

d_s el diámetro equivalente de la piedra.

σ factor de aireación definido como la relación entre el peso específico de la mezcla de agua y aire y el peso específico del agua.

α ángulo del talud con la horizontal.

En esta línea también Skoglund et al. [18] llevaron a cabo ensayos físicos para analizar la erosión, concluyendo, de la misma manera que Hartung y Scheuerlain, que es posible evitarla según sean la granulometría del material, el caudal circulante y el talud.

Knauss [20] realizó una revisión de los distintos estudios de erosión llevados a cabo por varios autores, entre ellos Olivier [21] o Hartung y Scheuerlain. El autor propuso modificar la expresión de Hartung y Scheuerlain según:

$q=0.84\cdot {\sqrt {Gs}}\cdot (1.9+0.8\cdot \varnothing -3sen\alpha )$	(14)
$\varnothing =0.0575\cdot Gs\cdot {N}^{1.5}$	(15)

Siendo:

q caudal unitario de vertido crítico.

Gs peso unitario de la partícula.

α ángulo del talud con la horizontal.

N nº de partículas por unidad de área.

Toledo [22] incluyó un coeficiente de seguridad frente a la erosión en base a la fórmula de Hartung y Scheuerlain modificada por Knauss, basado en mayorar el caudal de vertido crítico a partir del cual se obtiene el tamaño del material no erosivo. El autor propuso utilizar el caudal real de vertido para situaciones en las que resulten admisibles movimientos aislados de piedras (coeficiente de seguridad 1) y duplicar el caudal real de vertido para el cálculo cuando no se permita admitir ningún tipo de movimiento en las piedras (coeficiente de seguridad 2). Además ofrece valores para incluir el efecto de compacidad de las partículas por el parámetro, siendo 0.625 para escollera vertida y 1.125 para escollera colocada manualmente.

Recientemente Bartsch y Nilsson [23] han propuesto un procedimiento para dimensionar el tamaño medio de la piedra necesaria para evitar la erosión por arrastre, el método se basa en determinar la permeabilidad de la escollera. La formulación propuesta es la siguiente:

${D}_{50}=0.6\cdot {S}^{0.43}\cdot {q}^{0.78}$

(16)

Siendo:

S₀ el talud de presa.

q el caudal unitario crítico.

Una vez evitada la erosión superficial de las partículas, el mecanismo de rotura que puede provocar el colapso del espaldón de presa en presencia de presiones intersticiales es el deslizamiento en masa [24].

Parkin [2] definió que la forma de rotura del espaldón por deslizamiento en masa tiene carácter circular, y es un fenómeno rápido e imprevisible, por lo que resulta más difícil de prever que la erosión. Según este autor existen diferencias sobre la profundidad de los círculos de rotura pésimos calculados con los métodos de equilibrio límite y los observados en los casos estudiados en laboratorio, cuya profundidad es sensiblemente mayor.

Cruz et al. [13] concluyeron que los factores que más condicionan el deslizamiento en masa son el caudal unitario de vertido, la altura de la línea de saturación en la zona de emergencia de la infiltración y las características de permeabilidad de la escollera. Establece que el patrón de rotura está compuesto por un deslizamiento progresivo que va remontando desde el pie de presa hasta su coronación.

Toledo [6] indicó que el deslizamiento en masa en materiales no cohesivos se produce al desarrollarse el campo de presiones intersticiales en el espaldón a medida que éste se va saturando. Además también indica que la filtración es un fenómeno acoplado al proceso de rotura porque al variar la geometría del espaldón durante la rotura varía el dominio de filtración y sus contornos. El autor estudió numéricamente el comportamiento hidráulico de espaldones totalmente saturados sin circulación superficial de agua, empleando geometrías sin deformar y leyes de resistencia de carácter exponencial. En sus conclusiones principales indica cómo la zona del pie de presa es la más susceptible de sufrir deslizamiento por concentrar los mayores valores de presiones relativas, además pone de manifiesto cómo los taludes mayores dan como resultado líneas de filtración más largas, y por ello gradientes menores, lo que los hace más estables frente al deslizamiento en masa.

Toledo define el gradiente máximo como:

${i}_{max}={\frac {1}{N}}$

(17)

Siendo:

N talud de aguas abajo del espaldón.

El autor justificó la anterior expresión del gradiente máximo por la impermeabilidad del cimiento de la presa hace que las líneas de filtración sean horizontales en la zona del pie de presa en el caso de espaldón saturado. Toledo también concluyó que la dependencia del caudal de saturación con la altura de la presa es lineal.

Una vez estudiado el comportamiento hidráulico el autor abordó el estudio de la estabilidad a deslizamiento, definiendo el área inestable a deslizamiento como la envolvente de círculos de deslizamiento con coeficiente de seguridad inferior a la unidad, según el método de Bishop [25] y en base a un estudio paramétrico con variación del talud, el ángulo de rozamiento interno, el peso específico saturado de la escollera, la profundidad de los círculos de rotura, la linealidad o no de la fórmula de resistencia y la magnitud del área inestable.

Las conclusiones más importantes del trabajo fueron que los círculos de rotura pésimos se producen en el pie de presa y son superficiales, así como que adoptar una ley de filtración lineal no afecta sustancialmente al equilibrio del talud. Lo que coincide con los resultados de Parkin [7] que indicaban una mínima diferencia del campo de presiones en el pie de presa entre la ley de filtración lineal y la no lineal.

Finalmente Toledo propone una fórmula de estabilidad para espaldón saturado:

$F={\frac {1}{{\gamma }_{e,sat}}}\cdot \left({\gamma }_{e,sat}-{\frac {\beta \cdot {\gamma }_{w}}{{cos}^{2}\alpha }}\right)\cdot {\frac {tan\Phi }{tan\alpha }}$	(18)
${\textstyle \beta =-0.32\cdot {N}^{2}+\,1.52\cdot N-0.77}$, si 1.5<N<2	(19)
${\textstyle \beta =1}$ si , N>2	(20)

Siendo:

F coeficiente de seguridad frente al deslizamiento en masa.

γ _e,sat peso específico saturado de la escollera.

γ_w peso específico del agua.

φ ángulo de rozamiento de la escollera.

α ángulo de la superficie del espaldón con la horizontal.

N talud del espaldón.

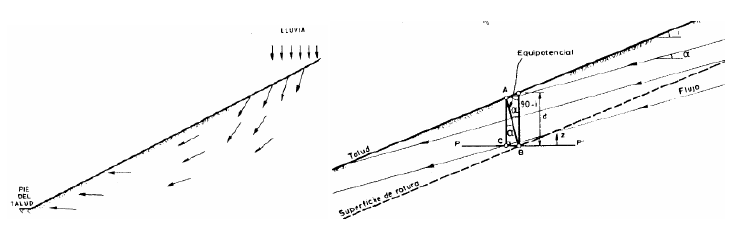
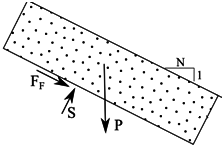
Alonso [26], desde un punto de vista distinto al de la ingeniería de presas, propuso una expresión para definir la estabilidad de taludes naturales sometidos a flujos internos de agua (Figura 8), y propuso la siguiente expresión para el coeficiente de seguridad a deslizamiento, que tiene en cuenta la dirección del flujo de agua en el interior del talud:

Figura 8. Parámetros geométricos utilizados por Alonso para definir la estabilidad de taludes naturales sometidos a flujos internos de agua. Fuente: Alonso [26].

$F={\frac {c}{\mathrm {{\gamma }_{e,sat}\cdot d\cdot seno} \,\left(i\right)\cdot \mathrm {cos} \,\left(i\right)}}+$$\left[\left(1-{\frac {{\gamma }_{w}\cdot \mathrm {cos} \,\left(\alpha \right)}{{\gamma }_{e,sat}\cdot \mathrm {cos} \,\left(i\right)\cdot \mathrm {cos} \,\left(\alpha -i\right)}}\right)\cdot {\frac {tan\Phi }{tani}}\right]$

(21)

Siendo:

F coeficiente de seguridad frente al deslizamiento en masa.

γ _e,sat peso específico saturado de la escollera.

γ_w peso específico del agua.

φ ángulo de rozamiento de la escollera.

i ángulo de la superficie del espaldón con la horizontal.

α ángulo del flujo de agua con la horizontal.

c cohesión del talud.

d profundidad de la superficie de rotura.

Como se puede observar las expresiones a las que llegaron Toledo y Alonso por caminos distintos son muy similares. De tal forma que operando en la fórmula de Alonso para que tenga la misma estructura exacta que la de Toledo se obtiene lo siguiente:

$F={\frac {1}{{\gamma }_{e,sat}}}\cdot \left({\gamma }_{e,sat}-{\frac {{\beta \cdot \gamma }_{w}}{{cos}^{2}i}}\right)\cdot {\frac {tan\Phi }{tani}}$	(22)
$\beta ={\frac {\mathrm {cos} \,\left(\alpha \right)\cdot \mathrm {cos} \,\left(i\right)}{\mathrm {cos} \,\left(\alpha -i\right)}}$	(23)

Siendo:

F coeficiente de seguridad frente al deslizamiento en masa.

γ _e,sat peso específico saturado de la escollera.

γ_w peso específico del agua.

φ ángulo de rozamiento de la escollera.

i ángulo de la superficie del espaldón con la horizontal.

α ángulo del flujo de agua con la horizontal.

β coeficiente de subpresión.

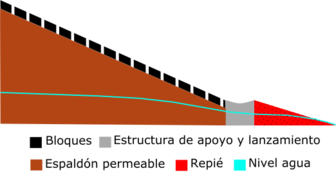
2.1.5. Las protecciones con repiés

La protección mediante repiés es un método habitual de estabilización de laderas frente deslizamiento y consiste en disponer un material de alta permeabilidad con un talud tendido en la zona próxima al pie de la estructura que se desea proteger. El principio teórico de esta protección es crear un talud quebrado más tendido en la zona del pie, que es donde se concentran los mayores gradientes hidráulicos [22].

En el campo de la ingeniería de presas se ha empleado esta solución tradicionalmente como protección frente a la erosión interna de espaldones, si bien en los últimos años, fundamentalmente en los países nórdicos [27],[28], se han empleado los repiés como protección frente al deslizamiento en masa ante posibles fallos del elemento impermeable o sobrevertidos accidentales.

En el campo de las protecciones de presas de materiales sueltos con repié se han llevado a cabo diversas investigaciones en los últimos años.

En concreto en 2005 se publicó el estudio noruego EBL Kompetanse [29] que presentaba un procedimiento de diseño de protecciones tipo repié de escollera frente a la rotura por arrastre, obteniendo una expresión de dimensionamiento del tamaño de piedra para conseguir un repié estable.

${D}_{50}=0.31\cdot {S}^{0.43}\cdot {q}^{0.78}$

(24)

Siendo:

S₀ el talud de presa.

q: el caudal unitario crítico.

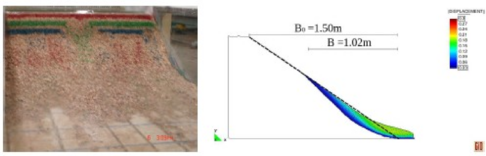
El trabajo más reciente en esta línea de protecciones ha sido el de Morán [16], quién propuso un procedimiento completo de diseño para repiés de escollera, basándose en simulaciones físicas y numéricas. Estudió la influencia de múltiples parámetros que afectan a la eficacia del repié ante el fenómeno del deslizamiento en masa, tales como la anchura de la berma, el talud exterior y su altura máxima desde la base. En concreto el autor concluye que la anchura óptima de berma es la mínima que permita una correcta puesta en obra del material del repié, para así reducir al máximo la longitud de las líneas de corriente, y por tanto la pérdida de carga y nivel de agua dentro del repié. También indicó como un talud de repié excesivamente tendido aumenta la pérdida de carga, y por tanto puede resultar contraproducente para la estabilidad del mismo. El autor también introdujo los conceptos de “caudal de incubación” y “camino crítico de rotura” para caracterizar los procesos de rotura de presas de materiales sueltos [30]. En la Figura 9 se muestra uno de los ensayos llevados a cabo por Morán [16] para validar su procedimiento de diseño de repiés, de hecho se observa en la imagen superior el deslizamiento en masa que se produce para un cierto caudal y presa sin proteger, y en la imagen inferior cómo al introducir el repié calculado basándose en la metodología propuesta la estructura no sufre daños.

Figura 9. Ensayos de validación del procedimiento de diseño de protecciones tipo repié realizados por Morán. Fuente: Morán [16].

2.1.6. Modelación numérica

Muchos autores durante las últimas décadas han propuesto modelos numéricos para analizar el flujo en medios porosos de baja permeabilidad y flujo laminar [31][32][33], sin embargo estos enfoques clásicos no son aplicables para medios de alta permeabilidad y flujo turbulento, en los que los niveles de saturación pueden variar de forma rápida. Ha habido varios enfoques para afrontar este problema, desde considerar modelos estacionarios para evaluar el gradiente hidráulico debido a la filtración [34][35], como aquellos basados en resolver las Ecuaciones de Navier-Stokes considerando la estructura porosa como impermeable [36][37][38]. Recientemente se han concebido algunos modelos RANS para simular flujos en estructuras costeras [39][40][41].

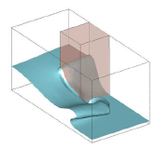
Larese et al.[42], desarrollaron un algoritmo en código abierto para resolver de manera acoplada la dinámica de fluidos en dominios con medio poroso y no poroso, para altas permeabilidades y régimen turbulento, mediante implementación de leyes de pérdida de carga parabólica que promedian la velocidad en el dominio global. Para ello modificaron las ecuaciones clásicas de Navier-Stokes, con el objetivo principal de simular de manera unificada la filtración dentro del medio poroso y la superficie libre. Un resumen esquemático del proceso seguido se muestra en la Figura 10.

Figura 10. Esquema de la formulación propuesta por Larese et al., promedio de velocidad entre zonas vacías y llenas u y esquemas de conservación de masa y momento Fuente:[42]

Este problema acoplado se resuelve utilizando un algoritmo estabilizador semi-explícito de paso fraccional, donde la velocidad se calcula usando un esquema de Runge-Kutta de 4º orden. La formulación numérica se desarrolla en un marco Euleriano utilizando una técnica Level Set para rastrear la evolución de la superficie libre. El código de elementos finitos resultante permite su fácil paralelización OpenMP, y se encuentra disponible en código abierto en el entorno Kratos Multiphisys [43]. En la Figura 11 se muestran algunos test realizados con el código numérico desarrollado por Larese et al., donde se observa la evolución de la superficie de agua tanto en la zona libre como en el interior de un medio poroso.

Figura 11. Simulación numérica del fenómeno de “dam break” a través de dominios poroso y libre con el código desarrollado por Larese et al. Fuente:[42]

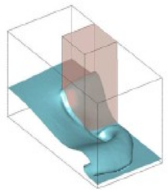
En el desarrollo de su tesis doctoral Larese [44] acopló el código de simulación hidráulica en medios porosos y no porosos antes descrito con un código de simulación estructural, lo que le permitió modelar el fenómeno de rotura de un espaldón de presa de materiales sueltos de manera evolutiva [45] (Figura 12), es decir, modificando de manera dinámica el dominio medio poroso-medio libre y recalculando su saturación y estabilidad.

Figura 12. Comparación entre deformaciones de espaldón en modelo físico y predichas por modelo numérico acoplado desarrollado por Larese. Fuente:[44]

El código que utilizó para el cálculo de la estabilidad estructural del espaldón fue PFEM [46][47] (Método de partículas y elementos finitos). Es un método lagrangiano, que considera los nodos de la malla de elementos finitos como partículas, que según las condiciones de presión y velocidad modifican su posición haciendo necesario el remallado entre cada paso de cálculo. Hay que destacar que la combinación de un código basado en un método euleriano (código hidráulico) con otro basado en un método lagrangiano (código estructural) hace que su acoplamiento sea complejo.

2.2. Los aliviaderos de bloques en forma de cuña

2.2.1. Introducción histórica

La utilización de los bloques prefabricados de hormigón como protección frente al sobrevertido en presas de materiales sueltos tuvo su origen en el Instituto de Ingeniería Civil de Moscú al final de la década del los 60 del siglo XX.

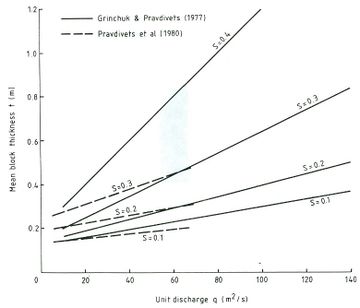
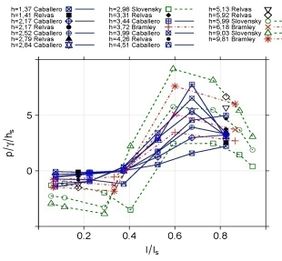
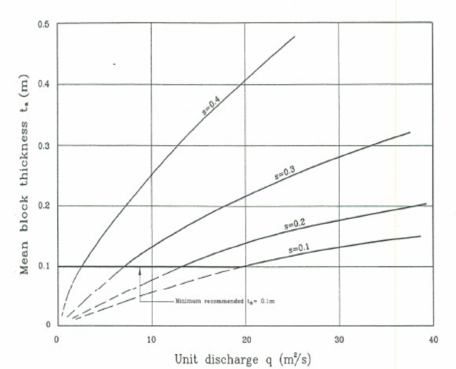
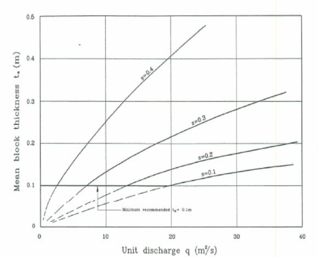
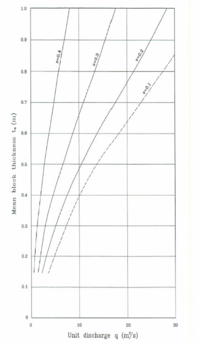
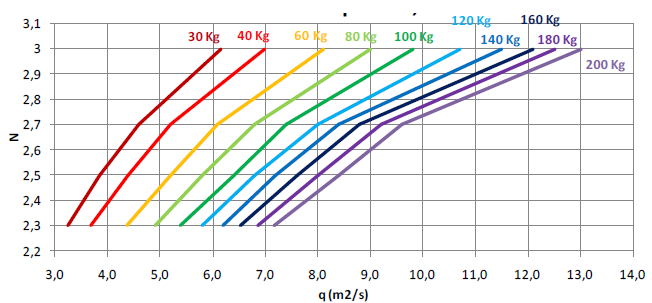
Los primeros trabajos en esta línea desarrollados en la antigua URSS fueron los de Gordienko [48] y Grinchuk et al. [49][50] que comenzaron el ensayo de protecciones formadas por losas de hormigón prefabricado. Estos primeros trabajos desembocaron en un primer diseño de bloque en forma de cuña (WSB en adelante) y fueron el comienzo de desarrollos posteriores en la década de los años 80 [51][52][53][54][55]. Definiendo con estos estudios unas curvas de diseño (Figura 13) que estiman el espesor promedio de bloque para asegurar su estabilidad, con diferentes pendientes muy tendidas para distintos caudales unitarios de vertido y factor de seguridad 1.5 [56].

Figura 13. Curvas de diseño de WSB, siendo s la pendiente. Fuente: Bramley [56].

A pesar de los prometedores resultados que lograron los soviéticos en este campo la política de bloques de la época impidió la exportación de esta tecnología a los países occidentales. Sin embargo tras la caída de la URSS en la década de los 90 comenzó el desarrollo de la tecnología en los países occidentales, tras conocerse los estudios rusos.

2.2.2. Trabajos recientes de investigación

Recientemente se han llevado a cabo investigaciones en el campo de los bloques en forma de cuña (WSB) en Reino Unido, EE.UU., Portugal y España. A continuación se describen brevemente cada uno de estos trabajos.

Reino Unido

Los ensayos del grupo británico se realizaron en la Universidad de Salford, liderados por el Prof. Baker que desarrollo su tesis doctoral en este ámbito [57]. La instalación de ensayo tenía una altura de 4 m y una pendiente fija (s) de 0.4, (2.5H: 1V) y se usaron tres tamaños diferentes de WSB.

De los ensayos llevados a cabo se obtuvo un mapa de presión promedio en las caras de los bloques, que venía a confirma la distribución de presión teórica esperada por los flujos inducidos por el escalonado de los bloques. Se observó una zona de alta presión en la zona final de la huella y de baja presión en la zona inicial, lo que garantiza la estabilidad del bloque por su solapamiento (Figura 14).

Figura 14. Distribución de presiones observada en contornos de bloque. Fuente: Morán [59].

El grupo también realizó ensayos para determinar la superficie óptima de aireadores en el WSB testado. Así mismo se comprobó que es conveniente que los bloques se dispongan lo más juntos posibles para maximizar los efectos estabilizantes de la succión por los conductos de aireación. También los ensayos demostraron que incrementar la descarga unitaria aumentaba la succión y estabilidad de los bloques para las condiciones de talud, caudal y bloque ensayados.

El grupo británico confirmó la recomendación de Pravdivets de no permitir la formación de resaltos hidráulicos sobre bloques no específicamente dispuestos para el efecto. Los ensayos llevados a cabo mostraron dos modos de fallo por resalto hidráulico diferentes (Figura 15): bloques individuales que vibran de forma normal a la superficie del terraplén y grupos de bloques que se balancean arriba y abajo.

Figura 15. Modos de fallo de bloques bajo resalto hidráulico. Fuente: Bramley [60].

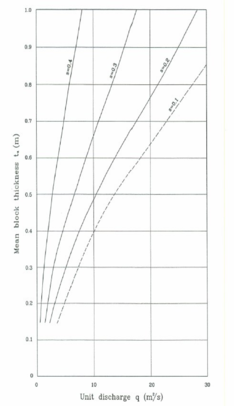
En consecuencia se propusieron nuevas curvas de diseño para bloques bajo un resalto hidráulico, recomendando tamaños de bloque mucho mayores a los de canal de descarga y taludes más tendidos.

Figura 16. Tabla de diseño de bloques bajo resalto hidráulico en función de pendiente (s), espesor medio de bloque y caudal. Fuente: [58].

Los trabajos realizados dieron como resultado el manual Design of stepped- block spillways de la Asociación de Información de la Industria de la Construcción (CIRIA) del Reino Unido [58], que es en la actualidad uno de los principales referentes para el diseño de aliviaderos WSB.

EE.UU.

Los primeros estudios con WSB en EE. UU. fueron promovidos por la Administración Federal de Carreteras [61]. Con un trabajo experimental desarrollado en el laboratorio de hidráulica de la Colorado State University (CSU) para diferentes protecciones de bloques articulados, entre ellos los WSB. Estos se colocaron sobre geotextil y una geomalla, con fines de drenaje. Los WSB se diseñaron según los criterios rusos y se probaron para calados de 1.2 m, que correspondían a una descarga de aproximadamente 2.07 m²/s aproximadamente. Se concluyó que los WSB eran estables en tales condiciones, con una velocidad de 5.2 m/s y un esfuerzo cortante de 5.2 kN / m2, pero se observaron vibraciones. En base a esta investigación, se publicó una metodología para analizar el factor de seguridad de estabilidad de diferentes sistemas de protección de bloques de hormigón articulados, incluidos los WSB [62] [63].

Posteriormente continuaron esta línea de investigación el United States Bureau of Reclamation (USBR) y la CSU, considerando las evidencias de los beneficios del sistema de protección WSB puestas de manifiesto. En estas nuevas investigaciones se desarrollaron tests en dos instalaciones experimentales. La instalación más pequeña tenía un canal de 0.46 m de ancho y 4.6 m de alto, con una descarga de unidad disponible de 1.3 m2 / s. El más grande era una instalación al aire libre (Figura 17), con dimensiones próximas a prototipo, con un canal de pendiente de 0.5 (2 H: 1 V), 15 m de altura con una descarga de unidad máxima de 2.94 m²/s.

Figura 17. Instalación de ensayo al aire libre CSU. Fuente: Colorado State University.

En esta investigación se encontró el límite de velocidad mínimo para desarrollar presiones negativas en la contrahuella del WSB en torno a los vértices exteriores del escalonado [64]. Este fenómeno está relacionado con el desarrollo de cavitación para lo que se propuso un índice [65]:

${\sigma }_{w}={\frac {{P}_{0}-{P}_{v}}{{\rho }_{w}.\,{\frac {{{V}_{0}}^{2}}{2}}}}$

(25)

Siendo:

P₀ es presión absoluta.

P_v es la presión de vapor del agua a una cierta temperatura.

ρ_wes la densidad del agua.

V₀ es la velocidad del agua sobre la pseudosolera del escalonado.

σ_wσ coeficinete de cavitación.

σ_wσ > 3 No hay cavitación.

σ_wσ σϵЄ (3, 1.8) Cavitación incipiente.

σ_wσ σ Єϵ (1.8, 3) Desarrollo de la cavitación.

σ_wσ σ< 0.3 Fuerte cavitación.

También cuantificaron los beneficios del adecuado drenaje para la estabilidad de los bloques y del efecto predominante de la pendiente del canal sobre la disipación de energía [66][67][68]. Así mismo confirmaron los resultados británicos que indicaban un aumento de la estabilidad de los bloques a medida que aumentaba la descarga.

También se estudio la concentración de aire en el flujo, llegando a la conclusión de que la concentración media de aire del flujo era del 33% para una pendiente del canal de 0.5 (2H: 1V) con una influencia reducida de la macro-rugosidad del fondo escalonado. Además, observó que la distribución de la concentración de aire a lo largo de una sección transversal del canal es independiente del caudal para regímenes de flujo uniformes [69]. El éxito de tales investigaciones [70] llevó a la obtención de una patente de WSB denominada ArmorwedgeTM (Patente de los Estados Unidos Nº 5.544.973), propiedad de la empresa Contech® (Figura 18).

Figura 18. Esquema de bloque ArmorwedgeTM. Fuente: Elaboración propia.

En base a las investigaciones llevadas a cabo en EE. UU. La Agencia Federal para el Manejo de Emergencias (FEMA, por sus siglas en inglés) cataloga a los WSB en su manual de protecciones frente al sobrevertido en presas [71] como una opción para presas de materiales sueltos, sin embargo no ofrece unas directrices de diseño para estas soluciones.

Portugal

El Instituto Superior Técnico (IST) de Lisboa también ha desarrollado su propia línea de investigación en WSB desde hace más de 15 años [72]. El grupo de investigación ha estudiado la efectividad económica de los WSB respecto a soluciones de aliviadero exento, concluyendo que los vertederos de WSB logran una reducción del costo de 40% a 60% en comparación con las alternativas tradicionales [73]. También llevaron a cabo estudios hidráulicos completos [74][75], incluyendo los resultados sobre la aireación, la distribución de la velocidad y la resistencia a la fricción que generan los bloques, así como caudales de infiltración al drenaje. Las investigaciones concluyeron que el caudal infiltrado al drenaje, una vez saturado este, disminuía a medida que el caudal de descarga era mayor.

España

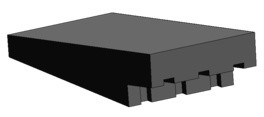
En los últimos años, en España, el Grupo de Investigación en SEguRidad de Presas y Aliviaderos (SERPA) de la UPM, CIMNE y PREHORQUISA, con el apoyo del CEDEX, han abierto su propia línea de investigación relativa a aliviaderos WSB. Fruto de este trabajo han desarrollado y patentado (ES2595852) un nuevo bloque en forma de cuña denominado ACUÑA (Figura 19), el cual mejorara el rendimiento de los diseños existentes desde un punto de vista hidráulico y estructural [76].

Figura 19. Esquema de bloque ACUÑA (patente ES2595852). Fuente: Elaboración propia.

El bloque ACUÑA presenta como principal diferencia respecto a los precedentes la ubicación de los orificios de aireación y drenaje en la zona superior de la contrahuella biselada, con objeto de aumentar las presiones negativas o de succión en esa zona y así potenciar los efectos de succión y la estabilidad del bloque [77].

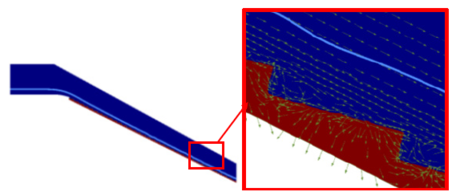
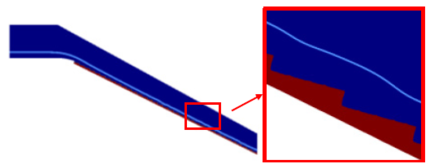
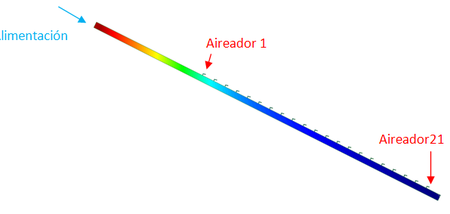
Para alcanzar el diseño final del bloque se recurrió a procedimientos de modelación física (Figura 20) y numérica (Figura 21) destinados al estudio de las distribuciones de presiones en los contornos de los bloques [78].

Figura 20. Izquierda: instalación de ensayo físico. Derecha: resultados de distribución de presiones en huella de bloque. Fuente: Caballero et al., [77].

Figura 21. Modelos numéricos para determinar la eficiencia de la posición del aireador. Fuente: elaboración propia.

También dentro de la línea de investigación española el profesor Morán hizo una amplia recopilación de los trabajos de investigación realizados hasta 2016 [59], agrupándolos en tres grupos:

El primero de ellos estudió el bloque como una unidad singular o con solo unos pocos bloques adyacentes (modelos a gran escala).

El segundo grupo de estudios incluyó pruebas de los WSB tratando de replicar el perfil longitudinal del canal del vertedero con diferentes anchos en modelos a pequeña escala.

El tercer grupo de estudios generalmente reproduce todo el vertedero en condiciones de laboratorio, en una escala determinada de modelo, para verificar su correcto funcionamiento como un todo: estructura de entrada, canal escalonado y disipador de energía.

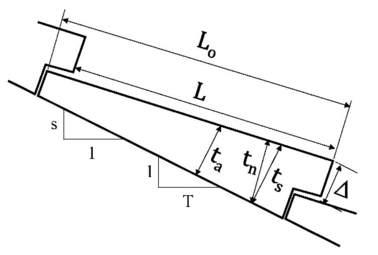
Los principales datos recopilados por Morán se resumen en la Tabla 1, donde Ref., Es la referencia o nombre de la instalación, Tipo, representa el tipo de WSB, W es el ancho del canal, Ss es la pendiente de los lados del canal, V son las paredes laterales verticales, H es la vertical caída disponible en la instalación, q es la descarga de la unidad, y SM es la escala geométrica del modelo (1 real: modelo SM). Unidades: L, B, ta, Lo y Δ, en milímetros. W y H, en metros. q en m²/s. El resto de parámetros empleados se exponen en la Figura 22.

Figura 22. Esquema de algunos de los parámetros empleados en la tabla 1. Fuente: Moran[59].

Tabla 1. Sumario de ensayos de laboratorio de WSB. Fuente: Moran [59].

Ref.	Tipo	L	B	ta	Lo	Δ	s	W	ss	H	q	SM
MCEI	-	-	20	3-6	20	-	0.10	-	-	-	0.10	30;50
MCEI	-	-	30	5.1	40	-	0.20	-	-	-	-	100;120
MCEI	WSB/O	25	20	7*		2.5*	0.35	0.18	V	0.317	0.10	100
MCEI	WSB/O		22	8*	28	4*	0.35	0.18	V	0.317	0.10	100
MCEI	WSB/BJ	-	-	21.2	89	18	0	0.46	V	-	-	-
MCEI	WSB/BJ	-	-	22.3	79	15	0	0.46	V	-	-	-
MCEI	WSB/BJ	-	-	23.9	62	12	0	0.46	V	-	-	-
MCEI	WSB/BJ	-	-	25.4	46	9	0	0.46	V	-	-	-
IHE	-	-	-	-	-	-	0.25	-	-	-	-	6;10
Kolyma Dam	WSB/O	-	200	40*	200	-	0.40	-	V	5.0	2.85	10
Noori	WSB/BJ	63.5	63.5	12.5*	63.5	13*	0.20	-	V	-	0.156	-
Jiang	WSB/BJ	63	63	12*	63	12*	0.20	-	-	-	0.180	20
Jiang	WSB/BJ	53	53	18.5*	53	13*	0.25	-	-	-	0.241	40
El Kashab	RSS	-	-	-	40	4*	0.10	-	-	-	-	-
El Kashab	RSS	-	-	-	65	13*	0.20	-	-	-	-	-
El Kashab	WSB/BJ	26	24	8	24.2	3	0.21	-	-	-	0.10	-
El Kashab	WSB/BJ	26	24	8	24.2	3	0.083	-	-	-	0.10	-
Clopper	WSB/O	203	203	102	158	44	0.50	1.22	V	1.8	1.94	-
Clopper	WSB/O	203	203	102	158	44	0.33	1.22	V	1.8	2.07	-
CIRIA	WSB/BJ	50	50	17	50	12	0.40	0.60	V	4.0	0.50	6
CIRIA	WSB/O	30	25	8.5	25	4.5	0.40	0.60	V	4.0	0.50	12
CIRIA	WSB/O	60	50	17	50	9	0.40	0.60	V	4.0	0.50	6
CIRIA	WSB/O	180	150	50	150	31	0.40	0.60	V	4.0	0.50	2
CIRIA	WSB/O	240	200	60	200	40	0.286	-	V	-	-	5
Frizell	RSS	-	-	-	102	51*	0.50	0.46	V	4.72	1.09	-
Frizell	RSS	-	-	-	104	33*	0.50	0.46	V	4.72	1.09	-
Frizell	RSS	-	-	-	106	24*	0.50	0.46	V	4.72	1.09	2.7
CSU	WSB/O	373	610	92	297	64*	0.50	1.52	V	15.2	2.94	-
Kumar	RSS	-	-	-	72	12*	0.167	1.25	V	0.78	0.11	16.76
LNEC	RSS	-	-	-	-	-	0.5	0.80	0.5	0.80	0.082	25
CSU	WSB/O	457	304.8	90.5	380	75	0.5	1.22	V	9.0	3.94	-
IST	WSB/O	240	200	50	200	40	0.4	0.675	0.66	2.5	0.361	-
IST	WSB/O	240	200	50	200	40	0.4	0.60	V	2.5	0.361	-
IST	WSB/O		80	20	80	16	0.4	0.27	0.66	2.25	0.184	-
UPM CEDEX	WSB/O	243	165	46.55	203.3	40	0.5	0.50	V	4.7	0.24	-

2.2.3. Procedimientos de diseño propuestos

En la literatura técnica actual solo existe una guía con directrices específicas para el diseño de aliviaderos WSB, la guía CIRIA [58], que no cubre todos los aspectos del diseño de un aliviadero, por lo que los criterios de diseño adicionales utilizados hasta ahora se basan en la experiencia y en estudios específicos, en aspectos tales como la capacidad de drenaje, la estabilidad del pie, la estabilidad interna del cuerpo de presa y la restitución al cauce entre otros.

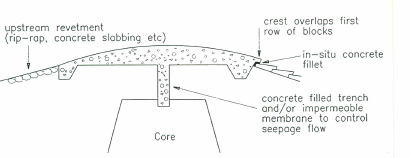
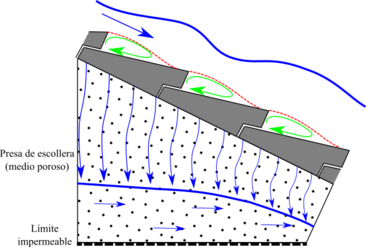
Las Directrices CIRIA establecen la conveniencia de la instalación de los aliviaderos WSB sobre taludes impermeables, para así asegurar su estabilidad, si bien la experiencia ha demostrado que también pueden emplearse sobre taludes permeables, siempre que se consiga la estabilidad del talud, la evacuación adecuada de caudales infiltrados para que no se produzca levantamiento de bloques y la condición de filtro de los materiales del espaldón. Un caso de éxito de aliviadero WSB sobre talud permeable es la presa de Barriga [79].

En cuanto a las descargas unitarias en un aliviadero WSB las directrices CIRIA recomiendan un límite de 2.0 m²/s, si bien este es un límite conservador, pues como se ha demostrado la estabilidad del bloque crece con el caudal de descarga.

La estructura de embocadura del aliviadero WSB se excava en la coronación de la presa y debe ser una extensión del elemento impermeable de la presa. Esto se consigue con una losa de hormigón con forma hidrodinámica. El manual CIRIA recomienda una sección parabólica (Figura 23), si bien según sea la geometría de la presa esta puede no ser la más eficiente ni hidráulicamente ni constructivamente.

Figura 23. Esquema de embocadura de aliviadero WSB. Fuente: CIRIA [58].

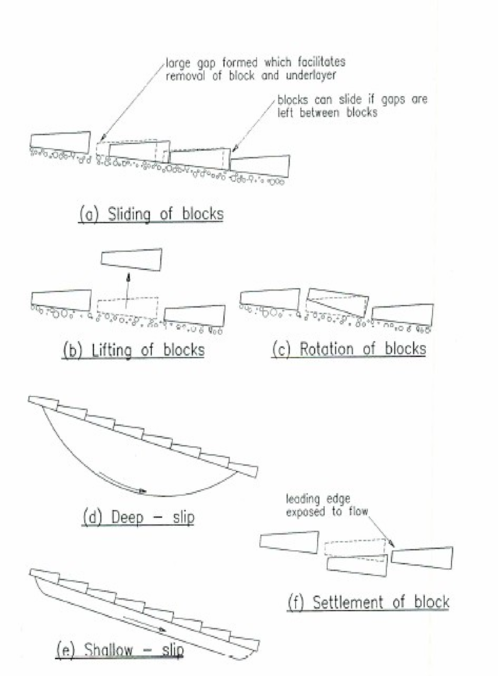
En cuanto al canal de descarga la guía CIRIA describe seis posibles formas de fallo (Figura 24), que son deslizamiento, levantamiento, rotación, deslizamiento superficial, deslizamiento profundo y hundimiento. En vista de ello recomienda una adecuada estabilización del talud de apoyo de los bloques y evitar las holguras en su puesta en obra.

Figura 24. Esquema de posibles fallos en canal de descarga de aliviadero WSB. Fuente: CIRIA [58].

La sección transversal del canal suele ser trapezoidal y, en raras excepciones, rectangular por razones constructivas. Los cajeros del canal generalmente también se construyen con WSB, y se debe prestar especial atención al diseño de las juntas de unión entre solera y cajero.

A lo largo del canal de descarga los bloques estarán sometidos a distintas condiciones hidráulicas según sea su posición más aguas arriba o aguas abajo. Estas condiciones dependerán de la longitud necesaria para que el flujo turbulento alcance la superficie libre (Inception point) y se produzca la aireación del flujo, lo que resulta beneficioso para atenuar efectos de fluctuaciones de presiones y cavitación. Existen diferentes formulaciones para determinar la posición del Inception point [80][81][82].

Figura 25. Esquema de aireación del flujo en canal de descarga WSB. Fuente: CIRIA [58].

Los bloques del canal de descarga se disponen sobre un material granular con fines de drenaje y regularización que puede tener varias capas. La guía CIRIA recomienda su dimensionamiento hidráulico según la formulación de Martins [83] y espesores de drenaje no inferiores a 20 cm o 4 veces el tamaño d₈₅ del material.

$Q={\frac {A\cdot E}{{\frac {{d}_{60}}{{d}_{10}}}^{0.26}}}\cdot {\frac {{e}^{1.5}}{1+e}}\cdot {\left(2\cdot g\cdot i\cdot {d}_{50}\right)}^{0.5}$

(26)

Siendo:

Q caudal circulante.

A sección transversal del drenaje.

E factor de forma de piedra, con 0.56 piedra machacada y 0.75 piedra redondeada.

d₆₀d₅₀ d₁₀Tamaño de la abertura del tamiz que deja pasar el % del índice.

e espesor del drenaje.

g aceleración de la gravedad.

i gradiente hidráulico igual al talud.

Esta fórmula es solo válida para capas de drenaje sobre presa homogénea, pero no sobre presa de escollera permeable. Además hay que destacar que no permite introducir la ley de pérdida de carga del material, en caso que sea conocida.

El manual CIRIA recomienda criterios adicionales para que el material del drenaje tenga la condición de filtro, si bien deben tenerse en cuenta sus afecciones a la capacidad hidráulica del drenaje.

La metodología CIRIA también ofrece una tabla (Figura 26) para el dimensionamiento del espesor medio de bloque considerando los parámetros hidráulicos y la pendiente del aliviadero. La tabla establece un espesor mínimo que no se debe sobrepasar para evitar riesgos de acciones vandálicas.

Figura 26. Tabla de dimensionamiento del espesor medio WSB. Fuente: CIRIA [58].

En cuanto a la forma de los WSB se recomiendan las siguientes relaciones para los parámetros de la Figura 22:

• L/Δ debe ser de 5 a 6.5. Esta relación es determinante para formar el vórtice que caracteriza el funcionamiento de los bloques en forma de cuña.

• L/t_a, debe ser de 3 a 4, con un espesor constructivo mínimo es de aproximadamente 10 cm, este valor puede incrementarse por aspectos de resistencia al vandalismo o durabilidad.

• B/L debe ser de 0.8 a 2 para adaptarse a asientos diferenciales del talud.

• La superficie de aireadores recomendada es del 2.5% a 5% de la superficie de la contra huella, si bien estos valores dependerán de la posición de los mismos.

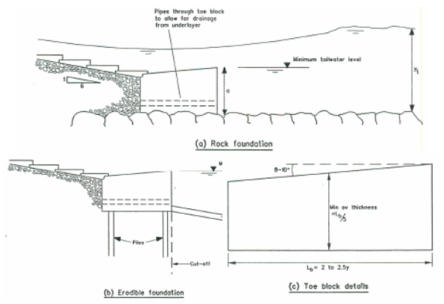
Por último se recomienda en la metodología CIRIA el diseño de una estructura de pie de aliviadero que sea capaz de soportar las filas de bloques e impida holguras que conduzcan a su fallo. Además esta estructura deberá ser lo suficientemente permeable como para no impedir el desagüe del drenaje y debe evitar que un posible resalto hidráulico alance los bloques. Los diseños propuestos se muestran en la Figura 27.

Figura 27. Soluciones de estructura de pie propuesta por CIRIA. Fuente:[58].

En caso de que sea inevitable la formación de resalto sobre los bloques se recomienda el hormigonado de las filas susceptibles de verse afectadas por el resalto (Figura 28), aunque hay que destacar que este tipo de estructuras puede generar problemas con la descarga del caudal del drenaje. También es posible aumentar el tamaño de los WSB en el extremo aguas abajo del canal según la tabla de la Figura 16 para así ser estables bajo resalto hidráulico, aunque solo para taludes muy tendidos.

Figura 28. Solución propuesta por CIRIA para bloques resistentes bajo resalto. Fuente:[58].

Hay que destacar que la metodología CIRIA no contempla el trampolín de lanzamiento como restitución al cauce del agua, que generalmente es la solución más económica, si las características del terreno aguas abajo de la presa lo permiten.

2.2.4. Aplicación de la tecnología

La aplicación de la tecnología de los aliviaderos WSB a nivel mundial ha sido escasa hasta el momento, a pesar de los prometedores resultados. Se ha empleado esta tecnología fundamentalmente en los países con grupos de investigación activos en este campo, como son Rusia, UK, EE. UU. y España. A continuación se describen brevemente algunos de los aliviaderos llevados a cabo.

Central hidráulica de Dneiper (Rusia)

La pendiente del aliviadero fue de 0.15 (6.5H: 1V), con descargas unitaria sin fallo de hasta 60 m²/s. Los movimientos de bloques máximos medidos fueron de 2 a 3 cm en las zonas sin pérdida de material de filtro de la capa de drenaje, y de 50 a 70 cm donde se eliminó el material granular subyacente. Las fuerzas hidrodinámicas máximas alcanzaron 4.5 t (vertical) y 2 t (horizontal).

Figura 29. Aliviadero de Dneiper. Fuente: CIRIA [58].

Aliviadero auxiliar en Kolyma (Rusia)

Se construyó un aliviadero WSB de emergencia cierre lateral con un caudal de diseño de 5 m²/s.

Figura 30.Aliviadero WSB de Kolym. Fuente: Morán [59].

Presas de granjas esatales (Rusia)

Este grupo de casos involucra varias presas pequeñas para el suministro agrícola en Rusia con aliviaderos compuestos por losas rectangulares superpuestas. Dos de estas presas son las de Maslovo y Sosnovski.

Figura 31. Aliviadero de Maslovo. Fuente: CIRIA [58].

Figura 32. Aliviadero de Sosnovski. Fuente: CIRIA [58].

Brushes Clough (Reino Unido)

Actualmente está fuera de servicio. Fue diseñado para una descarga de 2.2 m² /s con pendiente 0.33 (3H: 1V). Las dimensiones de los bloques fueron de 0.4 m de ancho, 0.56 m de largo, con un espesor promedio de 0.21 m y contrahuella de 0.12 m.

Figura 33.Aliviadero WSB de Clough Fuente: Morán [59].

Fue la primera instalación diseñada con las directrices y recomendaciones publicadas por CIRIA probando y supervisando su rendimiento. El CIRIA financió el trabajo de prueba y monitoreo con descargas controladas por un período de dos años para descargas de hasta 1 m³/s. Las pruebas incluyeron medidas de movimiento, presiones, aireación y profundidades de flujo de WSB.

Este caso mostró uno de los problemas importantes que debe enfrentar esta tecnología, que es el vandalismo. Algunos de los WSB se dañaron seriamente y tuvieron que ser reparados a pesar de que su grosor estaba excesivamente diseñado.

Preas Bruton (Reino Unido)

Este aliviadero WSB se diseñó para una descarga total de 500 m³/s [84][85]. La pendiente del canal del vertedero fue de 0.25 (4 H: 1 V) y los WSB se instalaron sobre una capa de drenaje y un geotextil. El canal WSB finalizó en una viga de hormigón armado, cimentada con tablestacas.

Figura 34.Aliviadero WSB de Bruton.

Preas de Odgen (Reino Unido)

La construcción se completó en 2013 y el diseño siguió las directrices del CIRIA, siendo el vertedero más grande de este tipo en el Reino Unido. Las últimas filas del canal son de hormigón armado para formar un contorno rígido de resalto con un diseño similar al de la Presa de Bruton. Se construyó un cuenco amortiguador aguas abajo del aliviadero.

Figura 35.Aliviadero WSB de Odegen Fuente: Morán [59].

Friendship Village (Estados Unidos)

El aliviadero auxiliar de la presa Friendship Village se construyó en 2008 utilizando la patente ArmorwedgeTM. La altura del vertedero es de aproximadamente 18 m y la descarga de diseño fue de 0.92 m² /s. Los bloques se colocaron sobre una capa de grava, debajo de un geotextil.

Presa Barriga (España)

Fue el primer aliviadero principal de presa con tecnología WSB. Se proyectó con bloques ArmorwedgeTM escalados hasta alcanzar una masa de 111 kg para un caudal unitario de diseño de 8 m²/s [79]. El canal de descarga trapezoidal se construyó con una pendiente de 0.5 (2H: 1V). Se trata de una presa de escollera sobre la que se colocaron dos capas de material drenante para regularizar la superficie de apoyo de los bloques. La cresta se diseñó con una losa de hormigón armado y la restitución al cauce se hizo con un trampolín de lanzamiento. La presa ha estado en operación desde 2007 sin daños reportados hasta ahora.

El proyecto incluyó modelación física específica realizada en el CSU y LNEC [86]. Se añadió al diseño ArmorwedgeTM un agujero interior transversal al bloque para permitir que se introduzca en él un cable, para así unir cada bloque con los que están en la misma fila, y así evitar fallos de bloques aislados. Además, este agujero fue útil en el transporte y la colocación de los bloques.

Figura 36.Aliviadero WSB de Barriga Fuente: Morán [59].

Presa de Wadi Sahal nawt (Omán)

Se proyectó un aliviadero auxiliar con una descarga de diseño de 5.2 m²/s y un canal rectangular de 980 m de ancho limitado por muros verticales de hormigón. Las dimensiones del WSB usado fueron de 1 metro cuadrado en planta y su espesor promedio era de 0.2 m. Este aliviadero fue modelado físicamente en la Universidad de Salford.

2.2.5. Modelación numérica

La modelación numérica de un aliviadero WSB en su conjunto resulta compleja por el gran número de fenómenos implicados, como son los flujos que induce el escalonado de las cuñas, los fenómenos de infiltración y drenaje y los movimientos de los bloques como sólidos rígidos. De tal manera que para poder afrontar el problema es común modelar de manera aislada cada uno de estos fenómenos.

Simulación CFD del flujo sobrevertido

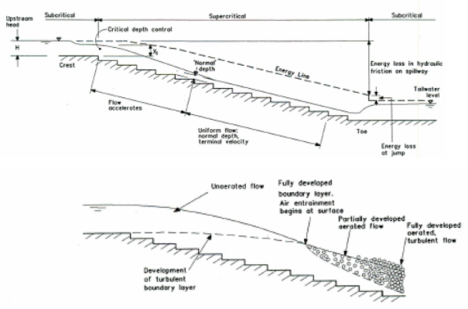
El fenómeno que más se ha estudiado, desde el punto de vista de la modelación numérica es el del flujo en aliviaderos escalonados, debido al gran desarrollo en las últimas décadas de las presas de hormigón compactado con rodillo (HCR o RCC), que suelen disponer un aliviadero escalonado fruto de su proceso constructivo. Tradicionalmente los aliviaderos escalonados se han modelado como aliviaderos lisos a los que se les impone una rugosidad ficticia que intenta reproducir los efectos del escalonado. Si bien esta simplificación permite utilizar modelos sencillos no es capaz de reproducir los flujos específicos que genera el escalonado (vórtices, depresiones locales de presión…) que resultarán de gran importancia para su diseño y optimización. Con el aumento de las capacidades de computación producidas en los últimos años es habitual que los modelos numéricos reproduzcan el contorno real de los aliviaderos escalonados, pudiendo así modelar los flujos inducidos por los escalones. De esta forma mediante modelación numérica se han estudiado recientemente aspectos como la disipación de energía para distintos regímenes de vertido del escalonado [87], así como efectos de entumecimiento de lámina, turbulencia superficial, intercepción de capa límite o aireación.

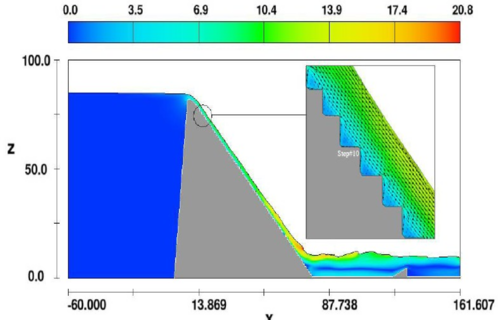
En la Figura 37 se muestra un ejemplo de modelación numérica de un aliviadero escalonado completo y su estructura de restitución [88], se muestra el campo de velocidades del agua, observándose el flujo rasante de mayor velocidad sobre la envolvente del escalonado y zonas de baja velocidad en el interior de los escalones.

Figura 37.Ejemplo de modelación numérica de vertido en aliviadero escalonado. Fuente: [88]

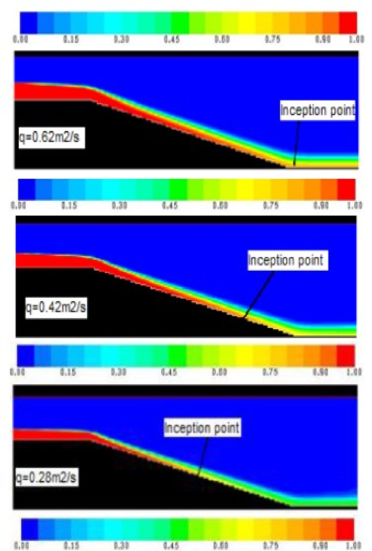
En la línea de la detección de la intercepción de la capa límite con la superficie libre se han realizado varios estudios. Chakib [89] detectó con modelos numéricos que el caudal de vertido afecta tanto a la posición del punto de intercepción como al campo de velocidades desarrollado aguas debajo del mismo y al calado por el fenómeno de entumecimiento. Algunos de los modelos realizados por el autor se muestran en la Figura 38.

Figura 38. Modelos numéricos para detección del inception point. Fuente: Chakib [89].

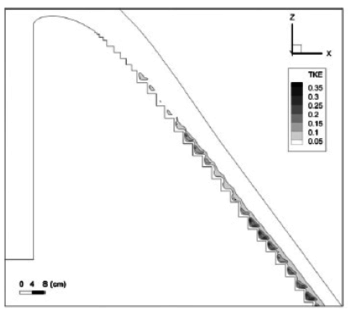
Por último dentro de esa línea Bombardelli [90] desarrolló trabajos destinados a relacionar la turbulencia en el flujo de agua con al aireación, observando que la turbulencia del flujo se concentra en las cavidades del escalonado y es creciente desde aguas arriba hacia aguas abajo (Figura 39).

Figura 39.Simulación numérica de Bombardelli para determinar la turbulencia del flujo en aliviadero escalonado. Fuente: Bombardelli [90].

Simulación de fenómenos de infiltración y drenaje

La simulación numérica de la infiltración que se produce hacia el drenaje en un aliviadero WSB no se ha abordado hasta el momento en la literatura técnica. Por una parte por la complejidad que representa modelar elementos de pocos milímetros de espesor, como son los aireadores o las ranuras entre bloques, de manera acoplada con las condiciones de sobrevertido en un aliviadero completo. Por otra parte la escasez de los diseños hechos con esta tecnología no ha requerido el desarrollo de un modelo numérico apropiado a tal efecto hasta el momento. Uno de los objetivos de esta tesis es desarrollar un modelo numérico adecuado y eficiente.

La modelación numérica del flujo circulante por el drenaje, bien sea espaldón permeable o capa de drenante, se afronta con las mismas estrategias ya descritas de modelación numérica de flujos en presas de materiales sueltos.

Simulación del movimiento de bloque como sólidos rígidos

Los aliviaderos de bloques en forma de cuña se conforman mediante bloques individuales colocados uno junto a otro sin ningún tipo de mortero o elemento que los una, de tal forma que son susceptibles de moverse de manera independiente según sean las acciones hidráulicas que sufra por el sobrevertido circulante.

Si bien en la literatura técnica no se ha estudiado el caso particular de los bloques WSB, sí es común la simulación de la dinámica de sólidos rígidos ante distintas acciones por diversas técnicas, siendo clave la modelación numérica eficiente del contacto entre sólidos. Algunas de estas técnicas se citan a continuación:

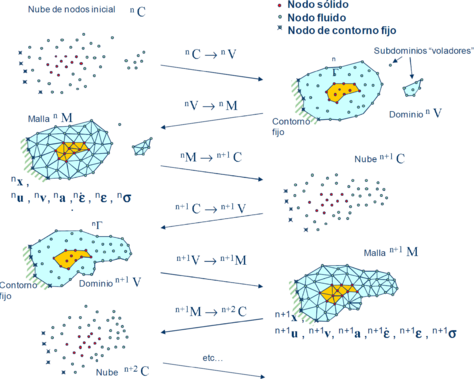
Algunos autores han utilizado el Método de las Partículas y los Elementos Finitos (PFEM)[91] para modelar el movimiento y contacto entre sólidos [92]. Esta técnica permite modelar el movimiento de sólidos embebidos en fluidos. Se basa en una particular de formulación Lagrangiana que trata los nodos de una malla de elementos finitos como partículas que pueden moverse libremente según las ecuaciones de gobierno de la mecánica de fluidos y de la mecánica de sólidos. La calidad de la solución numérica depende del tamaño de la malla utilizada, que debe actualizarse de manera dinámica en cada paso de cálculo, lo que puede conllevar altos costes computacionales. El método afronta el contacto entre sólidos mediante elementos de contacto con propiedades determinadas por el usuario, lo que requiera una calibración específica. A continuación se muestra un esquema de las etapas de resolución mediante PFEM en la Figura 40 y un ejemplo de aplicación en la Figura 41.

Figura 40.Secuencia de etapas que comprende la resolución de las ecuaciones mediante PFEM.

Figura 41.Simulación de estabilidad de escollera portuaria por el método PFEM. Fuente: Proyecto SAYOM [93].

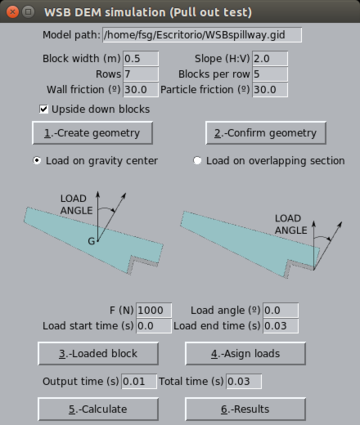
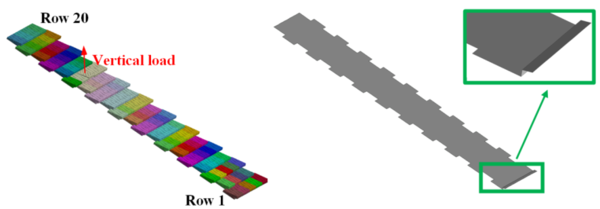
Otro método comúnmente utilizado para la modelación numérica de la dinámica de sólidos rígidos y sus contactos es el Método de los Elementos Discretos (DEM) [94][95]. Se trata de una tecnología en la que se discretiza el dominio de análisis en partículas rígidas con dimensiones conocidas, que se mueven siguiendo las leyes standard de la dinámica de partículas, por efecto de la gravedad y de las fuerzas de contacto con las partículas adyacentes o con los contornos del dominio. Suelen emplearse como partículas esferas que simplifican la generación de geometrías y el cálculo de las interacciones, lo que da como resultado un menor coste computacional (Figura 42).

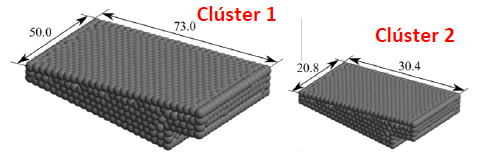
Para modelar sólidos con formas no esféricas, se debe implementar la posibilidad de generar agrupaciones rígidas de esferas (Clúster de esferas), siendo el resultado un elemento rígido de contornos esféricos y con el centro de gravedad y de inercia adecuados para su forma y densidad reales (Figura 43) [96]. Esta es una tecnología actualmente en desarrollo, y que encuentra uno de sus principales escollos en la búsqueda eficiente de partículas vecinas para el cálculo del contacto [97]. Este proceso puede ralentizar en gran medida las simulaciones para números de elementos crecientes.

Figura 42.Simulación numérica de vertido y ángulo de reposo de partículas esféricas con DEM. Fuente: Irazábal [98].

Figura 43.Aproximación de sólido rígido mediante clúster de esferas. Fuente: Irazábal [98].

3. METODOLOGÍA

En este capítulo se define la metodología seguida para desarrollar las campañas de modelación numérica de esta investigación. El capítulo se ha estructurado en tres subapartados que describen el método seguido para caracterizar la capacidad hidráulica de capas de drenaje, caracterizar caudales de infiltración entre bloques y determinar condiciones de estabilidad de los mismos.

3.1. Caracterización del comportamiento de la capa de drenaje

3.1.1. Introducción

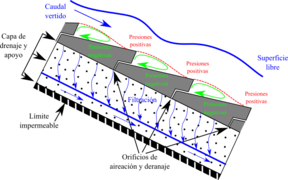
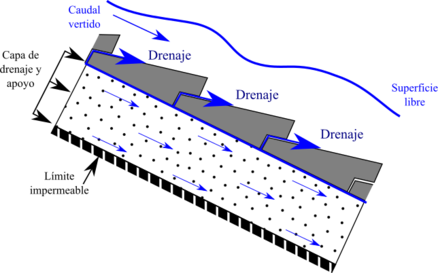
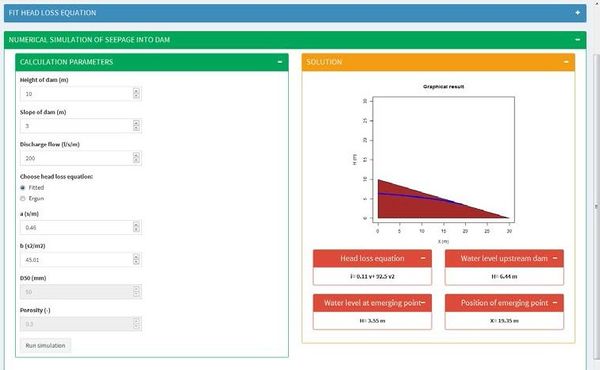
Uno de los aspectos que resultan fundamentales a la hora de diseñar un aliviadero de bloques en forma de cuña es el dimensionamiento adecuado de la capa granular de drenaje, sobre la que se apoyan estos bloques. Dicha capa de drenaje recoge las derivaciones del caudal sobrevertido que se producen por las juntas existentes entre bloques contiguos, así como por los elementos de aireación, para presas homogéneas o de escollera y tierras anisótropas. Esta capa de drenaje puede entrar en carga si su capacidad hidráulica es insuficiente para recoger esos caudales infiltrados (Figura 44), de tal manera que aparecerán subpresiones bajo los bloques, lo que puede afectar a la estabilidad de los mismos, de ahí la importancia de un buen diseño de la capa de apoyo y drenaje granular.

Figura 44.Esquemas de funcionamiento de la capa de drenaje. Izquierda: parcialmente saturado. Derecha: completamente saturado.

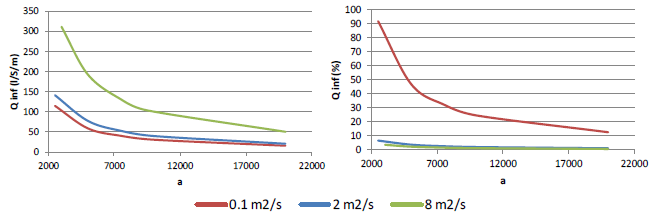
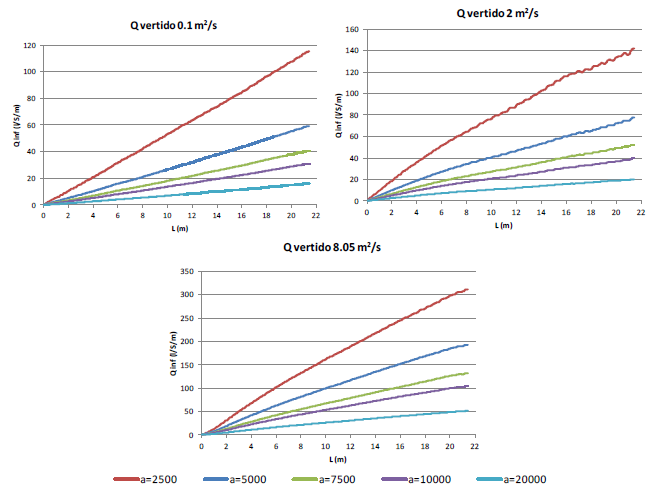
En consecuencia se ha tratado de caracterizar el comportamiento hidráulico de la capa de drenaje y su estabilidad, para distintos materiales, taludes y tamaños de bloques suprayacentes. Para ello se llevó a cabo una campaña de modelación numérica en la que se simuló la circulación de un cierto caudal infiltrado a lo largo de una capa de material poroso (capa de drenaje), mediante una simplificación bidimensional.

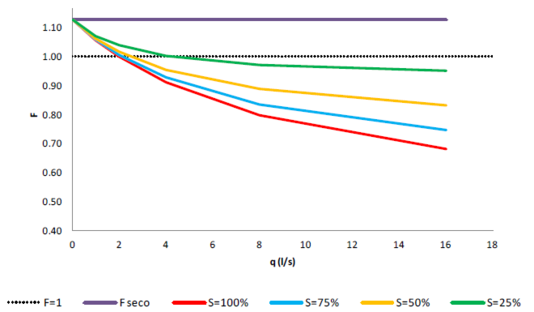
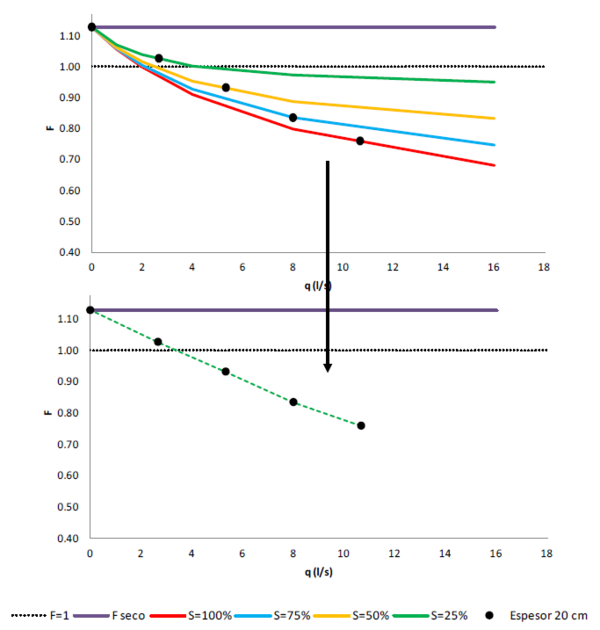
De manera complementaria a las simulaciones numéricas se desarrolló una formulación para el cálculo del coeficiente de seguridad a deslizamiento de una capa de drenaje parcialmente saturada por las infiltraciones de los bloques superiores. De tal manera que se puedan obtener curvas que relacionen el coeficiente de seguridad a deslizamiento del drenaje con su capacidad hidráulica de desagüe.

3.1.2. Modelación del comportamiento hidráulico

Materiales y sus características

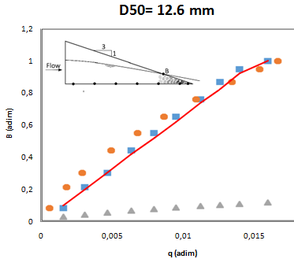
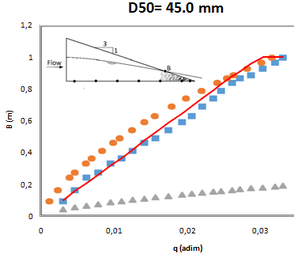
Los materiales porosos estudiados fueron dos, correspondientes a gravas reales de diámetro medio (d₅₀) 12.6 y 35.04 mm, con las características que se resumen en la Tabla 2. Se eligieron estos materiales en concreto debido a que ya fueron ensayados físicamente en laboratorio de Hidráulica de la ETSI de Caminos, Canales y Puertos de la UPM [16].

Tabla 2. Características de los materiales porosos d₅₀ diámetro medio, γγ_e,sat peso específico saturado del material, γγ_e,seco peso específico de material seco, θ ángulo de rozamiento interno, n porosidad.

	d50 (mm)	γe,sat (kN/m3)	γe,seco (kN/m3)	θ (º)	n
Material 1	12.6	18.34	14.32	36.94	0.41
Material 2	35.0	18.49	14.47	41.97	0.41

Para modelar numéricamente el comportamiento hidráulico de estos materiales es necesario conocer su ley de pérdida de carga asociada Ec.(27), de tipo parabólico según lo expuesto en el estado del arte de esta tesis

$i=a\cdot v+b\cdot {v}^{2}$

(27)

Siendo:

a,b coeficientes dependientes del material.

v la velocidad media del agua en el medio poroso.

Los valores de los coeficientes a y b pueden determinarse mediante leyes analíticas o mediante ensayo experimental. En esta tesis se han empleado ambos caminos.

Para la determinación de la ley de pérdida de carga analítica, de entre las formulaciones descritas en el estado del arte, se ha elegido emplear la propuesta por Ergun [11] Ec.(28), y se ha aplicado a los dos materiales a estudio, obteniendo los coeficientes de la Tabla 3

$i=150\cdot {\frac {{(1-n)}^{2}}{{n}^{3}}}\cdot {\frac {V}{g\cdot {d}_{50}}}\cdot v+$$1.75\cdot {\frac {(1-n)}{{n}^{3}}}\cdot {\frac {{\rho }_{w}}{{d}_{50}}}\cdot {v}^{2}$

(28)

Siendo:

i gradiente hidráulico.

n porosidad.

g aceleración de la gravedad.

v la velocidad media del agua en el medio poroso.

V viscosidad dinámica del agua.

d₅₀ diámetro medio de las partículas.

ρ_w densidad del agua.

Tabla 3. Coeficientes a y b de la ley de pérdida de carga obtenidos por fórmula analítica de Ergun.

	a	b
Material 1	12.6	18.34
Material 2	35.0	18.49

También se calibraron y validaron valores de los coeficientes a y b en base a ensayos experimentales y numéricos según un método de desarrollo propio, el cual se describe a continuación.

Los ensayos experimentales empleados se realizaron en el Laboratorio de Hidráulica de la ETSI de Caminos, Canales y Puertos de la Universidad Politécnica de Madrid. La instalación del laboratorio es un canal de 13.7 m de longitud, 1.4 m de altura y 1.32 m de ancho con una pendiente horizontal y se divide en tres áreas. Desde aguas arriba hasta aguas abajo, hay una entrada de 1 m de longitud y un área de disipación de energía, un área de ensayo de 9.5 m de largo, una zona de drenaje de 3.2 m de largo. En su pared izquierda hay dos ventanas de vidrio de 2.3 m de largo y 1.1 m de alto para la inspección visual y también para el video y la grabación fotográfica durante las pruebas. La instalación del laboratorio tiene una tubería de entrada que puede proporcionar un flujo máximo de 95 l/s [99].

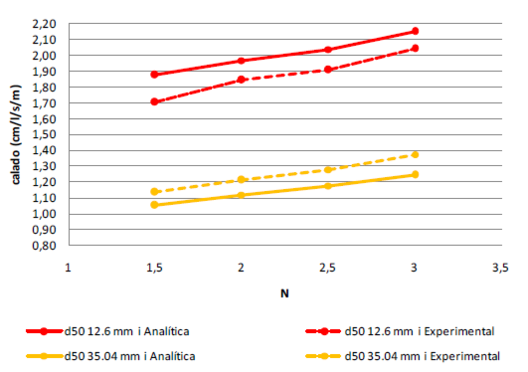
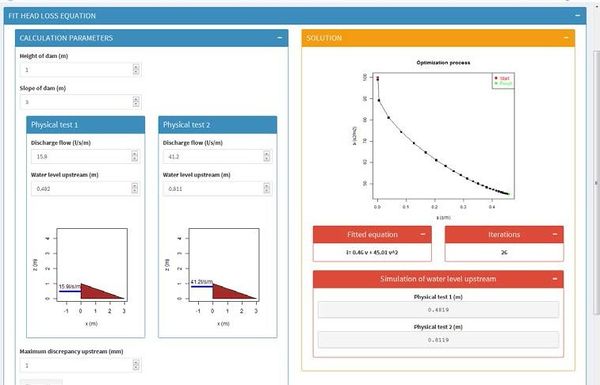
Se utilizaron dos ensayos físicos del proyecto eDams [16], en los que se construyó una presa en el canal de ensayo con 1 m de altura y talud 3, con geometría exterior reforzada por una malla de alambre para evitar deformaciones geométricas. En cada uno de los dos ensayos se construyo la presa con un material distinto, en concreto los materiales descritos en la Tabla 3. Las presas construidas para cada ensayo se muestran en Figura 45.

Figura 45.Ensayos físicos del proceso de calibración y validación de coeficientes de ley de pérdida de carga. Fuente: Morán [16].

Sobre cada geometría se ensayaron tres caudales distintos, de los cuales dos se emplearon para el proceso de calibración y el restante para la validación. En la Tabla 4 se muestran los valores de caudal ensayados. Para cada ensayo se registró la altura de la superficie de agua libre aguas arriba de la presa y el punto de emergencia del caudal sobre el talud de aguas abajo.

Tabla 4. Caudales ensayados en instalación experimental para la calibración y validación de ley de pérdida de carga.

	Caudales de calibración (l/s/m)	Caudales de validación (l/s/m)
Material 1	10.9, 26.0	21.0
Material 2	15.9, 41.2	26.1

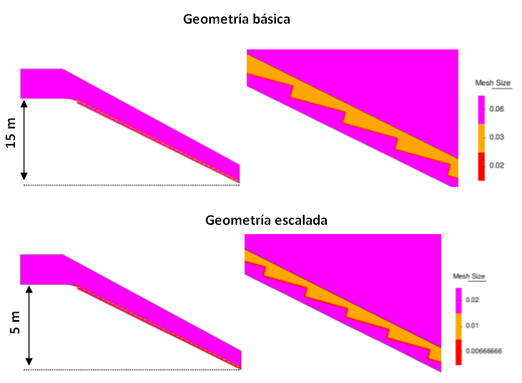
Los ensayos numéricos modelaron los mismos caudales y materiales que los modelos físicos, utilizando como código de cálculo una de las aplicaciones implementadas en el entorno KratosMulti-Physics de código abierto [100]. La malla de elementos finitos utilizada en todas las simulaciones contaba con un tamaño de elemento de 0.6 cm en el contorno exterior del modelo de la presa y en el resto del dominio de cálculo 3.5 cm (Figura 46). Todas las simulaciones numéricas fueron 2D (Figura 47).

Figura 46.Mallado en el dominio numérico del proceso de calibración y validación de coeficientes de ley de pérdida de carga.

Figura 47.Ejemplo de simulación numérica para calibrar ley de pérdida de carga de material poroso.

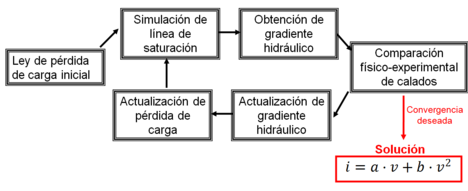
Los valores de los parámetros a y b que se debían implementar en la ley de pérdida de carga del modelo numérico eran en principio desconocidos, por lo que se debieron realizar múltiples simulaciones para su ajuste. La bondad del ajuste logrado en cada simulación numérica se valoraba comparando el nivel aguas arriba de la presa con respecto a lo registrado en el ensayo físico con sus caudales de calibración.

Para lograr la convergencia entre modelo numérico y físico en cada simulación numérica se actualizaba el valor de los parámetros a y b según el siguiente procedimiento:

1.- Fijar una ley de pérdida de carga. Para la inicialización del bucle se empleó Ergurn.

2.- Simular numéricamente la línea de saturación con la ley de pérdida de carga inicial para dos caudales.

3.- Obtener el gradiente hidráulico en la sección de más aguas arriba de la presa, según las Ec.(29) y Ec.(30)

${i}_{1}=a\cdot {\frac {{q}_{1}}{{y}_{1}}}+b\cdot {\left({\frac {{q}_{1}}{{y}_{1}}}\right)}^{2}$	(29)
${i}_{2}=a\cdot {\frac {{q}_{2}}{{y}_{2}}}+b\cdot {\left({\frac {{q}_{2}}{{y}_{2}}}\right)}^{2}$	(30)

Siendo:

i₁es el gradiente hidráulico en la sección de más aguas arriba del modelo que simula un primer caudal.

q₁ es el caudal unitario del primer caudal simulado.

y₁ es el calado aguas arriba obtenido de la simulación del primer caudal.

i₂ es el gradiente hidráulico en la sección de más aguas arriba del modelo que simula un segundo caudal.

q₂ es el caudal unitario del segundo caudal simulado.

y₂ es el calado aguas arriba obtenido de la simulación del segundo caudal.

a,b son coeficientes específicos de cada medio granular.

4.- Comparar los calados aguas arriba de la presa obtenidos para el primer caudal en ensayo físico y numérico.

Si el calado físico es mayor al de la simulación se actualiza i₁ según

i₁ⁿ= i₁ + (0.01· i₁)

Si el calado físico es menor al de la simulación se actualiza i₁ según

i₁ⁿ = i₁ - (0.01· i₁)

5.- Comparar los calados aguas arriba de la presa obtenidos para el segundo caudal en ensayo físico y numérico.

Si el calado físico es mayor al de la simulación se actualiza i₁ según

I₂ⁿ= i₂ + (0.01· i₂)

Si el calado físico es menor al de la simulación se actualiza i₁ según

i₂ⁿ = i₂ - (0.01· i₂)

6.- Con los nuevos valores actualizados de i₁ y i₂ ser resuelve el sistema de ecuaciones siguiente, siendo las variables a obtener a_n y b_n

${{i}_{1}}^{n}={a}_{n}\cdot {\frac {{q}_{1}}{{y}_{1}}}+{b}_{n}\cdot {\left({\frac {{q}_{1}}{{y}_{1}}}\right)}^{2}$	(31)
${{i}_{2}}^{n}={a}_{n}\cdot {\frac {{q}_{2}}{{y}_{2}}}+{b}_{n}\cdot {\left({\frac {{q}_{2}}{{y}_{2}}}\right)}^{2}$	(32)

Siendo:

i₁ⁿ es el gradiente hidráulico actualizado en el paso 4.

q₁ es el caudal unitario del primer caudal simulado.

y₁ es el calado aguas arriba obtenido de la simulación del primer caudal.

i₂ⁿ es el gradiente hidráulico actualizado en el paso 5.

q₂es el caudal unitario del segundo caudal simulado.

y₂es el calado aguas arriba obtenido de la simulación del segundo caudal.

a_n, b_n son las variables a obtener del sistema de ecuaciones.

7.- Se vuelve al paso 1 y se actualiza la ley de pérdida de carga con a_n y b_n.

8.- Se repite el proceso descrito desde el paso 1 tantas veces como sea necesario, hasta lograr la convergencia del nivel aguas arriba entre las simulaciones numéricas y los resultados físicos. En este proceso de calibración en concreto se estableció como criterio de salida del bucle una convergencia de menos de 1 cm, si bien de manera general puede establecerse el que desee el usuario. En la Figura 48 se muestra un esquema del proceso propuesto.

Figura 48. Esquema de proceso de calibración de ley de pérdida de carga.

Finalmente se realizó un ensayo numérico de validación para cada material testado como forma de verificar la ley de pérdida de carga lograda en la calibración.

De esta manera fue posible contar con dos leyes de pérdida de carga para cada material, obtenidas de manera experimental y analítica, permitiendo modelar numéricamente con ambas leyes el comportamiento de una capa de drenaje, y así determinar en qué medida afecta la ley de pérdida de carga a la capacidad del mismo.

Modelos de drenaje

La campaña de modelación numérica consistió en simular la circulación del caudal infiltrado a lo largo de una capa de drenaje, mediante una simplificación con dominio bidimensional. Esta campaña constó de dos etapas, una primera en la que se modeló el drenaje sin saturar y una segunda de modelación de drenaje saturado.

Drenaje sin saturar

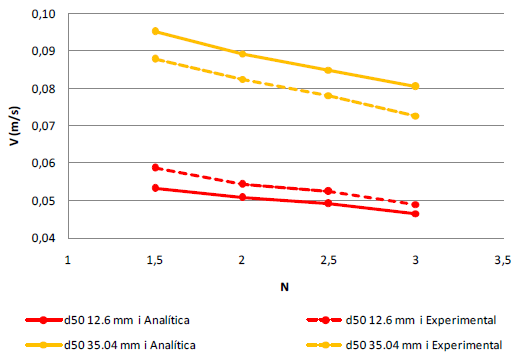
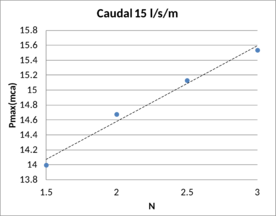
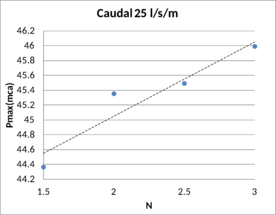
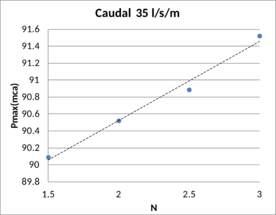
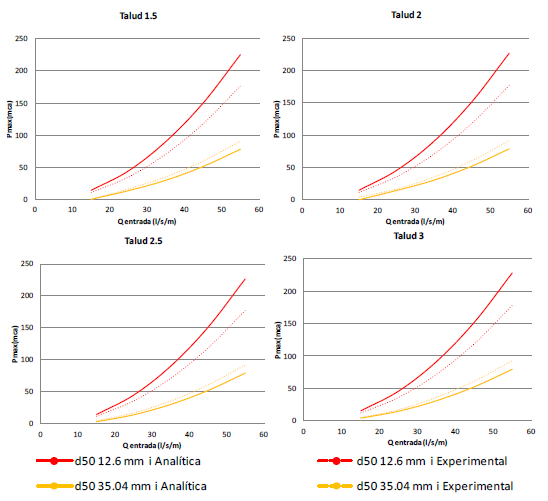
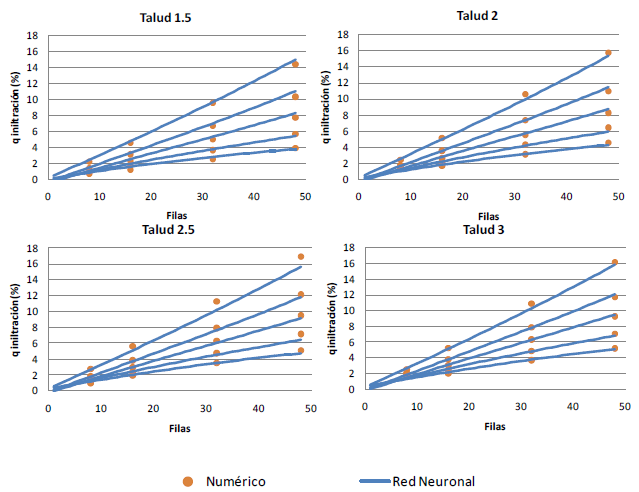
En concreto en la primera etapa de esta campaña de modelación se simularon cuatro taludes de capa drenante (H/V=1.5, 2, 2.5 y 3), que resultan habituales en los espaldones de presas de materiales sueltos sobre los que se implementan los aliviaderos de bloques en forma de cuña. El simular varios taludes permite estudiar el efecto del talud en la capacidad hidráulica. En la Tabla 5 se muestra un resumen de las simulaciones realizadas en base a la combinación de materiales, taludes y leyes de pérdida de carga descritas.

Tabla 5. Resumen de escenarios modelados numéricamente para determinar la capacidad de una capa de drenaje.

Simulación numérica	Material	Talud	Ley de pérdida de carga
1	1	1.5	Experimental
2	1	2	Experimental
3	1	2.5	Experimental
4	1	3	Experimental
5	1	1.5	Analítica
6	1	2	Analítica
7	1	2.5	Analítica
8	1	3	Analítica
9	2	1.5	Experimental
10	2	2	Experimental
11	2	2.5	Experimental
12	2	3	Experimental
13	2	1.5	Analítica
14	2	2	Analítica
15	2	2.5	Analítica
16	2	3	Analítica

El caudal de infiltración modelado en todos los escenarios de la primera etapa fue fijo (5 l/s/m), así como el espesor de capa (10 cm) y la diferencia de altura entre embocadura y salida del drenaje (5 m). No resulta necesario modelar más caudales debido a las características del flujo en un canal inclinado relleno de material poroso, ya que según los trabajos del USBR [14] la posición de la superficie libre del agua circulante por el canal resulta ser paralela a la solera del mismo, lo que equivale a decir que el calado se mantiene constante en todo su recorrido o que la velocidad se mantiene siempre constante [83]. De esta forma si la velocidad de circulación del agua resulta constante, independientemente del caudal circulante, el calado unitario (cm/l/s/m) resulta constante, y por tanto el calado aumenta de manera lineal con el caudal. De tal manera que solo resulta necesario simular numéricamente un caudal de circulación en cada configuración de capa de drenaje para obtener el calado unitario, para cada material y talud.

El código de cálculo utilizado para todas las simulaciones de esta campaña es una de las aplicaciones implementadas en el entorno KratosMulti-Physics de código abierto [100], que resuelve las ecuaciones completas de Navier-Stokes según un esquema Euleriano. El dominio de cálculo se discretiza mediante una malla de elementos finitos con tamaño máximo de elemento de mallado 0.5 cm.

Un ejemplo representativo del dominio tipo de cálculo empleado en la etapa de modelación de drenaje no saturado se muestra en la Figura 49.

Figura 49. Ejemplo de simulación numérica de circulación de un caudal infiltrado por un medio poroso. Se indica en amarillo dominio del medio poroso y en gris posición de la superficie libre.

De esta primera etapa de la campaña de modelación se obtuvieron como resultados el calado unitario de vertido para los materiales y taludes modelados con las leyes de pérdida de carga descritas.

Drenaje saturado

En esta segunda etapa de la campaña se simularon capas de drenaje en carga y los efectos de alivio de presión que generan los aireadores de los bloques, para obtener resultados desde un punto de vista cualitativo. Al igual que en la primera etapa de esta campaña todos los modelos han sido 2D y con longitudes y espesores similares a los de la etapa anterior. Así mismo se modelaron los cuatro taludes y dos materiales descritos en para la etapa anterior, con las leyes de pérdida de carga experimentales y analíticas indicadas anteriormente. Sin embargo las condiciones de alimentación sí fueron diferentes para esta etapa respecto a la anterior. En concreto las condiciones de alimentación del drenaje fueron bien uniformemente distribuida a lo largo de la base del drenaje, o bien concentrado en embocadura, con caudales de 15, 25, 35, 45 y 55 l/s/m.

La geometría y espaciamiento de los aireadores modelados se corresponde con los del bloque ArmorwedgeTM de 111 kg. En los modelos de esta etapa de la campaña se modelaron configuraciones sin aireadores o con 21 aireadores, y se consideró la presión en el extremo libre del aireador igual a la atmosférica.

Al igual que para la primera etapa el código de cálculo empleado fue una de las aplicaciones implementadas en el entorno KratosMulti-Physics, siendo el mallado del dominio también similar.

De esta segunda etapa de la campaña de modelación se obtuvieron como resultados los efectos sobre la presión del drenaje producidos por la forma de alimentación y por la presencia de aireadores, así como los efectos que producen la variación de caudales de vertido, el talud y la ley de pérdida de carga adoptada.

3.1.3. Estabilidad al deslizamiento

Para estudiar la estabilidad frente a deslizamiento en masa para la capa de drenaje se tomó como punto de partida la expresión propuesta por Toledo [6]. La cual permite la obtención del coeficiente de seguridad a deslizamiento de una rebanada de material poroso saturada, tomando como hipótesis de partida el equilibrio de fuerzas en dicha rebanada (Figura 50), donde F_F es la fuerza de fricción, S es la fuerza de subpresión, P es el peso del material.

Figura 50.Equilibrio de fuerzas sobre rebanada saturada empleado por Toledo para obtener su ecuación de deslizamiento en masa.

Para adaptar la expresión propuesta por Toledo, para que sea aplicable a capas de drenaje de aliviaderos con bloques en forma de cuña, se proponen añadir dos nuevas fuerzas sobre la rebanada de medio poroso saturado descrita: la acción del espesor de capa de drenaje seca que se encuentra por encima del nivel de la superficie libre y la acción del peso de los bloques (Figura 51). Planteando el nuevo equilibrio de fuerzas sobre la rebanada se obtiene una nueva expresión del coeficiente de seguridad a deslizamiento (Ec.(33)), dependiente de los parámetros que se ilustran en la Figura 52

${F}_{d}=\left(1-{\frac {{\gamma }_{w}{\frac {\beta }{\mathrm {cos} \,\alpha }}}{{\gamma }_{e,sat}+\left({\gamma }_{e,dry}\cdot ({\frac {1}{S}}-1)\right)+\left({\frac {\left({\frac {{P}_{B}}{({S}_{B})}}\right)}{{e}_{sat}}}\right)}}\right)\cdot {\frac {Tan\,(\varphi )}{Tan\,(\alpha )}}$

(33)

Siendo:

F_d es el coeficiente de seguridad a deslizamiento.

γ_e,sat es el peso específico saturado del material.

γ_e,dry es el peso específico seco del material.

γ_w es el peso específico del agua.

β es el coeficiente de subpresión.

ϕ es el ángulo de fricción del material.

α es la pendiente de la presa en grados.

S es el grado de saturación del drenaje en tanto por uno

e_sat es el espesor saturado de la capa de drenaje

P_B es el peso del bloque

S_B es la superficie de apoyo del bloque

Figura 51.Equilibrio de fuerzas sobre rebanada parcialmente saturada considerando las acciones del peso de los bloques y del material seco.

Figura 52.Esquema de parámetros utilizados en la fórmula propuesta de deslizamiento en masa de aliviaderos WSB.

Con esta nueva fórmula propuesta se puede obtener el coeficiente de seguridad a deslizamiento para distintos caudales de vertido, en función del grado de saturación (S). Un ejemplo esquemático de las familias de curvas que pueden obtenerse con la nueva formulación se muestra en la Figura 53, donde se aprecia que conforme aumenta S, para un mismo caudal de vertido, la capa de drenaje se hará más inestable.

Figura 53.Ejemplo esquemático de evolución del coeficiente de seguridad al deslizamiento en función S.

Para simplificar la forma de conocer si una cierta capa de drenaje es estable y para qué rango de caudales, se propone proceder a calcular el coeficiente de seguridad para distintos espesores totales de capa de drenaje, y para grados de saturación prefijados. Un esquema del proceso de simplificación para una capa de drenaje de espesor total 20 cm se muestra en la Figura 54.

Siguiendo el proceso de simplificación antes descrito se obtuvieron en base a los resultados caudal unitario obtenidos de la campaña de modelación numérica los coeficientes de seguridad al deslizamiento para tres espesores de capa de drenaje que resultan razonables desde un punto de vista constructivo (10 cm, 20 cm, 30 cm). En la Figura 55 se muestra un esquema de gráficos obtenidos para un cierto medio poroso, talud y tipo de bloque en forma de cuña, y que se muestran en el capítulo de resultados.

Figura 54.Esquema de obtención del coeficiente de seguridad al deslizamiento en función del caudal para una capa de drenaje de espesor total 20 cm, a partir de los puntos negros indicados.

Figura 55.Esquema de gráfico del coeficiente de seguridad obtenido en campaña de modelación numérica.

3.2. Caracterización y cuantificación de caudales de infiltración

3.2.1. Introducción

Los aliviaderos de bloques en forma de cuña están constituidos por bloques independientes de hormigón prefabricado, dispuestos uno junto al otro, sin ningún tipo de mortero que los una. De tal manera que las zonas de unión de un bloque con el contiguo constituyen unas ranuras por las que se puede infiltrar el agua que circula sobre ellos. También se pueden producir infiltraciones por los elementos de aireación dispuestos en los bloques, en función de las condiciones (calado y velocidad) de circulación del agua sobre los mismos.

Con el objetivo de caracterizar y cuantificar el circulante sobre los bloques, se ha propuesto una campaña de modelación numérica, en la que se plantean dos etapas para la obtención del caudal infiltrado: una primera 2D, que permitió realizar un gran número de simulaciones en un corto espacio de tiempo a partir de las cuales obtener conclusiones generales y tendencias del fenómeno de infiltración. En la segunda etapa se realizaron ensayos 3D, que si bien requieren tiempos significativamente mayores de cálculo fueron susceptibles de calibración en base a resultados de ensayos físicos.

3.2.2. Método matemático para la modelación de la infiltración

Como se ha expuesto en la introducción la infiltración de caudales a la capa de drenaje se produce a través de las ranuras que quedan entre bloques contiguos, y por los elementos de aireación, según sea su régimen de funcionamiento. De tal manera que se puede contemplar el sistema como una serie de conductos (ranuras y aireadores) embebidos en una matriz sólida e impermeable (cuerpo del bloque). Este sistema de conductos y zonas sólidas descrito es similar al que se observa en un material granular poroso, donde existen conductos definidos por huecos entre granos del material (sólidos impermeables) por los cuales puede circular el agua, como se ilustra en la Figura 56.

Figura 56.Esquema de medio granular, donde se indican algunos conductos definidos por huecos entre piedras por donde podría circular agua.

El problema de modelar matemáticamente la circulación de flujos de agua a través de medios granulares se suele afrontar considerando que el agua puede circular por todo el medio poroso, sin tener en cuenta la forma de los conductos o las zonas sólidas impermeables de los granos como se ha descrito en el estado del arte. Para que el flujo real sea equivalente al modelado matemáticamente se introduce una ley de pérdida de carga parabólica (i), que simula y promedia la pérdida de carga que se produciría al circular el agua por los conductos reales del medio poroso (Figura 57).

Figura 57.Comparación de flujo real en medio granular (izquierda) y aproximación matemática (derecha).

Un procedimiento de aproximación matemática similar al explicado para medios granulares es de aplicación para simular las infiltraciones a través de bloques en forma de cuña. De manera análoga a lo expuesto anteriormente, se considera que el agua infiltrada no solo circulará por los conductos, ranuras y aireadores en este caso, sino por todo el cuerpo del bloque, al que se le asignará una ley de pérdida de carga adecuada para reproducir la infiltración real. Esa variación en las zonas de infiltración consideradas para la aproximación matemática se muestra en la Figura 58.

Figura 58.Comparación de infiltraciones reales en bloque y aproximación matemática. Las flechas indican las zonas de infiltración en cada caso.

La ley de pérdida de carga adoptada para simular matemáticamente la infiltración tiene la expresión de la Ec.(34), que resulta ser igual a la de la Ec.(27), a excepción del término cuadrático. Este término se puede despreciar por considerarse la separación entre bloques lo suficientemente pequeña como para que no se desarrolle un flujo turbulento en el interior de las ranuras entre bloques o en los conductos de aireación. El principal inconveniente de tener que implementar esta ley de pérdida es que el coeficiente a debe ser calibrado en base a datos experimentales de infiltración

$i=a\cdot v$

(34)

Siendo:

a coeficiente dependiente de la forma de bloques y su colocación.

v la velocidad media del agua infiltrada.

Gracias a esta simplificación matemática deja de ser necesario reproducir en los modelos numéricos las ranuras y los conductos para poder obtener las infiltraciones, lo que debido a las pequeñas dimensiones de los mismos, mejora de manera muy notable la respuesta y eficacia de los modelos numéricos. En consecuencia se hace factible el modelar numéricamente el vertido sobre los bloques y de manera acoplada la infiltración, con dominios de cálculo del aliviadero al completo. Un ejemplo de ello se muestra en la Figura 59.

Figura 59.Ejemplo de simulación numérica acoplada de sobrevertido e infiltración 2D.

3.2.3. Etapa de modelación 2D

Influencia la ley de pérdida de carga en el caudal infiltrado

Con el objetivo de observar como varía la infiltración en un cierto aliviadero frente a distintos caudales de sobrevertido y leyes de pérdida de carga se han llevado a cabo una serie de simulaciones numéricas 2D.

La geometría de aliviadero modelada se corresponde con una rápida con altura de 15 m, un talud 2 y bloques en forma de cuña de 111 kg ArmorwegdgeTM. Los caudales de sobrevertido modelados fueron 3 (0.1 m²/s, 2 m²/s y 8.05 m²/s), que presentan distintos regímenes de funcionamiento del aliviadero. El modelo con caudal de vertido 0.1 m²/s presenta régimen de caídas sucesivas y los modelos con caudales 2 m²/s y 8.05 m²/s regímenes rasantes [103].

El código de cálculo usado fue una de las aplicaciones implementadas en el entorno KratosMulti-Physics, como en la campaña de modelación anterior. El dominio de cálculo se discretizó mediante una malla de elementos finitos similar en todos los modelos, según la distribución de tamaño máximo de elemento que se muestra en la Figura 60. Se definieron 3 tamaños máximos de elemento: 2 cm en los contornos de los bloques en forma de cuña, 3 cm en la zona inmediatamente superior al bloque y 6 cm en el resto del dominio.

Figura 60.Distribución de tamaños máximos de elemento de mallado, unidades en metros. Izquierda: vista general del dominio de cálculo. Derecha: detalle del mallado en torno a los bloques.

Los modelos numéricos realizados simularon la infiltración a través de los bloques, según la simplificación matemática expuesta con la implementación de leyes de pérdida de carga. De tal manera que el dominio de cálculo engloba tanto una zona superior al bloque para el desagüe de los sobrevertidos, como también la geometría del propio bloque asociada a una cierta ley de pérdida de carga de carácter lineal (Figura 61).

Figura 61.Domino de cálculo de las simulaciones numéricas de infiltración 2D.

Las simulaciones numéricas se realizaron para distintos valores del coeficiente a de la ley de pérdida de carga, para caracterizar su influencia en el caudal infiltrado. Los escenarios modelados se resumen en la Tabla 6.

Tabla 6. Resumen de escenarios modelados numéricamente para determinar la infiltración en 2D.

Simulación numérica	q (m2/s)	Coeficiente a de ley pérdida de carga
1	0.1	2500
2	0.1	5000
3	0.1	7500
4	0.1	10000
5	0.1	20000
6	2	2500
7	2	5000
8	2	7500
9	2	10000
10	2	20000
11	8.05	3000
12	8.05	5000
13	8.05	7500
14	8.05	9500
15	8.05	20000

Efectos de escala

De manera general el ensayo en laboratorio de aliviaderos de presas (por sus dimensiones y caudales a ensayar) se realiza en modelo reducido según la semejanza de Froude. En consecuencia, los ensayos físicos necesarios para obtener los caudales infiltrados en un aliviadero de bloques en forma de cuña, con los que calibrar el coeficiente a del modelo numérico, también se llevarán a cabo en modelo reducido. De ahí el interés de estudiar los posibles efectos de escala en el fenómeno de infiltración entre bloques.

Según la técnica del análisis dimensional cualquier problema hidráulico puede expresarse en función de los ocho parámetros que intervienen en la ecuación general de la hidráulica:

$F({\frac {b}{a}};{\frac {c}{a}};{\frac {d}{a}};F;Re;C;W;E)$

(35)

Siendo:

a, b y c son magnitudes de longitud en cada dirección del espacio tridimensional.

d es una magnitud de longitud asociada a fenómenos de rugosidad.

F es el número de Froude.

Re es el número de Reynolds.

C es el número de Cauchy.

W es el número de weber.

E es el número de Euler.

La condición para que exista semejanza entre un prototipo hidráulico y un modelo a escala reducida es que la ecuación general de la hidráulica sea la misma en ambos casos. Pero esto resulta inabordable ya que si se impone una semejanza geométrica y se obliga a que haya una semejanza en cualquiera de las fuerzas que actúan (gravedad, tensión superficial, elasticidad, etc.) esto impide que las demás fuerzas cumplan la semejanza, por ello se debe recurrir a imponer semejanzas parciales en cada fuerza actuante. Esto obliga a elegir las acciones que tengan mayor relevancia en el fenómeno a estudiar en el modelo reducido a ensayo.

A la hora de elegir establecer una semejanza u otra es importante recordar el significado físico de cada uno de los parámetros adimensionales que intervienen en la ecuación general de la hidráulica.

Los monomios b/a y c/a muestran relaciones entre dimensiones geométricas, y el monomio d/a representa la rugosidad relativa de los contornos. El número de Froude relaciona las fuerzas inerciales con las de gravedad, mientras que el número de Reynolds relaciona la fuerza inercial con la fuerza de viscosidad. El número de Cauchy indica la relación entre la velocidad y las ondas de presión, el número de Weber relaciona las fuerzas de inercia con las de tensión superficial y el número de Euler crea la relación entre presión y energía cinética [104].

Por tanto si la semejanza utilizada es la de Froude, se considera que las fuerzas predominantes son las gravitatorias y se impone que el prototipo hidráulico y el modelo a escala reducida tengan el mismo número de Froude. Esta semejanza es la aplicada habitualmente en estructuras hidráulicas como aliviaderos de presas.

Si se denomina el factor de escala que condiciona la semejanza de Froude como f las principales relaciones entre modelo real y modelo a escala reducida son:

$Longitud\,modelo\,real=f\ast Longitud\,modelo\,reducido$	(36)
$Velocidad\,modelo\,real={f}^{0.5}\ast Velocidad\,modelo\,reducido$	(37)

Para estudiar el comentado efecto de escala se modelaron dos geometrías de aliviadero, que se han denominado como geometría básica y geometría escalada.

La geometría básica se corresponde con un aliviadero de altura de 15 m, un talud 2 y bloques en forma de cuña de 111 kg Armorwegdge. El caudal de sobrevertido modelado para esta geometría fue de 2 m²/s.

La geometría escalada es la resultante de aplicar una semejanza de Froude de factor f=3 a la geometría básica. Resultando, altura de presa 5 m, talud 2 y bloques homotéticos a escala 1/3. El caudal unitario modelado fue 0.385 m²/s, que es el resultante de aplicar la semejanza de Froude al caudal 2 m²/s.

La semejanza de Froude que se aplicó para obtener la geometría escalada de aliviadero a partir de la geometría básica, también se aplicó al tamaño máximo de elemento de mallado, para mantener así la densidad de nodos del mallado constante con la misma distribución espacial. En concreto para la geometría básica se definieron 3 tamaños máximos de elemento: 2 cm en los contornos de los bloques en forma de cuña, 3 cm en la zona inmediatamente superior al bloque y 6 cm en el resto del dominio. Para la geometría escalada se definieron también tres tamaños máximos de elemento: 0.66 cm en los contornos de los bloques en forma de cuña, 1 cm en la zona inmediatamente superior al bloque y 2 cm en el resto del dominio. Estas distribuciones de tamaños máximos de elemento de mallado para ambas geometrías se ilustran en la Figura 62.

Figura 62.Distribución de tamaños máximos de elemento de mallado en campaña de efectos de escala, unidades en metros. Superior: geometría básica. Inferior: geometría escalada.

Las simulaciones numéricas se realizaron para distintos valores del coeficiente a de la ley de pérdida de carga, para así comparar la equivalencia entre ambas geometrías modeladas. Un resumen de las simulaciones realizadas se muestra en la Tabla 7.

Tabla 7. Resumen de escenarios modelados numéricamente para determinar los efectos de escala en 2D.

Simulación numérica	Geometría modelada	Coeficiente a de ley pérdida de carga
1	Básica	2500
2	Básica	5000
3	Básica	7500
4	Básica	10000
5	Básica	20000
6	Escalada	3000
7	Escalada	5000
8	Escalada	8000
9	Escalada	10000
10	Escalada	20000

3.2.4. Etapa de modelación 3D

En esta etapa se llevó a cabo en primer lugar un ensayo para comprobar que el modelo numérico era capaz de reproducir correctamente el sobrevertido en un aliviadero de bloques en forma de cuña. Posteriormente se calibró y validó el coeficiente a de la ley de pérdida de carga para simular las infiltraciones entre bloques. Para por último, y una vez que la ley de pérdida de carga fue validada, se procedió a realizar nuevas simulaciones numéricas para taludes y caudales distintos al de calibración.

Validación hidráulica del modelo numérico

Para comprobar que el modelo numérico 3D simula correctamente el fenómeno de sobrevertido en un aliviadero de bloques en forma de cuña, se procedió a reproducir numéricamente la geometría de la instalación construida para los ensayos físicos del proyecto DIABLO [105] en el Centro de Estudios Hidrográficos del CEDEX, que consiste en una rápida de talud 2:1 y una altura de 4.7 m (Figura 63).

Figura 63.Instalación de ensayo físico del proyecto DIABLO [105].

Los bloques empleados fueron los ACUÑA de 111 kg a escala 1/3. El caudal de vertido simulado fue de 200 l/s/m. El mallado empleado en el modelo numérico consistió en una malla desestructurada de tetraedros con tamaño máximo de elemento 4.5 cm de manera general en el dominio, y de tamaño máximo de elemento 1 cm en torno a los contornos de los bloques, como se muestra en la Figura 64.

Figura 64.Tamaños máximos de elementos de mallado empleados en el modelo de validación hidráulica.

Una vez obtenidos los resultados numéricos se realizó el ensayo de la misma geometría y caudal de vertido en las instalaciones de laboratorio, y se midieron en el bloque central de la fila número 25 desde la coronación la concentración de aire en el espesor del calado de agua [78]. Cuando la concentración de aire es del 90%, se alcanza el calado característico, que es el que define el calado en flujos de agua altamente turbulentos y aireados [106][107], como es el caso de los aliviaderos con bloques en forma de cuña. Por lo tanto para valorar la capacidad del modelo numérico para reproducir el sobrevertido sobre los bloques se procedió a comparar los calados registrados en el bloque 25 en la modelación numérica y el calado característico en los ensayos experimentales.

Calibración y validación de la ley de pérdida de carga

Para poder obtener el caudal real infiltrado a través de un aliviadero de bloques, mediante el método de la ley de pérdida de carga propuesto, resultó necesario calibrar a partir de ensayos físicos el valor del parámetro a. Para ello en la instalación de ensayo construida en el Centro de Estudios Hidrográficos del CEDEX se registraron los caudales infiltrados acumulados en el drenaje para un caudal de vertido de 240 l/s/m hasta la fila 32 desde embocadura y cavidad de drenaje sin material poroso (Figura 63 izquierda) [108] . A partir de esos resultados experimentales se procedió a calibrar el parámetro a de la ley de pérdida de carga numérica, mediante múltiples simulaciones numéricas.

Para la validación del parámetro, previamente calibrado, se llevó a cabo una simulación numérica con un caudal de 200 l/s/m y la misma geometría modelada en el proceso de calibración. La validación se produjo mediante ensayo ciego, es decir, en primer lugar se realizó la simulación numérica y se obtuvo el caudal infiltrado, para posteriormente realizar la simulación física y comparar resultados. La ley de pérdida de carga obtenida es función únicamente del tipo de bloque empleado y de su colocación, pero no varía para distintos caudales vertidos o taludes, por ello sería redundante validar la expresión para más de un talud y vertido.

Extensión del campo de simulación numérica

Una vez que la ley de pérdida de carga fue calibrada y validada, se pudo proceder a realizar nuevas simulaciones numéricas para taludes y caudales distintos a los de la instalación física. En concreto se llevaron a cabo 80 simulaciones numéricas 3D, según cuatro taludes (1.5, 2.0, 2.5 y 3.0), varios caudales de vertido (200, 300, 400, 600, 1000 l/s/m) y cuatro longitudes de aliviadero (8, 16, 32, 48 filas).

3.3. Determinación de las condiciones de estabilidad

3.3.1. Introducción

Uno de los aspectos fundamentales que se deben considerar en el diseño de un aliviadero de bloques en forma de cuña es la estabilidad de los bloques que lo constituyen, ante acciones de vandalismo o frente a solicitaciones hidráulicas debidas al sobrevertido [58]. A continuación se detallan los trabajos realizados para estudiar la estabilidad de los bloques ante las dos acciones antes indicadas.

En concreto para el estudio de la estabilidad de bloques ante acciones de vandalismo se ha desarrollado una aplicación de simulación numérica, que permite obtener la fuerza que es necesario realizar para extraer un bloque aislado de una matriz de bloques.

Por otra parte para el estudio de la estabilidad de bloques ante acciones hidráulicas se ha recurrido a estudios de estabilidad dinámica publicados en la literatura técnica, y se han adaptado a la geometría específica del bloque ACUÑA y ArmorwedgeTM.

3.3.2. Estabilidad ante vandalismo

La extracción de un bloque aislado por una carga de tracción de origen vandálico es desde un punto de vista numérico un problema dinámico de grandes deformaciones. Este problema requiere considerar la interacción entre los bloques adyacentes: el desplazamiento de los situados en las filas superiores, y la interacción con los laterales e inferiores, que en caso de estar en contacto con el que se pretende extraer, generan fuerzas de fricción que se oponen al movimiento. La modelación numérica de este tipo de problemas puede realizarse con el método de elementos discretos (DEM). Se trata de una tecnología en la que se discretiza el dominio de análisis en partículas rígidas con dimensiones conocidas, que se mueven siguiendo las leyes estándar de la dinámica de partículas, por efecto de la gravedad y de las fuerzas de contacto con las partículas adyacentes o con los contornos. Suelen emplearse partículas esféricas para simplificar la generación de geometrías y el cálculo de las interacciones, lo que da como resultado un menor coste computacional. Para modelar elementos no esféricos (como es el caso de los WSB), se ha implementado la posibilidad de generar agrupaciones rígidas de esferas (Clúster de esferas). El resultado es un elemento rígido de contornos esféricos y con el centro de gravedad y de inercia adecuados para su forma y densidad (Figura 65). En este trabajo se ha empleado el código DEM implementado en el entorno KratosMulti-Physics.

Figura 65.Perspectiva del clúster de esferas desarrollado con la forma del WSB a estudio, no se han considerado los conductos de aireación ni el biselado del bloque ACUÑA.

Para simplificar la realización de las simulaciones numéricas desarrolló una aplicación específica en el entorno GiD. El cual es un programa para pre y post proceso gráfico de datos y visualización de resultados provenientes de análisis por diversos métodos de simulación numérica (MEF, DEM, PFEM…) [109].

La aplicación permite de forma automática elegir tamaño de bloque a emplear, a partir de la anchura del mismo, definir la forma del aliviadero a estudio según los parámetros: número de bloques por fila, número de filas, talud y contrapeo de bloques (Figura 66). La aplicación también permite definir la posición, dirección y valor de la carga extractiva, así como el intervalo de tiempo de aplicación. Por último es posible visualizar de manera directa los resultados de la simulación realizada. Con la ayuda de la aplicación descrita se han llevado a cabo una serie de simulaciones numéricas para extraer conclusiones generales del comportamiento de los bloques en forma de cuña ante acciones de vandalismo. En concreto se ha modelado una geometría de aliviadero formada por 90 bloques situados en 20 filas, que se apoyan en un contorno rígido de pendiente 1V/2H. La numeración de filas adoptada comienza desde aguas abajo hacia aguas arriba. No se restringe el movimiento de los bloques laterales, ni de los de la fila 20. La fila 1 se apoya en un contorno rígido cuya forma se adapta a la del bloque, lo que genera fuerzas de fricción que dificultan su movimiento (Figura 67). Se estudió el comportamiento de 2 tamaños de bloques (Figura 68), y se consideró un coeficiente de rozamiento entre bloques de 33º y entre bloques y contorno rígido de 33º ó 0º, según el escenario. Se tomaron esos 33º por ser un valor conservador para el rozamiento con la capa de apoyo y el hormigón, el cual evitaba el deslizamiento aislado de los bloques [110]. La carga aplicada para estudiar el fallo fue vertical en el centro de cara vista, y se aplicó en los bloques situados sobre el eje de simetría de las filas 1, 3, 5, 9 y 15. En la Tabla 8 se resumen los escenarios modelados:

Figura 66.Interfaz de la aplicación para GiD de cálculo de estabilidad de bloques en forma de cuña ante acciones de vandalismo.

Figura 67. Izquierda: Vista general del aliviadero de bloques modelado con DEM. Derecha: contorno rígido de apoyo de los bloques y detalle de forma en el apoyo de la fila 1.

Figura 68. Bloques modelados con DEM. Izquierda: Clúster 1. Derecha: Clúster 2.

Tabla 8. Resumen de escenarios modelados numéricamente con DEM.

Clúster	Fila de aplicación de carga	Rozamiento bloque-contorno	Rozamiento bloque-bloque
1	1	33º	33º
	3
	5
	9
	15
	1	0º
	3
	5
	9
	15
2	1	33º
	3
	5
	9
	15
	1	0º
	3
	5
	9
	15

A partir de las simulaciones numéricas de los escenarios descritos previamente se obtuvieron dos resultados: la carga absoluta de fallo y la carga adimensional de fallo en función del peso de cada bloque modelado.

3.3.3. Estabilidad ante acciones hidráulicas

Para caracterizar la estabilidad de los bloques ante las solicitaciones hidráulicas que genera el flujo vertido sobre ellos se ha tomado como base las tablas publicadas en el manual CIRIA [58] (Figura 69). En estas tablas se relaciona el caudal vertido unitario sobre los bloques con el parámetro que denomina espesor medio de bloque, para varios taludes. Las hipótesis de estabilidad que asumen estas tablas son: capa de drenaje en carga, y factor de seguridad de 1.5. Las tablas permiten el dimensionamiento de bloques tanto en canal de descarga como bajo resalto hidráulico.

Figura 69. Tablas CIRIA para el dimensionamiento de bloques en forma de cuña estables ante acciones hidráulicas. q caudal unitario de descarga, s talud, ta espesor medio del bloque. Izquierda: tabla para dimensionar bloques del canal de descarga. Derecha: tabla para dimensionar bloques bajo resalto hidráulico. Fuente [58].

Teniendo en cuenta que las dimensiones de los bloques que se estudiam en esta campaña son conocidas se crearon tablas específicas de aplicación directa para el bloque en cuestión, que relacionan caudal de vertido unitario, talud y masas de bloque homotético estable, para un factor de seguridad 1,5 y drenaje saturado. Se consideraron como rangos de masas razonables para incluir en las tablas entre 30 Kg y 200 Kg, tanto por razones constructivas de los propios bloques como para facilitar su puesta en obra.

4. RESULTADOS Y DISCUSIÓN

En este capítulo se exponen y discuten los resultados obtenidos en esta investigación, agrupados según las tres campañas de modelación descritas en la metodología.

4.1. Caracterización del comportamiento de la capa de drenaje

4.1.1. Modelación del comportamiento hidráulico

Calibración y validación de la ley de pérdida de carga

En esta tesis se calibraron y validaron valores de los coeficientes a y b de ley de pérdida de carga parabólica para los dos materiales descritos en la metodología, en base a ensayos experimentales y numéricos según el método desarrollado.

Los coeficientes obtenidos para la ecuación parabólica en la fase de calibración se muestra en la Tabla 9.

Tabla 9. Coeficientes a y b de la ley de pérdida de carga de los materiales calibrados numéricamente.

	a	b
Material 1	1.29	93.65
Material 2	0.19	50.22

Utilizando estas leyes de pérdida de carga se modelaron numéricamente los caudales reservados para la validación de entre los ensayos físicos disponibles. Como parámetros de comparación se emplearon el nivel del agua aguas arriba de la presa y la posición del punto de emergencia desde el pié medido sobre el talud. En la Tabla 10 se muestra la comparativa de resultados.

Tabla 10. Comparativa de resultados del proceso de validación de las leyes de pérdida de carga.

	Numérico		Físico
	Nivel aguas arriba (m)	Punto de emergencia (m)	Nivel aguas arriba (m)	Punto de emergencia (m)
Material 1	0.70	1.45	0.71	1.30-1.50
Material 2	0.63	1.22	0.64	1.15-1.35

De los resultados de validación expuestos cabe destacar que el error máximo registrado entre las simulaciones numéricas y los ensayos físicos en cuanto a nivel aguas arriba de presa fue de 1.2 cm, lo que se corresponde con el 1.9% del nivel de agua. Por otro lado, la posición del punto de emergencia en los modelos numéricos queda para ambos materiales dentro de los rangos registrados en el modelo físico.

Teniendo en cuenta estos resultados el procedimiento para lograr los valores de los parámetros de la ecuación parabólica de pérdida de carga se considera validado.

Los resultados completos del ajuste de parámetros de ley de pérdida de carga y otros análisis complementarios de estabilidad fueron expuestos en el Congreso Dam Protections against Overtopping and Accidental Leakage [102].

En resumen se puede destacar que para etapas posteriores se adoptaron como leyes de pérdida de carga las descritas en la Tabla 11, donde son valores experimentales los obtenidos con el método físico-numérico y son valores analíticos los obtenidos según la expresión de Ergun.

Tabla 11. Coeficientes de leyes de pérdida de carga parabólicas empleadas en caracterizar el comportamiento de la capa de drenaje.

	Experimental		Analítica
d50	a	b	a	b
12.6	1.29	93.65	0.49	121.20
35.04	0.19	50.22	0.06	43.58

Modelos de drenaje

Drenaje sin saturar

A continuación se muestran los resultados relativos al calado unitario de vertido obtenido al modelar una capa de drenaje de distintos taludes y materiales sin que alcance la saturación, según las leyes de pérdida de carga descritas. En la Figura 70 se muestran los resultados de las simulaciones numéricas que relacionan el talud (N) y el calado unitario registrado en cada simulación. Se observa que para cada medio poroso la variación de calado con el talud presenta una tendencia sensiblemente lineal y de calado creciente conforme aumenta el talud. También se observa que dependiendo del material modelado el utilizar una ley de pérdida de carga calibrada numéricamente puede sobrevalorar o infravalorar el resultado del calado unitario. En la Figura 71 se muestra la relación obtenida entre el talud y la velocidad de circulación del agua por la capa de drenaje, observándose que conforme crece el talud disminuye la velocidad de circulación del agua, así como que cuanto más fino es el material más despacio circula el agua por el medio poroso.

Figura 70. Evolución del calado unitario registrado en las simulaciones numéricas en relación al talud de la capa de drenaje.

Figura 71. Evolución de velocidad de circulación registrada en las simulaciones numéricas en relación al talud de la capa de drenaje.

Como resumen de esta primera etapa de la campaña de modelación relativa a drenajes sin saturar se concluye que la capacidad hidráulica de un drenaje crece cuanto mayor sea el tamaño del material, a igualdad de porosidad, y cuanto menor sea el talud.

Drenaje saturado

En esta segunda etapa de la campaña de modelación se ha tratado de caracterizar el comportamiento de capas de drenaje saturadas y los efectos de disponer aireadores, con el objetivo de obtener unas nociones básicas de cuál es su comportamiento y los aspectos fundamentales que le afectan.

En base a las simulaciones llevadas a cabo se ha observado que la distribución de presiones que presenta la capa de drenaje saturada depende de cómo sea su alimentación. De tal forma que se ha constatado que para un caudal fijo si la alimentación se produce concentrada en la embocadura la presión máxima en el drenaje es muy superior a si la alimentación se realiza uniformemente distribuida a lo largo de la base del drenaje. Además se ha observado que en el caso de alimentación por embocadura la presión máxima se produce en la zona de más aguas arriba, mientras que en los modelos de alimentación distribuida la máxima presión se produce en una zona intermedia. Para lograr dicha presión máxima en una zona intermedia se forma un remanso, con superficie libre que avanza hacia aguas arriba hasta estabilizarse, por encima de la sección teórica de saturación del drenaje, esta elevación del nivel de la superficie libre es responsable de generar la carga de presión suficiente en el drenaje para desaguar los caudales suministrados. En la Figura 72 se muestra un ejemplo ilustrativo de lo anteriormente expuesto.

También se han realizado varios modelos comparando presiones en capa de drenaje sin aireadores y con aireadores, observándose un significativo descenso de carga debido a la acción de los aireadores (Figura 73).

Figura 72. Ejemplo de distribución de presiones en simulaciones de drenaje en carga sin aireadores, caudal de saturación 5 l/s/m y alimentación de 10 l/s/m, material modelado con d₅₀ 12.6 mm y ley analítica, talud 2. Arriba: alimentación concentrada en embocadura. Abajo: alimentación distribuida.

Figura 73. Ejemplo de acción de los aireadores en drenaje en carga. Se muestra distribución de presiones para caudal de saturación 5 l/s/m y alimentación de 10 l/s/m, material modelado con d₅₀ 12.6 mm y ley analítica, talud 2.

Se ha observado que los aireadores al entrar en carga pasan a actuar como elementos de drenaje, derivando parte del caudal circulante por la capa granular (Figura 74). La eficacia de la acción de los aireadores dependerá tanto de la presión en cada punto de la capa granular como de la presión en cada instante en el punto de conexión del aireador con el exterior del bloque, presión que estará condicionada por la condiciones de vertido sobre los bloques y por su forma específica, la cual condicionará la formación de depresiones localizadas y vórtices (Figura 75).

Figura 74. Ejemplo de distribución vectorial de velocidades en modelo de drenaje saturado con dispositivos de aireación donde se observa la salida de caudal por los aireadores.

Figura 75. Esquema de funcionamiento de capa granular en carga y aireadores actuando como drenaje.

A continuación se abordó como varía la presión máxima en un drenaje en carga conforme aumenta el caudal circulante, tanto en una configuración sin aireadores como con aireadores (Figura 76). Se ha observado que la presión máxima en el drenaje en carga aumenta con el caudal de manera no lineal, además de que la presencia de aireadores disminuye para todos los caudales modelados la presión máxima registrada.

Figura 76. Ejemplo de variación de presión máxima en drenaje en función del caudal drenado a la capa granular. Se muestran resultados de los modelos con material d₅₀ 12.6 mm y ley analítica con talud 2. Entrada de caudal por sección superior.

También se estudió como varía la presión máxima en un drenaje en carga para distintos taludes, observándose un tendencia creciente y sensiblemente lineal conforme aumenta el talud de la capa granular (Figura 77), si bien este aumento es despreciable comparado con el aumento de presión que genera un moderado aumento de caudal circulante por el drenaje.

Figura 77. Ejemplo de tendencia de variación de presión en función del talud (N). Modelos con material modelado con d₅₀ 12.6 mm y ley analítica, entrada de caudal por sección superior.

Por último se estudió cómo afecta la ley de pérdida de carga empleada a la presión máxima del drenaje en carga (Figura 78). Se observa que dependiendo del material modelado el utilizar una ley de pérdida de carga calibrada numéricamente (Experimental) puede sobrevalorar o infravalorar el resultado, al igual que sucedía para el calado unitario para drenaje sin carga. Hay que señalar que la discrepancia de resultados entre leyes es menor para el material más grueso.

Figura 78. Evolución de presión máxima en drenaje frente al caudal circulante para diversos materiales y leyes de pérdida de carga. Entrada de caudal por sección superior.

Como conclusiones a los resultados expuestos cabe destacar que la disposición de aireadores en una capa de drenaje saturada permite reducir significativamente su presión, sin embargo esta disminución no será constante, sino que vendrá condicionada por factores como el caudal de vertido sobre bloques y el desarrollo de zonas de bajas presiones por el escalonado inducido por los bloques, a su vez dependientes del caudal vertido e infiltrado, o también la posición de cada aireador en la rápida. De manera que se considera que para una correcta caracterización de las condiciones de drenaje por aireadores se debe estudiar cada caso particular en concreto en todo su rango de funcionamiento. También se concluye que al aumentar el caudal de vertido la presión máxima en el drenaje crece de manera exponencial, por lo que reducir al máximo el caudal infiltrado que llega al drenaje se revela como un factor clave para el diseño. También se ha observado que aumentar el talud del drenaje aumenta la presión para un mismo caudal, aunque de manera moderada.

4.1.2. Estabilidad al deslizamiento

En este apartado se muestran los resultados de aplicar la fórmula de estabilidad a deslizamiento propuesta (Ec.(33)) para drenaje parcialmente saturado bajo bloques de hormigón.

En primer lugar en la Figura 79 se comparan los coeficientes de seguridad a deslizamiento obtenidos para los dos materiales de estudio con coeficientes de ley de pérdida de carga analíticos y experimentales. Se muestran los resultados para los cuatro taludes modelados (1.5, 2, 2.5 y 3) y espesores de capa de drenaje 10, 20 y 30 cm.

Figura 79. Comparación de coeficiente de seguridad a deslizamiento de capas de drenaje de varios espesores y taludes para leyes de pérdida de carga en medio poroso analítico y experimental.

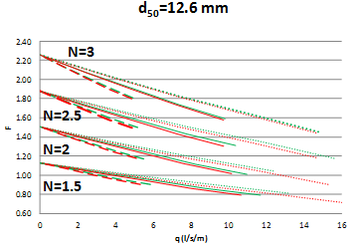
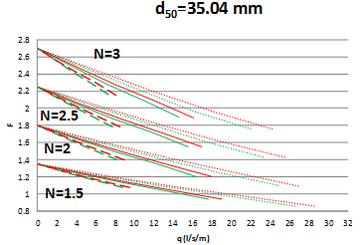
Se aprecia que para el material de diámetro medio 12.6 mm la ley de pérdida de carga adoptada no tiene repercusión significativa en los valores de F. En cuanto al material de 35.04 mm la repercusión sobre F es mayor, pero sigue siendo poco relevante, de hecho la discrepancia máxima en F por considerar una u otra ley de pérdida de carga es menor del 4%. En consecuencia, ante la poca afección que presenta sobre F la forma de definir la ley de pérdida de carga de medio poroso para un mismo material, se podría considerar suficiente aproximación obtenerla según fórmulas analíticas, aunque teniendo en cuenta la posible afección a la precisión de cálculo del calado de saturación.

En la Figura 80 se procede a comparar el coeficiente de seguridad a deslizamiento de capas de drenaje de 10, 20 y 30 cm de espesor, bajo dos tipos de bloques en forma de cuña. En concreto un bloque de 111 kg y otro 22.7 kg con dimensiones bloque ACUÑA o ArmorwedgeTM (dimensiones exteriores equivalentes).

Figura 80. Comparación de coeficiente de seguridad a deslizamiento de capas de drenaje de varios espesores bajo bloques de 111 kg y 22.7 kg.

Se aprecia que el bloque más pesado mejora las condiciones de estabilidad a deslizamiento de la capa de drenaje. Además se observa que conforme aumenta el talud y el espesor de la capa de drenaje el coeficiente de seguridad a deslizamiento aumenta. Un incremento en la estabilidad del drenaje también se aprecia cuando aumenta el tamaño del material.

Como principales conclusiones de las simulaciones realizadas se observa que conforme aumenta el caudal que circula a través del drenaje, aumenta su tendencia al deslizamiento. Cuanto mayor sea el espesor de la capa de drenaje, más estable resultará para un mismo caudal de infiltración al estabilizar la capa seca a la saturada. También al aumentar el peso de bloques en forma de cuña que se disponen sobre la capa de drenaje disminuye la tendencia de esta al deslizamiento.

4.2. Caracterización y cuantificación de caudales de infiltración

En este apartado se muestran los resultados de la campaña de modelación numérica para caracterizar y cuantificar el circulante sobre los bloques. Se plantearon dos etapas para la obtención del caudal infiltrado: una primera 2D, que permitió realizar un gran número de simulaciones en un corto espacio de tiempo a partir de las cuales obtener conclusiones generales y tendencias del fenómeno de infiltración. En la segunda etapa se realizaron ensayos 3D que fueron susceptibles de calibración en base a resultados de ensayos físicos.

4.2.1. Etapa de modelación 2D

Influencia la ley de pérdida de carga en el caudal infiltrado

En este epígrafe se muestran los resultados obtenidos de las simulaciones numéricas en cuanto a los caudales de infiltración registrados en 2D. En concreto se obtuvo en la sección de apoyo de los bloques (Figura 81) el caudal infiltrado que llega al drenaje por cada nodo, y se realizó posteriormente la suma acumulativa, de aguas arriba hacia aguas abajo, de todos estos caudales para obtener el caudal máximo que circularía por la capa de drenaje.

Figura 81. Izquierda: detalle de una zona del dominio de simulación de caudal infiltrado 2D, donde se indica en amarillo la zona de apoyo de los bloques en la que se calcula la infiltración. Derecha: esquema explicativo del parámetro L para la medida de infiltración 2D.

A continuación se muestran los resultados que relacionan el caudal infiltrado con el valor del parámetro de pérdida de carga a (Figura 82) y con la longitud del aliviadero (Figura 83).

Figura 82. Evolución del caudal máximo acumulado por filtraciones en el drenaje en función del coeficiente a, para distintos caudales de sobrevertido. Izquierda: infiltración en l/s/m. Derecha: infiltración en %.

Figura 83. Evolución del caudal infiltrado acumulado a lo largo del aliviadero 2D. Valores promedios en 5 s.

De los resultados expuestos cabe resaltar que en todas las simulaciones realizadas se observó que conforme aumenta el valor del coeficiente a la infiltración disminuye, aunque no de manera lineal. También se observa que el caudal máximo que circularía por la capa de drenaje depende del caudal vertido sobre los bloques, registrándose mayores valores absolutos de caudal infiltrado acumulado cuanto mayor es el caudal que circula por el aliviadero. Sin embargo si se observa cuál es el porcentaje del caudal circulante por el aliviadero que termina llegando a la capa de drenaje sucede lo contrario, es decir, cuanto menor es el caudal de vertido mayor es el porcentaje infiltrado. Este comportamiento ya ha sido observado en ensayos de laboratorio previos [74].

La evolución del caudal infiltrado acumulado a lo largo del aliviadero, para cualquiera de los valores de a simulados y para cualquiera de los caudales de sobrevertido, crece de manera lineal conforme se avanza hacia aguas abajo del aliviadero. Intuitivamente podría parecer que en la zona alta del aliviadero la infiltración sería mayor que en la zona baja, por existir un mayor calado de agua, pero las condiciones hidráulicas que genera el escalonado de los bloques hacen que no suceda eso, sino que la infiltración se mantenga sensiblemente constante a lo largo del aliviadero. En la Figura 84 se muestra un ejemplo de cómo las condiciones hidráulicas que genera el escalonado de los bloques afectan a los caudales de infiltración, generando especialmente en la zona del pie del aliviadero zonas contiguas con fuertes oscilaciones en los valores de infiltración.

Figura 84. Izquierda: Valores promedios en 5 s de caudal infiltrado en cada nodo a lo largo del aliviadero. Derecha: distribución vectorial de velocidades en un instante de la simulación, se aprecian zonas de infiltración nula y otras contiguas con infiltración, que variarán en el tiempo.

Efectos de escala

En este epígrafe se muestran los resultados obtenidos de las simulaciones numéricas en cuanto a los caudales de infiltración registrados para las geometrías básica y escalada según lo descrito en la metodología. En concreto se muestran los gráficos que relacionan el caudal infiltrado con la longitud del aliviadero (Figura 85) y con el valor del parámetro a (Figura 86).

Figura 85. Evolución del caudal infiltrado acumulado a lo largo del aliviadero. Valores promedios en 5 s.

Figura 86. Evolución del caudal máximo acumulado por filtraciones en el drenaje en función del coeficiente a. Izquierda: infiltración en l/s/m. Derecha: infiltración en %. Valores promedios en 5 s.

En los gráficos expuestos anteriormente se observa que, tanto en la geometría básica como en la escalada, la evolución del caudal infiltrado acumulado crece de manera lineal conforme se avanza hacia aguas abajo del aliviadero.

En la Figura 87 se comparan en una misma gráfica la evolución del caudal máximo (en porcentaje sobre el de vertido) que circula por la capa de drenaje en función del valor del coeficiente a, para ambas geometrías modeladas. Se puede observar que los resultados de las dos geometrías no son coincidentes, como sería de esperar al estar la geometría básica y la escalada relacionadas por la semejanza de Froude. Esta discrepancia puede ser debida a que la semejanza de Froude se ha aplicado a las dimensiones geométricas y a los caudales de vertido, pero no así a los valores del coeficiente a de la ley de pérdida de carga. Por lo que para que los resultados sean coincidentes resultará necesario introducir un factor de corrección a los valores del coeficiente a de la geometría escalada.

Figura 87. Comparativa de la evolución del caudal máximo acumulado por filtraciones en el drenaje en función del coeficiente a, para geometría básica y escalada.

Para establecer el factor de corrección que se debe aplicar a los valores del coeficiente se ha recurrido a aplicar la semejanza de Froude correspondiente a las unidades dimensionales de dicho coeficiente, que son s/m. En consecuencia se obtiene la expresión de equivalencia siguiente:

$Coeficiente\,a\,modelo\,real={f}^{-0.5}\ast Coeficiente\,a\,modelo\,reducido$

(38)

En la Figura 88 se muestran los resultados de aplicar la expresión de equivalencia de la Ec.(38) a los resultados de la geometría escalada, observándose que pasan a solaparse con los resultados de la geometría básica.

Figura 88. Resultados de aplicar la relación de equivalencia a la geometría escalada para obtener la curva de caudal infiltrado de la geometría básica.

4.2.2. Etapa de modelación 3D

Validación hidráulica del modelo numérico

Para comprobar que el modelo numérico 3D simula correctamente el fenómeno de sobrevertido en un aliviadero de bloques en forma de cuña, se procedió a reproducir numéricamente la geometría de la instalación construida en el Centro de Estudios Hidrográficos del CEDEX según se ha descrito en la metodología.

Los resultados se muestran en la Figura 89, donde se indican con líneas continuas de color rojo, azul y verde los calados máximo, promedio en 5 segundos y mínimo respectivamente medidos en la modelación numérica. También aparecen puntos rojo, naranja y morado, y sus líneas auxiliares respectivas de posicionamiento, que indican calados característicos (concentración de aire del 90%) en tres puntos obtenidos del ensayo en laboratorio. Se aprecia que estos calados característicos son casi coincidentes con la línea que define el calado máximo numérico. Este hecho se asocia a que al existir una gran turbulencia superficial en este tipo de aliviaderos hay regiones de aire que quedan atrapadas por esta turbulencia superficial, entumeciendo la lámina y por tanto aumentando el calado [90]. En la modelación numérica no se considera la interacción agua-aire y por tanto la lámina no se entumece al no atrapar aire, reflejándose únicamente la turbulencia superficial en la envolvente de máximos del calado, que es por tanto la más similar al calado entumecido que se registra en los ensayos físicos.

Figura 89. Simulación 3D. Comparación de calados numéricos y experimentales en el bloque 25.

Calibración y validación de la ley de pérdida de carga

Para poder obtener el caudal real infiltrado a través de un aliviadero de bloques, mediante el método de la ley de pérdida de carga propuesto, resulta necesario calibrar a partir de ensayos físicos el valor del parámetro a de la ley de pérdida de carga. Para ello en la instalación de ensayo construida en el Laboratorio de Estudios Hidrográficos del CEDEX se registraron los caudales infiltrados al drenaje para un caudal de vertido de 240 l/s/m en la fila 32 desde embocadura [108].

A partir de esos resultados experimentales se procedió a calibrar el parámetro a de la ley de pérdida de carga numérica, mediante múltiples simulaciones numéricas con diversos valores del parámetro (Figura 90) y el mallado adecuado para reproducir el calado adecuadamente. Para un valor a=8400 se consiguió un ajuste adecuado, con una discrepancia físico-numérica del 2.03%.

Figura 90. Calibración. Comparativa de resultados físico-numéricos 3D.

Para la validación del parámetro a, previamente calibrado, se llevó a cabo una simulación numérica con un caudal de 200 l/s/m y la misma geometría modelada en el proceso de calibración. La validación se produjo mediante ensayo ciego, es decir, en primer lugar se realizó la simulación numérica y se obtuvo el caudal infiltrado, para posteriormente realizar la simulación física y comparar resultados. Según este procedimiento la discrepancia entre la infiltración física y numérica fue del 4.4% (Figura 91). Estas pequeñas discrepancias confirman la bondad de la solución calibrada.

Figura 91. Validación. Comparativa de resultados físico-numéricos 3D. Se indica barra de erros de resultados físicos.

Extensión del campo de simulación numérica

Una vez que la ley de pérdida de carga fue calibrada y validada, se pudo proceder a realizar nuevas simulaciones numéricas para taludes y caudales distintos a los de la instalación física. En concreto se llevaron a cabo 80 simulaciones numéricas 3D, según 4 taludes (1.5, 2.0, 2.5 y 3.0), varios caudales de vertido (200, 300, 400, 600, 1000 l/s/m) y cuatro longitudes de aliviadero (8, 16, 32, 48 filas). Los resultados relativos a caudales de infiltración acumulados se muestran en Figura 92 y Figura 93. En todos los escenarios modelados se observa cómo el caudal infiltrado crece conforme lo hace el caudal vertido. Así mismo se observa que conforme aumenta el talud también lo hace el caudal infiltrado. También se confirma que al aumentar la longitud del aliviadero (número de filas) aumenta el caudal infiltrado.

Figura 92. Caudales de infiltración obtenidos mediante modelación numérica 3D. Taludes 1.5 y 2.

Figura 93. Caudales de infiltración obtenidos mediante modelación numérica 3D. Taludes 2.5 y 3.

4.3. Determinación de las condiciones de estabilidad

4.3.1. Estabilidad ante vandalismo

En este apartado se muestran los resultados relativos a los ensayos numéricos realizados con DEM para modelar las condiciones de extracción de bloques aislados. En concreto se muestran (Figura 94 y Figura 95) las cargas necesarias para la extracción de dos bloques homotéticos, situados en distintas posiciones del aliviadero y para distintas relaciones de rugosidad bloque-apoyo. Se ofrecen resultados de carga absoluta y adimensionalizadas en base al peso de cada bloque.

Figura 94. Carga absoluta de fallo de bloque a tracción según simulación numérica 3D.

De estos resultados se puede observar que la carga máxima necesaria para extraer un bloque se registró en la fila 1, que es donde los bloques tienen un mayor contacto con el contorno rígido. Conforme se asciende hacia aguas arriba de la rápida la carga de fallo desciende de una manera moderada.

Figura 95. Carga adimensional de fallo de bloque a tracción según simulación numérica 3D. Adimensionalización según masa de bloque.

En los resultados expuestos se aprecia cómo la carga absoluta para provocar el fallo del bloque más pesado (Clúster 1) es mayor que para el bloque más ligero (Clúster 2). Sin embargo en valores adimensionalizados las cargas para extraer cada uno de los bloques presentan valores similares. También se observa que en los escenarios sin rozamiento entre los bloques y el contorno se debe aplicar una mayor carga para la extracción del bloque traccionado. Esto se debe a que al no existir rozamiento entre contorno y bloques estos deslizan, comprimiéndose unos contra otros, de tal forma que al intentar sacar un bloque se deben movilizar un número importante de bloques a su alrededor. Sin embargo cuando los bloques no están comprimidos unos con otros solo se han de movilizar los dos bloques superiores al traccionado (Figura 96 y Figura 97).

Figura 96. Ejemplos de movilización de bloques en torno a bloque traccionado indicado en verde. Izquierda: rozamiento bloques-contorno 33º. Derecha: rozamiento bloques-contorno 0º.

Figura 97. Vista en planta de bloques movilizados más de 3 mm en situación de fallo.

4.3.2. Estabilidad ante acciones hidráulicas

Para caracterizar la estabilidad de los bloques ante las solicitaciones hidráulicas que genera el flujo vertido sobre ellos se ha tomado como base las tablas publicadas en el manual CIRIA [58]. Conocidas las proporciones de un diseño de bloque es posible adaptar las tablas a la familia de bloques homotéticos. Siguiendo esta línea se han adaptado las tablas CIRIA a los bloques ArmorwedgeTM y ACUÑA, que por tener las mismas proporciones exteriores pueden compartir las mismas tablas adaptadas de diseño.

De esta forma se han obtenido la tabla de base CIRIA que relaciona el caudal de vertido unitario, el talud y la masa del bloque estable, para un factor de seguridad 1.5 y drenaje saturado. En la Figura 98 se muestra la tabla obtenida, donde se ha considerado como rangos de masas razonables entre 30 Kg y 200 Kg, tanto por razones constructivas de los propios bloques como para facilitar su puesta en obra. Se observa cómo conforme crece el talud para un bloque de masa fija el caudal para el cual no sufre daños crece. También se observa que cuanto mayor es la masa del bloque mayor es el caudal frente al que es estable y más tendida su curva de evolución.

Figura 98. Tabla para el dimensionamiento estable en canal de descarga ante acciones hidráulicas y drenaje saturado para bloques ArmorwedgeTM y ACUÑA. N talud, q caudal unitario de vertido.

En cuanto a las tablas de dimensionamiento bajo resalto hidráulico se ha comprobado, en base a la tabla CIRIA específica, que para que resulten estables los bloques deben tener masas muy superiores a los 200 kg o taludes muy superiores a los razonables en presas o balsas, con lo que se recomienda no permitir el resalto hidráulico sobre los bloques en aliviaderos de presas, al tener que recurrir para asegurar su estabilidad a tamaños de bloques o taludes no razonables y antieconómicos. Si resultara imprescindible para un diseño que el resalto hidráulico se produzca sobre los bloque se recomienda usar las soluciones rígidas recogidas en el estado del arte.

5. PROCEDIMIENTO DE DISEÑO

En este capítulo se presenta un procedimiento para el diseño asistido por ordenador de aliviaderos WSB. El procedimiento incluye el diseño del drenaje y la capa de soporte, considerando su capacidad de filtración y estabilidad. El caudal infiltrado a través de las uniones entre bloques se estima por medio de los resultados obtenidos de los modelos numéricos calibrados y validados las campañas de ensayo. El procedimiento también sugiere la protección del pie de presa mediante un repié granular.

5.1. Soluciones propuestas para cada tipo de presa

La forma de drenar el caudal de infiltración es un aspecto clave para diseñar los aliviaderos WSB y depende del tipo de presa.

En las presas homogéneas el espaldón consiste en un material impermeable, por lo que para evitar que la subpresión bajo los bloques comprometa su estabilidad debe disponerse una capa de drenaje con una capacidad hidráulica adecuada para evacuar el caudal de infiltración al pie de presa (Figura 99).

Figura 99. Esquema de operación de WSB sobre presa homogénea.

En las presas de escollera su espaldón es permeable y las filtraciones pueden fluir libremente hasta el contorno impermeable definido por la cimentación (Figura 100). Por lo tanto, la permeabilidad del espaldón debe ser suficiente para evacuar el caudal infiltrado sin que afecta a la estabilidad de los bloques.

Figura 100. Esquema de operación de WSB sobre presa de escollera.

El procedimiento de diseño propuesto [111] se ha basado en evitar que el drenaje bajo los bloques entre en carga. Se ha decidido adoptar esta hipótesis de diseño dadas las incertidumbres observadas en las campañas numéricas realizadas en esta tesis, relativas a la disipación de presiones por los elementos de aireación de los bloques. Esta hipótesis de drenaje no saturado garantiza que no exista subpresión bajo los bloques, lo que asegura su estabilidad por su particular distribución de presiones en las caras vistas y la ausencia de presión desestabilizante en la cara de apoyo evitando el pandeo [112]. Para lograr este objetivo, se proponen dos soluciones según el tipo de presa (Figura 101).

Figura 101. Esquema de soluciones propuestas en el procedimiento de diseño. Superior: Solución para presa homogénea. Inferior: Solución para presa de escollera.

Para presas homogéneas o de escollera con una marcada anisotropía se propone disponer bajo los bloques una capa de drenaje de material poroso con condición de filtro, donde se recojan las infiltraciones entre bloques y se conduzcan hacia la zona del pie de presa. El espesor del drenaje se propone que sea constante y con dimensiones suficientes para recoger la totalidad del caudal infiltrado entre bloques en condiciones de estabilidad frente a deslizamiento. La capa de drenaje, según el diseño propuesto cubre todo el espaldón de la presa hasta alcanzar el plano de cimentación, donde enlazará con un repié de escollera mediante una estructura de transición, constituida por un marco perimetral de hormigón de ancho el ancho del canal de descarga del aliviadero, y relleno con el mismo material drenante del repié. Sobre el marco de hormigón se dispondrá un trampolín que permitirá independizar el desagüe de los caudales de sobrevertido y de infiltración. Una estructura de este tipo que permite independizar el desagüe de caudales ya se utilizó con éxito en la presa Barriga, como se ilustra en la Figura 102.

Figura 102. Presa de Barriga. Detalle de trampolín y marcos de hormigón rellenos de material poroso.

Cabe destacar que la estructura de transición descrita tiene como objetivo secundario ayudar a estabilizar los bloques al apoyarlos sobre un contorno rígido que impide holguras, que pueden llevar a fallos de los bloques por deslizamiento, giro o elevación [58].

Para presas de escollera isótropas se propone disponer los bloques sobre el propio espaldón de la presa o sobre una capa superficial de regularización, si el tamaño de la escollera no permite una correcta puesta en obra. Las infiltraciones entre bloques serán recogidas por el propio cuerpo de presa y dirigidas hacia el pie, donde de manera análoga al diseño para presas homogéneas se propone disponer una estructura de transición y un repié de escollera. Este repié comenzará aguas abajo del pie de presa y debe tener una permeabilidad mayor al material del cuerpo de presa para que su funcionamiento sea adecuado [16]. Hay que destacar que en el diseño para presas de escollera isótropas el marco de hormigón de la estructura de transición, sobre el que apoya el trampolín, se propone rellenar del mismo material del cuerpo de presa, ya que apoya parcialmente en el propio pie de presa.

Para ambas soluciones se recomienda disponer sobre el repié una protección superficial tipo rip-rap, que permita asegurar que no se producen daños por erosión superficial al desaguar los caudales infiltrados a través del repié. En el caso de que el diseño del aliviadero lleve a alturas de repié reducidas este puede eliminarse, siempre que se asegure la estabilidad del material granular del interior de la estructura de transición mediante estructuras de retención [113], como se hizo en al presas de Barriga. Así mismo se debe asegurar la condición de filtro para que los materiales de drenaje sean autoestables [114].

En la Figura 103 se muestra un render ilustrativo del diseño exterior resultante de la solución de aliviadero planteada en este procedimiento.

Figura 103. Dibujo esquemático en 3D de la solución propuesta. Se indica en rojo el repié para el drenaje de caudales infiltrados, así como la zona de protección con rip-rap del repié.

5.2. Procedimiento de cálculo

En este apartado se expondrán las características generarles del procedimiento de diseño propuesto, el cual a partir de unos datos de entrada devuelve los resultados necesarios para el diseño completo de un aliviadero WSB. Un esquema de los datos de entrada y resultados de salida del procedimiento se muestran en la Figura 104.

	ENTRADA				SALIDA
Tipo de presa				Volumen de materiales
Forma del valle				Talud del repié (αr)
Características mecánicas e hidráulicas de los materiales porosos				Altura de repié (HT)
				Espesor de capa de drenaje (et)
Coste de los materiales				Número de bloques (W)
Altura del labio del aliviadero (H)				Altura de cajeros (hc)
Caudal de descarga (Q)				Diámetro de rip-rap (drr)
Talud del espaldón de aguas abajo (α)
Nivel de agua en el cauce (yc)
Ancho de aliviadero (B)
Masa del bloque de diseño (M)
Talud de cajeros (Tc)
Grado de saturación máxima admisible (GS)
Factor de seguridad a deslizamiento del repié (Fr)
Factor de seguridad a deslizamiento de la capa de drenaje (Fd)
Ancho de fondo de valle (Bv)
Masa del bloque testado (MB)
Dimensiones del bloque testado
Caudal de infiltración (qi)

Figura 104. Resumen de datos de entrada del procedimiento y resultados de salida del mismo.

Figura 105. Esquema de dimensiones del bloque testado para obtener el caudal de infiltración

El procedimiento de diseño se sintetiza en un algoritmo (Figura 106), el cual alcanza la solución por un proceso de tentativas sucesivas. Una vez alcanzada la solución se recomienda comprobar la condición de filtro de los materiales así como el caudal límite estable ante acciones hidráulicas por tablas CIRIA particularizadas.

Figura 106. Algoritmo del procedimiento de diseño propuesto.

A continuación se detallan los procedimientos a seguir en cada paso del algoritmo propuesto.

5.2.1. Paso 0. Inicialización de parámetros

Este es el paso de inicialización del algoritmo, en él se calculan unas dimensiones geométricas iniciales que en pasos posteriores pueden ser modificadas según las condiciones hidráulicas de diseño.

Cálculo del talud saturado estable para el repié (α_r)

En primer lugar se procederá a calcular el talud saturado estable para el repié por el que se aliviarán los caudales infiltrados. Este talud es independiente de los caudales infiltrados, por lo tanto no le afectarán las condiciones hidráulicas del diseño, sino únicamente las características mecánicas del material que el diseñador desee disponer. Para obtener el talud estable se empleará la formulación desarrollada en esta tesis, considerando el flujo paralelo a la cimentación.

${F}_{r}={\frac {1}{{\gamma }_{e,sat}}}\cdot \left({\gamma }_{e,sat}-{\frac {{\gamma }_{w}}{{\mathrm {cos} \,{\alpha }_{r}}^{2}}}\right)\cdot {\frac {Tan(\varphi )}{Tan({\alpha }_{r})}}$

(39)

Siendo:

F_r es el coeficiente de seguridad a deslizamiento del repié fijado por el usuario.

γ_e,sat es el peso específico saturado del material.

α_res el talud del repié en grados.

γ_w es el peso específico del agua.

ϕ es el ángulo de fricción del material en grados.

Cálculo de la altura inicial de los cajeros (h_c0)

Posteriormente se procede a calcular la altura inicial de los cajeros del canal de descarga. Su mínimo geométrico será el que determine el calado en el labio para el caudal de diseño del aliviadero. Para obtener este calado se empleará la ecuación del aliviadero de labio grueso con un factor de seguridad 1.5. Esta altura de cajeros será modificada en pasos posteriores en función de la longitud del canal de descarga y las dimensiones del repié requerido.

$q={\frac {Q}{B}}$	(40)
$q={\frac {2}{3}}\cdot 0.577\cdot {\sqrt {2\cdot g}}\cdot {h}^{\frac {3}{2}}$	(41)
${h}_{c0}=1.5\cdot h$	(42)

Siendo:

q es el caudal unitario de descarga.

Q es el caudal de descarga.

B es el ancho del aliviadero.

h es la altura de los cajeros sin factor de seguridad.

h_c0 es la altura inicial de los cajeros con factor de seguridad.

g es la aceleración de la gravedad.

Cálculo de la altura inicial del repié (H_T0)

Por último se procede a obtener la altura inicial del repié según la expresión siguiente:

${H}_{T0}={\frac {{h}_{c0}}{\mathrm {cos} \,\alpha }}$

(43)

Siendo:

H_t0 es la altura del repié inicial.

h_c0 es la altura inicial de los cajeros con factor de seguridad 1.5.

α es la pendiente de la presa en grados.

Figura 107. Esquema de relación geométrica entre altura de repié y altura de cajeros.

Cálculo del factor de homotecia (${\textstyle \,\lambda }$)

A continuación se procede a calcular el factor de homotecia del bloque de diseño respecto al bloque testado para obtener el caudal de infiltración, según la Ec.(44).

$\lambda ={\frac {M}{{M}_{B}}}$

(44)

Siendo:

λ factor de homotecia.

M es la masa del bloque definido por el usuario para diseñar el aliviadero.

M_B es la masa del bloque testado para obtener el caudal de infiltración.

5.2.2. Paso 1. Actualización de la geometría

Actualización de la altura del repié (H_T)

En la primera etapa de este paso se procede a actualizar la altura del repié, según la expresión de la Ec.(45).

${H}_{T}={{H}_{T}}^{0}+{\Delta H}_{T}$

(45)

Siendo:

H_t es la nueva altura del repié actualizada para pasos posteriores.

H_t⁰ es la altura del repié en la tentativa anterior de solución del algoritmo

ΔH_t es un incremento de altura del repié definido por el usuario.

Figura 108. Esquema de actualización geométrica.

Si el algoritmo va a ser programado para su resolución asistida por ordenador se recomienda un valor de ΔH_t dinámico. En concreto en este trabajo se propone utilizar el valor de la centésima parte de la altura del labio de vertido. En caso de ser la primera vez que se ejecuta el Paso 1 en el algoritmo, se impone queH_T⁰ =H_T0, y ΔH_T=0.

Actualización de la altura de cajeros (h_c)

En función de la altura del repié actualizada se calcula la nueva altura de cajeros según la expresión siguiente:

${h}_{c}={H}_{t}\cdot \mathrm {cos} \,\alpha$

(46)

Siendo:

H_t es la altura del repié.

h_c es la altura de los cajeros.

α es la pendiente de la presa en grados.

Cálculo del número de filas de bloques (R_w)

El número de filas de bloques en el aliviadero se obtiene con la Ec.(47) si la presa es homogénea y con Ec.(48) si la presa es de escollera.

${R}_{w}={\frac {\left({\frac {H}{\mathrm {sin} \,\alpha }}\right)}{\lambda \cdot {A}_{B}}}$

(47)

Siendo:

R_w es el número de filas de bloques.

H es la altura del labio del aliviadero.

α es la pendiente de la presa en grados.

A_B es la dimensión longitudinal del apoyo del bloque testado para obtener el caudal de infiltración.

λ factor de homotecia.

${R}_{w}={\frac {\left({\frac {H-{H}_{t}}{\mathrm {sin} \,\alpha }}\right)}{\lambda \cdot {A}_{B}}}$

(48)

Siendo:

R_w es el número de filas de bloques.

H es la altura del labio del aliviadero.

H_t es la altura del repié.

α es la pendiente de la presa en grados.

A_B es la dimensión longitudinal del apoyo del bloque testado para obtener el caudal de infiltración.

λ factor de homotecia.

5.2.3. Paso 2. Obtención del caudal infiltrado

Determinación del caudal de infiltración (q_i)

El caudal infiltrado, como se observó en las campañas de modelación, depende de tres parámetros: La pendiente del aliviadero, el caudal de sobrevertido y el tamaño del WSB, que determina la longitud de las uniones por unidad de superficie. Este caudal infiltrado afecta a la estabilidad del espaldón de aguas abajo de la presa, y por lo tanto a todo el diseño del aliviadero. En consecuencia, para cada diseño se deberá determinar el caudal de infiltración con la mayor precisión posible, bien sea por ensayos físicos o numéricos específicos. En caso de no contar con ensayos de infiltración para el diseño específico planteado se tomarán como base los resultados obtenidos en las campañas de modelación 3D de esta tesis. En las que se emplearon modelos numéricos para obtener el caudal infiltrado en base al enfoque matemático de asignar una ley de pérdida de carga a los bloques en su conjunto, demostrando que con una ley de pérdida de carga adecuadamente calibrada y validada es posible reproducir el proceso de infiltración. En base a esos resultados se entrena una red neuronal que permite obtener resultados para combinaciones de valores de taludes, caudales y escalones de caudal no simulados numéricamente de manera específica. De tal forma que introduciendo en la red neuronal el talud de la presa, el caudal unitario de vertido y el número de filas de bloques del aliviadero, se obtiene el caudal de infiltración como tanto por ciento del caudal vertido.

En la Figura 109 se muestra el ajuste de la red neuronal a los ensayos numéricos realizados. Se han establecido como valores límite para el uso de la red taludes de hasta 3, 50 filas de bloques, considerando bloques homotéticos al ensayado según semejanza de Froude. Para valores fuera de estos rangos establecidos se deberá realizar el ensayo de infiltración específico, para así obtener el caudal infiltrado para el caso de estudio.

Figura 109. Comparativa de resultados obtenidos con los modelos numéricos y con la red neuronal.

5.2.4. Paso 3. Cálculo de saturación en repié y bajo estructura de trampolín

Cálculo del nivel de agua en el repié (y_r)

En esta primera fase del Paso 3 se calcula la línea de saturación que provoca en el repié el caudal infiltrado entre bloques, siendo el calado pésimo el que se produce en el entronque con la estructura del trampolín. Para ello se ha desarrollado un método de aproximación unidimensional, que contempla una ley de pérdida de carga para el medio poroso de tipo cuadrático, que implementada en la ecuación clásica de conservación de energía simplificada de la hidráulica, entre un punto 1 y otro 2 de una línea de corriente, permite obtener la Ec.(49):

${Z}_{1}+{\frac {{P}_{1}}{{\gamma }_{w}}}+{\frac {{{v}_{1}}^{2}}{2g}}={Z}_{2}+{\frac {{P}_{2}}{{\gamma }_{w}}}+$${\frac {{{v}_{2}}^{2}}{2g}}+\left[L\cdot (a\cdot {v}_{m}+b\cdot {{v}_{m}}^{2})\right]$

(49)

Siendo:

Z₁ cota de la línea de corriente en el punto 1 del medio poroso.

Z₂ cota de la línea de corriente en el punto 2 del medio poroso.

P₁ presión hidrostática en el punto 1 de la línea de corriente.

P₂ presión hidrostática en el punto 2 de la línea de corriente.

γ_w es el peso específico del agua.

v₁ velocidad en el punto 1 de la línea de corriente.

v₂ velocidad en el punto 2 de la línea de corriente.

g es la aceleración de la gravedad.

a, b son coeficientes específicos de cada medio granular.

v_m es el promedio de v₁ y v₂ .

L es la longitud entre los puntos 1 y 2 sobre la línea de corriente.

En base a la anterior ecuación es posible definir un sistema compatible de 5 ecuaciones con 5 incógnitas, partiendo de las siguientes hipótesis:

• El control hidráulico se establece en el punto de emergencia y su dirección es hacia aguas arriba.

• Se considera la línea de corriente entre los puntos 1 y 2 sobre la solera del repié.

• La presión hidrostática en la solera se corresponde con el nivel de agua en ese punto.

• El caudal circulante dentro del repié es constante.

• La pendiente de la línea de saturación es máxima en el punto de emergencia y no puede ser mayor en ningún caso al talud del repié [115][115].

• Se considera la distancia L, entre los puntos de cálculo 1 y 2 como constante y conocida. En concreto en esta tesis se propone utilizar la milésima parte de la longitud de ocupación en planta del repié.

${y}_{1}+{\frac {{{v}_{1}}^{2}}{2g}}={y}_{2}+{\frac {{{v}_{2}}^{2}}{2g}}+\left[L\cdot (a\cdot {v}_{m}+\right.$$\left.b\cdot {{v}_{m}}^{2})\right]$	(50)
${q}_{i}\cdot {\frac {B}{{B}_{v}}}={y}_{1}\cdot {v}_{1}$	(51)
${y}_{1}\cdot {v}_{1}={y}_{2}\cdot {v}_{2}$	(52)
$\mathrm {tan} \,\left(\alpha \right)={\frac {({y}_{2}-{y}_{1})}{L}}$	(53)
$L={\frac {{H}_{t}}{\mathrm {1000\cdot tan} \,\left(\alpha \right)}}$	(54)

Siendo:

y₁ nivel de la línea de saturación en el punto 1.

y₂ nivel de la línea de saturación en el punto 2.

v₁ velocidad en el punto 1 de la línea de corriente.

v₂ velocidad en el punto 2 de la línea de corriente.

g es la aceleración de la gravedad.

a, b son coeficientes específicos de cada medio granular.

v_m es el promedio de v₁ y v₂ .

α es la pendiente de la presa en grados.

B es el ancho del aliviadero.

B_v es el ancho de fondo de valle.

q_i es el caudal unitario de infiltrado.

L es la longitud entre los puntos 1 y 2.

H_t es la altura del repié.

Resolviendo el sistema anterior de 5 ecuaciones es posible obtener el calado del punto de emergencia para cualquier repié.

En caso de que exista un cierto calado en el cauce aguas abajo del repié el valor de y₁ debe actualizarse según la expresión siguiente:

${y}_{1}={{y}_{1}}^{0}+{y}_{c}$

(55)

Siendo:

y_c nivel del cauce aguas abajo del repié.

y₁⁰calado de emergencia sin considerar nivel del cauce.

y₁ calado de emergencia considerando el nivel del cauce.

Para comprobar que las hipótesis adoptadas son admisibles se procedió a comparar los resultados obtenidos resolviendo el sistema de ecuaciones con resultados obtenidos por ensayo en modelo físico en las instalaciones del laboratorio de Hidráulica de la ETSI de Caminos, Canales y Puertos de la UPM [16]. En concreto se utilizaron ensayos de dos materiales en modelo físico con talud 3, diámetro medio (d₅₀) 12.6 y 45.5 mm, con porosidad 41% y varios caudales, con registro del nivel de punto de emergencia. Paralelamente se resolvió matemáticamente el problema de filtración, según el procedimiento del sistema de ecuaciones indicado, y con una ley de pérdida de carga obtenida por el método analítico de Ergun, para finalmente comparar los resultados obtenidos con los del ensayo físicos y con formulaciones propuestas por otros autores [115] [116] (Figura 110), observándose el significativo ajuste del método propuesto.

Figura 110. Punto de emergencia. Comparación de resultados numéricos, físicos y de ecuaciones analíticas de autores varios.

Conocido el calado del punto de emergencia es posible obtener el nivel de saturación en todo el interior del repié, resolviendo un sistema de ecuaciones análogo al anteriormente propuesto, en el que se considere libre la pendiente de la línea de saturación, pero a cambio se fije el calado y₁ igual al calado y₂obtenido de la etapa anterior de resolución del sistema de ecuaciones. Actualizando de manera sucesiva el valor de y₁ igual al y₂ de la etapa anterior es posible calcular la línea de saturación completa. De esta manera resolviendo el sistema de ecuaciones anterior de manera sucesiva desde el punto de emergencia hacia aguas arriba, es posible generar la línea de saturación completa dentro del repié según el siguiente sistema de ecuaciones:

${y}_{1}+{\frac {{{v}_{1}}^{2}}{2g}}={y}_{2}+{\frac {{{v}_{2}}^{2}}{2g}}+\left[L\cdot (a\cdot {v}_{m}+\right.$$\left.b\cdot {{v}_{m}}^{2})\right]$	(56)
${q}_{i}={y}_{1}\cdot {v}_{1}$	(57)
${y}_{1}\cdot {v}_{1}={y}_{2}\cdot {v}_{2}$	(58)
$\mathrm {{y}_{1}=} \,{{y}_{2}}^{0}$	(59)
$L={\frac {{H}_{t}}{\mathrm {1000\cdot tan} \,\left(\alpha \right)}}$	(60)

Siendo:

y₁ nivel de la línea de saturación en el punto 1.

y₂ nivel de la línea de saturación en el punto 2.

v₁ velocidad en el punto 1 de la línea de corriente.

v₂ velocidad en el punto 2 de la línea de corriente.

g es la aceleración de la gravedad.

a, b son coeficientes específicos de cada medio granular.

v_m es el promedio de v₁ y v₂ .

α es la pendiente de la presa en grados.

q_i es el caudal unitario de infiltrado.

L es la longitud entre los puntos 1 y 2.

H_t es la altura del repié.

y₂⁰ nivel de la línea de saturación en el punto 2 de la etapa previa de resolución del sistema de ecuaciones.

Para comprobar la calidad de la reproducción de la línea de saturación por este procedimiento se compararon sus resultados con los resultados de los ensayos físicos de validación, utilizados para validar el procedimiento de obtención de la ley de pérdida de carga numérico-experimental de esta tesis, ya descritos en apartados anteriores.

En concreto se compararon los niveles aguas arriba del medio poroso para una presa de ensayo de talud 3 y materiales con diámetro medio (d₅₀) 12.6 y 35.04 mm con porosidad 41% y caudales de 21 l/s y 26.1 l/s respectivamente.

Resolviendo el sistema de ecuaciones propuesto con ley de Ergun se alcanza una discrepancia con el modelo físico al reproducir el nivel de aguas arriba de la presa del 4.3% para el caso de material 12.6 mm y del 5% para el material del 35.04 mm. En caso de utilizar como ley de pérdida de carga una ajustada específicamente para estos materiales [102] la discrepancia de resultados disminuye, alcanzando el 2.9 % para el caso de material 12.6 mm y el 0.3 % para el material del 35.04 mm, lo que se considera una aproximación suficiente, y de discrepancia similar a la observada al validar simulaciones por el método de elementos finitos más complejo y lento.

Cálculo del nivel de agua en la estructura de apoyo del trampolín (y_t)

En esta segunda parte del Paso 3 se calcula el nivel de agua en el interior del marco que sustenta el trampolín y que esta relleno de material poroso, siendo el punto pésimo el de más aguas arriba con calado y_t. El procedimiento de cálculo es similar al de la primera etapa de este paso en que se calculaba la línea de saturación del repié, con la única salvedad de que en vez de iniciarse el cálculo de la línea de saturación desde el punto de emergencia, se hace desde el último punto de la línea de saturación del repié, con calado y_r ya calculado.

Se debe tener en cuenta que según el tipo de presa el caudal circulante por la estructura bajo el trampolín será diferente, siendo q_i para presas homogéneas y q_i·(B/B_v) para presas de escollera, ya que el caudal infiltrado se distribuye por todo el ancho del valle al ser el cuerpo de presa poroso.

Comprobación del grado de saturación del repié y de la estructura del trampolín

Entre los parámetros que debe fijar el diseñador antes de comenzar el proceso de diseño propuesto está el grado de saturación máximo admisible (GS), el cual no se permite que sea rebasado en ninguna de las zonas de drenaje del aliviadero, para ello se deben cumplir las siguientes inecuaciones. En caso de no cumplirse alguna de estas se vuelve al Paso 1.

$GS\geq 100\cdot \left({\frac {{y}_{r}}{{H}_{t}}}\right)$	(61)
$GS\geq 100\cdot \left({\frac {{y}_{t}}{{H}_{t}}}\right)$	(62)

Siendo:

GS es el grado de saturación máximo fijado por el usuario.

H_t es la altura del repié.

y_r es el calado en la sección de más aguas arriba del repié.

y_t es el calado en la sección de más aguas arriba de la estructura de apoyo del trampolín.

5.2.5. Paso 4. Cálculo de saturación en presa de escollera

Cálculo del nivel de agua en el cuerpo de presa (y_p)

En este paso se calcula el nivel de saturación en el cuerpo de presa aplicando las Ec.(56) a Ec.(60), iniciando el cálculo de la línea de saturación desde el punto final de la línea de saturación de la estructura bajo el trampolín, con calado y_t ya calculado. El punto de mayor altura de la línea de saturación en el cuerpo de presa se encontrará en la sección de más aguas arriba con un calado y_p.

Comprobación del grado de saturación del cuerpo de presa

Para que el grado de saturación máximo (GS) no sea rebasado por la línea de saturación del cuerpo de presa se debe cumplir la siguiente inecuación. En caso de no cumplirse se vuelve al Paso 1.

$GS\geq 100\cdot \left({\frac {{y}_{p}}{H}}\right)$

(63)

Siendo:

GS es el grado de saturación máximo fijado por el usuario.

H es la altura del labio del aliviadero.

y_p es el calado en la sección de más aguas arriba de la presa.

5.2.6. Paso 4. Cálculo de saturación y estabilidad en presa homogénea

Cálculo del nivel de agua en la capa de drenaje (y_d)

Para el cálculo del nivel de agua en la capa de drenaje se emplean las Ec.(64) y Ec.(65) que consideran un calado constante y paralelo al talud de la presa como indica el USBR [14] y , así como una ley de pérdida de carga no lineal.

$sen(\alpha )=a\cdot v+b\cdot {v}^{2}$	(64)
${q}_{i}={y}_{d}\cdot v$	(65)

Siendo:

α es la pendiente de la presa en grados.

a, b son coeficientes específicos de cada medio granular.

v es la velocidad de circulación del agua por el drenaje.

q_i es el caudal unitario de infiltrado.

y_d calado en el drenaje.

Definición del espesor de la capa de drenaje estable a deslizamiento en masa (e_t)

Para que el drenaje sea estable a deslizamiento en masa debe cumplir las Ec.(66), Ec.(67) y Ec.(68). Estas ecuaciones incorporan los efectos estabilizantes de bloques y material no saturado, además de considerar la dirección del flujo circulante paralelo a la solera, así como el cumplimiento del grado máximo de infiltración prescrito por el usuario.

${F}_{d}=\left(1-{\frac {{\gamma }_{w}}{{\gamma }_{e,sat}+\left({\gamma }_{e,dry}\cdot ({\frac {1}{S}}-1)\right)+\left({\frac {\left({\frac {M\cdot g}{({A}_{B}\cdot {B}_{B})}}\right)\cdot \lambda }{{y}_{d}}}\right)}}\right)\cdot {\frac {Tan\,(\varphi )}{Tan\,(\alpha )}}$	(66)
${e}_{t}=100\cdot {\frac {{y}_{d}}{S}}$	(67)
$GS\geq S$	(68)

Siendo:

F_d es el coeficiente de seguridad a deslizamiento del drenaje fijado por el usuario.

γ_e,sat es el peso específico saturado del material.

γ_e,dry es el peso específico seco del material.

γ_w es el peso específico del agua.

ϕ es el ángulo de fricción del material.

α es la pendiente de la presa en grados.

S es el porcentaje saturado del drenaje.

y_d calado en el drenaje.

e_t espesor total de la capa de drenaje.

M es la masa del bloque definido por el usuario para diseñar el aliviadero.

A_B es la dimensión longitudinal del apoyo del bloque testado para obtener el caudal de infiltración.

B_B es la dimensión transversal del apoyo del bloque testado para obtener el caudal de infiltración.

λ factor de homotecia respecto al bloque testado para obtener el caudal de infiltración.

g es la aceleración de la gravedad.

GS es el grado de saturación máximo fijado por el usuario.

Comprobación de la compatibilidad geométrica de capa de drenaje y repié

Para comprobar que el drenaje y el repié son compatibles geométricamente debe cumplirse la siguiente ecuación. En caso negativo se vuelve al paso 1.

${H}_{t}={e}_{t}\cdot \mathrm {cos} \,\left(\alpha \right)$

(69)

Siendo:

e_t espesor total de la capa de drenaje.

α es la pendiente de la presa en grados.

H_t es la altura del repié.

5.2.7. Paso 5. Cálculo del rip-rap

Cálculo del diámetro del rip-rap (d_rr)

Para calcular el diámetro medio del rip-rap de protección ante la erosión superficial del repié (d_rr) se proponen los métodos HSK [20] y de Bartsch y Nilsson [23].

El método HSK emplea la Ec.(70), donde se impone un coeficiente de seguridad de 2 y puesta en obra por vertido, lo que resulta más conservador que suponer rip-rap colocado.

${q}_{i}=0.5\cdot {\sqrt {g}}\cdot {{(d}_{rr})}^{1.5}\cdot (1.9+(0.8\cdot 0.625)-$$3\cdot \mathrm {sin} \,{\alpha }_{r})$

(70)

Siendo:

q_i es el caudal unitario de infiltrado.

g es la aceleración de la gravedad.

d_rr es el diámetro medio del rip-rap.

α_r es el talud del repié en grados.

El método de Bartsch y Nilsson emplea la Ec.(71), donde se impone también un coeficiente de seguridad de 2.

${d}_{rr}=0.5\cdot {\left({\frac {1}{\mathrm {tan} \,{\alpha }_{r}}}\right)}^{0.43}\cdot {({q}_{i})}^{0.78}$

(71)

Siendo:

d_rr es el diámetro medio del rip-rap.

α_r es el talud del repié en grados.

q_i es el caudal unitario de infiltrado.

5.2.8. Paso 6. Mediciones y presupuesto

Obtener el número de bloques (W)

Para obtener el número de bloques necesarios para construir el aliviadero WSB se emplea la siguiente expresión:

$W=\left({R}_{w}\cdot {\frac {B}{{B}_{B}\cdot \lambda }}\right)+2\cdot \left({R}_{w}\cdot {\frac {\frac {{h}_{c}}{sen({T}_{c})}}{{B}_{B}\cdot \lambda }}\right)$

(72)

Siendo:

W es el número de bloques del aliviadero.

R_w es el número de filas de bloques.

B es el ancho del aliviadero.

B_B es la dimensión transversal del apoyo del bloque testado para obtener el caudal de infiltración.

λ factor de homotecia.

T_c es el talud del cajero en grados.

h_c es la altura de los cajeros.

Obtener volúmenes de materiales y presupuesto

Obtener los volúmenes de cada material resulta inmediato una vez definida la geometría completa del aliviadero en los pasos anteriores. No obstante se deben precisar los conceptos objeto de medición en este procedimiento:

• El volumen del repié se considera que se extiende horizontalmente a lo largo de todo el ancho del valle por debajo de la altura de repié definida por el algoritmo.

• El volumen de presa incluye tanto el material bajo el aliviadero como los recrecimientos laterales.

• El volumen de capa de drenaje se corresponde con el dispuesto bajo la solera del canal de descarga y bajo los cajeros.

• El volumen de rip-rap se obtiene considerando partículas esféricas sobre todo el repié y dispuesto en dos capas.

• Para el cálculo del hormigón se considera un recubrimiento en toda la embocadura de espesor igual al de los bloques dispuestos. En cuanto a la estructura bajo el trampolín se considera un muro de hormigón con muros perimetrales de 1 m de espesor y sin apoyos intermedios.

El presupuesto total del aliviadero se obtiene al multiplicar los volúmenes calculados para los distintos materiales por el precio unitario de cada uno de ellos, más el precio de los bloques a disponer.

5.3. Automatización del algoritmo

El algoritmo expuesto anteriormente alcanza la solución mediante un proceso tentativo que puede resultar complejo para su realización manual. Por ello el algoritmo se ha programado en el código abierto R [117] para su automatización. Adicionalmente se ha desarrollado una herramienta interactiva en Shiny de Rstudio [118][119], que permite su publicación web con una interfaz interactiva (Figura 111).

Figura 111. Ventana de bienvenida a la herramienta, donde se debe introducir la contraseña para entrar en el área privada de la aplicación.

La herramienta permite obtener en unos pocos segundos el diseño de aliviadero WSB buscado, aplicando el algoritmo descrito con anterioridad, pero mostrando una interfaz sencilla de ventanas dinámicas y botones independientes de la estructura interna del algoritmo, lo que lo hace más intuitivo y sencillo para el usuario. A continuación se muestra la estructura general de la aplicación.

5.3.1. Ventanas de entrada de parámetros

En la aplicación existen dos ventanas iniciales específicas para la introducción de parámetros de entrada. En la primera de ellas se introduce la geometría del cuerpo de presa y la forma del valle, como se aprecia en la Figura 112. En la segunda de las ventanas se introducen los datos relativos a los materiales que se emplearán posteriormente en el diseño de la presa, en aspectos relativos a características mecánica, de permeabilidad y coste (Figura 113). Una vez introducidos los parámetros se pueden ejecutar varias utilidades de cálculo.

Figura 112. Ventana de introducción de parámetros relativos a geometría de cuerpo de presa y valle.

Figura 113. Ventana de introducción de parámetros relativos a propiedades de materiales y costes.

5.3.2. Utilidad de diseño de aliviadero para tamaño de bloque fijo

La primera de las utilidades que permite ejecutar la aplicación es la de diseño de aliviadero para un tamaño de bloque definido por el usuario (Figura 114). En esta utilidad el usuario debe fijar parámetros como la anchura de aliviadero, el caudal de vertido, el nivel de agua en el cauce, los coeficientes de seguridad y grados de saturación admisibles, el método de obtención del caudal infiltrado, el talud de los cajeros y la masa del bloque para el diseño. Una vez fijados estos parámetros el usuario en pocos segundos obtiene la solución de diseño del aliviadero WSB, por aplicación directa del algoritmo descrito en epígrafes anteriores. Los resultados que ofrece la utilidad son tanto geométricos como de medición de volúmenes y presupuesto. Un ejemplo de la solución que ofrece la utilidad se muestra en Figura 115 y Figura 116.

Figura 114. Ventana la utilidad de diseño de aliviadero para un tamaño de bloque definido por el usuario.

Figura 115. Solución gráfica de la utilidad de diseño de aliviadero para un tamaño de bloque definido.

Figura 116. Resultados de la solución de la utilidad de diseño de aliviadero para un tamaño de bloque definido.

5.3.3. Utilidad de optimización económica de aliviadero

La segunda de las utilidades que permite ejecutar la aplicación es la de optimización económica del diseño del aliviadero WSB en función del tamaño de bloque y la anchura de aliviadero. En esta utilidad el usuario debe fijar el caudal de vertido, el nivel de agua en el cauce, los coeficientes de seguridad y grados de saturación admisibles y el talud de los cajeros (Figura 117).

Figura 117. Ventana de la utilidad de optimización económica del aliviadero.

La utilidad resuelve el diseño de aliviadero para una cierta gama de bloques que el usuario puede cargar en la aplicación (Figura 118), para anchuras de aliviadero variable desde una mínima del 5% de la anchura de fondo de valle hasta una máxima del 100%, con incrementos entre tentativas del 5% de la anchura de fondo de valle. Una vez calculados todos los escenarios la utilidad muestra el presupuesto estimado para cada uno de ellos, detectando el óptimo económico. Para la combinación óptima de anchura de aliviadero y peso de bloque se muestran en pantalla todos los resultados relevantes para su diseño. Un ejemplo de resultados obtenidos con la utilidad se muestra en Figura 119 y Figura 120.

Figura 118. Ventana de carga de gama de bloques del fabricante.

Figura 119. Ejemplo de solución gráfica obtenida con la utilidad de optimización económica del aliviadero.

Figura 120. Resultados de la solución óptima obtenida con la utilidad de optimización económica del aliviadero.

5.3.4. Utilidades adicionales

Además de las utilidades de diseño de aliviadero ya mostradas la aplicación cuenta con otras tres utilidades para el cálculo hidráulico en medio poroso con leyes no lineales.

'Utilidad de ajuste de ley de pérdida de carga

La primera de estas utilidades permite ajustar de manera automática una ley de pérdida de carga parabólica a partir de dos ensayos físicos, en los que se haya registrado caudal y nivel aguas arriba de la presa de ensayo (Figura 121).

Figura 121. Utilidad para el ajuste de ley de pérdida de carga parabólica a partir de dos ensayos físicos.

La utilidad mediante iteraciones sucesivas obtiene los coeficientes a y b de la ley de pérdida de carga según una particularización del método de ajuste propuesto en esta tesis. El procedimiento consiste en los siguientes pasos:

1. Fijar una ley de pérdida de carga. Para inicializar el proceso se toman valores de a=0.01 y b=100, acordes con la relación entre a y b de la expresión de Ergun.

2. Simular la línea de saturación que se obtendría con la ley de pérdida de carga inicial para las geometrías y caudales de los 2 ensayos físicos realizados, según la simplificación unidimensional desarrollada en este trabajo.

3. Obtener el gradiente hidráulico en la sección de más aguas arriba de las dos simulaciones realizadas, según las Ec.(73) y Ec.(74).

${i}_{1}=a\cdot {\frac {{q}_{1}}{{y}_{1}}}+b\cdot {\left({\frac {{q}_{1}}{{y}_{1}}}\right)}^{2}$	(73)
${i}_{2}=a\cdot {\frac {{q}_{2}}{{y}_{2}}}+b\cdot {\left({\frac {{q}_{2}}{{y}_{2}}}\right)}^{2}$	(74)

Siendo:

i₁es el gradiente hidráulico en la sección de más aguas arriba del modelo que simula el ensayo físico 1.

q₁es el caudal unitario del ensayo físico 1.

y₁es el calado aguas arriba obtenido de la simulación del ensayo físico 1.

i₂ es el gradiente hidráulico en la sección de más aguas arriba del modelo que simula el ensayo físico 2.

q₂es el caudal unitario del ensayo físico 2.

y₂es el calado aguas arriba obtenido de la simulación del ensayo físico2.

a, b son coeficientes específicos de cada medio granular.

4. Comparar los calados aguas arriba de la presa obtenidos del ensayo físico 1 y de su simulación.

• Si el calado físico es mayor al de la simulación se actualiza i₁ según

i₁ⁿ= i₁+(0.01· i₁)

• Si el calado físico es menor al de la simulación se actualiza i₁ según

i₁ ⁿ = i₁-(0.01· i₁)

5. Comparar los calados aguas arriba de la presa obtenidos del ensayo físico 2 y de su simulación.

• Si el calado físico es mayor al de la simulación se actualiza i₂ según

i₂ ⁿ = i₂+(0.01· i₂)

• Si el calado físico es menor al de la simulación se actualiza i₂ según

i₂ ⁿ = i₂-(0.01· i₂)

6. Con los nuevos valores actualizados de i₁ y i₂ ser resuelve el sistema de ecuaciones siguiente, siendo las variables a obtener a_n y b_n.

${{i}_{1}}^{n}={a}_{n}\cdot {\frac {{q}_{1}}{{y}_{1}}}+{b}_{n}\cdot {\left({\frac {{q}_{1}}{{y}_{1}}}\right)}^{2}$	(75)
${{i}_{2}}^{n}={a}_{n}\cdot {\frac {{q}_{2}}{{y}_{2}}}+{b}_{n}\cdot {\left({\frac {{q}_{2}}{{y}_{2}}}\right)}^{2}$	(76)

Siendo:

i₁ⁿ es el gradiente hidráulico actualizado en el paso 4

q₁es el caudal unitario del ensayo físico 1.

y₁es el calado aguas arriba obtenido de la simulación del ensayo físico 1.

i₂ⁿes el gradiente hidráulico actualizado en el paso 5.

q₂es el caudal unitario del ensayo físico 2.

y₂es el calado aguas arriba obtenido de la simulación del ensayo físico2.

a_n, b_n son la variables a obtener del sistema de ecuaciones.

7. Se vuelve al paso 1 y se actualiza la ley de pérdida de carga con a_n y b_n.

8. Se repite el proceso descrito desde el paso 1 tantas veces como sea necesario, hasta lograr la convergencia de nivel aguas arriba deseada entre los ensayos físicos y las simulaciones.

Utilidad para cálculo de línea de saturación en presa

La segunda de estas utilidades adicionales permite definir la posición de la línea de saturación en el interior de una presa de materiales sueltos, en función de su geometría, material y caudal, con ley de pérdida de carga automática (Ergun) o previamente calibrada con la anterior utilidad. La formulación empleada es la simplificación unidimensional desarrollada anteriormente. Los resultados obtenidos son la línea de saturación completa, el nivel aguas arriba y la altura y posición del punto de emergencia, como se muestra en la Figura 122. El procedimiento de cálculo es similar al descrito en el Paso 3 del algoritmo para el cálculo de la línea de saturación en repiés.

Figura 122. Utilidad para el ajuste de cálculo hidráulico en presas de materiales sueltos.

Utilidad para cálculo de línea de saturación en capa de drenaje

La última de las utilidades adicionales permite calcular el espesor necesario de una capa de drenaje porosa para drenar un cierto caudal, considerando ley de pérdida de carga automática (Ergun) o previamente calibrada (Figura 123). El cálculo se realiza de acuerdo a las expresiones de las Ec.(64) y Ec.(65).

Figura 123. Utilidad para el cálculo de capas de drenaje.

6. RESUMEN Y CONCLUSIONES

6.1. Resumen y conclusiones

En esta tesis doctoral se ha desarrollado un procedimiento para el diseño de aliviaderos con bloques en forma de cuña, el cual se ha automatizado mediante el desarrollo de un código informático propio. El procedimiento permite obtener los parámetros fundamentales de diseño geométrico y de drenaje del aliviadero, a partir de unos datos de entrada geométricos, hidráulicos y de propiedades de materiales. Como base para el procedimiento de diseño se han desarrollado varias campañas de modelación numérica, respaldadas por ensayos de validación en modelo físico.

Un resumen de los trabajos realizados y conclusiones alcanzadas para los cuatro objetivos planteados al comienzo del documento se expone a continuación.

Caracterización del comportamiento de la capa de drenaje

La campaña de modelación numérica realizada para caracterizar el comportamiento de la capa de drenaje se basó en un modelo numérico bidimensional que permitió definir para varios taludes y materiales, las condiciones de drenaje, tanto con drenaje parcialmente saturado como en carga, así como la acción de los aireadores cuando el drenaje está en carga. De manera complementaria se desarrolló un método para el ajuste numérico-experimental de leyes de pérdida de carga parabólica en medios porosos, además de una formulación propia para el cálculo del coeficiente de seguridad a deslizamiento de una capa de drenaje parcialmente saturada por las infiltraciones entre los bloques superiores, obteniéndose tablas que relacionan el coeficiente de seguridad a deslizamiento del drenaje con su capacidad hidráulica de desagüe.

Las principales conclusiones obtenidas de estos trabajos fueron:

• La variación del calado con respecto al talud de la capa de drenaje parcialmente saturado presenta una tendencia sensiblemente lineal, creciente con el talud. Esto indica que cuanto mayor es el talud de la capa de drenaje menor es su capacidad hidráulica.

• La disposición de aireadores en una capa de drenaje saturada permite reducir significativamente su presión, sin embargo esta disminución no será constante, sino que vendrá condicionada por diversos factores complejos acoplados entre sí. De manera que se considera que para una correcta caracterización de las condiciones de drenaje por aireadores se debe estudiar cada caso particular en concreto en todo su rango de funcionamiento.

• Aumentar el caudal de vertido aumenta la presión máxima en el drenaje saturado de manera exponencial, por lo que reducir al máximo el caudal infiltrado que llega al drenaje se revela como un factor clave para el diseño.

• Aumentar el talud del drenaje saturado aumenta la presión para un mismo caudal, aunque de manera muy moderada.

• La forma de obtener los coeficientes a y b de la ley de pérdida parabólica de carga del medio poroso, por vías experimentales o analíticas, tiene muy escasa afección en el valor del coeficiente de seguridad a deslizamiento, aunque sí puede afectar para el cálculo del espesor saturado de drenaje y la presión máxima.

• Para un cierto espesor de capa de drenaje conforme aumenta el caudal que circula a través de él, aumenta su tendencia al deslizamiento. Cuanto mayor sea el espesor de la capa de drenaje, más estable resultará para un mismo caudal de infiltración, al presentar una mayor proporción de material seco que ayuda a estabilizar el conjunto.

• El aumentar la masa de los bloques en forma de cuña que se disponen sobre la capa de drenaje disminuye la tendencia de esta al deslizamiento.

• El aumento del diámetro medio del material poroso del drenaje a porosidad constante mejora sus condiciones de estabilidad a deslizamiento.

Caracterización y cuantificación de los caudales infiltrados a la capa de drenaje

En esta segunda campaña de modelación numérica se afrontó la manera de determinar el caudal infiltrado a la capa de drenaje, en función de las condiciones del flujo circulante sobre los bloques.

Para ello se propuso un método para reproducir el fenómeno de la infiltración mediante la asignación de una ley de pérdida de carga lineal al dominio definido por bloques, juntas y aireadores, estudiando también los posibles efectos de escala en su aplicación.

En la campaña se plantearon dos etapas para la obtención del caudal infiltrado: una primera 2D que permitió obtener conclusiones generales y tendencias del fenómeno de infiltración, y una segunda etapa donde se realizaron ensayos 3D susceptibles de calibración en base a resultados de ensayos físicos.

Como principales conclusiones cabe destacar que:

• El caudal total infiltrado a lo largo del aliviadero crece en valor absoluto conforme aumenta el caudal de vertido, si bien tiene tendencia decreciente en términos porcentuales.

• Conforme aumenta el valor del coeficiente a de la ley de pérdida de carga lineal la infiltración disminuye, aunque no de manera lineal.

• La infiltración depende del caudal vertido, del talud y del tipo de bloque y su colocación únicamente.

• Para simular en modelo reducido un aliviadero de bloques en forma de cuña, y obtener resultados consistentes con los que se obtendrían en el aliviadero real, se debe escalar el modelo reducido aplicando la semejanza de Froude, tanto a dimensiones geométricas como a caudales de sobrevertido y a la ley de pérdida de carga que se asigna al dominio de bloques, juntas y aireadores para simular las infiltraciones.

• Se ha constatado la bondad del modelo numérico empleado a la hora de reproducir los calados de sobrevertido en un aliviadero de bloques en forma de cuña, reproduciendo la envolvente de máximos del modelo el calado entumecido del ensayo físico.

• El método propuesto de introducir una ley de pérdida de carga lineal para reproducir la infiltración en el modelo numérico se ha demostrado capaz de reproducir numéricamente el fenómeno observado en el modelo físico.

Determinación de las condiciones de estabilidad de los bloques en forma de cuña

En esta campaña de modelación se trató de caracterizar la estabilidad de los bloques en forma de cuña ante acciones de vandalismo y frente a solicitaciones hidráulicas debidas al sobrevertido. Para el estudio de la estabilidad de bloques ante acciones de vandalismo se desarrolló una aplicación de simulación numérica con el Método de Elementos Discretos (DEM) en el entorno GiD, y se llevó a cabo una campaña de modelación para caracterizar los factores que influyen en la carga de extracción de un bloque. Para el estudio de la estabilidad de bloques ante acciones hidráulicas se ha recurrido a particularizar las tablas CIRIA para los bloques ACUÑA y ArmorwedgeTM, los cuales comparten formas exteriores. En concreto se obtuvieron tablas de estabilidad de bloques con rangos de masa de 30 kg a 200 kg.

Las principales conclusiones de los trabajos realizados fueron:

• La carga máxima necesaria para extraer un bloque aislado se registra en la fila más inferior de la rápida, que es donde los bloques apoyan su solape en el contorno rígido. Conforme se asciende hacia aguas arriba la carga de fallo desciende hasta estabilizarse, pasando a ser independiente de la fila donde se encuentre el bloque traccionado.

• La carga máxima necesaria para extraer un bloque es varias veces superior a su peso.

• La carga absoluta para provocar el fallo de un bloque es mayor cuanto más pesado sea este, si bien en valores relativos al peso del propio bloque la carga adimensional de extracción es similar para cualquier masa de bloque.

• La carga de extracción se ve fuertemente incrementada si los bloques pueden deslizar sobre el contorno de apoyo, quedando comprimidos unos con otros, y afectando en este escenario la rotura a un gran número de bloques entorno al traccionado. Si el rozamiento entre bloque y capa de apoyo es tal que impide el deslizamiento de bloques la rotura afectará sólo al bloque traccionado, generando pequeños desplazamientos en los de la fila superior al de fallo.

• La estabilidad de los bloques ante acciones hidráulicas crece con la masa de los mismos y el talud de la capa de apoyo.

• Se recomienda evitar la formación de resalto hidráulico sobre los bloques, ya que para lograr la estabilidad frente a esas condiciones requeriría bloques de masas muy superiores a los 200 kg y taludes muy tendidos que llevarían a secciones antieconómicas para presas y balsas.

Desarrollo de un algoritmo de diseño

El objetivo final de la tesis es el desarrollo de un procedimiento para el diseño de aliviaderos de bloques en forma de cuña, para ello se desarrolló un algoritmo de cálculo (Figura 124), que permite definir la geometría apropiada de aliviadero, garantizando la estabilidad del cuerpo de presa, de la capa de drenaje y de los propios bloques, al evitar la subpresión en el apoyo granular de los mismos. Por tanto el algoritmo define el diseño del drenaje y la capa de soporte, considerando su capacidad de filtración y estabilidad. El caudal infiltrado a través de las uniones entre bloques puede estimarse por medio de los resultados obtenidos de los modelos numéricos calibrados y validados en la campaña previa desarrollada. El algoritmos sugiere la protección del pie de presa mediante un repié granular, y comprueba la saturación en los drenajes con una simplificación unidimensional para el cálculo de la línea de saturación.

Figura 124.Algoritmo de diseño de aliviaderos de bloques en forma de cuña propuestos.

En base a este algoritmo se ha desarrollado una aplicación informática en R para el diseño asistido por ordenador, publicable vía web (https://wsb-diablo.shinyapps.io/WSB-APP_v3/), y que permite obtener la solución de diseño en unos pocos segundos (Figura 125). Además la aplicación cuenta con utilidades para el cálculo hidráulico en medio poroso con leyes no lineales y su calibración.

Figura 125. Aplicación desarrollada en R en base al algoritmo propuesto.

6.2. Aportaciones originales

Las aportaciones principales que introduce esta tesis en el campo del diseño de los aliviaderos de bloques en forma de cuña son:

• Método para el ajuste numérico-experimental de leyes de pérdida de carga parabólica en medios porosos.

• Formulación para el cálculo del coeficiente de seguridad a deslizamiento de una capa de drenaje parcialmente saturada considerando la acción de los bloques superiores.

• Método para reproducir numéricamente el fenómeno de la infiltración en aliviaderos de bloques en forma de cuña mediante la asignación de una ley de pérdida de carga lineal al dominio definido por bloques, juntas y aireadores.

• Desarrollo de aplicación de simulación numérica con el Método de Elementos Discretos para el estudio de la estabilidad de bloques ante acciones de vandalismo. Caracterización de factores que afectan a la carga de extracción.

• Desarrollo de un algoritmo para el diseño completo de aliviaderos de bloques en forma de cuña.

• Desarrollo de una aplicación informática para el diseño asistido por ordenador de aliviaderos de bloques en forma de cuña.

6.3. Líneas futuras

Las líneas de investigación que se proponen para continuar los trabajos realizados en esta tesis son:

• Estudio del comportamiento de capas de drenaje multicapa.

• Desarrollo de un modelo numérico acoplado DEM-CFD que permita estudiar y caracterizar de manera precisa las condiciones de estabilidad de bloques en escenarios de drenaje saturado.

• Estudio de efectos dinámicos es la estabilidad de bloques.

• Estudio del intercambio de caudales entre flujo sobre vertido y capa de drenaje según la posición en el aliviadero y las condiciones hidráulicas de vertido.

• Estudio específico del drenaje en presas de escollera anisotrópicas.

• Validación experimental del procedimiento propuesto en modelo a escala prototipo.

BIBLIOGRAFÍA

[1] TROLLOPE, D.H., (1956). The stability of wedges of granular materials. PhD Thesis., University of Melbourne, School of Engineering.

[2] PARKIN, A.K., (1963). Rockfill Dams with Inbuilt Spillways Hydraulic Characteristics. Melbourne, Australia: Water Research Foundation of Australia LTD. Department of Civil Engineering, University of Melbourne.

[3] YU, X., JI, S. y JANOYAN, K.D., (2006). Direct Shear Testing of Rockfill Material, Proceedings of the GeoShanghai International Conference 2006, ASCE.

[4] DE CEA, J.C. y OLALLA, C., (1991). Monografía M 18. Resistencia al corte de escolleras. Centro de Estudios y Experimentación de Obras Públicas (CEDEX), Madrid, España.

[5] Guía para el proyecto y la ejecución de muros de escollera en obras de carretera. (2006). Serie normativa. Ministerio de Fomento.

[6] TOLEDO, M.A., (1997). Presas de escollera sometidas a sobrevertido. Estudio del movimiento del agua a través de la escollera y de la estabilidad frente al deslizamiento en masa. Tesis doctoral. Universidad Politécnica de Madrid.

[7] PARKIN, A.K., (1971). Field solutions for turbulent seepage flow. Journal of the soil mechanics and foundations division, 97(1).

[8] PARKIN, A.K., TROLLOPE, D. y LAWSON, J., (1966). Rockfill structures subject to water flow. Journal of the Soil Mechanics and Foundations Division, 92(SM6).

[9] LELIAVSKY, S., (1965). Percolation of water as a structural design factor. Design of dams for percolation and erosion. London, Great Britain: Chapman & Hall.

[10] SOLVIK, O., 1991. Throughflow and stability problems in rockfill dams exposed to exceptional loads. Proceedings of ICOLD Viena Congress, Austria, Q67(R20).

[11] ERGUN S., (1952) Fluid flow through packed columns. Chem Eng Prog 48:89–94.

[12] WARD, S., (1964) Turbulent flow in porous media. ASCE, Journal o Hydraulics Division. September 1964

[13] CRUZ, P.T., MATERÓN, B. y FREITAS, M., (2009). Concrete face rockfill dams. Gran Bretaña: CRC Press/Balkema.

[14] ZEIGLER, E. R., (1972). Laboratory tests to study drainage from sloping land. REC-ERC-72-4. U.S. Bureau of reclamation.

[15] SPARKS, A.D., (1967). The sloughing, overtopping, and reinforcement of rockfill and earth dams. Proceedings of ICOLD Istambul Congress, Turkia, Q35(R9).

[16] MORÁN, R., (2013). Mejora de la seguridad de las presas de escollera frente a percolación accidental mediante protecciones tipo repié. Tesis doctoral. Universidad Politécnica de Madrid.

[17] STEPHENSON, D., (1979). Rockfill and gabions for erosion control. Rockfill in hydraulic engineering. Amsterdam, Holanda: Elsevier Publishing Company.

[18] SKOGLUND, M. y SOLVIK, O., (1995). External and internal erosion in rockfill dams. International Journal on Hydropower & Dams, 2(3).

[19] HARTUNG, F. y SCHEUERLEIN, H., (1970). Design of overflow rockfill dams. Proceedings of ICOLD Montreal Congress, Q36(R35).

[20] KNAUSS, J., (1979). Computation of maximum discharge at overflow rockfill dams. (A comparison of different model test results). Proceedings of ICOLD New Delhi Congress, India., Q50(R9).

[21] OLIVIER, H., (1967). Through and overflow rockfill dams. New design techniques. Institution of Civil Engineers Proceedings, 36(3).

[22] TOLEDO, M.A., (1998). Diseño de presas de escollera resistentes al sobrevertido. Madrid: Comité Nacional Español de Grandes Presas.

[23] BARTSCH, M. y NILSSON, Å., (2007). Leakage in embankment dams. Functional analysis and strengthening by adding a downstream berm. Proceedings of Talsperren Symposium. Deutschen TalsperrenKomitee. Freising, Germany.

[24] SALMON, G.M., (2004). Notes for presentation on embankment dams. Design for accidental overopping and throughflow. International Seminar Stability and Breaching of Embankment Dams, Oslo, Norgay, 2004.

[25] BISHOP, A.W., (1954). The use of the slip circle in the stability analysis of slopes. Geotechnique, 5(1).

[26] ALONSO, E. (1989). Métodos generales de equilibrio límite. En Corominas, J. (editor), Estabilidad de Taludes y Laderas Naturales”, Monografía nº 3, Sociedad Española de Geomorfología.

[27] NILSSON, Å., (2004). RIDAS Tillämpningsvägledning – Fyllningsdammar. Utvikling av tillämpningsvägledning for fyllingsdammer i Sverige, Proceedings of the NNCOLD Fagseminar 2004.

[28] NILSSON, A., (2009). Maximal credible leakage for large rockfill dams due to internal erosion. International Workshop on Internal Erosion in Dams and Foundations 2009.

[29] EBL KOMPETANSE, (2005). Stability and breaching of embankment dams. Report on Subproject 2: Stability of downstream shell and dam toe during large throughflow. Oslo, Noruega: EBL Kompetanse AS.

[30] MORÁN, R., CAMPOS, H., GARCÍA, J. y TOLEDO, M.A., (2011). Estudio de protecciones frente al sobrevertido de presas de materiales sueltos mediante repié de escollera. Dam Maintenance & Rehabilitation II. Zaragoza, España: CRC Press. Taylor & Francis Group. Balkema 2010

[31] ANDRADE JA JR, COSTA UMS, ALMEIDA MP, MAKSE HA, STANLEY HE (1998) Inertial effects on fluid flow through disordered porous media. Phys Rev Lett 82(26):5249–5252.

[32] KHOEI AR, MOHAMMADNEJAD T (2011) Numerical modeling of multiphase fluid flow in deforming porous media: a comparison between two- and three-phase models for seismic analysis of earth and rockfill dams. Comput Geotech 38(2):142–166

[33] NIESSNER J, HASSANIZADEH SM (2008) A model for two-phase flow in porous media including fluid-fluid interfacial area. Water Resourc Res 44(8). doi:10.1029/2007WR006721

[34] CHEN Y, HU R, LU W, LI D, ZHOU C (2011) Modeling coupled processes of non-steady seepage flow and non-linear deformation for a concrete faced rockfill dam. Comput Struct 89:1333–1351

[35] LI B, GARGA VK (1998) Theoretical solution for seepage flow in overtopped rockfill. J Hydraul Eng Comput 124:213–217

[36] LI T, TROCH P, DE ROUCK J (2004) Wave overtopping over a sea dike. J Comput Phys 198(2):686–726

[37] LUBIN P, VINCENT S, CALTAGIRONE J-P, ABADIE S (2003) Fully three- dimensional direct numerical simulation of a plunging breaker. Comptes Rendus Mecanique 331(7):495–501

[38] WANG Z, ZOU Q, REEVE D (2009) Simulation of spilling break- ing waves using a two phase flow cfd model. Comput Fluids 38(10):1995–2005

[39] DE LEMOS MJS (2006) Turbulence in porous media. Elsevier, UK

[40] DEL JESUS M, LARA JL, LOSADA IJ (2012) Three-dimensional interac- tion of waves and porous coastal structures. Part i: nomerical model formulation. Coast Eng 64:57–72

[41] HSU T-J, SAKAKIYAMA T, LIU PL-F (2002) A numerical model for wave motions and turbulence flows in front of a composite break- water. Coast Eng 46(1):25–50.

[42] LARESE, A., ROSSI, R., AND OÑATE, E. (2015). Finite element modeling of free surface flow in variable porosity media. Arch. Comput. Meth. Eng., 22(4), 637-653.

[43] DADVAND, P., ROSSI,R., AND OÑATE,E. (2010). An object-oriented environment for developing finite element codes for multi-disciplinary applications. Archives of Computational Methods in Engineering, 17, 253–297.

[44] LARESE A (2012) A coupled Eulerian–PFEM model for the simulation of overtopping in rockfill dams. PhD Thesis. Universitat Politècnica de Catalunya. UPC BarcelonaTech, Barcelona

[45] LARESE, A., ROSSI, R., OÑATE, E., TOLEDO, M.A., MORÁN, R., CAMPOS, H. (2013). Numerical and experimental study of overtopping and failure of rockfill dams. International Journal of Geomechanics. ASCE.August 2013

[46] OÑATE, E. , IDELSOHN S.R., DEL PIN F. AND AUBRY R. (2004). The particle finite element method. An overview. International Journal of Computational Methods, 1 (2), 267‐307.

[47] OÑATE, E., IDELSOHN, S.R., CELIGUETA, M.A., ROSSI, R. (2006). Advances in the finiteelement method for fluid structure interaction problems. Comput Meth Appl. Mech. Engng. Submitted October 2006.

[48] GORDIENKO, P. (1967). The influence of channel roughness and flow states of hydraulic resistances in turbulent flow.

[49] GRINCHUK, A., AND PRAVDIVETS, Y. P. (1977). "Precast reinforced-concrete revetment of earth slopes used for discharging water." Power Technology and Engineering (Formerly Hydrotechnical Construction), 11(7), 682-687.

[50] GRINCHUK, A., PRAVDIVETS, Y. P., AND SHEKHTMAN, N. (1977). "Test of earth slope revetments permitting flow of water at large specific discharges." Hydrotech.Constr., 11(4), 367-373.

[51] PRAVDIVETS, Y., AND SLISSKY, S. (1981). Passing Floodwaters Over Embankment Dams. Water Power & Dam Construct., 33(7), 30-32.

[52] PRAVDIVETS, Y. P. (1987). Industrial design of an earth overflow dam. Power Technology and Engineering (Formerly Hydrotechnical Construction), 21(12), 685-689.

[53] PRAVDIVETS, Y. P. (1980). Designing and construction of earth-fill overflow dams. Gidrotekhnika i Melioratsiia, .

[54] PRAVDIVETS, Y. P., AND BRAMLEY, M. E. (1989). Stepped protection blocks for dam spillways. Int.Water Power Dam Constr., 41(7), 6.

[55] KREST'YANINOV, A., AND PRAVDIVETS, Y. P. (1986). Stepped spillways for small dams. Gidrotekhnicheskoe Melioratsiya, (8), 27-30.

[56] BRAMLEY, M., MAY, R., AND BAKER, R. (1989). Performance of wedge-shaped blocks in high velocity flow. Stage 1.

[57] BAKER, R. (1992). Concrete blocks for dam spillways. University of Salford.

[58] HEWLETT, H., BAKER, R., MAY, R., AND PRAVDIVETS, Y. (1997). Design of stepped block spillways. Construction Industry Research and Information Association.London, UK,

[59] MORÁN, R., (2016). Wedge-shaped blocks: a historical review. 2nd International Seminar on Dam Protection Against Overtopping. Colorado State University.Libraries.

[60] BRAMLEY, M., MAY, R., AND BAKER, R. (1991). Performance of wedge-shaped blocks in high velocity flow. Stage 2.

[61] CLOPPER, P. E. (1989). Hydraulic stability of articulated concrete block revetment systems during overtopping flow.

[62] FEDERAL HIGHWAY ADMINISTRATION PUBLICATION no.FHWA-RD-89-199, Washington, DC.

[63] CLOPPER, P. E. (1991). Protecting embankment dams with concrete block systems. Hydro Review;(United States), 10(2).

[64] FRIZELL, W. K. AND RENNA, F. M. (2010). Laboratory studies on the cavitation potential of stepped spillways. Engineering Monograph nº 42.Bureau of reclamation.United States Department of the Interior.Denver.

[65] FALVEY, H. T. (1990). Cavitation in chutes and spillways.Engineering Monograph nº 42.Bureau of reclamation.United States Department of the Interior. Denver.

[66] FRIZELL, K. (1992). Hydraulics of stepped spillways for RCC dams and dam rehabilitations. Roller Compacted Concrete III, ASCE, 423-439.

[67] FRIZELL, K. H., AND RUFF, J. F. (1993). Large-scale embankment overtopping protection tests. Hydraulic Engineering, ASCE, 1951-1956.

[68] SLOVENSKY, G. G. (1993). Near-prototype testing of wedge-block overtopping protection.

[69] GASTON, M. L. (1995). Air entrainment and energy dissipation on a stepped block spillway. Hydraulic Research, 5(4), 247-261.

[70] FRIZELL, K. (1997). Protecting embankment dams with concrete stepped overlays. Hydro Review, 16(5).

[71] FEMA. (2014). Technical Manual: Overtopping Protection for Dams. U.S. Department of Homeland Security.

[72] PINHEIRO, A., AND FAEL, C. (2000). Nappe flow in stepped channels–occurrence and energy dissipation. International Workshop on Hydraulics of Stepped Spillways, Balkema Publ, 119-126.

[73] CUSTÓDIO, C. A. M. (1999). Descarregadores de Blocos de Betão Pré-Fabricados sobre Barragens de Aterro. Dissertação de Mestrado, IST.

[74] RELVAS, A. J. (2008). Descarregadores de cheias de blocos de betao prefabricados em forma de cunha sobre barragens de aterro. Instituto Superior Tecnico.

[75] RELVAS, A. T., AND PINHEIRO, A. N. (2008). Inception Point and Air Concentration in Flows on Stepped Chutes Lined with Wedge-Shaped Concrete Blocks. 134(8), 1042-1051.

[76] RUANO, L., CABALLERO, F.J.; SAN MAURO, J.; TOLEDO, M.A.; MORAN, R. Y SALAZAR, F., MONTERDE, M. (2018). Protección de presas de materiales sueltos y balsas frente a sobrevertido: El bloque ACUÑA. Jornadas Españolas de Presas 2018.

[77] CABALLERO, F.J.; SAN MAURO, J.; TOLEDO, M.A.; MORAN, R. AND SALAZAR, F. (2017). Advances in the understanding of the hydraulic behavior of wedge-shape block spillways. 2nd International Seminar on Dam Protections against Overtopping. Protections 2016. Colorado State University (CSU). https://dspace.library.colostate.edu/handle/10217/179778.

[78] CABALLERO, F.J.; TOLEDO, M.A.; SAN MAURO, J. AND SALAZAR, F. (2015). Physical and numerical modeling for understanding the hydraulic behavior of wedge-shaped-blocks (WSB) spillways. Dam Protections against Overtopping and Accidental Leakage. CRC Press/ Balkema, ISBN 978-1-138-02808-1, pp. 193-206

[79] MORÁN, R., AND TOLEDO, M. (2015). Barriga Dam spillway: a case study of wedge-shaped blocks technology. Dam Protections Against Overtopping and Accidental Leakage, 181.

[80] SÁNCHEZ-JUNY, M., BLADÉ, E., AND DOLZ, J. (2008). "Analysis of pressures on a stepped spillway." Journal of Hydraulic Research, 46(3), 410.

[81] BOES, R. M., AND HAGER, W. H. (2003). Two-phase flow characteristics of stepped spillways. J.Hydraul.Eng., 129(9), 661-670.

[82] CHANSON, H. (2006). Hydraulics of skimming flows on stepped chutes: The effects of inflow conditions Journal of Hydraulic Research, 44(1), 51.

[83] MARTINS, R. (1990). "Turbulent seepage flow through rockfill structures." Int.Water Power Dam Constr., 42(3), 41- 42.

[84] PETHER, R. (2010). Design and construction of improvement works at Bruton flood storage reservoir, Somerset. Dams and Reservoirs, 20(1), 33-38.

[85] PETHER, R., MARSH, P., AND CARTWRIGHT, P. (2009). An innovative new spillway for Bruton flood storage reservoir. Dams and Reservoirs, 19(2), 67-72.

[86] COUTO, T. L., PINTO, A., TOLEDO, M. A., AND MORÁN, R. (2007). A new solution for a concrete spillway over a rockfill dam. Hydraulic model study of Barriga Dam in Spain. Proceedings of the 5th International Conference on Dam Engineering, C. Pina, E. Portela, and J. Pereira, eds., LNEC, Lisboa, Portugal, 139-146.

[87] CHANSON H (2002) The hydraulics of stepped chutes and spillways. Balkema, Lisse

[88] ABBASI, S., & KAMANBEDAST, A. A. (2012). Investigation of effect of changes in dimension and hydraulic of stepped spillways for maximization energy dissipation. World Applied Sciences Journal, 18(2), 261-267.

[89] CHAKIB, B. (2013). Numerical computation of inception point location for flat-sloped stepped spillway. International Journal of Hydraulic Engineering, 2(3), 47-52.

[90] BOMBARDELLI, F. A., MEIRELES, I., & MATOS, J. (2011). Laboratory measurements and multi-block numerical simulations of the mean flow and turbulence in the non-aerated skimming flow region of steep stepped spillways. Environmental Fluid Mechanics, 11(3), 263-288.

[91] OÑATE, E., IDELSOHN, S. R., CELIGUETA, M. A., AND ROSSI, R. (2008). Advances in the particle finite element method for the analysis of fluid–multibody interaction and bed erosion in free surface flows, Comput. Methods Appl. Mech. Eng., vol. 197, no. 19, pp. 1777–1800.

[92] OÑATE, E., CELIGUETA, M. A., IDELSOHN, S. R., SALAZAR, F., AND SUÁREZ, B. (2011) Possibilities of the particle finite element method for fluid-soil-structure interaction problems, in Computational Mechanics, 2011, vol. 48, no. 3, pp. 307–318.

[93] PROYECTO SAYOM. http://www.cimne.com/pfem/harbour.asp

[94] CUNDALL, P. A., & STRACK, O. D. (1979). A discrete numerical model for granular assemblies. geotechnique, 29(1), 47-65.

[95] CUNDALL, P. A., & HART, R. D. (1992). Numerical modelling of discontinua. Engineering computations, 9(2), 101-113.

[96] IRAZÁBAL, F. SALAZAR, E. OÑATE. (2017). Numerical modelling of granular materials with spherical discrete particles and the bounded rolling friction model. Application to railway ballast. Comput Geotech, 85, 220–229. https://doi.org/10.1016/j.compgeo.2016.12.034

[97] SANTASUSANA, M., IRAZÁBAL, J., OÑATE, E., AND CARBONELL, J. M. (2016). “The Double Hierarchy Method. A parallel 3D contact method for the interaction of spherical particles with rigid FE boundaries using the DEM”. Computational Particle Mechanics, 1-22.

[98] IRAZÁBAL, J. (2017) Numerical analysis of railway ballast behaviour using the Discrete Element Method. PhD thesis. Universitat Politècnica de Catalunya.

[99] MORÁN, R. AND TOLEDO, M.A., 2011. Research into protection of rockfill dams from overtopping using rockfill dowmstream toes. Canadian Journal of Civil Engineering. 38, pp. 1314-1326.

[100] ROSSI, R., LARESE, A., DADVAND, P., AND OÑATE, E.(2013) An efficient edge-based level set finite element method for free surface flow problems." International Journal for Numerical Methods in Fluids, 71(6), 687-716.

[101] SAN MAURO, J., LARESE, A., SALAZAR, F., IRAZÁBAL, J., MORÁN, R., & TOLEDO, M. A. (2016). Hydraulic and stability analysis of the supporting layer of wedge-shaped blocks. 2nd International Seminar on Dam Protection Against Overtopping. Colorado State University. Libraries.

[102] SAN MAURO, J., TOLEDO, M.A. AND MORÁN, R. (2015). CFD study of the time dependent flow pattern around the slope of rockfill dams in overtopping scenario. Dam Protections against Overtopping and Accidental Leakage, 123-130. CRC BALKEMA. ISBN 9781138028081

[103] CHANSON, H. (1995). Hydraulic design of stepped cascades, channels, weirs and spillways.

[104] MARTÍNEZ, E., (2000). Hidráulica. Colegio de Ingenieros de Caminos, Canales y Puertos. Servicio de Publicaciones. ISBN: 9788438001714

[105] DESARROLLO DE UN CÓDIGO DE DISEÑO ÓPTIMO DE ALIVIADEROS FORMADOS POR BLOQUES EN FORMA DE CUÑA. DIABLO (RTC-2014-2081-5). (2014-2017). Programa Estatal de Investigación, Desarrollo e Innovación Orientada a los Retos de la Sociedad. Ministerio de Economía, Industria y competitividad la financiación prestada al proyecto de investigación

[106] TÁBOAS, A. (2005). Comportamiento hidráulico de los aliviaderos escalonados en presas de hormigón compactado. Universidad Politécnica de Cataluña.

[107] WOOD, I. (1983). Uniform region of self aerated flow. Journal of Hydraulic Engineering, 109-3:447–461.

[108] CABALLERO, F.J., SAN MAURO, J., TOLEDO, M. A., MORÁN, R., SALAZAR, F.,& MORENO, E. (2018). A new evolution on the wedge-shaped block for overtopping protection of embankment dams: the ACUÑA block. III International Seminar on Dam Protection Against Overtopping. Grange-over-sands, United Kingdom.

[109] GiD. (2004). The personal pre/postprocessor. CIMNE, Barcelona, www.gidhome.com.

[110] OÑATE, E., ZÁRATE, F., MIQUEL, J., SANTASUSANA, M., CELIGUETA, M. A., ARRUFAT, F.,& RING, L. (2015). A local constitutive model for the discrete element method. Application to geomaterials and concrete. Computational particle mechanics, 2(2), 139-160.

[111] SAN MAURO, J., TOLEDO, M. A., SALAZAR, F. & CABALLERO, F.J., (2018). A methodology for the design of dam spillways with wedge shaped blocks based on numerical modeling. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería.

[112] AYALA, F.J.; ANDREU, F.J.; FE, M.; FERRER, M.; DE SIMÓN, A.; FERNÁNDEZ, I.; OLALLA, C.; GÓMEZ, J.; SANPEDRO, J. Y CIENFUEGOS, F.J. (1987). Manual de Taludes”. Serie Geotecnia. IGME. Madrid. Pp 237-247.

[113] SUÁREZ, L. M. (1993). Presas de corrección de torrentes y retención de sedimentos. Venezuela: Ministerio del Ambiente y de los Recursos Naturales Renovables.

[114] SHERARD, J.L.; DUNNIGAN, L.P. (1985) Filters and leakage control in embankment dams. Seepage and leakage from dams and impoundments. ASCE, 1985. p. 1-30.

[115] STEPHENSON, D. J. (1979). Rockfill in hydraulic engineering. Elsevier.

[116] HANSEN, D., ZHAO, W. Z., & HAN, S. Y. (2005). Hydraulic performance and stability of coarse rockfill deposits. Proceedings of the Institution of Civil Engineers - Water Management -Water Management,158(WM4), 163–175.

[117] R CORE TEAM (2017). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. <URL: >. https://www.R-project.org/>.

[118] RSTUDIO TEAM (2016). RStudio: Integrated Development Environment for R. RStudio, Inc., Boston, MA. <URL: >. http://www.rstudio.com/>.

[119]CHANG W, CHENG J, ALLAIRE J, XIE Y AND MCPHERSON J (2017). Shiny: Web Application Framework for R. R package version 1.0.5, <URL: https://CRAN.R-project.org/package=shiny