Resumen
En este trabajo se describe la formulación corrotacional de un elemento de viga que utiliza distintas teorías, Euler-Bernoulli, Timoshenko y Euler-Bernoulli incluyendo el acoplamiento entre los efectos de los esfuerzos de flexión y axil lo que genera coeficientes no lineales en la matriz de rigidez elástica de dicho elemento. La cinemática corrotacional se basa en la separación del movimiento de un sólido en una parte deformacional y otra en movimiento de cuerpo rígido. La parte deformacional del movimiento es representada por tres grados de libertad: una traslación debido al esfuerzo axil y por las rotaciones nodales debidas a la flexión del elemento. A nivel local se obtienen los esfuerzos internos mediante el princípio de los trabajos virtuales una vez definidas las funciones de interporlación que describen el movimiento deformacional para cada teoría de viga utilizada. Se describe de forma detallada la obtención de las matrices de rigideces elástica para los tres tipos de elementos de viga. A través de algunos ejemplos numéricos se muestra la habilidad del elemento para obtener el comportamiento no lineal de vigas, pórticos y arcos.
Palabras claves: Elemento de viga Euler-Bernoulli. Elemento de viga Timoshenko, Elemento de viga Euler-Bernoulli no lineal, Formulación corrotacional.
Abstract
The present work uses a co-rotating approach for obtain the internal forces and tangent stiffness matrices for three plane beam elements. All of them are based on the same co-rotational approach, and differ by the strain definition used in the local co-rotational coordinate system. Based on the Bernoulli assumption, the first two elements use a linear and a shallow arch strain definition, respectively. The third element is based on the Timoshenko assumption with linear interpolations for the displacements. Some examples are presented and the numerical results demonstrate that the beam elements here presented are able to perform the nonlinear analysis of plane frames and 2D arches and to handle large rotations too.
1. Introducción
En las últimas dos décadas se ha observado un creciente interés en la comunidad de mecánica computacional referente a la aplicación de la formulación corrotacional en el análisis no lineal de estructuras utilizadas en la industria aeronáutica, aeroespacial y petrolera. Felippa y Haugen [1] describen en detalle una reseña del desarrollo de la formulación corrotacional y de sus aplicaciones en mecánica computacional. La idea principal de la formulación corrotacional es descomponer el movimiento de un sólido en la suma de un movimiento de cuerpo rígido y un movimiento deformacional. Esta formulación es un caso particular de la cinemática Lagrangiana para modelar los efectos de la no linealidad geométrica en el análisis estructural, haciendo uso del método de los elementos finitos. En esta formulación se asume que tanto las traslaciones como las rotaciones de cuerpo rígido podrán ser grandes, pero las deformaciones han de ser pequeñas y por ello existe la posibilidad del uso de elementos finitos lineales en problemas que involucran no linealidad geométrica, siendo esta la principal motivación del uso de la formulación corrotacional. En el panorama actual se puede citar algunos trabajos que han aplicado la formulación corrotacional utilizando otros métodos de discretización, por ejemplo, en Yaw et al. [2] se muestran aplicaciones de la formulación corrotacional y los métodos sin malla en el análisis de sólidos 2D incluyendo no linealidad geométrica y física; Xu et al [3] aplican el método de elementos finitos extendidos para el tratamiento de problemas de localización y la formulación corrotacional en elementos de viga de Timoshenko en el análisis no lineal de estructuras reticulares. Aún en el contexto de la aplicación de la formulación corrotacional en la actualidad, en Bisegna y Caselli [4] se describe la formulación corrotacional de un elemento de lámina hiperelástico y su aplicación en el estudio de fibras de tejidos biológicos. Como ejemplo más reciente de aplicación de la formulación corrotacional en el análisis no lineal de estructuras se puede citar el trabajo de Li et al. [5] que describe la formulación corrotacional de um elemento triangular de lámina de 6 nodos y su aplicación en el análisis elastoplastico de cáscaras finas. En este trabajo se aplica la formulación corrotacional junto a diferentes teorías de vigas en el análisis no lineal geométrico de vigas, pórticos y arcos. Para ello, se utilizan las teorías clásicas de viga de Euler-Bernoulli y de Timoshenko. En el tercer elemento de viga se incluye en la teoría de Euler-Bernoulli el efecto del acoplamiento de los esfuerzos axil y de flexión, dicho acoplamiento genera coeficientes no lineales en la matriz de rigidez elástica del elemento, razón por la cual se le denonima elemento de viga de Euler- Bernoulli no lineal. La cinemática corrotacional aquí descrita sigue la formulación propuesta por Crisfield [6], esta formulación permite obtener la matriz de rigidez tangente en coordenadas globales independientemente del tipo de elemento de viga adoptado. El objetivo en este trabajo es comparar el desempeño de los tres tipos de elementos de viga 2D al retratar el comportamiento no lineal de vigas, pórticos planos y arcos.
2. Cinemática corrotacional
|
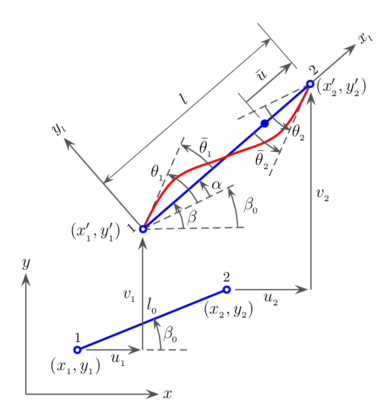
| Figura 1: Movimiento del elemento de viga 2D. |
La Figura 1 muestra las variables cinemáticas utilizadas en la descripción corrotacional del elemento de viga 2D. Las coordenadas nodales del elemento en la configuración de referencia son y , respectivamente. En la configuración deformada dichas coordenadas se definem como y A cada elemento se le asigna el sistema de referencia local que lo acompaña durante su movimiento. El sistema de referencia local es utilizado para definir la parte deformacional del movimiento. El vector de desplazamientos globales es definido por
|
|
(1) |
La parte deformacional del movimiento es dada por el vector de desplazamientos locales como
|
|
(2) |
donde es el desplazamiento relativo entre los nodos 1 y 2 en la dirección del eje local . y son las rotaciones deformacionales de los nodos 1 y 2, respectivamente. Las componentes de son definidas de la siguiente manera
|
|
(3) |
donde y denotan la longitud inicial y actual del elemento. Dichas longitudes son dadas por
|
|
(4) |
con
|
|
(5) |
y denota la rotación de cuerpo rígido que puede ser calculada como
|
|
(6) |
donde es la inclinación del elemento en la configuración de referencia y la inclinación de la línea que une los nodos del elemento en la configuración actual. Estos ángulos pueden ser calculados con el uso de las siguientes expresiones
|
|
(7) |
Usando la ecuación (7) se puede reescribir la ecuación (6) como
|
|
(8) |
donde y estan relacionadas con las diferencias entre las traslaciones de cuerpo rígido de los nodos del elemento en las direciones e , respectivamente. Por otra parte, utilizando la relación , la rotación de cuerpo rígido es dada por
|
|
(9) |
Esta expresión es singular si , por lo que será asignado el valor de para o para . Para el cálculo de las rotaciones deformacionales se utilizan las ecuaciones (3b) y (3c). Con el objeto de asumir cualquier magnitud en el valor de los ángulos, las expresiones para las rotaciones deformacionales deben ser calculadas usando la función módulo [7], tal que:
|
|
(10) |
La función módulo asigna un valor arbitrario en el intervalo , y el último término restablece la simetría en relación al valor cero. La omisión de este paso puede llevar a problemas de divergencia cuando el elemento de viga sufra rotaciones
2.1 Relación entre variables locales y globales
Para obtener la relación entre variables locales y globales se aplica una variación virtual en los desplazamientos locales, tal que
|
|
(11) |
La ecuación (11a) se obtiene diferenciando la ecuación (4b) respecto a los desplazamientos globales. Por otra parte, la variación virtual de es calculada diferenciando la ecuación (3.7d) respecto a los desplazamientos globales y se escribe como
|
|
(12) |
Reagrupando en forma matricial las relaciones entre las variaciones virtuales de las variables locales y globales, se escribe la matriz de transformación como
con
|
|
(13) |
Por otro lado, para obtener la relación entre los esfuerzos internos y los esfuerzos globales se impone que el trabajo virtual sea igual entre dichos esfuerzos, asi que
|
|
(14) |
La igualdad descrita en la ecuación (14) es válida para cualquier valor arbitrario de , de modo que
|
|
(15) |
donde el vector de esfuerzos internos depende de la definición del elemento de viga utilizado. En los próximos apartados se obtienen dichos vectores.
2.2 Matriz de rigidez tangente global
La relación entre las variaciones virtuales del vector de fuerzas global y del vector de desplazamientos global es descrita por
|
|
(16) |
donde es la matriz de rigidez tangente global que se obtiene diferenciando la ecuación (15) como
|
|
(17) |
donde , y son la primera, segunda y tercera columna de la matriz . Para auxiliar en el desarrollo algebraico son definidos los siguientes vectores
|
|
(18) |
cuyas variaciones virtuales son
|
|
(19) |
De modo que, las ecuaciones (11a) y (12) pueden reescribirse de la siguiente forma
|
|
(20) |
Con esta notación los vectores , y se escriben como
|
|
(21) |
cuyas variaciones virtuales son dadas por
|
|
(22) |
El primer término de la ecuación (17) es calculado al introducir la matriz de rigidez elástica local , que depende del tipo de elemento de viga adoptado. Esta matriz será calculada en los próximos apartados. Por lo tanto, la relación entre la variación virtual de los esfuerzos internos y los desplazamiento globales es definida por
|
|
(23) |
Finalmente, de las ecuaciones (16), (17), (22a), (22b) y (23), se obtiene la expresión de la matriz de rigidez tangente global como
|
|
(24) |
El primer término de la ecuación (24) representa la matriz de rigidez material. Así mismo, teniendo en cuenta que el esfuerzo cortante se define como , la matriz de rigidez geométrica global puede ser escrita mediante la siguiente expresión
|
|
(25) |
Por otra parte, la matriz de rigidez elastica es obtenida por medio de la deferenciación de los esfuerzos internos respecto a los desplazamientos locales , tal que
|
|
(26) |
En los próximos apartados se obtiene la matriz de rigidez elástica para los elementos de viga de Euler-Bernoulli, de Timoshenko y de Euler-Bernoulli no lineal. Para el último elemento se tiene en cuenta el acoplamiento entre los efectos de los esfuerzos de flexión y axil lo que genera coeficientes no lineales en la matriz de rigidez elástica, por esta razón se le denomina aquí con el adjetivo no lineal.
3. Elemento de viga Euler-Bernoulli
El movimiento deformacional de este elemento es descrito por las siguientes funciones de forma
|
|
(27) |
Es importante destacar que los desplazamientos transversales y son nulos, esto debido a que las funciones de forma están descritas en relación al sistema de referencia local en la configuración deformada del elemento conforme se muestra en la Figura 1. Por consiguiente, la curvatura y la deformación de un punto en el interior del elemento se escriben como
|
|
(28) |
Al aplicar una variación virtual en el vector de desplazamientos locales , se tiene una variación virtual de la deformación y por el princípio de los trabajos virtuales se tiene que
|
|
(29) |
Asumiendo que y sustituyendo la ecuación (28b) en la ecuación (29b) se obtiene el vector de esfuerzos internos que escrito como
|
|
(30) |
Ahora diferenciando cada componente del vector de esfuerzos internos en la ecuación (30) respecto a los desplazamientos locales , se obtiene la matriz de rigidez elástica dada por
|
|
(31) |
4. Elemento de viga Timoshenko
En el elemento de viga de Timoshenko son utilizadas funciones de interpolaciones lineales para los desplazamientos , y en el sistema de referencia local como
|
|
(32) |
La curvatura , la deformación por corte y la deformación axial son dadas por
|
|
(33) |
Las ecuaciones constitutivas se definen como and . Los esfuerzos internos son calculados usando el princípio de los trabajos virtuales teniendo en cuenta las deformaciones por cortante. Así, dicho princípio puede ser escrito como
|
|
(34) |
Además las variaciones virtuales y se calculan a partir de las ecuaciones (33b) y (33c), respectivamente, lo que permite escribir que
|
|
(35) |
Utilizando solo un punto de gauss, , para evitar el bloqueo por cortante en la ecuación (35) y la ecuación (34), los esfuerzos internos son obtenidos como
|
|
(36) |
Teniendo en cuenta las ecuaciones constitutivas definidas anteriormente y las ecuaciones (33b) y (33c), se obtiene la siguiente expresión para el vector de esfuerzos internos
|
|
(37) |
Por último, diferenciando cada componente del vector de esfuerzos internos en la ecuación (37) respecto a los desplazamiento locales se obtiene la matriz de rigidez elástica dada por
|
|
(38) |
5. Elemento de viga Euler-Bernoulli no lineal
La denominación no lineal se refiere al acoplamiento entre los efectos de los esfuerzos axil y de flexión, esto resulta en la obtención de coefcientes no lineales en la matriz de rigidez elástica del elemento. Por lo tanto, la deformación en un punto del elemento viene dada por
|
|
(39) |
donde es una medida de distribución média de deformación axial a lo largo del elemento, esto con el objetivo de evitar el bloqueo por deformación de membrana. Se nota en el intregando de la ecuación (39) que para el cálculo de dicha deformación se incluye tanto la deformación axial, , como la rotación de la sección transversal, . Usando las funciones de interpolación dadas por la ecuación (27) y la definición de la curvatura dada en la ecuación (28a), la ecuación anterior se escribe como
|
|
(40) |
cuya variación virtual se expresa de la siguiente manera
|
|
(41) |
Al aplicar el principio de los trabajos virtuales y teniendo en cuenta la ecuación (41) se obtienen los esfuerzos internos como
|
|
(42) |
Suponiendo que y utilizando la ecuación (40) se obtiene el vector de esfuerzos internos como
|
|
(43) |
con
|
|
(44) |
Por último, diferenciando cada componente del vector de esfuerzos internos en la ecuación (37) respecto a los desplazamiento locales se obtiene la matriz de rigidez elástica dada por la siguiente expresión
|
|
(45) |
Se puede observar que los términos , , y son funciones cuadráticas de las variables y , por lo tanto los coeficientes de la matriz en (45) que poseen estos términos son no lineales respecto a y .
6. Ejemplos numéricos
Es importante resaltar que entre los tres elementos de viga presentados en este trabajo, el elemento de viga de Timoshenko es el menos refinado, pues utiliza funciones de interpolaciones lineales, mientras que el elemento de viga de Euler-Bernoulli no lineal es el más refinado pues además de utilizar funciones de interporlación de grado 3 tiene en cuenta el acoplamiento entre los efectos de los esfuerzos axil y de flexión. En consecuencia, la respuesta no lineal de un sistema estrutural obtenida utilizando los tres tipos de elementos, será la misma si las magnitudes de las deformaciones fueran inifinitesimales, mientras que si las deformaciones son pequeñas o medianas la respuesta será distinta. Para realizar el análisis no lineal geométrico de los ejemplos presentados en este apartado, se utilizó un programa escrito en lenguaje Fortran90 denominado 2Dbeamnl.f90 escrito por los autores de este artículo. Se utilizará a continuación la denominaco EB para el elemento de viga de Euler-Bernoulli, EBNL para el elemento de viga Euler-Bernoulli no lineal y TI para el elemento de viga de Timoshenko. En todos los ejemplos presentados a continuación fue adoptada una tolerancia para convergencia de . El objetivo es mostrar el desempeño de estos elementos de viga para reproducir el comportamiento fuertemente no lineal de algunos sistemas estructurales. Cabe destacar, como será visto en los siguientes ejemplos, que los elementos de viga aquí descritos poseen habilidad de tratar grandes rotaciones de cuerpo rígido, y además que el elemento de viga de Timoshenko no presenta bloqueo por cortante.
6.1 Columna de Euler
En este ejemplo se considera el pandeo de la columna de Euler con una extremidad empotrada y la otra libre conforme la Figura 2a. En dicha figura se detallan las propiedades geométricas y mecánicas de la columna que fue discretizada con 10 elementos de viga EB, EBNL y TI, respectivamente.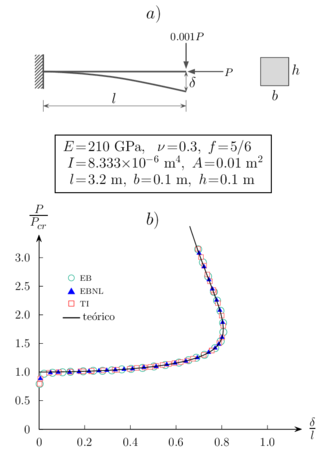
|
| Figura 2: Columna de Euler. (a) Propiedades geométricas y mecánicas. (b) Trayectoria secundaria de equilibrio. |
Para obtener la trayectoria secundaria de equilibrio fue aplicada en la extremidad livre de la columna una carga de en el sentido transversal como se muestra en la Figura 2a. En la Figura 2b se muestra dicha trayectoria obtenida por la aplicación de la integral elíptica completa de primera especie [8] que fue comparada con los caminos de equilibrio obtenidos con los tres tipos de elementos de viga. Se puede observar la buena concordancia entre los resultados analítico y numéricos, y también se observa una coincidencia entre los resultados numéricos obtenidos con los diferentes elementos de viga, lo que implica que las deformaciones son infinitesimales en el comportamiento postcrítico de la columna, aunque la misma sufre grandes traslaciones y rotaciones de cuerpo rígido. Para obtener la respuesta no lineal del pandeo de la columna de Euler se utilizó el método de control variable de los desplazamientos presentados en la referencia [9]. El valor de la longitud de arco fue de 0.01 para 500 pasos de carga. El número medio de iteraciones fue de 2.0. Estos datos fueran constantes para los tres modelos de elementos de viga utilizados en el análisis numérico.
6.2 Pórtico de Lee
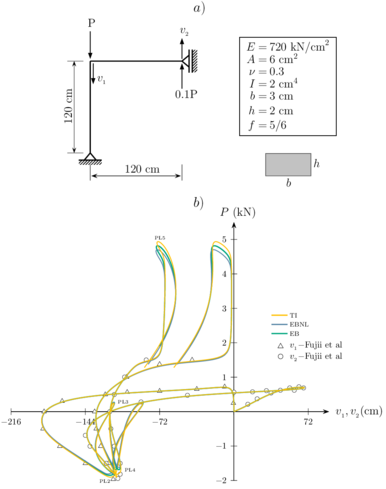
Este ejemplo consiste en la unión de una viga y una columna formando entre si un ángulo recto. Uno de los extremos posee un apoyo con dos restricciones mientras que el otro extremo presenta un apoyo con una restricción que permite el desplazamiento en la dirección del eje . Las condiciones de carga, así como las propiedades geométricas y mecánicas están descritas en la Figura 3a. Este pórtico fue discretizado con 20 elementos de viga EB, EBNL y TI, respectivamente. En la Figura 3b se muestran las trayectorias de equilibrio, donde se describen la evolución de los desplazamientos verticales del nodo rígido del pórtico y del apoyo de una restricción, durante el proceso de carga para los tres modelos de elementos de viga. Se puede observar que en la mayor parte del camino de equilibrio las trayectorias son coincidentes, tanto para como para , excepto a los valores próximos a los puntos limites PL2, PL4 y PL5 como se muestra en Figura 3b. Las diferencias se dan debido a que las deformaciones en estos tramos de la trayectoria son medianas. Los resultados de ambas trayectorias de equilibrio fueron comparados con los obtenidos por Fuji et al. [10] donde fue usada una malla con 10 elementos de viga 2D. En la Figura 3b se muestra que hay una buena concordancia con las trayectorias obtenidas por dichos autores con excepción de los puntos limites PL2 y PL3 donde se forman unos loopings cuando se utiliza la malla de 20 elementos. Para obtener la respuesta no lineal del pórtico de Lee se utilizó el método de longitud de arco con restricción cilíndrica. La longitud de arco inicial utilizada para los tres tipos de elemento de viga fue de 12.5. Para el elemento EB fueron 285 pasos de carga con 43 cortes automáticos debido a la divergencia del proceso iterativo. El número medio de iteraciones fue de 4.43. Con el elemento EBNL fueron 300 pasos de carga, 55 cortes automáticos y un número medio de iteraciones de 4.41. Por último, para el elemento TI fueron 350 pasos de carga con 78 cortes automáticos y un número medio de iteraciones de 4.65. Se puede notar que el comportamiento del Pórtico Lee es fuertemente no lineal con la presencia de algunos limit points, turning points y loopings como se muestra en la Figura 3b.
|
| Figura 3: Pórtico de Lee. (a) Propiedades geométricas y mecánicas. (b) Trayectorias de equilibrio. |
6.3 Arco circular biarticulado rebajado
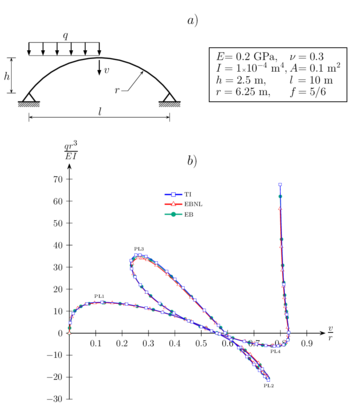
En este ejemplo se considera un arco rebajado de directriz circular, ambos extremos apoyados y sometido a una carga uniformemente distribuida en la mitad de la luz del arco conforme se muestra en la Figura 4a. En dicha figura se detallan las propiedades geométricas y mecánicas del arco que fue discretizado con 20 elementos de viga EB, EBNL y TI, respectivamente. En la Figura 4b se muestran las curvas de la carga normalizada versus el desplazamiento vertical del vértice normalizado , para los tres modelos de elementos de viga. Se puede observar que no hay diferencias significativas entre las tres trayectorias de equilibrio, excepto en los valores próximos a los puntos limite PL2, PL3 y PL4, respectivamente. Los valores normalizados de la carga en los puntos limites PL1, PL2 y PL3 fueron comparados con los valores obtenidos por Xu y Mirmiran [11]. Estos autores utilizaran la formulación corrotacional y un elemento de viga que incluye los términos no lineales de la deformación axial de Green. Además, utilizaron una malla con 20 elementos. Los valores de estas cargas son detalladas en la Tabla 1. Para el elemento EB la mayor diferencia es de 3.1%, observada en el punto limite PL2. Para el elemento EBNL la mayor diferencia fue de 0.53% en el punto limite PL3. Se puede observar que para este elemento fueran encontradas las menores diferencias, esto debido a la inclusión del término definido en la ecuación (39), en la deformación infinitesimal del elemento. Para el elemento TI la mayor diferencia fue de 5.92% en el punto limite PL2. Por otra parte, las mayores diferencias fueron detectadas para este elemento pues utiliza funciones de interpolaciones lineales para evaluar la deformación axial.
|
| Figura 4: Arco circular biarticulado rebajado. (a) Propiedades geométricas y mecánicas. (b) Desplazamiento vertical del vértice. |
| PL1 | PL2 | PL3 | |
| Xu y Mirmiran | 13.77 | -20.09 | 33.99 |
| EB | 13.92 | -20.71 | 34.86 |
| diferencia (%) | 1.09 | 3.09 | 2.56 |
| EBNL | 13.83 | -20.25 | 34.17 |
| diferencia (%) | 0.44 | 0.8 | 0.53 |
| TI | 14.02 | -21.28 | 35.62 |
| diferencia (%) | 1.82 | 5.92 | 4.8 |
Para obtener las trayectorias de equilibrio fue utilizado el método de control variable de los desplazamientos. El valor inicial de la longitud de arco fue de 0.1 para los tres tipos de elementos de viga. Para el elemento EB fue utilizado 177 pasos de carga con 12 cortes automáticos debido a la divergencia del proceso iterativo. El número medio de iteraciones fue de 4.18. Con el elemento EBNL fueron 173 pasos de carga, 10 cortes automáticos y un número medio de iteraciones de 4.20. Por último, para el elemento TI fueron 173 pasos de carga con 9 cortes automáticos y un número medio de iteraciones de 4.22. Se puede notar que las trayectorias de equilibrio del arco mostrado en la Figura 4b son fuertemente no lineales con la presencia de algunos limit points, turning points y un looping.
6.4 Arco semicircular biarticulado
En este ejemplo se considera un arco semicircular con ambos extremos apoyados, sometido a la acción de una carga excéntrica respecto al vértice del arco, como se muestra en la Figura 5a. En dicha figura se detallan las propiedades geométricas y mecánicas del arco que fue discretizado con 50 elementos de viga EB, EBNL y TI. En la Figura 5b se muestran las curvas carga versus el desplazamiento del vértice, obtenidas para los tres modelos de elementos de viga. Se puede observar que hay una buena concordancia entre las tres trayectorias de equilibrio, excepto en los valores próximos a los puntos limite PL6, PL7, PL8 y PL9, respectivamente. Sin embargo, las diferencias se acentuan en los puntos limite PL8 y PL9, debido probablemente, a que en estos tramos de equilibrio la elástica del arco presenta deformaciones medianas. Los valores de la carga en los nueve puntos limites fueron comparados con los valores presentados por Yang y Kuo [12]. Estos autores utilizaran la formulación Lagrageana Actualizada, un elemento de viga que incluye los términos no lineales de la deformación axial de Green y una malla con 26 elementos. Los valores de estas cargas se detallan en la Tabla 2. Para el elemento EB la mayor diferencia es de 3.82% observada en el punto limite LP9. Para el elemento EBNL la mayor diferencia fue de 1.76% en el punto limite PL8. Para el elemento TI la mayor diferencia ha sido de 6.88% en el punto limite PL9. Para los puntos PL1, PL2, PL3 y PL4 las diferencias no son significativas, sin embargo para los puntos PL6, PL7, PL8 y PL9 se han detectado las mayores diferencias.

|
| Figura 5: Arco semicircular biarticulado. (a) Propiedades geométricas y mecánicas. (b) Desplazamiento vertical del vértice. |
Para obtener las trayectorias de equilibrio fue utilizado el método de control variable de los desplazamientos. El valor inicial de la longitud de arco fue de 2.2 para los tres tipos de elementos de viga. Para el elemento EB se ha utilizado 859 pasos de carga con 91 cortes automáticos debido a la divergencia del proceso iterativo. El número medio de iteraciones fue de 4.23. Con el elemento EBNL fueron 820 pasos de carga, 93 cortes automáticos y un número medio de iteraciones de 4.25. Por último, para el elemento TI fueron 859 pasos de carga con 89 cortes automáticos y un número medio de iteraciones de 4.22. Se puede notar que las trayectorias de equilibrio del arco mostrado en la Figura 5b son fuertemente no lineales con la presencia de varios limit points, turning points y loopings.
| Tabla 2. Valores de la carga en los puntos limites - (lb) | |||||||||
| PL1 | PL2 | PL3 | PL4 | PL5 | PL6 | PL7 | PL8 | PL9 | |
| Yang y Kuo | 5.813 | -8.498 | 16.149 | -22.162 | 38.566 | -49.896 | 64.875 | -82.420 | 104.611 |
| EB | 5.811 | -8.495 | 16.204 | -22.086 | 38.932 | -50.206 | 66.786 | -83.138 | 108.61 |
| diferencia (%) | 0.03 | 0.04 | 0.34 | 0.34 | 0.95 | 0.62 | 2.95 | 0.87 | 3.82 |
| EBNL | 5.802 | -8.464 | 16.108 | -21.912 | 38.453 | -49.394 | 65.274 | -80.967 | 104.99 |
| diferencia (%) | 0.19 | 0.40 | 0.25 | 1.13 | 0.29 | 1.00 | 0.62 | 1.76 | 0.36 |
| TI | 5.816 | -8.518 | 16.278 | -22.24 | 39.328 | -50.909 | 68.081 | -85.055 | 111.81 |
| diferencia (%) | 0.05 | 0.24 | 0.80 | 0.35 | 1.98 | 2.03 | 4.94 | 3.20 | 6.88 |
7. Conclusiones
Los elementos de viga 2D de Euler-Bernoulli, de Euler-Bernoulli no lineal y de Timoshenko presentaron un excelente desempeño en el análisis no lineal de vigas, pórticos y arcos. Estos elementos obtuvieron trayectorias de equilibrio casi idénticas para las diferentes tipologías estructurales presentadas en este trabajo, cuando estas sufren deformaciones infinitesimales. Cuando la estructura analisada ha presentado en algunos estados de carga deformaciones medianas, los caminos de equilibrio difieren un poco. Asi que de manera general los resultados obtenidos con los tres modelos de vigas han tenido una buena coincidencia comparados con resultados de otros autores. En este trabajo se mostró, a través de los ejemplos numéricos, la habilidad de los tres modelos viga de tratar con grandes rotaciones de cuerpo rígido cuando se utiliza la formulación corrotacional. A través de operaciones algebraicas bastante simples se describió de manera explícita el movimiento de sólido rígido del elemento de viga y la obtención de la matriz de rigidez tangente expresada en coordenadas globales. La formulación corrotacional aquí descrita es independiente del modelo de elemento de viga 2D que será utilizado. Cabe destacar como principal ventaja de la formulación corrotacional el desacoplamiento entre los efectos locales y globales, esto permite utilizar una biblioteca de elementos finitos oriundos del análisis lineal. La extensión de estos al análisis no lineal geométrico se da al tener en cuenta los efectos globales debido al movimiento de sólido rígido. Por otro lado, diferentes no linealidades físicas pueden ser fácilmente incorporadas a la formulación corrotacional debido a que son efectos locales.
Referencias
[1] C.A. Felippa and B. Haugen, A unified formulation of small-strain corotational finite elements: I. Theory. Computer Methods in Applied Mechanics and Engineering, 81:131-150, (2005).
[2] L.L. Yaw, N. Sukumar and S.K. Kunnath, Meshfree co-rotational formulation for two-dimensional continua. International Journal for Numerical Methods in Engineering, 79(8):979–1003, (2009).
[3] Xu, J., C. K. Lee, C.K., Tan, K.H., A two-dimensional co-rotational Timoshenko beam element with XFEM formulation. Computational Mechanics, 49(5):667–683, (2012).
[4] Caselli, F. and Bisegna, P., A corotational flat triangular element for large strain analysis of thin shells with application to soft biological tissues. Computational Mechanics, 54(3):847–864, (2014).
[5] Li, Z.X., Xiang, Y., Izzuddin, B.A., Vu-Quoc, L., Zhuo, X., Zhang, C., A 6-node co-rotational triangular elasto-plastic shell element. Computational Mechanics, 55(5):837–859, (2015).
[6] Crisfield, M.A., Non-linear finite element analysis of solids and structures. Volume 1: Essentials, Wiley, (1991).
[7] S. Krenk, Non-linear modeling and analysis of solids and structures. Cambridge University Press, (2009).
[8] Timoshenko, S.P. y Gere, J.M., Theory of elastic stability. Second Edition, Dover, (2009).
[9] W.T. Matias, El control variable de los desplazamientos en el análisis no lineal elástico de estructuras de barras. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 18(4):549–572, (2002).
[10] F. Fujii, K.K. Choong and S.X. Gong, Variable displacement control to overcome turnning points of nonlinear elastic frames. Computers & Structures, 44(1/2):133-136, (1992).
[11] Xu, Z. and Mirmiran, A., Looping behavior of arches using corotational finite element. Computers & Structures, 62(6):1059-1071, (1997).
[12] Yang, Y.B. and Kuo, S.R., Theory & analysis of nonlinear framed strucutures. Prentice Hall, (1994).
Document information
Published on 02/01/18
Accepted on 05/06/17
Submitted on 22/02/17
Volume 34, Issue 1, 2018
DOI: 10.23967/j.rimni.2017.6.004
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?