Resumen
Las aplicaciones gobernadas por datos dinámicos (DDDAS) pueden considerarse un nuevo paradigma en el campo de las ciencias aplicadas y la ingeniería, en particular en la denominada Ingeniería basada en simulación (Simulation-based Engineering Sciences) . Se denomina DDDAS a un conjunto de técnicas que permiten la unión de herramientas de simulación con dispositivos de medida, de forma que se hace posible el control en tiempo real de procesos y sistemas. Las DDDAS permiten incorporar de forma dinámica datos adicionales en una aplicación en ejecución y, viceversa, permiten que una aplicación controle el proceso de medida. Las DDDAS exigen herramientas de simulación precisas y rápidas, haciendo uso en lo posible de procesos off-line para limitar el uso de procesos on-line . Para construir herramientas de simulación eficientes, en este trabajo se introducen todas las fuentes de variabilidad como coordenadas adicionales del modelo, de manera que este puede resolverse una única vez y calcular off-line todas las soluciones para cualquier valor de los mencionados parámetros. Esta estrategia necesita de la resolución de modelos definidos en espacios de un alto número de dimensiones, sometidos a lo que se conoce como la maldición de la dimensionalidad . Los autores han propuesto recientemente una técnica denominada descomposición propia generalizada (PGD), que permite evitar dicha « maldición». La yuxtaposición de las DDDAS y el uso de simulaciones PGD realizadas off-line abre posibilidades hasta ahora nunca exploradas en este campo. En el presente trabajo se exploran estas posibilidades en su aplicación a la estimación de parámetros.
Abstract
Dynamic Data Driven Application Systems (DDDAS) appear as a new paradigm in the field of applied sciences and engineering, and in particular in simulation-based engineering sciences. By DDDAS we mean a set of techniques that allow the linkage of simulation tools with measurement devices for real-time control of systems and processes. DDDAS entails the ability to dynamically incorporate additional data into an executing application, and in reverse, the ability of an application to dynamically steer the measurement process. DDDAS needs for accurate and fast simulation tools making use if possible of off-line computations for limiting as possible the on-line computations. We could define efficient solvers by introducing all the sources of variability as extra-coordinates in order to solve off-line only once the model to obtain its most general solution to be then considered in on-line purposes. However, such models result defined in highly multidimensional spaces suffering the so-called curse of dimensionality. We proposed recently a technique, the Proper Generalized Decomposition (PGD), able to circumvent the redoubtable curse of dimensionality. The marriage of DDDAS concepts and tools and PGD off-line computations could open unimaginable possibilities in the field of dynamics data-driven application systems. In this work we explore some possibilities in the context of parameter estimation.
Palabras clave
Descomposición propia generalizada ; Aplicaciones gobernadas por datos dinámicos ; Tiempo real ; Reducción de modelos
Keywords
Proper generalized decomposition ; Dynamic data driven application systems ; Real time ; Model order reduction
1. Introducción
Tradicionalmente, la simulación en ingeniería ha hecho uso de datos estáticos. Estos datos pueden ser parámetros de los modelos, condiciones de contorno, resultados en distintos instantes de tiempo, etc., obtenidos usualmente a través de experimentos. Por tanto, estático se refiere aquí a los parámetros que no pueden cambiarse a lo largo de la simulación.
Un nuevo paradigma ha emergido en el campo de la ingeniería, particularmente en la basada en la simulación (Simulation-based Engineering Sciences) . Las aplicaciones gobernadas por datos dinámicos (DDDAS, siglas de Dynamic Data Driven Application Systems ) constituyen hoy día uno de los más importantes retos a los que se enfrenta la simulación en ingeniería y en las ciencias aplicadas. Con DDDAS nos referimos aquí a un conjunto de técnicas que permiten la yuxtaposición de herramientas de simulación con dispositivos de medida para el control en tiempo real de las propias simulaciones. Tal como las definió la NSF norteamericana, «…las DDDAS permiten incorporar dinámicamente datos adicionales en una aplicación en ejecución y, viceversa, permiten a una aplicación controlar el proceso de medida» [1] .
El término DDDAS fue acuñado por Darema en un workshop sobre el tema en 2000. El documento que inicialmente puso en marcha esta iniciativa decía que las DDDAS «constituyen aplicaciones de simulación que pueden aceptar dinámicamente y responder a medidas realizadas on-line y, a su vez, controlar dichas medidas. Esta retroalimentación simbiótica y sinérgica controla el bucle entre aplicaciones, simulaciones y medidas, constituyendo una nueva línea que puede abrir nuevos dominios en la capacidad de simulación, con una capacidad de repuesta potencial muy alta y crear nuevas aplicaciones mejoradas. Tiene el potencial de transformar la forma en que la ciencia y la ingeniería son realizadas e induce un cambio potencialmente benéfico en la forma en que muchas tareas son realizadas actualmente en nuestra sociedad, en campos tales como la fabricación, el comercio, la predicción de riesgos y la medicina, por nombrar algunos» [2] .
Un sistema DDDAS está constituido típicamente por diferentes bloques:
- Un conjunto de modelos de simulación, muy frecuentemente heterogéneos.
- Un sistema capaz de manejar datos obtenidos de fuentes tanto estáticas como dinámicas.
- Algoritmos para predecir de una manera eficiente el comportamiento del sistema mediante la resolución de los modelos bajo las restricciones impuestas por los datos.
- Una infraestructura de software que integre los datos, las predicciones de los modelos, los algoritmos de control, etc.
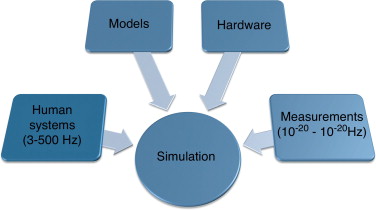
Casi una década después del establecimiento del concepto, la importancia del reto se valora hoy más que nunca. Como puede apreciarse, se trata con disciplinas transversales de caracteres muy diferentes: técnicas de simulación, conceptos numéricos, control, modelado, ingeniería del software, manejo de datos y telecomunicaciones, entre otras. Las características de una DDDAS pueden verse resumidas en la figura 1 .
|
|
|
Figura 1. Estructura de una aplicación gobernada por datos dinámicos y velocidad típica de comunicación entre bloques. |
La figura 1 identifica 3 tipos de interacciones:
- La propia de los humanos y la simulación.
- La interacción entre la simulación y el sistema físico.
- La simulación y la infraestructura de software y hardware.
Los sistemas físicos operan en escalas de tiempo muy dispares. En la figura 1 (adaptada de [3] ) se incluyen algunos valores representativos: desde 10−20 Hz para sistemas cosmológicos hasta 1020 Hz para sistemas a la escala atómica. Los seres humanos, por contra, pueden considerarse sistemas cuando operan a frecuencias entre 3 Hz hasta 500 Hz para sistemas hápticos1 capaces de transmitir sensaciones de tacto realistas. Como puede observarse, un aspecto crucial en las DDDAS es la simulación en tiempo real , esto es, que la simulación debe correr al mismo tiempo (o más rápido) que los datos que están siendo recolectados simultáneamente. Esto no es siempre estrictamente necesario, como en el caso de la meteorología, donde los datos recogidos no se incorporan generalmente de manera inmediata a las simulaciones, pero la mayoría de las aplicaciones requieren diferentes formas de simulación en tiempo real. En los simuladores quirúrgicos de tipo háptico, por ejemplo, el resultado de la simulación, esto es, la fuerza de reacción en el instrumental quirúrgico, debe trasladarse a los periféricos a una frecuencia de unos 500 Hz, que es la frecuencia de oscilación de la mano. En otras aplicaciones, como algunos procesos de fabricación, por ejemplo, las escalas de tiempo son mucho mayores y, por tanto, las simulaciones en tiempo real pueden durar segundos o incluso minutos.
Como se desprende de la introducción anterior, las DDDAS pueden revolucionar la manera de realizar la simulación en las próximas décadas. Nunca más una única simulación va a ser considerada como medio de validar un diseño sobre la base de un conjunto de datos estáticos.
La importancia de las DDDAS en las próximas décadas queda de manifiesto en el informe Blue Ribbon Panel on Simulation Based Engineering Sciences realizado por el NSF, que en 2006 incluyó a las DDDAS como uno de los 5 núcleos principales de actividad o retos en el campo para la próxima década, junto con la simulación multiescala, la validación y la verificación de modelos, el manejo de grandes conjuntos de datos y la visualización. Este panel de expertos concluyó que «…las aplicaciones gobernadas por datos dinámicos van a reescribir el libro sobre la validación y verificación de modelos de simulación» y que «…se necesita de la investigación para usar e integrar de manera efectiva los sistemas de computación, los sensores ubicuos, los detectores de alta resolución, aparatos de imagen, y otros sistemas de almacenamiento y distribución de datos y para desarrollar metodologías y marcos teóricos para su integración en los sistemas de simulación» [4] . Además, la NSF opina que «... la comunidad de DDDAS necesita alcanzar una masa crítica tanto en términos de número de investigadores en el campo como en términos de profundidad, alcance y madurez de las tecnologías que las constituyen» [1] .
Mientras que la investigación en DDDAS debe involucrar necesariamente aplicaciones, algoritmos matemáticos y estadísticos, sistemas de medida y software, el trabajo aquí presentado se centra en el desarrollo de algoritmos matemáticos para la simulación dentro de estos sistemas. En pocas palabras, nuestro trabajo se centra en la incorporación de una nueva generación de técnicas de simulación en este campo de las DDDAS que permita realizar simulaciones más rápidas, y que sea capaz de manejar incertidumbre en los datos, fenómenos multiescala, problemas inversos y otros aspectos que se discutirán más adelante. Esta nueva generación de técnicas de simulación ha recibido el nombre de descomposición propia generalizada (PGD, siglas de Proper Generalized Decomposition ) y está recibiendo un grado de atención creciente en la comunidad dedicada a la simulación en ingeniería. La PGD se desarrolló inicialmente para la simulación con modelos definidos en espacios con un alto número de dimensiones, para ser extendida posteriormente a modelos generales en mecánica computacional, donde puede considerarse una técnica de reducción de modelos a priori. En la siguiente sección se desarrollan las ideas principales de esta técnica.
1.1. Modelos que sufren la maldición de la dimensionalidad
Existen modelos en ingeniería que, a pesar del impresionante desarrollo de la capacidad de los ordenadores actuales, siguen siendo todavía intratables y que, previsiblemente, nunca lo serán por métodos tradicionales. Por ejemplo, en química cuántica, que constituye el nivel más fino de descripción de los enlaces atómicos y moleculares responsables de la estructura de los materiales, la función de onda Ψ, que representa la distribución de una partícula elemental, se define en el espacio físico, esto es, Ψ = Ψ(x , t ). Su evolución está gobernada por la ecuación de Schroedinger, que define un modelo tridimensional transitorio [5] . Sin embargo, cuando se consideran N partículas, la evolución de la función de onda asociada Ψ(x1 , x2 , …, xN , t ) está gobernada por una ecuación de evolución en un espacio de dimensión 3N . Si se intenta resolver dicho modelo por una técnica estándar que se apoye en un mallado del espacio y en la que se consideren, por ejemplo, M nodos en cada dirección del mismo, xi , el número de nodos resultante alcanza la cifra de MN . Con M ~ 203 (una descripción grosera en la práctica) y N ~ 30 (un sistema atómico muy moderado) la complejidad numérica del problema resulta ser de MN ~ 1090 . Es importante recordar que el número de partículas elementales que se presumen en el universo es del orden de 1080 .
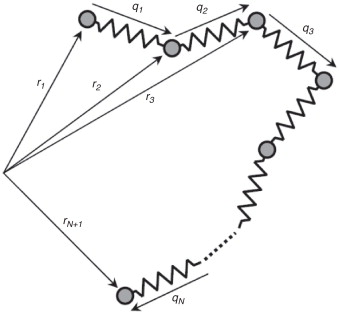
La maldición de la dimensionalidad está presente, sin embargo, en muchas otras escalas en la descripción de la estructura y la mecánica de los materiales. Por ejemplo, cuando se considera una macromolécula lineal, su conformación puede expresarse dando la posición de algunos puntos representativos a lo largo de su longitud o, de manera equivalente, dando los vectores que unen 2 de esos puntos consecutivos como se muestra en la figura 2 . Dentro de la Teoría Cinética [6] and [7] los sistemas moleculares se describen por una función de distribución en vez de por la especificación de la conformación de cada segmento individual de la cadena, puesto que en los sistemas reales hay demasiadas moléculas. Así, la representación vendrá dada por una función Ψ(x , q1 , q2 , …, qN , t ) que proporciona la fracción de moléculas que en la posición x y en el instante t tienen una conformación dada por los vectores q1 , q2 , …, qN . La ecuación de conservación de esta función de densidad de probabilidad proporciona una ecuación conocida como ecuación de Fokker-Planck, cuya resolución está así mismo afectada de la maldición de la dimensionalidad, ya que está definida en un espacio de dimensión 3 + 3 × N + 1 (el espacio físico, los N vectores de conformación y el tiempo). Incluso para una descripción grosera con N ~ 10, el modelo está definido en un espacio de i34 dimensiones!
|
|
|
Figura 2. Descripción de una macromolécula en el ámbito de la Teoría Cinética. |
Otras ramas de la ciencia sufren de esta maldición de la misma manera. Por ejemplo en química, cuando el número de moléculas presentes en un sistema es demasiado bajo, la aproximación continua basada en la introducción del concepto de concentración no resulta válida. Esta situación se da, por ejemplo, en el modelado de la expresión genética [8] . En este caso, el estado del sistema se define por el número de moléculas de cada una de las N especies coexistentes: Ψ(# S1 , # S2 , …, # SN , t ). De nuevo, la evolución del sistema, gobernada por la denominada «ecuación maestra» (Chemical Master Equation ), se define en un espacio multidimensional que hace imposible su tratamiento por técnicas tradicionales basadas en el mallado de dicho espacio. Pueden encontrarse ejemplos similares en multitud de ramas de la ciencia y la ingeniería, pero los expuestos son suficientes para los propósitos del presente trabajo.
Los modelos anteriores parecen estar alejados de la práctica habitual de la mecánica computacional, pero a lo largo del presente trabajo se mostrará cómo los modelos habituales en esta disciplina pueden enriquecerse mediante la adición de nuevas coordenadas, dando lugar a nuevas posibilidades hasta ahora no exploradas. Imagínese el lector, por ejemplo, que está interesado en la resolución de la ecuación de Fourier de transmisión del calor, pero que desconoce el valor de la conductividad térmica del material en cuestión. Esto puede deberse a su naturaleza estocástica o simplemente a que antes de resolver el modelo debe haberse realizado una medida experimental de dicho parámetro. En este caso, existen 3 posibilidades al alcance del ingeniero: a) esperar hasta que dicha conductividad sea medida (una solución conservadora a todas luces); b) resolver la ecuación para un número suficientemente grande de valores de la conductividad de forma que cuando la conductividad sea medida la solución pueda evaluarse (una aproximación al problema que podría denominarse de «fuerza bruta»); c) resolver la ecuación una única vez, pero para cualquier valor de la conductividad (sin duda, la opción a priori más inteligente).
Obviamente la tercera posibilidad es la más excitante. Para calcular esta solución «mágica», válida para cualquier valor de la conductividad, basta introducir la conductividad como una nueva coordenada, jugando el mismo papel que las coordenadas espaciales y temporales habituales, incluso si la ecuación no incorpora derivadas de esta nueva variable. Como se verá, este procedimiento funciona, y muy bien, y puede generalizarse a cualquier otra extra-coordenada: término fuente, condiciones iniciales … Es fácil imaginar, asimismo, que tras realizar este tipo de cálculos, la identificación inversa de parámetros o la optimización son procesos fáciles de realizar.
Pero el sueño no ha terminado. Son muchos los modelos que esperan nuevas reformulaciones. En el campo de la optimización de forma, los parámetros geométricos pueden introducirse en el modelo como nuevas coordenadas, permitiendo así el cálculo de la solución para todas las geometrías posibles y, a partir de ellas, identificar la óptima (en muchos casos un óptimo global en vez del óptimo local que a menudo proporcionan las estrategias habituales). En el modelado multiescala, las escalas fina y grosera de la descripción (y eventualmente cualquier otra escala intermedia) pueden coexistir y ser resueltas simultáneamente si se evita la maldición de la dimensionalidad. De la misma forma, la homogeneización no lineal puede realizarse resolviendo el problema termomecánico al nivel microestructural para cualquier trayectoria de carga, consideradas estas como nuevas dimensiones del modelo.
1.2. Rutas hacia la eliminación de la maldición de la dimensionalidad
Todo lo anterior parece apasionante, pero la cuestión principal permanece sin respuesta cómo resolver la maldición de la dimensionalidad. Para ello se han propuesto diferentes técnicas, siendo la simulación de Monte Carlo la más común. La principal desventaja es el ruido estocástico asociado cuando se calculan variables que no sean los momentos de la función de distribución. Otra posibilidad es el uso de sparse grids[9] , en un marco determinista, pero esta técnica no proporciona una solución definitiva cuando el número de dimensiones sobrepasa un cierto valor, que suele cifrarse en unas 20 dimensiones.
Hasta donde llega nuestro conocimiento, existen pocos precedentes de técnicas deterministas capaces de evitar la maldición de la dimensionalidad de manera eficiente para un gran número de dimensiones. Las aproximaciones de tipo Hartree-Fock son habituales en la química cuántica [5] . Los autores han propuesto recientemente una técnica basada en la representación separada de la solución [10] and [11] que opera mediante la expresión de una función genérica multidimensional u (x1 , x2 , …, xN ) como .
Nota 1.
En la expresión anterior, las coordenadas xidenotan cualquier coordenada, escalar o vectorial, incluyendo el espacio físico, el tiempo o cualquier otra coordenada del espacio de conformación, como puede ser la conductividad discutida en el ejemplo anterior.
De esta forma, si se utiliza un total de M nodos para discretizar cada coordenada, el número total de incógnitas del problema es Q × N × M en vez de MN en un método que utilice un mallado del espacio. Debe resaltarse que las funciones anteriores no se conocen a priori, sino que se calculan por el propio método al introducir la representación separada de la solución en la forma débil del problema, dando lugar a un problema no lineal. El lector interesado puede acudir a Chinesta et al. [12] para encontrar más detalles sobre los aspectos algorítmicos y de implementación del método. La construcción de la aproximación detallada anteriormente se ha denominado Proper Generalized Decomposition o descomposición propia generalizada, ya que dicha descomposición no es ortogonal en general, pero en muchos casos el número de términos es muy próximo al óptimo que se obtiene al aplicar la Proper Orthogonal Decomposition o descomposición propia ortogonal o la equivalente descomposición en valores singulares.
Como se desprende de lo anterior, la complejidad de la solución escala linealmente con la dimensión del espacio en el cual se define el modelo, en vez de la mencionada evolución exponencial de los métodos que utilizan una malla. En general, para un gran número de modelos, el número de funciones necesarias para una buena aproximación de la solución, Q , es muy reducido (unas decenas, habitualmente muy pocas) y en todos los casos la aproximación converge hacia la solución asociada al producto tensorial completo de las funciones de base en cada dimensión, xi . Puede concluirse, por tanto, que la representación separada de la solución tiene un carácter totalmente general, pero que la optimalidad depende de las características de la solución.
Este tipo de representación separada no es, de hecho, nuevo en la literatura. Hace muchos años ya se usaban aproximaciones similares en el campo de la química cuántica [5] . La principal diferencia estriba en la construcción de la representación separada. En mecánica computacional hay —hasta donde llega nuestro conocimiento— un único precedente, la denominada aproximación radial de Pierre Ladeveze, incluida en el método LATIN a mediados de los años ochenta. En esa época, Ladeveze buscaba un método eficiente para resolver modelos no lineales, tras observar que, en general, dichos modelos habitualmente constan de una parte no lineal que suele ser local en el espacio físico y una parte lineal (la relativa al equilibrio) que es global. Este fue el primer ingrediente de un método numérico muy eficiente, denominado LATIN (LArge Time INcrement method ). Pero para acelerar la solución hacía falta un nuevo ingrediente. Ladeveze propuso para ello emplear una solución separada en el espacio-tiempo [13] :
|
|
Si analizamos la eficiencia de esta aproximación separada la conclusión es que para muchos modelos es simplemente sorprendente [14] . Si se considera un modelo transitorio estándar en el espacio físico tridimensional y, asociado a él, P pasos de tiempo de integración, las estrategias habituales deben resolver P problemas tridimensionales, generalmente no lineales (téngase en cuenta que P puede ser del orden de millones). Sin embargo, la aproximación radial de Ladeveze (que hoy denominaríamos PGD en espacio-tiempo) debe resolver alrededor de Q · m problemas tridimensionales para calcular las funciones de espacio Xi (x ) y Q · m problemas unidimensionales para las funciones Ti (t ), donde m es el número de iteraciones necesarias para calcular cada término de la aproximación, debidas a la naturaleza no lineal del problema resultante). Puesto que Q · m ~ 100 en la mayoría de los modelos, el ahorro computacional puede alcanzar varios órdenes de magnitud (millones o más).
Pero si volvemos a los modelos multidimensionales que involucran al espacio físico, al tiempo y a un cierto número de extra-coordenadas «exóticas», el veredicto resulta implacable: la PGD multidimensional permite resolver modelos nunca resueltos con anterioridad y que han sido calificados de irresolubles en innumerables ocasiones. En muchos casos, la PGD permite resolverlos en minutos en un ordenador portátil. Paradojas de la Historia.
La solución de modelos físicamente multidimensionales de la química cuántica, la descripción proporcionada por la teoría cinética para fluidos complejos y la Chemical Master Equation han sido analizadas en profundidad en algunos de los trabajos anteriores de Chinesta et al. [10] , [11] and [15] . Los modelos paramétricos se analizaron en Pruliere et al. [16] . El modelo térmico analizado en Lamari et al. [17] contenía 25 parámetros, todos ellos considerados como extra-coordenadas. El acoplamiento entre EDO y EDP en un contexto multiescala se analizó en Pruliere et al. [18] . Finalmente, en Leygue y Verron [19] se analiza la optimización de forma suponiendo que todos los parámetros que definen la geometría son extra-coordenadas.
2. Sistemas dinámicos paramétricos gobernados por datos dinámicos
Como se ha mencionado en la introducción, el objetivo del presente trabajo no es dar a conocer las DDDAS, sino proponer un nuevo método de simulación que permite aprovechar de manera ventajosa las características de este en el ámbito de las DDDAS. A continuación se presenta un modelo simple gobernado por una ecuación diferencial ordinaria paramétrica. Esta clase de modelos se encuentra a menudo en el modelado de la fisiología, de la epidemiología y muchos otros ámbitos [20] and [21] , en los cuales los parámetros del modelo deben ser identificados a partir de los datos dinámicos que provienen de sensores y aparataje médico.
Se considera un sistema dinámico gobernado por la siguiente ecuación diferencial ordinaria (EDO):
|
|
( 1) |
donde u = u (t ), t ∈ (0, tmax ] y cuya condición inicial es u (t = 0) = ug con ug ≤ u∞ .
El estado estacionario de la ecuación (1) , esto es, la solución a largo plazo, viene dada por u (t → ∞) = u∞ , mientras que la velocidad de aproximación a esta solución depende del parámetro k que se supone desconocido (así es, en efecto, en el control de la diabetes, por ejemplo) y que es susceptible de evolucionar en el tiempo de una forma no predecible a priori.
La solución de la ecuación (1) , con el parámetro k supuesto constante, puede obtenerse fácilmente:
|
|
( 2) |
La identificación del parámetro k es un punto clave en muchas aplicaciones tales como el diagnóstico de la diabetes [22] . Para identificar dicho parámetro deben realizarse diversas medidas experimentales en diferentes instantes de tiempo, que constituyen precisamente el aporte de datos dinámicos reflejado en el título de este trabajo:
|
|
( 3) |
El reto fundamental radica entonces en la identificación, tan rápida como sea posible, del mejor parámetro k en cada intervalo , con i = 1, …, D − 1.
En lo que sigue, y sin pérdida de generalidad, se supone que los intervalos tienen la misma longitud, esto es, , i = 1, …, D − 1. El parámetro desconocido k toma valores en el intervalo [kmin , kmax ] con kmin > 0 y kmax > kmin . La solución más general que permite un conocimiento completo de u (t ) bajo todas las circunstancias posibles consiste en la resolución, una única vez, y realizada off-line , como se probará después, de la ecuación:
|
|
( 4) |
suponiendo que la condición inicial u0 y el parámetro del modelo k son extra-coordenadas. Así, se debería calcular la solución tridimensional u (t , k , u0 ), con t ∈ (0, tmax ], k ∈ [kmin , kmax ] y u0 ∈ [ug , u∞ ].
Nota 2.
El cálculo off-line de u (t , k ), con t ∈ (0, tmax ], k ∈ [kmin , kmax ], basta únicamente cuando el parámetro k es constante en (0, tmax ]. Esto se probará más adelante. De esta forma, resulta estrictamente necesario el cálculo tridimensional que involucre tanto al parámetro del modelo como a la condición inicial, tomados como coordenadas adicionales del modelo.
El modo más sencillo de resolver la ecuación (4) consiste en la definición de valores discretos de todas las coordenadas del modelo: (t1 , t2 , …, tP ), (k1 , k2 , …, kN ) y finalmente . Sin pérdida de generalidad se supone aquí que estos valores están uniformemente distribuidos, por ejemplo ti +1 − ti = ht , i = 1, …, P − 1; ki +1 − ki = hk , con i = 1, …, N − 1 y, finalmente, , con i = 1, …, M − 1. La ecuación (4) puede integrarse, por ejemplo, usando un esquema de diferencias finitas, cuyas limitaciones se expondrán posteriormente. Se considera aquí la estrategia más simple, un esquema de Euler explícito aunque, obviamente, existen otros más precisos. Puesto que la ecuación (4) no presenta derivadas respecto de las extra-coordenadas (el parámetro del modelo y la condición inicial), la integración de la susodicha ecuación (4) se reduce a la solución de un sistema de N × M ecuaciones diferenciales ordinarias desacopladas:
|
|
( 5) |
∀r , s ∈ [1, …, N ] × [1, …, M ], y donde . La integración de la ecuación (5) por diferencias finitas mediante un esquema de primer orden proporciona ∀r , s , ∈ [1, …, N ] × [1, …, M ],
|
|
( 6) |
que permite calcular .
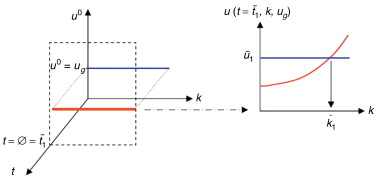
Una vez conocido el valor de , se ilustra ahora la forma de identificar el parámetro k . Se considera la restricción de u (t , k , u0 ) a , y se busca la intersección de dicha solución con el valor experimental , punto que determina el mejor valor del parámetro k en el intervalo , , tal como se ilustra en la figura 3 .
|
|
|
Figura 3. Primer paso en el proceso de identificación del parámetro k . |
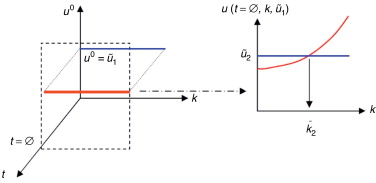
Se considera ahora la restricción de u (t , k , u0 ) a . Se busca la intersección de esta solución con el valor experimental , punto que determina el mejor valor del parámetro k en el intervalo , , tal como se muestra en la figura 4 .
|
|
|
Figura 4. Segundo paso en el proceso de identificación del parámetro k . |
Este proceso continúa hasta la identificación de todos los parámetros óptimos , relativos al modelo definido en todo el dominio temporal (0, tmax ].
Puede observarse que la integración en el dominio temporal se realiza únicamente a partir del conocimiento de , a pesar de la usual variabilidad del parámetro del modelo, k , y que esta es calculada una única vez y off-line (es decir, estos cálculos no tienen que realizarse in situ en presencia del paciente, sino que se calculan y se almacenan los resultados previamente). Puesto que la condición inicial u0 se introdujo como una coordenada adicional del modelo, el proceso de integración se puede adaptar dinámicamente (on-line) a partir de los datos medidos por los sensores, adaptando el valor del parámetro k para alcanzar el valor registrado por aquellos, valor que se considera como condición inicial para la integración en el siguiente intervalo temporal Δ.
Tal como se mencionó anteriormente, si en vez de calcular u (t , k , u0 ), con t ∈ (0, Δ], se calcula u (t , k ) con t ∈ (0, tmax ] a partir de la condición inicial dada, ug , se podría calcular el valor de k tan pronto se dispusiera de un valor medido experimentalmente, o bien tomando el compromiso para ajustar el valor para todos los datos experimentales disponibles. Sin embargo, no sería posible tener en cuenta el cambio del valor del parámetro y ello implicaría la integración on-line (esto es, en presencia del paciente) del modelo u (t , k ) en cada intervalo de tiempo , tomando el dato disponible como condición inicial. La desventaja de dicha aproximación al problema radica precisamente en la necesidad de realizar integraciones on-line , un hecho que limita seriamente su aplicabilidad en el control en tiempo real y por tanto en el ámbito de las DDDAS.
Nota 3.
Si el paso de tiempo entre 2 medidas consecutivas Δ es constante, se puede asegurar que el último paso de integración tPcoincide con Δ. Sin embargo, el dato raramente coincidirá con la condición inicial . A este respecto, existen diferentes posibilidades :
- Considerar el valor más cercano a .
- Considerar los 2 valores vecinos y que permitan definir un intervalo al que pertenezca .
- Considerar la solución interpolada a partir de y . En lo que sigue se consideran estas tres alternativas .
2.1. Un ejemplo numérico
Para ilustrar los métodos desarrollados anteriormente, se considera ahora un modelo dinámico como el dado por la ecuación (1) , donde u∞ = 1, ug = 0, t ∈ (0, 2] y el parámetro desconocido de la ecuación, k ∈ [0, 2]. El campo u se mide a intervalos de tiempo , con i = 1, …, 10 y Δ = 0,2. Finalmente, la representación de la solución se realizó en una malla uniforme definida por P = 200, N = 60 y M = 160.
Se consideran 2 escenarios posibles. El primero es aquel en el que las medidas experimentales provienen de la solución analítica de la ecuación (1) con k = 0,5, supuesta constante en todo el intervalo temporal. En este caso, los valores medidos en los instantes vienen dados respectivamente por , 0,181, 0,259, 0,329, 0,393, 0,451, 0,503, 0,451, 0,503, 0,551, 0,593, 0,632.
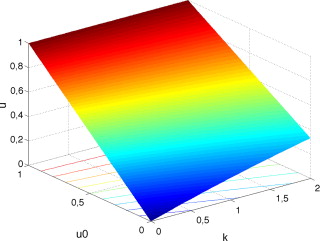
La figura 5 muestra la solución u , restringida al instante t = Δ, esto es u (t = Δ, k , u0 ).
|
|
|
Figura 5. Solución u (t = Δ, k , u0 ). |
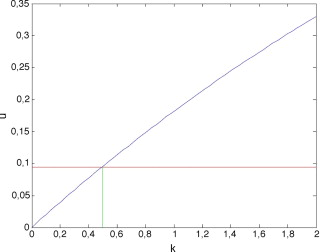
La figura 6 muestra la restricción de la solución u (t = Δ, k , u0 ) de la figura 5 para la condición inicial dada u0 = ug = 0, esto es, u (Δ, k , 0). La solución u (Δ, k , 0) se muestra en azul, mientras que la solución de referencia se muestra en rojo. La intersección de ambas curvas muestra el parámetro óptimo k que en este caso resulta muy cercano al exacto, k = 0,5 usado para calcular los valores que actúan como medidas «experimentales», , puesto que el valor u0 = 0 coincide con el valor discreto del eje de condiciones iniciales. Así, nos encontramos con una única curva .
|
|
|
Figura 6. Solución u (k ) = u (t = Δ, k , 0). |
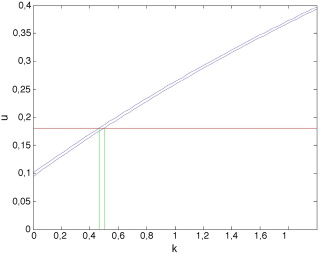
La solución para el instante se obtiene al particularizar la solución general u (t , k , u0 ) de nuevo para t = Δ, pero para una condición inicial . Puesto que dicho valor no coincide con ninguno de los valores discretos del eje de condiciones iniciales, se consideran ahora las soluciones para los dos valores más próximos, en este caso y . La figura 7 muestra ambas curvas, y , cuyas intersecciones con la curva de referencia determinan el intervalo al cual pertenece el parámetro k óptimo: .
|
|
|
Figura 7. Soluciones y . |
Se podría obtener una estimación más exacta del parámetro por interpolación. La interpolación más simple, lineal, consiste en la construcción del valor uint a partir de los valores y de acuerdo con
|
|
( 7) |
La tabla 1 muestra los diferentes intervalos obtenidos en la estimación del parámetro, . Obviamente, cuanto más refinada sea la representación, esto es, mayores N y M , menor es el intervalo de estimación. La última columna de la tabla muestra la identificación mejorada obtenida por interpolación según la ecuación (7) .
| kexacto | |||||
|---|---|---|---|---|---|
| 0,2 | 0,095 | 0,5 | 0,500 | 0,500 | 0,500 |
| 0,4 | 0,181 | 0,5 | 0,469 | 0,504 | 0,499 |
| 0,6 | 0,259 | 0,5 | 0,493 | 0,531 | 0,499 |
| 0,8 | 0,329 | 0,5 | 0,466 | 0,508 | 0,499 |
| 1,0 | 0,393 | 0,5 | 0,473 | 0,519 | 0,499 |
| 1,2 | 0,451 | 0,5 | 0,477 | 0,529 | 0,499 |
| 1,4 | 0,503 | 0,5 | 0,485 | 0,542 | 0,499 |
| 1,6 | 0,551 | 0,5 | 0,439 | 0,502 | 0,499 |
| 1,8 | 0,593 | 0,5 | 0,469 | 0,539 | 0,499 |
| 2,0 | 0,632 | 0,5 | 0,450 | 0,527 | 0,499 |
2.2. Un segundo ejemplo numérico con variación aleatoria del parámetro
En esta sección se considera un segundo escenario ligeramente diferente. En este caso el parámetro k se define de manera aleatoria en cada intervalo de tiempo , i = 1, …, D = 10, de acuerdo con la expresión
|
|
( 8) |
donde kref = 1,0, ε = 0,5 y denota una variable aleatoria con distribución uniforme en el intervalo [− 1, 1]. La tabla 2 muestra los parámetros identificados. De nuevo puede apreciarse la gran exactitud obtenida mediante la técnica de interpolación.
| kexacto | |||
|---|---|---|---|
| 0,2 | 0,150 | 0,811 | 0,811 |
| 0,4 | 0,360 | 1,423 | 1,422 |
| 0,6 | 0,469 | 0,930 | 0,930 |
| 0,8 | 0,537 | 0,685 | 0,685 |
| 1,0 | 0,650 | 1,405 | 1,404 |
| 1,2 | 0,740 | 1,480 | 1,479 |
| 1,4 | 0,784 | 0,939 | 0,938 |
| 1,6 | 0,809 | 0,611 | 0,611 |
| 1,8 | 0,836 | 0,758 | 0,758 |
| 2,0 | 0,863 | 0,909 | 0,908 |
2.3. Una formulación alternativa
Dado el carácter lineal de la ecuación (1) , es posible escribir la solución de la misma como la suma de la solución general de la ecuación homogénea (en adelante, uh ) más una solución particular de la ecuación completa (en adelante, uc ):
|
|
( 9) |
y
|
|
( 10) |
Si se realiza ahora el cambio de variable se tiene, para la ecuación (9) ,
|
|
( 11) |
La solución de las ecuaciones (10) y (11) se busca ahora acudiendo a la PGD, ampliamente analizada en algunos de los trabajos anteriores de los autores (véase, por ejemplo, [12] and [23] ) y que se resume brevemente en la sección final de este artículo.
|
|
( 12) |
a partir de la cual, la solución general de la ecuación (1) puede construirse como
|
|
( 13) |
que verifica, a su vez,
|
|
( 14) |
Esta sencilla técnica permite resolver problemas bidimensionales en vez de los tridimensionales que resultarían de la resolución para cualquier condición inicial. Sin embargo, su aplicación está restringida al caso lineal. En el caso no lineal podría aplicarse tras la linealización consiguiente.
2.4. Discusión
En el presente trabajo se ha propuesto una metodología de estimación de parámetros dinámicos haciendo uso de una solución general calculada off-line . Los primeros resultados mostrados en las secciones precedentes permiten concluir que la técnica desarrollada puede ser aplicada potencialmente en el entorno de una DDDAS.
La solución general u (t , k , u0 ) se pensó en un espacio tridimensional en el cual se definió el sistema dinámico original. La introducción de extra-coordenadas ha sido el precio a pagar para poder calcular una solución suficientemente general que pueda ser usada on-line sin la necesidad de posteriores integraciones del sistema dinámico. De esta forma, las tareas que deben realizarse on-line constituyen un mero post-proceso de la solución general. Dado que el sistema resultante era tridimensional, de una dimensionalidad moderada, esta integración pudo realizarse numéricamente aplicando un esquema de diferencias finitas extremadamente sencillo, que en el caso de las secciones anteriores contenía un total de N × M ecuaciones diferenciales ordinarias desacopladas.
Los modelos que involucran muchos campos o muchos parámetros (o ambos) limitan el uso de técnicas de discretización estándar, debido precisamente a la multidimensionalidad del modelo resultante. La necesidad de usar mallas suficientemente finas para representar las soluciones impide su integración e incluso el almacenamiento de los resultados.
Una posibilidad para evitar las dificultades asociadas con la maldición de la dimensionalidad consiste en el uso de PGD, tal como se discutió en la primera sección. En la siguiente sección se aplican estas descomposiciones en la solución del sistema dinámico considerado anteriormente.
3. Descomposición propia generalizada de sistemas dinámicos
A partir de este momento se ilustra la construcción de la PGD aplicada a los sistemas dinámicos analizados en las secciones previas:
|
|
( 15) |
con t ∈ I = (0, Δ], k ∈ ℵ = [kmin , kmax ] y u0 ∈ ℑ = [ug , u∞ ].
Como se ha comentado anteriormente, se pretende introducir tanto el parámetro del modelo, k , como la condición inicial, u0 , como coordenadas adicionales en la definición del problema. Para introducir la condición inicial en la EDO, se practica el siguiente cambio de variable:
|
|
( 16) |
que, introducido en la ecuación (15) anterior proporciona:
|
|
( 17) |
Una característica fundamental de la PGD es que busca la solución de la ecuación (17) en la forma:
|
|
( 18) |
Puesto que la PGD es un método a priori, es decir, no supone ninguna forma particular de las funciones Ti , Ki o Ui , estas deben generarse durante la ejecución del método, dando lugar a un problema no lineal que se describe a continuación. Dentro del proceso iterativo inherente a los problemas no lineales, supóngase que se tiene construida la aproximación en la iteración n < Q :
|
|
( 19) |
de forma que en la iteración actual se busca el siguiente producto funcional Tn +1 (t ) · Kn +1 (k ) · Un +1 (u0 ). Con el objeto de simplificar la notación, este producto de funciones se denotará en adelante como R (t ) · S (k ) · W (u0 ). Antes de resolver el problema no lineal a que da lugar la búsqueda de estas 3 funciones, se impone una linealización de este. La elección más sencilla consiste en el uso de un esquema de iteración por punto fijo en direcciones alternadas, que supone secuencialmente que tanto S (k ) como W (u0 ) se conocen de la iteración precedente y procede calculando R (t ). Con esta función R (t ) recién actualizada y con la W (u0 ) anterior, procede a determinar S (k ) y, finalmente, con las funciones R (t ) y S (k ) recién obtenidas, procede a determinar W (u0 ). El procedimiento continúa hasta alcanzar la convergencia. Las funciones así determinadas permiten definir el siguiente término de la aproximación, Tn +1 (t ) = R (t ), Kn +1 (k ) = S (k ) y Un +1 = W (u0 ).
Se ilustran a continuación cada uno de los pasos anteriores.
3.1. Cálculo de R (t ) a partir de S (k ) y W (u0 )
Considérese la forma débil del problema (15) :
|
|
( 20) |
en la que las funciones de aproximación y ponderación, respectivamente, son
|
|
( 21) |
y
|
|
( 22) |
Introduciendo (21) y (22) en la forma débil (20) se obtiene:
|
|
( 23) |
Puesto que todas las funciones dependientes de la coordenada paramétrica k y de la condición inicial u0 son conocidas, puede realizarse la integración de las mismas en sus dominios respectivos ℵ× ℑ. Teniendo en cuenta la siguiente notación para facilitar el desarrollo que sigue:
|
|
( 24a) |
|
|
( 24b) |
|
|
( 24c) |
la ecuación (23) se reduce a:
|
|
( 25) |
La ecuación (25) representa la forma débil de la EDO que define la evolución temporal del campo R (t ) y que puede resolverse mediante cualquier técnica de discretización estabilizada habitual (SU, Discontinuous Galerkin , etc.). La forma fuerte de la ecuación (25) quedaría entonces:
|
|
( 26) |
con
|
|
( 27) |
ecuación que puede integrarse usando alguna técnica apropiada (Euler, Runge-Kutta, etc.).
3.2. Cálculo de S (k ) a partir de R (t ) y de W (u0 )
En este caso, la función de ponderación puede escribirse como:
|
|
( 28) |
La forma débil del problema así definido quedaría:
|
|
( 29) |
que, tras integración en el espacio I × ℑ y teniendo en cuenta de nuevo la notación definida en la ecuación (24) , proporciona:
|
|
( 30) |
A diferencia del caso anterior, la ecuación (30) no involucra ningún operador diferencial, quedando la forma fuerte del problema:
|
|
( 31) |
donde
|
|
( 32) |
que representa una ecuación algebraica. Se observa, por tanto, que la introducción de parámetros como coordenadas adicionales del problema no tiene un efecto relevante en el coste computacional del problema en su formulación PGD.
3.3. Cálculo de W (u0 ) a partir de R (t ) y S (k )
En este último caso la función de ponderación resulta ser:
|
|
( 33) |
La forma débil del problema resulta ahora:
|
|
( 34) |
que, tras integración en el espacio I × ℵ y teniendo en cuenta la notación establecida en la ecuación (24) , (3.1 ), proporciona:
|
|
( 35) |
La ecuación (35) no involucra ningún operador diferencial. Por tanto, la forma fuerte de (35) quedaría:
|
|
( 36) |
con
|
|
( 37) |
que resulta ser, de nuevo, una ecuación algebraica.
3.4. Descomposición de la solución
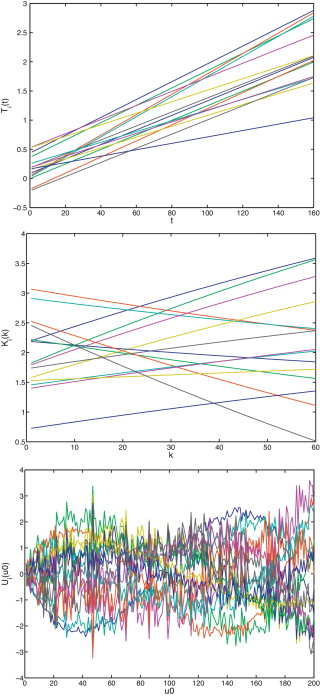
La solución del problema presentado en la ecuación (15) se puede descomponer, como se ha comentado, en sumas de productos de funciones separadas de las variables t , k , y u0 , tal y como se muestra en la figura 8 .
|
|
|
Figura 8. Funciones que proporcionan la aproximación de la ecuación (23) en las extra-coordenadas t (a), k (b) y u0 (c). |
En dicha aproximación se han empleado 15 sumas de productos, para obtener una precisión en la aproximación de 10−4 . Obviamente, es posible obtener menores cotas de error empleando un número mayor de funciones en la aproximación.
4. Conclusiones
El presente trabajo constituye un primer intento de definir métodos rápidos capaces de realizar simulaciones on-line a partir de una solución suficientemente general definida off-line . Este algoritmo podría ser incluido en un marco de aplicaciones gobernadas por datos dinámicos (DDDAS) para realizar simulaciones dinámicas en tiempo real.
Las soluciones generales requieren la reformulación del modelo en espacios de más alta dimensionalidad, que involucran frecuentemente la conversión de todos los datos sobre los cuales existe incertidumbre o son susceptibles de evolucionar en el tiempo (parámetros del modelo, condiciones de contorno...) en coordenadas adicionales, lo que, a su vez, provoca la conocida maldición de la dimensionalidad . Las técnicas basadas en la descomposición propia generalizada (PGD) permiten eludir esta maldición, tal como se ha probado en una serie de trabajos anteriores de los autores.
A pesar de lo prometedor de este matrimonio entre los conceptos de DDDAS y las herramientas derivadas de la PGD, existen diversas dificultades que deben abordarse todavía. En general, las soluciones calculadas con la PGD están definidas en espacios altamente dimensionales. De esta forma, será necesario desarrollar técnicas capaces de encontrar óptimos con respecto a criterios definidos en estos espacios altamente dimensionales y en tiempo real. En estos momentos la dificultad se ha trasladado desde la integración de los modelos al postproceso, mucho menos estudiado, al menos en espacios que involucran miles de dimensiones, por ejemplo.
Agradecimientos
El trabajo recogido en el presente artículo ha sido financiado parcialmente por el Ministerio de Ciencia e Innovación de España, a través del proyecto CICYT DPI2011-27778-C02-01.
References
- [1] Various Authors. Final report. DDDAS workshop at Arlington, VA. Technical report, National Science Foundation, 2006.
- [2] F. Darema; Engineering/Scientific and commercial applications: differences, simmilarities, and future evolution; Proceedings of the Second Hellenic Conference on Mathematics and Informatics (1994), pp. 367–374
- [3] Various Authors. Final report. DDDAS workshop at Arlington, VA. Technical report, National Science Foundation, 2000.
- [4] J.T. Oden, T. Belystchko, J. Fish, T.J.R. Hughes, C. Johnson, D. Keyes, A. Laub, L. Petzold, D. Srolovitz, and S. Yip, Simulation Based Engineering Science: Revolutionizing Engineering Science through Simulation. Technical report, National Science Foundation blue ribbon panel on SBES, 2006.
- [5] E. Cancès, M. Defranceschi, W. Kutzelnigg, C. Le Bris, Y. Maday; Computational quantum chemistry: a primer; Handbook of Numerical Analysis, volume X (2003) pp. 3-270
- [6] R.B. Bird, C.F. Curtiss, R.C. Armstrong, O. Hassager; Dynamics of polymerics liquids; Wiley (1987)
- [7] R. Keunings; Micro-Macro Methods for the Multiscale Simulation of Viscoelastic Flow using Molecular Models of Kinetic Theory; D.M. Binding, K. Walters (Eds.), Rheology Reviews 2004, British Society of Rheology (2004), pp. 67–98
- [8] S.N. Sreenath, K-H. Cho, P. Wellstead; Modelling the dynamics of signalling pathways; Essays in biochemistry, 45 (2008), pp. 1–28
- [9] H.-J. Bungartz, M. Griebel; Sparse grids; Acta Numerica, 13 (2004), pp. 1–123
- [10] A. Ammar, B. Mokdad, F. Chinesta, R. Keunings; A new family of solvers for some classes of multidimensional partial differential equations encountered in kinetic theory modeling of complex fluids; J. Non-Newtonian Fluid Mech., 139 (2006), pp. 153–176
- [11] A. Ammar, B. Mokdad, F. Chinesta, R. Keunings; A new family of solvers for some classes of multidimensional partial differential equations encountered in kinetic theory modeling of complex fluids. Part II: Transient simulation using space-time separated representations; J. Non-Newtonian Fluid Mech., 144 (2007), pp. 98–121
- [12] F. Chinesta, A. Ammar, E. Cueto; Recent advances in the use of the Proper Generalized Decomposition for solving multidimensional models; Archives of Computational Methods in Engineering, 17 (2010), pp. 327–350
- [13] P. Ladeveze; Nonlinear Computational Structural Mechanics; Springer, N.Y (1999)
- [14] A. Ammar, M. Normandin, F. Naim, D. González, E. Cueto, F. Chinesta; Non-incremental strategies based on separated representations: Applications in Computational Rheology; Communications in Mathematical Sciences, 8 (3) (2010), pp. 671–695
- [15] F. Chinesta, A. Ammar, E. Cueto; On the use of Proper Generalized Decompositions for solving the multidimensional Chemical Master Equation; European Journal of Computational Mechanics, 19 (2010), pp. 53–64
- [16] E. Pruliere, F. Chinesta, A. Ammar; On the deterministic solution of parametric models by using the proper generalized decomposition; Mathematics and Computer Simulation, 81 (2010), pp. 791–810
- [17] H. Lamari, A. Ammar, P. Cartraud, G. Legrain, F. Jacquemin, F. Chinesta; Routes for the efficient non-concurrent homogenization of non-linear heterogeneous materials by using the proper generalized decomposition; Archives of Computational Methods in Engineering, 17 (4) (2010), pp. 373–391
- [18] E. Pruliere, A. Ammar, N. El Kissi, F. Chinesta; Multiscale modelling of flows involving short fiber suspensions; Archives of Computational Methods in Engineering, 16 (2009), pp. 1–30
- [19] A. Leygue, E. Verron; A first step towards the use of proper generalized decomposition methods for structural optimization; Archives of Computational Methods in Engineering, 17 (4) (2010), pp. 465–472
- [20] A. Boutayeb and A. Chetouani, A critical review of mathematical models and data used in diabetology. Biomedical Engineering online, 5, 2006.
- [21] A. Boutayeb, E. H. Twizell, K. Achouayb, and A. Chetouani, A mathematical model for the burden of diabetes and its complications. Biomedical Engineering online, 3, 2004.
- [22] E. Ackerman, L. Gatewood, J. Rosevar, G. Molnar; Blood glucose regulation and diabetes; F. Heinmets (Ed.), Concepts and Models in Biomathematics, Marcel Dekker (1969), pp. 131–156 chapter 3
- [23] F. Chinesta, P. Ladeveze, E. Cueto; A short review on model order reduction based on Proper Generalized Decomposition; Archives of Computational Methods in Engineering, 18 (2011), pp. 395–404
Notes
1. Los sistemas hápticos son aquellos capaces de trasladar al usuario reacciones en forma de fuerza. Como ejemplo se podrían citar los simuladores quirúrgicos. Los sistemas que, como el cine, solo transmiten sensaciones visuales realistas operan a unos 30 Hz.
Document information
Published on 01/06/13
Accepted on 28/12/11
Submitted on 08/11/10
Volume 29, Issue 2, 2013
DOI: 10.1016/j.rimni.2013.04.001
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?