Abstract
In the present study heat transfer and entropy generation analysis of boundary layer flow of an incompressible viscous fluid over hyperbolic stretching cylinder are taken into account. The governing nonlinear partial differential equations are normalized by using suitable transformations. The numerical results are obtained for the partial differential equations by a finite difference scheme known as Keller box method. The influence of emerging parameters namely curvature parameter and Prandtl number on velocity and temperature profiles, skin friction coefficient and the Nusselt number is presented through graphs. A comparison for the flat plate case is given and developed code is validated. It is seen that curvature parameter has dominant effect on the flow and heat transfer characteristics. The increment in the curvature of the hyperbolic stretching cylinder increases both the momentum and thermal boundary layers. Also skin friction coefficient at the surface of cylinder decreases but Nusselt number shows opposite results. Temperature distribution is decreasing by increasing Prandtl number. Moreover, the effects of different physical parameters on entropy generation number and Bejan number are shown graphically.
Keywords
Boundary layer flow; Hyperbolic stretching cylinder; Heat transfer analysis; Entropy generation
1. Introduction
The boundary layer flow and heat transfer with stretching boundaries received remarkable attention in modern industrial and engineering practice. The attributes of end product are greatly reliant on stretching and rate of heat transfer at final stage of processing. Due to this real-world importance, interest developed among scientists and engineers to comprehend this phenomenon. Common examples are the extrusion of metals into cooling liquids, food, plastic products, the reprocessing of material in the molten state under high temperature. During this phase of manufacturing process, the material passes into elongation (stretching) and a cooling process. Such types of processes are very handy in the production of plastic and metallic made apparatus, such as cutting hardware tools, electronic components in computers, rolling and annealing of copper wires. In many engineering and industrial applications, the cooling of a solid surface is a primary tool for minimizing the boundary layer. Due to these useful and realistic impacts, the problem of cooling of solid moving surfaces has turned out to be an area of concern for scientists and engineers. Recently researchers have shown deep interest in analyzing the characteristics of flow and heat transfer over stretching surfaces. In this context, analysis of flow and heat transfer phenomena over a stretching cylinder has its own importance in processes such as fiber and wire drawing, hot rolling. Based on these applications, the boundary layer flow and heat transfer due to a stretching cylinder was initially studied by Wang [1]. He extended the work of Crane [2] to study the flow of heat transfer analysis of a viscous fluid due to stretching hollow cylinder. During last few years many researchers gave attention to analyze the fluid flow and heat transfer over the stretching cylinder and found the similarity solutions. Nazar et al. [3], [4] and [5] produced numerical solution of laminar boundary layer flow, uniform suction blowing and MHD effects over stretching cylinder in an ambient fluid. After that a lot of research problems have been done on the analysis of flow and heat transfer over stretching cylinder. Mukhopadhyay [6], [7], [8] and [9] considered chemical solute transfer, mixed convection in porous medium, and MHD slip flow along a stretching cylinder. Effect of magnetic field over horizontal stretching cylinder in the presence of source/sink with suction/injection is studied by Elbashbeshy [10]. Fang and Yao [11], Vajravelu et al. [12], Munawar et al. [13] and [14], Wang [15], Lok et al. [16], Abbas et al. [17], and Butt and Ali [18] have considered viscous swirling flow, axisymmetric MHD flow, unsteady vacillating flow, natural convection flow, axisymmetric mixed connection stagnation point flow, radiation effects in porous medium and entropy analysis of magnetohydrodynamics flow over stretching cylinder, respectively. More recently, Majeed et al. [19] applied Chebyshev Spectral Newton Iterative Scheme (CSNIS) and studied the heat transfer influence by velocity slip and prescribed heat flux over a stretching cylinder. Sheikholeslami [20] has calculated the effective thermal conductivity and viscosity of the nanofluid by Koo–Kleinstreuer–Li (KKL) model and provided the nanofluid heat transfer analysis over cylinder. Javed et al. [21] discussed the combined effects of MHD and radiation on natural convection flow over horizontal cylinder. Hajmohammadi et al. [22] considered flow and heat transfer of Cu-water and Ag-water nanofluid over permeable surface with convective boundary conditions. Their main focus was to discuss the effects of nano-particles volume fraction, and non-dimensional permeability parameter on skin friction and convection heat transfer coefficient. Dhanai et al. [23] investigated mixed convection nanofluid flow over inclined cylinder. They utilized Buongiorno’s model of nanofluid and found dual solutions with the velocity and thermal slip effects in the presence of MHD.
Aforementioned studies reveal that vast literature is present on study of linearly stretching cylinder but to the best of our knowledge, the problem over a cylinder with hyperbolic stretching velocity and entropy generation has not been addressed yet. The governing equations related to flow problem solved numerically and the effects of involving parameters on flow behavior are shown graphically. Entropy generation is the quantification of thermodynamics irreversibility and it exists in all types of heat transfer phenomenon. Due to this fundamental importance the present work is optimized with the inclusion of entropy generation analysis. In this context the studies [24], [25], [26], [27], [28], [29] and [30] are quite useful to explore many aspects of entropy generation which have not been taken into account yet.
2. Problem formulation
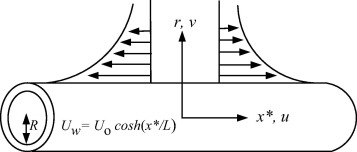
Consider the two-dimensional steady incompressible flow of a viscous fluid over a hyperbolic stretching circular cylinder of fixed radius R (see Fig. 1). The basic equations that govern the flow and heat transfer phenomena will take the form as
|
|
(1) |
|
|
(2) |
|
|
(3) |
where and are be velocity components along and directions, be the temperature and be the thermal diffusivity of the fluid. The relevant boundary conditions for the governing problem are as follows:
|
|
(4) |
where is a constant. Now introducing the following suitable transformation
|
|
(5) |
where stream function is the non-dimensional function defined through usual relationship as
|
|
(6) |
which satisfies the continuity Eq. (1). Upon using Eqs. (5) and (6) into Eqs. (2) and (3), we arrived at following transformed equations
|
|
(7) |
|
|
(8) |
where (local Reynolds number) and (Prandtl number). Using the stretching velocity in Eqs. (7) and (8), we get
|
|
(9) |
|
|
(10) |
and boundary conditions take the new form as
|
|
(11) |
where K represents curvature parameter.
|
|
|
Figure 1. Geometry of the flow. |
If we consider and then Eq. (9) reduces to the Sakiadis flow equation [31]
|
|
(12) |
with boundary conditions
|
|
(13) |
The quantities of physical significance are the skin friction coefficient and Nusselt number which are defined as
|
|
(14) |
where be the wall shear stress and the constant heat flux from the surface, which are defined as
|
|
(15) |
After using Eq. (15) into Eq. (14), the local skin friction coefficient and local Nusselt number take the form
|
|
(16) |
3. Solution methodology
To solve nonlinear system of partial differential Eqs. (9) and (10) subject to the set of boundary conditions (11), we employed a very accurate and efficient implicit finite difference method commonly known as Keller box which is explained in detail in the book of Cebeci and Bradshaw [32]. In present problem, the solution is obtained through following steps.
- Step-1: Eqs. (9) and (10) are written in terms of first order differential equations. Then functions and derivatives are replaced by central difference form in both coordinate directions. This results in a set of nonlinear difference equations for the number of unknown equal to the number of difference equations.
- Step-2: obtained nonlinear difference equations are then linearized by using Newton’s quasi-linearization technique.
- Step-3: and are solved using block tri-diagonal algorithm.
Now to initiate the process at , it is first provided guess profile for all five dependent variables arising after reduction to first order system and then obtained the solution outlined in steps 1-3. Iteration process is continued for all values of , until the difference in velocity and temperature profiles between the consecutive iteration is less than . The accuracy of the employed numerical scheme has been established in Table 1 by comparison with the known results obtained by Rees and Pop [31] for flat plate This comparison gives us confidence that the developed code is correct and has achieved the desired level of accuracy. Moreover, the values of and are given in Table 2.
| Ref. [31] | −0.4439 | −0.3509 |
| Present | −0.4439 | −0.3509 |
| 0 | −0.55387 | 0.41012 |
| 0.5 | −0.71911 | 0.60043 |
| 1 | −0.88994 | 0.78894 |
| 1.5 | −1.05690 | 0.96676 |
4. Result and discussion
An inspection of the governing partial differential equations indicates the presence of two emerging parameters: (a) the curvature parameter , (b) and the Prandtl number Pr.
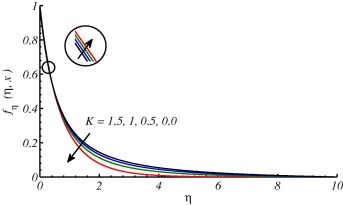
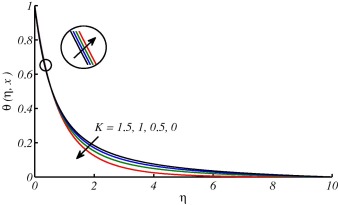
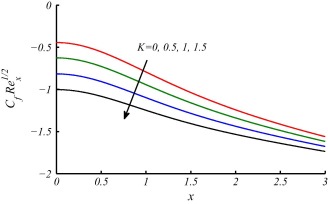
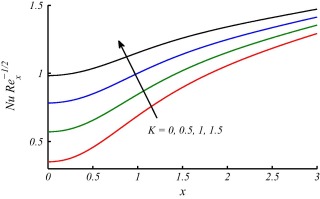
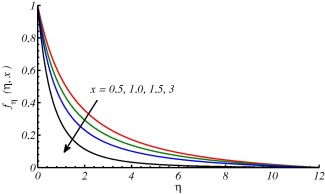
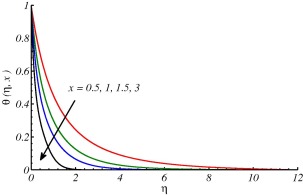
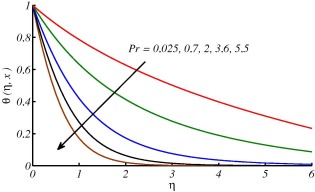
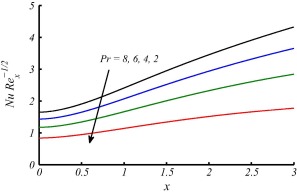
The effects of these parameters are discussed in the forthcoming figures. In Figure 2 and Figure 3, effects of curvature parameter on velocity and temperature profile are plotted. It is observed that curvature has significant effects on velocity and temperature profiles. In Fig. 2 the trend for velocity profile is rapidly decreasing in the region () and then increasing after for increasing values of curvature parameter and consequently as a result the boundary layer thickness increases with the increase in curvature of the cylinder. This behavior of the fluid velocity is due to the fact that curvature and radius of cylinder have reciprocal relationship. In other words increase in tends to decrease in radius of cylinder. In this way, due to lesser surface area of the cylinder, the increase in velocity gradient at the surface increases and consequently enhances the shear stress per unit area. Fig. 2 also depicts that an increase in the curvature of the cylinder leads to augment in boundary layer thickness, as compared to the flat plate case (). In Fig. 3 the temperature profiles decrease near the surface of the cylinder as increases, and afterward rise significantly and the thermal boundary-layer thickness increases. This variation of the temperature profile is due to the reason that as the curvature increases, the radius of cylinder reduces the surface area which is intact with the fluid also decreases. It is also important to mention that heat is transferred into the fluid in modes: conduction at the cylinder surface and convection for the region . Now, as the area of surface of the cylinder decreases, a slender reduction in the temperature profile occurs close to the surface of the cylinder, since a smaller amount of heat energy is transferred from the surface to the fluid through conduction phenomena. On the other hand, the thermal boundary-layer thickness increases, because of the heat transport in the fluid due to enhanced convection process all around the cylinder, which is evident from Fig. 3. Fig. 4 is plotted to observe the consequence of curvature parameter on the coefficient of skin friction . It is noticed that as increases, the wall skin friction coefficient decreases. This is due to the reason that, for larger curvature of the cylinder, the velocity gradient at the surface becomes increased rapidly as compared to the flat plate (). Fig. 5 is plotted to observe the consequence of curvature parameter on the Nusselt number . It is noticed that as increases the Nusselt number also increases. In Figure 6 and Figure 7, it is observed that both velocity and temperature boundary layer thickness decrease by increasing the value of . The effects of different values of Prandtl number Pr on temperature profile have been discussed in Fig. 8. It is observed that temperature is rapidly decreasing for increasing Pr and thermal boundary layer thickness decreases. It is obvious from the graph that fluids with low Prandtl number slow down the cooling process and fluids with high Prandtl number speed up the cooling process. The behavior of temperature profile shows that Prandtl number can be used to control the cooling process. This could be managed by using high Prandtl number fluids such as oils and lubricants. Fig. 9 shows that Nusselt number increases along the surface of cylinder and with the increase of Pr. This is because of fact that by increasing the value of Pr thermal boundary layer decreases and heat transfer rate enhances. This finding also testify the results shown in Fig. 8.
|
|
|
Figure 2. Effects on velocity profile due to different values of at . |
|
|
|
Figure 3. Effects on temperature profile due to different values of while and . |
|
|
|
Figure 4. Variations in Skin-friction coefficient for different values of against . |
|
|
|
Figure 5. Variations in Nusselt number for different values of against while . |
|
|
|
Figure 6. Velocity profile for different values of at . |
|
|
|
Figure 7. Temperature profile for different values of at and . |
|
|
|
Figure 8. Temperature profile for different value of at . |
|
|
|
Figure 9. Variation in Nusselt number for different values of against . |
5. Entropy generation analysis
Using the boundary layer approximation, the local volumetric rate of entropy generation EG for a Newtonian fluid over a hyperbolic stretching cylinder is defined as follows:
|
|
(17) |
After using results of Eq. (5) and Eq. (6) in Eq. (17), following form is obtained
|
|
(18) |
Above equation can be written as
|
|
(19) |
where is the entropy generation number which is the ratio of local volumetric rate of entropy generation and characteristic entropy generation rate , is the Reynolds number, is the Brinkman number, and is the dimensionless temperature difference and the ratio is group parameter. The Bejan number Be serves as a substitute of entropy generation parameter and it represents the ratio between the entropy generation due to heat transfer and the total entropy generation due to heat transfer and fluid friction. It is defined by
|
|
(20) |
Here
|
|
(21) |
|
|
(22) |
Bejan number Be can also be written as , where is called irreversibility ratio.
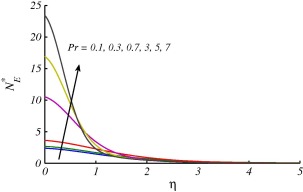
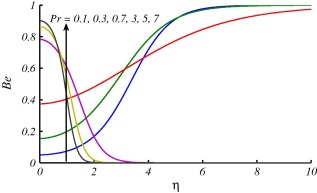
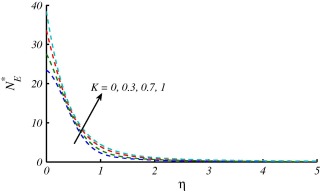
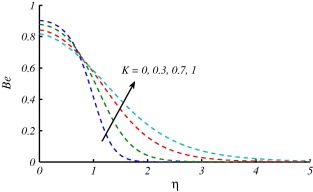
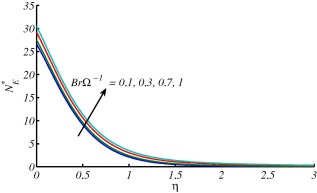
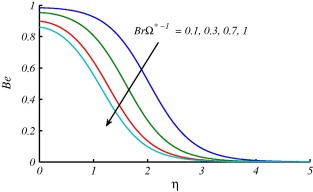
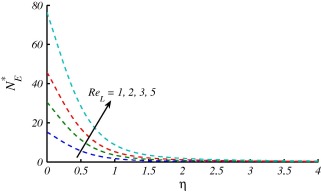
Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16 are drawn to discuss the influence of Prandtl number , curvature parameter , group parameter and Reynolds number on entropy generation number and Bejan number . In Figure 10 and Figure 11, the overall effect of Prandtl number is the enhancement in and . This is because the temperature gradient increases with the larger values of . It is also noted that when a small variation in values of at surface of the cylinder is observed and it increases for larger and attains maximum value i.e., . On the other hand when , large values of at surface of the cylinder are reported. These effects start decreasing and far away from the surface. Figure 12 and Figure 13 are plotted to see the effects of on and . Both figures depict that entropy generation is more dominant for stretching cylinder case in comparison with flat plat case . In Fig. 13, decrease at the surface stretching cylinder () and reverse behavior is observed far away from the surface. The variations of group parameter on and are depicted in Figure 14 and Figure 15. The enhancement in results in augmentation of and these effects are opposite on . The values of are decreasing with increase in because the fluid friction dominates when increases and this results in decrement of . The effects of on entropy generation number are expressed in Fig. 16. This figure reveals that the entropy generation number has gained an increasing trend with increase in .
|
|
|
Figure 10. Effects of on when at . |
|
|
|
Figure 11. Effects of on when at . |
|
|
|
Figure 12. Effects of on when at . |
|
|
|
Figure 13. Effects of on when at . |
|
|
|
Figure 14. Effects of on when at . |
|
|
|
Figure 15. Effects of on when at . |
|
|
|
Figure 16. Effects of on when at . |
6. Concluding remarks
A study is performed to investigate the flow and heat transfer characteristics over a nonlinear stretching cylinder. The nonlinear stretching velocity is considered as hyperbolic function. An analysis of entropy generation is also presented and results are computed numerically with Keller box method. From above study it is observed that:
- Increase in the values of curvature parameter leads to increase in velocity and temperature distribution.
- skin-friction coefficient reduces and Nusselt number enhances with an increase in curvature parameter .
- The temperature reduces and Nusselt number enhances by increasing Prandtl number .
- Increasing trend of curvature parameter, Prandtl number and group parameter results in enhancement of entropy generation.
Acknowledgment
The authors are grateful to reviewers for their constructive guideline which definitely improve this version of manuscript.
References
- [1] C.Y. Wang; Fluid flow due to a stretching cylinder; Phys. Fluids, 31 (1988), pp. 466–468
- [2] L.J. Crane; Flow past a stretching plate; Z Angew. Math. Phys., 21 (1970), pp. 645–647
- [3] A. Ishak, R. Nazar; Laminar boundary layer flow along a stretching cylinder; Eur. J. Sci. Res., 36 (2009), pp. 22–29
- [4] A. Ishak, R. Nazar, I. Pop; Uniform suction/blowing effect on flow and heat transfer due to a stretching cylinder; Appl. Math. Model., 32 (2008) 2059-6
- [5] A. Ishak, R. Nazar, I. Pop; Magnetohydrodynamic (MHD) flow and heat transfer due to a stretching cylinder; Energy Convers. Manage., 49 (2008), pp. 3265–3269
- [6] S. Mukhopadhyay; Chemically reactive solute transfer in a boundary layer slip flow along a stretching cylinder; Int. J. Chem. Sci. Eng., 5 (2011), pp. 385–391
- [7] S. Mukhopadhyay; Mixed convection boundary layer flow along a stretching cylinder in porous medium; J. Petrol. Sci. Eng., 96 (2012), pp. 73–78
- [8] S. Mukhopadhyay, R.S.R. Golra; Slip effects on boundary layer flow and heat transfer along a stretching cylinder; Int. J. Appl. Mech. Eng., 2 (2013), pp. 447–459
- [9] S. Mukhopadhyay; MHD boundary layer slip flow along a stretching cylinder; Ain Shams. Eng. J., 4 (2013), pp. 317–324
- [10] E.M.A. Elbashbeshy; Effect of magnetic field on flow and heat transfer over a stretching horizontal cylinder in the presence of a heat source/sink with suction/injection; J. Appl. Mech. Eng., 1 (2012), p. 1000106
- [11] T. Fang, S. Yao; Viscous swirling flow over a stretching cylinder; Chin. Phys. Lett., 28 (2011), p. 114702
- [12] K. Vajravelu, K.V. Prasad, S.R. Santhi; Axisymmetric magneto-hydrodynamic (MHD) flow and heat transfer at a non-isothermal stretching cylinder; Appl. Math. Comput., 21 (2012), pp. 3993–4005
- [13] S. Munawar, A. Mehmood, A. Ali; Unsteady flow of viscous fluid over the vacillate stretching cylinder; Int. J. Num. Meth. Fluids, 70 (2012), pp. 671–681
- [14] S. Munawar, A. Mehmood, A. Ali; Time-dependent flow and heat transfer over a stretching cylinder; Chin. J. Phys., 50 (2012), pp. 828–848
- [15] C.Y. Wang; Natural convection on a vertical stretching cylinder; Commun. Nonlinear Sci. Num. Simul., 17 (2012), pp. 1098–1103
- [16] Y.Y. Lok, J.H. Merkin, I. Pop; Mixed convection flow near the axisymmetric stagnation point on a stretching or shrinking cylinder; Int. J. Therm. Sci., 59 (2012), pp. 186–194
- [17] Z. Abbas, A. Majeed, T. Javed; Thermal radiation effects on MHD flow over stretching cylinder; Heat Transf. Res., 44 (2013), pp. 703–718
- [18] A.S. Butt, A. Ali; Entropy analysis of magnetohydrodynamics flow and heat transfer due to a stretching cylinder; J. Taiwan Inst. Chem. Eng., 45 (2014), pp. 780–786
- [19] A. Majeed, T. Javed, A. Ghaffari, M.M. Rashidi; Analysis of heat transfer due to stretching cylinder with partial slip and prescribed heat flux: a Chebyshev Spectral Newton Iterative Scheme; Alexandria Eng. J., 54 (2015), pp. 1029–1036
- [20] M. Sheikholeslami; Effect of uniform suction on nanofluid flow and heat transfer over a cylinder; J. Brazil. Soc. Mech. Sci. Eng., 37 (2015), pp. 1623–1633
- [21] T. Javed, A. Majeed, Irfan Mustafa; MHD effects on natural convection laminar flow from a horizontal circular cylinder in presence of radiation; Revista Mexicana de Fısica, 61 (2015), pp. 450–457
- [22] M.R. Hajmohammadi, H. Maleki, G. Lorenzini, S.S. Nourazar; Effects of Cu and Ag nano-particles on flow and heat transfer from permeable surfaces; Adv. Powder Technol., 26 (2015), pp. 193–199
- [23] R. Dhanai, P. Rana, L. Kumar; MHD mixed convection nanofluid flow and heat transfer over an inclined cylinder due to velocity and thermal slip effects: buongiorno’s model; Powder Technol., 288 (2016), pp. 140–150
- [24] T.H. Ko, K. Ting; Optimal Reynolds number for the fully developed laminar forced convection in a helical coiled tube; Energy, 31 (2006), pp. 2142–2152
- [25] M.R. Hajmohammadi, G. Lorenzini, O.J. Shariatzadeh, C. Biserni; Evolution in the design of V-shaped highly conductive pathways embedded in a heat-generating piece; J. Heat Transf., 137 (6) (2015), pp. 061001–061007
- [26] G. Xie, Y. Song, M. Asadi, G. Lorenzini; Optimization of pin-fins for a heat exchanger by entropy generation minimization and constructal law; J. Heat Transf., 137 (2015), pp. 061901–61903
- [27] A. Pouzesh, M.R. Hajmohammadi, S. Poozeshi; Investigations on the internal shape of constructal cavities intruding a heat generating body; Therm. Sci., 19 (2015), pp. 609–618
- [28] Giulio. Lorenzini, Simone. Moretti; Bejan’s constructal theory and overall performance assessment: the global optimization for heat exchanging finned modules; Therm. Sci., 18 (2014), pp. 339–348
- [29] M.R. Hajmohammadi, A. Campo, S.S. Nourazar, A. Masood Ostad; Improvement of forced convection cooling due to the attachment of heat sources to a conducting thick plate; J. Heat Transf. Trans. ASME, 135 (2013), p. 124504
- [30] H. Najafi, B. Najafi, P. Hoseinpoori; Energy and cost optimization of a plate and fin heat exchanger using genetic algorithm; Appl. Therm. Eng., 31 (2011), pp. 1839–1847
- [31] D.A.S. Rees, I. Pop; Boundary layer flow and heat transfer on a continuous moving wavy surface; Acta Mech., 112 (1995), pp. 149–158
- [32] T. Cebeci, P. Bradshaw; Physical and Computational Aspects of Convective Heat Transfer; Springer, New York (1984)
Document information
Published on 12/04/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?