Una alternativa numérica en la solución de un sistema que modela la producción de biogás

Abstract

We study a simplified model of the Anaerobic Digestion Model Number One (ADM1) that represents Anaerobic Digestion for the biogas production and wastewater treatment. This system is modeled by systems of nonlinear differential equations. First, we implemented the Dimensional Analysis to obtain an equivalent model with non-dimensional variables and parameters. Then, numerical solutions are solved both the initial model and the non-dimensional model, and we comparative graph between their corresponding numerical solutions. where we see the advantages of working with the non-dimensional model with respect to the original model.

Keywords. Anaerobic digestion, biogas, dimensional analysis, Pi-Buckingham theorem.

1 Introducción

Iniciamos recordando que dentro del objetivo de crear una plataforma común y facilitar la simulación de una gran variedad de procesos anaerobios, la Asociación Internacional del agua IWA (2002) publicó el Modelo para Digestión Anaerobia No. 1 (ADM1) con el cual pretende proporcionar una base unificada para la modelización de la digestión anaerobia. De este modelo se derivan otros modelos como los de lodos activados (ASM1, ASM2, ASM2d, ASM3), entre otros [8].

En la literatura se encuentra como aplicación de la digestión anaerobia el tratamiento de aguas industriales [3], aguas residuales [11],[14] y en la biodegradación de aguas en el despulpado del café [10],[19], caña de azúcar [13] entre otras. De igual forma se han hecho estudios sobre su modelacion [16],[20],[21],[22] y de análisis de bifurcación y estabilidad [2],[9] y de estrategias de optimización apropiadas [18].

La digestión anaerobia es un proceso muy complejo debido a las reacciones bioquímicas que en ella ocurren y por la cantidad y variedad de bacterias involucradas, las cuales difieren en cuanto a su velocidad de crecimiento y a la sensibilidad a cada producto intermedio como los inhibidores (hidrógeno, ácido acético o amoniaco producido en la acidogénesis de aminoácidos). El proceso de digestión anaerobia está dividido en cuatro etapas subsiguientes: hidrólisis, acidogénesis, acetogénesis y metanogénesis, en las cuales se debe vigilar el equilibrio del proceso para evitar la acumulación de compuestos intermedios inhibidores que generan unos bajos niveles de pH y a la vez impiden la producción óptima de biogás [5],[6], otra de las aplicaciones directas de la digestión anaerobia.

El biogás es una mezcla de gases, considerado una fuente de energía renovable que se obtiene como resultado de la fermentación de materia orgánica con altas concentraciones de humedad, como lo son los desechos de animales, residuos vegetales, basuras domésticas, aguas residuales industriales o domésticas, entre otros; en condiciones anaeróbicas mediante la digestión de un grupo de bacterias, que puede suceder en condiciones naturales o en dispositivos específicos como los reactores. La composición del biogás depende principalmente del material utilizado en la digestión anaerobia y las condiciones en las que se realiza el proceso, sin embargo, está constituido aproximadamente por Metano entre 50% y 70%, Dióxido de Carbono entre 30% y 50% y un porcentaje menor al 5% de otros gases considerados impurezas (hidrógeno, nitrógeno, oxígeno, sulfuro de hidrógeno o ácido sulfhídrico). De este proceso también se obtiene una solución acuosa o lodo en donde se encuentran los microorganismos que se encargan de la degradación de la materia orgánica [13].

Luego de la publicación del modelo ADM1 el doctor Olivier Bernard del INRIA de Francia, junto con otros investigadores, publica un artículo en donde plantea un modelo matemático macroscópico simplificado que representa la dinámica del tratamiento de aguas residuales por medio de dos de las reacciones de la digestión anaerobia: la acidogénesis y la metanogénesis; y que además conserva parámetros cinéticos e incorpora equilibrios electroquímicos para poder incluir la alcalinidad, propiedad que desempeña un papel muy importante en relación con el monitoreo y estrategias de control de la planta. De igual manera propone un método de identificación de parámetros para la digestión anaerobia; a este modelo de denominó AMOCO [3].

De todos estos modelos simplificados del ADM1 que existen, consideramos el AMOCO debido a que, ha sido uno de los modelos más completos en la inclusión de parámetros cinéticos, después de ADM1.

Este modelo tiene las siguientes características:

• Es un modelo dinámico sobre el desarrollo y la identificación de los parámetros del proceso de digestión anaerobia.
• El balance de masas se ha considerado a dos pasos, acidogénesis y metanogénesis.
• El modelo incorpora los equilibrios electroquímicos a fin de incluir la alcalinidad.
• El modelo trabaja con la medida de demanda química de oxígeno (DQO), la cual determina la cantidad de oxígeno requerido para oxidar la materia orgánica en una muestra de agua residual.

Entre los factores ambientales que afectan el proceso de digestión anaerobia se encuentra el pH y el control de éste, en los sistemas anaerobios, es de vital importancia para el desarrollo del proceso, debido a la gran suceptibilidad de los microorganismos, especialmente las metanobacterias, frente a las especies ácidas. El equilibrio ácido-base que tiene lugar en la operación de los digestores anaerobios es muy importante por la presencia de diversas especies de esta naturaleza que están en el medio y que requieren ser neutralizadas para restituir el ${\textstyle pH}$ del medio, por lo que junto con este parámetro debe considerarse a la alcalinidad que es la forma de control del ${\textstyle pH}$ dice [6]. Por tanto, se considera la alcalinidad ${\textstyle A}$ como variable en el modelo.

Como se menciona en [7], para la estabilidad del pH es importante el equilibrio ${\textstyle CO_{2}}$-bicarbonato. Dado que el total de carbono inorgánico es la suma de las especies de carbono inorgánico en una solución, esto es, dioxido de carbono (${\textstyle {CO}_{2}}$), acido carbónico, bicarbonato y carbonato.

El total de Carbono inorgánico total es un parámetro que se utiliza para valorar la calidad de las aguas de un determinado lugar y debido a que éste se mide con la acidificación de una muestra de agua, lo que lleva a un equilibrio del ${\textstyle {CO}_{2}}$, entonces otra de las variables en el modelo será el total de carbono inorgánico ${\textstyle C}$.

1.1 El modelo

Un esquema en el que podemos observar la reacciones en el proceso es:

  $S_{1}$  ${\textstyle {\stackrel {r_{1}}{\longrightarrow }}}$   $S_{2}$ + ${CO}_{2}$

  $S_{2}$  ${\textstyle {\stackrel {r_{2}}{\longrightarrow }}}$   ${CH}_{4}+{CO}_{2}$

donde:

• ${\textstyle r_{1}=\mu _{1}(S_{1})X_{1}}$ es la tasa de reacción en la acetogénesis con tasa de crecimiento bacterial ${\textstyle \mu _{1}(S_{1})}$
• ${\textstyle r_{2}=\mu _{2}(S_{2})X_{2}}$ es la tasa de reacción en la metanogénesis con tasa de crecimiento bacterial ${\textstyle \mu _{2}(S_{2})}$.

Las variables en nuestra dinámica son:

$S_{1}:={\hbox{ Cantidad de sustrato organico}}[g/l]$ $X_{1}:={\hbox{ Cantidad de biomasa acetogenica}}[g/l]$ $S_{2}:={\hbox{ Cantidad de sustrato acetogenico}}[g/l]$ $X_{2}:={\hbox{ Cantidad de biomasa metanogenica}}[g/l]$ $A:={\hbox{ Cantidad de alcalinidad}}[mmol/l]$ $C:={\hbox{ Cantidad total de carbono inorganico ( }}CO_{2}{\hbox{)}}[mmol/l]$

y los parámetros son:

$\mu _{1_{max}}:={\hbox{ Velocidad especifica de crecimiento maximo, asociada a }}S_{1}$ $K_{S_{1}}:={\hbox{ Constante de saturacion media, asociada a }}S_{1}$ $\mu _{2_{max}}:={\hbox{ Velocidad especifica de crecimiento maximo, asociada a }}S_{2}$ $K_{S_{2}}:={\hbox{ Constante de saturacion media, asociada a }}S_{2}$ $K_{I2}:={\hbox{ Constante de inhibicion, asociada a }}S_{2}$ $k_{1}:={\hbox{ Coeficiente cinetico asociado al sustrato }}S_{1}$ $k_{2}:={\hbox{ Coeficiente cinetico asociado al sustrato }}S_{2}$ $k_{3}:={\hbox{ Coeficiente cinetico asociado al consumo de sustrato }}S_{2}$ $k_{4}:={\hbox{ Coeficiente cinetico asociado a la produccion de }}CO_{2}{\hbox{ por }}X_{1}$ $k_{5}:={\hbox{ Coeficiente cinetico asociado a la produccion de }}CO_{2}{\hbox{ por }}X_{2}$ $K_{L_{a}}:={\hbox{ Es el coeficiente volumetrico de transferencia de oxigeno}}$ $K_{H}:={\hbox{ Constante de Henry}}$ $P_{C}:={\hbox{ Presion parcial del gas }}C$

La modelo representa sólo dos pasos de la digestión anaerobia: acidogénesis y metanogénesis; el cual está dado por los siguientes balances ( ver [3] )

${\frac {dX_{1}}{dt}}=\left(\mu _{1_{max}}{\frac {S_{1}}{S_{1}+K_{S_{1}}}}-\alpha D\right)X_{1}\triangleq F_{1}$ (1.a) ${\frac {dS_{1}}{dt}}=D\left(S_{1in}-S_{1}\right)-k_{1}\mu _{1_{max}}{\frac {S_{1}}{S_{1}+K_{S_{1}}}}X_{1}\triangleq F_{2}$ (1.b) ${\frac {dX_{2}}{dt}}=\left(\mu _{2_{max}}{\frac {S_{2}}{{\frac {S_{2}^{2}}{K_{I2}}}+S_{2}+K_{S_{2}}}}-\alpha D\right)X_{2}\triangleq F_{3}$ (1.c) ${\frac {dS_{2}}{dt}}=D\left(S_{2in}-S_{2}\right)+k_{2}\left({\frac {\mu _{1_{max}}S_{1}}{S_{1}+K_{S_{1}}}}\right)X_{1}-k_{3}\left({\frac {\mu _{2_{max}}S_{2}}{{\frac {S_{2}^{2}}{K_{I2}}}+S_{2}+K_{S_{2}}}}\right)X_{2}\triangleq F_{4}$ (1.d) ${\frac {dA}{dt}}=D\left(A_{in}-A\right)\triangleq F_{5}$ (1.e) ${\frac {dC}{dt}}=D\left(C_{in}-C\right)+\left({\frac {k_{4}\mu _{1_{max}}S_{1}X_{1}}{S_{1}+K_{S_{1}}}}\right)$ $\;\;+\;\left({\frac {k_{5}\mu _{2_{max}}S_{2}X_{2}}{{\frac {S_{2}^{2}}{K_{I2}}}+S_{2}+K_{S_{2}}}}\right)-K_{L_{a}}[C+S_{2}-A-K_{H}P_{C}]\triangleq F_{6}$ (1.f)

con condiciones iniciales

$X_{1}(0)\;\;=\;\;c_{1},$ (1.g) $S_{1}(0)\;\;=\;\;c_{2},$ (1.h) $X_{2}(0)\;\;=\;\;c_{3},$ (1.i) $S_{2}(0)\;\;=\;\;c_{4},$ (1.j) $A(0)\;\;=\;\;c_{5},$ (1.k) $C(0)\;\;=\;\;c_{6},$ (1.l)

donde ${\textstyle t\in [0,T]=\Omega ,}$ con ${\textstyle T>0}$ y las partes derechas de las ecuaciones (${\textstyle F_{i};i=1,...6,}$) son funciones clase ${\textstyle C^{0}(\Omega )}$, es decir funciones contínuas en ${\textstyle \Omega }$. Con ${\textstyle \mu _{1max}>0}$, ${\textstyle \mu _{2max}>0}$, ${\textstyle K_{S_{1}}>0}$, ${\textstyle K_{S_{2}}>0}$, ${\textstyle K_{I2}>0}$, ${\textstyle A_{in}>0}$, ${\textstyle C_{in}>0}$, ${\textstyle K_{L_{a}}>0}$, ${\textstyle S_{1in}>0}$, ${\textstyle S_{2in}>0}$, y ${\textstyle k_{i}>0}$, ${\textstyle i=1,2,3,4,5.}$ constantes positivas. El parámetro ${\textstyle \alpha }$ (${\textstyle 0\leq \alpha \leq 1}$) refleja la heterogeneidad de este proceso: ${\textstyle \alpha =0}$ corresponde a un reactor ideal de lecho fijo, mientras que ${\textstyle \alpha =1}$ corresponde a un reactor ideal de tanque agitado continuamente(CSTR) [3].

La expresión ${\textstyle K_{L}a(C-K_{H}P_{C})}$ describe la tasa de flujo molar del carbono inorgánico desde su fase líquida hasta su fase gaseosa y el producto ${\textstyle K_{H}P_{C}=B>0}$ determina la concentración de oxígeno disuelto en ${\textstyle C}$.

Éste, es un sistema de ecuaciones diferenciales ordinarias no lineales de primer orden y autónomo. Dadas estas características se tiene que toda solución de una ecuación diferencial autónoma o es constante o estrictamente creciente o estrictamente decreciente en todo su intervalo de definición. Otra característica importante es que este tipo de sistemas no posee soluciones oscilatorias.

El sistema 1.1, se ha descompuesto en subsistemas de los cuales el primero conformado por las variables ${\textstyle (X_{1},S_{1})}$ tiene soluciones analíticas semitriviales presentadas en [15]. Para calcular soluciones analíticas no triviales se encuentra una relación directa entre la variable ${\textstyle S{1}}$ y la ecuación de Abel de primer tipo y aplicando el método propuesto en [17] se logra encontrar soluciones exactas no triviales, para mayores detalles ver [1].

1.2 Sobre el análisis adimensional

Por modelado matemático se entiende como el proceso por el cual se formula un modelo matemático que representa una realidad, donde se incluyen hipótesis, cantidades importantes y variables que intervienen en el fenómeno. Al resolver una ecuación, que represente un modelo, por alg'un método se hacen las simulaciones o aproximaciones pertinentes por medio de alg'un software, cuyos resultados se comparan con datos reales (validar) y de acuerdo a sus diferencias se puede decir si el modelo es predictivo para otras observaciones similares. En general, el objetivo primordial del modelado matemático es darle sentido al mundo tal y como lo observamos [12].

Entonces, como consecuencia de la importancia del modelado es necesario desarrollarlo e interpretarlo por medio de técnicas que permitan esto. Dentro de estas se destacan el análisis dimensional y el reescalamiento. La primera permite comprender la dimensión de las cantidades en las ecuaciones y las implicaciones resultantes de la homogeneidad dimensional y la segunda es una técnica que ayuda a entender la magnitud de los términos que aparecen en el modelo comparando las cantidades con las cantidades de referencia que aparecen naturalmente en el fenómeno físico[12].

Las magnitudes se clasifican según su origen en magnitudes fundamentales y derivadas. Una magnitud fundamental es aquella que se define por sí misma y es independiente de las demás. Estas están elegidas adecuadamente y son las que permiten expresar cualquier magnitud física en términos de ellas. Entre ellas se encuentran las contenidas dentro del Sistema Internacional de Unidades (SI) establecidas en la XI Conferencia General de Pesos y Medidas (1960) a las que más adelante en la XIV Conferencia General sobre Pesas y Magnitudes en 1971, se les agregó la unidad más reciente, el mol que representa la cantidad de sustancia (1971). Fourier en su libro “Théorie analytique de la chaleur” (1822), define que “Es necesario hacer notar que cada magnitud, indeterminada o constante, tiene una dimensión que le es propia, y que los términos de una no podrán ser comparados si no tuviesen los mismos exponentes de dimensiones”, lo que nos remite al principio de homogeneidad que debe tener cualquier ecuación. A diferencia de la anterior, una magnitud derivada es toda aquella que se puede formar a partir de expresiones matemáticas que relacionen magnitud {${\textstyle F_{1},\ldots ,F_{m}}$, (${\textstyle m<n}$) de menor cantidad de elementos que permite derivar todas las magnitudes involucradas en un fenómeno específico. Recordemos las 7 magnitudes fundamentales definidas por el Bureau International des Points et Mesures, estas son: longitud (L), masa (M), tiempo (${\textstyle T}$), intensidad de corriente eléctrica (I), cantidad de sustancia (N), temperatura termodinánica (T) e intensidad luminosa (K).

Magnitudes adimensionales: En general, si

$[X_{j}]=F_{1}^{a_{1j}}F_{2}^{a_{2j}}...F_{m}^{a_{mj}}$

(2)

Con ${\textstyle j=1,\ldots ,n}$. Si ${\textstyle [X_{j}]=1}$. Entonces se dice que ${\textstyle X_{j}}$ es adimensional. Por lo tanto, las magnitudes adimensionales son un conjunto de ${\textstyle n-}$magnitudes variables o constantes, donde cada una está definida por ${\textstyle m-}$magnitudes fundamentales, que generan un nuevo sistema de ecuaciones.

Matriz de dimensión: Dado un conjunto de magnitudes adimensionales ${\textstyle [\mu _{1_{max}},\ldots ,M_{n}]=[M_{j}]_{j=1}^{n}}$ representado por el sistema de magnitudes fundamentales ${\textstyle F_{1},\ldots ,F_{m}}$ con (${\textstyle m<n}$), entonces las magnitudes adimensionales tienen la forma descrita en la ecuación 2. Entonces se denomina matriz de dimensión a la matriz que tiene la forma:

${\mathbf {A} }={\begin{bmatrix}a_{11}&a_{12}&...&a_{1n}\\a_{21}&a_{22}&...&a_{2n}\\\vdots &\ddots &\ddots &\vdots \\a_{m1}&a_{m2}&...&a_{mn}\end{bmatrix}}$

Ley libre de unidades: Se define que, dada una ley ${\textstyle f(q_{1},q_{2},\ldots q_{n})=0}$ se dice libre de unidades si para todo real positivo ${\textstyle \lambda _{1},\ldots ,\lambda _{m}}$ se cumple que: ${\textstyle {\overline {f}}({\overline {q}}_{1},{\overline {q}}_{2},\ldots {\overline {q}}_{n})=0\Longleftrightarrow f(q_{1},q_{2},\ldots q_{n})=0}$, con ${\textstyle {\overline {q}}_{1}=\lambda _{1}^{b_{1}}...\lambda _{m}^{b_{m}}q_{j}}$.

Ahora debemos mencionar lo que se considera la escencia de la adimensionalización y es el conocido Teorema de Pi-Buckingham. Aunque enunciado por primera vez por Aimé Vaschy en su obra “Sur les lois de similitude en physique” (1982), no fue publicado sino hasta 1914 por Edgar Buckingham. El teorema de Pi es conocido como la piedra angular del análisis dimensional, pues este indica que si hay una ley física que da una relación entre cierto n'umero de cantidades físicas dimensionadas, entonces hay una ley equivalente que puede expresarse como una relación entre ciertas cantidades adimensionales independientes que pueden formarse a partir de las variables fundamentales, denotadas como ${\textstyle \pi _{1},\pi _{2},\ldots ,\pi _{n}}$, de dónde se le ha asignado su nombre [12].

Teorema 1: [Pi-Buckingham]

Sea

$f(q_{1},q_{2},\ldots q_{n})=0$

(3)

una ley física libre de unidades que relaciona magnitudes dimensionales ${\textstyle q_{1},q_{2},\ldots q_{n}}$. Y sean ${\textstyle [F_{1},\ldots ,F_{m}]}$ con (${\textstyle m<n}$) magnitudes fundamentales con ${\textstyle [q_{j}]=F_{1}^{a_{1j}}F_{2}^{a_{2j}}...F_{m}^{a_{mj}}}$ con ${\textstyle j=1,\ldots ,n}$ y sea ${\textstyle r}$ el rango de la matriz ${\textstyle \mathbf {A} }$, siendo ${\textstyle \mathbf {A} }$ la matriz de dimensión de ${\textstyle [q_{j}]}$. Entonces existen ${\textstyle n-r}$ magnitudes adimensionales independientes ${\textstyle \pi _{1},\pi _{2},\ldots ,\pi _{n-r}}$, que se pueden formar a partir de ${\textstyle q_{1},q_{2},\ldots q_{n}}$, y además la ecuación ${\textstyle f(\pi _{1},\pi _{2},\ldots ,\pi _{n-r})=0}$, que está expresada sólo en términos de las cantidades adimensionales, es equivalente a la ley física 1. Su prueba se encuentra en [12].

2 Resultados principales

Se toma la ecuación

$f\left(t;S_{1},X_{1},\mu _{1_{max}},K_{S_{1}},D,S_{1in},S_{2},X_{2},\mu _{2_{max}},K_{S_{2}},K_{I2},S_{2in},k_{2},k_{3},A,A_{in},C,C_{in},k_{4},k_{5},K_{L_{a}},B\right)=0$

Para probar que el sistema se puede adimensionalizar tomamos las unidades de cada uno de los parámetros y variables, y comprobamos que estén bien definidos en el sistema. Se revisan las unidades

$S_{1}=g/l\;;\;X_{1}=g/l\;;\;\mu _{1_{max}}={\frac {1}{dia}}\;;\;K_{S_{1}}=g/l\;;\;D={\frac {1}{dia}}\;;\;S_{1in}=g/l\;;\;S_{2}={\frac {m\;mol}{l}}\;;$

$X_{2}=g/l\;;\;\mu _{2_{max}}={\frac {1}{dia}}\;;\;K_{I2}={\frac {m\;mol}{l}}\;;\;K_{S_{2}}={\frac {m\;mol}{l}}\;;\;S_{2in}={\frac {m\;mol}{l}}\;;k_{2}={\frac {m\;mol}{g}}\;;$

$k_{3}={\frac {m\;mol}{g}}\;;\;A={\frac {m\;mol}{l}}\;;\;A_{in}={\frac {m\;mol}{l}}\;;\;C={\frac {m\;mol}{l}}\;;\;C_{in}={\frac {m\;mol}{l}}\;;\;k_{4}={\frac {m\;mol}{g}}$

$k_{5}={\frac {m\;mol}{g}}\;;\;K_{L_{a}}={\frac {1}{dia}}\;;\;B={\frac {m\;mol}{l}}\;;\;t=dia$

Se sustituyen las unidades en el sistema 1.1. De aquí deteminamos las magnitudes fundamentales: ${\textstyle T}$: tiempo, ${\textstyle M}$: masa,  ${\textstyle N}$: cantidad de sustancia  y la magnitud derivada:  ${\textstyle V}$: volúmen que intervienen en el proceso. El paso siguiente es la contrucción de la matriz de dimensiones ${\textstyle \mathbf {A} }$ con ${\textstyle Rank\left(\mathbf {A} \right)=3}$ y se determina que: el total de magnitudes (parámetros y variables) en el modelo son 25, dos de los cuales no tienen dimensiones (${\textstyle \alpha }$ y ${\textstyle k_{1}}$). Entonces se tiene que hay 23 magnitudes dimensionales. Ahora se calcula el número de magnitudes adimensiones que quedarán en el modelo adimensional, esto es ${\textstyle n-Rank\left(\mathbf {A} \right)=23-3=20}$, de donde se tiene que el modelo adimensional es de 20.

Por el Teorema de Pi se tiene que la ecuación

$F\left(\pi _{1},\pi _{2},\pi _{3},\pi _{4},\pi _{5},\pi _{6},\pi _{7},\pi _{8},\pi _{9},\pi _{10},\pi _{11},\pi _{12},\pi _{13},\pi _{14},\pi _{15},\pi _{16},\pi _{17},\pi _{18},\pi _{19},\pi _{20}\right)=0$

es equivalente a la ley

$f\left(t;S_{1},X_{1},\mu _{1_{max}},K_{S_{1}},D,S_{1in},S_{2},X_{2},\mu _{2_{max}},K_{S_{2}},K_{I2},S_{2in},k_{2},k_{3},A,A_{in},C,C_{in},k_{4},k_{5},K_{L_{a}},B\right)=0.$

2.1 Adimensionalización del modelo

Se inicia con el reescalamiento

$\left[\pi _{1}\right]=S_{1in}^{-1}S_{1}\quad ;\quad \left[\pi _{2}\right]=S_{1in}^{-1}X_{1}\quad ;\quad \left[\pi _{3}\right]=t\;\mu _{1_{max}}\quad ;\quad \left[\pi _{4}\right]=S_{1in}^{-1}K_{S_{1}}$ $\left[\pi _{5}\right]=t\;D\quad ;\quad \left[\pi _{6}\right]=S_{2in}^{-1}S_{2}\quad ;\quad \left[\pi _{7}\right]=S_{1in}^{-1}X_{2}\quad ;\quad \left[\pi _{8}\right]=t\;\mu _{2_{max}}$ $\left[\pi _{9}\right]=S_{2in}^{-1}K_{S_{2}}\quad ;\quad \left[\pi _{10}\right]=S_{2in}^{-1}K_{I2}\quad ;\quad \left[\pi _{11}\right]=S_{1in}S_{2in}^{-1}k_{2}\quad ;\quad \left[\pi _{12}\right]=S_{1in}S_{2in}^{-1}k_{3}$ $\left[\pi _{13}\right]=S_{2in}^{-1}A\quad ;\quad \left[\pi _{14}\right]=S_{2in}^{-1}A_{in}\quad ;\quad \left[\pi _{15}\right]=S_{2in}^{-1}C\quad ;\quad \left[\pi _{16}\right]=S_{2in}^{-1}C_{in}$ $\left[\pi _{17}\right]=S_{1in}S_{2in}^{-1}k_{4}\quad ;\quad \left[\pi _{18}\right]=S_{1in}S_{2in}^{-1}k_{5}\quad ;\quad \left[\pi _{19}\right]=t\;K_{L_{a}}\quad ;\quad \left[\pi _{20}\right]=S_{2in}^{-1}B$

luego,

${\overline {t}}=\pi _{5}=t\;D\rightarrow t={\frac {1}{D}}{\overline {t}}\rightarrow {\frac {dt}{d{\overline {t}}}}={\frac {1}{D}}$ ${\overline {S}}_{1}={\pi _{1}}={\frac {S_{1}}{S_{1in}}}\rightarrow S_{1}=S_{1in}{\overline {S}}_{1}$ ${\overline {X}}_{1}={\pi _{2}}={\frac {X_{1}}{S_{1in}}}\rightarrow X_{1}=S_{1in}{\overline {X}}_{1}$ $\vdots \;\;\;\;\;\;\;\;\;\ldots \;\;\;\;\;\;\;\;\;\vdots$

y así sucesivamente con todas las magnitudes, de donde se obtiene el sistema adimensional

${\begin{array}{l}{\frac {d{\overline {X}}_{1}}{d{\overline {t}}}}&=\left({\frac {{\overline {\mu }}_{1_{max}}{\overline {S}}_{1}}{{\overline {S}}_{1}+{\overline {K}}_{S_{1}}}}-\alpha \right){\overline {X}}_{1}\\{\frac {d{\overline {S}}_{1}}{d{\overline {t}}}}&=1-{\overline {S}}_{1}-k_{1}{\frac {{\overline {\mu }}_{1_{max}}{\overline {S}}_{1}}{{\overline {S}}_{1}+{\overline {K}}_{S_{1}}}}{\overline {X}}_{1}\\{\frac {d{\overline {X}}_{2}}{d{\overline {t}}}}&=\left({\frac {{\overline {\mu }}_{2_{max}}{\overline {K}}_{I2}{\overline {S}}_{2}}{{\overline {S}}_{2}^{2}+{\overline {K}}_{I2}\;{\overline {S}}_{2}+{\overline {K}}_{I2}\;{\overline {K}}_{S_{2}}}}-\alpha \right)\\{\frac {d{\overline {S}}_{2}}{d{\overline {t}}}}&=1-{\overline {S}}_{2}+{\overline {k}}_{2}\;{\frac {{\overline {\mu }}_{1_{max}}{\overline {S}}_{1}}{{\overline {S}}_{1}+{\overline {K}}_{S_{1}}}}{\overline {X}}_{1}-{\overline {k}}_{3}{\frac {{\overline {\mu }}_{2_{max}}{\overline {K}}_{I2}{\overline {S}}_{2}}{{\overline {S}}_{2}^{2}+{\overline {K}}_{I2}\;{\overline {S}}_{2}+{\overline {K}}_{I2}\;{\overline {K}}_{S_{2}}}}{\overline {X}}_{2}\\{\frac {d{\overline {A}}}{d{\overline {t}}}}&=\;{\overline {A}}_{in}-{\overline {A}}\\{\frac {d{\overline {C}}}{d{\overline {t}}}}&={\overline {C}}_{in}-{\overline {C}}+{\overline {k}}_{4}\;{\frac {{\overline {\mu }}_{1_{max}}{\overline {S}}_{1}}{{\overline {S}}_{1}+{\overline {K}}_{S_{1}}}}{\overline {X}}_{1}\\&\;\;+\;{\overline {k}}_{5}{\frac {{\overline {\mu }}_{2_{max}}{\overline {K}}_{I2}{\overline {S}}_{2}}{{\overline {S}}_{2}^{2}+{\overline {K}}_{I2}\;{\overline {S}}_{2}+{\overline {K}}_{I2}\;{\overline {K}}_{S_{2}}}}{\overline {X}}_{2}-K_{L_{a}}[C+S_{2}-A-B]\end{array}}$

(4.f)

con condiciones iniciales

${\overline {X}}_{1}(0)\;\;=\;\;{\overline {c}}_{1},$ (5.a) ${\overline {S}}_{1}(0)\;\;=\;\;{\overline {c}}_{2},$ (5.b) ${\overline {X}}_{2}(0)\;\;=\;\;{\overline {c}}_{3},$ (5.c) ${\overline {S}}_{2}(0)\;\;=\;\;{\overline {c}}_{4},$ (5.d) ${\overline {A}}(0)\;\;=\;\;{\overline {c}}_{5},$ (5.e) ${\overline {C}}(0)\;\;=\;\;{\overline {c}}_{6},$ (5.f)

2.2 Aproximaciones numéricas

La solución numérica de una Ecuación Diferencial Ordinara (EDO) se utiliza cuando no es posible obtener una solución analítica mediante integración de la función ${\textstyle f(x,y)}$ y se obtiene mediante algunos métodos como Runge-Kutta, métodos multipaso y los métodos de extrapolación. No sobra mencionar que cuando se halla la solución numérica, no se obtiene una expresión analítica sino un conjunto de valores numéricos.

Los métodos numéricos para resolver EDO se pueden agrupar en dos conjuntos:

• Métodos de un paso: Euler (simple) y Euler modificado, Taylor y Runge-Kutta (R-K).
• Métodos multipaso: Adams-Bashfort y Adams-Moulton.

Para determinar qué método numérico aplicar a un sistema de EDO, lo primero es determinar si dicho sistema es Stiff (rígido) o No.

La concepción de un sistema Stiff aún no tiene una definición como tal en la solución numérica de EDOs. En la literatura se encuentran dos aproximaciones [4]:

• Un sistema de EDOs es Stiff cuando los métodos Backward Differentiation Formulae, normalmente funcionan mejor que los métodos explícitos.
• Un sistema de EDOs es Stiff cuando para algunos métodos se necesita una disminución del tamaño de paso para evitar inestabilidad del sistema.

Una manera practica para identificar(presunción) si un sistema de EDOs es Stiff es apoyarnos en la estabilidad de sus equilibrios, esto es (i) si un equilibrio es estable y todos sus autovalores asociados tienen parte real distinta, se podría asumir que el sistema es Stiff. (ii) Si el equilibrio es inestable o algún par de sus autovalores tienen parte real igual, se prodría asumir que el sistema es No-Stiff.

Dicho esto, para sistemas Stiff se recomienda aplicar métodos implícitos y para los no-Stiff los métodos explícitos ver [4].

Tomando el sistema original 1.1, lo primero es determinar si el sistema es estable, y para ello linealizamos el sistema en uno de los equilibrios más representativos para el proceso (punto de operación). Después de varias pruebas con distintos valores se observa:

1. En todos los casos se presentan uno o dos autovalores con parte real positiva, esto nos dice que el sistema en el equilibrio es inestable.
2. De igual forma en todos los casos se presenta un autovalor con parte real negativa pero de multiplicidad algebraica 3, esto es, que aparece tres veces.

Con estos resultados se puede asumir que el sistema es No-Stiff (no rígido) y por esto se utiliza un Runge-Kutta de orden 2-3 o de orden 4-5. De igual manera después de varias pruebas se obseva que para este modelo AMOCO 1.1 se obtienen mejores salidas con un R-K de 4o orden como se puede ver en la Figura 1 y la Figura 2:

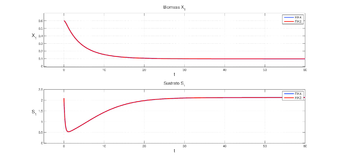
Figure 1: Graficas de $X_{1}$ y $S_{1}$ comparando los RK

Figure 2: Graficas de $X_{2}$, $S_{2}$, $A$ y $C$ comparando los RK

A simple vista parece que no se encontraran mayores diferencias entre los RK2 y RK4. Pero haciendo una ampliación en una de ellas, en particular en la grafica de ${\textstyle C}$, como se muestra en la Figura 3 se puede detallar que el trazo del RK4 en más contíuo que el del RK2.

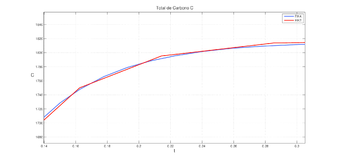
Figure 3: Ampliación de la gráfica de $C$

0.85

Table. 1 Los parámetros para las gráficas fueron tomados de [3].

Parámetro	Valor	Unidades	Desviación estandar
$S_{1}(0)$	2	[g/l]	2.5
$D$	0.395	[d$^{-1}$]	0.135
$S_{1in}$	10	[g/l]	5
$K_{S_{1}}$	7.1	[mmol/l]	5
$S_{2}(0)$	10	[mmol /l]	10
$S_{2in}$	87.5	[mmol /l]	12.5
$K_{I2}$	256	[mmol/l]	320
$K_{S_{2}}$	9.28	[mmol/l]	13.7
$A(0)$	87.5	[mmol/l]	12.5
$A_{in}$	87.5	[mmol/l]	12.5
$C(0)$	87.5	[mmol/l]	12.5
$C_{in}$	9	[mmol/l]	1
$K_{L_{a}}$	19.8	[d$^{-1}$]	3.5
$B$	1777.6	[mmol/l ]

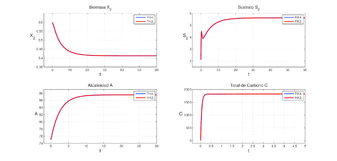
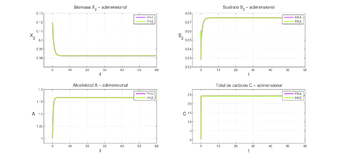
Ahora graficamos las soluciones numéricas del modelo adimensional 2.1

Figure 4: Gráficas de ${\overline {X}}_{1}$ y ${\overline {S}}_{1}$ comparando los RK

Figure 5: Graficas de ${\overline {X}}_{2}$, ${\overline {S}}_{2}$, ${\overline {A}}$ y ${\overline {C}}$ comparando los RK

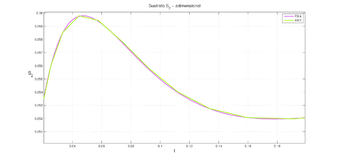
Aquí se presenta una situación similar a la del modelo original y es que en forma aparente no hay mayores diferencias entre los RK2 y RK4. Pero haciendo una ampliación en la gráfica de ${\textstyle {\overline {S}}_{2}}$ (Figura 6) se obserba, también, que el trazo del RK4 en más contíuo que el del RK2.

Figure 6: Ampliación de la gráfica de ${\overline {S}}_{2}$

2.3 Comparación de ambos modelos

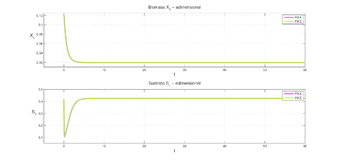
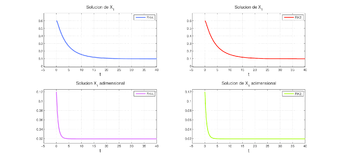
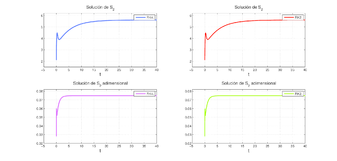
Si observamos las salidas de las graficas del RK4 (o RK2) del modelo inicial y lo comparamos con el RK4 (o RK2) del modelo adimensional, se observa que el modelo adimensional tiende a estabilizarse en menos tiempo que el modelo inicial como se puede ver en las Figuras 7 y 8.

Figure 7: Comparación de las salidas de ambos modelos para $X_{1}$

Figure 8: Comparación de las salidas de ambos modelos para $S_{2}$

Conclusiones

• Comparando las gráficas de los dos sistemas podemos observar que las salidas de las aproximaciones del sistema adimensional se estabilizan en menos tiempo que el sistema original, esto es un resultado relevante en el proceso dado que para este tipo de modelos al llevarlos a escala industrial el ahorro del tiempo minimiza costos y puede optimizar resultados.
• Por lo anterior se puede afirmar que además de reducir parámetros en el modelo AMOCO, la adimensionalización del sistema, permite conservar todas las propiedades, principios y leyes que están presentes en el proceso de Digestión Anaerobia para la producción de biogás.
• Se presentó una metodología práctica para el estudio de sistemas de ecuaciones diferenciales ordinarias no lineales que modela la Digestión Anaerobia y que puede ser extendida a otros bioprocesos representados por este tipo de ecuaciones.

BIBLIOGRAFÍA

[1] P.B. Acosta-Humánez, M. Machado-Higuera and A.V. Sinitsyn, A Model Of Anaerobic Digestion For Biogas Production Using Abel Equations, Far East Journal of Mathematical Sciences (FJMS), 101(6), 1295–1311, (2017). http://dx.doi.org/10.17654/MS101061295.

[2] Abdelhamid Ajbar, Khalid Alhumaizi. (2012). Dynamics of the Chemostat: A Bifurcation Theory Approach; CRC Press Taylor & Francis Group. http://www.crcpress.com/Dynamics-of-the-Chemostat-A-Bifurcation-Theory-Approach/Ajbar-Alhumaizi/p/book/9781138112780.

[3] O. Bernard, Z. Hadj-Sadok, D. Dochain, A. Genovesi and J-P. Steyer, Dynamical model development and parameter identification for an anaerobic wastewater treatment process, Biotechnology and Bioengineering, 75(4), 424–438, (2001). https://www.ncbi.nlm.nih.gov/pubmed/11668442.

[4] C.F. Curtiss and J.O. Hirschfelder, Integration of Stiff equations, Proceedings of the National Academy of Sciences, 38(3), 235–243, (1952). https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1063538/.

[5] María Teresa Varnero Moreno. (2011). Manual de Biogás. Santiago de Chile: FAO; Organización de las Naciones Unidas para la Alimentación y la Agricultura (FAO). http://www.fao.org/family-farming/detail/es/c/342734/.

[6] G.M. Mejía Sánchez. (1996). Digestión anaerobia; Universidad Autónoma de Yucatán (UADY). http://www.libreria.uady.mx/viewlib.php?i=398.

[7] Besel, S. A. (Departamento de Energía). (2007). Biomasa: Digestores anaerobios; Instituto para la Diversificación y Ahorro de la Energía. http://www.idae.es/publicaciones/biomasa-digestores-anaerobios.

[8] D.J. Batstone, J. Keller, I. Angelidaki, S.V. Kalyuzhnyi, S.G. Pavlostathis, A. Rozzi, W.T.M. Sanders, H. Siegrist and V.A. Vavilin, The IWA Anaerobic Digestion Model No.1 (ADM1), Water Science and Technology, 45(10), 65–73, (2002). http://wst.iwaponline.com/content/45/10/65.

[9] B. Benyahia, T. Sari, B. Cherky, J. Harmand, Bifurcation and stability analysis of a two step model for monitoring anaerobic digestion processes, Elsevier Ltd., Journal of Process Control 22(6), 1008–1019, (2012). http://www.sciencedirect.com/science/article/pii/S0959152412000972.

[10] J. Del Real Olvera and J. Islas Gutiérrez, Biodegradación anaerobia de las aguas generadas en el despulpado del café, Revista Colombiana de Biotecnología, 12(2), 230–239, (2010). https://revistas.unal.edu.co/index.php/biotecnologia/article/view/18773.

[11] W.J. Jewell, Anaerobic Sewage Treatment. Part 6, Environmental Science and Technology, 21(1), 14–21, (1987). http://pubs.acs.org/doi/abs/10.1021/es00155a002.

[12] J. David Logan. (2006). Applied Mathematics; Wiley Interscience. https://books.google.com.co/books?id=nUk_AQAAIAAJhl=essource=gbs_book_other_versions.

[13] Y. Lorenzo Acosta y M.C. Obaya Abreu, La Digestión Anaerobia. Aspectos teóricos. Parte I, ICIDCA. Sobre los Derivados de la Caña de Azúcar, XXXIX(1), 35–48, (2005). http://www.redalyc.org/articulo.oa?id=223120659006.

[14] M. Hernández y L. Delgadillo, Aplicación del modelo Adm1 en la digestión anaerobia de aguas residuales y desechos sólidos, Revista Tumbaga, 1(6), 29–42, (2011). http://revistas.ut.edu.co/index.php/tumbaga/article/view/46.

[15] M. Machado-Higuera and A.V. Sinitsyn, Existence of lower and upper solutions in reverse order with respect to a variable in a model of acidogenesis to anaerobic digestion, Bulletin of the South Ural State University. Ser. Mathematical Modelling, Programming & Computer Software, 8(2), 55–68, (2015). https://www.scilit.net/article/00cd41ee5077298166fe0d2ff968ca97.

[16] F. Mariet, O. Bernard, M. Ras, L. Lardon and J. Steyer, Modeling anaerobic digestion of microalgae using ADM1, Bioresource Technology 102(13), 6823–6829, (2011). doi:10.1016/j.biortech.2011.04.015.

[17] E. Salinas, R. Muñoz, J. Sosa, B. López, Analysis to the solutions of Abel's Differential Equations of the first kind under transformation $y=u(x)z(x)+v(x)$, Applied Mathematical Sciences 7(42), 2075–2092, (2013). http://www.m-hikari.com/ams/ams-2013/ams-41-44-2013/index.html.

[18] M. Sbarciog, M. Loccufier and E. Noldus, Determination of appropriate operating strategies for anaerobic digestion systems, Elsevier Ltd., Biochemical Engineering Journal 51(3), 180–188, (2010). https://www.sciencedirect.com/science/article/pii/S1369703X10001865

[19] B. Sialve, N. Bernet and O. Bernard, Anaerobic digestion of microalgae as a necessary step to make microalgal biodiesel sustainable, Biotechnology Advances 27(4), 409–416, (2009). doi:10.1016/j.biotechadv.2009.03.001.

[20] V.M. Trejos, J. Fontalvo y M.A. Gómez, Descripción Matemática y Análisis de Estabilidad de Procesos Fermentativos, Dyna 76(158), 111–121, (2009). https://revistas.unal.edu.co/index.php/dyna/article/view/10251.

[21] A.O. Wagner, C. Malin, P. Lins, G. Gstraunthaler and P. Illmer, Reactor performance of a 750 m$^{3}$ anaerobic digestion plant: Varied substrate input conditions impacting methanogenic community, Anaerobe 29, 29–33, (2014). https://www.sciencedirect.com/science/article/pii/S1075996414000328.

[22] M. Weedermann, G. Seo and G.S. Wolkowicz, Mathematical model of anaerobic digestion in a chemostat: effects of syntrophy and inhibition, Journal of Biological Dynamics 7(1), 59–85, (2013). [ ]http://www.tandfonline.com/doi/abs/10.1080/17513758.2012.755573.