Highlights

  • Ejection fraction has a limited value in predicting mortality and functional capacity.
  • Myocardial mechanics including the relationship between myocardial strain and ejection fraction are currently poorly understood.
  • We showed that there is biophysical relationship between end-diastolic wall thickness, myocardial strain and ejection fraction.
  • Such a relationship explains the poor correlation of ejection fraction with prognosis and functional capacity.
  • The study provides the foundation for determining the relationship between ventricular hypertrophy, ejection fraction and prognosis.
  • words

Abstract

Objectives

The purpose of this study was to determine the mathematical relationship between left ventricular ejection fraction and global myocardial strain. A reduction in myocardial strain would be expected to cause a fall in ejection fraction. However, there is abundant evidence that abnormalities of myocardial strain can occur with a normal ejection fraction. Explanations such as a compensatory increase in radial or circumferential strain are not supported by clinical studies. We set out to determine the biomechanical relationship between ejection fraction, wall thickness and global myocardial strain.

Methods

The study used an established abstract model of left ventricular contraction to examine the effect of global myocardial strain and wall thickness on ejection fraction. Equations for the relationship between ejection fraction, wall thickness and myocardial strain were obtained using curve fitting methods.

Results

The mathematical relationship between ejection fraction, ventricular wall thickness and myocardial strain was derived as follows: φ = e(0.14Ln(ε) + 0.06)ω + (0.9Ln(ε) + 1.2), where φ is ejection fraction (%), ω is wall thickness (cm) and ε is myocardial strain (−%).

Conclusion

The findings of this study explain the coexistence of reduced global myocardial strain and normal ejection fraction seen in clinical observational studies. Our understanding of the pathophysiological processes in heart failure and associated conditions is substantially enhanced. These results provide a much better insight into the biophysical inter-relationship between myocardial strain and ejection fraction. This improved understanding provides an essential foundation for the design and interpretation of future clinical mechanistic and prognostic studies.

Keywords

Ejection fraction;Heart failure;Mathematical modelling;Pathophysiology

1. Introduction

The terms global left ventricular function and ejection fraction are usually used synonymously. Ejection fraction is measured by assessing changes in the lumen of the ventricle. In contrast, myocardial muscle function is evaluated using displacement, velocity or deformation of the wall of the ventricle. These quantities may be measured using mitral annular displacement, tissue Doppler velocities, Doppler or speckle tracking derived myocardial strain and strain rate.

A reduction in myocardial systolic strain might be expected to result in a fall in ejection fraction; however this is often not the case in hypertrophic left ventricular diseases and heart failure with a normal ejection fraction (HFNEF) (Table 1) [1]; [2]; [3]; [4] ;  [5]. Systolic myocardial abnormalities such as long-axis displacement, systolic velocities of basal myocardial and mitral annular motion and strain rate are often observed in HFNEF [4]; [5]; [6]; [7] ;  [8]. Similar abnormalities of myocardial strain occur in patient groups with thick walled ventricles such as hypertension and aortic stenosis (Table 1 ;  Table 2). In addition, abnormalities of global strain occur in hypertrophic cardiomyopathy with the lowest values in the segments with the most hypertrophy [3]. Furthermore, abnormalities of midwall and longitudinal fractional shortening in the presence of a normal ejection fraction have been described in hypertensive hypertrophic left ventricular disease (Table 2) [9]; [10]; [11]; [12]; [13] ;  [14]. Of note, as wall thickness increases in hypertensive left ventricular disease, midwall fractional shortening decreases [15]. Depressed midwall fractional shortening also occurs in cardiac amyloid despite a preserved ejection fraction [16].

Table 1. Left ventricular strain in hypertrophic left ventricular diseases. The table shows either trend or significant reduction in average myocardial strain in various cohorts with an increased left ventricular wall thickness despite a preserved ejection fraction. Note the lower (less negative) longitudinal and circumferential strains and lower (less positive) radial strains despite unchanged ejection fractions. HFREF is shown for comparison.
Cohort Longitudinal strain (%) Circumferential strain (%) Radial strain (%) EF (%) Ref.
Control Patient Control Patient Control Patient Control Patient
cLVH − 22.9 − 17.9** − 23.7 − 20.4** + 74.4 + 62.7** 77 70* [1]
AS − 20.3 − 14.6** − 19.5 − 15.2** + 38.9 + 33.9ns 62 61ns [2]
HBP − 20.3 − 17.2** − 19.5 − 17.0ns + 38.9 + 34.4ns 62 61ns [2]
HCM − 20.3 − 15.1** − 19.6 − 16.8** + 36.8 + 25.2** 67 69ns [3]
HFNEF − 19.0 − 12.0* − 20.0 − 15.0ns + 47.0 + 28.0* 64 63ns [4]
− 20.0 − 14.6* − 27.1 − 22.9* NA NA 61 59ns [5]
− 20.9 − 18.9* NA NA + 49.2 + 41.8* 62 61ns [6]
− 20.9 − 15.9** − 26.4 − 20.8ns + 44.5 + 32.9** 68 61ns [7]
HFREF − 19.0 − 4.0* − 20.0 − 7.0* + 47.0 + 14.0* 64 24* [4]
− 20.9 − 9.6** − 26.4 − 9.5** + 44.3 + 18.0** 68 31* [7]

cLVH, concentric left ventricular hypertrophy. AS, aortic stenosis. HBP, high blood pressure. HCM, hypertrophic cardiomyopathy. HFNEF, heart failure with a preserved ejection fraction. HFREF, heart failure with reduced ejection fraction. EF, ejection fraction. *significant, ns, non-significant. NA, data not available.

Table 2. Left ventricular shortening in hypertension. The table shows reduced midwall fractional shortening in hypertensive hypertrophic left ventricular disease despite a normal (or increased) ejection fraction. Note longitudinal shortening is also decreased.
Cohort Longitudinal fractional shortening (%) Midwall fractional shortening (%) Endocardial fractional shortening (%) EF (%) Ref.
Control Patient Control Patient Control Patient Control Patient
HBP NA NA 21.4 16.7* NA NA 64.2 64.7ns [9]
HBP NA NA 21.0 16.0* 35 35ns 65 66ns [10]
HBP NA NA 19 16* 37 35ns 67 64ns [11]
HBP 21 18* 21 18* 37 42* 63 69* [12]
HBP NA NA 17.6 15.6* 38.2 36.6* NA NA [15]

HBP, high blood pressure. EF, ejection fraction. NA, data not available. *significant, ns, non-significant.

How can the presence of widespread myocardial abnormalities and a normal ejection fraction be reconciled? One viewpoint is that myocardial function (strain) and global function (ejection fraction) are distinct entities. For example, some authorities see the muscular pump and haemodynamic compression pump as intrinsically different [17]. However, the mechanical or physical reasons as to how this might arise are unexplained. Another possibility is that longitudinal strain may be reduced and a compensatory increase in circumferential strain or shortening maintains the ejection fraction. However, observational data (Table 1 ;  Table 2) does not support this viewpoint. The final option is that there is another factor influencing the ejection fraction [8]. Previously, we have shown that increasing left ventricular wall thickness increases the ejection fraction independently of all other variables [18].

Studies have shown the importance of left ventricular ejection fraction in predicting prognosis [19]. For example, following myocardial infarction there is a reciprocal relationship between ejection fraction and mortality [20]; [21] ;  [22]. However, increasing left ventricular wall thickness or concentric hypertrophy is also associated with a higher mortality in the presence of a preserved ejection fraction [23]; [24]; [25]; [26]; [27] ;  [28]. The greater the left ventricular mass the greater the risk [24]. An increase in left ventricular wall thickness may be a consequence of either myocyte hypertrophy, such as that occurs in hypertension and hypertrophic cardiomyopathy or ‘pseudohypertrophy’ as in infiltrative disorders such as cardiac amyloidosis.

These findings indicate that myocardial wall thickness and ejection fraction are independent risk factors for mortality [29]. This observation may explain why heart failure with a reduced ejection fraction has the same mortality as HFNEF when presenting symptoms are similar [30] ;  [31]. These data would also explain why measures of myocardial mechanics such as global longitudinal and circumferential strain are better markers of mortality and morbidity than ejection fraction [32]; [33] ;  [34].

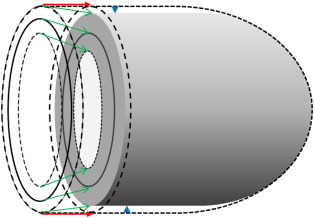
A combination of longitudinal and circumferential shortening of 20% results in a radial wall thickening of approximately 56% [35]. This wall thickening results in an inward displacement of the endocardium (absolute wall thickening) and, when combined with movement of the mitral annulus (and a minor outer contour change), causes a reduction in left ventricular cavity volume generating the stroke volume (Fig. 1). Previous modelling has shown that ejection fraction in normal and thick walled ventricles, is predominantly determined by absolute wall thickening (change in wall thickness) rather than relative wall thickening (radial strain) [36]. Furthermore, absolute wall thickening is determined by both end-diastolic wall thickness and radial strain [36]. The contribution of midwall circumferential shortening has a greater impact on stroke volume and ejection fraction (67%) than longitudinal shortening (33%); importantly these values do not change with increasing concentric hypertrophy [37].


Left ventricular contraction.The figure represents diastole (external dashed ...


Fig. 1.

Left ventricular contraction.

The figure represents diastole (external dashed lines) and systole (shaded figure). Stroke volume is determined from the difference in internal end-diastolic and end-systolic volumes. It is also determined by the change in total external volume assuming the myocardium is incompressible. Therefore, the stroke volume is the sum of the volume of atrioventricular displacement (red arrows) and is disc shaped. In addition, there is a smaller contribution from external epicardial displacement (blue arrow heads) and is approximately cylindrically shaped. Note that midwall fractional shortening is less than endocardial fractional shortening (green arrows) as shown in Table 2.

Adapted from MacIver [37].

Normal tissue perfusion is viewed as a fundamental physiological requirement with potent feedback mechanisms designed to maintain the net stroke volume [38]; [39] ;  [40]. In heart failure syndromes due to myocardial diseases, a reduced myocardial strain is compensated for by concentric or eccentric remodelling which preserves the normal stroke volume [39] ;  [40]. Contrary to a commonly held view, most patients with heart failure have a normal resting stroke volume [8], although an inadequate increase in stroke volume with exertion is commonly observed [39] ;  [40]. Only a minority of individuals, usually with severely reduced ejection fractions and hypotension, have a low stroke volume at rest [41]. This cohort may be related to insufficient time for the compensatory mechanism to fully occur or because of functional limits to these processes.

Biomechanical theoretical studies are used to gain a greater comprehension of physical processes of complex biological systems. Abstract modelling may improve understanding of myocardial mechanics and the relationship between measures of myocardial strain and ejection fraction. Such modelling complements existing investigational in vitro, experimental and observational methods and often has a number of distinct advantages. For example it enables the exclusion of confounding factors e.g., body size, valvular disease, inotropic effects, heart rate, rhythm, filling pressures, blood pressure, ventricular–arterial interaction, reflected waves and peripheral vascular resistance. More importantly, modelling is particularly helpful in studying complex systems where multiple, and often linked, processes are taking place as well as studying the specific effects of certain physiological changes or variables. Specifically, it is not possible to examine the independent or isolated effects of differing strain and wall thickness in either clinical or biological experimental studies.

This study sets out to determine if there is a biophysical relationship between left ventricular wall strain, ejection fraction and wall thickness. To test this hypothesis, we implemented an abstract model of the left ventricle to elucidate the functional connection between left ventricular ejection fraction and myocardial muscle mechanics. Based on simulation data, we derive an equation to describe this relationship. Such an equation allows a deeper understanding of the processes involved in generating the ejection fraction beyond simply a ratio of stroke volume to end-diastolic volume.

2. Methods

A simple computer model of left ventricular contraction was used thus avoiding the complexity and computational costs of finite element modelling and numerical analysis techniques [42]. The endocardium of the left ventricle is represented by the cylindrical-hemispheroidal shape [43]. This shape was chosen as it matches internal and muscle volumes at least as closely as other methods such as the simpler ellipsoidal model [43]; [44] ;  [45]. The modelling assumed that the midwall and epicardium have the same shape in order to more accurately assess muscle volume and mass [45]. The middle layer of the left ventricle is the site of the circumferential fibres with longitudinal fibres present in the sub-endocardial (inner shell) and sub-epicardial (outer shell) layers. Left ventricular end-diastolic length from annulus to the middle of the wall of the apex was presumed to be 9 cm and equivalent to a normal size adult [46] ;  [47]. The apical thickness was assumed to be 50% of the wall thickness of the body of the left ventricle (at the level of the mitral valve tips). The inner, outer and midwall volumes were calculated from the formula V = 5 × A × L / 6, where V = volume, A = area perpendicular to the long-axis at the level of the mitral valve and L = length of long-axis. Short axis area (A) was calculated from width where, A = πR2 and R is radius (Fig. 1). Total midwall volume (intra-ventricular volume plus inner shell volume) was obtained from the short axis area (middle ring in Fig. 1) and length in diastole. Volumes of outer and inner shells were then calculated and the diastolic external and internal ventricular volumes were obtained, followed by the total left ventricular myocardial volume derived from the difference. The variables for midwall short-axis width and longitudinal length were reduced to simulate circumferential and longitudinal shortening respectively and the new midwall volume derived. The myocardium was assumed to be a non-compressible isotropic elastomer [48]. The internal end-systolic volume was calculated by subtracting the total muscle volume from the external end-systolic volume. The midwall circumferential and longitudinal strains were kept the same to mimic observational data as closely as possible (Table 1) [39]. Wall thickness was adjusted from 0.6 cm to 2.8 cm and systolic longitudinal and midwall circumferential per cent shortening (normal engineering strain) was altered from − 20% (normal) to − 4% (severely reduced). The different values for wall thickness and strain were incorporated into the model as input variables and the resulting change in volumes used to calculate the resulting ejection fraction etc. For simplicity, we assumed a homogeneous distribution of wall thickness and myocardial strain.

The modelling assumed an average adult with a normal body mass, body/organ proportions including adiposity and the same tissue flow requirements [40]. Stroke volume remained constant to simulate a fully compensatory state [38] and mimic published data on adaptive remodelling for ejection fractions above 20% [41]. Ejection fraction was calculated by dividing the stroke volume by the end-diastolic volume. The volume of the papillary muscles, muscle bands, trabeculae and non-compacted myocardium were ignored as their anatomic ‘dead space’ does not change during the cardiac cycle and therefore would have no impact on stroke volume. All other factors including external end-diastolic long-axis length were kept constant because of its poor correlation with end-diastolic volume [41]. It was assumed that heart rate and rhythm, body habitus, valvular regurgitation, blood pressure, systemic vascular resistance and all other known physiological variables etc. were identical.

3. Results

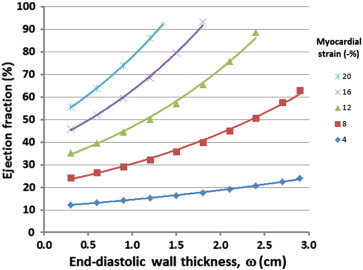
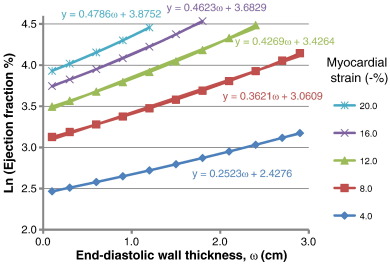
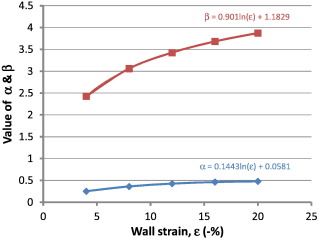
Fig. 2 shows the curvilinear relationship between ejection fraction and end-diastolic wall thickness at various values of myocardial strain. As end-diastolic wall thickness increases, the ejection fraction increases exponentially. Analytic methods were considered too complex and therefore standard curve fitting methods were employed. A number of different curves fitting methods were used including exponential and second order polynomial equations, however log transforming provided the best fit and resulted in the simplest mathematical relationship. Ejection fraction (%) was log transformed and analysed in the form Ln(φ) = αω + β (or φ = eαω + β), where φ = ejection fraction (%), and ω = mean mid end-diastolic wall thickness (cm) (Fig. 3). The values α and β were then derived from the strain curves in Fig. 4 such that α = 0.14Ln(ε) + 0.058 and β = 0.90Ln(ε) + 1.2, where ε is strain (−%).


Effect of myocardial shortening (peak systolic strain) and left ventricular ...


Fig. 2.

Effect of myocardial shortening (peak systolic strain) and left ventricular end-diastolic wall thickness on ejection fraction.

The ejection fraction increases as end-diastolic wall thickness increases. Decreasing (less negative) myocardial strain leads to a fall in ejection fraction.


The figure is showing log transformed data for ejection fraction vs. ...


Fig. 3.

The figure is showing log transformed data for ejection fraction vs. end-diastolic wall thickness.

Using log transformed data shows a linear relationship between ejection fraction and mean midwall thicknesses for various values of myocardial strain.


Values for α and β derived from strain.The α and β strain values are calculated ...


Fig. 4.

Values for α and β derived from strain.

The α and β strain values are calculated from the curves as shown. Where ε = strain (−%), ω = mean mid end-diastolic wall thickness (cm).

The relationship between the ejection fraction (φ, %), wall thickness (ω, cm) and myocardial strain (ε, −%) may be described to 2 significant figures as:

(1)

(2)

Rearranging for strain (ε, −%) gives:

(3)

And for mean wall thickness (ω, cm)

(4)

The ejection fraction calculated from different myocardial strains and end-diastolic wall thicknesses using Eq. (2) are shown in Table 3.

Table 3. Table showing interrelationship between left ventricular ejection fraction (%), wall strain (−%) and mid end-diastolic wall thickness (cm). Increasing (more negative) systolic myocardial strain and increasing wall thickness both result in increasing ejection fraction. Values of ejection fraction above 90% are deemed not possible because of geometric constraints of the left ventricle. Values calculated from Eq. (1) using 3 significant figures.
Strain (−%) Wall thickness (cm)
0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0 2.2 2.4 2.6 2.8 3.0
4 13.3 14.0 14.7 15.5 16.3 17.2 18.1 19.1 20.1 21.1 22.3 23.4 24.7
6 19.8 21.1 22.5 24.0 25.5 27.2 29.0 30.9 32.9 35.1 37.4 39.8 42.4
8 26.3 28.3 30.4 32.7 35.1 37.7 40.5 43.5 46.7 50.2 53.9 57.9 62.2
10 32.8 35.5 38.4 41.5 44.9 48.5 52.5 56.7 76.6 66.3 71.7 77.5 83.8
12 39.3 42.7 46.5 50.5 54.9 59.6 64.8 70.5 76.6 83.2
14 45.8 50.0 54.6 59.6 65.1 71.0 77.5 84.6
16 52.2 57.3 62.8 68.8 75.4 82.6
18 58.7 64.5 71.0 78.0 85.8
20 65.1 71.8 79.2 87.4
22 71.6 79.1 87.5

4. Discussion

This study describes the mathematical relationship between left ventricular ejection fraction, wall thickness and myocardial wall strain using an exponential function. The results provide a deeper understanding compared to simply a ratio of stroke volume to end-diastolic volume by linking the important myocardial variables of strain and wall thickness. In doing so, it also unifies the seeming inconsistency associated with the concept of global versus myocardial measures of myocardial function.

We have shown that ejection fraction is determined by both myocardial strain and end-diastolic wall thickness. As end-diastolic wall thicknesses increases there is an exponential effect on ejection fraction. As the walls become thinner then strain alone is increasingly important and wall stresses rise dramatically [49]. As ejection fraction falls the end-diastolic volume increases in a reciprocal manner resulting in a normalisation of stroke volume [38]. A greater end-diastolic volume may be viewed as a compensatory mechanism that normalises stroke volume and returns tissue perfusion towards normal [39].

The role of diastolic function in heart failure is beyond the scope of this paper but has been discussed elsewhere [8]; [39] ;  [40]. A reduction in strain may be caused either by a failure of contraction (systolic strain) or restriction in relaxation limiting complete sarcomere expansion (diastolic strain). The latter explanation is less likely as many patients with hypertension and HFNEF usually have a relatively normal or increased end-diastolic volume and normal stroke volume [50] ;  [51].

5. Clinical implications

This study explains the apparent paradox of seemingly normal global ‘function’, i.e., preserved ejection fraction, and widespread abnormalities of myocardial strain. A preserved ejection fraction can occur in the presence of a thick walled ventricle even though global myocardial strain is reduced ( Table 3). The presence of abnormal resting strain or an inadequate increase in strain with effort may contribute to symptoms such as breathlessness despite a normal ejection fraction [39]; [40] ;  [52]. If these equations are validated in clinical trials, they may be used to estimate ejection fraction from strain and wall thickness or allow the estimation of average strain values from ejection fraction and wall thickness. The conclusions of this study are of significant clinical relevance. For example, these findings may improve the reliability of assessing likely mortality and morbidity from ejection fraction by allowing for ventricular wall thickness [36]. It may also prevent clinicians from over-relying on ejection fraction alone when determining systolic function. We suggest that the ejection fraction should be ‘corrected’ to allow for any increase in wall thickness [36]. These equations cited here would enable the automation of the calculation of such a corrected ejection fraction (EFc) if strain is known and wall thickness normalised (using Eq. (2)) [36]. Alternatively, global strain may be calculated from the ejection fraction and wall thickness by using Eq. (3) negating the need for measuring strain where imaging is suboptimal.

6. Limitations and future studies

The study was based on abstract modelling with an idealised left ventricular shape in order to mimic findings in clinical practice [36]. The model assumes an average human adult body size and constant resting tissue requirements and therefore cannot be extrapolated to extremes of body size, children or non-human animals. Variables such as heart rate and presence of valvular regurgitation were not modelled in this study but have been elsewhere [39] ;  [53]. The study only assessed myocardial shortening rather than other measures of systolic function such as velocities of contraction. Arguably better measures of contractility, such as force of contraction, systolic wall stress or velocity of contraction with no load, were not assessed; however, this is also a limitation of in vivo studies. Rotational motion and twist of the left ventricle has not been specifically considered. Changes in torsion correlate closely with longitudinal strain [54] and stress-corrected strain and torsion are similarly related to ejection fraction [7]. Modelling torsion and twist was deemed unnecessary as this would not impact on the volume determinations or other outcomes. The presence of dyssynchrony was not modelled; it was assumed that strain was the total shortening between the maximum and minimum end-diastolic volumes. Therefore, this would not reflect regional peak systolic strain in the presence of mechanical dyssynchrony.

Ejection fraction was calculated from the ventricular internal volume, which included the volume of the papillary muscles, trabeculae and muscle bands, as this is the commonest method used in clinical practice. Alternatively, blood pool volumes (as calculated using nuclear techniques and some modern CT scanners) may have been used instead to give slightly higher ejection fractions [55] ;  [56]. With further developments in the abstract modelling it may also be possible to determine similar equations for children and adults at extremes of body size.

This study only models for a single value of wall thickness i.e., the mean wall thickness at the mid-section of the body ventricle (equator). This is similar to the thickness measured at the level of the tips of the mitral valve on M-mode echocardiography. Future biomechanical studies could model heterogeneity in wall thickness and myocardial strains at different segments of the wall and will require finite element analysis and numerical methods [57]; [58] ;  [59]. These more advanced modelling techniques could also be applied to the wall thinning that occurs in ischaemic heart disease with, for example, a subendocardial infarction resulting in a thinned but healthy rim of sub-epicardial muscle. Similar issues would arise with marked wall variation as may occur in hypertrophic cardiomyopathy.

As this study is a theoretical exploration of myocardial mechanics it does not include a clinical cohort. However, it does lay the scientific foundation for better and more precise clinical investigations. Nevertheless, the results do match closely those of previously published studies in terms of the relationship between ejection fraction, end-diastolic volume and myocardial shortening [36]. Future clinical studies with accurate measurements of mean midwall thickness, myocardial strain and ejection fraction in a variety of body sizes will be required to confirm the reliability and reproducibility of the equations. We expect these to require 3D assessment as M-mode echocardiography is unlikely to have the accuracy required.

7. Summary

This is the first study that describes the biophysical relationship between ejection fraction, end-diastolic wall thickness and myocardial strain using a relatively simple equation. It would not be possible to determine such a relationship using clinical observational data. The equation quoted also substantially improves our understanding of left ventricular myocardial mechanics. The ejection fraction, derived only from changes to the ventricular lumen, does not necessarily reflect myocardial muscle or sarcomeric shortening. This study explains the discrepancy in observational data shown in Table 1 ;  Table 2 as well as the mortality described in relation to ejection fraction, concentric hypertrophy and myocardial strain. The results may improve our ability to provide a more accurate prognosis and better assessment of actual systolic function. The biophysical relationship outlined creates a solid theoretical foundation that could be used to improve both the design and interpretation of future clinical studies in both myocardial mechanics and prognosis assessment.

It is important to note that measures of regional or segmental function such as myocardial strain may actually reflect ‘global’ systolic function better than the ejection fraction. Since ejection fraction may not accurately reflect true global systolic function, we suggest use of such a term is misleading. In order to avoid confusion and misinterpretation, we propose the phrase ‘global systolic function’ should be avoided.

Conflict of interest

The authors report no relationships that could be construed as a conflict of interest.

References

  1. [1] Y. Mizuguchi, Y. Oishi, H. Miyoshi, A. Iuchi, N. Nagase, T. Oki; Concentric left ventricular hypertrophy brings deterioration of systolic longitudinal, circumferential, and radial myocardial deformation in hypertensive patients with preserved left ventricular pump function; J Cardiol, 55 (2010), pp. 23–33
  2. [2] V. Delgado, L.F. Tops, R.J. van Bommel, F. van der Kley, N.A. Marsan, R.J. Klautz, et al.; Strain analysis in patients with severe aortic stenosis and preserved left ventricular ejection fraction undergoing surgical valve replacement; Eur Heart J, 30 (2009), pp. 3037–3047
  3. [3] K. Serri, P. Reant, M. Lafitte, M. Berhouet, V. Le Bouffos, R. Roudaut, et al.; Global and regional myocardial function quantification by two-dimensional strain: application in hypertrophic cardiomyopathy; J Am Coll Cardiol, 47 (2006), pp. 1175–1181
  4. [4] J. Wang, D.S. Khoury, Y. Yue, G. Torre-Amione, S.F. Nagueh; Preserved left ventricular twist and circumferential deformation, but depressed longitudinal and radial deformation in patients with diastolic heart failure; Eur Heart J, 29 (2008), pp. 1283–1289
  5. [5] E. Kraigher-Krainer, A.M. Shah, D.K. Gupta, A. Santos, B. Claggett, B. Pieske, et al.; Impaired systolic function by strain imaging in heart failure with preserved ejection fraction; J Am Coll Cardiol, 63 (2014), pp. 447–456
  6. [6] Y.T. Tan, F. Wenzelburger, E. Lee, G. Heatlie, F. Leyva, K. Patel, et al.; The pathophysiology of heart failure with normal ejection fraction: exercise echocardiography reveals complex abnormalities of both systolic and diastolic ventricular function involving torsion, untwist, and longitudinal motion; J Am Coll Cardiol, 54 (2009), pp. 36–46
  7. [7] G.W. Yip, Q. Zhang, J.M. Xie, Y.J. Liang, Y.M. Liu, B. Yan, et al.; Resting global and regional left ventricular contractility in patients with heart failure and normal ejection fraction: insights from speckle-tracking echocardiography; Heart, 97 (2011), pp. 287–294
  8. [8] D.H. MacIver; Current controversies in heart failure with a preserved ejection fraction; Future Cardiol, 6 (2010), pp. 97–111
  9. [9] Y.S. Koh, H.O. Jung, M.W. Park, J.Y. Baek, S.G. Yoon, P.J. Kim, et al.; Comparison of left ventricular hypertrophy, fibrosis and dysfunction according to various disease mechanisms such as hypertension, diabetes mellitus and chronic renal failure; J Cardiovasc Ultrasound, 17 (2009), pp. 127–134
  10. [10] G. Shimizu, Y. Hirota, Y. Kita, K. Kawamura, T. Saito, W.H. Gaasch; Left ventricular midwall mechanics in systemic arterial hypertension. Myocardial function is depressed in pressure-overload hypertrophy; Circulation, 83 (1991), pp. 1676–1684
  11. [11] C.S. Vinch, G.P. Aurigemma, H.U. Simon, J.C. Hill, D.A. Tighe, T.E. Meyer; Analysis of left ventricular systolic function using midwall mechanics in patients > 60 years of age with hypertensive heart disease and heart failure; Am J Cardiol, 96 (2005), pp. 1299–1303
  12. [12] G.P. Aurigemma, K.H. Silver, M.A. Priest, W.H. Gaasch; Geometric changes allow normal ejection fraction despite depressed myocardial shortening in hypertensive left ventricular hypertrophy; J Am Coll Cardiol, 26 (1995), pp. 195–202
  13. [13] G. de Simone, R.B. Devereux, M.J. Roman, A. Ganau, P.S. Saba, M.H. Alderman, et al.; Assessment of left ventricular function by the midwall fractional shortening/end-systolic stress relation in human hypertension; J Am Coll Cardiol, 23 (1994), pp. 1444–1451
  14. [14] A. Ganau, R.B. Devereux, M.J. Roman, G. de Simone, T.G. Pickering, P.S. Saba, et al.; Patterns of left ventricular hypertrophy and geometric remodeling in essential hypertension; J Am Coll Cardiol, 19 (1992), pp. 1550–1558
  15. [15] G. Schillaci, G. Vaudo, L. Pasqualini, G. Reboldi, C. Porcellati, P. Verdecchia; Left ventricular mass and systolic dysfunction in essential hypertension; J Hum Hypertens, 16 (2002), p. 117
  16. [16] S. Perlini, F. Salinaro, F. Musca, R. Mussinelli, M. Boldrini, A. Raimondi, et al.; Prognostic value of depressed midwall systolic function in cardiac light-chain amyloidosis; J Hypertens, 32 (2014) [Published ahead of print]
  17. [17] G.W. De Keulenaer, D.L. Brutsaert; Systolic and diastolic heart failure are overlapping phenotypes within the heart failure spectrum; Circulation, 123 (2011), pp. 1996–2004
  18. [18] D.H. MacIver, M. Townsend; A novel mechanism of heart failure with normal ejection fraction; Heart, 94 (2008), pp. 446–449
  19. [19] R.S. Vasan, M.G. Larson, E.J. Benjamin, J.C. Evans, C.K. Reiss, D. Levy; Congestive heart failure in subjects with normal versus reduced left ventricular ejection fraction prevalence and mortality in a population-based cohort; J Am Coll Cardiol, 33 (1999), pp. 1948–1955
  20. [20] A. Volpi, C. De Vita, M.G. Franzosi, E. Geraci, A.P. Maggioni, F. Mauri, et al.; Determinants of 6-month mortality in survivors of myocardial infarction after thrombolysis. Results of the Gissi-2 data base. The Ad Hoc Working Group of the Gruppo Italiano Per Lo Studio Della Sopravvivenza Nell'infarto Miocardico (Gissi)-2 Data Base; Circulation, 88 (1993), pp. 416–429
  21. [21] J.A. Puma, M.H. Sketch Jr., T.D. Thompson, R.J. Simes, D.C. Morris, H.D. White, et al.; Support for the open-artery hypothesis in survivors of acute myocardial infarction: analysis of 11,228 patients treated with thrombolytic therapy; Am J Cardiol, 83 (1999), pp. 482–487
  22. [22] J.P. Curtis, S.I. Sokol, Y. Wang, S.S. Rathore, D.T. Ko, F. Jadbabaie, et al.; The association of left ventricular ejection fraction, mortality, and cause of death in stable outpatients with heart failure; J Am Coll Cardiol, 42 (2003), pp. 736–742
  23. [23] A. Barbieri, F. Bursi, F. Mantovani, C. Valenti, M. Quaglia, E. Berti, et al.; Left ventricular hypertrophy reclassification and death: application of the recommendation of the American Society of Echocardiography/European Association of Echocardiography; Eur Heart J Cardiovasc Imaging, 13 (2012), pp. 109–117
  24. [24] G. Schillaci, P. Verdecchia, C. Porcellati, O. Cuccurullo, C. Cosco, F. Perticone; Continuous relation between left ventricular mass and cardiovascular risk in essential hypertension; Hypertension, 35 (2000), p. 580
  25. [25] R.B. Devereux, K. Wachtell, E. Gerdts, K. Boman, M.S. Nieminen, V. Papademetriou, et al.; Prognostic significance of left ventricular mass change during treatment of hypertension; JAMA, 292 (2004), pp. 2350–2356
  26. [26] J.K. Ghali, Y. Liao, B. Simmons, A. Castaner, G. Cao, R.S. Cooper; The prognostic role of left ventricular hypertrophy in patients with or without coronary artery disease; Ann Intern Med, 117 (1992), pp. 831–836
  27. [27] M.J. Koren, R.B. Devereux, P.N. Casale, D.D. Savage, J.H. Laragh; Relation of left ventricular mass and geometry to morbidity and mortality in uncomplicated essential hypertension; Ann Intern Med, 114 (1991), p. 345
  28. [28] D. Levy, R.J. Garrison, D.D. Savage, W.B. Kannel, W.P. Castelli; Prognostic implications of echocardiographically determined left ventricular mass in the Framingham Heart Study; N Engl J Med, 322 (1990), pp. 1561–1566
  29. [29] M.A. Quinones, B.H. Greenberg, H.A. Kopelen, C. Koilpillai, M.C. Limacher, D.M. Shindler, et al.; Echocardiographic predictors of clinical outcome in patients with left ventricular dysfunction enrolled in the SOLVD Registry and Trials: significance of left ventricular hypertrophy. Studies of left ventricular dysfunction; J Am Coll Cardiol, 35 (2000), pp. 1237–1244
  30. [30] R.S. Bhatia, J.V. Tu, D.S. Lee, P.C. Austin, J. Fang, A. Haouzi, et al.; Outcome of heart failure with preserved ejection fraction in a population-based study; N Engl J Med, 355 (2006), pp. 260–269
  31. [31] T. Owan, D. Hodge, R. Herges, S. Jacobsen, V. Roger, M. Redfield; Trends in prevalence and outcome of heart failure with preserved ejection fraction; N Engl J Med, 355 (2006), pp. 251–259
  32. [32] T. Stanton, R. Leano, T.H. Marwick; Prediction of all-cause mortality from global longitudinal speckle strain: comparison with ejection fraction and wall motion scoring; Circ Cardiovasc Imaging, 2 (2009), pp. 356–364
  33. [33] G.-Y. Cho, T.H. Marwick, H.-S. Kim, M.-K. Kim, K.-S. Hong, D.-J. Oh; Global 2-dimensional strain as a new prognosticator in patients with heart failure; J Am Coll Cardiol, 54 (2009), pp. 618–624
  34. [34] H.M. Su, T.H. Lin, P.C. Hsu, W.H. Lee, C.Y. Chu, C.S. Lee, et al.; Global left ventricular longitudinal systolic strain as a major predictor of cardiovascular events in patients with atrial fibrillation; Heart, 99 (2013), pp. 1588–1596
  35. [35] D.H. MacIver; Understanding myocardial deformation, ‘global systolic function’ and abnormal geometry; Heart (2009) http://doi.org/10.1136/hrt.2009.172569
  36. [36] D.H. MacIver; A new method for quantification of left ventricular systolic function using a corrected ejection fraction; Eur J Echocardiogr, 12 (2011), pp. 228–234
  37. [37] D.H. MacIver; The relative impact of circumferential and longitudinal shortening on left ventricular ejection fraction and stroke volume; Exp Clin Cardiol, 17 (2012), pp. 5–11
  38. [38] D.H. MacIver; Is remodeling the dominant compensatory mechanism in both chronic heart failure with preserved and reduced left ventricular ejection fraction?; Basic Res Cardiol, 105 (2010), pp. 227–234
  39. [39] D.H. MacIver, M.J. Dayer; An alternative approach to understanding the pathophysiological mechanisms of chronic heart failure; Int J Cardiol, 154 (2012), pp. 102–110
  40. [40] D.H. MacIver, M.J. Dayer, A.J. Harrison; A general theory of acute and chronic heart failure; Int J Cardiol, 165 (2013), pp. 25–34
  41. [41] B. Ky, T. Plappert, J. Kirkpatrick, F.E. Silvestry, V.A. Ferrari, M.G. Keane, et al.; Left ventricular remodeling in human heart failure: quantitative echocardiographic assessment of 1,794 patients; Echocardiography, 29 (2012), pp. 758–765
  42. [42] D.H. MacIver; A mathematical model of left ventricular contraction and its application in heart disease; M. Atherton, M. Collins, M. Dayer (Eds.), Repair and redesign of physiological systems, WIT Press, Boston (2008), pp. 65–86
  43. [43] E.D. Folland, A.F. Parisi, P.F. Moynihan, D.R. Jones, C.L. Feldman, D.E. Tow; Assessment of left ventricular ejection fraction and volumes by real-time, two-dimensional echocardiography. A comparison of cineangiographic and radionuclide techniques; Circulation, 60 (1979), pp. 760–766
  44. [44] H.L. Wyatt, M.K. Heng, S. Meerbaum, P. Gueret, J. Hestenes, E. Dula, et al.; Cross-sectional echocardiography. II. Analysis of mathematic models for quantifying volume of the formalin-fixed left ventricle; Circulation, 61 (1980), pp. 1119–1125
  45. [45] H.L. Wyatt, M.K. Heng, S. Meerbaum, J.D. Hestenes, J.M. Cobo, R.M. Davidson, et al.; Cross-sectional echocardiography. I. Analysis of mathematic models for quantifying mass of the left ventricle in dogs; Circulation, 60 (1979), pp. 1104–1113
  46. [46] K. Emilsson, R. Egerlid, B.M. Nygren, B. Wandt; Mitral annulus motion versus long-axis fractional shortening; Exp Clin Cardiol, 11 (2006), pp. 302–304
  47. [47] K. Emilsson, L. Brudin, B. Wandt; The mode of left ventricular pumping: is there an outer contour change in addition to the atrioventricular plane displacement?; Clin Physiol, 21 (2001), pp. 437–446
  48. [48] Y. Zhu, X. Papademetris, A.J. Sinusas, J.S. Duncan; A coupled deformable model for tracking myocardial borders from real-time echocardiography using an incompressibility constraint; Med Image Anal, 14 (2010), pp. 429–448
  49. [49] D.H. MacIver; a new understanding and definition of non-compaction cardiomyopathy using analysis of left ventricular wall mechanics and stresses; Int J Cardiol, 174 (2014), pp. 819–821
  50. [50] M.S. Maurer, D. Burkhoff, L.P. Fried, J. Gottdiener, D.L. King, D.W. Kitzman; Ventricular structure and function in hypertensive participants with heart failure and a normal ejection fraction: the Cardiovascular Health Study; J Am Coll Cardiol, 49 (2007), pp. 972–981
  51. [51] M.S. Maurer, D.L. King, R.L. El-Khoury, M. Packer, D. Burkhoff; Left heart failure with a normal ejection fraction: identification of different pathophysiologic mechanisms; J Card Fail, 11 (2005), pp. 177–187
  52. [52] H. Casey, A.G. Dastidar, D.H. MacIver; Swimming induced pulmonary oedema in two triathletes: a novel pathophysiological explanation; J R Soc Med (2014) http://doi.org/10.1177/0141076814543214 [in press]
  53. [53] D.H. MacIver; The impact of mitral regurgitation on left ventricular ejection fraction using mathematical modelling; Exp Clin Cardiol, 20 (2014), pp. 4994–5008
  54. [54] F. Carreras, J. Garcia-Barnes, D. Gil, S. Pujadas, C.H. Li, R. Suarez-Arias, et al.; Left ventricular torsion and longitudinal shortening: two fundamental components of myocardial mechanics assessed by tagged cine-MRI in normal subjects; Int J Cardiovasc Imaging (2011), pp. 1–12
  55. [55] B. Sievers, S. Kirchberg, A. Bakan, U. Franken, H.J. Trappe; Impact of papillary muscles in ventricular volume and ejection fraction assessment by cardiovascular magnetic resonance; J Cardiovasc Magn Reson, 6 (2004), pp. 9–16
  56. [56] T.A. Foley, S.V. Mankad, N.S. Anavekar, C.R. Bonnichsen, M.F. Morris, T.D. Miller, et al.; Measuring Left ventricular ejection fraction — techniques and potential pitfalls; Eur Cardiol, 8 (2012), pp. 108–114
  57. [57] I. Adeniran, D.H. MacIver, J.C. Hancox, H. Zhang; Abnormal calcium homeostasis in heart failure with preserved ejection fraction is related to both reduced contractile function and incomplete relaxation: An electromechanically detailed biophysical modelling study; Frontiers Physiology, 6 (78) (2015), pp. 1–14
  58. [58] I. Adeniran, D.H. MacIver, H. Zhang; Myocardial electrophysiological, contractile and metabolic properties of hypertrophic cardiomyopathy: Insights from modelling; Comput Cardiol., 41 (2014), pp. 1037–1040
  59. [59] D.H. MacIver, A.L. Clark; The vital role of the right ventricle in the pathogenesis of acute pulmonary edema; The Am J Cardiol, 115 (7) (2015), pp. 992–1000
Back to Top
GET EPUB

Document information

Published on 19/05/17
Submitted on 19/05/17

Licence: Other

Document Score

0

Views 15
Recommendations 0

Share this document

Keywords

• • •

claim authorship

Are you one of the authors of this document?

I am an author