Abstract
Due to the growing number of emergency accidents occurring around students, evacuation issues have become significantly important for both school officials and architects. Simply following construction codes cannot ensure that a building׳s layout is suitable for evacuation behaviors; therefore, to discover the suitable planning schemes, we have introduced an agent-based simulation model via Netlogo to investigate the interrelationships between evacuation efficiency and classroom layouts. Before conducting modeling experiments, both the simulation structure and the sensitivity to its parameter settings are examined by validation research and sensitivity analysis. Furthermore, to demonstrate the importance of conducting fire drills with students, two different types of behavior rules are designed to reflect the distinctive characteristics of students evacuating without instructions and students evacuating in good order. The general comparison results show us that the classroom layout with two exits shortens students׳ evacuation time, and the premeditated behavior rules, meaning that students who follow preset instructions to arrange their activities, not only escape faster but also have some advantages in ensuring their safety during the evacuation process. Moreover, at the end of this paper, several methods of improving this simulation model are proposed for more complex research in the future.
Keywords
Agent-Based Modeling (ABM) ; Evacuation ; Classroom layout ; Netlogo ; Safety ; Architectural design
1. Introduction
Effectively organizing evacuation routes inside buildings, especially densely populated buildings such as theaters or schools, is always one of the most important aspects architects take into consideration during the design process. However, due to limited knowledge of human׳s behavior, architects usually create these evacuation designs from pure statistics instead of their practical usage. Therefore, as long as the critical statistics of the planning layout meet the demand of the construction codes, the planning scheme will be automatically identified as a qualified design by law. This type of static evaluation method can hardly tell the difference among all of the alternative designs in terms of safety, so it is unable to help us to select the most appropriate planning schemes for the building. Although some researchers would let people actually participate in evacuation tests and compare their results to determine which layouts could best facilitate building evacuation, this method cannot be considered good for evaluating performance. After all, exposing people to real emergency situations can be both time-consuming and dangerous; and applying such a complex research method in a small-scale design project is not very cost effective (Almeida et al ., 2012 ; Camillen et al ., 2009 ).
Therefore, to quickly assess their safety performance, other controllable alternatives should be taken into consideration, among which simulation models are the most commonly used. As previous research shows, the main operational mechanisms in traditional simulation models describe people׳s evacuation behaviors through a set of differential equations, assuming that they are completely homogeneous to reduce the calculation difficulty. One of the obvious drawbacks for this approach is that the idealized environment settings cannot fully reflect the dynamic characteristics of people׳s evacuation behaviors in the real world, which may cause some deviations in the analysis results. Fortunately, with the improving theory of complex system and computer technology, we are able to show these heterogeneous and dynamic characteristics through agent-based modeling (ABM) techniques (Steven and Volker, 2011 ). The basic principle of this research method is to establish a series of behavior rules for the agents based on real world experiences and to let them interact freely with each other and the virtual environment. As a result, unlike traditional models, the evacuating behaviors in this model are mainly driven by the dynamic interactions between agents and their environment, not just some pre-arranged rules.
Our particular interest in this paper is the case of a middle school teaming with young students. Because these juveniles have limited capacities to escape and that the classroom is the most densely populated place in the school, designing an appropriate education space should be the initial task for the architects. Therefore, the main focus of this paper is to use Netlogo, a popular ABM (Agent-Based Modeling) tool, to create simulation models for two different types of classroom layouts and to compare their evacuation performances from various angles. In addition, to demonstrate the importance of fire drills, we design the premeditated behavior rules based on the reaction patterns in the real world after people have received fire drill training, and compare its performances to the non-trained (self-organized) scenario to see whether it can help students escape from the classroom more quickly and more safely.
2. Related works
Integrating evacuation research with ABM techniques requires us to have a detailed understanding of people׳s decision-making mechanisms and transform them into computer programming languages. It is not easy to transform people׳s highly abstract psychological activities into logical relationships that can be recognized by computers. Therefore, many research efforts have been devoted to combining sociology and computer science to set up the simulation models.
According to the research of Craig, (1987) , those collective patterns of motion that we have seen in evacuation processes, such as clogging or arching, are mainly driven by the "social force" and they are closely connected to individualistic and herding behaviors. Similarly, Colin and Tony (2005) have established a crowded evacuation model to investigate the interrelationships between the power of pushing forward and population density (Ansgar and Andreas, 2002 ). Su et al. (2008) used the simulation model as an evaluation tool to assess the performance of different evacuation plans for a hospital in the event of a terrorist attack. Unlike others, Xiaohui et al. (2012) adopted cellular automata theory as their simulation basis and created a new set of evaluation standards, including "escape income" to help agents decide on the most suitable place for evacuation. For convenience, Ganting Xia did not code the model by herself. Instead, she chose to use a well-developed modeling software to set up the simulation research and design a series of comparison experiments to explore the differences between two different types of evacuation behaviors (Tinxia, 2015 ).
Some scholars have already obtained good results on modeling people׳s evacuation processes by combining the ABM techniques with evacuation research. For example, Almeida et al. (2012) used Netlogo to test agent׳s evacuation performances in various scenarios and validate their simulation results through the Van Bogaer and Predetchenky formulae before applying any detailed analysis. Tariq et al. (2010) set up a bomb explosion scenario in Netlogo and changed the location of the rescue area randomly for each run to determine how different components of the layout would affect the final evacuation results. Vani and Sumam(2013) focused their attention on analyzing the impacts of different evacuation behaviors and measuring their efficiency in terms of the evacuation rate. In addition, Camillen et al. (2009) conducted a similar comparison research in his paper to test various evacuation strategies in a museum and demonstrated that due to its ever-changing environment, evacuation behaviors are difficult to predict using traditional simulation methods and that only ABM can successfully capture their dynamic characteristics. In conclusion, traditional equation-based modeling techniques and statistical analysis methods are not qualified for these types of non-stationary scenes; only ABM, where virtual individuals can freely move and interact with each other, could successfully capture these ever-changing characteristics and make accurate evaluations about the evacuation performance.
3. Model construction
3.1. Simulation software
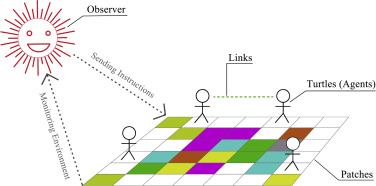
As mentioned above, this simulation research is conducted in Netlogo (Uri, 1999 ), an easy to install and non-programmer friendly ABM software. Because most architects have little knowledge about computer science, it is important for us to find a suitable tool to set up the whole simulation program that is reproducible for these designers. Therefore, we select Netlogo for our simulation research. Basically, four major parts constitute the simulation environment in Netlogo, which include turtles, patches, links and observer. Detailed descriptions about these four components are shown in both Table 1 and Fig. 1 (Bibo, 2005 ; Jin, 2009 ; Uri, 1999 ).
| Item | Functions |
|---|---|
| Turtles | Agents that can move around the simulation world, and are usually used to represent the main research target. |
| Patches | A series of grids that constitute the two-dimensional world, and are mainly used to represent the physical environment of the real world. |
| Links | Special agents that have two ends to connect two different turtles, and can be used to represent both social and physical connections. |
| Observer | The invisible control center that can supervise the activities of agents and give instructions to them during the simulation process. |
|
|
|
Fig. 1. Simulation environment in Netlogo. |
3.2. Environment setup
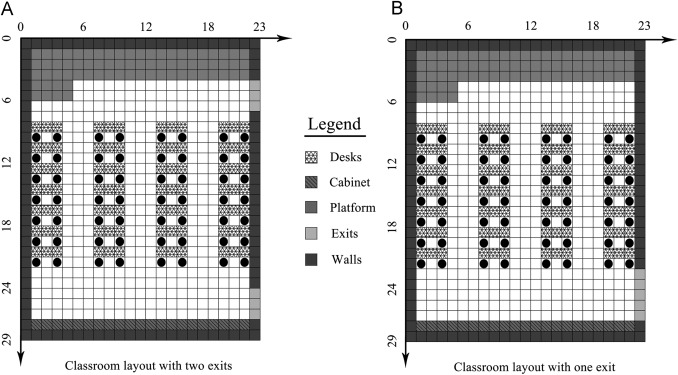
To further resemble the evacuation behaviors in real world, the general classroom layouts suggested by Chinese construction codes are chosen as the main references to set up the simulation scenes. Compared to some other classrooms with special functions, students would spend most of their time in these general types and they are more likely to encounter emergency situations here. Therefore, to make the analysis results more practical, the whole simulation project strictly follows the Chinese construction codes to set up the simulation environment. Two major types of general classroom layouts and their design details are illustrated in Table 2 and Fig. 2 (Shaobo et al., 2009 ).
| Item | Content |
|---|---|
| Requirements in the construction code | Excerpted from "Design Standards for Primary and Middle Schools" (GB 50099-2011). |
| |
| Planning scheme for the simulation environment | Considering that 300 mm is the basic module for Chinese construction projects and that the sizes of most objects can be divided by exactly 300 mm, we select 300 mm as the basic unit length to setup the simulation environment. |
|
|
|
|
Fig. 2. The planning schemes for different classroom types. |
3.3. Behavior rules
According to previous research (Aldis, 2014 ; Camillen et al., 2009 ; Lishen, 2014 ; Rong and Long, 2014 ; Shaobo et al., 2009 ; Yuling et al., 2008 ), when people encounter emergency situations, they first evaluate the surrounding environment, make individual judgments based on their knowledge, and then follow their own decisions to escape from the dangerous place. People׳s evacuation behavior can be basically divided into two parts: decision-making and moving. Therefore, to keep consistent with reality, the student agents in this model will use the same behavior strategies during the simulation process.
3.3.1. Decision-making
To verify the effects of the fire drills, two different types of evacuation scenarios are designed for this research project: a self-organized scene and a premeditated scene. Similar to most people׳s reactions to emergency events, student agents with self-organized behaviors would consider only their own safety and run to any place as long as they can get out of the room quicker. However, after people have received fire drill training from the department, they act more cooperatively and orderly, and they are willing to follow the instructions of signboards or firefighters to escape. As a result, student agents in the premeditated scenarios take fewer factors into consideration and move only within a specific route that has been set up for them in advance.
- Self-organized scene
As described above, in the self-organized scenario, agents act selfishly and independently. They prefer to move to the place with fewer people and closer to the door when they are deciding where to escape. Therefore, the population density and the distance to the nearest exit are considered the main influence factors in students׳ decision-making processes. After the student agents calculate the composite scores for each patch within their moving capabilities, they select the patch with the highest score as their moving target and move forward to it. Specific details about calculation Eqs. (1) , (2) , (3) ; (4) are listed below (Hui et al., 2011 ).
The equation (1) for calculating the population density Pi :
|
|
( 1) |
- “i ” is the ID number of the target patch.
- Ni is the total number of agents that are standing within the searching range.
- R is the searching radius.
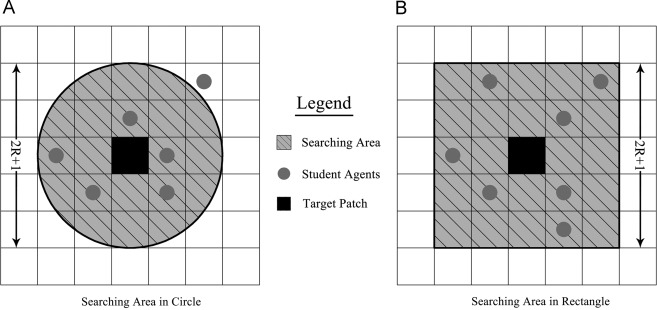
Because the simulation world consists of a series of grids and agents always located at the grid׳s center, some agents would be left out if we used a circle to mark the calculation area, as shown in Fig. 3 . For this reason, we choose the rectangle as an alternative to identify those agents qualified for calculation within its searching areas.
|
|
|
Fig. 3. Illustration of different types of searching areas. |
The equation (2) for calculating the attraction value of population density Fp :
|
|
( 2) |
- Pi is the population density of the target patch.
- Pmax is the maximum population density of all of the patches.
- Pmin is the minimum population density of all of the patches.
Because people in the self-organized scenes prefer to locate to areas with more space to move, population density has a negative effect on agents׳ evaluation processes. Therefore, we choose to use the normalization method of extreme values to recalculate its relative importance among all patches. Through this equation, the denominator, which is the difference between the maximum population density and the minimum population density, will be the same constant for all of the patches during each time-step, and patches with less population will naturally gain more attraction values because they create a more positive difference in the numerator.
The equation (3) for the attraction value of distance Fd :
|
|
( 3) |
- Di is the travel distance from the target patch i to its nearest exit.
- Dmax is the maximum travel distance of all of the patches.
- Dmin is the minimum travel distance of all of the patches.
Similar to the evaluation process of the population density, the travel distance to the nearest exit also has a negative effect on the student agents׳ evacuation behaviors. Therefore, all of the patches will use the same normalization method of population density to calculate its relative importance on travel distance.
The equation (4) for calculating the final attraction values Fi :
|
|
( 4) |
- α is the weight factor for the attraction value of the population density.
- β is the weight factor for the attraction value of the travel distance.
The influence factors of both population density and travel distance play important roles in calculating the overall attraction values, but there are some differences between their relative importance. As a result, we use two weight factors (α and β ) as indicators of different importance levels and multiply them with their corresponding attraction values, then we add the results together for the final composite attraction values.
- Premeditated scene
As discussed previously, people act more regularly after they received fire drill training, and they are willing to follow the premeditated instructions to arrange their evacuation activities. Therefore, student agents in this scenario are designed to act in a not very strict order and they can only move within certain safe areas that are chosen by our experts based on their experiences. Therefore, unlike students in the self-organized scene have to take both density and distance into consideration, agents in this scenario only have to follow the pre-defined routes to move towards their nearest exit, regardless of how many other agents are waiting in line in front of them. Thus, the travel distance becomes the only thing that student agents need to consider when they are making moving decisions. Specific details about how they calculate the attraction values for the target patch can be seen in Eq. (5) (Hui et al., 2011 ).
The equation (5) for calculating the attraction value of target patch Fi :
|
|
( 5) |
- i is the ID number of the target patch
- Di is the travel distance from patch i to its nearest exit.
- Dmax is the maximum travel distance of all of the patches.
- Dmin is the minimum travel distance of all of the patches.
3.3.2. Moving
- Speed limits
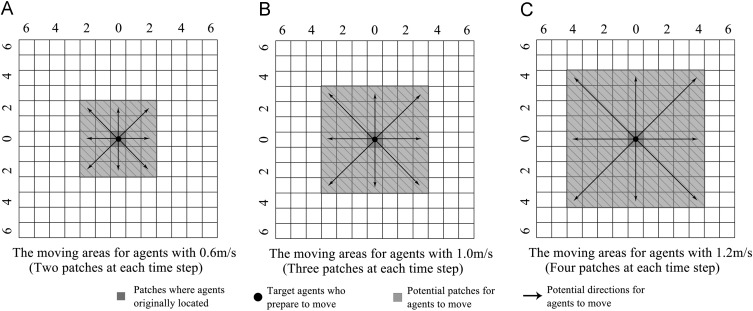
According to previous research on human behavior (Aldis, 2014 ; Camillen et al., 2009 ; Preston et al., 2015 ; Rong and Long, 2014 ; Victor and Jeffrey, 2001 ; Yuling et al., 2008 ), the average speed for evacuation is usually one meter per second (1 m/s). Sometimes, under extreme circumstances, they can reach one and two-tenths of a meter per second (1.2 m/s) or even more. However, those less capable students, especially young girls, will walk slower than average speed, only reaching approximately six-tenths of a meter per second (0.6 m/s) Therefore, to reflect this heterogeneous characteristic in our model and make the simulation results more reliable, student agents are randomly divided into three groups with different evacuation speeds, varying among 0.6 m/s, 1.0 m/s and 1.2 m/s. Considering that the length of each patch represents 0.3 m in the real world, for calculation convenience, we transfer the speed limits into the number of patches that agents can cross at each time step. For example, 0.6 m/s would equal two patches (2×0.3) in a single time step, 1.2 m/s would equal four patches (4×0.3) in a single time step and so on. Detailed instructions about this translation process are shown in Fig. 4 , where all of the patches marked with gray hatching indicate the areas that student agents could possibly reach at each time step if they are not occupied by other agents at that time. To determine the exact number of students in each group, three different parameters are used to control their overall proportions, which should be entered separately by researchers through the interface before running the experiments.
- Moving patterns
|
|
|
Fig. 4. The illustration of moving areas at different evacuation speeds. |
Because the virtual environment in Netlogo consists of an array of grids and one of the most important characteristics in ABM software is to simulate discrete actions in the space, all of the student agents in this model are restricted to move from one patch׳s center to another, including both vertical and diagonal directions (as shown in Fig. 4 ). In addition, for the average width of one person׳s shoulders is equal to the length of each patch (0.3 m), it is automatically assumed that every student agent can only occupy one patch at each time and no overlap is allowed in this model. Thus, if their target patch is occupied by another agent, the student has to wait until this patch is available or change to another patch with similar attraction values.
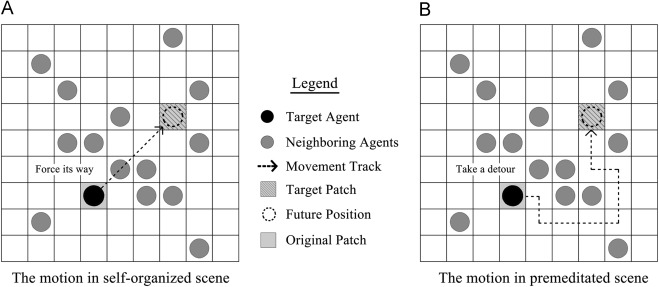
Moreover, agents in the self-organized scenarios tend to behave in completely different ways than those in the premeditated scenarios. To avoid being close to the source of danger and get out of the room as quickly as possible are the only goals for them during the evacuation process. Therefore, when self-organized agents come across some barriers on their way to the target patch, they act selfishly and choose to cross them directly without considering any consequences, just as people in the real world prefer to push other people away or jump across the desk and so on, as shown in Fig. 5 (A). Conversely, to reflect the characteristic of sequentially evacuating the room after people received fire drill training, agents in the premeditated scenarios are set up to care more about their surroundings. Therefore, unlike the hasty motions in the self-organized scene, student agents in the premeditated scene constantly change their actions to avoid any possible collisions between each other, such as shoving or pushing. When these agents happen to meet another agent standing in front of them, they would adjust their headings to another adjacent patch without any barriers. If all of the possible choices are occupied, they will choose to stay where they are and wait patiently until one of the adjacent patches is available, as shown in Fig. 5 (B).
|
|
|
Fig. 5. The illustration of moving patterns with different behavior rules. |
To conclude, student agents in the self-organized scene would always maintain their movement in a straight line, while the walking tracks in the premeditated scene tend to look more twisted and complex than the self-organized ones due to the ongoing adjustment decisions.
- Route arrangements
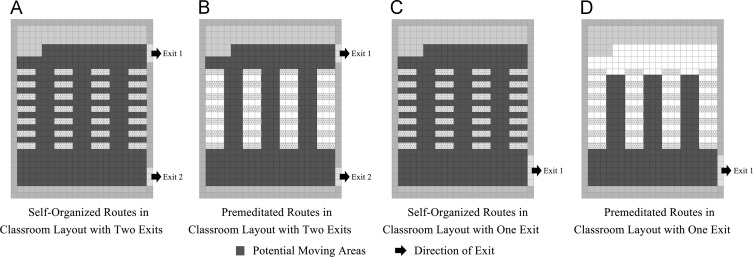
Other than the evacuation behaviors, another obvious difference between people who have received training or not is their range of moving activities. As stated by the scenario׳s name, agents in the self-organized scene make decisions individually and there are no limits for them to move. They can walk to any place they choose even if those places are not suitable for them to stay or have potential risk, such as the seating area surrounded by desks and chairs that students may stumble over while they are walking. However, in the premeditated scenarios, agents must follow the instructions received from the "fire drill" (in this context, from researchers) to arrange their moving activities for safety reasons, and they can only move within areas marked as "potential evacuation routes," where all places with unsafe features have already been eliminated. Specific details about these route arrangements in different classroom layouts are shown in Fig. 6 .
|
|
|
Fig. 6. The evacuation routes in different classroom layouts. |
3.4. Modeling procedures
3.4.1. Data preparation
Although Netlogo is able to draw simple geometric graphs on its simulation interface, it is a very time-consuming job for researchers to design an complex architecture layout through digital codes. Therefore, before compiling simulation codes in the ABM modeling platform, we use other specialized software, such as the AutoCAD and ArcGIS, to finish all of the graphic drawing work and to transform them into an appropriate file type that can be read by Netlogo, as illustrated in Fig. 7 .
|
|
|
Fig. 7. Data preparation process. |
3.4.2. Simulation framework
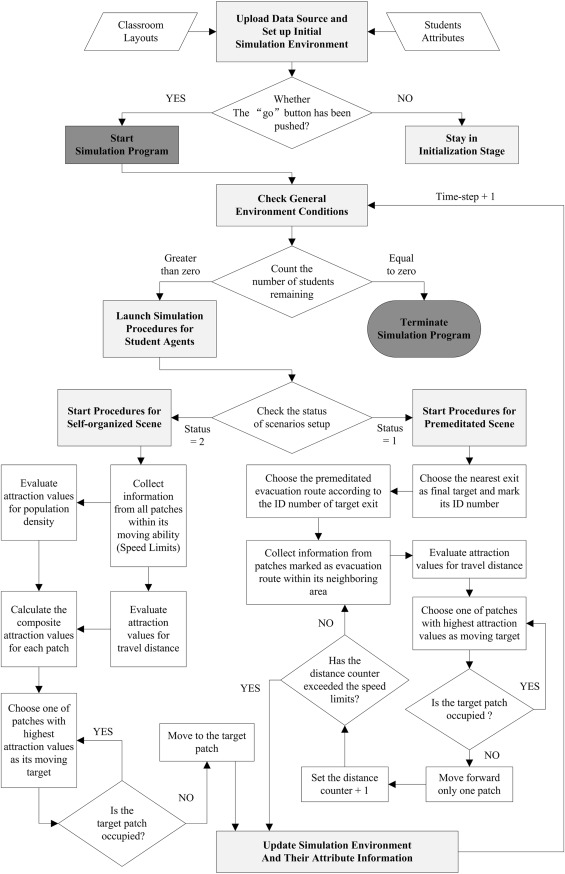
Because modular design can help programmers avoid unnecessary coding work and make it easier for them to check or replace error codes, we adopt this compiling method in our simulation program and divide the whole modeling procedures into five independent parts based on their main functions, as follows:
- upload relevant data source into Netlogo and set up the modeling environment;
- start the simulation program after researchers click the "go" button on the interface;
- check the total number of students remaining in the classroom and decide whether there is a need to continue the procedures;
- launch different types of rational thinking and moving procedures among student agents according to the scenario setup (self-organized or premeditated);
- recalculate the attribute information of the environment after all of the agents finish their moving actions to prepare for the same simulation work in the next time step.
The five steps mentioned above are arranged in chronological order, and some of them would be executed over and over again until the last student agent escapes from the classroom. Details about how these independent simulation modules cooperate with each other in the model are illustrated by the flow chart in Fig. 8 .
|
|
|
Fig. 8. Flow chart of the simulation procedures. |
4. Simulation research
4.1. Interface design
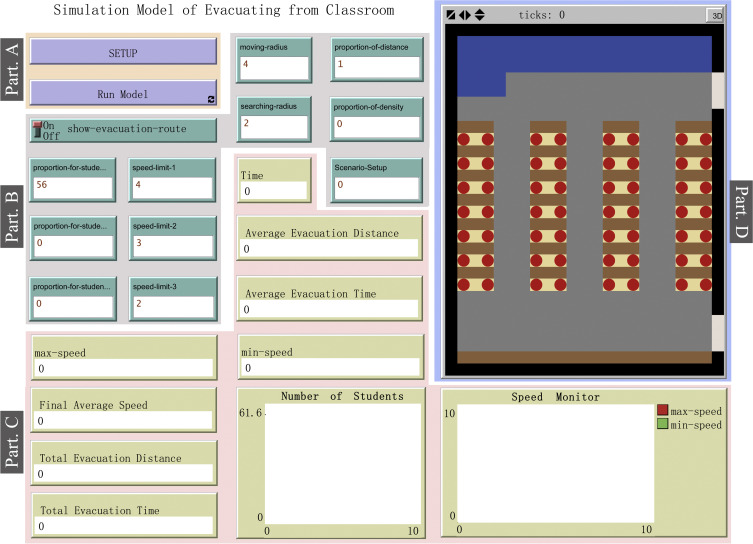
Fig. 9 shows the basic operation interface of this simulation program in Netlogo. Based on their function settings and the chronological order of the application process, all of these elements can be classified into four categories, which are marked with different background colors and labels. More specifically, "Part A" is the control center of whole simulation program, which is mainly used to initialize the simulation environment or send instructions to others so that they can start or terminate their corresponding procedures, just like switches. The green ones in part B are the input areas where researchers can assign strings or numbers to relevant parameters. In part C, the yellow buttons with pink base belong to the monitoring section, through which researchers can observe the model׳s development history from the perspective of statistical data. Similarly, part D, the viewer on the right side. is also used for observations but in a more dynamic way that researchers can watch student agents moving around the classroom directly.
|
|
|
Fig. 9. Snapshots of the operational interface in Netlogo. |
4.2. Structure verification
Before further discussing how the simulation model performed or what information it could provide us, we need to test its robustness on the system structure, which means that we should analyze whether these simulation results are caused by the essentials of the modeling structure or just a series of detailed assumptions. If a model depends too much on its parameter settings, then this model likely does not capture the real operation mechanisms (Steven and Volker, 2011 ). Therefore, we design several simplified versions of this model where unnecessary parameter settings are eliminated, such as preferences on population density, and all agents are assumed to be homogeneous with the same evacuation speed (1.0 m/s). Then, we use Togawa׳s equation (Jake, 1996 ; Tzu-sheng, 2003 ), as shown in Eq. (6) , to calculate the maximum evacuation time that students could spend in the real world with the same environment conditions, and compare them to the simplified models to determine whether there is any simulation result beyond its corresponding standard.
Togawas equation (6) for calculating the evacuation time Te
|
|
( 6) |
- Te is the time estimated for evacuation (s).
- Na is the total number of student agents in the model (person).
- B is the width of the narrowest passage in the layout (m).
- N is the flow capacity of the narrowest passage in unit time (person/m/s).
- Ks is the travel distance for the agent who evacuated from the classroom first (m).
- V is the speed settings of the agents (m/s).
Because all of the agents have the same speed limit (1.0 m/s) in this validation research, we set up four different simplified models mainly based on their behavior rules (self-organized and premeditated) and layout designs (classroom with one exit and classroom with two exits) to conduct this validation experiment. Specific details about the models׳ attribute settings and their comparison results with Togawa׳s equation are shown in Table 3 and Table 4 . In addition, due to the impact of stochastic elements in Netlogo, there may be a slight difference among the simulation results in each run. Therefore, to minimize the deviations from stochastic elements, all of the experiments in this study are run 10 times each and take the average as the final simulation results.
| Model categories | Model 1 | Model 2 | Model 3 | Model 4 |
|---|---|---|---|---|
| Classroom layout | 6.9 m x 8.7 m with one exit | 6.9 m x 8.7 m with two exits | 6.9 m x 8.7 m with one exit | 6.9 m x 8.7 m with two exits |
| Behavior rules | Self-organized | Self-organized | Premeditated | Premeditated |
| Speed limit | 1.0 m/s | 1.0 m/s | 1.0 m/s | 1.0 m/s |
| Preference ontravel distance | 100% | 100% | 100% | 100% |
| Flow capacity | 3 persons/m/s | 3 persons/m/s | 3 persons/m/s | 3 persons/m/s |
| Width ofnarrowest Passage | 0.3 m | 0.3 m | 0.3 m | 0.3 m |
| Shortest distance to exit | 1.2 m | 0.6 m | 1.2 m | 0.6 m |
| Model categories | Model 1 | Model 2 | Model 3 | Model 4 |
|---|---|---|---|---|
| General evacuation time in Togawa (s) | 19.33 | 20 | 19.33 | 20 |
| General evacuation time in model (s) | 17.2 | 14.9 | 17 | 11.6 |
As Table 4 shows, all of the simulation results are within the limitations of the maximum evacuation time imposed by Togawa, and they also agree well with the common sense that students in a classroom with two exits spend less time on their evacuation than those in a classroom with only one exit. Therefore, because this simulation model can reproduce realistic characteristics from its essential structure, we can conclude that the model is a detail-free model and it can successfully capture the mechanisms in the real world driving people׳s evacuation behaviors. It is therefore appropriate for us to use this model as a dynamic analysis tool to distinguish evacuation performances among different classroom layouts.
4.3. Sensitivity analysis
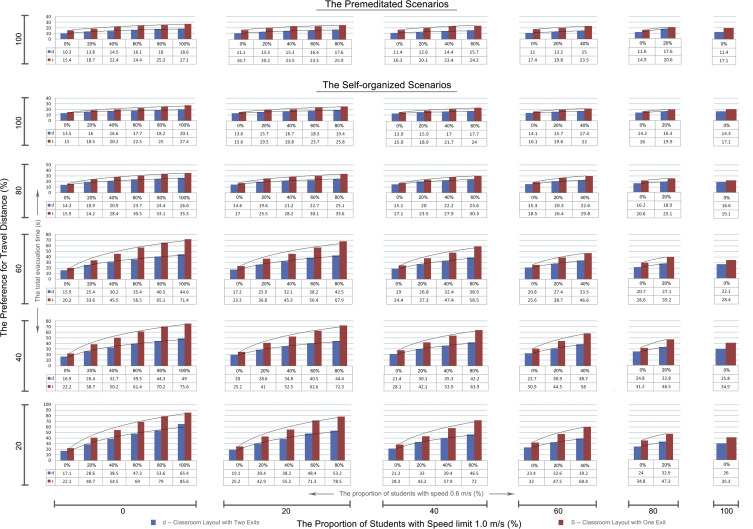
Unlike the homogeneous assumptions of agents׳ evacuation behaviors in the previous section, students in the real world not only have different walking speeds but also vary greatly in their preferences for different influence factors during the decision-making process. There is no unified standard for us to refer to when we set up the parameters, which may produce various simulation results using different data combinations. Therefore, the traditional evaluation method of making accurate judgments based on particular parameter settings is not suitable for this simulation research. To further analyze the effects of uncertainties and variations in parameters on the simulation results, we conduct sensitivity analysis to obtain a general understanding about how the evacuation time changes with different walking speeds and preferences (Andrew et al., 2008 ; Broeke et al., 2014 ).
The basic principle of sensitivity analysis is to vary the parameters one at a time and examine the small changes in the final simulation result (Steven and Volker, 2011 ). Because the general evacuation time is the most important indicator of evacuation performance and we have two types of parameters to examine, including the proportions of different walking speeds and the preference for different space factors, we choose multiple bar charts as the display tool to represent the interrelationships among the evacuation time and its two corresponding parameters in a single graph. As shown in Fig. 10 , the chart has a two-tier coordinated system, in which the outer one is used to identify factors of proportion on travel distance and proportion on students with a speed of 1.0 m/s, and the inner one is used to identify factors of total evacuation time and proportion on students with a speed of 0.6 m/s. Even if they have three different walking speeds (0.6 m/s, 1.0 m/s, 1.2 m/s) and two types of space influence factors (travel distance, population density), the chart only shows part of them as the coordinate indicators. The rest can be estimated by the difference between 100% and other summations, so there is no need to repeat the calculation results in the graph. In addition, to simplify the analysis process, the units for the proportion change for walking speed and preference on space factors were both set to 20% at each time. Although the proportion for different speed limits can range from 0 to 100, the preference for travel distance must remain greater than zero to match reality. Therefore, the variation range for travel distance is 20–100%, while the population density changes from 80% to 0% accordingly. However, in the premeditated scenarios, the population density is not taken into consideration, so the proportion of travel distance will stay at 100% through-out the entire study.
|
|
|
Fig. 10. The chart graphs for sensitivity analysis. |
These bar charts show that both the preference of travel distance to the nearest exit and the proportion of students with a speed limit of 1.0 m/s negatively impact the increase of evacuation time, meaning that the total time for people evacuating the scene will decrease accordingly as these two factors increase their proportions. However, compared to the general variation trends, the impact from travel distance is greater than that from walking speed because the total evacuation time will decrease down dramatically after the proportion of travel distance adds up to 60%, while the slope declines relatively slowly in the section of the walking speed. The main reason for this is that people who have a high preference for travel distance tend to choose places closer to the exit as their moving targets, so the evacuation route here is more goal-oriented and they save significant time in finding more comfortable places(with less population density).
For the coordinate axis in the inner tier, following the growth trend of students with a speed limit of 0.6 m/s, the total evacuation time increases steadily in all of the analysis scenarios when the other two factors (students with a speed of 1.0 m/s and a preference for travel distance) remain the same. Both the total number of students and the number of students with 1.0 m/s are already fixed in each scenarios, and increasing the students with a speed of 0.6 m/s will consequently decrease the number of students with a speed of 1.2 m/s, which is not shown in the bar charts for simplification. So the average evacuation speed overall will decrease accordingly as the model increases the proportion of students with lower evacuation speed.
The comparison results between the different classroom layouts basically follow the trend that students spend 20% less time evacuating from the classroom with two exits than the classroom with only one exit. However, this type of advantage is slightly decreased when the travel distance increases its percentage. As discussed previously, students with a high preference for travel distance tend to give up seeking less densified places and gather around the exit more quickly, so the flow of students in unit time will gradually become the dominant factor in determining the length of the evacuation time. Other factors, including walking speed or route arrangements, decrease their impacts on the evacuation time accordingly and leave the width of the exit, which is used to decide the maximum flow rate, as the only difference between these two classroom layouts.
In addition to the detailed analysis on scenarios with self-organized behavior rules, the multiple bar charts also include the change situations of total evacuation time in the premeditated scene as a part of the comparison research. However, because the students do not consider the population density, the proportion of travel distance in this scenario will always remain the same (100%) in all six experiments. As shown in the top two rows of Fig. 10 , the total evacuation time in the classroom layout with two exits is generally 11% less than that in self-organized scenes. However, when the comparison research is conducted in the classroom layout with only one exit, no significant improvements are shown between the evacuation performance in scenarios with different behavior rules or, in some cases, the students with premeditated rules spend more time on their evacuation. The limited door area in the one exit scene greatly hinders the evacuation flow in the unit time step, and regardless of whether the students are queued up or not, they have to spend most of their time waiting in line. Unlike students with premeditated behaviors who often take detours when walking on the designated evacuation route assigned by experts, students in the self-organized scene may save slightly more time by crossing the desk directly. So the benefits of fire drills do not come into play under such restricted environment conditions.
To conclude, the results of this sensitivity analysis show us that the proportions of different space factors (travel distance and population density) have a greater influence on the final evacuation time than the composition ratio of students with different speed limits. And the evacuation efficiency in the classroom layout with two exits is generally higher than the classroom layout with a single exit. In addition, due to the limits of flow rate in an objective environment, the advantage of evacuating in an organized way cannot be fully represented in the one exit׳s scene. Opposite to their considerably different performance in the classroom layout with two exits, both the self-organized behavior rules and the premeditated behavior rules have similar simulation results on the evacuation time in a classroom layout with one exit, and in some rare cases, the student agents in the premeditated scenarios could even spend more time than those in the self-organized ones on their way out.
4.4. Performance evaluation
To further learn about the benefits of fire drills and the distinction between evacuation performance of two types of classroom layouts, comparison research is also conducted on four evacuation scenes, which are organized under different combinations of classroom layouts and behavior rules. To obtain a more accurate comparison result, this research mainly focuses on analyzing the variations in research objects and ignores the impacts of other elements such as walking speed. Therefore, this experiment uses the same parameter settings as the structure validation research (Table 3 ), which means that all of the simulation models in this section will have similar attribute values except for their classroom layouts and the agent׳s behavior rules. Specific details about this analysis research are provided in the following two sections.
4.4.1. Motion
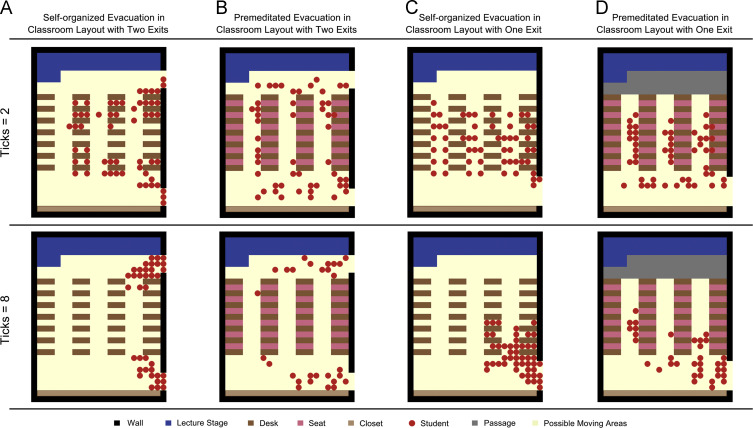
As shown in Fig. 11 , the moving patterns for students with self-organized behavior rules are more direct and more targeted than those in the premeditated scenarios. And they basically turn their headings towards the exit at the very beginning of the simulation research and walk that direction without many detours. However, when students in the premeditated scene choose to follow the instructions to evacuate the room, instead of running to the exit directly, they first find the nearest evacuation route designed by researchers and then keep walking along this way until they get to the target exit. During the evacuation process, students in the self-organized scene tend to act inconsiderately and rudely while forcing their way through the crowd or barriers, and they always clog around the exit areas due to the disparity between the number of students waiting in line and the limited capacity that allows students to pass at a unit time. In emergency situations, this type of crossing and clogging behavior could be very harmful to students׳ evacuation safety. Because students in a large crowd can easily feel nervous; once their anxiety is raised to a certain level, they start to push each other to get out, which may cause serious accidents such as a stampede. Conversely, students with premeditated rules rarely form clogging patterns on their way out. As we can see in Fig. 11 , they have a bit looser intervals than in the self-organized ones, and a few distinct queues also gather along the route in both two types of classroom layouts. Although these queues are not as orderly as an army, they can still provide the students some necessary cushion space and help them to avoid collisions between each other. Therefore, from the perspective of safety, the orderly evacuation behavior in the premeditated scenarios is more suitable for students when they are organizing their moving activities in emergency circumstances.
|
|
|
Fig. 11. Snapshots of the simulation process in different scenarios. |
4.4.2. Efficiency
Table 5 shows the comparison results evaluating from six different aspects. The performance of the total evacuation time in the classroom layout with two exits is generally better than that in the classroom layout with only one door. After all, the flow rate of students is directly related to the length of the exit and increasing the number of exits consequently allows more students to escape quickly. In addition, the section of evacuation distance reflects that when the students have two alternative exits to evacuate, their walk is approximately 20% shorter than in a classroom with one exit. In one-exit scenarios, students who sit in front of the classroom have to walk through the entire space to get to the door located at the back, so all of the students in the front half increase their evacuation distance from a few centimeters to several meters. Similarly, as the distance of escaping gets extended in the classroom layout with one exit and the maximum walking speed remains the same (1.0 m/s), students would automatically spend more time on their evacuation when they only get one choice of exit.
| Evaluation factors | Two exits with self-organized rules | One exit with self-organized rules | Two exits with premeditated rules | One exit with premeditated rules |
|---|---|---|---|---|
| Ticks (s) | 14.6 | 17.2 | 11.7 | 17 |
| Average speed (m/s) | 0.7038 | 0.6841 | 0.9976 | 0.971 |
| Total distance (m) | 292.0825 | 340.5352 | 316.788 | 430.2806 |
| Average distance (m) | 5.2157 | 6.0809 | 5.6569 | 7.6836 |
| Total time (s) | 415 | 497.8 | 317.549 | 443.1156 |
| Average time (s) | 7.4107 | 8.8893 | 5.6705 | 7.9128 |
Another interesting fact revealed from this comparison research is that, although the evacuation distance in the self-organized scenarios is shorter than that in the premeditated scenarios, students do not receive any benefits from this during their evacuation. Conversely, they surprisingly spend more time than the students who walk farther. This result is not hard to understand if we combine this finding with the analysis results of motion in the previous section. As shown in Fig. 11 , students with self-organized behavior rules tend to arrive at the exit areas earlier by forcing their way through the barriers, but after a large crowd has gathered around the door, the fast moving actions immediately stop and students have to spend the rest of their time waiting in line due to the flow limits of the exit. Therefore, even in the premeditated scenarios, the designated evacuation route is not the shortest path for all of the students and causes them to spend extra time walking; students here can still obtain a better performance by saving time from useless waiting behavior in the dense crowd, which is also at a high risk of accidents. Therefore, from the view point of evacuation efficiency, both the planning scheme with two exits and the orderly evacuating behaviors in the premeditated scenarios can help students to escape from the classroom more quickly and more safely. Fire drills need to be conducted regularly among students so that they could learn how to evacuate in an orderly way in emergency situations.
5. Conclusion
In this paper, several simulation experiments were built based on four different types of evacuation scenarios using Netlogo. The main objective of this study is to provide architects or school administrations with preliminary insight on how evacuation efficiency and students׳ safety are connected to classroom planning schemes and what type of behavior rules best serve students while they are escaping. The detailed analysis results proves that the classroom layout with two exits has a better performance than that with one exit in all of the simulation scenarios. If people cannot avoid designing the classroom layout with one exit in some restricted circumstances, certain remedial measures must be taken before the classroom come into use, of which receiving fire drill training is one possible choice. In addition, as shown in the comparison research between self-organized and premeditated scenarios, students who follow the instructions to walk on the designated routes can generally spend less time on their way out, further demonstrating the importance of conducting regular fire drills among students and developing the habit of evacuating in good order.
Due to the limited calculation capacity of Netlogo, this simulation model had to make several simplified assumptions during its setup process, including rasterized movements and categorized attribute settings. However, a series of validation research and sensitivity analysis proved that the basic operational mechanisms underlying this simplified model can successfully capture the major characteristics of the observed system in the real world. Therefore, except for calculating the total evacuation time, this model can also be used to watch the specific details of student׳s moving actions, such as clogging or queuing up, helping to make a more accurate evaluation of the performance of different simulation scenarios. To achieve a higher degree of similarity with reality, several aspects still have plenty of room for improvement. Taking the student agents for example, in addition to the three different speed limits, more categories and flexible walking speed settings could be introduced into this model, and their reaction time before taking any action is also worth adding. Moreover, students may show different types of responses to specialized emergency situations, such as a bombing or earthquake, so we need to build evacuation models based on different reaction mechanisms to determine whether there is any differences among their simulation results. To conclude, using ABM software (Netlogo) to simulate the evacuation process in emergencies has very important application values for architectural design. With the help of its dynamic visualization function, we can not only use it as an evaluation tool to distinguish the evacuation performance among different planning schemes but also use it as a medium to observe the specific details of student׳s moving activities during the evacuation process. Therefore, ABM can play a vital role in both scientific research and architectural design.
Acknowledgment
I would like to extend my sincere gratitude to my adviser Wayne Wakeland at Portland State University, for his instructive advice and useful suggestions on my paper. I am deeply grateful of his help in the completion of this paper.
References
- Aldis, 2014 R.L. Aldis; Evacuation of Children: Focusing on Daycare Centers and Elementary Schools, Technical University of Denmark, Denmark: Kongens Lyngby (2014) (This is a thesis, not a book)
- Almeida et al., 2012 Almeida, J.E., Kokkinogenis, Z., Rossetti, R.J.F., 2012. Netlogo implementation of an evacuation scenario. In: Proceedings of the Iberian Conference on Information Systems & Technologies, CISTI, Madrid, Spain, pp. 1–4.
- Andrew et al., 2008 C. Andrew, C. Christian, B. Michael; Key challenges in agent-based modeling for geo-spatial simulation; Comput., Environ. Urban Syst., 32 (6) (2008), pp. 417–430
- Ansgar and Andreas, 2002 K. Ansgar, S. Andreas; Simulation of evacuatio processes using a bionics-inspired cellular automaton model for pedestrian dynamics; Phys. A: Stat. Mech. Appl, 312 (1) (2002), pp. 260–276
- Bibo, 2005 Y. Bibo; The Application of Complex System Simulation in Urban Research, Zhejiang University, China: Hangzhou, Zhe Jiang (2005) (This is a thesis, not a book)
- Broeke et al., 2014 Broeke, G.A.T., Voorn, G.A.KV., Ligtenberg, A., 2014. Sensitivity analysis for agent-based models: a low complexity test-case. In: Proceedings of the Social Simulation Conference, Barcelona, Spain.
- Camillen et al., 2009 Camillen, F., Capri, S., Garofalo, C., Ignaccolo, M., Inturri, G., Pluchino, A. et al., 2009. Multi agent simulation of pedestrian behavior in closed spatial environments. In: Proceedings of the Toronto International Conference on Science and Technology for Humanity, TIC-STH, Toronto, Canada.
- Colin and Tony, 2005 Colin, M.H., Tony, W., 2005. Agent-based modeling of forces in crowds. In: Proceedings of the International Conference on Multi-Agent and Multi-Agent-Based Simulation, Berlin, German, pp. 173–184.
- Craig, 1987 W.R. Craig; Flocks, herbs and schools: a distributed behavioral model, ACM SIGGRAPH Comput; Graph., 21 (4) (1987), pp. 25–34
- Hui et al., 2011 L. Hui, W. Hanning, Z. Wencong, X. Muzhou, D. Minggang, T. Jian; Research on micro-agent simulation model of evacuation under direction of macro-scene; Appl. Res. Comput, 28 (11) (2011), pp. 4111–4114
- Jake, 1996 P. Jake; Movement of people; The SFPE Handbook of Fire Protection Engineering (2nd ed.) 3rd.,), National Fire Protection Association, USA, Boston, Massachusetts (1996), pp. 263–285
- Jin, 2009 G. Jin; Dynamic Simulation of Vegetation Spatial Pattern Based on Multi-Agent, Beijing Forestry University, China: Beijing (2009) (This is a thesis, not a book)
- Lishen, 2014 W. Lishen; Research on Pedestrian Density and Pedestrians Working Rules in Commercial Complex Building, Central South University, China: Changsha, Hunan (2014) (This is a thesis, not a book)
- Preston et al., 2015 J. Preston, J.M. Binner, L. Branicki, T. Galla, N. Jones, J. King, et al.; City Evacuations: An Interdisciplinary Approach, Springer, German: Berlin Heidelberg (2015)
- Rong and Long, 2014 X. Rong, L. Long; Simulation of optimized evacuation processes in complex building using cellular automata model; J. Softw, 9 (6) (2014), pp. 1428–1434
- Shaobo et al., 2009 L. Shaobo, Y. Lizhong, F. Tingyong, L. Jian; Evacuation from a classroom considering the ccupant density around exits; Phys. A: Stat. Mech. Appl, 388 (9) (2009), pp. 1921–1928
- Steven and Volker, 2011 F.R. Steven, G. Volker; Agent-Based and Individual Based Modeling, Princeton University Press, USA: Princeton, New Jersey (2011)
- Su et al., 2008 Su, S., Tsai, S.T., Shih, C.L., Kuo, R.J., Wang, H.C., Chen, J.C., 2008. Use of computer simulation in the evacuation system for hospitals. In: Proceedings of the Summer Computer Simulation Conference. Edinburgh, Scotland.
- Tariq et al., 2010 Tariq, M. E., Jun, Z., Mahmoud, T. K., Ra’ed, M. J., 2010. The incorporation of layout design into an agent-based evacuation model. In: Proceedings of the Modeling, Simulation, and Gaming Student Capstone Conference, Suffolk, Virginia.
- Tinxia, 2015 G. Tinxia; Research on Application of Ordered Evacuation in Campus Emergencies, Southwest Jiaotong University, China: Chengdu, Sichuan (2015) (This is a thesis, not a book)
- Tzu-sheng, 2003 S. Tzu-sheng; Building Planning Evacuations for Emergency Evacuation, Worcester Polytechnic Institute, USA: Worcester, Massachusetts (2003) (This is a thesis, not a book)
- Uri, 1999 Uri, W., 1999. Netlogo. Center for Connected Learning and Computer-Based Modeling. Northwestern University, Evanston, Illinois. 〈〈http://ccl.northwestern.edu/netlogo/〉 〉.
- Vani and Sumam, 2013 K. Vani, M.I. Sumam; Agent based evacuation simulation using leader-follower model; Int. J. Sci. Eng. Res., 4 (8) (2013)
- Victor and Jeffrey, 2001 J.B. Victor, L.A. Jeffrey; Cellular automata microsimulation for modeling bi-directional pedestrian walkways; Transp. Res. Part B: Methodol, 35 (3) (2001), pp. 293–312
- Xiaohui et al., 2012 H. Xiaohui, Z. Feng, C. Yong, H. Xiaoqing; Simulation study of urgent evacuation in large public place; Comput. Eng. Appl, 48 (29) (2012), pp. 230–233
- Yuling et al., 2008 L. Yuling, O. Norio, T. Yukiko; Dynamic route decision model-based multi-agent evacuation simulation-case study of Nagata Ward, Kobe; J. Nat. Disaster Sci, 28 (2) (2008), pp. 91–98
Document information
Published on 12/05/17
Submitted on 12/05/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?