Abstract
Genetic Algorithm (GA) is widely adopted in optimization and the improvement of its optimization performance is attracting many researchers’ attentions. In solving practical problems in the process of architectural design, the ways of converting design problems into mathematical models that can be addressed by GA are of great significance in achieving final optimal results. However, no such rule that can be applied to such conversion has been developed so far. In general, problems which can be addressed by GA can be divided into combinatorial problems and numerical problems. In this paper, by means of attempting to disintegrate a complicated architectural problem into combinatorial and numerical problems, the author discusses feasibility and practicality of solving these two types of problems simultaneously utilizing GA and discloses both advantages and disadvantages of GA by comparing with other algorithms.
Keywords
Genetic Algorithms ; Unfolding ; Combinatorial problems ; Numerical problems ; Architectural design
1. Introduction
Genetic Algorithms have been introduced into architectural design field in general since a dozen years ago due to its special robustness and relatively simple implementation. Ever since then, they have been adopted in particular in optimizing the layouts of floor plans (Michalek et al., 2002 ) and site plans (Finucane et al., 2006 ), optimizing building façade designs(Caldas and Norford, 1999 ), optimizing forms of building structures (Papapavlou and Turner, 2009 ), and in some conceptual design (Soddu, 2005 ). However, unlike in other purely scientific research fields, problems in architectural designs are often mixed with social and esthetic factors which cannot be described by mathematical models. When a designer attempts to optimize design problems with the help of GA, facing such complexities inherent in architectural designs, he or she has to convert specific problems into combinatorial and/or numerical problems that can be addressed by GA. Particularly in the case of combination of these two kinds of problems, drastic expansion of searching space can be seen as a tough test for GAs searching ability. How to utilize Genetic Algorithms, how to convert design problems and how to effectively control the scale of searching space are three major subjects in optimizing architectural designs using GA. In this paper, the optimization of modeling for schematic design of ancient Yangzhou South City-Gate Ruins Museum exemplifies the introduction of the application process for optimizing architectural designs with the help of GA, as well as the disclosure of both advantages and disadvantages of GA by comparing it with other non-heuristic algorithms.
2. Background
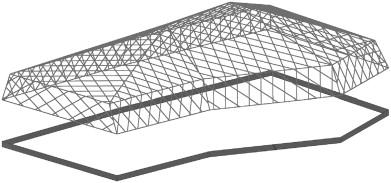
In order to preserve the historical remains – the ancient Yangzhou South City-Gate Site – a large shell structure is designed as a museum to shelter the ruins. For the sake of avoiding any damage to the site, no strut is provided within the site area to support this large-span structure with the scale of 80 m long, 40 m wide and 11 m tall. As designed, the whole structure is composed of several irregular triangular faces while each face is filled with textures of regular angles formed by steel beams interconnected horizontally and vertically (Figure 1 ). It is clear that continuity and completeness of the textures are important factors affecting the performance of the whole structure. However, since the shell shape is irregular, it is difficult to ensure the textures’ continuity at turning points of some triangular faces. Therefore, the primary task of optimization is to minimize such discontinuous edges.
|
|
|
Figure 1. Structure of the shell. |
In addition, in order to guarantee sufficient spaces for the convenience of construction treatment, the intersection points, i.e., vertexes of each regular triangle in the textures, should be kept away from the turning points as further as possible.
Since building structures and shapes are subject to changes of design purposes during the design process, optimization programming is also required to provide immediate and direct feedbacks on design changes.
3. Modeling
In order to simplify issues, an abstract geometrical model is introduced to describe the building structure as a whole, with beams and nodes turned into abstract line segments and points (Figure. 2 ). To avoid ambiguity, triangular faces of structures and shapes are defined as triangular faces , edges shared by two triangular faces as shared edges , edges of single triangular face as border edges , end points of shared edges as vertexes , end points of border edges as border vertexes , vertexes of regular triangles too proximate to shared edges as close points , and shared edges which will be split in their unfolding process as split edges .
|
|
|
Figure 2. Abstract geometrical model. |
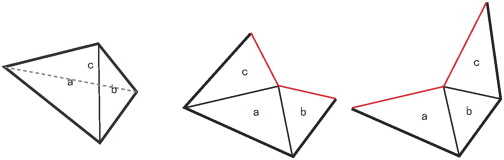
Discontinuity of textures is associated with unfolding ways of three-dimensional bodies onto a two-dimensional plane. In doing so, some shared edges need to be split. For instance, there are many ways to unfold a simple triangular pyramid. The longer the split edges are, the poorer the continuity of textures will be (Figure 3 ). So this problem has been transformed into the one targeting at searching for a combination way of the shortest split edges. It is obvious that this is a combinatorial problem.
|
|
|
Figure 3. Different ways to unfold a triangular pyramid. |
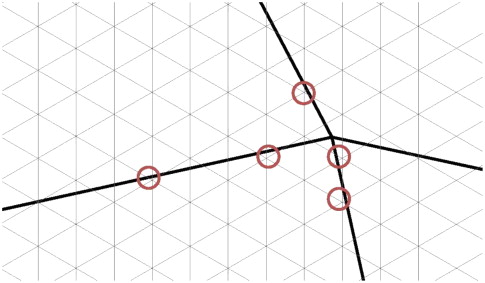
Furthermore, the quantity of close points depends on the textures of the regular triangles and the relative position and angle of graphics after unfolding (Figure 4 ).
|
|
|
Figure 4. Close points. |
4. Algorithms
4.1. Split edge optimizing algorithm
Concerning the way of searching for unfolding algorithm for the shortest split edges, Genetic Algorithm is applied tentatively. However, in doing so, its searching scope expands at an exponential order with increasing number of vertexes and it is difficult to determine whether the optimal solution has been identified. As a result, it will bring about difficulties for subsequent optimization. Therefore, an alternative sorting algorithm is designed by analyzing rules for the unfolding process. Here lists both algorithms and the comparison between them.
4.1.1. Based on Genetic Algorithm
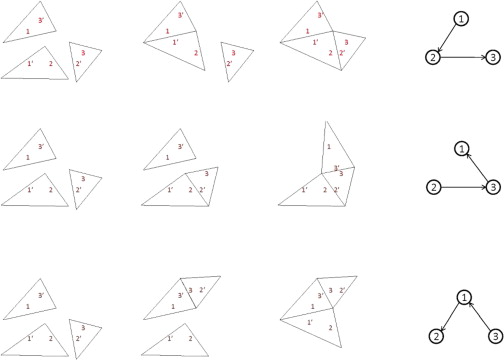
Selection of split edges is associated with the sequence of joining shared edges together. For example, for a triangular pyramid without bottom face, first, its three faces are unfolded into a two-dimensional space. If their shared edges are joined together in different sequences, the results obtained are diversified (Figure 5 ).
|
|
|
Figure 5. Different results of different sequences. |
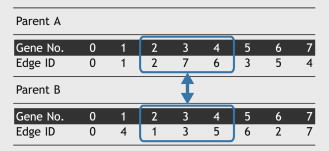
In turn, chromosome is coded according to permutation encoding style. Each gene represents the ID number of the shared edge while chromosomes are various combinations of these ID numbers. Length of the chromosomes is the total number of the shared edges (Table 1 ). If there are n shared edges, then searching space will be as large as n !.
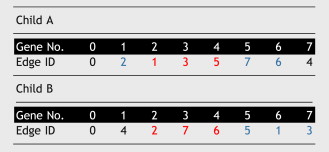
Since the chromosomes are ordered sequences, the commonly used single-point crossover algorithm will break the sequence and generate illegal solutions. Alternatively, partially matched crossover is adopted. Two chromosome fragments are taken out from parent chromosomes for exchange (Table 2 ). In offspring chromosomes generated from the process, the repetitive genes produced from exchange are replaced by corresponding genes inside chromosome fragments (Table 3 ).
Mutation operator randomly selects two genes from chromosomes, i.e., ID numbers of shared edges and exchanges their positions (Table 4 ).
Chromosomes fitness is the total length of un-split shared edges. The longer the length is the better continuity and fitness will be. Its formula is as following:
|
|
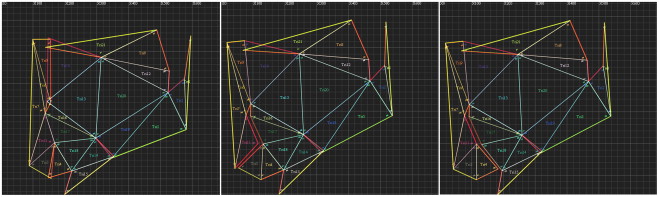
In which, s is fitness, n is the total number of shared edges; Li is the length of i th shared edge. When shared edges are not split, Hi =1; otherwise Hi =0. At the same time, roulette algorithm is used to select chromosomes from the population. Figure 6 shows the changes of optimal solutions during the unfolding process.
|
|
|
Figure 6. Changes of optimal solutions during unfolding. |
4.1.2. Based on sorting
It is clear that when a three-dimensional shell structure is unfolded, each vertex owns at least one shared edge starting from itself to be split. For instance, a triangular pyramid has only one vertex, so splitting one of the edges starting from this point can unfold this shape (Figure 3 ). In the case of objects with numerous vertexes, their shapes can be unfolded so that all shared edges of the three-dimensional object can be arranged according to their lengths from the shortest to the longest if each vertex has its own split edge. The following rules can be applied to determine whether this edge should be assumed to be the split edge.
- If its two ends are vertex and border vertex, respectively, assume it to be the split edge attributed to the vertex.
- If its two ends are both vertexes which do not own their own split edges, assume it to be the undetermined edge shared by the two vertexes. Once either of them gets another split edge in the later determination process, this undetermined edge is attributed to the other vertex. If one of them has already owned one split edge, this edge can be attributed to the other vertex. If both vertexes own split edges, this edge can be abandoned. If one of the two vertexes owns one undetermined edge and the other of them owns un-split edge, this edge will be attributed to the one owning undetermined edge on a prioritized basis. If two vertexes both own undetermined edges, it will be attributed to the vertex with the shorter undetermined edge on a prioritized basis. Continue to put each shared edge into the formula until all vertexes have their own split edges.
- If some split edges form a circle, it means that the shape is split into two sections, which is not desired. In this case, we need to select the second shortest edge with the smallest length increment to substitute one split edge in the circle.
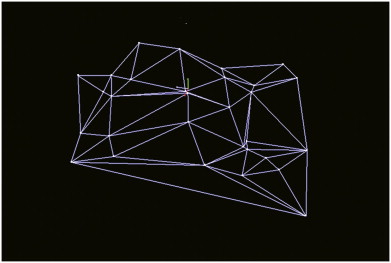
The speed of unfolding becomes much faster after introducing this algorithm, enabling dealing with a large amount of vertexes (Figure 7 ).
|
|
|
Figure 7. The result of unfolding a 3d shape with 100 vertexes. |
4.2. Projection optimization algorithm
During projection process, two approaches can be applied to reduce the number of critical points. The first one is to adjust relative positions and angles of projected textures on the unfolded shape. The second is to tune position of the shells vertex. Therefore, the chromosome is a sequence composed of vectors of three elements (Table 5 ).The three elements of a vector represent its values on axes x , y and z, respectively. The first two vectors of the chromosome represent relative position and angle of the textures of the regular triangle. Other vector represents the displacement of each vertex. Values of vectors are limited to a certain range to ensure that changes of the structure and shape are not too drastic.
Single-point crossover is applied to crossing process. Once one crossover point is randomly selected, new offspring will be generated when two parent chromosomes exchange their chromosome fragments behind crossover points.
In order to ensure the chromosome mutate, genes inside chromosomes are randomly selected and replaced with randomly generated vectors.
Chromosomes fitness is reciprocal of the total number of close points. When a regular triangle is projected onto an unfolded shape, positions of its vertexes and distances between them and the surrounding shared edges can be calculated. If the distance is less than certain threshold, it is marked as a close point.
5. Processes
Here we have proposed corresponding algorithms for major problems in design. The next step will be how to select and arrange these algorithms. In split edge optimization algorithm, genetic-algorithms-based approach is apparently not as effective as sequence-based algorithm in terms of searching ability. Since in projection optimization algorithm, splitting and unfolding ways for newly generated objects may possibly change with operations in positions of each objects vertexes, we need to embed split edge optimization algorithm into projection optimization algorithm before obtaining relatively complete searching space. If we embed one Genetic Algorithm into another Genetic Algorithm, the amount of calculations required is huge. If changes brought about by vertex movements are uncounted and two Genetic Algorithms are combined in successive order for application, some searching space will be neglected. Considering all the above factors, sequence-based split edge optimization algorithm embedded into projection optimization algorithm is adopted in the optimization process.
The optimization program is written with java language and JMonkey Engine is used to provide 3d rendering and shading. The whole optimization process can be conducted in the following three steps:
|
1st step: Enter the vertexes of the shells triangular faces (Figure 8 ).
| ||
|
2nd step: Delaunay Triangulation is used to generate triangular faces (Figure 9 ). During this generation process, connecting relations between points and edges, connecting relations between points and triangular faces, and neighboring relations between triangular faces are also established for further calculating.
|
- 3rd step: Use Genetic Algorithm to accomplish the optimization.
Generate certain number of random chromosomes.
- Adjust the position of each vertex of the three-dimensional object according to each gene inside the chromosome to produce new corresponding object.
- Use split edge optimization algorithm to calculate splitting ways for each object and unfold it into a two-dimensional plane (Figure 10 ).
|
|
|
Figure 10. Unfolding. |
- Project the textures of the regular triangle onto the unfolded shape according to the first two genes inside chromosome (Figure 11 ).
|
|
|
Figure 11. Projection. |
- Calculate fitness of each projecting way.
- Select the chromosome with the optimal fitness. If it is better than current maximum fitness, update this fitness, recover the projected and unfolded shape back to three-dimensional state, and draw it on the image interface (Figure 12 ).
|
|
|
Figure 12. Refolding. |
- Determine whether optimization needs to be continued. If not, stop the program.
- Use roulette algorithm to select chromosome to be inherited by the next generation.
- Perform crossover and mutation operations to the chromosome of new generation and return to the 2nd step operation.
6. Conclusions
By comparing the two unfolding algorithms, it can be seen that Genetic Algorithm is less difficult to realize. Generally speaking, so long as one knows how to code chromosome and how to assess fitness, he or she can optimize problems by using Genetic Algorithm and do not need to consider functional relations between inputs and outputs. It has special advantages in optimizing np problems. If one has no other better algorithm in optimization, Genetic Algorithms can be a reasonable choice. However, as a heuristic random searching algorithm, it involves huge computation load. First, it is a parallel searching algorithm, which means calculation load will multiply with the increase of the number of chromosome lengths and individuals in a population. Second, calculations cannot be once for all, the optimal solution must be approached by continuous iterations. Its ability for achieving optimal solution and the time consumed for achieving the solution are random to a great degree. When considering two optimization problems embedded within each other, it is difficult to achieve optimization. In case that some requirements in terms of optimization efficiency are put forward, or the optimal solution must be obtained, Genetic Algorithm is not an appropriate choice. In this case, functional relations have to be considered. However, with regard to some of the architectural design problems, the optimal solutions expressed in numbers or values are not necessarily what architects would like. Genetic Algorithm may provide diversified approximately optimal solutions for architects for their references. In turn, architects can make their own judgments after considering all other design factors on a comprehensive basis.
References
- Caldas and Norford, 1999 L.G. Caldas, L.K. Norford; A Genetic Algorithm Tool for Design Optimization; ACADIA ‘99, Salt Lake City (1999)
- Finucane and Derix, 2006 E.L. Finucane, C. Derix, et al.; Evolving urban structures using computer optimisation techniques; Generative Art (2006)
- Michalek and Choudhary, 2002 J. Michalek, R. Choudhary, et al.; Architectural layout design optimization; Engineering Optimization, 34 (2002), pp. 461–484
- Papapavlou and Turner, 2009 Papapavlou, A., Turner A., 2009. Structural evolution: a genetic algorithm method to generate structurally optimal delaunay triangulated space frames for dynamic loads. In: 27th eCAADe Conference, Istanbul.
- Soddu, 2005 Soddu, C., 2005. Visionary Variations of Milano, from 〈http://soddu2.dst.polimi.it/asialink/de1.htm〉 .
Document information
Published on 12/05/17
Submitted on 12/05/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?