Posibilidades de un modelo sustituto de incendios mediante el empleo de redes neuronales

Resumen

En los últimos años ha tenido lugar un amplio desarrollo de los modelos de simulación computacional de incendios (MSCI) y se ha intensificado su empleo para el estudio de la seguridad contra incendios y otras investigaciones relacionadas con estos. Los 2 principales tipos de MSCI son los modelos de campo y los modelos de zona. El primero obtiene mejores aproximaciones a la dinámica del incendio, mientras que el segundo requiere mucho menor tiempo de cómputo.

Hay que destacar además los grandes avances que se han conseguido en los últimos años en el procesamiento de información, mediante el empleo de las redes neuronales artificiales, que se han convertido en una herramienta de gran utilidad y con aplicación en campos muy diversos.

El presente artículo trata de analizar las posibilidades del empleo de redes neuronales artificiales en los modelos computacionales de incendios. En la primera aproximación a este objetivo se pretende conseguir en un recinto conocido resultados similares a los que se obtienen con los modelos de campo, y reducir así el tiempo de cómputo necesario para realizar las simulaciones con respecto al empleado en modelos de zona. En este caso se empleará una red neuronal de regresión general (GRNN) y se realizará su entrenamiento con simulaciones llevadas a cabo con el modelo de campo FDS (Fire Dynamics Simulator) , validando el modelo resultante con los datos obtenidos en un ensayo a escala real. En etapas posteriores se evaluarán otros fenómenos y diferentes tipos de redes.

Abstract

In recent years there has been extensive development of the fire computer models, and its use in the study of the fire safety, fire investigation, etc. has been increased. The most important types of fire computer models are the field model and the zone model. The first model reaches a better approximation to fire dynamics, but the second one requires less computational time.

Additionally, in the last years, it should be noted the great advances in information processing using artificial neural networks, and it has become a useful tool with application in very diverse fields.

This paper analyzes the possibilities of develop a new fire computer model using artificial neural networks. In the first approach to this objective, a simple compartment was analyzed with a field model. After that, simulations employing General Regression Neural Network were performed. This method achieves similar results that the field model employing computational times closer to the zone models. The neural network has been trained with FDS field model and validating the resulting model with data from a full scale test. In later stages other phenomena and different types of networks will be evaluated.

Palabras clave

Modelado y simulación computacional de incendios ; Redes neuronales

Keywords

Fire computer models ; Artificial neural networks

1. Modelos de simulación computacional de incendios

Los modelos de simulación computacional de incendios (MSCI) nacen con el objetivo de representar el desarrollo del incendio en un recinto, para su posterior estudio. Estos modelos surgen de la necesidad de mejorar la seguridad frente a un incendio tanto de las personas como, en la medida posible, de los bienes materiales involucrados. Se emplean en diversos campos, como la caracterización de materiales frente al fuego, para analizar cuán seguro es frente a un incendio un edificio, un vehículo de transporte, etc. [1]  and [2] .

La clasificación clásica distingue en primer lugar los modelos de zona, los cuales utilizan diversas simplificaciones en las ecuaciones de gobierno del incendio, de modo que el modelo matemático que emplean es más sencillo y por tanto el tiempo de cómputo requerido es pequeño. Sin embargo, estas asunciones hacen que estos modelos sean poco precisos, aunque válidos para una primera aproximación. Una de las simplificaciones más significativas es que consideran 2 zonas a la hora de realizar el estudio del incendio, suponiendo propiedades homogéneas en cada una de ellas (zona superior o de gases calientes y zona inferior o de gases fríos) [3] .

Los resultados de estos modelos vienen dados también como valores promedios de temperatura de la capa caliente, de la capa fría y de la altura de la interfase de separación de ambas capas. El modelo de zona más empleado en la actualidad, tanto por su continuo desarrollo como por las numerosas validaciones que presenta, es el CFAST [4] , desarrollado por el National Institute of Standards and Technology (NIST) estadounidense, que se empleará en el presente artículo de cara a la comparación de los resultados del modelo desarrollado con los actuales modelos de zona.

Más recientes son los modelos de campo, los cuales resuelven con más detalle las ecuaciones de gobierno del incendio ya que se basan en la fluidodinámica computacional (CFD), lo que hace que se obtenga una mejor aproximación a la realidad aunque ello implique un mayor tiempo de cómputo. Estos modelos ya no dividen el recinto en 2 zonas sino que lo dividen en miles o incluso millones de celdas de control de pequeño tamaño, en cada una de las cuales se consideran las propiedades homogéneas. Esto proporciona una mayor precisión a la hora de obtener los parámetros de salida. El modelo de campo más empleado en la actualidad, y que se utiliza en el presente trabajo, es el Fire Dynamics Simulator (FDS) [5] , desarrollado también por el NIST.

2. Redes neuronales artificiales

Las redes neuronales artificiales nacen del deseo de obtener un sistema de procesamiento de información que imite al cerebro humano. Este último tiene un funcionamiento paralelo y no lineal, por lo que no puede representarse mediante modelos lineales, y es además propenso a almacenar información experimental para su posterior uso [6]  and [7] .

Las redes neuronales artificiales consisten en unidades de procesamiento que:

• Intercambian datos e información.
• Son capaces de aprender mediante un entrenamiento mejorando así su funcionamiento.
• Son capaces de realizar tareas complejas de reconocimiento de patrones y estimación de parámetros.

Además, tienen la capacidad de generalizar y son adaptables ya que pueden adaptar sus pesos sinápticos a los cambios en el ambiente que las rodea, y con ellas se consiguen bajos tiempos de procesamiento debido a su funcionamiento en paralelo.

2.1. Estructura de la neurona

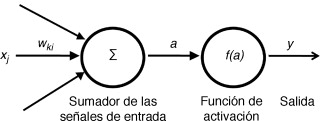
El bloque constituyente básico de una red neuronal artificial es la neurona, que es la unidad básica de procesamiento y tiene múltiples entradas pero una única salida, como podemos observar en la figura 1 . Se pueden identificar 3 elementos básicos en el modelo neuronal:

• Las conexiones, cada una de las cuales tiene un peso propio (el peso sináptico, ${\textstyle w_{kj}}$ ), que varía mediante el entrenamiento para adaptarse a la salida deseada. Es aquí donde se une la señal de entrada (x_j ) con la neurona k, la cual es multiplicada por el peso.
• El sumador de las señales de entrada, variadas ya por los pesos sinápticos.
• La función de activación, que se encarga de limitar la amplitud de la salida. Las redes neuronales se conforman poniendo las neuronas en diversas capas y conectando las salidas de una capa a la entrada de la siguiente. Matemáticamente una neurona se puede representar como:

Figura 1. Estructura de una neurona.

$a=\sum _{j=1}^{n}w_{kj}\cdot x_{j}+{\theta }_{k}$

( 1)

donde a   es la salida del sumatorio de las señales de entrada modificadas, ${\textstyle w_{kj}}$ son los pesos sinápticos de la neurona, θ_k es el sesgo y x_j es el valor de las señales de entrada.

Obteniéndose la salida (y ) como:

$y=f(a)$

( 2)

2.2. Arquitectura de la neurona

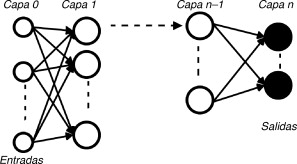
A la hora de desarrollar la red neuronal es importante tener en cuenta su arquitectura, que viene definida por los pesos sinápticos, el número de capas y la conexión entre los distintos elementos que forman la red neuronal. Estas conexiones pueden ser de alimentación unidireccional (feedforward) o de retroalimentación (feedback) , entre otras.

Con la alimentación unidireccional, las capas están conectadas entre sí en una única dirección y las salidas de una se conectan en la entrada de la siguiente (fig. 2 ). La retroalimentación permite que alguna de las salidas de alguna capa no tenga que conectarse con la capa siguiente, sino que se pueda conectar con una capa anterior.

Figura 2. Unión de las capas de una red neuronal.

2.3. Diseño del modelo de red neuronal

La red neuronal elegida para realizar el presente modelo es una red neuronal de regresión general (GRNN) [8] . Este tipo de red se entrena rápidamente en un único paso ya que, a diferencia de otros tipos de redes neuronales, no realiza sucesivas iteraciones variando los pesos sinápticos, y puede entrenarse nuevamente tan pronto como se disponga de nuevos datos. Por otra parte, la red GRNN es capaz de capturar el comportamiento de los sistemas no lineales.

La expresión (3) es la ecuación fundamental de la GRNN y calcula el valor más probable de Y para cada valor de X basado en un número finito de datos de entrenamiento. Es una red paralela y permite aprender y estimar los valores de Y para cada valor de entrada X . Para ello, como se observa en la ecuación, se ayuda de la distribución gaussiana.

${\overset {\mbox{ˆ}}{Y}}(x)={\frac {{\sum }_{i=1}^{n}Y_{i}exp({\frac {-D_{i}^{2}}{2{\sigma }^{2}}})}{{\sum }_{i=1}^{n}exp({\frac {{\left(-D_{i}^{2}\right)}^{2}}{2{\sigma }^{2}}})}}$

( 3)

siendo D_i la matriz de distancias entre los valores del entrenamiento y los puntos de predicción.

$D_{i}^{2}={\left(X-X_{i}\right)}^{T}(X-X_{i})$

( 4)

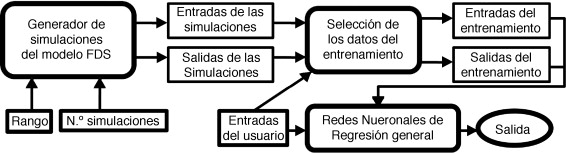
Para el desarrollo de la red neuronal se ha empleado la herramienta Matlab, concretamente su Neural Network Toolbox^TM 6 [9] , en la cual está implementada la función newgrnn que se encarga de generar esta red. Esta función recibe directamente como entradas todos los datos de entrenamiento y crea con ellos la red neuronal deseada. En el caso de disponer de un número adecuado de datos, la creación y el entrenamiento de la red son muy rápidos, aunque si introducimos en el modelo un número muy elevado de valores de entrenamiento puede ralentizarse la operación. Para mejorar este elevado coste computacional se han desarrollado una serie de funciones adicionales con las cuales se seleccionan los valores del entrenamiento de los que va a disponer la red para efectuar su entrenamiento (fig. 3 ).

Figura 3. Esquema de las funciones empleadas.

La primera función desarrollada tiene como objetivo la creación y ejecución de un número de simulaciones del modelo FDS a partir de una selección aleatoria del tamaño del recinto, la potencia y localización del incendio y las condiciones ambientales de ese espacio, dentro de un rango de valores establecido por el usuario. Se obtienen de esta primera función los parámetros antes mencionados que se emplean para definir dichas simulaciones, y la temperatura y la altura de la capa caliente de los humos calculadas por esos determinados incendios.

El resultado de esta primera función, junto con los valores de entrada deseados por el usuario para su caso de estudio particular, sirven a la segunda función para realizar una selección de los valores de entrada del entrenamiento más cercanos a ese caso de estudio, salvo para la posición de la fuente de ignición que solo dispone de 3 posiciones (posición esquina, en una pared o por el resto del recinto). Igualmente, selecciona también los resultados más próximos del entrenamiento asociados a los anteriores. Con esta función se obtienen dichos valores de entrada y resultados del entrenamiento, que finalmente se emplearán en la red.

Por último, se creó una tercera función en la cual se desarrollan 2 redes neuronales, para la temperatura y para la altura de la capa de humos respectivamente. Para ello se empleó la función newgrnn de Matlab, con los valores de entrada obtenidos mediante las funciones anteriores. En esta función se introducen los datos que empleará la red para su entrenamiento, que se lleva a cabo mediante 45 simulaciones, las cuales constan de 45 vectores de entrada con sus respectivos 45 vectores de salida. Cada uno de estos vectores de entrada está formado por los 7 parámetros considerados por el modelo y cada vector de salida consta de 40 datos de temperatura o de altura de los humos en función del tiempo. Introduciendo en la red creada los 7 parámetros de entrada deseados, se obtienen sus salidas correspondientes.

La GRNN está formada por 2 capas. La primera tiene tantas neuronas como los vectores de entradas y salidas, en nuestro caso 45. Cada una de las entradas a la función radial de la primera capa es el producto de su entrada por su sesgo, que se toma como 0,8326/SPREAD. Cada salida de las neuronas de la primera capa es su entrada de red pasada por la función radbas de Matlab. Esta es una red neuronal radial que requiere más neuronas que las redes de realimentación pero que se diseña en mucho menor tiempo, en la cual si el vector de pesos de la neurona es igual al vector de entrada, su entrada ponderada será 0, su entrada de red será 0 y su salida 1. Si la distancia euclídea entre el vector de pesos de la neurona y el vector de entrada es igual al valor SPREAD, su entrada ponderada será SPREAD y su salida será 0,5.

La segunda capa también tiene tantas neuronas como los vectores de entradas/salidas, con lo que hacen entre las 2 capas 90 neuronas, y emplea la función lineal de transferencia purelin.

Un SPREAD grande permite una gran área alrededor del vector de entrada en la que la capa 1 de neuronas responderá con salidas significativas. Por su parte, si el SPREAD es pequeño, los pesos cercanos a la entrada tendrán mucha más influencia. El SPREAD por defecto toma el valor de 1.

3. Entrenamiento de la red neuronal

Tal y como se comentó anteriormente, el entrenamiento de la red neuronal se ha llevado a cabo mediante el empleo del modelo FDS [10]  and [11] . A fin de conseguir un amplio número de simulaciones para el entrenamiento, se ha creado un proceso automatizado que permite optimizar el tiempo empleado en el lanzamiento de las simulaciones.

Los parámetros de entrada que se han seleccionado por ser considerados los más significativos para el escenario de incendio analizado son: las dimensiones del recinto que contendrá el incendio, la fuente de ignición definida por su posición en el recinto y por su velocidad de cesión de calor por unidad de área (HRRPUA) y la temperatura ambiente en el recinto.

En la tabla 1 se muestran los rangos empleados para los valores de los parámetros de entrada. Estos parámetros se considerarán para un recinto cerrado en el cual se disponen unas pequeñas aberturas en la parte inferior para evitar el aumento de presión en su interior.

Tabla 1. Rango de variables de entrada de la red neuronal.

	Valor mínimo	Valor máximo
Temperatura ambiente (°C)	19	22
HRRPUA (kW/m2 )	225	1.000
Largo recinto (m)	2,5	5,2
Ancho recinto (m)	2,5	5,2
Alto recinto (m)	1,6	2,5
Posición de la fuente de ignición	Pared/Esquina/Interior

El rango de valores anterior ha sido seleccionado según el trabajo realizado en la tesis doctoral del Dr. Espina: ”Método para la determinación de la interfase térmica de los humos del incendio en atrios basado en el modelado a escala de Froude” [12] .

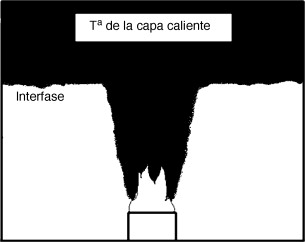
Como salidas del modelo se obtendrá la temperatura de la capa caliente y de la altura de la interfase de separación capa caliente-capa fría (fig. 4 ). Se recogerán valores de estos parámetros cada 10 s y la simulación total constará de 400 s, por lo que se obtendrán un total de 40 salidas para cada uno de los 2 parámetros.

Figura 4. Parámetros de salida proporcionados por el modelo.

Uno de los ejemplos del compartimento del estudio se muestra en la figura 5 . Se realizaron 4.640 simulaciones para el entrenamiento que permitieron disponer de un amplio número de datos dentro del rango de la tabla 1 .

Figura 5. Ejemplo de simulación del entrenamiento con FDS.

4. Validación de los resultados frente a FDS y CFAST

Los resultados obtenidos con el modelo desarrollado mediante el empleo de redes neuronales artificiales se compararán en el presente apartado con los obtenidos por los modelos CFAST y FDS. Con ello se pretende comprobar su validez para el modelado de la dinámica computacional del incendio en recintos cerrados [13] , [14]  and [15] .

Se considera el caso 1 mostrado en la tabla 2 con los parámetros de entrada mostrados en esta misma tabla.

Tabla 2. Parámetros de entrada de casos comparativos.

Caso	Temperatura ambiente	HRRPUA	Largo	Ancho	Alto	Localización de la fuente
1	20	662	3	3,4	2	Interior
2	19	375	2,7	2,7	2	Pared
3	19	375	2,7	2,7	2	Interior
4	19	375	2,7	2,7	2	Esquina

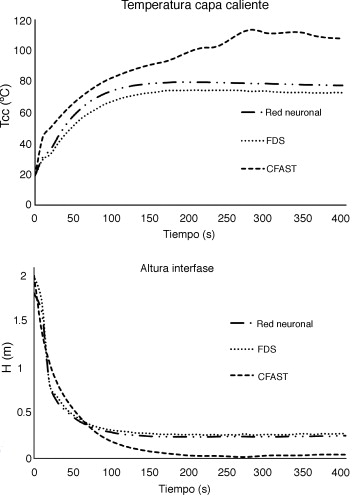
En la figura 6 se exponen las gráficas comparativas de la temperatura de la capa caliente y de la altura de la interfase, comparando los modelos FDS, CFAST y la red neuronal desarrollada. En dichas gráficas se puede observar el comportamiento del incendio en un recinto cerrado con la fuente de ignición situada en un punto interior del recinto con las características descritas en la tabla 2 . Se observa cómo, partiendo de una temperatura de 19 °C, la capa caliente va calentándose hasta alcanzar alrededor de 40 °C en el modelo de FDS y en el basado en la red neuronal, mientras que se alcanza un valor de alrededor de 49 °C con CFAST. Se puede observar que en un instante inicial la pendiente del modelo CFAST es mucho mayor, y a partir de los 110 s los modelos FDS y el de la red neuronal mantienen la temperatura constante, mientras que en CFAST sigue aumentando. En lo que respecta a la altura de la interfase el modelo CFAST tiene una pendiente más suavizada y alcanza una altura final de 13 cm, mientras que los otros 2 modelos tienen inicialmente una gran pendiente y se estabilizan antes alcanzando los 26 cm.

Figura 6. Gráficas comparativas de temperatura en la capa caliente y de la altura de la interfase, con FDS, CFAST y el modelo de la red neuronal. Caso 1.

Además, se ha podido comprobar en otras simulaciones realizadas que los modelos FDS y el de redes neuronales tienen en cuenta el efecto esquina mientras que el modelo CFAST no lo tiene en cuenta.

A continuación, la tabla 3 muestra los errores relativos de los modelos, tomando como referencia el modelo de campo FDS ya que este es el que mejor se aproxima a la realidad.

Tabla 3. Errores relativos de la red neuronal y de CFAST con respecto a FDS

ERROR RELATIVO			Ej.1	Ej.2	Ej.3	Ej.4
	PROMEDIO	Red Neuronal	7,75%	1,27%	0,60%	5,23%
		CFAST	37,61%	32,03%	25,56%	36,20%
TEMPERATURA CAPA CALIENTE	ERROR MÁXIMO	Red Neuronal	12,55%	4,97%	2,00%	6,54%
		CFAST	54,32%	46,40%	41,24%	50,88%
	ERROR MÍNIMO	Red Neuronal	0,00%	0,00%	0,00%	0,00%
		CFAST	0,00%	0,00%	0,00%	0,00%
	PROMEDIO	Red Neuronal	7,73%	2,69%	2,52%	9,45%
		CFAST	65,38%	60,29%	57,42%	62,68%
ALTURA INTERFASE	ERROR MÁXIMO	Red Neuronal	10,73%	6,30%	13,47%	12,96%
		CFAST	93,65%	79,98%	78,80%	82,10%
	ERROR MÍNIMO	Red Neuronal	1,85%	0,16%	0,17%	6,30%
		CFAST	0,01%	0,01%	0,01%	0,01%

Como se puede observar en la tabla 3 , al estar entrenada la red con simulaciones realizadas con FDS, los errores cometidos por la red neuronal con respecto a los datos obtenidos con FDS dentro de los parámetros de entrenamiento considerados son mucho menores que los cometidos por el modelo de zona CFAST.

5. Validación de resultados frente al ensayo a escala reducida

Para poder llevar a cabo la validación del modelo basado en el empleo de redes neuronales se han vuelto a emplear el modelo de zona CFAST y el modelo de campo FDS, con unas simulaciones diferentes a las empleadas para el entrenamiento, y se emplearon además los resultados de un ensayo a escala reducida desarrollado para el Proyecto de Investigación del Grupo GIDAI ”Modelado Físico del Movimiento de Humos en Caso de Incendio en Atrios”, financiado por el Ministerio de Vivienda [16] .

Los resultados de los ensayos realizados son los que más peso tienen durante el proceso de validación, ya que los modelos tienen un error (mayor o menor), y con los ensayos reales se puede observar el ajuste que lleva a cabo la red neuronal a la dinámica del incendio en un recinto real para el que se ha diseñado.

En la tabla 4 se muestran las entradas para 2 de los ensayos realizados.

Tabla 4. Valores de los parámetros de entrada de los ensayos realizados

Ensayo	Temperatura ambiente	HRRPUA	Largo	Ancho	Alto	X Fuego	Y Fuego
1	20	225	3	3	1,8	1,5	1,5
1	20	225	3	3	2,2	1,5	1,5

Los resultados de la temperatura de la capa caliente de humos y de la interfase de separación de la capa caliente y la fría para el ensayo 1 se recogen en la figura 7 .

Figura 7. Resultados de la temperatura de la capa caliente y de la altura de la interfase de los modelos CFAST, FDS y el modelo desarrollado frente al Ensayo 1.

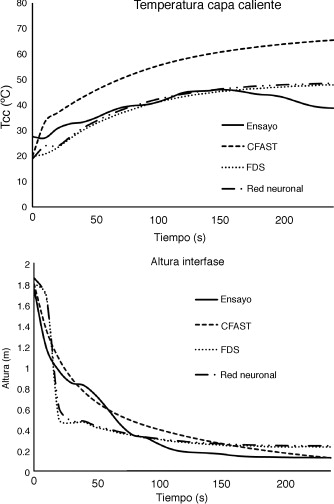
Se puede observar cómo, para el caso de la temperatura de la capa caliente de humos, los resultados obtenidos por la red neuronal y por el modelo FDS se aproximan a los obtenidos en el ensayo a escala real, diferenciándose únicamente en los instantes finales donde la fuente de ignición del ensayo de fuego a escala real pierde potencia debido a la propia fase de decaimiento, mientras que en los 2 modelos computacionales permanece prácticamente estable, debido a que ambos modelos consideran constante la velocidad de cesión de calor de la fuente de ignición.

Por otro lado, se comprueba cómo el modelo CFAST comienza ganando temperatura con mayor pendiente inicialmente, y se va alejando del valor obtenido por el ensayo a escala, con una diferencia de más de 25 °C durante gran parte del ensayo.

En cuanto a la altura de la interfase, se observa cómo en este caso es el modelo CFAST el que consigue un mejor ajuste a los datos proporcionados por el ensayo a escala real; sin embargo, los resultados de los otros modelos no se alejan en exceso, y aunque inicialmente el modelo FDS y el de la red neuronal disminuyen la altura de la capa caliente mediante una gran pendiente, finalmente alcanzan una diferencia de apenas 10 cm en los instantes finales.

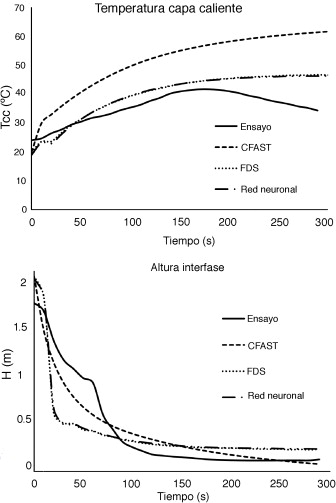
El ensayo 2, que se muestra en la figura 8 , es semejante al anterior, con la única variación de la altura del recinto, que ha pasado de 1,8 m a 2,2 m.

Figura 8. Resultados de la temperatura de la capa caliente y de la altura de la interfase de los modelos CFAST, FDS y el modelo desarrollado frente al Ensayo 2.

Se observa que el comportamiento es similar al caso anterior, donde el modelo FDS y el modelo de la red neuronal obtienen una buena aproximación a la temperatura de la capa caliente, mientras que el modelo de zona CFAST se ajusta ligeramente mejor en la altura de la interfase.

Se puede concluir que el modelo FDS y la red neuronal obtienen mejores resultados globales en su aproximación a la dinámica computacional de incendios, y se ajustan mejor a los ensayos de fuego realizados.

En lo que respecta a los tiempos de cómputo (tabla 5 ), se puede observar cómo con el empleo de las redes neuronales se obtienen unos tiempos de cómputo del orden de los obtenidos con el modelo de zona CFAST, mejorando enormemente los tiempos alcanzados por el modelo de campo FDS, lo que permite plantear su uso en aplicaciones que requieren una rápida respuesta.

Table 5. Tiempos de cómputo requeridos por los modelos

	Red neuronal	FDS	CFAST
Tiempo de cómputo	20 s	90 min	10 s

6. Conclusiones

Se ha presentado el diseño de un modelo sustituto de incendios basado en el empleo de redes neuronales artificiales, y se ha demostrado que alcanza las exigencias requeridas, al conseguir resultados similares a los obtenidos con modelos de campo, con menor tiempo de cómputo, y para el caso de un recinto que se encuentra dentro de un rango conocido. El presente artículo indica las posibilidades de este nuevo enfoque, y ofrece información de importancia vital a la hora de realizar el estudio de un incendio en tiempo real.

Es preciso, para que este nuevo enfoque sea válido, el desarrollo de modelos específicos para los escenarios que se deseen estudiar, a través de datos de entrenamientos relativos a cada escenario. Además, es necesario profundizar en otros tipos de redes neuronales a fin de poder seleccionar la que mejor se aproxime al fenómeno del incendio.

Agradecimientos

Los autores queremos agradecer al Ministerio de Ciencia e Innovación (Gobierno de España) por la subvención TRA2010-19006 otorgada por el proyecto ”Modelado Matemático de la Combustión de los Materiales Presentes en los Trenes de Pasajeros de Alta Velocidad”.

References

1. [1] D. Alvear, J. Capote, M. Lázaro, P. Espina; Heat Release Rate and Computer Fire Modeling vs. Real Scale Fire Tests in Passenger Trains; Fire and Materials, 32 (2008), pp. 213–229
2. [2] D. Alvear, J. Capote, M. Lázaro, G. Rein, J.L. Torero, O. Abreu, Modelado y Simulación Computacional de Incendios en la Edificación, Ediciones Díaz de Santos, Madrid, 2007.
3. [3] M.L. Janssens; An Introduction to Mathematical Fire Modeling; Technomic Publishing Company, Lancaster, EE. UU (2000)
4. [4] R.D. Peacock, W.W. Jones, P.A. Reneke, G.P. Forney, “CFAST - Consolidated Model of Fire Growth and Smoke Transport (Version 6) - Technical Reference Guide”. National Institute of Standards and Technology, NIST Special Publication 1026, April 2009.
5. [5] Kevin McGrattan, Simo Hostikka, Jason Floyd “Fire Dynamics Simulator (Version 5) - Technical Reference Guide”. National Institute of Standards and Technology (NIST). September 2009.
6. [6] R.M. Hritsev; The ANN Book; GNU Public License (1998)
7. [7] S. Haykin; Neural Network, A Comprehensive Foundation; Pearson Prentice Hall., Delhi, India (1999)
8. [8] D.F. Specht; A General Regression Neural Network; IEEE transactions on neural networks, 2 (6) (november 1991), pp. 568–576
9. [9] MATLAB R2008. The Language of Technical Computing. The MathWorks, Inc., 2008.
10. [10] M. Kowalczykiewicz, “Recurrent Neural Networks for CFD based Optimization”. Thesis. Cranfield University, Cranfield, 2007.
11. [11] E.W.M. Lee, R.K.K. Yuen, S.M. Lo, K.C. Lam, G.H. Yeoh; A novel artificial neural network fire model for prediction of thermal interface location in single compartment fire; Fire Safety Journal, 39 (2004), pp. 67–87
12. [12] P. Espina; Método para la determinación de la interfase térmica de los humos del incendio en atrios basado en el modelado a escala de Froude; Tesis Doctoral. Universidad de Cantabria (2009)
13. [13] B. Karlsson, J. Quintiere; Enclosure Fire Dynamics; CRC Press, Florida, EE. UU (2000)
14. [14] M. Janssens, H.C. Tran; Data reduction of room tests for zone model validation; Journal of Fire Sciences, 10 (6) (1992), pp. 528–555
15. [15] J. Capote, D. Alvear, O. Abreu, M. Lázaro, P. Espina, Analysis of the Smoke Management Approaches in Large Atriums using Fire Computer Modelling, Fire Computer Modeling, Universidad de Cantabria, GIDAI, Santander, 2007, pp. 147–167.
16. [16] J.A. Capote, D. Alvear, M. Lázaro, P. Espina, A. Cuesta; Scale Tests of Smoke Filling in Large Atria; Fire Technology, 45 (2) (2009), pp. 201–220 ISSN: 0015-2684,