Simplified thermal and hygric building models: A literature review

Abstract

This paper provides a systematic literature review on simplified building models. Questions are answered like: What kind of modelling approaches are applied? What are their (dis)advantages? What are important modelling aspects? The review showed that simplified building models can be classified into neural network models (black box), linear parametric models (black box or grey box) and lumped capacitance models (white box). Research has mainly dealt with network topology, but more research is needed on the influence of input parameters. The review showed that particularly the modelling of the influence of sun irradiation and thermal capacitance is not performed consistently amongst researchers. Furthermore, a model with physical meaning, dealing with both temperature and relative humidity, is still lacking. Inverse modelling has been widely applied to determine models parameters. Different optimization algorithms have been used, but mainly the conventional Gaus–Newton and the newer genetic algorithms. However, the combination of algorithms to combine their strengths has not been researched. Despite all the attention for state of the art building performance simulation tools, simplified building models should not be forgotten since they have many useful applications. Further research is needed to develop a simplified hygric and thermal building model with physical meaning.

Keywords

Literature review ; Building performance simulation ; Simplified building models ; Inverse modelling ; Climate change

1. Introduction

Within the European project Climate for Culture , researchers are seeking to find the influence of the changing climate on the built cultural heritage. The Building Physics and Systems group at the University of Technology of Eindhoven participate in this project ( Schijndel et al., 2010 ). Currently they are able to simulate the indoor climate of several monumental buildings for the next hundred years (for results see Kramer, 2011 ) using the model HAMLab (Schijndel, 2007 ) with artificial climate data for the years 2000 until 2100.

Due to the long simulation period (hundred years with time step 1 h), combined with detailed physical models, the simulation run time is long. Furthermore, the detailed modelling of the buildings itself requires much effort: the monumental buildings are old and protected. Therefore, blueprints are hard to find and destructive methods to obtain building material properties are not allowed.

A simplified model with physical meaning is desired which is capable of simulating both temperature and relative humidity. The parameters of the model will be derived by an inverse modelling technique which fits the output of the model to measured values of respectively temperature and relative humidity.

To create a clear starting point for modelling, a literature review on the field of simplified building models is needed. However, despite the large amount of research efforts on simplified building models, a literature review is missing.

This paper will be very interesting for anyone who wants to know more about simplified building models. Questions are answered like: what kind of modelling approaches are applied? What are their (dis)advantages? What are important modelling aspects? Section 2 gives a brief history.

Section 3 deals with simplified building models, with 3.1 , 3.2  ;  3.3 respectively on neural network models, linear parametric models and RC-models. Finally, Section 4 reviews the topic of inverse modelling.

2. Building simulation models: a brief history

Building simulation models have been developed over many years, starting with very simple models (e.g., Bruckmayer, 1940 ) which dealt with the analysis of conduction through one building element. These models were completely analytical.

Later, in the 1970s and 1980s, research was focused on four approaches which modelled one or more building zones:

• Response factor methods (e.g., Mitalas and Stephenson, 1967 ). A time series of responses is calculated from a time series of unit pulses based on building properties.
• Conduction transfer functions (e.g., Stephenson and Mitalas, 1971 ). Laplace transfer functions relate temperature and heat fluxes in (a layer of) a wall to boundary conditions.
• Finite difference methods (e.g., Clarke, 1985 ). A wall is divided into a finite number of control volumes for which the heat balance equation are solved.
• Lumped capacitance methods (e.g., Crabb et al., 1987 ). The electrical analogy is used to model a building element using resistances and capacitances. A capacitance represents the thermal capacitance of (a layer of) a wall.

Sometimes, different approaches are combined. For example, Xu and Wang (2008) use CTF for detailed modelling of the conduction through walls and use a thermal network model (Lumped capacitance model) for the modelling of the rest of the building zone. However, detailed wall properties are necessary to use the CTF approach. Santos and Mendes (2004) use the finite difference method for wall conduction and the lumped capacitance method for the rest of the building zone.

The most recent development in research is to achieve a synergy by using several simulators simultaneously (Trčka, 2008 ), which is referred to as co-simulation. In this way, the strength of different simulators can be combined.

3. Simplified building models

Due to the increase of computational power, the attention for simplified models has decreased. However, through the years it became clear that simplified models have benefits over complex models (Wang and Chen, 2001 ; Mathews et al., 1994 ): user friendliness, straight forward, and fast calculation.

The response factor method and lumped capacitance method are suitable for simplified modelling. More recently, linear parametric models and neural network models are used for simplified models.

Neural network models (e.g., Mustafaraj et al., 2011 ) can be classified as black box models. The parameters have no direct physical meaning, but the output is generated by the hidden layers (black box) from the input.

Some models are referred to as grey box models. An example in the field of simplified building models is the use of linear parametric models (Mustafaraj et al., 2010 ). The linear model itself is a black box model, but the parameters can be determined using physical data (Jimenez et al., 2008 ).

Some researchers stress out the importance of simplified models with physical meaning (Kopecký, 2011 ), so called white box models. The lumped capacitance model can be classified as a white box model. Another advantage of this approach is the representation of building elements using R (resistance) and C (capacitance), according to the electrical analogy, which makes a graphical representation of the model possible. Most of the simplified building models are based on this approach.

There are three approaches to create a simplified model:

• Create a detailed comprehensive model from known building properties and perform afterwards a model order reduction technique (e.g., Gouda et al., 2002 ).
• Create directly a simplified model from building properties (e.g., Nielsen, 2005 ).
• Create a simplified model and identify the parameter values with an inverse modelling technique (Balan et al., 2011 ).

Technique 1 is obviously the most labour intensive: building a detailed model and simplifying it afterwards. Detailed construction properties need to be available together with a methodology for simplifying an existing model. The lumped capacitance model can be used for this model order reduction (Mathews et al., 1994 ) and neural network models can be used to filter out unimportant parameters (Mustafaraj, 2011 ), called pruning. Technique 2 is faster, but a validated methodology should be known as to how to identify the parameters. Therefore, it is difficult to achieve good results with this technique. Fraisse (2002) has demonstrated a methodology how to incorporate multiple walls into one single order model. Technique 3 is not labour intensive and identification of the model parameters is done by an optimization algorithm. This technique can be used with the lumped capacitance model (Wang and Xu, 2006b ), neural network model (e.g., Mustafaraj, 2011 ) and linear parametric model (e.g., Moreno et al., 2007 ).

3.1. Neural network models

Neural network models belong to the group of black box models: no knowledge is needed about the physical properties of the building. It is a data driven modelling technique. This can be a huge advantage if no information about the physical properties is known, but the disadvantage is that the building cannot be characterized by its parameters. However, neural network nonlinear models can be used to validate and remove unimportant inputs while preparing for physical modelling (Seginer et al., 1994 ). Unlike physical models, neural network models can be made adaptive and self learning (Mustafaraj, 2011 ).

Creating a neural network model involves three or four steps:

• input–output data collection from measurements.
• Using linear model to determine input for neural network model (optional).
• Model structure selection.
• Optimization and model validation.

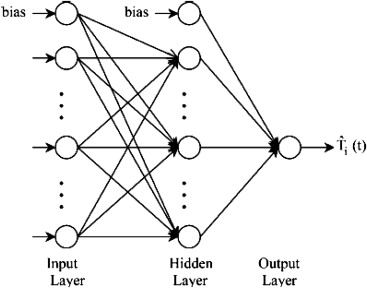
Neural networks are based on the same functioning principle as the human brain. The relationship between inputs and outputs is determined by linear or nonlinear relationships defined in the neuron layers, see Figure 1 . A neural network model can have several layers. Most past research works (Lu and Viljanen, 2009 ; Patil et al ., 2008  ;  Mechaqrane and Zouak, 2004 ) demonstrate that a three-layer feed forward neural network can approximate any function as long as a sufficient number of hidden neurons are provided. Mustafaraj (2011) found 12 neurons to be sufficient before training. Other researchers used slightly different numbers of neurons in the hidden layer, e.g., Mechaqrane and Zouak (2004) used 10 neurons in the hidden layer, but have not motivated why the particular number of neurons have been used.

Figure 1. Graphical representation of a simple neural network.

A common problem can be overfitting : overfitting means the network performs well in the training stage but has poor generalization ability. To avoid overfitting, a pruning algorithm called optimal brain surgeon (OBS) can be applied to determine the optimal network topology (optimal number of nodes and connections between them) ( Norgaard et al ., 2002  ;  Mechaqrane and Zouak, 2004 ). For example, Mechaqrane and Zouak (2004) have found a reduction of 73% of connections by pruning, resulting in a reduction of the summed-squared-error from 2.0632 to 0.9060.

Different types of neural network models exist. Ruano et al. (2006) used RBF (radial basic function) to model the output based on given input. An RBF model has no feedback. On the other hand, fully recurrent neural networks have feedback from the neurons in the hidden layer. Siegelmann et al. (1997) proved that these fully recurrent models are computationally rich. However, they compared the performance of these recurrent neural network models with NARX models (Nonlinear AutoRegressive models with eXogenous inputs) which have a limited feedback: only from the output. They concluded that NARX models can be used without any computational loss compared to fully recurrent models. Most researchers use NARX nowadays: Frausto and Pieters (2004) , Mechaqrane and Zouak (2004) , Mustafaraj (2011) , and Frausto and Pieters (2004) have used neural networks for the prediction of the indoor temperature of a greenhouse. Ruano et al. (2006) have used neural network models to predict the indoor temperature of a building. Only very few researchers have dealt both with temperature and relative humidity. Only Lu and Viljanen (2009) and Mustafaraj et al. (2011) have used neural networks for the prediction of temperature and relative humidity.

Whereas a linear model cannot predict nonlinear relationships (e.g., relative humidity) between variables with high accuracy, this problem does not exist with neural network models (Siegelmann et al ., 1997  ;  Menezes and Barreto, 2008 ). A simple solution to this restriction would be to calculate with specific moisture content, x (g/kg), because this property is linear in contrast to the nonlinear relative humidity (%).

3.2. Linear parametric models

A linear parametric model is also a black box model. No knowledge is needed about the physical properties of the building (Srinivas and Brambley, 2005  ;  Fraisse et al ., 2002 ). It is a data driven modelling technique.

According to Mustafaraj et al. (2010) , there are several advantages of linear parametric models versus non-linear neural network models: (i) they are simple (low number of model parameters); (ii) they are much easier to deal with due to the potential of connecting them with physical models of the system in contrast with non-linear neural networks which are not able to relate model parameters with the systems physical parameters; (iii) a disadvantage of non-linear networks is that their parameters (i.e., weights) vary after each trial (i.e., training the network on the same weekday many times), whereas this does not happen with linear models; (iv) linear models are easier to use in control schemes for HVAC plants.

The equations are simple and the parameters can be interpreted with the physical model of the building. This will help future research work to identify grey box models which are based partially on physical knowledge and partially on empiricism (Moreno et al ., 2007  ;  Balan et al ., 2011 ). Attempts at building grey box models can be seen in Norlén (1990) and Jimenez et al. (2008) .

Norlén (1990) developed a method based on an autoregressive ARMAX model to describe the dynamics of the heat flows in a test cell. Loveday and Craggs (1993) used Box–Jenkins to describe the thermal behaviour of a building influenced by a number of variables, including external temperature variation, ventilation rate fluctuations and occupancy pattern variation. Past research works have built linear models to predict room temperature for greenhouses (Moreno et al ., 2007  ; Boaventura Cunha et al ., 1997  ;  Frausto et al ., 2003 ) and an office building (Lowry and Lee, 2002 ).

There are several reasons why the research efforts of Mustafaraj et al. (2010) should be mentioned exclusively: (i) the research presented in their paper is related to developing models for a real office whereas previous researchers have applied these models mainly to experimental rooms and HVAC plants in which experimental conditions can be managed. (ii) Past research on thermal model development has been related mainly to linear parametric ARX and ARMAX models (Moreno et al ., 2007  ; Boaventura Cunha et al ., 1997  ;  Frausto et al ., 2003 ), with few research papers (e.g., Lowry and Lee, 2002 ) dealing with BJ and OE models. Mustafaraj et al. (2010) include ARX, ARMAX, BJ and OE models. (iii) Predictions of different time scales are investigated, i.e., 6, 12 and 24 steps ahead (30 min, 1 and 2 h) are produced, while in the past most papers mainly dealt with model simulation (Moreno et al ., 2007  ; Boaventura Cunha et al ., 1997  ; Frausto et al ., 2003  ;  Lowry and Lee, 2002 ). Also, the criteria of goodness of fit, mean absolute error, mean squared error and coefficient of determination are given particular importance. (iv) Their research uses linear models to predict relative humidity for long periods (nine months) whereas past researches, such as Boaventura et al. (1997) and Lu and Viljanen (2009) , built models based on short periods of data collection for 6 and 30 days respectively. (v) In the past, apart from Lu and Viljanen (2009) who used a NARX model to predict relative humidity, no research papers have used black box linear parametric models to predict relative humidity. (vi) In their research, models are developed using data collected over long periods (nine months), whilst in past research works models were developed using a limited period of data collection. For example, Boaventura Cunha et al. (1997) used 6 days, Loveday and Craggs (1993) recorded two weeks of hourly data, Lowry and Lee (2002) three weeks, Lu and Viljanen (2009) 30 days and Moreno et al. (2007) 36 days. Models developed and validated using a limited range of data are not reliable for predicting room temperature and relative humidity with high accuracy outside the range of data used for their development and validation.

3.3. RC-models

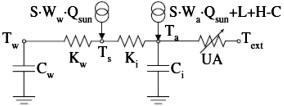
Lumped capacitance models are white box models. The parameters of the model have clear physical meaning (Wang and Xu, 2006b ). The model can be built by using the electrical network analogy: a thermal resistance is represented by an R (analogous to electrical resistance) and a thermal capacitance is represented by a C (analogous to electrical capacitance). The connecting nodes represent a certain temperature. The model order is equal to the number of used C s and for every C , the governing equations include a differential equation. Using these R s and C s, the network can be represented graphically as shown in Figure 2 , which shows the simplified model of Nielsen (2005) .

Figure 2. Graphical representation of a lumped capacitance model (Nielsen, 2005 ).

Research has been focused mainly on: (i) required model order (Hudson and Underwood, 1999 ; Fraisse et al ., 2002  ; Gouda et al ., 2002  ;  Xu and Wang, 2007 ); (ii) what part of the building should be wrapped into one C ( Antonopoulos and Koronaki, 1998 ; Antonopoulos and Koronaki, 1999 ; Fraisse et al ., 2002  ;  Wang and Xu, 2006b ).

Almost all research efforts using the RC-network method only deal with the simulation of temperature (Antonopoulos and Koronaki, 1998 ; Hudson and Underwood, 1999 ; Fraisse et al ., 2002  ; Gouda et al ., 2002  ; Nielsen, 2005 ; Wang and Xu, 2006b ; Penman, 1990  ;  Richards and Mathews, 1994 ). Only Santos and Mendes (2004) deal with both temperature and moisture, but they focused more on the numerical methods solving the differential equations.

Other important questions are: what are important input parameters and where should these input parameters be included in the model? Surprisingly, not one research article has dealt with this for the RC-models. All researchers started with certain chosen parameters, some researchers motivated and some researchers have not motivated why they have chosen for the parameter set. Only Frausto et al. (2003) have researched the input parameter set, but this was done for linear parametric models (ARX and ARMAX). Nevertheless, this may also be valuable information for RC-models. The objective of their study was to investigate the outside climate variables which must at least be included in linear auto-regressive models simulating the inside air temperature of a greenhouse. It was concluded that a general model for a complete year must include four input variables relating to the outside climate: air temperature, relative humidity, global solar radiation, and cloudiness. The relative humidity was least influencing the output and may be less important for other types of buildings, e.g., offices.

Schijndel (2009) has introduced the Crest factor to assess the power of an input parameter. The Crest factor is commonly used in electrical engineering to determine the input power of a signal. For example, one cannot find a Solar Gain factor for windows if measurements are taken during night. Furthermore, Schijndel (2009) states that the simulated objective data (e.g., temperature and relative humidity) should be sensitive enough for changes in the parameters, otherwise, a parameter can have a band width of possible solutions. This is especially a problem for characterizing a building by its parameters when searching for model parameters in an inverse problem.

Antonopoulos and Koronaki (1998) introduced the concept of an effective thermal capacitance (C_eff ), which is a fraction of the apparent thermal capacitance (C_a ). The apparent capacitance (C_a ) is the sum of the buildings capacitances. However, if this value is used for the C in the simplified model, the dynamics of the model do not match the buildings' dynamics. Antonopoulos and Koronaki (1998) found that the effective thermal capacitance (C_eff ) decreases if the heat losses increase. For insulated buildings he found 2.2<C_a /C_eff <3.1 and for uninsulated buildings C_a /C_eff ≈4.5. This is an important aspect because, if the parameters of the model are determined by inverse modelling (fitting the output of the model to measured values), the found values for the models' capacitances represent the C_eff , not the C_a . Antonopoulos and Koronaki (1999) subsequently divided the total capacitance (C_eff ) into a capacitance for the envelope (C_env ), for the furnishings (C_fur ) and indoor partitions (C_par ).

Hudson and Underwood (1999) used a first-order model and concluded that it performed well for the short term, but for the longer term a second order model is required. The model order is apparently not only depending on the mass of the building, but also on the length of the simulation period.

Richard and Mathews (1994) are the only ones who have dealt with the modelling of buildings in ground contact for use in simplified RC-models. They have validated their model in 53 existing buildings, covering a wide range of thermal characteristics. However, the model is a set of equations incorporating building parameters, which need to be calculated from the existing buildings properties. Of course, this is not a satisfactory method if one is seeking for a simplified model, in which the parameters are identified using inverse modelling.

The sun irradiation is modelled very differently amongst the researchers. According to Penman (1990) and Nielsen (2005) , the sun irradiation has much influence and therefore they model the influence of sun irradiation more detailed. Antonopoulos and Koronaki (1999) and Mathews et al. (1994) used the sol-air temperature to take into account the heat flow of the sun into the external envelope, but did not take into account the sun penetration through windows. Gouda et al. (2002) state that if the sun irradiates at the inner wall surface, a first-order model is inaccurate and therefore the walls should be split up into a second order model. Yohanis and Norton (1999) have researched the amount of sun that is absorbed by the buildings thermal mass and is used to lower the heating demand. They conclude that heavy weight buildings have a higher solar utilization factor. Therefore it is even more important for heavy weight building models to place the sun irradiation at the correct node and with a correct C (capacitance) connected to it. Nielsen (2005) connected a fraction of the sun irradiation to the capacitance of the air (C_i ) and a fraction to the capacitance of the inner walls (C_w ), see Figure 2 . Wang and Xu (2006a) mention another important aspect regarding sun irradiation: external walls should be treated, taking the orientation into account, because the dynamic models of the external walls at different orientations gain different sun irradiation due to the changing position of the sun.

Hudson and Underwood (1999) mentioned that the influence of initial values turned out to be a problem for short term simulations. This effect even increases with increasing thermal capacitance. So, especially for heavy weight buildings, a sufficiently long dummy simulation period is recommended to eliminate the influence of initial values. Santos and Mendez (2004) mention the same issue with the initial values and state that the use of dummy simulation days (1 week) will reduce the influence of the initial values significantly. Penman (1990) has used two weeks as dummy simulation period. They simply implemented a dummy simulation period of 2 weeks by simulating over a period of n weeks, but using only n −2 weeks (i.e., exclude the results of the first 2 weeks). However, sometimes all the results of a year are desired and climate data of the previous year might not be available. Therefore, de Wit (2006) used a clever method: mirroring the climate data of the first three weeks before the actual simulation period. In this way, a dummy simulation period can be constructed without additional previous climate data.

4. Inverse modelling: optimization

Simplified models can be applied for several reasons. One of the applications is inverse modelling, where the model parameters are determined by matching the output of the model as close as possible to measurement data. Simplified models are more suitable for this than complex models, because the less parameters which need to be optimized, the quicker and more reliable. The former is clear: a more complex model requires more time to optimize than a simple model. However, the latter is also important: if a model is very complex (vast amount of parameters), the chance increases that multiple sets of parameter values give almost the same output. The absolute values of the parameters are not reliable then for characterizing the building. Both neural network models, linear parametric models and lumped capacitance models are used for inverse modelling.

The matching of the models output with the measurement data is performed by an optimization algorithm. The optimization algorithm tries to minimize the objective function.

4.1. Objective functions

The objective function is a function determined by the researcher which formulates the objective that should be minimized. For example, Wang and Xu (2006a) used the root-mean-squared-error to define the difference between measured and simulated output parameters:

$l={\sqrt {\frac {{\sum }_{k=1}^{N}{\left(T{'}-T\right)}^{2}}{N-1}}}$

( 1)

where T ′ is the measured temperature and T the predicted temperature. The objective parameter, in this case temperature (T ), can differ and depends on the problem. For example, Schijndel and Schellen (2011) made a first attempt to model both temperature and relative humidity by setting up a preliminary 2 state 5 parameter model. He used the summed squared error as objective function:

$l=\sum _{1}^{n}{\left({\left(T_{isim}-T_{imeas}\right)}^{2}+(RH_{isim}-RH_{imeas}\right)}^{2})$

( 2)

Penman (1990) used also the summed squared error, but only for temperature. Mustafaraj et al. (2010) used multiple objective functions, such as goodness of fit, mean absolute error, mean squared error and coefficient of determination, and these are given particular importance: it is demonstrated how additional information can be derived from comparing the results of different objective functions. For example, a mean error is usually a very small number, which might be inconvenient. If two results are compared with the same number of simulation steps, the summed error might be more convenient since it is a bigger number. Remember to use a mean error if the compared results are from simulations with different number of steps. Furthermore, large errors contribute more to a squared-error than to a root-squared-error.

The objective function can be subjected to constraints: all equality, inequality and bounding constraints are possible (Gouda et al., 2002 ). These constraints determine the possible range of values for a certain parameter. If it is possible, make the optimization problem constraint, because this narrows down the domain of optimization, which results in a faster optimization. Constraints are formulated as follows:

$R1\leq x$ $C2_{eq}=y_{eq}$ $L_{bound}\leq R2\leq U_{bound}$

( 3)

The constraints are respectively, from top to bottom, inequality, equality and bound constraints.

4.2. Optimization algorithms

Through the years, a myriad of optimization algorithms have been developed and researched.

Penman (1990) used Gauss–Newton optimization without further motivation. Mustafaraj et al. (2011) used damped Gauss–Newton optimization with the following motivation: according to Akaikes final prediction error theory, the damped Gauss–Newton iterative method is recommended as the basic choice to produce a global minimum. The reason for choosing the Gauss–Newton method is that it gives one-step convergence for quadratic functions (see Ljung, 1999 for details).

However, Gauss–Newton belongs to the conventional algorithms which have limitations, for example if the function is not smooth, because it relies on derivatives. More recently, another group of algorithms are coming up, developed in computer science, metaheuristic methods, which are also referred to as direct search or derivative-free.

A subclass of metaheuristic methods is the evolutionary algorithm, in which a subclass exists, called genetic algorithm (GA). The GA has proved to be very promising in finding a near optimal solution in very big solution spaces.

Wang and Xu (2006a) used GA for parameter identification of their building model, with particular attention to the buildings internal mass. They state that, according to Mitchell (1997) , GAs are better optimization methods, especially if the problem is not smooth: they are able to find very quickly a sufficiently good solution. Of course, as a critic, one may react with the question: what is considered to be sufficiently good? Mathematical examples exist where GA has not found a sufficiently good solution. At least GA considerably scaled down the solution space. Therefore, an option is to use GA to find quickly a near optimal solution and then proceed with a more accurate, but slower, optimization algorithm to find the best solution.

Xu and Wang (2007) have developed a building model operating in the frequency domain, where they used GA for parameter identification. This illustrates that optimization algorithms can be applied on all sorts of objective functions, and also operates in the frequency domain.

Ruano et al. (2006) used a multi objective genetic algorithm for the optimization of their neural network model: the GA optimized both the neural network topology (i.e., models structure) and the input parameters.

Balan et al. (2011) used their own developed method to find the optimal parameter set: they used a bank of models. The models are introduced/removed from the bank using specific performance criteria. According to them, the method has some advantages and limitations. Some advantages would be: (i) significantly improves the speed of the identification of the parameters of the model; (ii) the risk for a divergent identification process decreases very much; (iii) the risk of a local minimum decreases also very much. However, optimization is a field of research on its own, where a lot of different algorithms have been developed, researched and validated. The mentioned advantages of the used method have not been made clear in the article, nor have they referred to another article where they validated the method. Because a lot of validated algorithms are available, it would be wiser to look for an appropriate existing algorithm which suites the problem. After all, developing a new optimization method was not the objective of the article.

5. Conclusions

Despite the myriad of researches concerning simplified building models, a literature review was missing. This literature review provided answers to the most important questions related to the field of simplified building models.

The review showed that simplified building models can be classified into black box, grey box and white box models. Respectively, nowadays these are neural network models, linear parametric models and lumped capacitance models (RC-networks).

Research has mainly dealt with network topology (structure of the network), but more research is needed on the influence of input parameters. The review showed that, for example, the modelling of the influence of sun irradiation is not performed consistently amongst researchers.

Furthermore, a systematically developed simplified building model with physical meaning, dealing with both temperature and relative humidity, is still lacking.

Inverse modelling has been widely applied to determine the models parameters. Different optimization algorithms have been used: mainly the conventional Gauss–Newton and the state of the art genetic algorithms. However, the combination of algorithms to combine their strengths has not been researched. For example, using GA to find quickly a near optimal solution and using a more accurate, yet slower, technique to get from the near-optimal to the optimal solution.

Despite all the attention for the state of art building performance simulation tools, simplified building models should not be forgotten since they have many useful applications. Research is still needed to develop a qualitative simplified hygric and thermal building model.

References

1. Antonopoulos and Koronaki, 1998 K. Antonopoulos, E. Koronaki; Apparent and effective thermal capacitance of buildings; Energy, 23 (1998), pp. 183–192
2. Antonopoulos and Koronaki, 1999 K. Antonopoulos, E. Koronaki; Envelope and indoor thermal capacitance of buildings; Applied Thermal Engineering, 19 (1999), pp. 743–756
3. Balan et al., 2011 R. Balan, J. Cooper, K. Chao, S. Stan, R. Donca; Parameter identification and model based predictive control of temperature inside a house; Energy and Buildings, 43 (2011), pp. 748–758
4. Boaventura Cunha et al., 1997 B. Boaventura Cunha, C. Couto, A. Ruano; Real time estimation of dynamic temperature models for greenhouse environment control; Control Engineering Practice, 5 (1997), pp. 1473–1481
5. Bruckmayer, 1940 F. Bruckmayer; The equivalent brickwall; Gesundheuts-Ingenieur, 63 (1940), pp. 61–65
6. Clarke, 1985 J. Clarke; Energy Simulation in Building Design; Adam Hilger, Bristol (1985)
7. Crabb et al., 1987 J. Crabb, N. Murdoch, J. Pennman; A simplified thermal response model; Building Services Engineering Research and Technology, 8 (1987), pp. 13–19
8. Wit, 2006 M. de Wit; Heat air and moisture model for building and systems evaluation; Bouwstenen, 100 (2006), p. 100
9. Fraisse et al., 2002 G. Fraisse, C. Viardot, O. Lafabrie, G. Achard; Development of a simplified and accurate building model based on electrical analogy; Energy and Buildings, 34 (2002), pp. 1017–1031
10. Frausto et al., 2003 H. Frausto, J. Pieters, J. Deltour; Modelling greenhouse temperature by means of auto regressive models; Biosystems Engineering, 84 (2003), pp. 147–157
11. Frausto and Pieters, 2004 H. Frausto, J. Pieters; Modeling greenhouse temperature using system identification by means of neural networks; Neurocomputing, 56 (2004), pp. 423–428
12. Gouda et al., 2002 M. Gouda, S. Danaher, C. Underwood; Building thermal model reduction using nonlinear constrained optimization; Building and Environment, 37 (2002), pp. 1255–1265
13. Hudson and Underwood, 1999 G. Hudson, C. Underwood; A simple building modeling procedure for MATLAB/Simulink; Proceedings of the 6th International Conference on Building Performance Simulation (IBPSA '99), September, Kyoto-Japan (1999), pp. 777–783
14. Jimenez et al., 2008 M. Jimenez, H. Madsen, K. Andersen; Identification of the main thermal characteristics of building components using Matlab; Building and Environment, 43 (2008), pp. 170–180
15. Kopecký, 2011 Kopecký, P., 2011. Experimental validation of two simplified thermal zone models. In: Proceedings of the 9th Nordic Symposium on Building Phsyics. Tampere, Finland.
16. Kramer, 2011 Kramer, R., 2011. The impact of climate change on the indoor climate of monumental buildings. Department of Architecture Building and Planning, University of Technology Eindhoven, Eindhoven.
17. Ljung, 1999 L. Ljung; System Identification: Theory for User; Prentice-Hall, Upper Saddle, River (1999)
18. Lowry and Lee, 2002 G. Lowry, M. Lee; Modeling the passive thermal response of a building using sparse BMS data; Applied Energy, 78 (2002), pp. 53–62
19. Loveday and Craggs, 1993 D. Loveday, C. Craggs; Stochastic modelling of temperatures for a full-scale occupied building zone subject to natural random influences; Applied Energy, 45 (1993), pp. 295–312
20. Lu and Viljanen, 2009 T. Lu, M. Viljanen; Prediction of indoor temperature and relative humidity using neural network models: model comparison; Neural Computing and Applications, 18 (2009), pp. 345–357
21. Mathews et al., 1994 E. Mathews, P. Richards, C. Lombard; A first-order thermal model for building design; Energy and Buildings, 21 (1994), pp. 133–145
22. Mechaqrane and Zouak, 2004 A. Mechaqrane, M. Zouak; A comparison of linear and neural network ARX models applied to a prediction of the indoor temperature of a building; Neural Computing and Applications, 13 (2004), pp. 32–37
23. Menezes and Barreto, 2008 J. Menezes, G. Barreto; Long-term time series prediction with the NARX network: an empirical evaluation; Neurocomputing, 71 (2008), pp. 3335–3343
24. Mitalas and Stephenson, 1967 G. Mitalas, D. Stephenson; Room thermal response factors; ASHRAE Transactions, 73 (1967), pp. 2.1–10
25. Mitchell, 1997 M. Mitchell; An Introduction to Genetic Algorithm; MIT Press, Cambridge, MA (1997)
26. Moreno et al., 2007 G. Moreno, M. Perea, R. Miranda, V. Guzmán, G. Ruiz; Modelling temperature in intelligent buildings by means of autoregressive models; Automation in Construction, 16 (2007), pp. 713–722
27. Mustafaraj et al., 2010 G. Mustafaraj, J. Chen, G. Lowry; Development of room temperature and relative humidity linear parametric models for an open office using BMS data; Energy and Buildings, 42 (2010), pp. 348–356
28. Mustafaraj et al., 2011 G. Mustafaraj, G. Lowry, J. Chen; Prediction of room temperature and relative humidity by autoregressive linear and nonlinear neural network models for an open office; Energy and Buildings, 43 (2011), pp. 1452–1460
29. Nielsen, 2005 T. Nielsen; Simple tool to evaluate energy demand and indoor environment in the early stages of building design; Solar Energy, 78 (2005), pp. 73–83
30. Norgaard et al., 2002 M. Norgaard, O. Ravn, N. Poulsen; NNSYSID-toolbox for system identification with neural networks; Mathematical and Computer Modelling of Dynamical Systems, 8 (2002), pp. 1–20
31. Norlén, 1990 P. Norlén; Estimating thermal parameters of outdoor test cells; Building and Environment, 25 (1990), pp. 17–24
32. Patil et al., 2008 S. Patil, H. Tantau, V. Salokhe; Modelling of tropical greenhouse temperature by autoregressive and neural network models; Biosystems Engineering, 99 (2008), pp. 423–431
33. Penman, 1990 J. Penman; Second order system identification in the thermal response of a working school; Building and Environment, 25 (1990), pp. 105–110
34. Richards and Mathews, 1994 P. Richards, E. Mathews; A thermal design tool for buildings in ground contact; Building and Environment, 29 (1994), pp. 73–82
35. Ruano et al., 2006 A. Ruano, E. Crispim, E. Coincecao, M. Lucio; Predictions of buildings temperature using neural networks models; Energy and Buildings, 38 (2006), pp. 682–694
36. Santos and Mendes, 2004 G. dos Santos, N. Mendes; Analysis of numerical methods and simulation time step effects on the prediction of building thermal performance; Applied Thermal Engineering, 24 (2004), pp. 1129–1142
37. Schijndel, 2007 Schijndel, A.W.M. van, 2007. Integrated Heat Air and Moisture Modeling and Simulation. Ph.D. Thesis. University of Technology Eindhoven, Eindhoven.
38. Schijndel, 2009 Schijndel, A.W.M. van, 2009. The exploration of an inversed modeling technique to obtain material properties of a building construction. In: Proceedings of the 4th International Building Physics Conference. Istanbul, pp. 91–98.
39. Schijndel et al., 2010 Schijndel, A.W.M. van, Schellen, H., Martens, M., Aarle, M. van, 2010. Modeling the effect of climate change in historic buildings at several scale levels. In: Proceedings of the International WTA Conference, Eindhoven, pp. 161–180.
40. Schijndel and Schellen, 2011 Schijndel, A.W.M. van, Schellen, H., 2011. Inverse modeling of the indoor climate using a 2-state 5-parameters model in Matlab. In: Climate for Culture, Third Annual Meeting. Visby, pp. 1–12.
41. Seginer et al., 1994 I. Seginer, T. Boulard, J. Bailey; Neural network models of the greenhouse climate; Journal of Agricultural Engineering Research, 59 (1994), pp. 203–216
42. Siegelmann et al., 1997 H. Siegelmann, B. Horne, C. Giles; Computational capabilities of recurrent NARX neural networks; IEEE Transactions on Systems, Man, and Cybernetics—Part B: Cybernetics, 27 (1997), pp. 208–215
43. Srinivas and Brambley, 2005 K. Srinivas, M. Brambley; Methods for fault detection, diagnostics, and prognostics; HVAC and R Research, 11 (2005), pp. 3–25
44. Stephenson and Mitalas, 1971 D. Stephenson, G. Mitalas; Calculation of heat conduction transfer functions for multilayer slabs; ASHRAE Transactions, 77 (1971), pp. 117–126
45. Trčka, 2008 Trčka, M., 2008. Co-simulation for Performance Prediction of Innovative Integrated Mechanical Energy Systems in Buildings. Ph.D. Thesis. University of Technology Eindhoven, Eindhoven.
46. Wang and Chen, 2001 S. Wang, Y. Chen; A novel and simple building load calculation model for building and system dynamic simulation; Applied Thermal Engineering, 21 (2001), pp. 683–702
47. Wang and Xu, 2006a S. Wang, X. Xu; Simplified building model for transient thermal performance estimation using GA-based parameter identification; International Journal of Thermal Sciences, 45 (2006), pp. 419–432
48. Wang and Xu, 2006b S. Wang, X. Xu; Parameter estimation of internal thermal mass of building dynamic models using genetic algorithm; Energy Conversion and Management, 47 (2006), pp. 1927–1941
49. Xu and Wang, 2007 X. Xu, S. Wang; Optimal simplified thermal models of building envelope based on frequency domain regression using genetic algorithm; Energy and Buildings, 39 (2007), pp. 525–536
50. Xu and Wang, 2008 X. Xu, S. Wang; A simplified dynamic model for existing buildings using CTF and thermal network models; International Journal of Thermal Sciences, 47 (2008), pp. 1249–1262
51. Yohanis and Norton, 1999 Y. Yohanis, B. Norton; Utilization factor for building solar-heat gain in for use in a simplified energy model; Applied Energy, 63 (1999), pp. 227–239