Abstract
In this work, the combined effects of magnetic field and ohmic heating on the entropy generation rate in the flow of couple stress fluid through a porous channel are investigated. The equations governing the fluid flow are formulated, non-dimensionalised and solved using a rapidly convergent semi-analytical Adomian decomposition method (ADM). The result of the computation shows a significant dependence of fluid’s thermophysical parameters on Joule’s dissipation as well as decline in the rate of change of fluid momentum due to the interplay between Lorentz and viscous forces. Moreover, the rate of entropy generation in the flow system drops as the magnitude of the magnetic field increases.
Keywords
Magnetic field; Entropy generation; Slip flow; Irreversibility ratio; ADM; Ohmic heating
Nomenclature
- dimensionless Navier slip parameter at the lower wall
- dimensionless Navier slip parameter at the upper wall
- coefficient of couple stress
- Navier slip coefficient at the lower plate
- Navier slip coefficient at the upper plate
- thermal conductivity
- dynamic viscosity
- parameter that measures the temperature difference between the two heat reservoirs
- fluid density
- electrical conductivity
- dimensionless fluid temperature
- couple stress parameter
- magnetic field strength
Br- Brinkman number
- specific heat at constant pressure
- volumetric rate of entropy
G- dimensionless pressure gradient
h- width of the channel
- Hartmann number
- entropy generation due to heat transfer
- entropy generation due to entropy generation due to fluid friction and ohmic heating
- entropy generation number
Pr- Prandtl number
s- suction/injection parameter
T- fluid temperature
- temperature at the lower plate
- final fluid temperature
u- dimensionless fluid velocity
- fluid velocity
- uniform suction/injection velocity
- cartesian coordinates
- dimensionless cartesian coordinates
1. Introduction
In recent times, there has been a renewed interest in the thermodynamic analysis involving channel fluid flows. This is due to the usefulness of the study in several renewable energy applications. For instance, it could be used to predict the efficiency of many thermal systems exchanging heat between two heat reservoirs and other Carnot systems. Moreover, in the energy generation, excessive energy is wasted or dissipated in the form of heat. Hence there is need to minimise the wastage by improving the energy of the system. Based on this fact, few research works have been reported in the literature. For example, Adesanya and Makinde [1] reported the entropy generation in couple stress fluid flowing steadily through a porous channel with slip at the isothermal walls. Similarly, Adesanya and Makinde [2] studied the entropy generation rate in the couple stress fluid flowing through a porous channel with convective heating at the walls. Also in the class of couple stress fluid, Makinde and Eegunjobi [3] investigated the inherent irreversibility of heat in steady flow of a couple stress fluid through a vertical channel filled with porous materials. Other important work on the entropy generation in a moving fluid includes [4], [5], [6] and [7].
In all the studies above on the thermodynamics analysis, the effect of magnetic field, placed in the transverse direction to the flow channel has been neglected. In reality, magnetic field plays a vital role in many industrial and thermal engineering applications. For instance, it is useful in controlling extremely hot moving fluid like molten steel and many more. Several researchers have investigated the entropy analysis in hydromagnetic fluid flow in recent times. For example, Das and Jana [8] presented the second law analysis for magnetohydrodynamic incompressible fluid flow through a porous channel by imposing Navier slip conditions at the walls. Adesanya and Falade [9] analysed the inherent irreversibility in the flow of hydrodynamic third grade fluid through a channel saturated with porous materials. Similarly, the effect of hall current was presented in a study by Das and Jana [10]. Interested readers can see more interesting work on the influence of magnetic field on entropy generation rate in Refs. [11], [12], [13], [14], [15], [16], [17], [18], [19] and [20].
Motivated by studies in [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19] and [20], the objective of the present study was to examine the influence of magnetic field and ohmic heating of the couple stress fluid on the entropy production within the flow channel, which has not been accounted for in the literature. The outcoming results are expected to enhance many industrial and thermal engineering processes whose working medium is a non-Newtonian fluid, with a view to minimise entropy generation which tends to deplete the amount of available energy for work.
To achieve this objective, flow governing equations are formulated, and non-dimensionalised and approximate solution of the dimensionless coupled non-linear boundary-value problem are obtained by using a semi-analytical Adomian decomposition method [21] and [22]. The choice of the method is due to the fact that the method does not require any linearisation, discretisation, use of initial guess or perturbation. These approximation solutions are used to compute the entropy generation rate and irreversibility ratio.
In the following section, the problem is formulated and non-dimensional analysis is also presented. Section 3 of the work contains the method of solution, results are presented and discussed in Section 4, while Section 5 concludes the paper.
2. Mathematical formulation
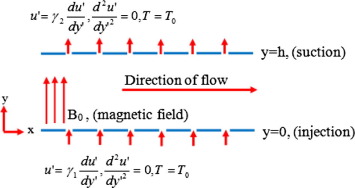
A fully developed hydromagnetic non-Newtonian fluid flow between two parallel plates is considered. The parallel plates are infinite, permeable and stationary relative to the fluid motion as shown in Fig. 1. We choose a 2-dimensional cartesian coordinate system with -axis along the flow direction and -axis orthogonal to the planes of the parallel plates, separated by width . Fluid injection occurs at the lower plate at a uniform rate , matched with a corresponding fluid suction at the upper plate. A constant magnetic field of strength is applied perpendicular to the direction of fluid flow. For most industrial applications, a non-chaotic fluid flow is desired such that the magnetic Reynolds number is very small, and since no external voltage is applied to the fully developed flow system, the induced magnetic field and Hall effect are negligible. We further assumed that all the fluid properties are constant and the Stokes constitutive model for the couple stresses is used. Consequently, the momentum and energy balance equations, with the local volumetric entropy generation rate () for the fluid flow can be written as follows [1] and [10]:
|
|
(1) |
|
|
(2) |
|
|
(3) |
with the boundary conditions
|
|
(4) |
|
|
(5) |
where and P are the fluid velocity and pressure respectively, is the injection/suction velocity at the channel walls, is the coefficient of couple stress, is the dynamic viscosity, corresponds to the Navier slip coefficients at the lower plate and upper plate, respectively for is the fluid density, is the fluid electrical conductivity, is the coefficient of thermal conductivity, is the isobaric specific heat, and are referenced fluid temperatures, and T is the fluid temperature. The present model has potential application in automated heat control mechanisms, especially in micro-channels. It is often desired in manufacturing processes that the rate of randomness (or entropy generation) be tamed to avoid system complexity.
|
|
|
Figure 1. The geometry of the model. |
Introducing the following dimensionless parameters and variables,
|
|
(6) |
|
|
we obtain the following boundary value problems:
|
|
(7) |
|
|
(8) |
together with the boundary conditions
|
|
(9) |
while the entropy generation can be computed using
|
|
(10) |
Our model given by Eqs. (7), (8) and (10) reduces to the asymptotic case as as obtained in Ref. [1].
3. Adomian decomposition method of solution
In this section, we seek the solution of the model Eqs. (7), (8) and (10) subject to the boundary condition (9), using the semi-analytical Adomian decomposition scheme. To achieve this, the boundary value problems are converted to the equivalent integral equations noting that . Thus,
|
|
(11) |
|
|
(12) |
where
|
|
The unknown coefficients and are to be determined by using the method of undetermined coefficients. Following ADM we seek solutions in the form of an infinite series:
|
|
(13) |
Substituting (13) into (11) and (12), we obtain
|
|
(14) |
and
|
|
(15) |
where
|
|
|
|
and
|
|
Evidently (13) may be written in the recursive form:
|
|
(16) |
|
|
(17) |
In order to reduce the computational load in (15), the modified recurrent relation
|
|
(18) |
is used, so that
|
|
(19) |
|
|
(20) |
|
|
(21) |
|
|
(22) |
Due to convergence of the ADM series solution conducted in Ref. [6] only few terms of the series will be required to obtain the approximate solutions of the problem. We set the number of iteration to m so that the approximate solutions (13) may be written as the finite series as follows:
|
|
(23) |
The irreversibility in the heat flow to the viscous fluid is analysed using (10) by expressing the entropy generation number as partial sum of the entropy generation due to heat transfer, and the irreversibility resulting from fluid friction and ohmic heating of the fluid. Therefore we set and as follows:
|
|
(24) |
The Bejan number Be, which is a parameter that measures the irreversibility ratio in the heat flow, may be defined as
|
|
(25) |
where is the irreversibility ratio, a parameter that measures the rate of destruction of available work in the flow system. The Bejan number in Eq. (25) is bounded in the interval . The irreversibility due to heat transfer is dominant when , while the irreversibility due to viscosity and magnetic field is dominant when . The dimensionless Eqs. (7), (8), (9) and (10), with the boundary conditions (9) were solved using the algorithm in (16), (17), (18), (19), (20), (21), (22) and (23), coded in MATHEMATICA symbolic package. Using the numerical procedure discussed above, we computed the dimensionless velocity, temperature, entropy generation and irreversibility ratio. In what follows, we discussed some interesting results from our findings.
4. Results and discussion
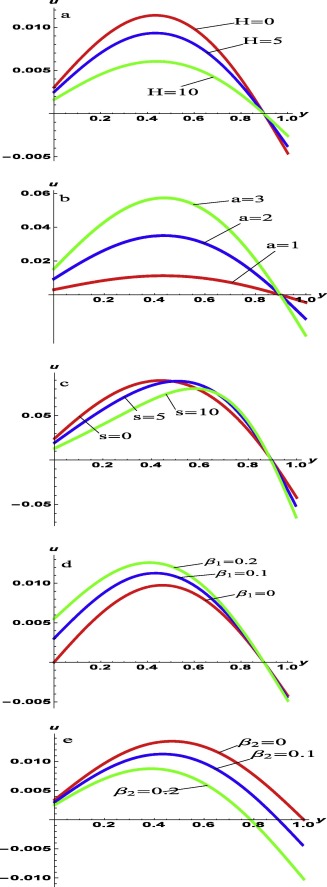
Let us begin by examining the effect of the applied magnetic field and couple stresses on the flow velocity, the variations of the dimensionless velocity with the width of the flow channel as presented in Fig. 2, for varying values of magnetic parameter (Hatman number, ), couple stress inverse parameter , suction/injection parameter s , upper wall Navier-slip parameter , and lower wall Navier-slip parameter . We showed in Table 1 that the ADM could guarantee a result comparable with the exact solution of the problem, with absolute error of order for . It is clear from Fig. 2a that by increasing the magnetic field the flow velocity would be inhibited. This could be explained by the action of Lorentz force, whose presence in the flow system constitutes resistance to the momentum of fluid parcels in the adjacent fluid layers. Fig. 2b depicts the implication of increasing couple stress inverse parameter on the flow velocity. Here, we find that an increase in couple stress inverse parameter corresponds to increase in fluid friction in the moving fluid. This friction arises from the effect of particle additives, constituting size dependent effect on couple stress fluids. Moreover, rotational field of the velocity is generated in couple stress fluid. Hence, an increase in couple stress results in decrease in the velocity profile of the fluid. Fig. 2c shows the effect of suction/injection on the velocity profile of the fluid flow. Clearly, the increase in suction/injection parameter breaks the symmetry of the fluid flow. This is because the continual injection of fluid into the channel, from a direction different from that of channel fluid flow, changes the momentum of (or slows down) the fluid parcels at the lower wall-fluid interface. This effect is propagated beyond the neighbourhood of the lower plate, which breaks the symmetry of the channel flow system. However, increasing the suction/injection parameter does not show any significant effect at the upper wall of the channel. Fig. 2d and e depicts the effects of Navier-slip parameters on the velocity profile of the fluid flow. Evidently, the fluid slippage has significant effect on the fluid motion, in that any change in any of the parameters impacts on the viscous drag on the flow, which scales the maximum velocity of the flow up or down. In clear terms, increasing the upper wall Navier-slip parameter decreases the fluid velocity significantly at the upper wall as well as the maximum velocity of the fluid flow. In contrast, increasing the slip parameter at the lower wall increases the velocity at the wall as well as the maximum velocity of the fluid flow.
|
|
|
Figure 2. Parameterised velocity profiles of the fluid flow: (a) at varying Hatman number H , with ; (b) at varying couple stress inverse a , with ; (c) at varying suction/injection parameter s , with ; (d) at varying lower wall Navier-slip parameter , with ; (e) at varying upper wall Navier-slip parameter , with . |
| u | Absolute error | ||
|---|---|---|---|
| 0 | 0.00303054 | 0.00303070 | |
| 0.1 | 0.00598827 | 0.00598858 | |
| 0.2 | 0.00854151 | 0.00854196 | |
| 0.3 | 0.01037320 | 0.01037370 | |
| 0.4 | 0.01125880 | 0.01125950 | |
| 0.5 | 0.01106440 | 0.01106510 | |
| 0.6 | 0.00974517 | 0.00974577 | |
| 0.7 | 0.00734506 | 0.00734554 | |
| 0.8 | 0.00399756 | 0.00399783 | |
| 0.9 | −0.00007304 | −0.00007305 | |
| 1.0 | −0.00454921 | −0.00454955 |
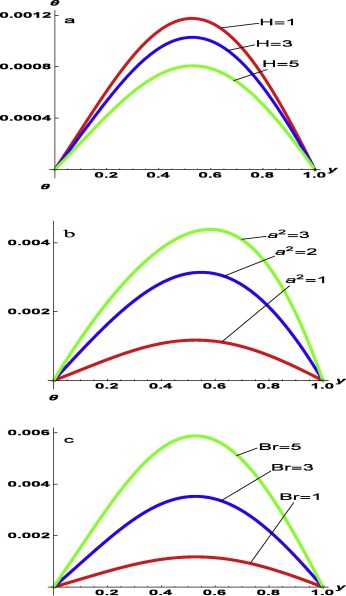
Next we describe the temperature response of the fluid with respect to flow to changes in the values of the magnetic parameter, couple stress parameter and the Brinkman number Fig. 3. Fig. 3a shows that increasing the magnetic field intensity (or parameter) translates into a decrease in the channel temperature. Fig. 3b reveals that increasing couple stresses decrease the temperature profile in the channel. Expectedly, couple stresses enhance the fluid’s intermolecular cohesion. This increases the fluid’s resistance to shear stress, resulting in temperature rise within the flow channel. Fig. 3c shows that an increase in Brinkman number results in the increase in the fluid temperature.
|
|
|
Figure 3. Parameterised temperature profiles of the fluid flow: (a) at varying values of Hatman number H , with ; (b) at varying values of couple stress inverse a , with ; (c) at varying values of the Brinkman number Br , with . |
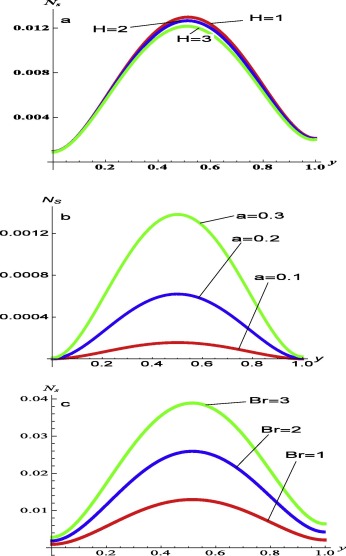
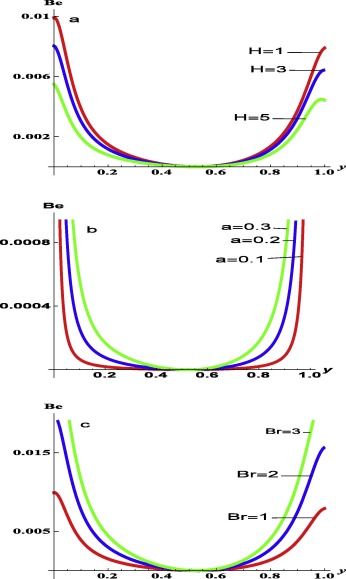
To complete the analysis, the effects of the magnetic parameter, , couple stress parameter, , and the Brinkman number, Br on the entropy generation are shown in Fig. 4. Interestingly, it is observed from Fig. 4a that the entropy generation, decreases with increase in magnetic parameter in the middle of the channel. The interplay between the two thermophysical phenomena, namely the intermolecular cohesion and entropy generation rate in viscous fluid becomes imperative. Viscosity increases as the intermolecular cohesion within the fluid rises, or vice versa. The applied Lorentz force reduces the intermolecular cohesion within the fluid resulting in decrease in entropy generation within the channel flow. Fig. 4b and c shows that the rate of entropy generation increases with increase in both couple stress parameter and the Brinkman number. Increase in Brinkman number raises both dissipations due to Joule heating and viscosity, which in turn increases the entropy generation rate. Fig. 5 shows the dominance of fluid viscosity on the irreversibility ratio, over heat transfer at the centreline of the channel. In Fig. 5a, it is observed that as the magnetic parameter increases, heat transfer dominates the irreversibility ratio at the walls, while Fig. 5a and b revealed that as the couple stress inverse and the Brinkman number increase, fluid viscosity dominates the irreversibility ratio.
|
|
|
Figure 4. Entropy generation rate: (a) at varying values of Hatman number H , with ; (b) at varying values of couple stress inverse a , with ; (c) at varying values of the Brinkman number Br , with . |
|
|
|
Figure 5. Irreversibility ratio: (a) at varying values of Hatman number H , with ; (b) at varying values of couple stress inverse a , with ; (c) at varying values of the Brinkman number Br , with . |
Following from the discussion above, at specific and Br, varying the magnetic field automatically changes the fluid’s rate of change of momentum, which in turn changes the fluid velocity. Reducing velocity in micro-channel fluid flow effectively reduces fluid temperature, rate of entropy production in the fluid, and the irreversibility ratio as shown in Figure 2, Figure 3, Figure 4 and Figure 5.
5. Conclusion
The effects of magnetic field and couple stresses on entropy generation in an MHD flow through a porous channel, with suction/injection and Navier slip have been examined. The Adomian decomposition method was employed to obtain semi-analytical solution that approximates the velocity and temperature profiles, which are used to obtain the entropy generation production as well as the Bejan number. It was found that the entropy generation rate reduces with increasing magnetic parameter. The magnetic field acts in such a way as to tame the degree of randomness in the fluid’s particles, resulting in the lowering of the fluid’s velocity and entropy generation rate in the system. In effect, the fluid velocity, the fluid temperature and entropy generation showed significant dependence on Joule dissipation. This result suggests a balanced mix between heat transfer irreversibility and fluid friction irreversibility, which would enhance entropy minimisation and hence system design and manufacturing applications. Our result would motivate applications in micro-channel automatic heat control systems.
Acknowledgement
UEV is supported by the Royal Society of London, through their Newton International Fellowship Alumni scheme.
References
- [1] S.O. Adesanya, O.D. Makinde; Entropy generation in couple stress fluid flow through porous channel with fluid slippage; Exergy, 15 (3) (2014), pp. 344–362
- [2] S.O. Adesanya, O.D. Makinde; Effects of couple stresses on entropy generation rate in a porous channel with convective heating; Comput. Appl. Math., 34 (2015), pp. 293–307
- [3] O.D. Makinde, A.S. Eegunjobi; Entropy generation in a couple stress fluid flow through a vertical channel filled with saturated porous media; Entropy, 15 (11) (2013), pp. 4589–4606
- [4] J.A. Esfahani, M. Modirkhazeni; Entropy generation of forced convection film condensation on a horizontal elliptical tube; C. R. Mcanique, 340 (7) (2012), pp. 543–551
- [5] Y. Wang, Z. Chen, X. Ling; Entropy generation analysis of particle suspension induced by Couette flow; Int. J. Heat Mass Transfer, 90 (2015), pp. 499–504
- [6] S.O. Adesanya, O.D. Makinde; Thermodynamic analysis for a third grade fluid through a vertical channel with internal heat generation; J. Hydrodyn., 27 (2) (2015), pp. 264–272
- [7] S.O. Adesanya, O.D. Makinde; Irreversibility analysis in a couple stress film flow along an inclined heated plate with adiabatic free surface; Physica A, 432 (2015), pp. 222–229
- [8] S. Das, R.N. Jana; Entopy generation due to MHD flow in a porous channel with Navier slip; Ain Shams Eng. J., 5 (2014), pp. 575–584
- [9] S.O. Adesanya, J.A. Falade; Thermodynamics analysis of hydromagnetic third grade fluid flow through a channel filled with porous medium; Alexandria Eng. J., 54 (3) (2015), pp. 615–622
- [10] S. Das, R.N. Jana; Effect of hall current on entropy generation in porous channel with suction/injection; Int. J. Energy Technol., 5 (25) (2013), pp. 1–11
- [11] C.K. Chen, B.S. Chen, C.C. Liu; Entropy generation in mixed convection magnetohydrodynamic nanofluid flow in vertical channel; Int. J. Heat Mass Transfer, 91 (2015), pp. 1026–1033
- [12] N. Saeid; Magnetic field effects on entropy generation in heat and mass transfer in porous cavity; Acad. J., 8 (17) (2013), pp. 728–739
- [13] M. Magherbi, A. El-Jery, N. Hidouri, A.B. Brahim; Evanescent magnetic field effects on entropy generation at the on set of natural convection; Indian Acad. J., 35 (2) (2010), pp. 163–176
- [14] A. El-Jery, N. Hidouri, M. Magherbi, A.B. Brahim; Effect of external oriented magnetic field on entropy generation in natural convection; Entropy, 12 (2010), pp. 1391–1417
- [15] S. Salas, S. Cuevas, M.L. Haro; Entropy analysis of magnetohydrodynamic induction devices; J. Phys. D: Appl. Phys., 32 (1999), pp. 2605–2608
- [16] S.H. Tasnim, M.A.H. Mahmud; Entropy generation in a porous channel with hydromagnetic effects; Exergy, 2 (2002), pp. 300–308
- [17] S. Mahmud, S.H. Tasnim, H.A.A. Mamun; Thermodynamics analysis of mixed convection in a channel with transverse hydromagnetic effect; Int. J. Therm. Sci., 42 (731–740) (2003)
- [18] D. Theuri, O.D. Makinde; Thermodynamic analysis of variable viscosity MHD unsteady generalized Coutte flow with permeable walls; Appl. Comput. Math., 3 (1) (2014), pp. 1–8
- [19] O. Mahian, H.F. Oztop, I. Pop, S. Mahmud, S. Wongwises; Design of vertical annulus with MHD flow using entropy generation analysis; Therm. Sci., 17 (4) (2013), pp. 1013–1022
- [20] S.O. Adesanya, S.O. Kareem, J.A. Falade, S.A. Arekete; Entropy generation analysis for a reactive couple stress fluid flow through a channel saturated with porous material; Energy, 93 (1) (2015), pp. 1239–1245
- [21] G. Adomian; Solving Frontier Problems of Physics: The Decomposition Method; Kluwer Academic Publishers, Dordrecht (1994)
- [22] J.S. Duan, R. Rach; A new modification of the Adomian decomposition method for solving boundary value problems for higher order nonlinear differential equations; Appl. Math. Comput., 218 (2011), pp. 4090–4118
Document information
Published on 12/04/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?