Abstract
Numerical computation of unsteady laminar three-dimensional natural convection and entropy generation in an inclined cubical trapezoidal air-filled cavity is performed for the first time in this work. The vertical right and left sidewalls of the cavity are maintained at constant cold temperatures. The lower wall is subjected to a constant hot temperature, while the upper one is considered insulated. Computations are performed for Rayleigh numbers varied as 103 ⩽ Ra ⩽ 105, while the trapezoidal cavity inclination angle is varied as 0° ⩽ Φ ⩽ 180°. Prandtl number is considered constant at Pr = 0.71. Second law of thermodynamics is applied to obtain thermodynamic losses inside the cavity due to both heat transfer and fluid friction irreversibilities. The variation of local and average Nusselt numbers is presented and discussed, while, streamlines, isotherms and entropy contours are presented in both two and three-dimensional pattern. The results show that when the Rayleigh number increases, the flow patterns are changed especially in three-dimensional results and the flow circulation increases. Also, the inclination angle effect on the total entropy generation becomes insignificant when the Rayleigh number is low. Moreover, when the Rayleigh number increases the average Nusselt number increases.
Keywords
Transient natural convection; Trapezoidal cavity; Three-dimensional flow; Entropy generation; Second law analysis
Nomenclature
Symbol- Description (unit)
g- gravitational acceleration (m/s2)
H- height of the trapezoidal cubical cavity (m)
k- fluid thermal conductivity (W/m °C)
n- unit vector normal to the wall
L- length of the cubical trapezoidal cavity (m)
Nu- Nusselt number
- dimensionless local generated entropy
Pr- Prandtl number
- heat flux (W/m2)
Ra- Rayleigh number
S- dimensionless entropy generation
- generated entropy (Kj/kg K)
T- dimensionless temperature
To- bulk temperature
t- dimensionless time ()
- dimensionless velocity vector
x- dimensionless Cartesian coordinate in x -direction ()
y- dimensionless Cartesian coordinate in y -direction ()
z- dimensionless Cartesian coordinate in z -direction ()
Greek symbols
α- thermal diffusivity (m2/s)
β- thermal expansion coefficient (K−1)
- dimensionless temperature difference
- dissipation function
- trapezoidal cavity inclination angle (degree)
υ- fluid kinematic viscosity (m2/s)
- dimensionless vector potential ()
- dynamic viscosity (kg/m s)
- dimensionless vorticity ()
Subscripts
av- average
c- cold
fr- friction
h- hot
Loc- local
th- thermal
tot- total
x, y, z- Cartesian coordinates
Superscripts
- dimensional variable
1. Introduction
Natural convection in cavities of various geometries has taken considerable attention in the past few decades due to its many significant applications such as electronic components, cooling, heating and preservation of canned foods, solar collectors, nuclear reactors, double-panel windows and heat exchangers [1] and [2]. The study of natural convection in a trapezoidal cavity is very difficult compared with classical square or rectangular cavities due to the presence of inclined walls. This complex geometry needs an accurate and large effect in grid generation and code construction. However, many studies were available on natural convection concerned trapezoidal cavity. Lam et al. [3] performed experimental and numerical studies of natural convection in trapezoidal cavities composed of two vertical insulated sidewalls, an inclined cold top wall and a horizontal hot bottom wall. Kumar [4] studied experimentally the natural convective heat transfer in a trapezoidal enclosure of a box-type solar cooker by using the simple proposed correlations for a wide range of absorber-plate temperature. He concluded that the major advantage of this geometry was the absorption of a higher fraction of incident solar radiation falling on the aperture at larger incidence angles. Basak et al. [5] investigated numerically the natural convection in trapezoidal enclosures for uniformly heated bottom wall, linearly heated vertical wall(s) in presence of insulated top wall. The results were presented for wide range of Rayleigh numbers (Ra = 103–105), Prandtl numbers (Pr = 0.7–1000) and various tilt angles of side walls (φ). For linearly heated sidewalls, symmetry in flow pattern was observed. Average Nusselt number plots showed higher heat transfer rates for (φ = 0°) and the overall heat transfer rates at the bottom wall were larger for the linearly heated left wall and cooled right wall. A non-monotonic trend in average Nusselt number against Rayleigh number due to presence of multiple circulations was observed for (φ = 0°). Lasfer et al. [6] investigated numerically the steady natural convection of air flow in a two-dimensional side-heated trapezoidal room. The considered geometry had an inclined left heated sidewall, a vertical right cooled sidewall, and two insulated horizontal upper and lower walls. Computations were performed for seven values of the heated sloping wall angle, three different values of aspect ratio, and five Rayleigh number values. The results indicated a great dependence of the flow fields and the heat transfer on inclination angle, aspect ratio and Rayleigh number. A correlation between the average Nusselt number, Rayleigh number, heated sloping wall angle and aspect ratio was proposed. Basak et al. [7] studied numerically using penalty finite element method the natural convection flow in closed trapezoidal enclosures with linearly heated sidewalls and linearly heated left wall and cold right wall. In both cases the bottom wall was uniformly heated while top wall was insulated. Numerical results were obtained for various values of Rayleigh number (103 ⩽ Ra ⩽ 105), Prandtl number (0.015 ⩽ Pr ⩽ 1000) and inclination angles (φ = 45°, 60° and 90°). It was found that, less intense circulations occurred in square cavity (φ = 90°) compared to other cavities (φ = 45° and 60°). They concluded that, overall heat transfer rates were larger for square cavity (φ = 90°) compared to other angles (φ = 45° and 60°) irrespective of heating patterns for side walls. Sahoo et al. [8] investigated numerically the heat loss due to radiation and steady laminar natural convection flow in a trapezoidal cavity having eight absorber tubes for a Linear Fresnel Reflector (LFR) solar thermal system with uniformly heated tubes and adiabatic top and sidewalls. Effect of emissivities of the tubes on the heat loss was simulated. They suggested a correlation between the total average Nusselt number and its influencing parameters for the proposed cavity. Natarajan et al. [9] performed by using FLUENT 6.3 a numerical study of combined natural convection and surface radiation in a solar trapezoidal cavity absorber for Compact Linear Fresnel Reflector (CLFR). The combined heat loss coefficients were predicted for various parameters such as Grashof number, absorber angles, surface emissivity, aspect ratio, temperature ratio and radiation–conduction number. The results were presented in terms of Nusselt number correlation to show the effect of these parameters on combined natural convection and surface radiation heat loss. Mustafa and Ghani [10] investigated numerically by finite volume method the natural convection in a trapezoidal enclosure with partial heating from below and symmetrical cooling from the sides. The heating was simulated by a centrally located heat source on the bottom wall and four different values of the dimensionless heat source length were considered. The results were presented for Rayleigh number (103 ⩽ Ra ⩽ 105) and Prandtl number (Pr = 0.7). They concluded that the average Nusselt number increased with the increase of the source length. Da Silva et al. [11] investigated numerically the natural convection in trapezoidal cavities, especially those with two internal baffles in conjunction with an insulated floor, inclined top surface, and isothermal left-heated and right-cooled vertical walls. The effect of three inclination angles of the upper surface, Rayleigh number (Ra), Prandtl number (Pr) and baffle’s height (Hb) on stream functions, temperature profiles, and local and average Nusselt numbers was investigated. The results were presented for a wide range of Rayleigh numbers (103 ⩽ Ra ⩽ 106), baffle’s height (Hb = H∗/3, 2H∗/3, and H∗), Prandtl number (Pr = 0.7, 10 and 130) and top angle (θ) ranged from 10° to 20°. A correlation for the average Nusselt number in terms of Prandtl and Rayleigh numbers, and the inclination of the upper surface of the cavity were proposed for each baffle height investigated. Tracy and Crunkleton [12] studied numerically the natural convective flow oscillations in isosceles trapezoidal enclosures for three vertex angles [22°, 45° and 67°]. For the largest angle, a completely periodic oscillation was calculated over different time scales. They concluded that as the base angle was decreased, various disturbances were superimposed over flow oscillations. Additional works concerning the natural convection in trapezoidal enclosures can be found in [13], [14], [15] and [16]. From the other side, the three-dimensional natural convection in cavities was investigated by many researchers. Hiller et al. [17] investigated experimentally and numerically the transient natural convection in a cube-shaped cavity with two isothermal copper walls kept at a prescribed temperature. The experiments were performed at a Rayleigh number of (1.66 × 105) and a Prandtl number of (1109). The theoretical predictions were found to be in a good agreement with the experimental results. Frederick [18] studied numerically the natural convection in a cubical enclosure with two equal active sectors on one vertical wall over a wide range of Rayleigh number. He concluded that Nusselt numbers exceeded the ones for a side heated cavity at low Rayleigh number. The flow patterns and temperature distribution were described and an expression for overall heat transfer was proposed. Frederick and Moraga [19] numerically investigated the three-dimensional natural convection of air in a cubical enclosure with a fin on the hot wall for Rayleigh numbers of (103–106). The fin with a thickness of (1/10) of the cavity side was placed horizontally on the hot wall. The solid to fluid thermal conductivity ratio (Rk) and the fin width were varied. It was concluded that for 105 ⩽ Ra ⩽ 106, a fin of partial width was more effective in promoting heat transfer than a fin of full width. Oosthuizen et al. [20] numerically studied the three-dimensional natural convective flow in a rectangular enclosure with vertical sidewalls and horizontal top and bottom surfaces. A heated isothermal rectangular element was mounted on the center of one vertical wall of the enclosure while the horizontal top surface of it cooled to a uniform temperature. All other enclosure surfaces were adiabatic. They concluded that the relative change in mean Nusselt number with decreasing dimensionless width of plate increased as the Rayleigh number decreased. Bocu and Altac [21] studied numerically the laminar natural convection heat transfer in 3D rectangular air filled enclosures, with pins attached to the active wall. Two cases of rectangular enclosures were considered (H/L = 1 and H/L = 2). The enclosure was heated from a lateral wall and was cooled from the opposite lateral wall while the other walls of the enclosure were insulated. A number of isothermal cylindrical pins were attached to the interior of the hot wall in various arrangements to enhance the heat transfer. The results explained that the Nusselt number ratio with respect to the enclosure without pins increased with pin length, pin number and for tall enclosures. Also, long pins increased the Nusselt number ratio by about 34%. Another work related with the three-dimensional natural convection in a three-dimensional cavity can be found in [22], [23] and [24]. Nowadays, a modern approach for the thermal system optimization is based on the second law of thermodynamics. In other words, the entropy generation is used as a parameter for evaluating the system efficiency. In fact, the system with minimum entropy generation is considered as the optimal design [25]. Anyway, the entropy generation due to natural convection in the two-dimensional trapezoidal cavity was analyzed by limited authors. Varol et al. [26] investigated numerically the entropy generation due to buoyancy induced convection and conduction in a right angle trapezoidal enclosure filled with fluid saturated porous medium. Left vertical solid wall of the trapezoidal enclosure had a finite thickness and conductivity. The outside temperature of the solid wall was higher than that of inclined wall, while horizontal walls were adiabatic. The study was performed for the Rayleigh number (50 ⩽ Ra ⩽ 1000), inclination angle of the inclined wall of the enclosure (γ = 35°, 45° and 60°), dimensionless thickness of the solid vertical wall (S = 0.05, 0.1 and 0.2) and thermal conductivity ratio (k = 0.1, 1.0 and 10). It was found that increasing the Rayleigh number decreased the Bejan number. Basak et al. [27] investigated numerically the entropy generation during natural convection in a trapezoidal cavity with isothermal and non-isothermal hot bottom wall. The study was performed with various inclination angles (φ = 45°, 60° and 90°), and various Prandtl numbers (Pr = 0.015, 0.7 and 1000) in the range of Rayleigh number (103–105). The total entropy generation was found to increase with Prandtl number. The non-isothermal heating strategy was found to be energy efficient values than isothermal heating for all inclination angles. Very recently, Ramakrishna et al. [28] analyzed heatlines and entropy generation during free convection within trapezoidal cavities. The left wall of the cavity was hot and right wall maintained at constant cold temperature while the top and bottom walls were adiabatic. The results were presented in terms of streamlines, heatlines, isotherms, entropy generation due to fluid friction and heat transfer, average Bejan number, average Nusselt number and total entropy generation. They concluded that, the trapezoidal cavity with (φ = 60°) was the optimal shape for thermal processing at (Pr = 0.015) while square cavity (φ = 90°) was the optimal design for the thermal processing at (Pr = 7.2) based on lower total entropy generation and higher average Nusselt number. The above literature review indicated that the published papers related with the analysis of natural convection and entropy generation are available in two-dimensional trapezoidal cavities only. According to our knowledge and experience, the investigation of this problem in a three-dimensional trapezoidal inclined cavity has not been considered yet in the literature. We think that the present work is a very significant attempt to fill this gap in the available literature.
2. Mathematical model
2.1. Definition of geometrical configuration
The three-dimensional natural convection and entropy generation problem inside an inclined cubical trapezoidal cavity of height (H) and length (L) filled with air [Pr = 0.71] are investigated in the present work as shown in Fig. 1. The vertical right and left sidewalls of a trapezoidal cavity are kept at isothermal cold temperatures (Tc). The upper and lower walls are considered insulated and subjected to an isothermal hot temperature (Th) respectively. The flow field inside the cubical cavity is considered three-dimensional, Newtonian, unsteady, incompressible and laminar. From the other side, the heat transfer due to thermal gradients and friction effects causes that the cubical trapezoidal cavity is subjected to a loss in energy and as a result an entropy generation is induced. The Rayleigh number is varied as 103 ⩽ Ra ⩽ 105, while the trapezoidal cavity inclination angle is varied as 0° ⩽ Φ ⩽ 180°. The Rayleigh number relates the relative magnitude of viscous and buoyancy forces in the fluid. The natural convection occurs when buoyancy forces are greater than viscous forces. The fluid inside the cubical cavity is assumed to have constant thermo-physical properties and Boussinesq approximation is used to model the density variation.
|
|
|
Figure 1. Schematic diagram of the present problem. |
2.2. Mathematical model and the numerical solution
To start the numerical approach, the vorticity-vector potential formalism is considered in the present work which allows in a three-dimensional geometry together with the elimination of the pressure term. Vector potential and the vorticity are defined respectively by the following two equations:
|
|
(1) |
The construction of these equations is described in more details in Ghachem et al. [29]. The dimensionless governing equations can be written as follows:
|
|
(2) |
|
|
(3) |
|
|
(4) |
where
|
|
Moreover, the dimensionless temperature, dimensionless time, dimensionless velocity, dimensionless vector potential and dimensionless vorticity are defined respectively as
|
|
while, the dimensionless Cartesian coordinates in x, y and z directions are defined as
|
|
2.2.1. Boundary conditions
The boundary conditions for the present problem are given as follows:
Temperature:
|
|
|
|
Vorticity:
|
|
|
|
|
|
Vector potential:
|
|
|
|
|
|
Velocity:
|
|
The generated entropy () is written by Kolsi et al. [30] in the following form:
|
|
(5) |
The first term represents the generated entropy due to the temperature gradient, while the second one is due to the friction effects. The heat flux vector is given by
|
|
(6) |
The dissipation function () is written as follows:
|
|
(7) |
Therefore, the generated entropy is written as
|
|
(8) |
The dimensionless local generated entropy () is written as follows:
|
|
(9) |
where
|
|
(10) |
where is the irreversibility coefficient.
The first term of (Ns) represents the local irreversibility due to the temperature gradients, and it is noted as (Ns–th). The second term of (Ns) represents the contribution of the viscous effects in the irreversibility and it is noted as (Ns–fr). It is useful to mention that Eq. (10) gives a good idea on the profile and the distribution of the dimensionless local generated entropy (Ns ). Also, the total dimensionless generated entropy () is written as
|
|
(11) |
The local and average Nusselt numbers are given by
|
|
(12) |
The mathematical model described above was written by a FORTRAN program. The control volume finite difference method is used to discretize governing (2), (3), (4) and (10) respectively. The central-difference scheme is used for treating convective terms while the fully implicit procedure is used to discretize the temporal derivatives. The grids are considered uniform in all directions with clustering nodes on boundaries. The successive relaxation iteration scheme is used to solve the resulting non-linear algebraic equations. The time step (10−4) and spatial mesh (71 × 71 × 71) are utilized to carry out all the numerical tests. The solution is considered acceptable when the following convergence criterion is satisfied for each step of time:
|
|
(13) |
In order to check the accuracy of our code, a verification is performed by using the present numerical algorithm to simulate the same problem considered by Basak et al. [31] using the same geometry and boundary conditions for laminar natural convection flow in a two-dimensional trapezoidal porous enclosure. The comparison for both streamlines and isotherms is shown in Fig. 2 using the dimensionless parameters: Pr = 0.7, Da = 10−3, Ra = 105 and and a good agreement is obtained. Therefore, the computational procedure is ready and can predict the three-dimensional natural convection and the entropy generation in an inclined trapezoidal cavity and as a result, the previous verification gives a good interest in the present numerical model to deal with the recent physical problem.
|
|
|
Figure 2. Comparison of streamlines and isotherms at Pr = 0.7, Da = 10−3, Ra = 105 and . |
3. Results and discussion
The unsteady laminar three-dimensional natural convection and entropy generation in an inclined cubical trapezoidal air-filled cavity are investigated numerically in this work. The effect of Rayleigh number (Ra) and cavity inclination angle () on the fluid flow, heat transfer and entropy generation has been performed. The results were presented via streamlines, trajectory of particles, isotherms, entropy contours together with local and average Nusselt numbers.
3.1. Effect of Rayleigh number on the thermal field
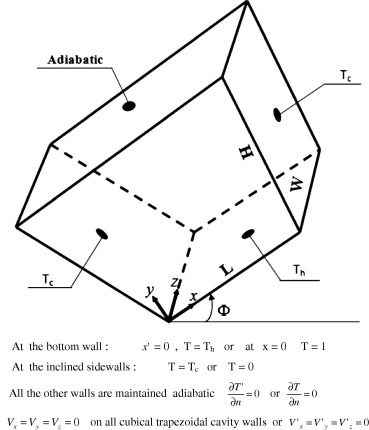
Fig. 3 illustrates isosurfaces of temperature around the all geometry (left) and isotherms along the mid-section [Z = 0.5] (right) in the cubical trapezoidal cavity [] for various values of Rayleigh number [(a) Ra = 103, (b) Ra = 104 and (c) Ra = 105]. When the Rayleigh number is low [Ra = 103] or when the effect of natural convection is slight, the isotherms are in general smooth, straight lines and parallel to cavity sidewalls. This behavior is due to flow weakness when the Rayleigh number is low [Ra = 103]. It can be seen from Fig. 3, that isotherms emanate from the lower wall (or base) where the heat source exists and end on cold right and left sidewalls, indicating the heat flow path. Heat conduction is the dominant mechanism of heat transfer inside the cubical cavity in this case. But, as the Rayleigh number increases to [Ra = 104 and Ra = 105], buoyancy force dominates over viscous force leading to increase the natural convection effect. Therefore, the shape of isotherms begins to deviate sharply from uniform one encountered in the case where [Ra = 103]. This is due to the fact that strong circulation occurs when the Rayleigh number is high. The concentration of isotherms adjacent to the lower wall increases as the Rayleigh number increases illustrating high amount of heat and large temperature gradient adjacent to the lower wall of the cubical trapezoidal cavity. Therefore, a thermal boundary layer is constructed at this region and can be observed especially when [Ra = 105]. Heat convection is the dominant mechanism of heat transfer in this case. Therefore, it can be concluded that there is a clear conversion in isotherms pattern from uniform smooth shape to a high confuse one as the Rayleigh number increases. This behavior gives a clear approval of natural convection effect on the thermal field inside the cubical trapezoidal cavity.
|
|
|
Figure 3. The isosurfaces of temperature around the all geometry (left) and isotherms along the mid-section (right) in the cubical trapezoidal cavity [] for various values of Rayleigh number (a) Ra = 103, (b) Ra = 104 and (c) Ra = 105. |
3.2. Effect of Rayleigh number on the flow field
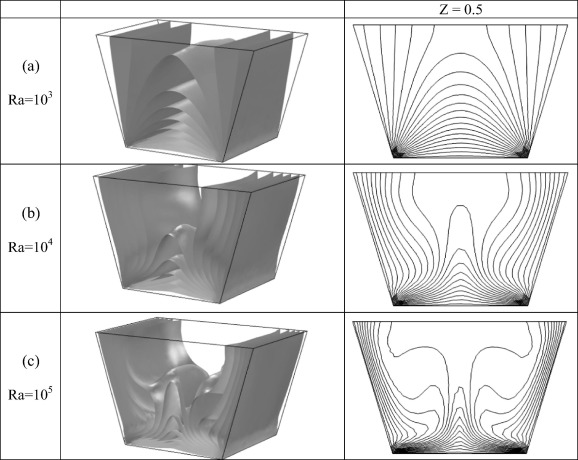
Fig. 4 presents the trajectory of particles around the all geometry (left) and streamlines along the mid section [Z = 0.5] (right) in the cubical trapezoidal cavity [] for various values of Rayleigh number [(a) Ra = 103, (b) Ra = 104 and (c) Ra = 105]. According to the natural convection effect, the flow field begins to move from the hot lower wall until it arrives to the insulated upper wall. Then, it changes its direction and moves toward the cold right and left sidewalls after passing secondly adjacent to the hot lower wall. This cyclic motion of the flow field generates the re-circulating vortices which occupy all span of the cubical trapezoidal cavity as seen in Fig. 4. It can be noticed that the air stream which moves upward adjacent to the hot lower wall separates into two re-circulating vortices as indicated in 3D results. This flow behavior can be seen for all the considered values of Rayleigh number, but there is a difference in the shape of vortices related with the value of Rayleigh number. In the case of low Rayleigh number [Ra = 103], the effect of buoyancy force [which is generated due to the temperature difference] is slight and the flow circulation is uniform. Therefore, the convection effect is weak. Now, when the Rayleigh number increases to [Ra = 104 and Ra = 105] or when the effect of buoyancy force is significant, the frictional resistance to the fluid motion diminishes gradually. Therefore, the flow circulation becomes less uniform. This notation is in a good agreement with the results of Fusegi et al. [32]. It can be observed that, the strict uniform pattern of re-circulating vortices encountered at [Ra = 103] is broken due to the strong effect of natural convection inside the cubical trapezoidal cavity, while, a weak fluid motion is noticed at the edges of the cubical cavity for all the considered range of Rayleigh number. Moreover, it can be seen also that the difference between the two-dimensional and three-dimensional results becomes clear as Rayleigh number increases from [Ra = 103] to [Ra = 105].
|
|
|
Figure 4. The trajectory of particles around the all geometry (left) and streamlines along the mid-section (right) in the cubical trapezoidal cavity [] for various values of Rayleigh number (a) Ra = 103, (b) Ra = 104 and (c) Ra = 105. |
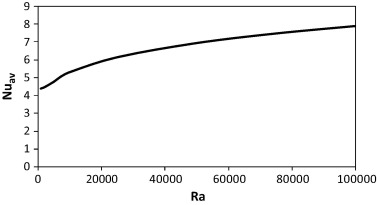
3.3. Effect of Rayleigh number on local and average Nusselt numbers
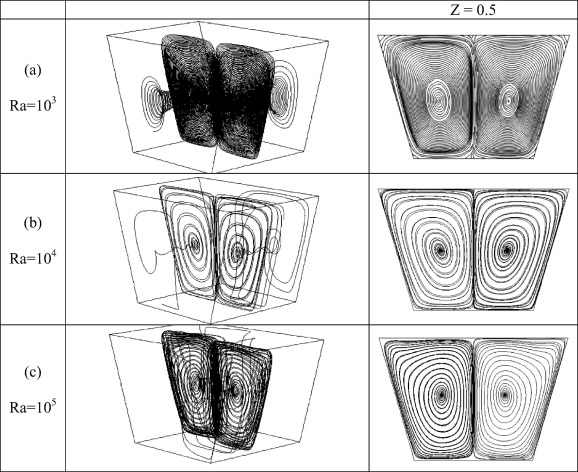
Fig. 5 demonstrates the profiles of the local Nusselt numbers (NuLoc) at the hot lower wall in the cubical trapezoidal cavity [] for various values of Rayleigh number [(a) Ra = 103, (b) Ra = 104 and (c) Ra = 105]. These profiles reveal that the local Nusselt number is linear at low Rayleigh number [Ra = 103] .This indicates that the heat is transferred inside the cubical trapezoidal cavity by pure conduction. But, as the Rayleigh number increases to [Ra = 104 and Ra = 105], local Nusselt number profiles start to change its shape indicating the onset of natural convection. However, at [Ra = 104], the local Nusselt profiles are still in the transition process from conduction mode to a fully convection one. Moreover, it is interesting to observe high values of the local Nusselt number adjacent to the cavity hot lower wall due to the existence of heat source at this place. Fig. 6 illustrates the effect of Rayleigh number on the average Nusselt number (Nuav) in the cubical trapezoidal cavity at []. The average Nusselt number is a measure of the heat transfer rate inside the cubical trapezoidal cavity. It can be seen as expected, that the average Nusselt number increases as the Rayleigh number increases. This is because the natural convection and flow circulation enhance when the Rayleigh number increases. Therefore, the highest average Nusselt number corresponds to the highest Rayleigh number and vice versa. The reason of this behavior is due to the increase in the temperature gradient when the Rayleigh number increases. This increase leads to the average Nusselt number increasing.
|
|
|
Figure 5. The variation in the local Nusselt numbers at the hot lower wall in the cubical trapezoidal cavity [] for various values of Rayleigh number [(a) Ra = 103, (b) Ra = 104 and (c) Ra = 105]. |
|
|
|
Figure 6. The variation in the average Nusselt numbers in the cubical trapezoidal cavity [] for various values of Rayleigh number. |
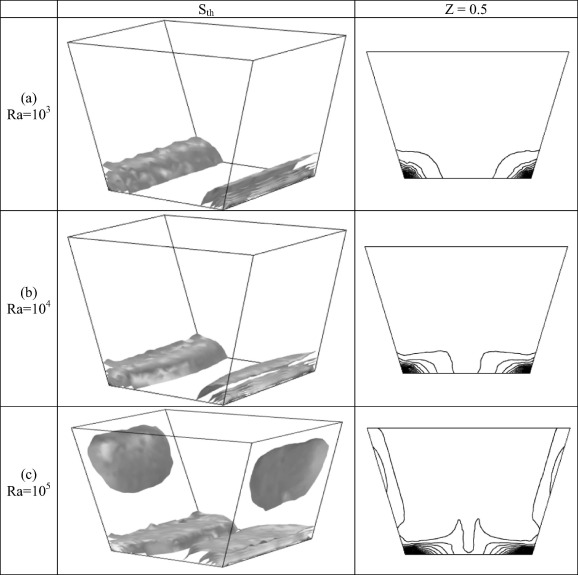
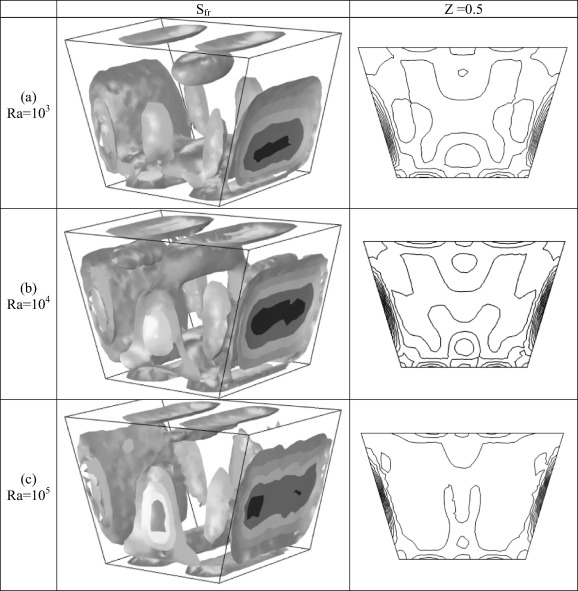
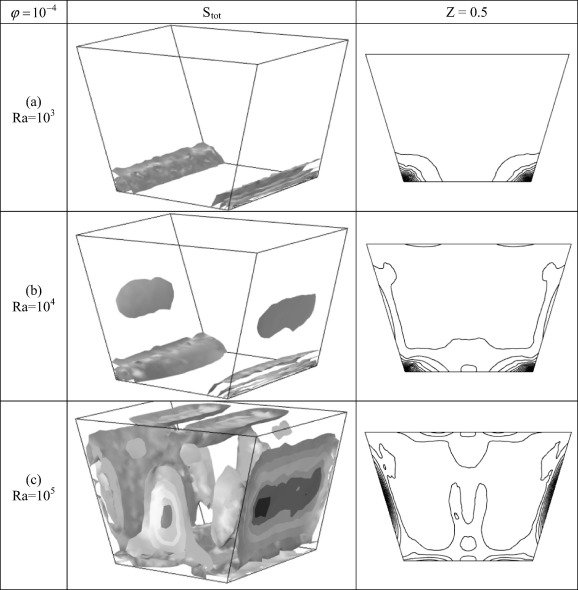
3.4. Effect of Rayleigh number on entropy generation
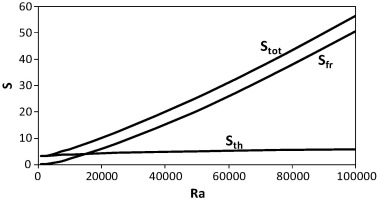
Fig. 7 displays iso-surfaces (left) and isolines (right) of the entropy generation due to the heat transfer (Sth) in the cubical trapezoidal cavity [] for various values of Rayleigh number [(a) Ra = 103, (b) Ra = 104 and (c) Ra = 105]. It can be noticed that the entropy generation contours extend deeply inside the cubical trapezoidal cavity as the Rayleigh number increases. This is due to the increase in the heat transfer losses with increasing the Rayleigh number, which leads to increase the entropy generation. Moreover, it can be seen that the entropy generation contours increase near the lower wall due to the heat source existence, while, they weak adjacent to the left and right cavity sidewalls even at [Ra = 105]. Furthermore, it can be seen from Fig. 7, that there is a space region in the cubical cavity core. This is because of stagnant or low fluid velocity. Fig. 8 demonstrates iso-surfaces (left) and isolines (right) of the entropy generation due to the friction (Sfr) in the cubical trapezoidal cavity [] for various values of Rayleigh number [(a) Ra = 103, (b) Ra = 104 and (c) Ra = 105]. It can be seen that the entropy generation contours due to the fluid friction are concentrated strongly adjacent to the cavity right and left sidewalls. This is due to the existence of boundary layer which leads to increase the entropy generation due to the friction there. This observation is in a good agreement with the results of Mukhopadhyay [33]. It is interesting to see that, the total entropy generation (Stot) and the entropy generation due to heat transfer (Sth) have an approximately similar pattern when [Ra = 103 and Ra = 104]. This behavior indicates the domination of the irreversibility due to the heat transfer at this range of Rayleigh number. But, when the Rayleigh number is high [Ra = 105] the total entropy generation (Stot) has a similar pattern with the entropy generation due to the fluid friction (Sfr). This behavior indicates the domination of the irreversibility due to the fluid friction at high Rayleigh number. This behavior will be highlighted in more detail later. Fig. 9 shows iso-surfaces (left) and isolines (right) of the total entropy generation (Stot) in the cubical trapezoidal cavity [] for various values of Rayleigh number [(a) Ra = 103, (b) Ra = 104 and (c) Ra = 105]. From this figure, one can notice that when the Rayleigh number is low [Ra = 103], the entropy contours are concentrated near the lower wall in a similar behavior to their corresponding contours noticed in Fig. 7. The main conclusion of this behavior is that the entropy generation due to heat transfer (Sth) is high and dominant, while the entropy generation due to the fluid friction (Sfr) is weak. Therefore, the contribution of the entropy generation due to heat transfer (Sth) is greater than the entropy generation due to the fluid friction (Sfr) which makes the contours of the total entropy generation (Stot) similar to the contours of entropy generation due to heat transfer (Sth). At [Ra = 104], the total entropy generation contours (Stot) are somewhat similar to the corresponding contours which are seen in Figure 7 and Figure 8 respectively. So, in this case the contribution of entropy generations due to heat transfer and fluid friction is comparable. But when the Rayleigh number is high [Ra = 105], the entropy contours are concentrated adjacent to the cavity right and left sidewalls in a similar behavior to their corresponding contours noticed in Fig. 8. The main conclusion of this behavior is that the entropy generation due to the fluid friction (Sfr) is high and dominant, while the entropy generation due to the heat transfer (Sth) is weak. Therefore, the contribution of the entropy generation due to fluid friction (Sfr) is greater than the entropy generation due to the heat transfer (Sth) which makes the contours of the total entropy generation (Stot) similar to the contours of the entropy generation due to fluid friction (Sfr). Fig. 10 presents the variation of different entropy generation [Sth, Sfr and Stot] in the cubical trapezoidal cavity with various values of Rayleigh number. It can be seen that the entropy generation rate due to the heat transfer (Sth) increases slightly as the Rayleigh number increases. From the other side, there is a clear increase of entropy generation due to friction (Sfr) and the total entropy generation (Stot) when the Rayleigh number increases. This is due to the slight increase in the heat transfer losses and high increase in fluid friction losses with increasing the Rayleigh number. Therefore, the maximum value of the total entropy generation (Stot) and entropy generation due to friction (Sfr) occurs at maximum value of Rayleigh number [i.e., Ra = 105].
|
|
|
Figure 7. The iso-surfaces (left) and isolines (right) of the entropy generation due to the heat transfer (Sth) in the cubical trapezoidal cavity [] for various values of Rayleigh number [(a) Ra = 103, (b) Ra = 104 and (c) Ra = 105]. |
|
|
|
Figure 8. The iso-surfaces (left) and isolines (right) of the entropy generation due to the friction (Sfr) in the cubical trapezoidal cavity [] for various values of Rayleigh number [(a) Ra = 103, (b) Ra = 104 and (c) Ra = 105]. |
|
|
|
Figure 9. The iso-surfaces (left) and isolines (right) of the total entropy generation (Stot) in the cubical trapezoidal cavity [] for various values of Rayleigh number [(a) Ra = 103, Ra = 104 and (c) Ra = 105] and φ = 10−4. |
|
|
|
Figure 10. The variation of different entropy generation in the cubical trapezoidal cavity [] with various values of Rayleigh number. |
3.5. Effect of inclination angle on the thermal field
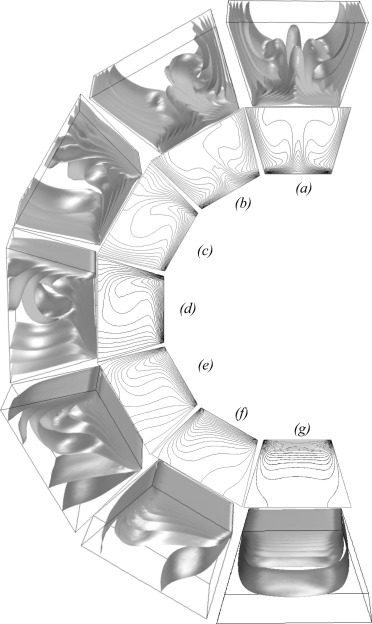
Fig. 11 shows the isosurfaces of temperature around the all geometry (upper) and isotherms along the mid-section [Z = 0] (lower) in the cubical trapezoidal cavity at [Ra = 105] and various values of inclination angle [(a) ; (b) ; (c) ; (d) ; (e) ; (f) and (g) ]. For horizontal cubical trapezoidal cavity [i.e., ], the thermal field is governed by the Rayleigh number effect only which is explained previously in Fig. 3. Since, the value of the selected Rayleigh number is high [i.e., Ra = 105], the natural convection effect is strong which causes to make the thermal field represented by isotherms and isosurfaces of temperature are non-uniform. Now, when the cavity inclination angle increases to and respectively, the effect of natural convection decreases slightly and the disturbance in the isotherms becomes less than the corresponding one which is observed at . Furthermore, the thermal boundary layers adjacent to the hot lower wall become less thicker than that observed at . For vertical cubical trapezoidal cavity [i.e., ], the thermal field becomes somewhat uniform indicating the beginning of the conduction mode of the heat transfer inside the cavity. But, when the cavity inclination angle increases to , and respectively, the pattern of isotherms will change completely especially at . The isotherms are uniformly distributed inside the cavity implying conduction as the dominant heat transfer mode.
|
|
|
Figure 11. The isosurfaces of temperature around the all geometry (upper) and isotherms along the mid-section (lower) in the cubical trapezoidal cavity at [Ra = 105] and various values of inclination angle [(a) ; (b) ; (c) ; (d) ; (e) ; (f) and (g) ]. |
3.6. Effect of inclination angle on the flow field
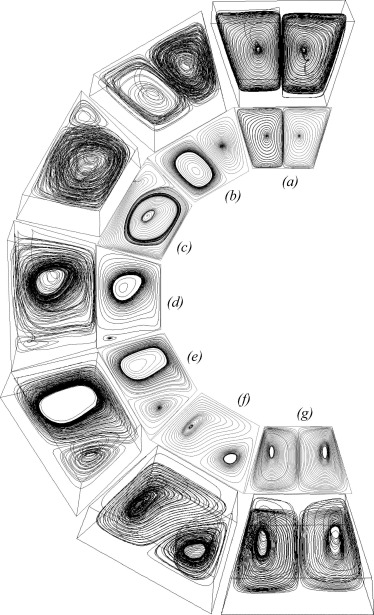
Fig. 12 displays the trajectory of particles around the all geometry (upper) and streamlines along the mid-section [Z = 0] (lower) in the cubical trapezoidal cavity at [Ra = 105] and various values of inclination angle [(a) ; (b) ; (c) ; (d) ; (e) ; (f) and (g) ]. The results demonstrate that the cavity inclination angle has a significant role on the flow pattern. When the inclination angle is and , the flow field inside the cavity can be represented by two symmetrical re-circulating vortices. The effect of buoyancy force in this case is high. But, when the cavity inclination angle increases to and , the flow field inside the cavity is represented by a single large re-circulating vortex. As, the cavity inclination angle jumps to , and respectively, the flow field inside the cavity is characterized again by two unsymmetrical re-circulating vortices. The effect of natural convection in this case begins to decrease gradually as the cavity inclination angle increases.
|
|
|
Figure 12. The trajectory of particles around the all geometry (upper) and streamlines along the mid-section (lower) in the cubical trapezoidal cavity at [Ra = 105] and various values of inclination angle [(a) ; (b) ; (c) ; (d) ; (e) ; (f) and (g) ]. |
3.7. Effect of inclination angle on average Nusselt numbers
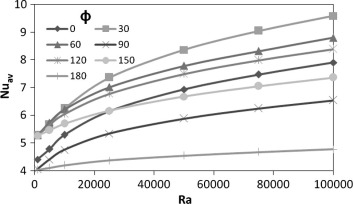
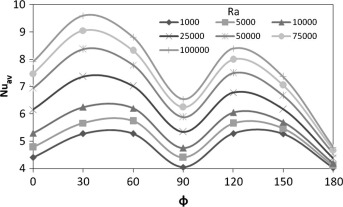
Fig. 13 illustrates the relationship between the average Nusselt numbers in the cubical trapezoidal cavity and Rayleigh number for various values of inclination angle. It is found that the average Nusselt number reaches its maximum value at , while, the minimum value of the average Nusselt number is reached at . The reason of this behavior is due to the increase of distance between the hot and cold cavity walls when the inclination angle increases to . This increase reduces the temperature gradient and causes to drop the average Nusselt number values. Fig. 14 depicts the relationship between the average Nusselt numbers in the cubical trapezoidal cavity and inclination angle for various values of Rayleigh number. It can be seen that the average Nusselt number is an increasing function of Rayleigh number due to the significant increase in the convection effect as expected. The results show also that when the inclination angle in the range is 0° ⩽ Φ ⩽ 90°, the effect of Rayleigh number is greater than its effect when the inclination angle in the range is 120° ⩽ Φ ⩽ 180°. The reason of this behavior is explained previously.
|
|
|
Figure 13. The relationship between the average Nusselt numbers in the cubical trapezoidal cavity and Rayleigh number for various values of inclination angle. |
|
|
|
Figure 14. The relationship between the average Nusselt numbers in the cubical trapezoidal cavity and inclination angle for various values of Rayleigh number. |
3.8. Effect of inclination angle on entropy generation
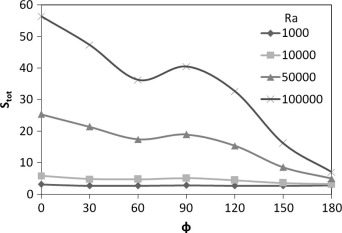
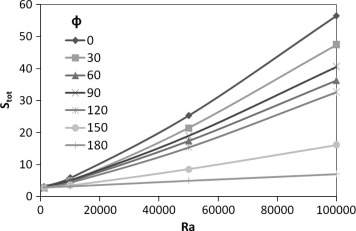
Fig. 15 displays the relationship between the total entropy generation (Stot) in the cubical trapezoidal cavity and inclination angle for various values of Rayleigh number. It can be seen from this figure, that the total entropy generation increases strongly for high Rayleigh number [i.e., Ra = 105] and []. This increase is due to an enhancement in the flow circulation when the Rayleigh number is high. But, as the cavity inclination angle increases, the profiles of the total entropy generation begin to decrease gradually. The result indicated also that the total entropy generation has an approximately linear profile when the Rayleigh number is low. Therefore, one can conclude that the inclination angle effect on the total entropy generation becomes insignificant when the Rayleigh number is low. Fig. 16 illustrates the relationship between the total entropy generation (Stot) in the cubical trapezoidal cavity and Rayleigh number for various values of inclination angle. Similar to the results noticed in Fig. 15, it can be seen that the total entropy generation has a maximum value for horizontal cubical trapezoidal cavity [i.e., ], while, it has a minimum value when the inclination angle equals to []. This behavior can be seen for all values of the Rayleigh number. Furthermore, the total entropy generation (Stot) increases as the Rayleigh number increases. But as mentioned previously, this increase is high for horizontal cubical trapezoidal cavity [i.e., ], while it decreases as the inclination angle increases.
|
|
|
Figure 15. The relationship between the total entropy generation (Stot) in the cubical trapezoidal cavity and inclination angle for various values of Rayleigh number. |
|
|
|
Figure 16. The relationship between the total entropy generation (Stot) in the cubical trapezoidal cavity and Rayleigh number for various values of inclination angle. |
4. Conclusions
The following conclusions can be detected from the results of the present work:
- When the natural convection is weak [i.e., Ra = 103], isotherms are in general smooth, nearly vertical and semi-parallel to the right and left cavity sidewalls and the heat is transferred by conduction.
- When the natural convection is strong [i.e., Ra = 105], the concentrated region of isotherms adjacent to the lower wall becomes more intense and isothermal lines are become more confuse due to strong circulation.
- The difference between the two-dimensional and three-dimensional flow pattern results becomes clear as the Rayleigh number increases.
- When the Rayleigh number increases, the flow circulation increases and some disturbances in the flow patterns are observed especially in 3D results.
- The flow pattern inside the cubical trapezoidal cavity consists of four spiral re-circulating vortices which cover all the span of it.
- The local Nusselt number distribution is almost parallel to the horizontal upper and lower cavity walls.
- When the Rayleigh number increases the average Nusselt number increases.
- The entropy generation contours due to the heat transfer (Sth) increase strongly when the Rayleigh number increases especially adjacent to the heat source location at the lower wall.
- The entropy generation contours due to the fluid friction (Sfr) are concentrated strongly adjacent to the cavity right and left sidewalls.
- The entropy generation due to the heat transfer (Sth) increases slightly as the Rayleigh number increases, while, a strong increase with the Rayleigh number is seen with respect to entropy generation due to friction (Sfr) and the total entropy generation (Stot).
- Different flow patterns can be seen inside the cubical trapezoidal cavity as the inclination angle increases from to . This gives an important indication that the flow field inside the cavity is significantly affected by the inclination angle.
- When the cavity inclination angle increases, isotherms are uniformly distributed, less compressed inside the cavity and the conduction is the dominant heat transfer mode. Also, the thickness of thermal boundary layer decreases as the cavity inclination angle increases.
- The minimum average Nusselt number inside the cubical trapezoidal cavity corresponds to the highest inclination angle [i.e., ], while, the results indicated that the average Nusselt number reaches its maximum value at .
- The inclination angle effect on the total entropy generation becomes insignificant when the Rayleigh number is low.
- The total entropy generation has a maximum value for horizontal cubical trapezoidal cavity [i.e., ], while, it has a minimum value when the inclination angle equals to [].
References
- [1] A. Hussein; Computational analysis of natural convection in a parallelogrammic cavity with a hot concentric circular cylinder moving at different vertical locations; Int. Commun. Heat Mass Transfer, 46 (2013), pp. 126–133
- [2] S. Hussain, A. Hussein; Numerical investigation of natural convection phenomena in a uniformly heated circular cylinder immersed in square enclosure filled with air at different vertical locations; Int. Commun. Heat Mass Transfer, 37 (8) (2010), pp. 1115–1126
- [3] S. Lam, R. Gani, J. Simons; Experimental and numerical studies of natural convection in trapezoidal cavities; ASME J. Heat Transfer, 111 (1989), pp. 372–377
- [4] S. Kumar; Natural convective heat transfer in trapezoidal enclosure of box-type solar cooker; Renewable Energy, 29 (2004), pp. 211–222
- [5] T. Basak, S. Roy, A. Singh, B. Pandey; Natural convection flow simulation for various angles in a trapezoidal enclosure with linearly heated side wall(s); Int. J. Heat Mass Transfer, 52 (2009), pp. 4413–4425
- [6] K. Lasfer, M. Bouzaiane, T. Lili; Numerical study of laminar natural convection in a side-heated trapezoidal cavity at various inclined heated sidewalls; Heat Transfer Eng., 31 (5) (2010), pp. 362–373
- [7] T. Basak, D. Ramakrishna, S. Roy, A. Matta, I. Pop; A comprehensive heatline based approach for natural convection flows in trapezoidal enclosures: effect of various walls heating; Int. J. Therm. Sci., 50 (2011), pp. 1385–1404
- [8] S. Sahoo, S. Singh, R. Banerjee; Analysis of heat losses from a trapezoidal cavity used for linear fresnel reflector system; Sol. Energy, 86 (2012), pp. 1313–1322
- [9] S. Natarajan, K. Reddy, T. Mallick; Heat loss characteristics of trapezoidal cavity receiver for solar linear concentrating system; Appl. Energy, 93 (2012), pp. 523–531
- [10] A. Mustafa, I. Ghani; Natural convection in trapezoidal enclosure heated partially from below; Al-Khwarizmi Eng. J., 8 (1) (2012), pp. 76–85
- [11] A. Da silva, E. Fontana, V. Mariani, F. Marcondes; Numerical investigation of several physical and geometric parameters in the natural convection into trapezoidal cavities; Int. J. Heat Mass Transfer, 55 (2012), pp. 6808–6818
- [12] N. Tracy, D. Crunkleton; Oscillatory natural convection in trapezoidal enclosures; Int. J. Heat Mass Transfer, 55 (2012), pp. 4498–4510
- [13] L. Iyican, L. Witte, Y. Bayazitoglu; An experimental study of natural convection in trapezoidal enclosures; ASME J. Heat Transfer, 102 (8) (1980), pp. 648–653
- [14] F. Moukalled, S. Acharya; Natural convection in a trapezoidal enclosure with offset baffles; J. Thermophys. Heat Transfer, 15 (2001), pp. 212–218
- [15] F. Moukalled, M. Darwish; Natural convection in a trapezoidal enclosure heated from the side with a baffle mounted on its upper inclined surface; Heat Transfer Eng., 25 (2004), pp. 80–93
- [16] E. Natarajan, S. Roy, T. Basak; Effect of various thermal boundary conditions on natural convection in a trapezoidal cavity with linearly heated side wall(s); Numer. Heat Transfer, Part B, 52 (6) (2007), pp. 551–568
- [17] W. Hiller, S. Koch, T. Kowalewski, F. Stella; Onset of natural convection in a cube; Int. J. Heat Mass Transfer, 13 (1993), pp. 3251–3263
- [18] R. Frederick; Natural convection heat transfer in a cubical enclosure with two active sectors on one vertical wall; Int. Commun. Heat Mass Transfer, 24 (4) (1997), pp. 507–520
- [19] R. Frederick, S. Moraga; Three-dimensional natural convection in finned cubical enclosures; Int. J. Heat Fluid Flow, 28 (2007), pp. 289–298
- [20] P. Oosthuizen, A. Kalendar, T. Simko, Three-dimensional natural convective flow in a rectangular enclosure with a rectangular heated section on one vertical wall and a cooled horizontal upper wall, in: 5th European Thermal-Sciences Conference, Netherlands, 2008, pp. 1–8.
- [21] Z. Bocu, Z. Altac; Laminar natural convection heat transfer and air flow in three-dimensional rectangular enclosures with pin arrays attached to hot wall; Appl. Therm. Eng., 31 (2011), pp. 3189–3195
- [22] A. Da silva, L. Gosselin; On the thermal performance of an internally finned 3D cubic enclosure in natural convection; Int. J. Therm. Sci., 44 (2005), pp. 540–546
- [23] B. Bennett, J. Hsueh; Natural convection in a cubic cavity: implicit numerical solution of two benchmark problems; Numer. Heat Transfer, Part A, 50 (2006), pp. 99–107
- [24] D. Lo, S. Leu; DQ analysis of 3D natural convection in an inclined cavity using an velocity-vorticity formulation; Proc. World Acad. Sci., Eng. Technol., 36 (2008), pp. 370–375
- [25] W. El-Maghlany, K. Saqr, M. Teamah; Numerical simulations of the effect of an isotropic heat field on the entropy generation due to natural convection in a square cavity; Energy Convers. Manage., 85 (2014), pp. 333–342
- [26] Y. Varol, H. Oztop, I. Pop; Entropy analysis due to conjugate-buoyant flow in a right-angle trapezoidal enclosure filled with a porous medium bounded by a solid vertical wall; Int. J. Therm. Sci., 48 (2009), pp. 1161–1175
- [27] T. Basak, R. Anandalakshmi, P. Kumar, S. Roy; Entropy generation vs energy flow due to natural convection in a trapezoidal cavity with isothermal and non-isothermal hot bottom wall; Energy, 37 (2012), pp. 514–532
- [28] D. Ramakrishna, T. Basak, S. Roy; Analysis of heatlines and entropy generation during free convection within trapezoidal cavities; Int. Commun. Heat Mass Transfer, 45 (2013), pp. 32–40
- [29] K. Ghachem, L. Kolsi, C. Mâatki, A. Hussein, M. Borjini; Numerical simulation of three-dimensional double diffusive free convection flow and irreversibility studies in a solar distiller; Int. Commun. Heat Mass Transfer, 39 (2012), pp. 869–876
- [30] L. Kolsi, H. Oztop, M. Borjini, K. Al-Salem; Second law analysis in a three-dimensional lid-driven cavity; Int. Commun. Heat Mass Transfer, 38 (2011), pp. 1376–1383
- [31] T. Basak, S. Roy, A. Singh, I. Pop; Finite element simulation of natural convection flow in a trapezoidal enclosure filled with porous medium due to uniform and non-uniform heating; Int. J. Heat Mass Transfer, 52 (2009), pp. 70–78
- [32] T. Fusegi, M. Hyun, K. Kuwahara, B. Farouk; A numerical study of three-dimensional natural convection in a differentially heated cubical enclosure; Int. J. Heat Mass Transfer, 34 (6) (1991), pp. 1543–1557
- [33] A. Mukhopadhyay; Analysis of entropy generation due to natural convection in square enclosures with multiple discrete heat sources; Int. Commun. Heat Mass Transfer, 37 (2010), pp. 867–872
Document information
Published on 12/04/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?