On the need for the use of error-controlled finite element analyses in structural shape optimization processes with evolutionary algorithms

Resumen

Este trabajo analiza la influencia del nivel de error de discretización de los análisis por elementos finitos (MEF) de las distintas configuraciones geométricas propuestas por los algoritmos de optimización de forma estructural sobre el comportamiento de dichos algoritmos. El artículo demuestra claramente que si los análisis mediante el MEF no presentan la suficiente precisión, la solución final proporcionada por el algoritmo de optimización no será ni el óptimo buscado ni cumplirá con las restricciones impuestas. Se demostrará la necesidad de la utilización de técnicas del MEF basadas en remallados adaptables. El artículo propone la combinación de dos estrategias para reducir el coste computacional relacionado con la utilización de dichos remallados adaptables junto con algoritmos evolutivos de optimización: (a) la utilización del algoritmo descrito por Bugeda et al. [1] que reduce el coste computacional asociado al análisis de cada configuración geométrica mediante el MEF con remallados adaptables y, (b) el incremento paulatino de la precisión requerida a cada análisis a fin de obtener una reducción sustancial del coste computacional en las etapas iniciales del proceso de optimización.

Abstract

This work analyzes the influence of the discretization error contained in the Finite Element (FE) analyses of each design configuration proposed by the structural shape optimization algorithms over the behavior of the algorithm. The paper clearly shows that if FE analyses are not accurate enough, the final solution provided by the optimization algorithm will neither be optimal nor satisfy the constraints. The need for the use of adaptive FE analysis techniques in shape optimum design will be shown. The paper proposes the combination of two strategies to reduce the computational cost related to the use of mesh adaptivity in evolutionary optimization algorithms: (a) the use of the algorithm described by Bugeda et al. [1] which reduces the computational cost associated to the adaptive FE analysis of each geometrical configuration and, (b) the successive increase of the required accuracy of the FE analyses in order to obtain a considerable reduction of the computational cost in the early stages of the optimization process.

Palabras clave

Optimización de forma estructural ; Estimación de error ; Refinamiento adaptativo ; Análisis de sensibilidades ; Algoritmos evolutivos

Keywords

Structural shape optimization ; Error estimation ; Adaptive remeshing ; Sensitivity analysis ; Evolutionary algorithms

1. Introducción

Desde el punto de vista matemático, un problema de optimización se puede considerar como la minimización de una función f (v ) que depende de un conjunto de variables v y que está sujeta a una serie de restricciones. La forma general de un problema de este tipo es:

${\begin{array}{lrcll}minimizar:&f({\boldsymbol {\mbox{v}}});{\boldsymbol {\mbox{v}}}&=&\lbrace v_{i}\rbrace &;i=1,\ldots ,n\\con:&{\boldsymbol {\mbox{g}}}({\boldsymbol {\mbox{v}}})&=&\lbrace g_{j}({\boldsymbol {\mbox{v}}})\rbrace &;j=1,\ldots ,m\\verificando:&g_{j}({\boldsymbol {\mbox{v}}})&\leq &0&;j=1,\ldots ,m\\&a_{i}&\leq &v_{i}\leq b_{i}&;i=1,\ldots ,n\\&&&&\end{array}}$

( 1)

donde f   es la función objetivo (FO), ${\textstyle v_{i}}$ son las variables de diseño y g_j son las restricciones en desigualdad, las cuales, en los problemas estructurales, normalmente se expresan en función de las tensiones y/o de los desplazamientos. Los valores a_i y b_i definen restricciones laterales. Cada individuo se caracteriza por un conjunto de valores de v que se corresponden con un diseño estructural específico. La definición de cada diseño en función de los valores de ${\textstyle v_{i}}$ se denomina la parametrización del problema de optimización. La resolución del problema de diseño óptimo consiste en hallar los valores de v que definen el mejor diseño.

Los algoritmos utilizados para la resolución de los problemas de optimización son, en general, iterativos. Con independencia del algoritmo utilizado, será necesario calcular los valores de f y g para cada uno de los distintos diseños propuestos durante el proceso iterativo de optimización. En este trabajo hemos considerado problemas de optimización de formas estructurales. Para este tipo de problemas los valores de f y g se obtienen normalmente mediante la utilización del método de los elementos finitos (MEF). Por tanto, es necesario construir una malla específica para cada uno de los distintos diseños a analizar y, a continuación, utilizar el MEF para obtener la respuesta estructural de cada diseño. Llegados a este punto se deben tener en cuenta dos aspectos principales, ligados a la evaluación de f y g mediante el MEF, que tienen una gran incidencia sobre el comportamiento global del proceso de optimización: el esfuerzo computacional requerido para la evaluación numérica de cada individuo (configuración geométrica) y la precisión de los resultados del MEF.

La importancia del esfuerzo computacional requerido para la evaluación de cada configuración geométrica es evidente. En los problemas de optimización como los que estamos considerando, la mayor parte del coste computacional está dedicado al análisis de los distintos individuos para la determinación de los valores de la FO y del grado de satisfacción de las restricciones.

Por otro lado, y en cuanto a la precisión de los resultados, se debe tener en cuenta que los métodos numéricos de análisis solo proporcionan valores aproximados para los datos que los algoritmos de optimización precisan (FO, restricciones,…). Si estos valores no son lo suficientemente precisos se puede introducir una cantidad de ruido excesivo en el proceso de optimización. Esto puede empobrecer la velocidad de convergencia del proceso de optimización, conducir la convergencia hacia una solución no óptima o incluso producir una solución final no factible que incumpla alguna de las restricciones. En el contexto del MEF, los métodos h -adaptables, p -adaptables y hp -adaptables se pueden utilizar para obtener soluciones con un nivel de precisión prescrito. No obstante, la utilización de estas técnicas implica un gran coste computacional que reduce la eficiencia computacional del proceso de optimización.

Este artículo mostrará que si no se garantiza una mínima calidad en los resultados del análisis de cada diseño, que son los que se utilizan para alimentar al algoritmo de optimización, no se puede asegurar un comportamiento correcto del proceso de optimización. Para ello, se mostrará la incidencia del valor máximo prescrito de la norma energética del error de discretización sobre los resultados finales obtenidos mediante un algoritmo evolutivo de optimización.

Tal como se ha comentado previamente, los métodos de remallado adaptable del MEF se pueden utilizar para obtener soluciones con un nivel prescrito de precisión. No obstante, la utilización de las técnicas de remallado adaptable tradicionales implica el análisis de una secuencia de modelos numéricos con precisión creciente, que se adaptan de forma automática a las características de la solución del problema. El coste computacional relacionado con la utilización de estas técnicas tradicionales de remallado adaptable puede ser crítico cuando se utilizan algoritmos evolutivos. Para resolver este problema, en este artículo se propone la utilización de la técnica de análisis h -adaptable para las distintas generaciones de individuos que se describe en [1] . El procedimiento consiste en utilizar el análisis de sensibilidad de la norma energética del error de discretización con respecto a las variables de diseño [2] , [3]  and [4] para proyectar el error obtenido en el análisis de un individuo representativo de la generación hacia las distintas configuraciones geométricas que se deben analizar. Las mallas h -adaptadas para el análisis de cada individuo particular se pueden generar utilizando esta información, lo que en la inmensa mayoría de los casos proporciona los resultados del MEF con la precisión requerida, evitando así el alto coste computacional derivado de los remallados h -adaptables completos.

2. Motivación mediante el estudio de un caso sencillo: sección transversal de un tubo

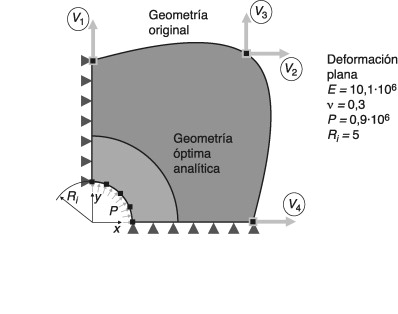
Como motivación de los desarrollos presentados en este artículo, esta sección muestra los resultados correspondientes a la resolución de un problema de optimización, cuya solución analítica es conocida, utilizando algoritmos evolutivos y distintos niveles de control en el error de discretización. La geometría a optimizar es la de la sección transversal de un tubo sujeto a una presión interna. Se han utilizado dos planos perpendiculares de simetría, por lo que solo se ha modelado un cuarto de la sección, tal como se muestra en la figura 1 . La forma se define mediante un total de 8 puntos, de los cuales 5 describen la forma circular interna y 3 describen la forma del contorno exterior del tubo. El problema de optimización consiste en hallar la forma del contorno exterior, manteniendo fijo el contorno interior y minimizando el área total. Las 4 variables de diseño mostradas en la figura 1 corresponden a las coordenadas de los puntos utilizados para definir la forma del contorno exterior. Nótese que este ejemplo no se corresponde con ningún caso real, por lo que no se han especificado unidades para las distintas magnitudes involucradas. En cualquier caso, se ha utilizado un sistema coherente de unidades.

Figura 1. Sección transversal de un tubo. Datos para el análisis, modelo original, solución óptima analítica y variables de diseño.

La máxima tensión de von Mises admisible en el modelo se ha restringido a 2,0 × 10⁶ .

Es bien conocido que la geometría analítica óptima del contorno exterior se corresponde con una forma circular. Las siguientes ecuaciones muestran los valores exactos de los desplazamientos y las tensiones para un punto dado en función de sus coordenadas cartesianas (x , y ), con k  = R₀ /R_i , ${\textstyle r={\sqrt {x^{2}+y^{2}}}}$ y ϕ  = arctg(y /x ) situado en un cilindro de pared gruesa sujeto a una presión interior P . Por tanto, estas ecuaciones se pueden utilizar para evaluar la solución analítica de este problema de optimización:

- Desplazamiento radial:

$u_{r}={\frac {P(1+\nu )}{E(k^{2}-1)}}\left[(1-2\nu )r+{\frac {R_{0}^{2}}{r}}\right]$

( 2)

- Tensiones en coordenadas cilíndricas y cartesianas:

${\sigma }_{r}={\frac {P}{k^{2}-1}}\left(1-{\frac {R_{0}^{2}}{r^{2}}}\right)$ ${\sigma }_{t}={\frac {P}{k^{2}-1}}\left(1+{\frac {R_{0}^{2}}{r^{2}}}\right)$ ${\sigma }_{xx}={\sigma }_{r}{cos}^{2}(\phi )+{\sigma }_{t}{sin}^{2}(\phi )$ ${\sigma }_{yy}={\sigma }_{r}{sin}^{2}(\phi )+{\sigma }_{t}{cos}^{2}(\phi )$ ${\sigma }_{xy}=({\sigma }_{r}-{\sigma }_{t})sin(\phi )cos(\phi )$ ${\sigma }_{z}=2\nu {\frac {P}{k^{2}-1}}$

( 3)

El radio externo de la solución analítica para este problema (1/4 de la sección transversal) evaluado a partir de (3) es R₀  = 10,67033824461. Esto corresponde a un área A_opt  = 69,787307715081.

2.1. Algoritmo evolutivo

Para estos análisis numéricos se ha utilizado el algoritmo evolutivo de optimización denominado Differential Evolution (DE). DE es un algoritmo robusto que ha proporcionado buenos resultados en su aplicación a problemas de muy distinto tipo. DE fue desarrollado por Storn y Price [5] . Su idea fundamental es el operador diferencial, que obedece al mismo propósito que el parámetro de cruce en los algoritmos genéticos estándar, es decir, el intercambio de información entre individuos para producir las nuevas generaciones. De las dos versiones diferentes propuestas por Storn y Price para este algoritmo se ha escogido la DE1 para este trabajo.

Los valores iniciales de las variables de diseño y sus restricciones tanto laterales como geométricas para este problema se muestran en la tabla 1 .

Tabla 1. Sección transversal de un tubo. Valores de las variables de diseño.

Variable de diseño	Valor inicial	Rango	Restricciones
V1	20	[5,2-50,0]
V2	19	[4,0-50,0]
V3	19	[4,0-50,0]	V3  < V1  − 0,5
V4	20	[5,2-50,0]	V4  > V2  + 0,5

Obsérvese que las restricciones entre los valores de las variables de diseño se han utilizado para minimizar la aparición de geometrías con formas extrañas.

2.2. Análisis mediante elementos finitos h -adaptables

Se ha utilizado un código de elementos finitos h -adaptables para obtener los valores de la función objetivo y del grado de satisfacción de las restricciones para cada una de las distintas configuraciones geométricas propuestas por los algoritmos de optimización. La utilización de la estrategia h -adaptable asegura la calidad del análisis proporcionando soluciones mediante el MEF con una estimación de la norma energética del error de discretización inferior a un valor prefijado por el analista. El programa utiliza el estimador del error en la norma energética propuesto por Zienkiewicz y Zhu [6] para controlar el análisis h -adaptable. El estimador de error está basado en la definición de la norma energética ||u ||:

$\Vert {\boldsymbol {\mbox{u}}}{\Vert }^{2}={\int }_{\Omega }{\boldsymbol {\sigma }}^{T}{\boldsymbol {\mbox{D}}}^{-1}{\boldsymbol {\sigma }}\quad d\Omega$

( 4)

Por tanto, se utiliza la siguiente expresión para evaluar la estimación del error en la norma energética, η :

${\eta }^{2}={\int }_{\Omega }{\left({\boldsymbol {\sigma }}^{\ast }-{\boldsymbol {\sigma }}^{h}\right)}^{T}{\boldsymbol {\mbox{D}}}^{-1}\left({\boldsymbol {\sigma }}^{\ast }-\right.$$\left.{\boldsymbol {\sigma }}^{h}\right)d\Omega$

( 5)

donde σ^h es el campo de tensiones obtenido directamente del análisis mediante el MEF, σ^* es un campo de tensiones mejorado, D relaciona las deformaciones con las tensiones mediante σ  = Dɛ y Ω es el dominio de análisis. Para cuantificar la tolerancia en el nivel del error de discretización presente en un determinado análisis se ha usado el error relativo en norma energética γ definido como:

$\gamma ={\frac {\eta }{\Vert {\boldsymbol {\mbox{u}}}\Vert }}\approx {\frac {\eta }{\sqrt {\Vert {\boldsymbol {\mbox{u}}}^{h}{\Vert }^{2}+{\eta }^{2}}}}$

( 6)

donde ||u^h || es el valor de norma energética proporcionado por la solución de EF.

En los ejemplos numéricos se han utilizado elementos triangulares cuadráticos y la técnica del alisado global por mínimos cuadrados [6] para obtener el campo de tensiones mejorado requerido por el estimador de error de Zienkiewicz y Zhu. Las tensiones reconstruidas en nodos del contorno obtenidas mediante esta técnica han sido utilizadas para verificar las restricciones de tensión en el modelo. También se podrían utiliza otras técnicas como el Superconvergent Patch Recovery (SPR) [7] , [8]  and [9] o cualquiera de sus mejoras posteriores [10] , [11] , [12]  and [13] .

Para definir cada una de las configuraciones geométricas en función de las coordinadas de algunos puntos de definición (parametrización) se han utilizado B -splines cúbicos [14]

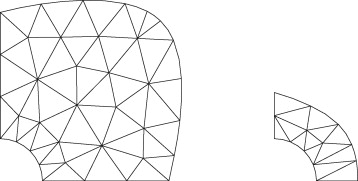
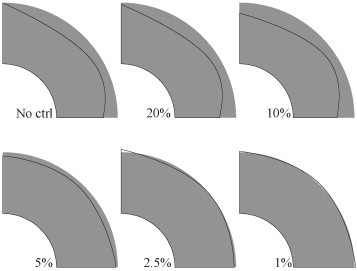
Para ver el efecto de la magnitud del error de discretización en norma energética contenido en el análisis de cada diseño sobre el comportamiento de los algoritmos de optimización se han estudiado 6 situaciones distintas correspondientes a diferentes niveles de error de discretización prescrito γ . Los valores del error prescrito para los primeros 5 análisis han sido 1, 2,5, 5, 10 and 20%. En el sexto caso se ha especificado una tolerancia γ  < 100 % lo cual, en la práctica, implica que no existe ningún control sobre la calidad de la solución y que el número de elementos generados para cada malla solo depende de criterios geométricos (ver los ejemplos en la figura 2 ).

Figura 2. Ejemplos de mallas previas a cualquier operación de adaptabilidad.

2.3. Optimización utilizando el algoritmo evolutivo

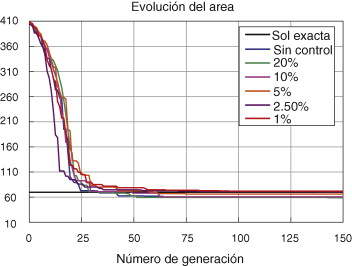
La figura 3 muestra el efecto del valor máximo prescrito para la estimación del valor relativo de la norma energética del error sobre la evolución del área de la sección transversal del tubo para cada uno de los procesos de optimización puestos en marcha. Se puede observar que, al menos para este problema, todos los casos estudiados presentan aspectos globales bastante similares entre sí.

Figura 3. Influencia de γ sobre la evolución de la función objetivo.

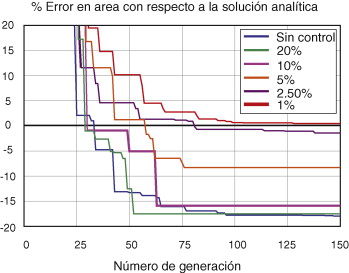
No obstante, y tal como se muestra en la figura 4 , el efecto de γ sobre la evolución del proceso de optimización es especialmente significativo si se comparan los resultados finales obtenidos para cada grado del error de discretización. La figura 4 muestra la evolución de la diferencia relativa entre el área proporcionada por el mejor individuo de cada generación y el área correspondiente a la solución óptima analítica. El gráfico muestra que la solución final asociada a cada proceso de optimización es significativamente distinta a la solución analítica para aquellos casos con valores altos del error prescrito γ , mientras que se aproxima hacia el valor exacto para los valores más bajos de γ .

Figura 4. Influencia de γ sobre la evolución del error en la función objetivo con respecto a la solución analítica.

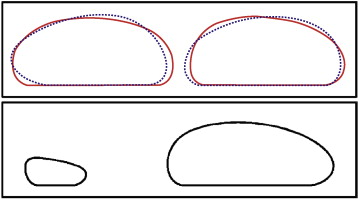
La figura 5 representa el efecto de γ sobre la forma de la solución final proporcionada por el algoritmo de optimización. Se puede observar claramente que para valores altos de γ el algoritmo converge hacia formas que son bastante distintas a la solución óptima analítica y solo se aproximan hacia esta última para valores decrecientes de γ . La diferencia en área entre la solución exacta y la obtenida para γ  = 1% es de solo un 0,38%. En cualquier caso, se debe tener en cuenta que la forma circular del contorno de la solución óptima analítica no se puede reproducir con total exactitud ya que los B -splines utilizados no son capaces de reproducir exactamente una forma circular.

Figura 5. Influencia de γ sobre la solución óptima final obtenida (contorno en negro) y comparación con la solución óptima analítica (zona sombreada).

En el modelo geométrico se ha impuesto que, en sus extremos, la superficie externa del tubo sea perpendicular a las superficies de simetría. Cuando no se controla el error de discretización o para los valores más altos de γ , el tamaño de los elementos resulta demasiado grande para capturar dicha restrición geométrica, tal y como se muestra en el área sombreada de la figura 6 .

Figura 6. Restricción geométrica y malla.

Por otro lado se puede observar que, debido a su tamaño, los elementos mostrados en la figura 6 son incapaces de representar adecuadamente el máximo nivel de tensiones producido por este tipo de detalle geométricos. Así pues, el algoritmo de optimización podría aceptar como válidos a individuos con geometrías similares a la representada en la figura 6 , tal y como se puede observar en la primera fila de geometrías de la figura 5 . Con los valores más restrictivos de γ , el proceso h -adaptivo adaptará adecuadamente la malla a las características locales de la geometría de cada individuo y la distribución de tensiones será evaluada con mayor precisión, lo que conducirá a que geometrías de este tipo no sean aceptadas.

En este problema, el proceso de optimización tiende a producir una solución con un valor de la FO (área) inferior a la de la solución analítica. Ello es debido a una subestimación del máximo valor de las tensiones proporcionado por el MEF para este problema. El valor de esta subestimación de las tensiones se incrementa con el tamaño de los elementos utilizados en el análisis. Para cuantificar la calidad de las soluciones obtenidas con los distintos niveles del error de discretización hemos efectuado un análisis h -adaptable completo para cada una de las geometrías mostradas en la figura 5 , requiriendo una estimación del error relativo final γ  ≤ 0,3%. Esto ha proporcionado aproximaciones mucho mejores de la distribución de tensiones para estas geometrías y, por tanto, una evaluación mucho más precisas del grado de satisfacción de las restricciones en tensión. La tabla 2 muestra los valores de las áreas A de las secciones transversales junto con la diferencia con respecto a la de la solución analítica A_opt y el valor de la tensión de von Mises máxima σ_vm evaluada con γ  < 0,3% junto con su diferencia con respecto al valor máximo admisible σ_adm . La tabla muestra que, excepto para el caso γ < 1 %, los valores de la máxima tensión de von Mises se han subestimado debido a la falta de precisión en el análisis por elementos finitos. Por tanto, estos diseños no son, en realidad, factibles ya que exceden ampliamente el máximo valor permitido para dicha magnitud. La tabla también muestra que A  − A_opt está muy relacionada con σ_vm  − σ_adm debido a la subestimación de la máxima tensión de von Mises el algoritmo de optimización reduce el área hasta que este valor alcanza el límite prefijado. Por tanto, el algoritmo de optimización produce soluciones con un área menor que la que se obtendría con una evaluación precisa de la tensión máxima de von Mises. Obsérvese que la solución obtenida con γ ≤ 1 % es casi idéntica a la solución analítica, con una diferencia en áreas de solo un 0,38% y excediendo la tensión máxima admisible en solo un 0,69%.

Tabla 2. Influencia de γ sobre la precisión de la función objetivo y el grado de satisfacción de las restricciones en tensión (tensiones de von Mises máximas de cada geometría final evaluadas con γ  ≤ 0,3%

γ	A	A  − Aopt	σvm	σvm  − σadm
Sin control	57,22	−18,00%	2222330	11,12%
20%	57,52	−17,58%	2229070	11,45%
10%	58,64	−15,97%	2265360	13,27%
5%	63,94	−8,39%	2074650	3,73%
2,5%	68,74	−1,50%	2025850	1,29%
1%	70,05	0,38%	2013710	0,69%

Este experimento numérico se ha reproducido utilizando programas de análisis MEF tanto comerciales como propios, modelos 2D y 3D de este experimento y algoritmos de optimización tanto genéticos como evolutivos, obteniéndose en todos los casos resultados muy similares.

3. Integración de los algoritmos evolutivos y los remallados h -adaptables mediante la proyección del estimador de error

Los resultados de la sección precedente han mostrado claramente que si no se asegura un nivel mínimo de precisión en los resultados utilizados para gobernar los procesos de optimización de formas estructurales, dichos procesos no convergerán hacia la verdadera solución óptima, produciendo soluciones que podrían violar notablemente las ecuaciones de restricción. No obstante, la utilización de técnicas h -adaptables para controlar la calidad de los análisis por elementos finitos implica un alto coste computacional adicional ya que cada configuración geométrica se debe evaluar más de una vez hasta alcanzar el nivel de precisión requerido. Debido al alto número de geometrías distintas que se deben analizar, el coste de la utilización de este tipo de técnicas puede ser crítico.

En el caso de la utilización de algoritmos evolutivos, y para reducir el coste computacional asociado con la generación de una malla adaptada para cada uno de los individuos (geometrías) a analizar, proponemos la utilización de la técnica descrita por Bugeda et al. [1] que a continuación se resume. El origen de esta técnica, y su aplicación a algoritmos de optimización deterministas, se puede ver en las referencias [2]  and [3] . En este trabajo hemos adaptado esta técnica para algoritmos evolutivos de optimización.

3.1. Algoritmo para la definición directa de mallas h -adaptadas para todos los individuos de una generación

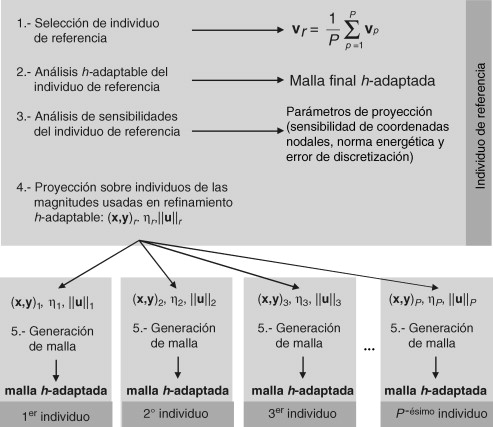
Para cada generación de individuos, la estrategia propuesta se resume como sigue (ver su representación gráfica en la figura 7 ):

Figura 7. Algoritmo para la definición directa de mallas h -adaptadas para todos los individuos de una generación.

• Selección de un individuo de referencia. Para cada generación se selecciona un individuo específico como referencia. Este individuo se puede fijar al inicio de todo el proceso de optimización como el diseño inicial. No obstante, los mejores resultados se han obtenido definiendo un individuo de referencia distinto para cada generación del proceso de optimización utilizando los valores medios de las variables de diseño de todos los individuos de la misma. Así, si se tiene una población con P individuos, los valores de v_r que definen al de referencia se calculan como

${\boldsymbol {\mbox{v}}}_{r}={\frac {1}{P}}\sum _{p=1}^{P}{\boldsymbol {\mbox{v}}}_{p}$

( 7)

donde v_p indica los valores de las variables de diseño v correspondientes al p -ésimo individuo utilizando la parametrización seleccionada

• Análisis h-adaptable del individuo de referencia. El individuo de referencia para la generación se analiza utilizando el MEF tradicional, incluyendo una estrategia de remallados adaptables para asegurar unos resultados de buena calidad.
• Análisis de sensibilidad del individuo de referencia. Una vez que se ha obtenido una malla adaptada para el análisis del individuo de referencia, se realiza un análisis de sensibilidad completo de todas las magnitudes usadas en la estrategia de remallados adaptables. Esto incluye la evaluación de la sensibilidad del estimador de error, ver (5) , para cada elemento de la malla. La siguiente expresión fue obtenida en [2] para evaluar dicha magnitud:

${\frac {\partial {\eta }_{e}^{2}}{\partial v_{i}}}={\int }_{{\Omega }_{\xi }}\left[{\left({\frac {\partial {\boldsymbol {\sigma }}^{\ast }}{\partial v_{i}}}-{\frac {\partial {\boldsymbol {\sigma }}^{h}}{\partial v_{i}}}\right)}^{T}{\boldsymbol {\mbox{D}}}^{-1}({\boldsymbol {\sigma }}^{\ast }-\right.$$\left.{\boldsymbol {\sigma }}^{h})+({\boldsymbol {\sigma }}^{\ast }-\right.$$\left.{\boldsymbol {\sigma }}^{h})^{T}{\frac {\partial {\boldsymbol {\mbox{D}}}^{-1}}{\partial v_{i}}}({\boldsymbol {\sigma }}^{\ast }-\right.$$\left.{\boldsymbol {\sigma }}^{h})+({\boldsymbol {\sigma }}^{\ast }-\right.$$\left.{\boldsymbol {\sigma }}^{h})^{T}{\boldsymbol {\mbox{D}}}^{-1}\left({\frac {\partial {\boldsymbol {\sigma }}^{\ast }}{\partial v_{i}}}-\right.\right.$$\left.\left.{\frac {\partial {\boldsymbol {\sigma }}^{h}}{\partial v_{i}}}\right)+\right.$$\left.({\boldsymbol {\sigma }}^{\ast }-{\boldsymbol {\sigma }}^{h})^{T}{\boldsymbol {\mbox{D}}}^{-1}({\boldsymbol {\sigma }}^{\ast }-\right.$$\left.{\boldsymbol {\sigma }}^{h})tr\left({\boldsymbol {\mbox{J}}}^{-1}{\frac {\partial {\boldsymbol {\mbox{J}}}}{\partial v_{i}}}\right)\right]\vert {\boldsymbol {\mbox{J}}}\vert d{\Omega }_{\xi }$

( 8)

donde Ω_ξ es el dominio del elemento en coordenadas locales y J es la matriz Jacobiana correspondiente a la transformación de coordenadas.

Fuenmayor et al. [4] extendieron el estimador de error de Zienkiewicz y Zhu [6] para el análisis de sensibilidad de formas para desarrollar un estimador del error de discretización en el análisis de sensibilidad, obteniendo también la expresión mostrada en (8) . Esto demuestra que la sensibilidad del error es equivalente al error en la sensibilidad.

Estos cálculos requieren la evaluación de las sensibilidades de las coordenadas nodales, las cuales describen como se modifica la malla al cambiar las variables de diseño. Para los nodos situados sobre el contorno del dominio estas sensibilidades se pueden obtener con facilidad a partir del análisis de sensibilidad de primer orden de los B -splines utilizados para definir su geometría. La referencia [15] presenta una descripción y comparación de distintos métodos utilizados habitualmente para la evaluación de las sensibilidades de los nodos internos. En los ejemplos numéricos presentados en este trabajo se ha utilizado el clásico alisado Laplaciano.

La evaluación de ${\textstyle \partial {\eta }_{e}^{2}/\partial v_{i}}$ también requiere la evaluación del campo de tensiones mejorado σ^* . En este trabajo se ha utilizado la técnica del alisado global por mínimos cuadrados [6] , aunque se podrían haber utilizado otros procedimientos como el SPR [7]  and [8] .

• Proyección de las magnitudes utilizadas en el proceso h-adaptable. Para cada uno de los individuos a analizar, los valores de todas las magnitudes involucradas en la estrategia de remallados adaptables, que se han obtenido en el paso anterior, se proyectan desde el individuo de referencia utilizando el correspondiente análisis de sensibilidad. Las magnitudes a proyectar son las coordenadas nodales (x e y ), el estimador de la norma energética del error η y la norma energética del error ||u ||. Para estas proyecciones se utilizan las siguientes expresiones:

$(x,y)_{p}=(x,y)_{r}+\sum _{i}^{n}(v_{p_{i}}-v_{r_{i}})\left({\frac {\partial x}{\partial v_{i}}},{\frac {\partial y}{\partial v_{i}}}\right)$

( 9)

${\eta }_{p}^{2}={\eta }_{r}^{2}+\sum _{i}^{n}(v_{p_{i}}-v_{r_{i}}){\frac {\partial {\eta }^{2}}{\partial v_{i}}}$

( 10)

$\Vert {\boldsymbol {\mbox{u}}}{\Vert }_{p}^{2}=\Vert {\boldsymbol {\mbox{u}}}{\Vert }_{r}^{2}+$$\sum _{i}^{n}(v_{p_{i}}-v_{r_{i}}){\frac {\partial \Vert {\boldsymbol {\mbox{u}}}{\Vert }^{2}}{v_{i}}}$

( 11)

donde los subíndices r y p   están relacionados, respectivamente, con el individuo de referencia y el individuo hacia el cual se proyecta la información. ${\textstyle v_{i}}$ son las variables de diseño utilizadas para definir la geometría (ver [1] ).

Esta proyección proporciona, sin ningún cálculo previo adicional, una aproximación a los valores que se obtendrían para cada individuo específico si este se hubiese analizado utilizando la misma malla de elementos finitos que para el individuo de referencia. Se proporciona así, por tanto, la información necesaria para realizar un remallado adaptable sobre el nuevo diseño, incluso antes de efectuar ningún nuevo cálculo sobre el mismo.

• Generación de la malla h-adaptada. Utilizando los valores proyectados en el último paso se genera una malla adaptada para cada individuo. Esta malla h -adaptada se utiliza para la evaluación de la función objetivo y las restricciones para el individuo.

La generación de cada nueva malla en el procedimiento de remallado requiere de la definición de un criterio de malla óptima. En este trabajo se considera que una malla es óptima cuando la densidad del error está uniformemente distribuida sobre todo el dominio (ver referencia [3] ).

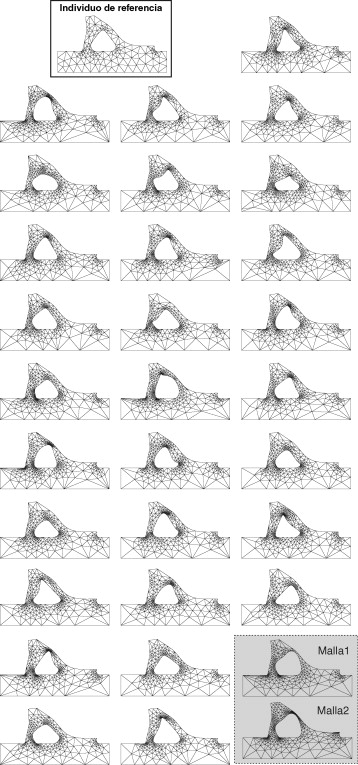
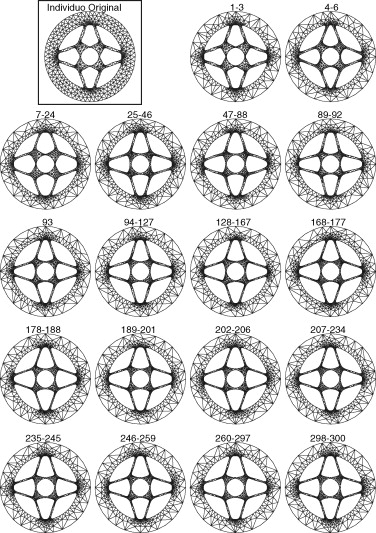
La figura 8 muestra un ejemplo de análisis con una generación de 30 individuos. En la figura se muestra la malla h -adaptada del individuo de referencia junto con las obtenidas para cada uno de los individuos de la generación. Obsérvese que tan solo uno de los individuos ha requerido un segundo paso de refinamiento.

Figura 8. Ejemplo de mallados de una generación de individuos obtenidos por proyección desde el individuo de referencia.

4. Ejemplos numéricos

Esta sección muestra cuatro ejemplos de optimización resueltos con la estrategia propuesta.

4.1. Sección transversal de un tubo

La metodología propuesta se ha utilizado para resolver el ejemplo de la optimización de la sección transversal de un tubo descrito en la sección 2. La técnica descrita en la sección 3 se ha utilizado para la definición directa de las mallas h -adaptadas utilizadas para el análisis de los individuos de cada generación. El máximo error relativo admisible en la norma energética se ha fijado en un γ  = 1%. Se han utilizado 150 generaciones con 30 individuos en cada una de ellas. Los resultados muestran que en un 97% de los 4.500 individuos analizados, la utilización de la técnica propuesta ha proporcionado de forma directa una malla apropiada para el MEF. Esto implica una considerable reducción del coste computacional asociado al análisis h -adaptable.

4.2. Optimización de la forma de un volante de inercia

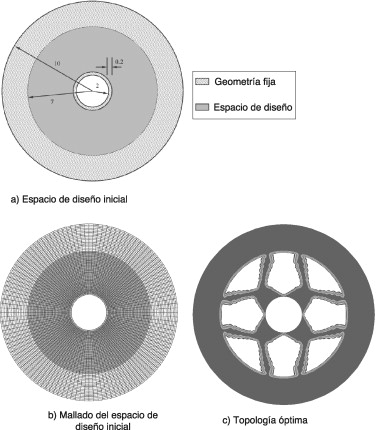
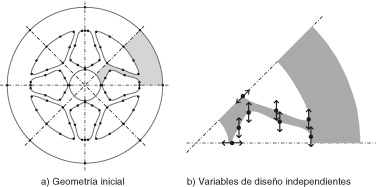
Consideremos el problema de diseño óptimo mostrado en la figura 9 a) en el que se define un volante de inercia cuya zona interior es susceptible de recibir mejoras geométricas. Se ha aplicado una fuerza centrífuga correspondiente a una velocidad de rotación de 3 rad/s, y una fuerza tangencial distribuida sobre el contorno exterior de 1 N/mm² . Las propiedades del material son E = 210 GPa, coeficiente de Poisson μ  = 0,29 y densidad ρ  = 7.860 kg/m³ .

Figura 9. Optimización de un volante de inercia. Optimización topológica.

Este problema ya fue resuelto con anterioridad, ver [16] , utilizando una combinación de dos herramientas de optimización. En una primera etapa, se utilizó la malla representada en la figura 9 b) (6.000 cuadriláteros bilineales en tensión plana) para proceder a una optimización topológica, obteniendo la topología representada en la figura 9 c). A continuación, para obtener una forma más refinada, en una segunda etapa se utilizó una estrategia de optimización de forma basada en un algoritmo determinista con análisis de sensibilidad. La geometría inicial para esta segunda etapa se muestra en la figura 10 a). Este proceso redujo el peso total desde 1,53 kg hasta 1,45 kg.

Figura 10. Optimización de un volante de inercia. Parametrización.

En este trabajo se presenta la resolución de este problema sustituyendo el algoritmo de optimización determinista por el algoritmo evolutivo con la integración de los remallados h -adaptables presentada.

La geometría de la solución obtenida mediante la optimización topológica presenta 4 ejes de simetría. No obstante, la carga tangencial aplicada no permite utilizar dichos ejes para simplificar el problema y, por ello, no es posible limitar la resolución del mismo a solo un octavo del total. De todos modos, teniendo en cuenta la presencia de los ejes de simetría se ha seguido el siguiente procedimiento:

• La geometría del problema se ha parametrizado utilizando un total de 60 variables de diseño que son algunas de las coordenadas de los puntos de definición cuyo movimiento está permitido.
• Se han aplicado restricciones lineales sobre dichas variables de diseño para conseguir que la solución del problema mantenga los ejes de simetría. De esta manera se han conseguido un total de solo 8 variables de diseño independientes (fig. 11 b).

Figura 11. Optimización de un volante de inercia. Evolución de la función objetivo (peso) y de la diferencia con respecto a la solución final (error%).

• La función objetivo adoptada es el peso total del volante de inercia.
• El máximo valor permitido para la tensión de von Mises es de 100 N/mm² .
• Para el algoritmo evolutivo de optimización se han utilizado 300 generaciones con 15 individuos cada una.
• El máximo error relativo admisible en la norma energética se ha fijado en un γ  = 5%.

La figura 11 muestra los valores del peso obtenidos a lo largo del proceso evolutivo de optimización, y la diferencia porcentual (error%) entre la función objetivo y el valor final obtenido. La figura 12 muestra la evolución de la geometría y las correspondientes mallas adaptadas. El peso total se reduce desde 1,53 kg hasta 1,4445 kg, lo cual es un resultado muy cercano al obtenido mediante el algoritmo determinista (1,45 kg). No obstante, si se tiene en cuenta solo la zona del dominio susceptible de ser modificada la reducción es de 0,25 a 0,17 kg.

Figura 12. Optimización de un volante de inercia. Evolución de la geometría. Mallas adaptadas.

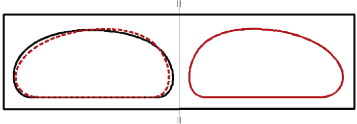
La figura 13 muestra una comparación entre la geometría original (línea discontinua) y la solución final obtenida (zona sombreada).

Figura 13. Optimización de un volante de inercia. Comparación entre las geometrías original (trazo discontinuo) y optimizada (area sombreada).

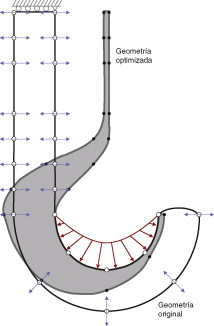
4.3. Optimización de la forma de un gancho

El tercer ejemplo numérico es la optimización de la forma de un gancho para minimizar su peso. La geometría inicial, los puntos de definición utilizados para la misma y la carga aplicada se muestran en la figura 14 . Se han utilizado las coordenadas de 19 puntos como variables de diseño, 16 de ellas se pueden mover horizontalmente, una se puede mover verticalmente y se ha forzado al resto para que se muevan sobre rectas inclinadas 45^∘ . Se ha aplicado una carga vertical con distribución parabólica sobre la cara interna del gancho con una fuerza resultante de 6.300 N. Las propiedades mecánicas del material son E = 21.000.000 N/cm² y ν  = 0,3. Se ha utilizado un modelo de tensión plana. La función objetivo es el área total de la sección transversal del gancho. La máxima tensión de von Mises admisible se ha limitado a 20.000 N/cm² . El grosor mínimo del eje del gancho se ha limitado a 0,5 cm.

Figura 14. Optimización de un gancho. Geometría inicial y variables de diseño. Geometría optimizada.

Durante el proceso de optimización se han utilizado 400 generaciones con 20 individuos cada una. El máximo error relativo admisible en norma energética se ha fijado en un γ  = 2%.

La figura 14 permite comparar la solución final obtenida, con un área de 88,71 cm² , con la geometría inicial que tenía un área de 181,22 cm² . Puede observarse cómo el proceso de optimización desplaza el eje vertical del gancho para que su directriz coincida con la de la fuerza resultante de la carga aplicada, eliminando así la presencia de momento flector sobre esa región.

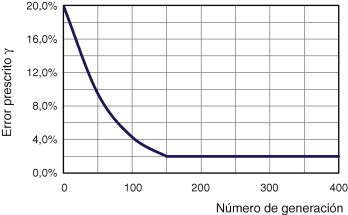
La figura 3 muestra que los resultados obtenidos durante las primeras etapas del proceso de optimización no están afectados de forma significativa por el nivel de precisión prescrito para el análisis. Esto ha permitido implementar una técnica muy simple, que también contribuye a reducir el coste computacional de la optimización, que ha sido utilizada en la resolución de este problema. Esta técnica consiste simplemente en definir el valor admisible para la estimación de la norma energética del error γ como una función del número de generación, haciendo decrecer su valor a medida que el proceso de optimización avanza. Esta técnica reduce considerablemente el coste computacional asociado a los análisis de las primeras generaciones de individuos sin afectar a la precisión de los resultados obtenidos en las últimas etapas del proceso. La evolución del error prescrito a lo largo de la optimización se puede ver en la figura 15 . Entre las generaciones 1 y 150 se ha definido un decrecimiento exponencial de γ desde un 20% hasta un 2%, habiéndose impuesto el límite más exigente de γ  = 2% solo a partir de la generación 150.

Figura 15. Optimización de un gancho. Evolución del nivel de precisión prescrito (γ ) a medida que progresa el proceso de optimización.

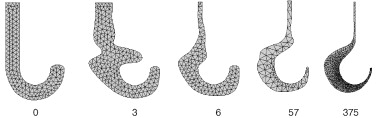
La figura 16 muestra ejemplos de las distintas densidades de malla utilizadas durante el proceso de optimización. Obsérvese que dicho proceso es capaz de proporcionar aproximaciones razonables a la geometría final a partir de las primeras etapas del proceso utilizando mallas groseras (ver las geometrías para las generaciones 6 y 57) que requieren un bajo coste computacional. La figura 17 muestra la evolución del mejor individuo obtenido para una serie de generaciones a lo largo del proceso.

Figura 16. Optimización de un gancho. Densidades de malla utilizadas durante el proceso de optimización. Las geometrías representadas corresponden a un individuo representativo de las generaciones 0, 3, 6, 57 y 375.

Figura 17. Optimización de un gancho. Evolución del mejor individuo durante el proceso de optimización. Debajo de cada geometría se indica la generación en la que la misma se ha generado.

4.4. Optimización de la forma de la sección transversal de un túnel doble sumergido

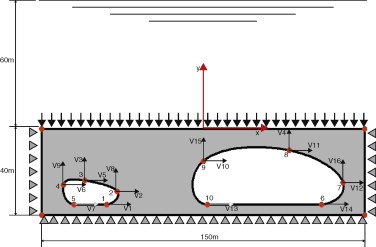
En este ejemplo se ha resuelto la optimización de forma de la sección transversal del túnel doble sumergido bajo una capa de agua de 60 m mostrado en la figura 18 . Se considera que los túneles son excavados en un material con E = 1,4 · 10⁷  N/m² , ν  = 0,4 y ρ  = 2.500 kg/m³ . En el análisis se han considerado las cargas de peso propio y de la presión que ejerce el agua. La geometría del modelo no presenta ningún punto anguloso para evitar la aparición de singularidades en la distribución de tensiones que podrían enmascarar la evolución del proceso de remallado adaptable. El problema de optimización de forma ha consistido en mejorar la forma de los túneles internos para aumentar el área total de la sección transversal destinada al paso de vehículos, manteniendo fijo el contorno exterior. Para ello se ha utilizado el algoritmo evolutivo de optimización con un total de 400 generaciones, con 40 individuos por generación. La forma de cada túnel interior se ha definido mediante la posición de un total de 5 puntos. Tal como se indica en la figura 18 , se ha considerado como variables de diseño las coordenadas de esos 5 puntos. Obsérvese que los puntos 1, 5, 6 y 10, definen la cota inferior de los túneles, por lo que en ellos solamente se considera variable su coordenada horizontal. El máximo valor de la tensión de von Mises se ha restringido a 7,5 · 10⁶  Pa.

Figura 18. Optimización de un túnel sometido a presión. Modelo de análisis (en la versión electrónica de este artículo se puede consultar esta figura a color).

El máximo error relativo admisible en la norma energética para el análisis de la solución final se ha fijado en un γ  = 2%.

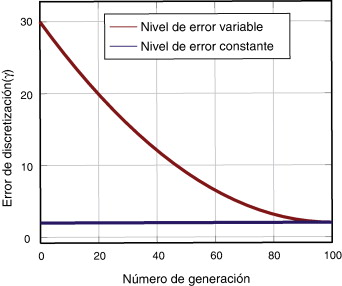
Al igual que en el ejemplo anterior, a lo largo del proceso se ha hecho variar en valor prescrito de γ con el número de generación. Se ha especificado una variación exponencial para el nivel de error admisible desde γ ≤ 30% para la primera generación hasta γ ≤ 2% para la generación 100, tal como se muestra en la figura 19 . A efectos de comparación, este problema se ha resuelto una segunda vez imponiendo un nivel de error constante γ ≤ 2% para todo el proceso.

Figura 19. Optimización de un túnel sometido a presión. Evolución del nivel de precisión prescrito (γ ) a medida que progresa el proceso de optimización (en la versión electrónica de este artículo se puede consultar esta figura a color).

Hay que tener en cuenta que la variació de γ con el número de generación no ha de ser necesariamente una función exponencial. Los mayores beneficios del uso de esta ténica se obtendrían si dicha variación de γ está adecuadamente acoplada a la evolución del proceso de optimización. Cómo obtener este adecuado acoplamiento será materia de nuestras investigaciones en el futuro.

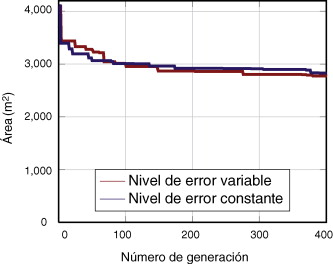
La figura 20 muestra la evolución de la función objetivo (área) durante ambos procesos de optimización. Esta figura muestra claramente que la utilización de valores altos de γ para las primeras generaciones y su progresiva reducción proporciona una evolución similar de los mejores individuos y reducciones del área similares después de 400 generaciones (de 4.105 m² a 2.824 m² para γ constante y a 2.772 m² para γ variable). Las diferencias en los valores finales de la figura 20 son razonables teniendo en cuenta la naturaleza del algoritmo evolutivo y el hecho de que el proceso de optimización no se pueda considerar que haya convergido después de 400 iteraciones.

Figura 20. Optimización de un túnel sometido a presión. Evolución del área (en la versión electrónica de este artículo se puede consultar esta figura a color).

La figura 21 muestra las diferencias entre la geometría original y las optimizadas en ambos casos. Se observa que la técnica de la reducción gradual de γ permite reducir sensiblemente el coste computacional sin perjudicar la evolución del proceso de optimización. Para este caso, con 400 iteraciones con error de discretización constante se ha necesitado un tiempo un 13% superior.

Figura 21. Optimización de un túnel sometido a presión. Comparación entre las geometrías original (negro) y optimizada, con error (γ ) variable (línea a trazos), con error (γ ) constante (línea punteada) (en la versión electrónica de este artículo se puede consultar esta figura a color).

Dado que tanto las condiciones de contorno como la geometría son simétricas, la solución óptima también tendrá que ser simétrica. La figura 22 muestra en trazos continuos la geometría final de ambos túneles y en trazo discontinuo, la imagen especular del túnel de la derecha representada sobre el de la izquierda. Una solución inicial considerablemente asimétrica como la utilizada podría hacer que un algoritmo de optimización basado en gradiente se quedase estancado en un mínimo local proporcionando una solución no simétrica. Este tipo de comportamientos representa uno de los principales problemas de estos algoritmos. Frente a este problema, una de las principales ventajas de los algoritmos evolutivos es que son capaces de proporcionar el mínimo global del problema de optimización. Así, la figura 22 muestra que sin aportar ninguna información relativa a la simetría de la solución final, el algoritmo evolutivo ha sido capaz de evaluar una solución que tiende a reponer la simetría geométrica característica del mínimo global.

Figura 22. Optimización de un túnel sometido a presión. Comparación entre los dos agujeros. Agujero izquierda linea negra. Agujero derecho línea continua. Imagen especular del agujero derecho sobre el izquierdo en la línea a trazos (en la versión electrónica de este artículo se puede consultar esta figura a color).

5. Conclusiones

Este artículo ha demostrado la necesidad de asegurar una mínima calidad en los resultados de los análisis utilizados para guiar los procesos de optimización; de otro modo se puede degradar, o incluso impedir, la convergencia hacia la solución óptima o se pueden obtener soluciones que violan notablemente la ecuaciones en restricción. Por ello, los procesos de optimización que utilizan el método de los elementos finitos para la evaluación de la función objetivo y del grado de satisfacción de las restricciones, requieren la utilización de técnicas para el control del error, preferentemente utilizando técnicas de remallados adaptables, ya que es conocido el hecho de que la malla más económica para alcanzar un determinado nivel de precisión es una malla adaptada.

Debido al alto número de individuos a analizar, el coste computacional asociado a la utilización de técnicas de remallado adaptable puede ser crítico cuando se utilizan algoritmos evolutivos. Para estos casos, este artículo propone la utilización de la técnica de remallados h -adaptables presentada por Bugeda et al. [1] . Esta técnica utiliza la proyección del estimador de la norma energética del error de discretización para la obtención de las mallas requeridas para el análisis de los distintos individuos presentes en cada generación. Los resultados presentados muestran la eficiencia de esta técnica la cual, en la inmensa mayoría de los casos, proporciona directamente la malla h -adaptada para el análisis con un nivel de error inferior al especificado por el analista, evitando así los procesos de remallados adaptables completos.

Los resultados preliminares han demostrado que el nivel de error de discretización máximo impuesto a los análisis por el MEF tiene poca incidencia durante las primeras etapas del proceso de optimización. Por ello, se ha propuesto una técnica de reducción paulatina del mismo. A pesar de su simplicidad, esta técnica permite reducir de forma considerable el coste computacional asociado los análisis de las primeras generaciones de individuos sin afectar a la precisión de los resultados obtenidos al final de la optimización.

Agradecimientos

Los autores primero, tercero y quinto agradecen el soporte económico recibido para el desarrollo de este artículo a través de los proyectos de investigación DPI2007-66773-C02-01 y DPI2010-20542 del Ministerio de Educación y Ciencia (España) y los fondos recibidos de la Generalitat Valenciana y de la Universitat Politècnica de València.

El segundo autor agradece el soporte económico recibido para el desarrollo de este artículo a través del proyecto de investigación DPI2008-05250 del Ministerio de Educación y Ciencia (España).

Los autores también agradecen a MsC Santos López Real su ayuda con la utilización de los algoritmos evolutivos.

References

1. [1] G. Bugeda, J.J. Ródenas, E. Oñate; An integration of a low cost adaptive remeshing strategy in the solution of structural shape optimization problems; Computers & Structures, 86 (2008), pp. 1563–1578
2. [2] G. Bugeda, J. Oliver; A general methodology for structural shape optimization problems using automatic adaptive remeshing; International Journal for Numerical Methods in Engineering, 18 (1993), pp. 3161–3185
3. [3] G. Bugeda, E. Oñate; A methodology for adaptive mesh refinement in optimum shape design problems; Computing Systems in Engineering, 5 (1994), pp. 91–102
4. [4] F.J. Fuenmayor, J.L. Oliver, J.J. Ródenas; Extension of the Zienkiewicz-Zhu error estimator to shape sensitivity analysis; International Journal for Numerical Methods in Engineering, 40 (1997), pp. 1413–1433
5. [5] R. Storn, K. Price, Differential Evolution - A simple and efficient adaptive scheme for global optimization over continuous space, International Computer Science Institute, Berkeley, CA, USA, Technical Report, March 1995 [consultado 10 Ene 2011], ftp://ftp.icsi.berkeley.edu/pub/techreports/1995/tr-95-012.pdf .
6. [6] O.C. Zienkiewicz, J.Z. Zhu; A simple error estimator and adaptive procedure for practical engineering analysis; International Journal for Numerical Methods in Engineering, 24 (1987), pp. 337–357
7. [7] O.C. Zienkiewicz, J.Z. Zhu; The superconvergent patch recovery and a posteriori error estimates. Part I: The recovery technique; International Journal for Numerical Methods in Engineering, 33 (1992), pp. 1331–1364
8. [8] O.C. Zienkiewicz, J.Z. Zhu; The superconvergent patch recovery and a posteriori error estimates. Part II: Error Estimates and Adaptivity; International Journal for Numerical Methods in Engineering, 33 (1992), pp. 1365–1382
9. [9] O.C. Zienkiewicz, J.Z. Zhu, J. Wu; Superconvergent Patch Recovery Techniques - some further Tests; Communications in Numerical methods in Engineering, 9 (1993), pp. 251–258
10. [10] N.E. Wiberg, F. Abdulwahab; Patch Recovery Based on Superconvergent Derivatives and Equilibrium; International Journal for Numerical Methods in Engineering, 36 (1993), pp. 2703–2724
11. [11] N.E. Wiberg, F. Abdulwahab, S. Ziukas; Enhanced superconvergent patch recovery incorporating equilibrium and boundary conditions; International Journal for Numerical Methods in Engineering, 37 (1994), pp. 3417–3440
12. [12] J.J. Ródenas, M. Tur, F.J. Fuenmayor, A. Vercher; Improvement of the Superconvergent Patch Recovery technique by the use of constraint equations: the SPR-C technique; International Journal for Numerical Methods in Engineering, 70 (2006), pp. 705–727
13. [13] P. Díez, J.J. Ródenas, O.Z. Zienkiewicz; Equilibrated Patch Recovery error estimates: simple and accurate upper bounds of the error; International Journal for Numerical Methods in Engineering, 69 (2007), pp. 2075–2098
14. [14] I.D. Faux, M.J. Pratt; Computational Geometry for Design and Manufacture; Ellis Horwood Limited (1987)
15. [15] J.J. Ródenas, F.J. Fuenmayor, J.E. Tarancón; A numerical methodology to asses the quality of the design velocity field computation methods in shape sensitivity analysis; International Journal for Numerical Methods in Engineering, 59 (2004), pp. 1725–1747
16. [16] J. Sienz, E. Hinton, G. Bugeda, S. Bulman; Some studies on Integrating Topology and shape optimization; M. Papadrakakis, B.H.V. Topping (Eds.), Innovative Computational Methods for Structural Mechanics, Saxe-coburg Publications (1999), pp. 223–256