Abstract
The temporal variability and spatial pattern of the Arctic Oscillation (AO) simulated in the historical experiment of 26 coupled climate models participating in the Coupled Model Intercomparison Project Phase 5 (CMIP5) are evaluated. Spectral analysis of the monthly AO index indicates that 23 out of the 26 CMIP5 models exhibit no statistically significant spectral peak in the historical experiment, as seen in the observations. These models are able to reproduce the AO pattern in the sea level pressure anomaly field during boreal winter, but the intensity of the AO pattern tends to be overestimated in all the models. The zonal-mean zonal wind anomalies associated with the AO is dominated by a meridional dipole in the mid-high latitudes of the Northern Hemisphere during boreal winter, which is well reproduced by only a few models. Most models show significant biases in both strength and location of the dipole compared to the observation. In considering the temporal variability as well as spatial structures in both horizontal and vertical directions, the MPI-ESM-P model reproduces an AO pattern that resembles the observation the best.
Keywords
Arctic Oscillation ; model evaluation ; coupled climate model ; CMIP5
1. Introduction
It is well known that the global mean surface temperature has been increased in recent decades [ Tang et al. , 2012 ]. Detection of recent climate changes, attribution of causes, and projection of parameter changes are the main topics in climate change research [ Wang et al. , 2012 ]. Coupled global climate models (CGCM) are the major objective tools available for climate change attribution and projection studies. In general, we assume that the models, which are able to reproduce past climate changes the best, might also be able to simulate future changes with high accuracy. For that reason, it is crucial to assess the ability of CGCMs in simulating the observed climate changes, especially the dominant modes of the atmospheric low-frequency variability [ Stoner et al. , 2009 ].
The Arctic Oscillation (AO) is the leading mode of the extra-tropical low-frequency variability and is characterized by a seesaw of pressure anomalies between the middle and high latitudes of the Northern Hemisphere [ Thompson and Wallace , 1998 ]. Due to the quasi-zonally symmetric structure of the AO, it is also referred to as the Northern Hemisphere annular mode [ Thompson and Wallace , 2000 ]. Many previous studies have demonstrated that the AO has important impact on the surface climate variability and storm track activity over wide regions of the Northern Hemi-sphere [ Thompson and Wallace, 2000 ; Thompson and Wallace, 2001 ]. In particular, the surface air temperature anomalies over North America, Greenland, Eurasia, and North Africa are closely related to the AO variability during winter. Also, the AO has an obvious influence on the East Asian winter monsoon as well as the winter surface air temperature and precipitation over China [ Gong et al ., 2001 ; Wu and Wang, 2002 ; Gong and Wang, 2003 ]. In the last two decades of the 20th century, the AO experienced a positive phase of extremes during winter, which intensified the warm anomalies over Eurasia, including Northeast Asia [ Thompson and Wallace, 2001 ; Jü et al ., 2004 ]. Therefore, changes in the phases of the AO tend to alter the range of surface climate conditions as experienced in many locations over the Northern Hemisphere, and may have implications on future changes.
The ability of CGCMs to simulate the AO variability is an important aspect of model evaluation. Previous studies show that atmospheric general circulation models (AGCM) and atmosphere-ocean coupled models are both able to reproduce the AO pattern, but have difficulties in simulating the observed positive trend of the winter AO in the second half of the 20th century [ Yamazaki and Shinya, 1999 ; Robertson, 2001 ]. The AO pattern as simulated by CGCMs has been widely evaluated using the outputs of 20th century simulations from the Coupled Model Intercomparison Project Phase 3 (CMIP3) [ Miller et al ., 2006 ; Xin et al ., 2008 ; Zhu and Wang, 2008 ; Stoner et al ., 2009 ]. It has been demonstrated that almost all the CMIP3 models are able to reproduce the spatial pattern of the AO, whereas their ability to simulate the magnitude and location of the pattern as well as its temporal variability needs to be improved.
The latest CMIP project, namely CMIP5, was coordinated by the World Climate Research Programme’s (WCRP’s) Working Group on Coupled Modeling (WGCM). This project involved about 30 climate modeling groups around the world. The CMIP5 project is designed to advance our knowledge of climate variability and climate change, and to provide simulations for evaluation in the IPCC Fifth Assessment Report (AR5) [ Taylor et al. , 2012 ]. Most CMIP5 models have been improved in physical processes and the coupled carbon cycle. For this reason, we will evaluate the ability of those state-of-the-art coupled climate models in simulating the AO variability. Here, the temporal variability and spatial pattern of the AO simulated in historical experiments of 26 CMIP5 models are focused on. A comparison of the simulated AO variability between CMIP5 and CMIP3 models was given by Zhu et al. [2013] .
2. Model simulations and calculation methods
In this paper, the simulations from 26 coupled climate models participating in the CMIP5 project are listed. Model provenance and resolution are provided in Table 1 . These models are from 18 institutions in 11 countries. Most of the atmospheric components have a horizontal resolution in the range of 2° to 3°, with the MRI-CGCM3 having the highest resolution of 1.1°. Ten models are physical climate system models that do not include the carbon cycle, while the other 16 models are Earth system models that incorporate a coupled carbon cycle.
| Model name | Country | Resolution |
|---|---|---|
| ACCESS1.0 | Australia | 1.875×1.25 |
| BCC-CSM1.1 | China | 2.8×2.8 |
| CanESM2 | Canada | 2.8×2.8 |
| CCSM4 | United States | 1.25×0.94 |
| CESM1-CAM5 (FV2) | United States | 2.5×1.9 |
| CNRM-CM5 | France | 1.4×1.4 |
| FGOALS-g2 | China | 2.8×2.8 |
| FIO-ESM | China | 2.8×2.8 |
| GFDL-CM3 | United States | 2.5×2.0 |
| GFDL-ESM2M | United States | 2.5×2.0 |
| GFDL-ESM2G | United States | 2.5×2.0 |
| GISS-E2-H | United States | 2.5×2.0 |
| GISS-E2-R | United States | 2.5×2.0 |
| HadCM3 | United Kingdom | 3.75×2.5 |
| HadGEM2-AO | Korea | 1.875×1.25 |
| HadGEM2-ES | United Kingdom | 1.875×1.25 |
| HadGEM2-CC | United Kingdom | 1.875×1.25 |
| INMCM4 | Russia | 2.0×1.5 |
| IPSL-CM5A-LR | France | 3.75×1.875 |
| IPSL-CM5A-MR | France | 2.5×1.25 |
| MIROC5 | Japan | 1.4×1.4 |
| MIROC-ESM | Japan | 2.8×2.8 |
| MPI-ESM-LR | Germany | 1.9×1.9 |
| MPI-ESM-P | Germany | 1.9×1.9 |
| MRI-CGCM3 | Japan | 1.1×1.1 |
| NorESM1-M | Norway | 2.5×1.875 |
Model outputs used in this study are obtained from the CMIP5 historical run, which is initiated from an arbitrary point of a quasi-equilibrium control run and integrating no less than 156 years (1850–2005). The CMIP5 historical run is forced by time-evolving greenhouse gases, ozone, aerosols, and a solar constant that are consistent with the observations, and, for the first time, including time-evolving land cover/land use pattern [ Taylor et al. , 2012 ]. All the model outputs are interpolated to a regular grid of 2.5°×2.5°before the actual analysis.
We compare the historical simulations with observed sea level pressure (SLP) obtained from the Hadley Centre HadSLP2 dataset at a resolution of 5°×5° [ Allan and Ansell , 2006 ] and quasiobservational zonal wind from the NCEP/NCAR reanalysis project at a resolution of 2.5°×2.5° [ Kalnay et al. , 1996 ]. The observation and reanalysis are both referred to as observation in this study, though the reanalysis is not a real observation.
According to Thompson and Wallace [2000] , we define the AO as the first leading empirical orthogonal function (EOF) mode of monthly mean SLP anomalies poleward of 20°N. To ensure equal area weighting for the covariance matrix for the EOF analysis, the SLP anomalies are weighted by the square root of the cosine of latitude. The AO index is defined as the normalized time series corresponding to the first leading EOF. The spatial pattern of the AO, comparable to the EOF, is presented as the regressions of SLP anomalies onto the time series of the AO index. The regression coefficients correspond to amplitudes of one standard deviation of the index. Simulations and observations for the period of 1950–2005 are analyzed in this study. Since the AO is most prominent in the cold season, and its activity centers always move northward in winter, as compared to summer [ Barnston and Livezey , 1987 ], only spatial patterns of the winter AO (December to next February) are shown in this study. All monthly data per year are used for the spectral analysis. The linear trends are removed prior to the correlation/regression analysis.
3. Comparison of AO patterns between simulations and observations
3.1. Temporal variability
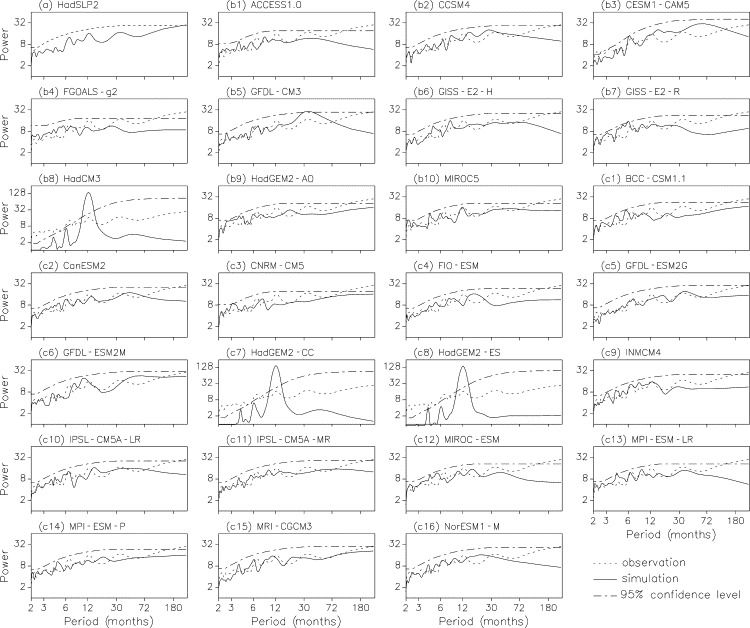
Figure 1 shows the power spectra for the monthly AO index derived from observations and from each model simulation. Notable peaks in observations are found near 6-, 12-, and 36-month cycles (Fig. 1 a), indicating semiannual and annual behavior and lower-frequency variability of the AO pattern, although all these peaks are not statistically significant at the 95% confidence level. All the spectral peaks in the model simulations are not statistically significant either, except those for three models (HadCM3, HadGEM2-CC, and HadGEM2-ES) from the Hadley Centre. Most models reproduce the semiannual behavior, as seen in the observations. However, less than half of the models capture the observed annual behavior. The GFDL-CM3, GFDL-ESM2G and MPI-ESM-LR exhibit a near 3-year cycle, similar to the observation, whereas this cycle in the GFDL-CM3 is obviously stronger than in the observation. The three models from the Hadley Centre exhibit a significant and tall peak near 1 year and two relatively smaller peaks near 4 and 6 months, indicating large seasonal and interannual variability of the AO pattern in these model simulations. In addition, some models display peaks at about 4 months, 8–9 months, 2 years and/or 4–5 years, which cannot be found in the observations.
|
|
|
Figure 1. Smoothed power spectra for the time series of monthly AO index derived from (a) observation (HadSLP2; also dotted line), and (b, c) the CMIP5 model simulations (solid lines) (the dashed line indicates the 95% confidence limit above the red noise spectrum; b1–b10 are the physical climate system models and c1–c16 the Earth system models) |
The observational analysis shows that the negative phase of the winter AO is more frequent from the 1950s to the 1970s, but less frequent thereafter. The phase of the winter AO tends to change from positive to negative in the first decade of the 21st century, indicating a large inter-decadal variability of the AO pattern. In Figure 1 a, the observed AO indices show a final peak beginning from near 6-year and increasing in power until the end of the analyzed period, which confirms the large inter-decadal variability of the AO pattern. However, only a few CMIP5 models, including BCC-CSM1.1, CNRM-CM5, HadGEM2-AO, MPI-ESM-P, and MRI-CGCM3, are able to capture the inter-decadal component in the observed AO variability. On the contrary, the power tends to decrease with the period in about half of the CMIP5 model simulations, indicating that the inter-decadal variability is weaker compared to the observations. In addition, the spectral analysis is applied to the wintermean AO index (Figures not shown), where the power spectrum for the winter-mean AO index agrees well with the monthly AO index at annual to inter-decadal time scales. Overall, the majority of the CMIP5 models simulate the AO temporal variability quite poor. There is no significant difference in the ability to simulate the AO temporal variability between the physical climate system models and the Earth system models.
3.2. Spatial patterns in the SLP field
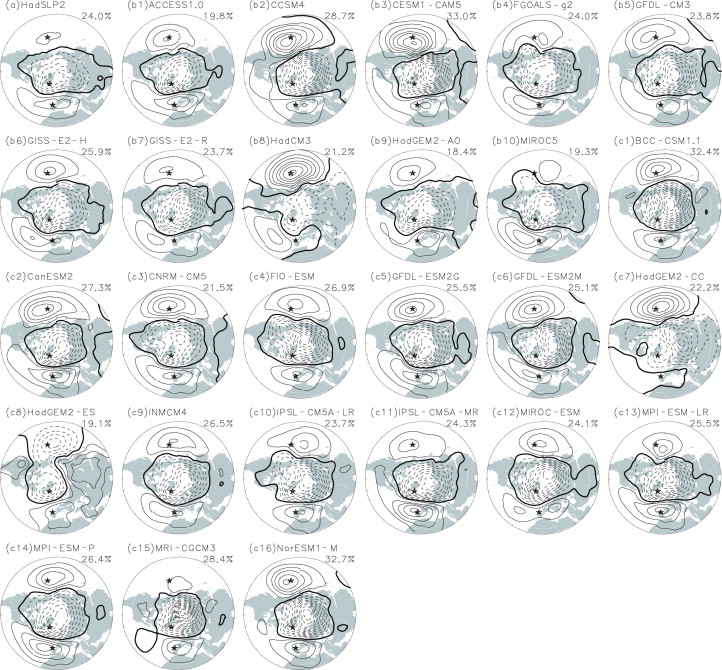
To assess the ability of the CMIP5 models in simulating the spatial patterns of the AO, Figure 2 shows the regression of SLP anomalies on the AO index during winter. It can be seen that all the CMIP5 models, except those from the Hadley Centre, clearly simulate a recognizable AO pattern. The first leading EOF for the winter SLP anomalies simulated by the HadCM3 (Fig. 2b8 ) and HadGEM2-CC (Fig. 2c7 ) are featured by a negative anomaly over the pole and Eurasia, with a maximum centered over northern Eurasia. For the HadGEM2-ES, a positive anomaly mainly occurs over the middle latitudes of North America, the northeastern Atlantic and Eurasia, whereas a negative anomaly occurs over the North Pacific, Greenland and the adjacent regions (Fig. 2c8 ). These results indicate that the models from Hadley Centre may have difficulties in simulating the spatial patterns of the winter AO. In particular, they all exaggerate the relationship between AO and SLP anomalies over Siberia.
|
|
|
Figure 2. Regressions of SLP anomalies in winter on the AO index derived from the observation (HadSLP2) and the CMIP5 model simulations (the dashed line indicates negative values and the thick solid line is zero; the percentage of variance explained by the winter AO pattern is given at the top right-hand corner of each frame; ★ shows the three activity centers of the AO obtained from the observation) |
The observed AO pattern consists of three activity centers as denoted by the star symbol (Fig. 2 a). One is located near the pole (A1), and the other two are located in the middle latitudes of the Atlantic (A2) and the Pacific (A3). The observed A1 is characterized by a single-pole structure and centered near the Atlantic. More than half of the CMIP5 models produce an A1 shifting to the Eastern Hemisphere and/or with a dipole structure. In addition, most models displace A2 more eastward or westward. Only five models, IPSL-CM5A-MR, MIROC5, MPI-ESM-LR, MPI-ESM-P and MRI-CGCM3, reproduce A3 with a weaker magnitude than A2, as is observed.
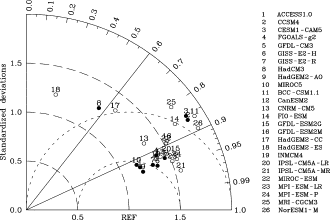
Almost all the models overestimate the magnitude of the AO pattern, especially the activity center in the North Pacific. To quantitatively measure the resemblance of the simulated AO pattern to the observed, the Taylor diagram [ Taylor , 2001 ], which summarizes the comparison of wintertime AO pattern between the observation and the CMIP5 model simulations, is shown in Figure 3 . The results indicate that the spatial correlation coefficient with the observation is above 0.80 for all the CMIP5 models, except the three models from Hadley Centre. More than half of the models have a spatial correlation coefficient with the observation of no less than 0.90. The amplitude of the AO pattern for each model is about 1.2 to 1.9 times as that of the observation, which further confirms that all models overestimate the amplitude of AO pattern.
|
|
|
Figure 3. Taylor diagram, comparison of wintertime AO pattern between observation and CMIP5 model simulations. The radial distance from the origin indicates the standard deviation of AO pattern for each model normalized by the observed value. The azimuthal position denotes the correlation between the observed and simulated AO pattern. A solid circle indicates a physical climate system model and a hollow circle an Earth system model |
The majority of the physical climate models reproduce an AO pattern that more resembles the observation than the Earth system models (Fig. 3 ). The AO is a dominant mode of the extra-tropical, low-frequency atmospheric variability, and its formation and maintenance are closely related to the atmospheric internal dynamics. Since the Earth system model in corporates a coupled carbon cycle, the reproduction may be more complicated than the physical climate model, which only consists of interactions between the ocean, land, atmosphere and sea ice. In other words, the latter is advantageous in simulating the AO pattern at the recent development in coupled models.
3.3. Vertical structure in the zonal-mean zonal wind field
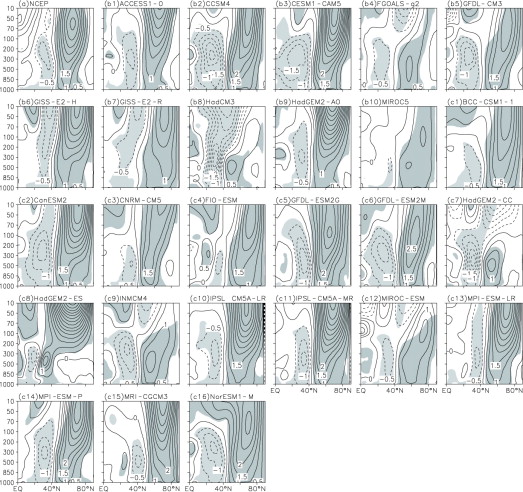
The AO is characterized by an equivalent barotropic structure from the surface upward into the lower stratosphere during boreal winter [ Thompson and Wallace , 2001 ]. The zonal-mean zonal wind anomalies associated with the AO exhibit a meridional dipole in the mid-high latitudes of the Northern Hemisphere. Corresponding to the positive phase of the AO, easterly anomalies occur in the middle latitudes south of 45°N, with a maximum in the upper troposphere, while westerly anomalies are observed in high latitudes, amplifying with height upward into the lower stratosphere (Fig. 4 a). These wind anomalies correspond to the weakened subtropical westerly jet and the strengthened polar jet [ Li and Wang , 2003 ].
|
|
|
Figure 4. Regressions of the wintertime zonal-mean zonal wind anomaly (m s–1 ) with the AO index derived from (a) the observation (NCEP) and (b, c) the CMIP5 model simulations (gray shading indicates significance at the 95% confidence level) |
To evaluate the vertical structure of the AO as simulated by the CMIP5 models, Figure 4 shows the regression of zonal-mean zonal wind anomaly onto the AO index derived from the observation and the model simulations during winter. It is indicated that almost all of the CMIP5 models exhibit a meridional dipole in the zonal-mean zonal wind anomaly field associated with the AO in the mid-high latitudes of the Northern Hemisphere, as seen in observation. But the models tend to overestimate or underestimate the observed amplitude of the dipole. In addition, there are significant biases in the location of the dipole between the simulations and the observation. The mid- and high-latitude activities of the dipole are hereafter referred to as SJ and PJ, respectively. The CMIP5 models, except GISS-E2-R (Fig. 4 b7), MRI-CGCM3 (Fig. 4c15 ) and the three models from the Hadley Centre (Fig. 4-b8, 4-c7 and 4-c8 ), are all able to reproduce the observed PJ amplifying and titling poleward with height. But most models tend to display the PJ more northward. Some models have difficulties in simulating the location of the wind maximum corresponding to the PJ. For example, the FGOALS-g2 (Fig. 4b4 ), GFDL-ESM2G (Fig. 4c5 ), GFDL-ESM2M (Fig. 4c6 ), INMCM4 (Fig. 4c9 ), MIROC5 (Fig. 4b10 ) and MIROCESM (Fig. 4c12 ) display the wind maximum of the PJ more downward to the upper or middle troposphere. The wind maximum of the SJ is centered in the troposphere in most of the model simulations, similar to the observation. However, there are some models, such as GISS-E2-H (Fig. 4b6 ) and GISS-E2-R (Fig. 4b7 ), which display the wind maximum of the SJ more upward to the lower stratosphere. In the CCSM4 (Fig. 4b2 ), CESM1-CAM5 (Fig. 4b3 ) and GFDL-CM3 (Fig. 4b5 ), the SJ extends more southward compared to the observation. Overall, the vertical structure of the AO is best simulated by the MPI-ESM-P than the other CMIP5 models.
4. Conclusions and discussion
The temporal variability and spatial pattern of the AO simulated in the historical experiment of 26 CMIP5 models were evaluated. The spectral analysis of monthly AO index indicates that only the HadCM3, HadGEM2-CC, and HadGEM2-ES, all from the Hadley Centre, exhibit a significant and tall peak near 1 year and two relatively small peaks near 4 and 6 months. The other 23 models exhibit no statistically significant spectral peak in the historical experiment, as similar to the observations. Also, these models are able to reproduce the AO pattern in the SLP anomaly field during winter. But the magnitudes of the AO pattern tend to be overestimated in all models. The majority of the physical climate models reproduce an AO pattern that resembles the observation better than the Earth system models. The observed zonal-mean zonal wind anomalies associated with the AO are characterized by a meridional dipole in the mid-high latitudes of the Northern Hemisphere during winter. Although almost all CMIP5 models can capture a dipole, there are significant biases in both magnitude and location of the dipole between the simulations and observation, indicating that the ability of most CMIP5 models to simulate the vertical structure of the AO needs to be improved. Considering the temporal variability and spatial structures in both horizontal and vertical directions, the MPI-ESM-P reproduces the best AO pattern in comparison of the 26 CMIP5 models and the observation.
Acknowledgements
The authors are grateful for the useful comments and suggestions of the two anonymous reviewers. We acknowledge the WCRP Working Group on Coupled Modeling, which is responsible for CMIP5, and we thank the climate modeling groups for producing and making available their model outputs. This work was supported by the National Basic Research Program of China (No. 2010CB950501 & 2010CB950404), the National Natural Science Foundation of China (No. 4120-5058), and the China Postdoctoral Science Foundation (No. 2012M510634).
References
- Allan and Ansell, 2006 R. Allan, T. Ansell; A new globally complete monthly historical gridded mean sea level pressure dataset (HadSLP2): 1850-2004; J. Climate, 19 (2006), pp. 5816–5842
- Barnston and Livezey, 1987 A.G. Barnston, R.E. Livezey; Classification, seasonality and persistence of low-frequency atmospheric circulation patterns; Monthly Weather Review, 115 (1987), pp. 1083–1126
- Gong and Wang, 2003 D.-Y. Gong, S.-W. Wang; Influence of Arctic Oscillation on winter climate over China; Acta Geographica Sinica (in Chinese), 58 (4) (2003), p. 559568
- Gong et al., 2001 D.-Y. Gong, S.-W. Wang, J.-H. Zhu; East Asian winter monsoon and Arctic Oscillation; Geophys. Res. Lett., 28 (2001), pp. 2073–2076
- Jü et al., 2004 J.-H. Jü, J.-Z. Ren, J.-M. LÜ; Effect of interdecadal variation of Arctic Oscillation on temperature increasing in North of East Asian winter; Plateau Meteorology (in Chinese), 23 (4) (2004), pp. 429–434
- Kalnay et al., 1996 E. Kalnay, M. Kanamitsu, R. Kistler, et al.; The NCEP/NCAR 40-year reanalysis project; Bull. Amer. Meteor. Soc., 77 (1996), pp. 437–472
- Li and Wang, 2003 J.-P. Li, J.X.L. Wang; A modified zonal index and its physical sense; Geophys. Res. Lett., 30 (2003) 1011029P2003GL017441
- Miller et al., 2006 R.L. Miller, G.A. Schmidt, D.T. Shindell; Forced annular variations in the 20th century Intergovernmental Panel on Climate Change assessment report models; J. Geophys. Res., 111 (2006) D18101
- Robertson, 2001 A.W. Robertson; Influence of oceanatmosphere interaction on the Arctic Oscillation in two general circulation models; J. Climate, 14 (2001), pp. 3240–3254
- Stoner et al., 2009 A.M.K. Stoner, K. Hayhoe, D.J. Wuebbles; Assessing general circulation model simulations of atmospheric teleconnection patterns; J. Climate, 22 (2009), pp. 4348–4372
- Tang et al., 2012 G.-L. Tang, Y. Luo, J.-B. Huang, et al.; Continuation of the global warming; Progressus Inquisitiones De Mutatione Climatis (in Chinese), 8 (4) (2012), pp. 235–242
- Taylor, 2001 K.E. Taylor; Summarizing multiple aspects of model performance in a single diagram; J. Geophys. Res., 106 (2001), pp. 7183–7192
- Taylor et al., 2012 K.E. Taylor, R.J. Stouffer, G.A. Meehl; An overview of CMIP5 and the experiment design; Bull. Amer. Meteor. Soc., 93 (2012), pp. 485–498
- Thompson and Wallace, 1998 D.W.J. Thompson, J.M. Wallace; The Arctic Oscillation signature in the wintertime geopotential height and temperature fields; Geophys. Res. Lett., 25 (1998), pp. 1297–1300
- Thompson and Wallace, 2000 D.W.J. Thompson, J.M. Wallace; Annular modes in the extratropical circulation; Part I: Month-to-month variability. J. Climate, 13 (2000), pp. 1000–1016
- Thompson and Wallace, 2001 D.W.J. Thompson, J.M. Wallace; Regional climate impacts of the Northern Hemisphere annular mode; Science, 293 (2001), pp. 85–89
- Wang et al., 2012 S.-W. Wang, Y. Luo, Z.-C. Zhao, et al.; Attribution of climate warming to the causes; Progressus Inquisitiones De Mutatione Climatis (in Chinese), 8 (4) (2012), pp. 308–312
- Wu and Wang, 2002 B.-Y. Wu, J. Wang; Winter Arctic Oscillation, Siberian High and East Asian winter monsoon; Geophys. Res. Lett., 29 (19) (2002) http://dx.doi.org/10.1029/2002GL015373 doi:
- Xin et al., 2008 X.-G. Xin, T.-J. Zhou, R.-C. Yu; The Arctic Oscillation in coupled climate models; Chinese Journal of Geophysics, 51 (2) (2008), pp. 223–239
- Yamazaki and Shinya, 1999 K. Yamazaki, Y. Shinya; Analysis of the Arctic Oscillation simulated by AGCM; Journal of Meterological Society of Japan, 77 (1999), pp. 1287–1298
- Zhu et al., 2013 X. Zhu, W.-J. Dong, Y. Guo; Comparison of simulated winter and spring Arctic Oscillation variability by CMIP5 and CMIP3 coupled models; Advances in Climate Change Research (in Chinese), 9 (3) (2013), pp. 165–172
- Zhu and Wang, 2008 Y.-L. Zhu, H.-J. Wang; The Arctic and Antarctic oscillations in the IPCC AR4 coupled models; Acta Meteorologica Sinica (in Chinese), 66 (6) (2008), pp. 993–1004
Document information
Published on 15/05/17
Submitted on 15/05/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?