Abstract
This study is devoted to investigate the steady fully developed natural convection flow in a vertical annular micro-channel having temperature dependent viscosity in the presence of velocity slip and temperature jump at the annular micro-channel surfaces. The governing equations of the motion are a set of ordinary differential equations and their analytical solutions in dimensionless form have been obtained for the temperature field and velocity field. The effect of various flow parameters entering into the problem is discussed with the aid of line graphs. During the course of numerical investigation, it is found that increase in viscosity variation parameter enhances the fluid velocity and velocity slip. Furthermore, an increase in viscosity variation parameter leads to increase in the volume flow rate and skin friction.
Keywords
Annular micro-channel; Natural convection; Temperature dependent viscosity; Velocity slip and temperature jump
Nomenclature
- viscosity variation parameter
- specific heat at constant pressure
- fluid–wall interaction parameter,
- gravitational acceleration
- radius of the inner cylinder
- radius of the outer cylinder
- Knudsen number,
- volume flow rate
- dimensionless volume flow rate
- Prandtl number
- dimensional radial coordinate
- dimensionless radial coordinate
- specific gas constant
- temperature of fluid
- reference temperature
- temperature at outer surface of the inner cylinder
- axial velocity
- dimensionless axial velocity
- dimensional gap between the cylinders
- thermal and tangential momentum accommodation coefficients, respectively
Greek letters
- thermal diffusivity
- coefficient of thermal expansion
- dimensionless variables
- ratio of specific heats
- dynamic viscosity
- dynamic viscosity at
- dimensionless temperature
- density
- fluid kinematic viscosity
- ratio of radii
- molecular mean free path
- thermal conductivity
- skin-friction
1. Introduction
Fluid flow in micro-channel has continued to attract interest because of its practical applications in space systems, manufacturing and material processing operations, and in high-power-density chips in supercomputers and other electronics. Several investigations have been accomplished on forced convection fluid flow in micro-channels and micro-tube. However, only a few studies have been carried out on natural and mixed convection in vertical micro-channels and micro-tube. Chen and Weng [1] studied the flow mechanism in a vertical micro-channel and obtained an exact solution of the fully developed natural convection in an open-ended vertical parallel-plate micro-channel due to asymmetric heating of micro-channel walls. They found that the rarefaction and fluid–wall interaction have significant effects on the flow and thermal fields. Jha et al. [2] extended this work by taking into account suction/injection on the micro-channel walls. They concluded in their work that skin friction as well as rate of heat transfer is strongly dependent on suction/injection parameter. The transient hydrodynamics and thermal behaviors of fluid flow in an open-ended vertical parallel-plate micro-channel, under the effect of the hyperbolic-heat-conduction model, were investigated semi-analytically in [3]. They concluded that, as Knudsen number increases, velocity slip and temperature jump increase at the boundaries. Haddad et al. [4] numerically investigated the developing hydrodynamical behaviors of free convection gas flow in a vertical open-ended parallel-plate micro-channel filled with porous media. Their results showed that the slip in velocity and jump in temperature decreased in the axial direction of the flow. Numerical solutions were obtained by Buonomo and Manca [5] for natural convection in parallel-plate vertical microchannels due to asymmetric heating by imposing constant heat flux on the boundaries. Buonomo and Manca [6] further performed a numerical study on transient mixed convection in a vertical micro-channel due to asymmetric as well as symmetric heat fluxes on the micro-channel surfaces. Chen and Weng [7] numerically studied the creep effect on the flow and heat transfer characteristics, for developing natural convective microflow in the same geometry.
In another related article, Weng and Chen [8] examined the influence of wall-surface curvature on the flow and thermal fields as well as the corresponding characteristics over the heated wall. The results of this work show the nonlinear behavior in temperature. It was also concluded that under certain rarefaction and wall interaction condition, by decreasing the curvature radius ratio, skin-friction decreases while rate of heat transfer increases. Jha et al. [9] extended the work of Weng and Chen [8] to the case in which the cylindrical surfaces forming the annulus are permeable, i.e. when there is a suction or injection through the annulus surfaces. They concluded that as suction/injection on the cylinder walls increases, the fluid velocity and temperature are enhanced. In another work, Jha and Aina [10] analyzed the work of Weng and Chen [8] by incorporating the pressure gradient in the vertical direction. It is observed that the probability of reverse flow formation increases at inner surface of outer cylinder of the micro-annulus by increasing curvature radius, while it decreases with increase in Knudsen number and fluid wall interaction parameter. Avci and Aydin [11] and [12] presented exact solutions for fully developed mixed convection in a vertical parallel-plate micro-channel with constant plate temperature and constant heat flux on the plates respectively. Also, Avci and Aydin [13] studied the fully developed mixed convective heat transfer of a Newtonian fluid in a vertical micro-annulus formed by two concentric micro-tubes. It is found that increasing mixed convection parameter enhances heat transfer while rarefaction effects considered by the velocity slip and the temperature jump in the slip flow regime decrease it. Jha and Aina [14] further extended the work of Avci and Aydin [13] to the case when suction/injection is imposed on the annulus surfaces. They concluded in their study that as suction/injection on the micro-porous-annulus (MPA) increases, the fluid velocity and temperature increase. Recently, Jha and Aina [15] investigated steady fully developed mixed convection flow in a vertical micro-annulus in the presence of transverse magnetic field. Das et al. [16] presented a theoretical analysis to investigate the effect of buoyancy force on mixed convective Couette flow of a reactive viscous incompressible nanofluid between two concentric cylindrical pipes under bimolecular, Arrhenius and sensitized reaction rates. In another article, Das et al. [17] studied the fully developed mixed convection flow in a vertical channel filled with nanofluids in the presence of a uniform transverse magnetic field. They reported that the magnetic field tends to enhance the nanofluid velocity in the channel. Makinde [18] investigated the thermal analysis of a reactive generalized Couette flow of power law fluids between concentric cylindrical pipes.
On the other hand, most of the existing analytical studies for such problems are based on the constant physical properties of the fluid. However, accurate prediction for the flow formation and heat transfer can be achieved by considering variation of physical properties with temperature [19], especially for fluid viscosity. Makinde and Chinyoka [20] presented numerical solution of unsteady flow of a variable viscosity reactive fluid in a slit with wall suction/injection. Tshehla et al. [21] investigated the entropy generation rate in a variable viscosity liquid flowing steadily through a cylindrical pipe with convective cooling at the pipe surface. They reported that a decrease in the fluid viscosity and an increase in viscous heating enhance total entropy generation in the flow fluid. Klemp et al. [22] studied numerically the effect of temperature dependent viscosity on the entrance flow in a channel in the hydrodynamic case. The effects of variable viscosity on hydromagnetic flow and heat transfer have been studied by Seddeek [23]. Grasset and Parmentier [24] investigated thermal convection in a volumetrically heated fluid with strongly temperature dependent viscosity cooled from above. In another article, Saravanan and Kandaswamy [25] analyzed the hydromagnetic stability of convective flow of variable viscosity fluids generated by internal heat sources. The effect of variable temperature dependent viscosity on the mixed convection flow from vertical plate is investigated by many authors, e.g. Hady et al. [26] and Mahmud [27]. The free-or-mixed convection boundary layer flow from a horizontal surface in a saturated porous medium taking into account the effect of variable viscosity has been studied by Kumari [28]. Recently, Umavathi and Ojjela [29] studied the effect of variable viscosity on free convection flow in a vertical rectangular duct. They observed that the negative values of viscosity variation parameter show intense velocity contour in the lower half region of the duct whereas positive values of viscosity variation parameter show the intense velocity contours in the upper half region of the duct. In another related article, Umavathi [30] studied analytically as well as numerically the combined effects of variable viscosity and variable thermal conductivity on double-diffusive convection flow of fluid in a vertical channel filled with porous material. However, derivation of any exact solution for steady fully developed natural convection flow in a vertical annular micro-channel with temperature dependent viscosity in the presence of velocity slip and temperature jump at the annular micro-channel surfaces with interfacial slip has not been attempted. It is well known that exact solutions have their own theoretical meaning, and many exact solutions played key roles in the early development of fluid mechanics and heat conduction [31] and [32]. Besides their theoretical importance, exact solutions can also be applied to checking the accuracy, convergence and effectiveness of various numerical computation methods and improving differencing schemes, grid generation ways and so on. Exact solutions are therefore very useful even for the newly rapidly developing computational fluid dynamics and heat transfer.
The objective of this work was to present exact solution of steady fully developed natural convection flow of fluid having temperature dependent viscosity in a vertical annular micro-channel in the presence of velocity slip and temperature jump at the annular micro-channel surfaces. The mathematical model employed herein represents a generalization of the work discussed in [8] to include temperature dependent viscosity.
2. Mathematical analysis
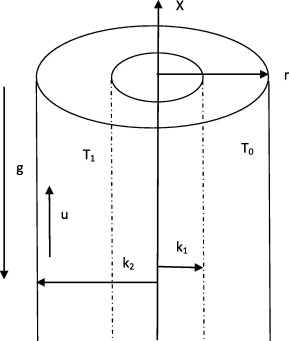
Consider a steady fully developed natural convection flow in a vertical annular micro-channel with temperature dependent viscosity in the presence of velocity slip and temperature jump at the annular micro-channel surfaces. A schematic geometry of the problem under investigation is shown in Fig. 1, where X-axis is parallel to the gravitational acceleration g but in the opposite direction while the r -axis is in the radial direction. The radius of the inner and outer cylinder walls is and , respectively. The outer surface of the inner cylinder is heated to a temperature greater than that of the surrounding fluid having temperature and the inner surface of the outer cylinder is maintained at temperature . Due to this temperature difference, natural convection occurs in the vertical annular micro-channel. Since the flow is fully developed and cylinders are of infinite length, the flow depends only on radial coordinate . Using Boussinesq’s approximation and considering temperature dependent viscosity, the governing momentum and energy equations, describing the present physical situation can be written in dimensional form as follows:
|
|
|
Figure 1. Flow configuration and coordinate system. |
Conservation of momentum
|
|
(1) |
Conservation of energy
|
|
(2) |
The boundary conditions for the velocity and temperature field in dimensional form are as follows:
|
|
(3) |
|
|
(4) |
|
|
(5) |
|
|
(6) |
The mathematical model used in the present work to capture the viscosity variation with temperature is [33]
|
|
(7) |
where is the viscosity when temperature is while the coefficient determine the strength of dependency between and .
Introducing the following dimensionless quantities in Eqs. (1), (2), (3), (4), (5), (6) and (7),
|
|
(8) |
Eqs. (1) and (2) can be written in dimensionless form as
|
|
(9) |
|
|
(10) |
subject to the following dimensionless boundary conditions [8]
|
|
(11) |
|
|
(12) |
The physical quantities used in the above equations are defined in the nomenclature.
By using the transformation , the Eqs. (9), (10), (11) and (12) can be written as follows:
|
|
(13) |
|
|
(14) |
subject to the boundary conditions
|
|
(15) |
|
|
(16) |
Integrating Eq. (14) and applying the boundary conditions (16) give the following:
|
|
(17) |
where
|
|
(18) |
Substituting Eq. (17) into the momentum Eq. (13) and solving it using the boundary condition (15) give
|
|
(19) |
Two important parameters for convective micro-flow are the volume flow rate, and skin-friction. The temperature solution as well as rate of heat transfer is exactly the same as discussed by Chen and Weng [8].
The dimensionless volume flow rate is as follows:
|
|
(20) |
By substituting Eqs. (19) into (20) and integrating Eq. (20) give the following:
|
|
(21) |
The skin-frictions () at the cylinder walls are as follows:
|
|
|
|
(22) |
|
|
(23) |
|
|
|
|
(24) |
|
|
(25) |
where are all constants given in the Appendix A.
In order to verify the accuracy of the present work, we have computed the numerical value for the velocity for small value of . Table gives a comparison of the numerical values of the velocity obtained in the present work when with those obtained by Weng and Chen [8] for . As can be seen from Table 1, the solutions of the present work agree with those of Weng and Chen [8] for small values of .
| Velocity | |||
|---|---|---|---|
| Weng and Chen [8] | Present work | ||
| 0.8 | 0.2 | 0.0713 | 0.0712 |
| 0.4 | 0.0838 | 0.0837 | |
| 0.6 | 0.0746 | 0.0744 | |
| 0.8 | 0.0505 | 0.0503 | |
| 0.5 | 0.2 | 0.0651 | 0.0650 |
| 0.4 | 0.0730 | 0.0725 | |
| 0.6 | 0.0624 | 0.0621 | |
| 0.8 | 0.0409 | 0.0405 | |
| 0.2 | 0.2 | 0.0527 | 0.0526 |
| 0.4 | 0.0538 | 0.0536 | |
| 0.6 | 0.0431 | 0.0430 | |
| 0.8 | 0.0270 | 0.0269 | |
3. Results and discussion
MATLAB program is written to compute and generate line graphs for velocity, volume flow rate, and skin friction at both cylinders for different values of the dimensionless parameters, such as rarefaction parameter , fluid–wall interaction parameter , radius ratio and viscosity variation parameter so as to comment on their relative significance in the flow formation. The present parametric study has been performed in the continuum and slip flow regimes . Also, for air and various surfaces, the values of and range from near 1 to 1.667 and from near 1.64 to more than 10, respectively. So, this study has been performed over the reasonable ranges of and . The selected reference values of , and for the present analysis are 0.05 and 1.64 respectively as given in Weng and Chen [8].
Temperature solution as well as rate of heat transfer is exactly the same as discussed by Weng and Chen [8]; therefore, we have only discussed the variation of velocity, volume flow rate and skin friction for different controlling parameters.
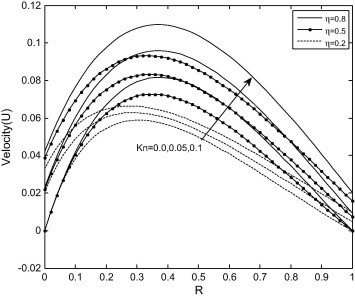
Fig. 2 shows the velocity distribution for different values of rarefaction parameter for fixed values of and . It is observed that, as rarefaction parameter increases, the velocity slip at the cylindrical surfaces increases which reduces the retarding effect of the boundaries. This yields an observable increase in the fluid velocity. Furthermore, the slip induced by rarefaction effect increases as radius ratio increases.
|
|
|
Figure 2. Velocity profile for different values of Kn with ln = 1.64, B = 0.5. |
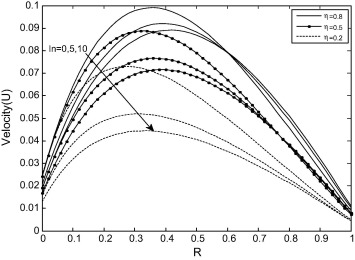
Fig. 3 depicts the effect of fluid–wall interaction parameter on the velocity distribution for fixed values of and . It is evident from Fig. 3 that, the increase in fluid–wall interaction parameter leads to the decrease in fluid velocity and increase in slip velocity near the outer surface of the inner cylinder while reverse trend is observed at inner surface of the outer cylinder. In addition, the slip induced by fluid–wall interaction parameter increases as radius ratio decreases while the impact of fluid–wall interaction parameter on the slip is more visible for smaller radius ratio .
|
|
|
Figure 3. Velocity profile for different values of ln with Kn = 0.05, B = 0.5. |
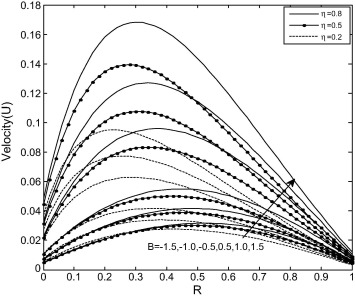
Fig. 4 exhibits the effect of viscosity variation parameter on velocity distribution for fixed values of and It is observed that increase in viscosity variation parameter enhances the fluid velocity and slip velocity while the profiles for constant viscosity lie above and below on velocity field. This is due to the fact that as viscosity variation parameter increases, the viscosity of the working fluid decreases due to exponentially decaying nature of viscosity which causes higher velocity and velocity slip while as the viscosity variation parameter increases, the viscosity of the working fluid increases which causes lower velocity and velocity slip. It is also evident in Fig. 4 that velocity slip increases for and decreases for with increase in radius ratio .
|
|
|
Figure 4. Velocity profile for different values of B with Kn = 0.05, ln = 1.64. |
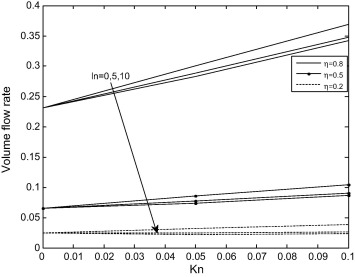
Fig. 5 illustrates the effects of rarefaction parameter and fluid–wall interaction parameter on volume flow rate . It is interesting to note that the volume flow rate is a decreasing function of fluid–wall interaction parameter . Furthermore, it is found that increase in radius ratio and rarefaction parameter leads to increase in the volume flow rate.
|
|
|
Figure 5. Variation of volume flow rate with Kn at different values of ln. |
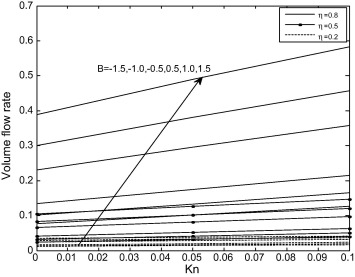
Fig. 6 reveals the influences of rarefaction parameter and viscosity variation parameter on volume flow rate It is observed from Fig. 6 that, the volume flow rate increases, as viscosity variation parameter increases. In addition, it is interesting to note that increase in rarefaction parameter leads to increase in the volume flow rate.
|
|
|
Figure 6. Variation of volume flow rate with Kn at different values of B. |
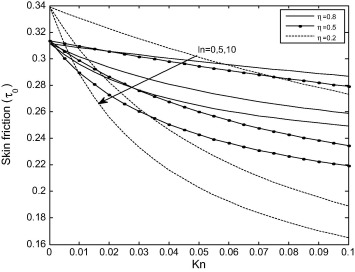
Fig. 7 exhibits the effects of rarefaction parameter and fluid–wall interaction parameter on skin-friction at outer surface of inner cylinder . It is clear that the skin-friction decreases with the increase in fluid–wall interaction parameter and rarefaction parameter . It is interesting to note that the impact of these parameters is significant for small value of radius ratio .
|
|
|
Figure 7. Variation of skin friction on the inner cylinder with Kn at different values of ln. |
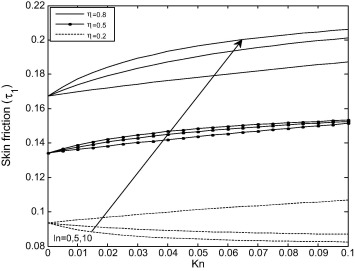
Fig. 8 shows the effects of rarefaction parameter and fluid–wall interaction parameter on skin-friction at inner surface of outer cylinder . It is evident from Fig. 8 that increases in radius ratio and rarefaction parameter lead to the increase in the skin-friction at inner surface of outer cylinder.
|
|
|
Figure 8. Variation of skin friction on the outer cylinder with Kn at different values of ln. |
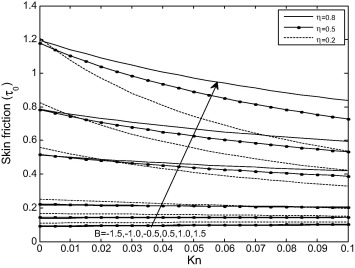
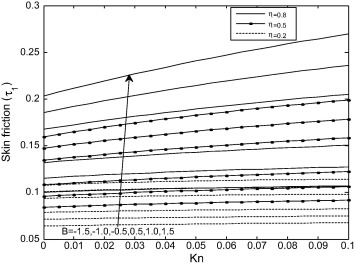
Figure 9 and Figure 10 illustrate the effects of rarefaction parameter and viscosity variation parameter on skin-friction at outer surface of inner cylinder and inner surface of outer cylinder , respectively. It is observed from the these Figures that skin friction increases, as viscosity parameter increases.
|
|
|
Figure 9. Variation of skin friction on the inner cylinder with Kn at different values of B. |
|
|
|
Figure 10. Variation of skin friction on the outer cylinder with Kn at different values of B. |
4. Conclusions
Steady fully developed natural convection flow formation in a vertical annular micro-channel having temperature dependent viscosity in the presence of velocity slip and temperature jump at the annular micro-channel surfaces is considered. The role of radius ratio , viscosity variation parameter , rarefaction parameter , and fluid–wall interaction parameter on the fluid velocity, volume flow rate and skin-friction is investigated. This study agrees with the findings of Weng and Chen [8] for vanishing viscosity variation parameter . The main findings are as follows:
- Increasing the values of viscosity variation parameter enhances the velocity and velocity slip.
- The volume flow rate increases with the increase in the values of both viscosity variation parameter and Knudsen number .
- Skin friction increases as viscosity variation parameter increases.
Appendix A
Constants used in the present work.
|
|
References
- [1] C.K. Chen, H.C. Weng; Natural convection in a vertical microchannel; J. Heat Transf., 127 (2005), pp. 1053–1056
- [2] B.K. Jha, B. Aina, S.B. Joseph; Natural convection flow in a vertical micro-channel with suction/injection; J. Process Mech. Eng., 228 (3) (2014), pp. 171–180
- [3] A.F. Khadrawi, A. Othman, M.A. Al-Nimr; Transient free convection fluid flow in a vertical micro-channel as described by the hyperbolic heat conduction model; Int. J. Thermophys., 26 (3) (2005), pp. 905–918
- [4] O.M. Haddad, M.A. Al-Nimr, M.M. Abuzaid; The effect of frequency of fluctuating driving force on basic slip micro-flows; Acta Mech., 179 (2005), pp. 249–259
- [5] B. Buonomo, O. Manca; Natural convection flow in a vertical micro-channel with heated at uniform heat flux; Int. J. Therm. Sci., 49 (2012), pp. 1333–1344
- [6] B. Buonomo, O. Manca; Transient natural convection flow in a vertical micro-channel with heated at uniform heat flux; Int. J. Therm. Sci., 56 (2012), pp. 35–47
- [7] C.K. Chen, H.C. Weng; Developing natural convection with thermal creep in a vertical microchannel; J. Phys. D, 39 (2006), pp. 3107–3118
- [8] H.C. Weng, C.K. Chen; Drag reduction and heat transfer enhancement over a heated wall of a vertical annular microchannel; Int. J. Heat Mass Transf., 52 (2009), pp. 1075–1079
- [9] Basant Kumar Jha, Babatunde Aina, S.A. Muhammad; Combined effects of suction/injection and wall surface curvature on natural convection flow in a vertical annular micro-channel; J. Thermophys. Aeromech., 22 (2) (2015), pp. 217–228
- [10] Basant K. Jha, Babatunde Aina; Steady fully developed mixed convection flow in a vertical annular microchannel: an exact solution; ASIAN J. Math. Comput. Res., 10 (4) (2016), pp. 332–347
- [11] M. Avci, O. Aydin; Mixed convection in a vertical parallel plate microchannel; ASME J. Heat Transf., 129 (2007), pp. 162–166
- [12] M. Avci, O. Aydin; Mixed convection in a vertical parallel plate microchannel with asymmetric wall heat fluxes; ASME J. Heat Transf., 129 (2007), pp. 1091–1095
- [13] M. Avci, O. Aydin; Mixed convection in a vertical microannulus between two concentric microtubes; ASME J. Heat Transf., 131 (2009), pp. 014502–014504
- [14] B.K. Jha, Babatunde Aina; Mathematical modelling and exact solution of steady fully developed mixed convection flow in a vertical micro-porous-annulus; J. Afr. Matematika, 26 (2015), pp. 1199–1213
- [15] Basant K. Jha, Babatunde Aina; MHD mixed convection flow in a vertical micro-annulus: an exact solution; Int. J. Fluid Mech. Res., 42 (6) (2015), pp. 537–552
- [16] S. Das, S. Chakraborty, R.N. Jana, O.D. Makinde; Mixed convective Couette flow of reactive nanofluids between concentric vertical cylindrical pipes; J. Nanofluids, 4 (4) (2015), pp. 485–493
- [17] S. Das, R.N. Jana, O.D. Makinde; Mixed convective magnetohydrodynamic flow in a vertical channel filled with nanofluids; Eng. Sci. Technol. Int. J., 18 (2) (2015), pp. 244–255
- [18] O.D. Makinde; Thermal analysis of a reactive generalized Couette flow of power law fluids between concentric cylindrical pipes; European Phys. J. Plus, 129 (2014), pp. 1–9
- [19] H. Herwig, G. Wicken; The effect of variable properties on laminar boundary layer flow; Warme-und Stof-Fubertrag, 20 (1986), pp. 47–57
- [20] O.D. Makinde, T. Chinyoka; Analysis of unsteady flow of a variable viscosity reactive fluid in a slit with wall suction or injection; J. Petrol. Sci. Eng., 94 (95) (2012), pp. 1–11
- [21] M.S. Tshehla, O.D. Makinde, G.E. Okecha; Heat transfer and entropy generation in a pipe flow with temperature dependent viscosity and convective cooling; Sci. Res. Essays, 5 (23) (2010), pp. 3730–3741
- [22] K. Klemp, H. Herwig, M. Selmann; Entrance flow in channel with temperature dependent viscosity including viscous dissipation effects; Int. Proceedings of the Third International Congress of Fluid Mechanics, Cairo, Egypt, 3 (1990), pp. 1257–1266
- [23] M.A. Seddeek; Effects of radiation and variable viscosity on a MHD free convection flow past a semi-infinite flat plate with an aligned magnetic field in the case of unsteady flow; Int. J. Heat Mass Transf., 45 (2002), pp. 931–935
- [24] O. Grasset, E.M. Parmentier; Thermal convection in a volumetrically heated, infinite Prandtl number fluid with strongly temperature-dependent viscosity: implications for planetary thermal evolution; J. Geophys. Res., 103 (1998), pp. 18171–18181
- [25] S. Saravanan, P. Kandaswamy; Hydromagnetic stability of convective flow of variable viscosity fluids generated by internal heat sources; Z. Angew. Math. Phys., 55 (2004), pp. 451–467
- [26] F.M. Hady, A.Y. Bakier, R.S.R. Gorla; Mixed convection boundary layer flow on a continuous flat plate with variable viscosity; Heat Mass Transf., 31 (1996), pp. 169–172
- [27] M.A.A. Mahmud; A note on variable viscosity and chemical reaction effects on mixed convection heat and mass transfer along a semi-infinite vertical plate; Math. Probab. Eng. (2007), Article Article ID 413237 doi:1155/2007/41323
- [28] M. Kumari; Variable viscosity effects on free and mixed convection boundary-layer flow from a horizontal surface in a saturated porous medium – variable heat flux; Mech. Res. Commun., 28 (2001), pp. 339–348
- [29] J.C. Umavathi, Odelu Ojjela; Effect of variable viscosity on free convection in a vertical rectangular duct; Int. J. Heat Mass Transf., 84 (2015), pp. 1–15
- [30] J.C. Umavathi; Combined effect of variable viscosity and variable thermal conductivity on double-diffusive convection flow of a permeable fluid in a vertical channel; Transp. Porous Med., 108 (2015), pp. 659–678
- [31] H. Lamb; Hydrodynamics; (sixth ed.)Cambridge Univ. Press, London (1932)
- [32] M. Jacob; Heat Transfer; John Wiley and Sons Inc, New York (1949)
- [33] H.T. Syeda, M. Shohel; Entropy generation in a vertical concentric channel with temperature dependent viscosity; Int. Commun. Heat Mass Transf., 29 (2002), pp. 907–918
Document information
Published on 12/04/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?