A new solution for nonlinear Dual Phase Lagging heat conduction problem

Abstract

The application of new methods to solution of non-Fourier heat transfer problems has always been one of the interesting topics among thermal science researchers. In this paper, the effect of laser, as a heat source, on a thin film was studied. The Dual Phase Lagging (DPL) non-Fourier heat conduction model was used for thermal analysis. The thermal conductivity was assumed temperature-dependent which resulted in a nonlinear equation. The obtained equations were solved using the approximate-analytical Adomian Decomposition Method (ADM). It was concluded that the nonlinear analysis is important in non-Fourier heat conduction problems. Significant differences were observed between the Fourier and non-Fourier solutions which stress the importance of non-Fourier solutions in the similar problems.

Keywords

Non-Fourier; Nonlinear analysis; DPL model; ADM; Laser heating

Nomenclature

c₀- reference speed of thermal wave (m s⁻¹)

c_p- specific heat (J kg⁻¹ K⁻¹)

FO- Fourier number

g- heat source (W m⁻³)

${\textstyle {\tilde {g}}}$- dimensionless heat source

g_l- dimensionless energy magnitude factor at the left boundary

g_r- dimensionless energy magnitude factor at the right boundary

k- thermal conductivity (W m⁻¹ K⁻¹)

k₀- reference thermal conductivity (W m⁻¹ K⁻¹)

L- characteristic length (m)

q- heat flux (W m⁻²)

${\textstyle {\tilde {q}}}$- dimensionless heat flux

T- temperature (K)

T₀- reference temperature (K)

${\textstyle {\tilde {T}}}$- dimensionless temperature

t- time (s)

t_p- dimensionless energy pulse time

Ve- Vernotte number

x- space direction (m)

${\textstyle {\tilde {x}}}$- dimensionless space direction

Greek symbols

α₀- reference thermal diffusivity (m² s)

β- the ratio of relaxation times

γ- dimensionless coefficient for taking into account of temperature-dependent conductivity

μ- dimensionless absorption coefficient

ρ- density (kg m⁻³)

τ_q- heat flux relaxation time (s)

τ_T- temperature relaxation time (s)

1. Introduction

Heat conduction is a mechanism of heat transfer during which thermal energy is transferred from an area with higher temperature to an area with lower temperature. A fundamental equation that can describe the mentioned mechanism well was first introduced in 1822 by a French physicist called Joseph Fourier in a thesis entitled “analytical theory of heat” [1]. Parabolic classic equation of Fourier heat conduction was used until 1950 in all analyses at that time, while all scientists accepted that hypothesis of this equation based on infinite motion speed of thermal energy inside matter was a non-physical hypothesis. Of course, this hypothesis is valid in many conventional applications but Fourier law was not able to predict correctly thermal behavior of the matter in some cases such as heat transfer at very low temperatures [2], heat transfer in very small sizes [3] or heat transfer with very high rate in short times [4].

Cattaneo [5] and Vernotte [6] presented a modified model for heat conduction in independent studies. The model was named after these two scientists as the Cattaneo–Vernotte (C–V) model. Their model accounts for the inertia caused by the acceleration of heat flux and, thus, resolves the paradox present in the Fourier model. Fourier model, due to its parabolic nature, states that thermal disturbances propagate in the body with an infinite velocity. This problem was resolved in the C–V non-Fourier model, where a specific velocity was considered for the propagation of thermal disturbances. The C–V model states that in the case of occurrence of a temperature gradient, a certain duration of time (heat flux relaxation time, τ_q) takes before the heat flux is established.

The development of non-Fourier models did not stop at the C–V model. In 1995, Tzou [7] introduced another macroscopic model known as the Dual Phase Lagging (DPL) model. The reason for the name was that it was suggested that a temperature gradient relaxation time (τ_T) also exists in addition to heat flux relaxation time (τ_q). This means that when a heat flux is established, duration of time is needed before it can create a temperature gradient. Some empirical studies have confirmed the validity of the model [8] and [9]. A number of well-established review studies have also addressed the development of non-Fourier models [10] and [11].

In most studies that have employed non-Fourier models for analyzing the conduction heat transfer, the assumption of constant thermal properties has yielded linear equations, and solving nonlinear equations has been less studied in the field’s literature. Nonlinear studies have utilized numerical methods, while challenges such as convergence and computational cost make the use of numerical methods difficult. New techniques have been recently proposed to solve nonlinear problems. They are known as semi-analytical or approximate-analytical methods. Some of the most common analytical-approximate methods include the following: Adomian Decomposition Method (ADM) [12], Homotopy Perturbation Method (HPM) [13] and [14], Homotopy Analysis Method (HAM) [15], Differential Transform Method (DTM) [16], and Variational Iteration Method (VIM) [17].

Semi-analytical methods have been widely used in solving various heat transfer problems in the past years. Ganji and Rajabi [18] used HPM to solve an unsteady nonlinear convective–radiative equation. Ganji [19] applied HPM to nonlinear equations arising in heat transfer and compared it with the perturbation and numerical methods. Ganji and Sadighi [20] investigated nonlinear heat transfer and porous media equations by HPM and VIM. Chakraverty and Behera [21] investigated the numerical solution of a fractionally damped dynamic system by HPM. HPM was used to present a mathematical model for biofilm inhibition for steady-state conditions by Meena et al. [22]. Gupta et al. [23] studied about the solution of various linear and nonlinear convection–diffusion problems arising in physical phenomena by HPM. Nadeem et al. [24] studied about the effects of nanoparticles on the peristaltic flow of tangent hyperbolic fluid in an annulus which were solved by ADM.

The application of semi-analytical methods to solve the nonlinear problems of non-Fourier heat conduction problems has been reported just in few studies. Torabi et al. [25] applied the homotopy perturbation method (HPM) to solve a nonlinear convective–radiative non-Fourier conduction heat transfer equation with variable specific heat coefficient. Saedodin et al. [26] used the variational iteration method (VIM) to solve the same problem. Differential transformation method (DTM) was applied for analysis of nonlinear convective–radiative hyperbolic lumped systems with simultaneous variation of temperature-dependent specific heat and surface emissivity by Torabi et al. [27]. In all of three mentioned references, the governing equations have been only dependent of time and in fact, ordinary differential equations (ODE) have been solved by semi-analytical methods and to the best knowledge of the authors, nonlinear partial differential equation (PDE) of non-Fourier heat conduction equation has not been solved yet by semi-analytical methods.

In the present paper, the heat transfer phenomenon within a one-dimensional slab subjected to an internal heat source was investigated. The DPL non-Fourier heat conduction model was employed for thermal analysis. A nonlinear equation was obtained since the thermal conductivity was assumed temperature-dependent. The obtained equations were solved by ADM. The main advantage of the ADM is the fact that it provides its user with an analytical approximation, in many cases an exact solution, in a rapidly convergent sequence with elegantly computed terms. Moreover, ADM approximates the nonlinear terms without linearization, perturbation, closure approximations, or discretization methods which can result in massive numerical computations. The application of a semi-analytical method such as ADM to solve a system of nonlinear PDEs of non-Fourier heat conduction problem is the novelty and originality of this study.

2. Physical modeling

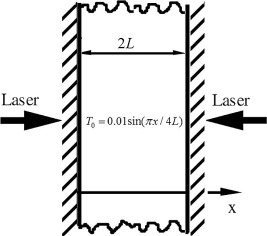
A simple schematic of the problem geometry is shown in Fig. 1. A 1-D thin film with the thickness of 2L   and the initial temperature ${\textstyle T(x{\mbox{,}}0)=0.01sin(\pi x/4L)}$ is insulated on its both sides and is subjected to a laser heat source. The energy conservation equation is as follows:

$\rho c_{p}{\frac {\partial T(x{\mbox{,}}t)}{\partial t}}+$${\frac {\partial q(x{\mbox{,}}t)}{\partial x}}-g=0$

(1)

where ρ is the density of the body, c_p is the specific heat of the body, T(x, t) is temperature function and q(x, t) is the function of heat flux, g is internal heat source, and x and t are spatial and temporal variables, respectively. The constitutive equation governing on the problem is based on the DPL model [7]:

${\tau }_{q}{\frac {\partial q(x{\mbox{,}}t)}{\partial t}}+$$q(x{\mbox{,}}t)+k\left[{\frac {\partial T(x{\mbox{,}}t)}{\partial x}}+\right.$$\left.{\tau }_{T}{\frac {{\partial }^{2}T(x{\mbox{,}}t)}{\partial t\partial x}}\right]=$$0$

(2)

where τ_q and τ_T are the heat flux and the temperature relaxation times, respectively and k is thermal conductivity of the body. Thermal conductivity is assumed a linear function of temperature [28]:

$k=k_{0}[1+\lambda T(x{\mbox{,}}t)]$

(3)

where k₀ is a reference value of thermal conductivity and λ is the coefficient of linear-dependency of thermal conductivity to temperature. The initial and boundary conditions are also as follows:

$T(x{\mbox{,}}0)=sin(\pi x/4L){\mbox{,}}\quad q(x{\mbox{,}}0)=$$0{\mbox{,}}\quad q(0{\mbox{,}}t)=0{\mbox{,}}\quad q(2L{\mbox{,}}t)=$$0{\mbox{.}}$

(4)

Figure 1. The schematic geometry of the problem.

Eqs. (1) and (2) are non-dimensionalized by introducing the following parameters:

${\begin{array}{ccccc}{\tilde {x}}={\frac {x}{2L}}{\mbox{,}}&{\overset {\sim }{T}}({\tilde {x}}{\mbox{,}}FO)={\frac {T(x{\mbox{,}}t)}{T_{0}}}{\mbox{,}}&{\alpha }_{0}={\frac {k_{0}}{\rho C_{p}}}{\mbox{,}}&c_{0}^{2}={\frac {{\alpha }_{0}}{{\tau }_{q}}}{\mbox{,}}&{Ve}^{2}={\frac {{\alpha }_{0}{\tau }_{q}}{L^{2}}}{\mbox{,}}\\FO={\frac {{\alpha }_{0}t}{2L^{2}}}{\mbox{,}}&{\tilde {q}}({\tilde {x}}{\mbox{,}}FO)={\frac {{\alpha }_{0}q(x{\mbox{,}}t)}{T_{0}k_{0}c_{0}}}{\mbox{,}}&\gamma =\lambda T_{0}{\mbox{,}}&{\tilde {g}}={\frac {4Lg}{\rho C_{p}T_{0}c_{0}}}{\mbox{,}}&\beta ={\frac {{\tau }_{T}}{{\tau }_{q}}}{\mbox{.}}\end{array}}$

(5)

The dimensionless form of Eqs. (1) and (2) is as follows:

$Ve{\frac {\partial {\overset {\sim }{T}}({\tilde {x}}{\mbox{,}}FO)}{\partial FO}}+$${\frac {\partial {\tilde {q}}({\tilde {x}}{\mbox{,}}FO)}{\partial {\tilde {x}}}}-$${\frac {\tilde {g}}{2}}=0$

(6)

$Ve{\frac {\partial {\tilde {q}}({\tilde {x}}{\mbox{,}}FO)}{\partial FO}}+$${\frac {2}{Ve}}{\tilde {q}}({\tilde {x}}{\mbox{,}}FO)+\left[1+\right.$$\left.\gamma {\overset {\sim }{T}}({\tilde {x}}{\mbox{,}}FO)\right]\left[{\frac {\partial {\overset {\sim }{T}}({\tilde {x}}{\mbox{,}}FO)}{\partial {\tilde {x}}}}+\right.$$\left.{\frac {\beta {Ve}^{2}}{2}}{\frac {{\partial }^{2}{\overset {\sim }{T}}({\tilde {x}}{\mbox{,}}FO)}{\partial FO\partial {\tilde {x}}}}\right]=$$0$

(7)

The dimensionless boundary and initial conditions are also as follows:

${\overset {\sim }{T}}({\tilde {x}}{\mbox{,}}0)=0.01sin\left({\frac {\pi {\tilde {x}}}{2}}\right){\mbox{,}}\quad {\tilde {q}}({\tilde {x}}{\mbox{,}}0)=$$0{\mbox{,}}\quad {\tilde {q}}(0{\mbox{,}}FO)=0{\mbox{,}}\quad {\tilde {q}}(1{\mbox{,}}FO)=$$0{\mbox{.}}$

(8)

The laser heat flux is considered as a heat source and it can be modeled as follows [29]:

${\tilde {g}}({\tilde {x}}{\mbox{,}}FO)=\left[g_{l}e^{-\mu {\tilde {x}}}+\right.$$\left.g_{r}e^{-\mu (1-{\tilde {x}})}\right]\left({\frac {FO}{t_{p}^{2}}}\right)e^{-{\frac {FO}{t_{p}}}}$

(9)

where g_l is dimensionless energy strength at the left boundary and g_r is dimensionless energy strength at the right boundary, μ is absorption coefficient and t_p is dimensionless energy pulse time.

3. The basic idea of ADM

Consider a general nonlinear differential equation in the following form:

$Lu+Ru+Nu=g$

(10)

where L is the highest-order invertible derivative. R is a linear differential operator with an order less than L, Nu includes the nonlinear terms, and g is the nonhomogeneous term. By applying the inverse operator L⁻¹ to both sides of Eq. (10) and using the given conditions, we have the following:

$u=-L^{-1}(Ru)-L^{-1}(Nu)+L^{-1}(g)$

(11)

For nonlinear differential equations, the nonlinear operator Nu = F(u) is expressed by an infinite series called the Adomian polynomials:

$F(u)=\sum _{m=0}^{\infty }A_{m}$

(12)

For A_m polynomials, A₀ depends only on u₀, A₁ depends only on u₀ and u₁, A₂ depends only on u₀, u₁, and u₂ and so on. ADM provides the solution as follows:

$u=\sum _{m=0}^{\infty }u_{m}$

(13)

For F(u), the infinite series is a Taylor series about u₀ as follows:

$F(u)=F(u_{0})+F^{'}(u_{0})(u-u_{0})+F^{''}(u_{0}){\frac {\left(u-u_{0}\right)}{2!}}+$$F^{'''}(u_{0}){\frac {{\left(u-u_{0}\right)}^{2}}{3!}}+\cdots$

(14)

By rewriting Eq. (13) in the form of ${\textstyle u-u_{0}=u_{1}+u_{2}+u_{3}+\cdots }$, and substituting in Eq. (14) and equating the two terms for F(u) in Eqs. (12) and (14), the relations for the Adomian polynomials are obtained in the following form:

$F(u)=A_{1}+A_{2}+\cdots =F(u_{0})+F^{'}(u_{0})(u_{1}+u_{2}+\cdots )+$$F^{''}(u_{0}){\frac {{\left(u_{1}+u_{2}+\cdots \right)}^{2}}{2!}}+$$\cdots$

(15)

By equating the terms of the above equation, the initial polynomials of the Adomian polynomials are obtained as follows:

$A_{0}=F(u_{0})$

(16)

$A_{1}=u_{1}F^{'}(u_{0})$

(17)

$A_{2}=u_{2}F^{'}(u_{0})+{\frac {1}{2!}}u_{1}^{2}F^{''}(u_{0})$

(18)

$A_{3}=u_{3}F^{'}(u_{0})+u_{1}u_{2}F^{''}(u_{0})+{\frac {1}{3!}}u_{1}^{3}F^{'''}(u_{0})$

(19)

$A_{4}=u_{4}F^{'}(u_{0})+\left({\frac {1}{2!}}u_{2}^{2}+u_{1}u_{3}\right)F^{''}(u_{0})+$${\frac {1}{2!}}u_{1}^{2}u_{2}F^{'''}(u_{0})+{\frac {1}{4!}}u_{1}^{4}F^{\left(iv\right)}(u_{0})$

(20)

Now that the (A_m) are obtained, the terms of Eq. (13) (i.e., the solution to the problem) are determined by inserting Eq. (12) into Eq. (11).

4. Application and modification of ADM

One of the shortcomings of semi-analytical methods, including ADM, in solving PDE is that they are unable to considering the boundary conditions in the solution process [30]. Therefore, ADM has to be improved so that it can include the boundary conditions, and consequently, obtain the correct solution. The method proposed by García-Olivares [31] for ADM improvement was used here. According to Eq. (10), Eqs. (6) and (7) can be rewritten as follows:

$L_{1}=-R_{1}+g$

(21)

$L_{2}=-R_{2}-N$

(22)

Then, the operators introduced in Eqs. (21) and (22) are as follows:

$L_{1}={\frac {\partial {\overset {\sim }{T}}({\tilde {x}}{\mbox{,}}FO)}{\partial FO}}{\mbox{,}}R_{1}=$${\frac {1}{Ve}}{\frac {\partial {\tilde {q}}({\tilde {x}}{\mbox{,}}FO)}{\partial {\tilde {x}}}}{\mbox{,}}g=$${\frac {1}{2Ve}}\left[g_{l}e^{-\mu {\tilde {x}}}+g_{r}e^{-\mu (1-{\tilde {x}})}\right]\left({\frac {FO}{t_{p}^{2}}}\right)e^{-{\frac {FO}{t_{p}}}}{\mbox{,}}$ $L_{2}={\frac {\partial {\tilde {q}}({\tilde {x}}{\mbox{,}}FO)}{\partial FO}}{\mbox{,}}R_{2}=$${\frac {2}{{Ve}^{2}}}{\tilde {q}}({\tilde {x}}{\mbox{,}}FO)+{\frac {1}{Ve}}{\frac {\partial {\overset {\sim }{T}}({\tilde {x}}{\mbox{,}}FO)}{\partial {\tilde {x}}}}+$${\frac {\beta Ve}{2}}{\frac {{\partial }^{2}{\overset {\sim }{T}}({\tilde {x}}{\mbox{,}}FO)}{\partial FO\partial {\tilde {x}}}}{\mbox{,}}$ $N={\frac {\gamma }{Ve}}{\overset {\sim }{T}}({\tilde {x}}{\mbox{,}}FO)\left[{\frac {\partial {\overset {\sim }{T}}({\tilde {x}}{\mbox{,}}FO)}{\partial {\tilde {x}}}}+\right.$$\left.{\frac {\beta {Ve}^{2}}{2}}{\frac {{\partial }^{2}{\overset {\sim }{T}}({\tilde {x}}{\mbox{,}}FO)}{\partial FO\partial {\tilde {x}}}}\right]{\mbox{.}}$

(23)

Once the given operators are determined, the values of ${\textstyle {\overset {\sim }{T}}({\tilde {x}}{\mbox{,}}FO)}$ and ${\textstyle {\tilde {q}}({\tilde {x}}{\mbox{,}}FO)}$ can be obtained according to Eq. (11). However, since the integration is performed in the FO direction, the boundary conditions are taken into account at any stage of the solution process which causes the solution to have errors compared to the accurate solution [30]. Therefore, the method proposed by García-Olivares [31] was then used to provide the solution.

Two perturbation functions were added to the initial conditions:

${\tilde {q}}^{_{\ast }}({\tilde {x}}{\mbox{,}}0)=p_{1}({\tilde {x}})$

(24)

${\overset {\sim }{T}}^{_{\ast }}({\tilde {x}}{\mbox{,}}0)=$$0.01sin\left({\frac {\pi {\tilde {x}}}{2}}\right)+p_{2}({\tilde {x}})$

(25)

Let the solution be in the form of ${\textstyle {\overset {\sim }{T}}={\overset {\sim }{T}}_{0}+{\overset {\sim }{T}}_{1}+}$${\overset {\sim }{T}}_{2}+\cdots$ and ${\textstyle {\tilde {q}}={\tilde {q}}_{0}+{\tilde {q}}_{1}+{\tilde {q}}_{2}+}$$\cdots$. Then, the functions ${\textstyle {\overset {\sim }{T}}_{0}}$ and ${\textstyle {\tilde {q}}_{0}}$ will be in the form of ${\textstyle {\tilde {q}}_{0}=p_{1}({\tilde {x}})}$ and ${\textstyle {\overset {\sim }{T}}_{0}=0.01sin(\pi {\tilde {x}}/2)+p_{2}({\tilde {x}})}$. The values of other terms are obtained successively using these two functions. Finally, the solution to the problem is obtained by summing up all the terms.

After obtaining the solution, the values of the function at the boundary are determined, e.g., ${\textstyle {\tilde {q}}^{_{\ast }}(0{\mbox{,}}FO)}$ and ${\textstyle {\overset {\sim }{T}}^{_{\ast }}(1{\mbox{,}}FO)}$. These values are certainly different from the boundary conditions of Eq. (8). The distance between the initial values and the new values has to be minimized at this stage. For this purpose, the distance between the new values and the values in Eq. (8) is defined as follows:

$d\left[{\tilde {q}}^{_{\ast }}(0{\mbox{,}}FO){\mbox{,}}{\tilde {q}}(0{\mbox{,}}FO)\right]=$${\int }_{0}^{1}{\left({\tilde {q}}^{_{\ast }}(0{\mbox{,}}FO)-{\tilde {q}}(0{\mbox{,}}FO)\right)}^{2}dFO$ $d\left[{\tilde {q}}^{_{\ast }}(1{\mbox{,}}FO){\mbox{,}}{\tilde {q}}(1{\mbox{,}}FO)\right]=$${\int }_{0}^{1}{\left({\tilde {q}}^{_{\ast }}(1{\mbox{,}}FO)-{\tilde {q}}(1{\mbox{,}}FO)\right)}^{2}dFO$ $d\left[{\tilde {q}}^{_{\ast }}({\tilde {x}}{\mbox{,}}0){\mbox{,}}{\tilde {q}}({\tilde {x}}{\mbox{,}}0)\right]=$${\int }_{0}^{1}p_{1}{\left({\tilde {x}}\right)}^{2}d{\tilde {x}}$ $d\left[{\overset {\sim }{T}}^{_{\ast }}({\tilde {x}}{\mbox{,}}0){\mbox{,}}{\overset {\sim }{T}}({\tilde {x}}{\mbox{,}}0)\right]=$${\int }_{0}^{1}p_{2}{\left({\tilde {x}}\right)}^{2}d{\tilde {x}}$

(26)

For the minimization problem, the bulk distance is now expressed as follows:

$d=d\left[{\tilde {q}}^{_{\ast }}(0{\mbox{,}}FO){\mbox{,}}{\tilde {q}}(0{\mbox{,}}FO)\right]+$$d\left[{\tilde {q}}^{_{\ast }}(1{\mbox{,}}FO){\mbox{,}}{\tilde {q}}(1{\mbox{,}}FO)\right]+$$d\left[{\tilde {q}}^{_{\ast }}({\tilde {x}}{\mbox{,}}0){\mbox{,}}{\tilde {q}}({\tilde {x}}{\mbox{,}}0)\right]+$$d\left[{\overset {\sim }{T}}^{_{\ast }}({\tilde {x}}{\mbox{,}}0){\mbox{,}}{\overset {\sim }{T}}({\tilde {x}}{\mbox{,}}0)\right]{\mbox{.}}$

(27)

To minimize the above expression, the forms of the perturbation functions ${\textstyle p_{1}({\tilde {x}})}$ and ${\textstyle p_{2}({\tilde {x}})}$ have to be known. The most common option is to select a polynomial form:

$p_{1}({\tilde {x}})=a_{0}+a_{1}{\tilde {x}}+a_{2}{\tilde {x}}^{2}+\cdots {\mbox{,}}\quad p_{2}({\tilde {x}})=$$b_{0}+b_{1}{\tilde {x}}+b_{2}{\tilde {x}}^{2}+\cdots$

(28)

Once the forms of the perturbation functions ${\textstyle p_{1}({\tilde {x}})}$ and ${\textstyle p_{2}({\tilde {x}})}$ are known, the coefficients ${\textstyle a_{0}{\mbox{,}}a_{1}{\mbox{,}}a_{2}{\mbox{,}}\ldots {\mbox{,}}b_{0}{\mbox{,}}b_{1}{\mbox{,}}b_{2}{\mbox{,}}\ldots }$ can be obtained through minimizing Eq. (27). Consequently, the values of perturbation functions ${\textstyle p_{1}({\tilde {x}})}$ and ${\textstyle p_{2}({\tilde {x}})}$ are obtained thereby yielding the problem solution, i.e. ${\textstyle {\overset {\sim }{T}}({\tilde {x}}{\mbox{,}}FO)}$ and ${\textstyle {\tilde {q}}({\tilde {x}}{\mbox{,}}FO)}$. All computations of mentioned process were calculated by Maple 15 package.

5. Results and discussion

To evaluate the accuracy of the obtained solution, the results were compared with the results of Lam [29], which is a linear analytical study (Fig. 2). Fig. 2 shows the temperature profile for two cases. Based on the conditions and parameters values of case 1, the bulk distance and the perturbation function coefficients and the dimensionless temperature function are as follows:

$d=0.00000244898149231{\mbox{,}}a_{0}=-0.001542779335579{\mbox{,}}a_{1}=$$0.02020571041553{\mbox{,}}$ $a_{2}=0.0252921158649449{\mbox{,}}a_{3}=-0.275753535197911{\mbox{,}}a_{4}=$$0.35863040092761{\mbox{,}}$ $a_{5}=-0.117845221675933{\mbox{,}}b_{0}=0.0008926043623460{\mbox{,}}b_{1}=$$0.009334213988682{\mbox{,}}$ $b_{2}=-0.005051864326525{\mbox{,}}b_{3}=-0.012580633028671{\mbox{,}}b_{4}=$$0.131409780625046{\mbox{,}}$ $b_{5}=-0.063327870215932.$

${\overset {\sim }{T}}({\tilde {x}}{\mbox{,}}FO)=(-500exp(-10+$$10{\tilde {x}}-100FO)-0.0001852317134exp(10{\tilde {x}}-$$100FO)$ $-504.08exp(-10{\tilde {x}}-100FO))FO+2\times {10}^{\left(-14\right)}exp(-$$10+10{\tilde {x}}-100FO)(-2.5\times {10}^{16}exp(-10+$$20{\tilde {x}})$ $-9.079985950\times {10}^{9}exp(20{\tilde {x}})-2.52\times {10}^{16})FO+$$0.01sin(\pi {\tilde {x}}/2)-20.10323640exp(-10+10{\tilde {x}}-$$100FO)$ $-0.000007513361496exp(10{\tilde {x}}-100FO)+(-0.003079929687-$$0.003771047093{\tilde {x}}^{2}$ $+1.25\times {10}^{\left(-7\right)}sin(0.5\pi {\tilde {x}}){\pi }^{4}+$$0.003070600247{\tilde {x}}-5.208333328\times {10}^{\left(-9\right)}sin(0.5\pi {\tilde {x}}){\pi }^{6}){FO}^{5}$ $+(0.01515384609+0.01284233263{\tilde {x}}-0.0388019220{\tilde {x}}^{2}+$$0.8012429018{\tilde {x}}^{3}-0.00125sin(0.5\pi {\tilde {x}}){\pi }^{2}$ $-0.5892261085{\tilde {x}}^{4}){FO}^{2}+(1.122163031{\tilde {x}}-$$1.191386191{\tilde {x}}^{2}+0.2670809671{\tilde {x}}^{3}-$$0.1964087028{\tilde {x}}^{4}$ $+0.00002604166665sin(0.5\pi {\tilde {x}}){\pi }^{4}-0.0004166666665sin(0.5\pi {\tilde {x}}){\pi }^{2}-$$0.1392924726){FO}^{4}$ $+(-0.1381420813-2.170138887\times {10}^{\left(-7\right)}sin(0.5\pi {\tilde {x}}){\pi }^{6}+$$0.00001041666666sin(0.5\pi {\tilde {x}}){\pi }^{4}$ $-0.00005555555553sin(0.5\pi {\tilde {x}}){\pi }^{2}+0.2564541244{\tilde {x}}-$$.3159784543{\tilde {x}}^{2}+0.03561079560{\tilde {x}}^{3}$ $-0.02618782703{\tilde {x}}^{4}){FO}^{6}+\cdots ({\mbox{many other terms}})$

Figure 2. Validation of ADM with a linear analytical study [29]. Case 1: gl = 10, gr = 10, tp = 0.001, μ = 10, β = 0.004, γ = 0, Ve = 1, FO = 0.3. Case 2: gl = 10, gr = 0, tp = 0.001, μ = 10, β = 0.004, γ = 0, Ve = 1, FO = 0.4.

As can be seen in the figures, there is a good agreement between the results of the analytical solution and the results obtained from ADM. Quantitatively, ADM has a 0.23% average error in case 1 and 0.2% average error in case 2 compared to the analytical solution. In both graphs, the behavior of ADM is consistent with the analytic solution.

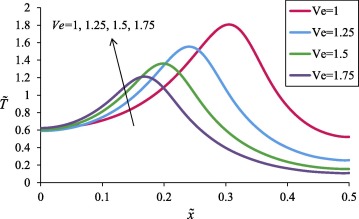
It should be noted that because of symmetry, only half of temperature profiles will be shown in next figures. Fig. 3 shows the effect of variations in the Vernotte number on the temperature profile. At the beginning of the body, variations in the Vernotte number did not significantly affect the temperature, but as ${\textstyle {\tilde {x}}}$ increased, an increased Vernotte number increased the temperature, and the diagrams moved apart. This behavior was reversed when the diagrams reached their peak. A deceased Vernotte number extended the temperature variation range and increased the amplitude, width, and velocity of the heat wave. A reduced Vernotte number formed stronger and faster wave; consequently, more parts of the body were affected by the wave. This behavior is due to the nature of the Vernotte number ${\textstyle \left(Ve={\frac {{\alpha }_{0}}{{Lc}_{0}}}\right)}$, where the thermal wave velocity is inversely related to the Vernotte number.

Figure 3. The effect of Vernotte number on temperature profiles. (gl = 10, gr = 10, tp = 0.01, μ = 10, β = 0.004, γ = 0.1, FO = 0.3).

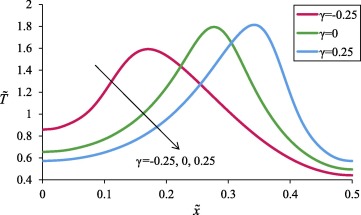
Fig. 4 shows the effect of variations in thermal conductivity coefficient (γ) on the temperature profiles. In the early parts of the body, an increased γ increased the temperature. The trend was reversed when temperature reached its peak. On the other hand, an increased γ increased both thermal wave velocity and the slope of the wave front. In fact, unlike Fig. 3, where the waveform did not change at different Vernotte numbers, in Fig. 4, an increase in γ caused the wave take a more aggressive form. In addition, the diagram showed lower maximum temperatures in the negative values of γ. Fig. 4 generally shows that to what extent the variations in the thermal conductivity with the temperature can affect the temperature profile.

Figure 4. The effect of γ on temperature profiles. (gl = 10, gr = 10, tp = 0.01, μ = 10, β = 0.004, Ve = 1, FO = 0.3).

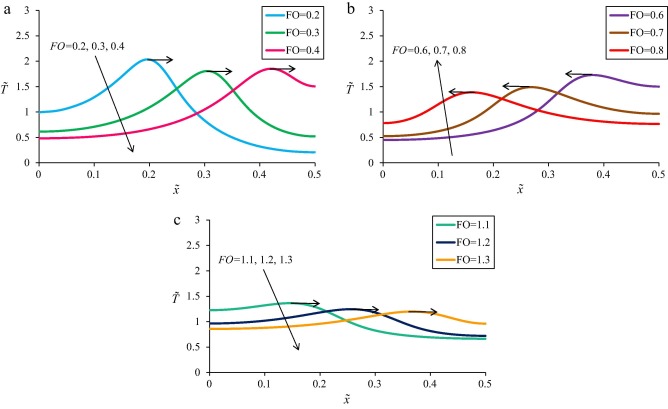
The effects of variations in the Fourier number on the temperature profile are shown in Fig. 5. As can be seen, temperature completely depended on the Fourier number. Since the Fourier number represents the dimensionless time, with increase in time (or the Fourier number), the heat wave continuously moved forward and reversed upon reaching the end point of the body and being reflected.

Figure 5. The effect of Fourier number on temperature profiles. (gl = 10, gr = 10, tp = 0.01, μ = 10, β = 0.004, Ve = 1, γ = 0.1).

In fact, Fig. 5 shows the position of a heat wave at different times. As time increased, the wave amplitude decreased, the peak point took lesser values, and the wave was gradually damped. The temperature throughout the body increased at the same time that the wave was being damped.

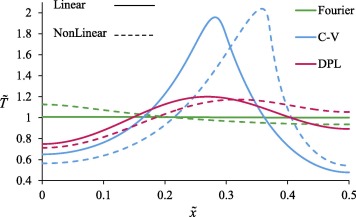
A comparison between different heat transfer models is made in Fig. 6, where the effects of variations in γ in the models are shown. Two values were considered for γ (linear case, i.e., γ = 0, and the nonlinear case, i.e., γ = 0.25). Different values of β yield different heat transfer models. For β = 0, we have the C–V non-Fourier heat transfer model; for β = 1, we have the Fourier heat transfer model; and for 0 < β < 1 we have the DPL model. As can be seen in Fig. 6, the effects of a non-constant thermal conductivity are more prominent in the non-Fourier models. As previously mentioned, non-Fourier models better predict the temperature distribution compared to the Fourier model in real-world applications. Therefore, when it is intended to use such models in order to obtain a more accurate temperature distribution, consideration of a variable thermal conductivity is essential, and a constant thermal conductivity coefficient creates significant errors.

Figure 6. The comparison between different models of heat transfer for linear (γ = 0) and nonlinear (γ = 0.25) cases. (gl = 10, gr = 10, tp = 0.01, μ = 10, Ve = 1, FO = 0.3, Fourier: β = 1, C–V: β = 0, DPL: β = 0.1).

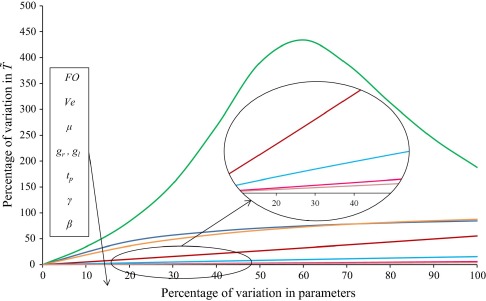
In this section, the sensitivity of the midpoint temperature (${\textstyle {\tilde {x}}}$ = 0.5) to the variations in different parameters in the problem was analyzed. Fig. 7 shows the percentage changes in temperature versus the percentage changes in different parameters. In fact, it indicates that how and to what extent (in percent) the dimensionless midpoint temperature changed when the value of a parameter was changed from its reference value. Variations in the Fourier number had the greatest effect on the temperature, with its effectiveness being much higher than other parameters. After the Fourier number, variations in the Vernotte number had greatest effect on the temperature, followed by the parameters related to the heat source. Finally, γ and β had the least effect. It is noteworthy that only the midpoint of the body was considered here, while, as seen in Fig. 4, variations in γ significantly affected the temperature throughout the body.

Figure 7. Sensitivity analysis of the dimensionless temperature with respect to different parameters. The reference values of parameters: (gl = 10, gr = 10, tp = 0.01, μ = 10, β = 0.004, Ve = 1, γ = 0.1, FO = 0.3).

6. Conclusion

The present study investigated heat transfer problem in a thin film. The Dual Phase Lagging (DPL) heat conduction model was employed for this purpose. Thermal conductivity was assumed temperature-dependent which resulted in a nonlinear equation. The modified semi-analytical Adomian Decomposition Method was used for solving the equations. Results are summarized as follows:

• It was concluded that the modified ADM used in this paper had a suitable accuracy in solving nonlinear PDE problems considering non-Fourier heat transfer.
• It was observed that a reduced Vernotte number increased the velocity, amplitude, and width of the heat wave.
• The assumption of temperature-dependent thermal conductivity caused significant differences in temperature profiles which makes nonlinear analysis important. Particularly, the difference was much more evident in the non-Fourier models.
• The Fourier and Vernotte numbers had the greatest effect on the temperature variations; therefore, dimensionless numbers significantly affected the analysis of non-Fourier heat transfer problems.

References

1. [1] J. Fourier; Analytical Theory of Heat; Dover, New York (1955)
2. [2] V. Peshkov; Second sound in Helium II; J. Phys., USSR, 3 (1944), p. 381
3. [3] R. Shirmohammadi; Thermal response of microparticles due to laser pulse heating; Nanoscale Microscale Thermophys. Eng., 15 (3) (2011), pp. 151–164
4. [4] M.M. Tung, M. Trujillo, J.A. López Molina, M.J. Rivera, E.J. Berjano; Modeling the heating of biological tissue based on the hyperbolic heat transfer equation; Math. Comput. Model., 50 (5–6) (2009), pp. 665–672
5. [5] C. Catteneo; A form of heat conduction equation which eliminates the paradox of instantaneous propagation; Comput. Rendus, 247 (1958), pp. 431–433
6. [6] P. Vernotte; Some possible complications in the phenomenon of thermal conduction; Comput. Rendus, 252 (1961), pp. 2190–2191
7. [7] D.Y. Tzou; A unified field approach for heat conduction from macro- to micro-scales; J. Heat Transfer, 117 (1) (1995), pp. 8–16
8. [8] D.Y. Tzou; Experimental support for the lagging behavior in heat propagation; J. Thermophys. Heat Transfer, 9 (4) (1995), pp. 686–693
9. [9] K. Liu, H. Chen; Investigation for the dual phase lag behavior of bio-heat transfer; Int. J. Therm. Sci., 49 (7) (2010), pp. 1138–1146
10. [10] D.D. Joseph, L. Preziosi; Heat waves; Rev. Mod. Phys., 61 (1) (1989), pp. 41–73
11. [11] M.N. Özişik, D.Y. Tzou; On the wave theory in heat conduction; J. Heat Transfer, 116 (3) (1994), pp. 526–535
12. [12] G. Adomian; Stochastic Systems; Academic Press, New York (1983)
13. [13] J. He; An approximate solution technique depending on an artificial parameter: a special example; Commun. Nonlinear Sci. Numer. Simul., 3 (2) (1998), pp. 92–97
14. [14] J. He; Newton-like iteration method for solving algebraic equations; Commun. Nonlinear Sci. Numer. Simul., 3 (2) (1998), pp. 106–109
15. [15] S.J. Liao; The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems; Tong University (1992)
16. [16] J.K. Zhou; Differential Transform and Its Applications for Electrical Circuits; Huarjung University Press (1986)
17. [17] J. He; Variational iteration method—a kind of non-linear analytical technique: some examples; Int. J. Nonlinear Mech., 34 (1999), pp. 699–708
18. [18] D.D. Ganji, A. Rajabi; Assessment of homotopy – perturbation and perturbation methods in heat radiation equations; Int. Commun. Heat Mass Transfer, 33 (2006), pp. 391–400
19. [19] D.D. Ganji; The application of He’s homotopy perturbation method to nonlinear equations arising in heat transfer; Phys. Lett. A, 355 (4–5) (2006), pp. 337–341
20. [20] D.D. Ganji, A. Sadighi; Application of homotopy-perturbation and variational iteration methods to nonlinear heat transfer and porous media equations; J. Comput. Appl. Math., 207 (2007), pp. 24–34
21. [21] S. Chakraverty, D. Behera; Dynamic responses of fractionally damped mechanical system using homotopy perturbation method; Alexandria Eng. J., 52 (3) (2013), pp. 557–562
22. [22] V. Meena, K. Indira, S. Kumar, L. Rajendran; A new mathematical model for effectiveness factors in biofilm under toxic conditions; Alexandria Eng. J., 53 (4) (2014), pp. 917–928
23. [23] S. Gupta, D. Kumar, J. Singh; Analytical solutions of convection–diffusion problems by combining Laplace transform method and homotopy perturbation method; Alexandria Eng. J., 54 (3) (2015), pp. 645–651
24. [24] S. Nadeem, H. Sadaf, N.S. Akbar; Effects of nanoparticles on the peristaltic motion of tangent hyperbolic fluid model in an annulus; Alexandria Eng. J., 54 (4) (2015), pp. 843–851
25. [25] M. Torabi, H. Yaghoobi, S. Saedodin; Assessment of homotopy perturbation method in non-linear convective-radiative non-fourier conduction; Therm. Sci., 15 (2011), pp. 263–274
26. [26] S. Saedodin, H. Yaghoobi, M. Torabi; Application of the variational iteration method to nonlinear non-Fourier conduction heat transfer equation with variable coefficient; Heat Transfer—Asian Res., 40 (6) (2011), pp. 513–523
27. [27] M. Torabi, H. Yaghoobi, K. Boubaker; Thermal analysis of non-linear convective – radiative hyperbolic lumped systems with simultaneous variation of temperature-dependent specific heat and surface emissivity by MsDTM and BPES; Int. J. Thermophys., 34 (1) (2013), pp. 122–138
28. [28] P. Malekzadeh, H. Rahideh; IDQ two-dimensional nonlinear transient heat transfer analysis of variable section annular fins; Energy Convers. Manag., 48 (1) (2007), pp. 269–276
29. [29] T.T. Lam; A unified solution of several heat conduction models; Int. J. Heat Mass Transfer, 56 (1–2) (2013), pp. 653–666
30. [30] J. Biazar, M.R. Islam; The adomian decomposition method for the solution of the transient energy equation in rocks subjected to laser irradiation; Iran. J. Sci. Technol. Trans. A, 30 (A2) (2006), pp. 201–212
31. [31] A. García-Olivares; Analytic solution of partial differential equations with Adomian’s decomposition; Kybernetes, 32 (3) (2003), pp. 354–368