Double criterion optimisation of transparent façades based on solar thermalprocesses

Abstract

This work aimed to find the best possible solution for transparent façades. The evaluation was formulated to assure the highest user comfort criteria corresponding to energy efficiency—two criterion optimisation. The analyses were based on BESTEST, south-oriented zone geometry. Computer model was designed using Finite Control Volume Techniques with assumptions for applied materials and specified boundary conditions, plus reference year for energy calculation (WYEC2). The natural ventilation façade system was designed to determine airflow network inside the façade. The adjustable size of openings (inlets and outlets) was selected at the level of 80% for the cold season and totally closed during the hot season. Environmental parameters for thermal comfort evaluation were: zone resultant temperature and solar radiation in zone space. Energy efficiency was assessed based on heat flux between the zone with controlled temperature and external environment. Results showed that well selected design of buffer zone section could improve energy efficiency of adjacent zones for both winter and summer periods. The most profitable Double Skin Façade solution is DGC (double glazing with low-e coating) combined with single glazing with internal blinds (SGB) or coloured glazing.

Keywords

Optimisation ; Solar radiation ; Energy ; Thermal comfort ; Double skin facade ; Glazing

1. Introduction

Solar thermal processes in transparent elements exposed to solar radiation are relatively easy to evaluate for single layer components and become complicated for multilayer structures. Different methods for calculating spectral properties of composites have been developed and presented (Jonsson, 2009 ; Liu and Jordan, 1960  ;  Roos et al ., 2000 ). Intensity of solar energy conversion into heat depends on specific thermophysical and optical properties. Commonly used solutions for controlling solar heat gains are based on thermo-, photo- and electro-chromic glazing systems, or the more traditional shading systems. In some cases, coloured glazing seems to be useful.

During last two decades, the use of double skin façade (DSF) in buildings located in moderate climatic conditions has been thoroughly investigated (Gertis, 1999  ;  Saelens and Hens, 2003 ). More recent experiments have been carried out (Gavan et al ., 2007  ;  Serra et al ., 2009 ) to study the energy aspects of DSF application. Such application is beset by this main problem, overheating during summer, due to the very low thermal mass of metal/glass construction Heim (2006) . DSF opponents argue that, during winter, similar insulation effect could be obtained for low-e double glazing windows, which is more cost-effective. Despite this problem, it is necessary to make good use of the advantages of DSF application. An important solution is to create natural buffer space between the zone with controlled temperature and the external environment. Additional facade equipment, e.g., shading devices, can shield the building from external elements, such as wind, snow, rain, etc. Still, the most important benefit is the improvement of thermal comfort parameters inside the building. In this paper, a formulation of double objective optimisation of DSF is presented.

2. Physical processes in DSF

Double glass curtain exposed to solar radiation and separating two zones with different temperatures is a complex system from physical point of view. The intensity of thermophysical processes obtaining in a DSF depends on climatic conditions and parameters of indoor heating/cooling control system. These three weather parameters should be taken into account: solar radiation, air temperature, and wind speed. Solar radiation affects the intensity of photothermal conversion in facade and adjacent zone. Air temperature determines the magnitude of heat flux between the façade and external environment and vicariously the heat flux from zone space. The wind speed is responsible for infiltration and mass flow in the façade. These weather parameters and thermophysical processes have an indirect effect on thermal comfort and energy efficiency of the whole building.

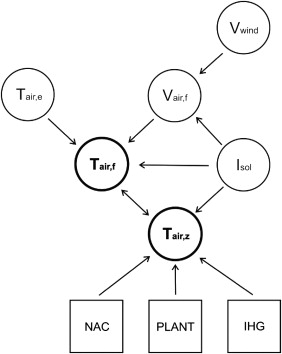
Heat exchange between solid volumes (walls) and air volume (inter-space), as well as heat storage potential, play a significant role in energy balance and in determining thermal comfort parameters. The energy flowpath between external environment (e ), facade space (f ) and zone with controlled temperature (z ) is presented in Figure 1 . The following symbols are used:

• T_air —air temperature,
• V_air —air flowspeed,
• V_air —wind speed,
• I_sol —solar radiation,
• NAC—number of air changes, heat flux lost by ventilation,
• PLANT—heat flux from heating system,
• IHG—heat flux from internal heatgains.

Figure 1. DSF energy flowpath.

In this study, the effect of occupancy (number of air changes and internal heat gains) and heating system (the heat flux from the system) is omitted. The following assumptions are used for this:

• air changes per hour is 0ac/h,
• internal heat gains is 0 W,
• air temperature in zone changes between 20 °C–26 °C between 8:00 and 16:00, 18 °C and 28 °C between 16:00 and 8:00.

Furthermore, the temperature is selected as a parameter for double objective optimisation, including energy efficiency and thermal comfort. For the purpose of task formulation, the following temperatures are considered:

• T_air —air temperature (dry bulb temperature),
• T_surf —surface temperature,
• T_mrt —mean radiant temperature,
• T_res —resultant temperature.

The interrelations between these temperatures with coefficients describing heat exchange are presented in Figure 2 .

Interrelations between temperatures.

Figure 2. Interrelations between temperatures.

Mean radiant temperature is calculated using the following formula (Sars et al., 1988 ):

$T_{mrt}={\frac {{\Sigma }_{i=1}^{n}T_{surf,i}\quad {\epsilon }_{surf,i}\quad A_{i}}{{\Sigma }_{i=1}^{n}A_{i}}}$

( 1)

where T_surf ,_i is the temperature of surface i , A_i is the area of surface i .

Resultant temperature is defined (Clarke 2001 ) as follows:

$T_{res}=0,5(T_{mrt}+T_{air})$

( 2)

3. Optimisation criteria for thermal behaviour of DSF

Assuming that glass components will still be popular among architects, then finding an optimal DSF solution remains a big challenge for experts.

An optimal solution of inter-space between outer and inner parts of a building envelope is well described for some certain energy applications. These thermal problems are associated with double façades: (1) considerable temperature fluctuation between day and night, and (2) temporary overheating or overcooling effects in facade. To reduce these effects and sustain stable thermal conditions in the inner part of the façade, shading devices with proper control mechanism are generally applied (Belgian Building Research Institute, 2002 ; Gratia and DeHerde, 2004a  ;  Gratia and DeHerde, 2004b ). However, the main question is what should be the best solution for buffer space in the context of geometry, construction (glazing properties) and control of internal parameters under different environmental conditions. In places with moderate climate, the weather exhibits some extreme conditions in the middle of summer or winter. Meanwhile, the temperature usually varies from −25 °C (winter) to +25 °C (summer) with different daily fluctuations depending on locations, altitude, or local conditions.

4. Formulation of optimisation task

4.1. Energy

The first criterion of DSF optimisation is minimum energy delivered to adjacent zone of controlled indoor air temperature. For assumed geometry of zone and façade (including ratio between transparent and opaque elements) and constant material thermophysical properties, the criterion of optimisation will be energy balance between zone and external environment, as a minimum of total heat flux between zone and façade in a day:

$f_{1}({\overline {X}})={\int }_{0}^{24}\left(\sum _{m=1}^{x_{1}}\sum _{n=1}^{x_{2}}q_{m,n}\right)d\tau$

( 3)

and a minimum of temperature difference of surfaces in a partition between zone and façade:

$f_{2}({\overline {X}})=\sum _{m=1}^{x_{1}}\sum _{n=1}^{x_{2}}\delta T_{surf\quad m,n}$

( 4)

where

$\Delta T_{surf}=(T_{surf},z-T_{surf,f})$

and

• (x₁ ) type of construction between zone and façade,
• (x₂ ) number of partition between zone and façade.

Decision variables (x₁ , x₂ ) are discrete and limited as follows:

• construction type is unambiguously defined as:

$x_{1}\in \left\{1,2\right\}$

where 1is transparent construction and 2is opaque construction.

• there is at least one partition between zone and facade,

$x_{2}\geq 1$

4.2. Thermal comfort

The second criterion of DSF optimisation is defined based on required values of temperatures, resultant and mean radiant. For the space (zone) built with a number of surfaces, the criterion will be the resultant and mean radiant temperatures defined below. For resultant temperature, the minimum of temperature differences:

$f_{3}({\overline {X}})=\sum _{m=1}^{x_{1}}\sum _{n=1}^{x_{2}}{\vert T_{res}-T_{air}\vert }_{m,n}$

( 5)

with the following limitation:

9 °C≤T_res ≤23°C

and for mean radiant temperature:

$f_{4}({\overline {X}})=\sum _{m=1}^{x_{1}}\sum _{n=1}^{x_{2}}{\vert T_{mrt}-T_{air}\vert }_{m,n}$

( 6)

with the following limitation:

−5 K≤(T_mrt −T_air )≤8 K

Both limitations were formulated based on CIBSE (1986) .

Decision variables (x₁ ), (x₂ ) are the same asabove.

5. Case study—optimised solution for solar energy conversion

All simulations were performed using worked out weather data, based on local data from meteorological station, and prepared in accordance with WYEC standards. The simulations covered the entire calendar year. One hour time step was assumed for the analysis of heat and massflow.

Thermal model of the building was created using a finite-volume heat balance discretisation method. Elements of building structures, zones, and surface areas were presented by the nodes – one node for each internal enclosed space, and three nodes for each homogeneous layer. The influence of solar radiation was considered by way of direct solar-tracking processor combined with the distribution of diffused radiation (Clarke, 2001 ). The airflow was modelled applying one-dimensional nodal airflow network (AFN) method in accordance with the principle of conservation mass law (Patankar, 1980 ). More detailed information about the difference between AFN and CFD modelling of DSF is presented in Samuel and Hand (2007 ).

5.1. Geometry

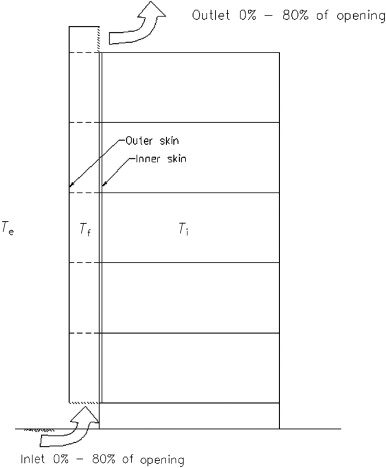
The area of façade was divided into a number of zones represented by the nodes and connected to create a set of flow paths. Two external nodes were assigned to inlet and outlet, and one internal node for each façade zone. Nodes were connected by components with a set of specified linkages. Zone was defined based on geometric assumptions of BESTEST Case 600 model (8 m×6 m×2.7 m) with additional façade at depth of 1.0 m.

The vertical cross section is presented in Figure 3 .

Figure 3. Cross section of analysed façade.

5.2. Construction

Table 1 lists the types of glazing systems and combinations were considered using simulation techniques. Different types of single or double glazing were assumed for inner (in) partition between zone and facade, and were combined with selected glazing on outer skin (out). Full descriptions of the symbols are presented in Table 2 . All physical parameters of glazing come from ESP-r database.

Table 1. Analysed glazing systems.

In	Out
	SG	DG	DGC	SGB	SGG	SGW	SGY
SG	×	×		×		×
DG	×	×		×
DGC	×			×		×
SGB	×
DGG	×
DGW	×
DGY	×

Table 2. Description of symbols.

Symbol	Description
SG	Single glazing
DG	Double glazing
DGC	Double glazing low-e coating
SGB	Single glazing with internal blinds
DGG	Double anti sun glazing—green
DGW	Double anti sun glazing—brown
DGY	Double anti sun glazing—grey

6. Simulation results

Results are from a whole year work-out according to WYEC2 standards. For better presentation, statistics of temperature differences characterised for both optimisation criteria were worked out. Additionally, for some extreme cases, the time history for the characteristic period is presented.

Table 3 shows the values of arithmetic mean (AM) and standard deviation (SD) for the following temperature differences:

• T_surf,z −T_surf,f
• |T_res −T_air |
• |T_mrt −T_air |

Table 3. Statistical results.

In–Out	Tsurf,z –Tsurf ,f		|Tres –Tair |		|Tmrt –Tair |
	AM	SD	AM	SD	AM	SD
SG–SG	0.130	0.069	1.672	1.459	0.836	0.730
DG–SG	3.162	1.665	1.669	1.478	0.834	0.739
DGC–SG	6.575	3.455	1.893	1.646	0.946	0.823
SGB–SG	0.131	0.070	1.749	1.525	0.874	0.762
DGG–SG	3.770	1.547	1.748	1.573	0.874	0.787
DGW–SG	3.514	1.530	1.709	1.538	0.854	0.769
DGY–SG	3.560	1.537	1.696	1.527	0.848	0.763
SG–DG	0.114	0.073	1.694	1.560	0.847	0.780
DG–DG	2.967	1.851	1.720	1.547	0.860	0.774
SG–SGB	0.161	0.112	1.224	1.006	0.612	0.503
DG–SGB	3.728	2.418	1.124	0.889	0.562	0.445
DGC–SGB	7.421	4.306	1.182	0.992	0.591	0.496
SG–SGW	0.137	0.121	1.200	1.097	0.600	0.548
DGC–SGW	6.484	4.873	0.934	0.854	0.467	0.427

Comparison of the surface temperature differences showed that, for the one-year period, the arithmetic mean varied from 0.130 to 7.421. The lowest values were obtained for inner skin with single glazed components. The highest arithmetic mean was obtained for double glazed outer skin with low emissivity coating. Arithmetic mean for the differences between resultant and air temperature was similar for all analysed cases. The lowest and highest values were derived for cases with double, low-e glazing on external surface. It means that the final results depend on construction of internal skin. Lower values of surface temperature differences were reported for coloured glass types. Similar relations are reported for differences between mean radiant and air temperature.

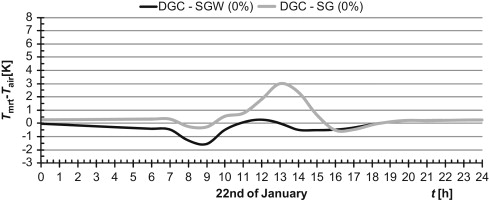
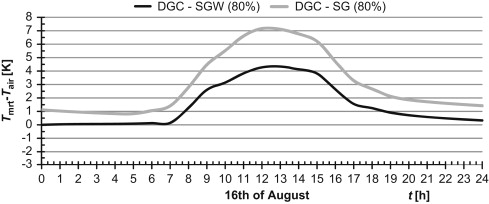
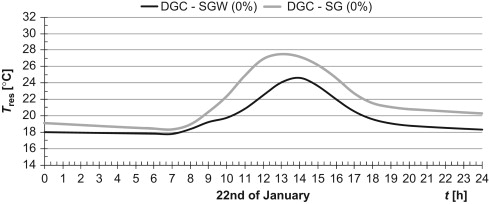
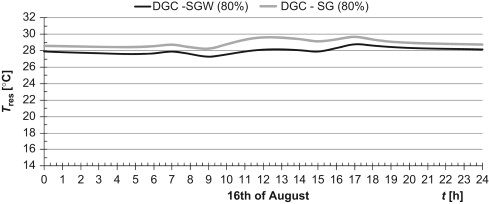
Exemplar results of resultant temperature and temperature differences for two extreme cases (DGC-SGW & DGC-SG) are presented (Figure 4 , Figure 5 , Figure 6  ;  Figure 7 ); these are for selected coldest and warmest days in a year. Differences between mean radiant and air temperature did not exceed 7 K for both analysed days. It means that such kind of construction meets CIBSE recommendation. Less promising results were obtained for resultant temperature (Figure 6  ;  Figure 7 ). In summer and, periodically also in winter, temperature exceeded 23 °C, achieving a level of 28–30 °C.

Figure 4. Differences between mean resultant temperature and air temperature for the coldest day in ayear.

Figure 5. Differences between mean resultant temperature and air temperature for the warmest day in ayear.

Figure 6. Resultant temperature for the coldest day in ayear.

Figure 7. Resultant temperature for the warmest day in ayear.

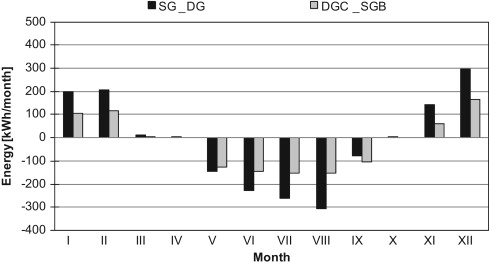
Finally, the energy balance for selected types of glazing configurations was analysed. Results showed that for March, April, and October, the monthly energy requirements for heating/cooling were almost zero. For the rest of the year, the more promising results were obtained for the case with lowest thermal transmittance (Figure 8 ).

Figure 8. Monthly energy demands for heating and cooling.

7. Conclusion

This study is an initial step towards multi-criterion optimisation of building façade.

An optimisation approach was presented and the main assumptions for zone temperatures (i.e., air, resultant, mean radiant, and surfaces) were described.

Regarding heat transmission through façade, the best results were obtained for single glazed inner curtain and double glazed outer curtain. The effect on comfort level in a zone was not significant and, for all cases, relatively high values of resultant temperatures were obtained. It is recommended that inner partition should be built using coloured glass for better absorption of solar radiation.

Acknowledgements

Funding for this Research Project (2059/B/T02/2011/40 ) comes from the state budget funds (2011–2013) .

References

1. Belgian Building Research Institute, 2002 Belgian Building Research Institute, 2002. Source book for better understanding of conceptual and operational aspects of active facades. Department of Building Physics, Indoor Climate and Building Services, BBRI. Version 1.
2. CIBSE, 1986 CIBSE: CIBSE Guide, Volume A, Design Data, 1986.
3. Clarke, 2001 J.A. Clarke; Energy Simulation in Building Design; (2nd edition)Butterworth-Heinemann, Oxford (2001)
4. Gavan et al., 2007 Gavan, V., Woloszyn, M., Roux, J-J., Muresan, C., Safer, N., 2007. An investigation into the effect of ventilated double-skin facade with venetian blinds: global simulation and assessment of energy performance, Proceedings of the X BS Conference, 127–133.
5. Gertis, 1999 Gertis, K., 1999. New façade developments—do they make sense from a building physics point of view? Part 2: Glass Double Façades, Bauphysik 2, 54–66 (in German).
6. Gratia and DeHerde, 2004a E. Gratia, A. DeHerde; Optimal operation of a south double-skin facade; Energy and Buildings, 36 (2004), pp. 41–60
7. Gratia and DeHerde, 2004b E. Gratia, A. DeHerde; Natural ventilation in double-skin façade; Energy and Buildings, 36 (2004), pp. 137–146
8. Heim, 2006 Heim, D., 2006. Comparison of sensible and latent thermal storage potential of double-skin façade, Research in Building Physics and Building Engineering, Taylor & Francis Publishers, 301–309.
9. Jonsson, 2009 A. Jonsson; Optical Characterization and Energy Simulation of Glazing for High-Performance Windows; Uppsala Universitet (2009)
10. Liu and Jordan, 1960 B.Y. Liu, R.C. Jordan; The interrelationship and characteristic distribution of direct, diffuse and total solar radiations; Solar Energy, 4 (3)) (1960), pp. 1–19
11. Patankar, 1980 S.V. Patankar; Numerical Heat Transfer and Fluid Flow; Hemisphere, Washington D.C. (1980)
12. Roos et al., 2000 A. Roos, P. Polato, P. van Nijnatten, M.G. Hutchins, F. Olive, C.H. Anderson; Angular-dependent optical properties of low-e and solar control windows—simulation versus measurements; Solar Energy, 69 (2000), pp. 15–26
13. Saelens and Hens, 2003 D. Saelens, H. Hens; Comparison of the Energy Demand of Multiple-Skin Façade. Research in Building Physics; J. Carmeliet, H. Hens, G Vermeir (Eds.)Balkema Publishers (2003), pp. 503–511
14. Samuel and Hand, 2007 Samuel, A., Hand, J., 2007. CFD assessments within strongly transient domains, Proceedings of the X IBPSA Conference BS 2007, Beijing, 945–951.
15. Sars et al., 1988 Sars, G., Pernot, C., De Wit, M., 1988. ESPmrt, A New Module for the ESP-System, Eindhoven University of Technology, Eindhoven.
16. Serra et al., 2009 V. Serra, F. Zanghirella, M. Perino; Experimental Energy Efficiency Assessment of a Hybrid Ventilated Transparent Façade. Energy Efficiency and New Approaches; Istanbul Technical University (2009)