Abstract
Nowadays, investors, customers, and even suppliers focus on the bankability of photovoltaic (PV) technologies. However, few studies have investigated the annual net effect of solar spectrum. In this study, we estimate the net effect of the solar spectrum on the annual energy yield of c-Si and a-Si modules by two parameters. One parameter is a direct calculation from spectral factor (SF). The other parameter uses average photon energy (APE) and a regression line or curve. The estimations by the two parameters are quite consistent, whereas there is 1.2% difference between the estimations at most. Therefore, APE would be a useful index to quantify the effect of the solar spectrum.
Introduction
The installation of photovoltaic (PV) power generation systems has shown high growth rates in recent years. The European Photovoltaic Industry Association (EPIA) [1] has reported that global Solar PV installations reached 29.7 GW in 2011. The rapid growth of the PV markets results in a decrease in the cost of solar electricity. Nowadays, investors, customers, and even suppliers focus on the bankability of PV technologies. In order to determine the bankability of solar PV projects, it is required to estimate the annual energy yield with accuracy and precision. The dominant factors, which influence the energy yield of PV modules, are solar irradiation, module temperature, and solar spectrum. However, few studies have investigated the net effect of solar spectrum on the annual energy yield of PV modules, because there would be few data sets of solar spectrum that cover a whole year.
The effect of solar spectrum is in particular sensitive to solar cells with narrow spectral response ranges, such as hydrogenated amorphous silicon (a-Si) solar cells, organic solar cells (OSC), and dye-sensitized solar cells (DSSC). The shapes of spectral responses are slightly different among the same kind of solar cells, because of differences in film thickness, amount of impurity or dopant, encapsulation, manufacturing process, etc. Furthermore, the shape of the spectral response of a given technology may be influenced by temperature, irradiance intensity, and voltage [2-4]. However, restrained variations in the spectral response (particularly if related to a scaling factor) should result in little change in the spectral factor (SF) or mismatch factor (MMF), because not the absolute but the relative spectral response is used to calculate these parameters. These parameters are defined in the following section according to IEC 60904-7 and IEC 61853-3 [5, 6]. Eventually, if the conversion efficiency of a solar cell were enhanced to the upper limit, the shape of the spectral response would be likely to converge on the ideal shape. Recently, seasonal performance variations due to the impact of solar spectrum have been actively investigated in European countries [7-11].
In this study, we use the spectral responses of a c-Si and a-Si single-junction device and assume them to be representative for these two technologies. The relative spectral responses of a crystalline silicon (c-Si) module and an a-Si module are used in this study. The purpose of this study is to investigate the impact of the solar spectrum on the annual energy yield of these technologies by using two parameters. One parameter uses SF or MMF, which is an index indicating the ratio of available solar irradiance between an actual solar spectrum and the standard AM1.5G spectrum [11-21]. The other parameter uses average photon energy (APE). APE is the average energy of the photons included in a solar spectrum, indicating that the solar spectrum is “blue-rich” or “red-rich” [22-30]. Theoretically, APE would not be a unique characteristic of solar spectrum, because the shape of the solar spectrum could be complexly changed by solar altitude and atmospheric conditions such as air mass (AM), aerosol optical depth (AOD), and the amount of precipitable water (PW) [31, 32]. Therefore, we investigate the relationship between these two parameters (SF, APE) for the above mentioned technologies. The regression line or curve of SF on APE is calculated by the least-squares method. If there is a general relationship between these two parameters, the influence of the solar spectrum on the energy yield of the above mentioned technologies can be evaluated using only APE simply and easily.
Experimental Methods
The solar spectrum at the optimum tilt angle for south-facing solar panels has been measured by Japan Weather Association (JWA) since 2008 at four locations in Japan: ST01 (Sapporo), ST02 (Tosu), ST04 (Gifu), and ST05 (Okinoerabu), as shown in Figure 1. The optimum tilt angles are 36°, 26°, 32°, and 22°, respectively. In addition, other meteorological parameters have been monitored in parallel, including both in-plane and horizontal global solar irradiance and solar spectrum, direct solar irradiance, ambient temperature, humidity, wind direction, and velocity. The measurement and data collection systems were compiled by CLIMATEC Inc., Japan. The measurement system at the Tsukuba Center of National Institute of Advanced Industrial Science and Technology (AIST) shown in Figure 2 has been installed in year 2011 only. We investigate the solar spectra measured at the optimum tilt angle at four stations except ST03 (TKB) for 3 years from 2008 to 2010.
|
|
|
Figure 1. Five locations where the various meteorological parameters have been measured by Japan Weather Association (JWA). |
|
|
|
Figure 2. Meteorological measurement station (ST03) at Advanced Industrial Science and Technology (AIST) Tsukuba Center. |
Solar spectra have been measured using a spectroradiometer with two measuring heads of MS-710 and MS-712 (EKO Instruments Co. Ltd., Japan), which cover the wavelength ranges from 350 to 900 nm and from 900 to 1700 nm, respectively. The measurement interval is one minute. In order to classify the solar spectra by irradiance intensity, we introduce integrated spectral irradiance (ISI) W/m2, which is given by,
|
|
(1) |
where E is the spectral irradiance and λ is the wavelength. The solar spectra were classified by ISI into four categories indicated in the legends of Figure 3. APE is given as follows:
|
|
(2) |
|
|
|
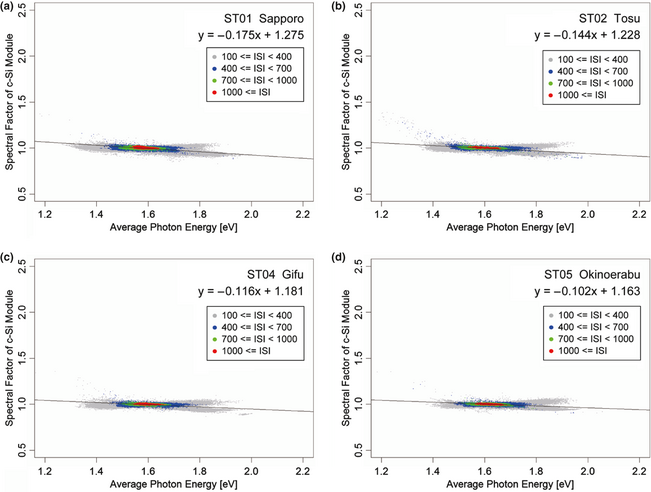
Figure 3. Relationship between average photon energy (APE) and spectral factor (SF) of the c-Si photovoltaic (PV) module at each site. The solid lines indicate the regression lines calculated by the least-squares method. |
where qe is the electronic charge and Φ is the photon flux density. It should be noted that APE is different from the integrated wavelength range. The APE of the standard AM1.5G spectrum in the range between 350 and 1700 nm is approximately 1.59 eV. APE expressed in the unit of electronvolt can be also expressed as effective wavelength (λeff) in the unit of wavelength [28, 31]. SF or MMF is given by the following:
|
|
(3) |
where SR is the relative spectral response and EAM1.5G is the standard AM1.5G spectrum [33]. The number of the analyzed solar spectra is more than 700 thousand in each location.
In order to estimate the effect of the solar spectrum on the energy yield of the PV modules, we introduce effective solar irradiance (Geff), which is solar irradiance corrected by the effect of the solar spectrum. Geff is given by the following:
|
|
(4) |
where G is the solar irradiance measured by a pyranometer (EKO/MS-802) at each site. Geff indicates G corrected by the ratio of available energy in the measured solar spectrum to available energy in the AM1.5G spectrum for a technology. The calculation is conducted for the data set in 2008, when the number of missing values is smallest among 3 years. We have confirmed that the tendency of the results is common among 3 years.
The manufacturer (personal communication) suggests that the measurement uncertainty of the spectroradiometers is approximately ±13% between 350 nm and 450 nm, ±5% from 450 nm to 1600 nm, and ±24% between 1600 nm and 1700 nm. The dominant source of the large uncertainty between 350 nm and 450 nm is stray light. Both stray light and measurement repeatability enlarge the uncertainty between 1600 nm and 1700 nm. Improvement of the uncertainty should be expected for the manufacturer. The pyranometer used in this investigation is classified in “secondary standard.” Therefore, the uncertainty of the pyranometer is expected to be less than the definition by the ISO 9060 standard and the World Meteorological Organization (WMO).
Results and Discussion
Figure 3 shows the relationship between APE and SF of the c-Si module at each site. Most of the solar spectra with high ISI (1000 W/m2 or more) show APE at around 1.59 eV, which is the APE of the standard AM1.5G spectrum, in all locations. However, APE values in Sapporo (Fig. 3A), which is located in the north of Japan (43.03°N), are slightly and systematically lower than those in Okinoerabu (Fig. 3D), which is located in the south of Japan (27.21°N). This would be mainly due to the difference in AM. The dispersion of both APE and SF increases with decreasing ISI, suggesting that the more ISI is small, the more the variation in the shape of solar spectrum is large.
The SF of the c-Si module depends only weekly on APE, the values of which are always around 1.0. The regression lines calculated by the least-squares method show a weak negative slope in all locations as shown by the solid lines in Figure 3. The SF seems to split into two branches at APE higher than 1.8 eV. The branch with lower SF indicates solar spectral distribution consisting of diffuse solar irradiance caused by Mie scattering under heavily cloudy weather conditions, while the branch with higher SF indicates solar spectral distribution composed of diffuse solar irradiance caused by Rayleigh scattering by atmospheric gas particles under fine weather but little or no direct solar irradiance conditions (i.e., the sun is behind a small cloud). The total energy of solar irradiance with such high APE is quite small. Therefore, the difference between the SF and regression line could be negligible for the total energy yield. The APE lower than 1.5 eV indicates “red-rich” solar spectral distribution dominated by direct solar irradiance that passes through a large AM in morning or evening.
The regression lines suggest that the performance of c-Si modules is only little influenced by the effect of the solar spectrum. This can be explained by the “offset effect” [21]. The range of the spectral response of c-Si modules is approximately between 350 and 1200 nm. The increase or decrease in spectral irradiance due to Rayleigh scattering at shorter wavelengths below 700 nm is considered offset by the decrease or increase in spectral irradiance due to absorption by water vapor at wavelengths around 730, 820, 930, and 1150 nm.
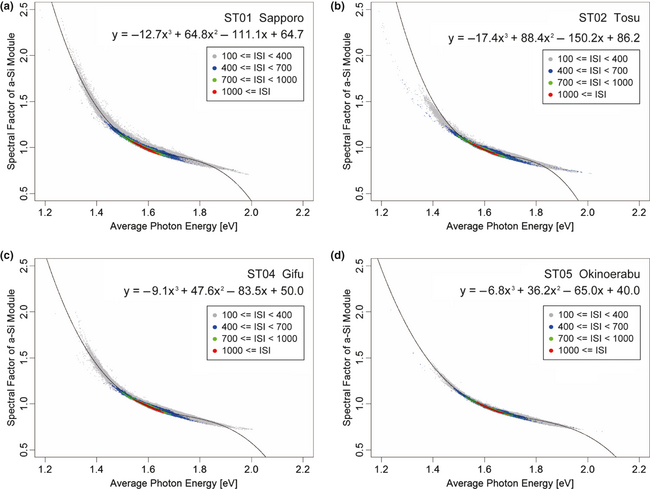
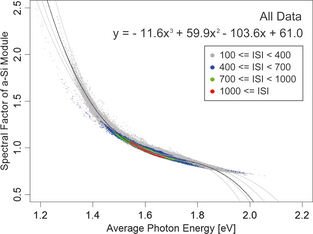
Figure 4 shows the relationship between APE and SF of the a-Si module at each site. As in the case of the relationship of the c-Si module, the dispersion of the SF of the a-Si module increases with decreasing ISI. The SF of the a-Si module clearly decreases with increasing APE, although the SF of the c-Si module seems to be constant for APE. The branches, which are shown by the SF of the c-Si module at APE higher than 1.8 eV, are not shown by the SF of the a-Si module. The range of the spectral response of a-Si modules is approximately between 350 and 800 nm. Because of the narrow spectral response biased toward shorter wavelength, it is well known that the performance of a-Si modules is significantly influenced by the effect of solar spectrum. The SF indicates that the performance of the a-Si module varies by about ± 20% only by the effect of the solar spectrum, even at ISI higher than 400 W/m2 around the latitude of Japan. Although the relationship of the c-Si module seems to be linear, the relationship of the a-Si module is not linear clearly. Consequently, we calculate the regression curves (cubic approximation) by the least-squares method.
|
|
|
Figure 4. Relationship between average photon energy (APE) and spectral factor (SF) of the a-Si photovoltaic (PV) module at each site. The solid lines indicate the regression curves calculated by the least-squares method. |
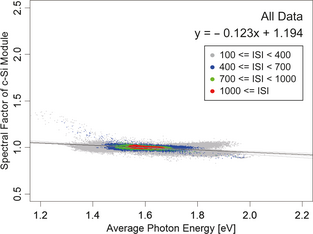
The regression lines in Figure 3 are quite similar to each other. The regression curves in Figure 4 are also similar each other. If there is a general relationship between APE and SF of solar cells, we can determine a unique regression line or curve for a kind of solar cell. Figure 5 shows the relationship between the APE and SF of the c-Si module for all solar spectra shown in Figure 3. The regression line is given by the following:
|
|
(5) |
|
|
|
Figure 5. Regression line (black color) of the spectral factor (SF) of the c-Si module calculated from all data. The gray lines indicate the regression lines at each site shown in Fig. 3. |
Figure 6 shows the relationship between the APE and SF of the c-Si module for all solar spectra shown in Figure 4. The regression curve is given as follows:
|
|
(6) |
|
|
|
Figure 6. Regression curve (black color) of the spectral factor (SF) of the a-Si module calculated from all data. The gray curves indicate the regression lines at each site shown in Fig. 4. |
In order to verify the above equations, we calculate the effective solar irradiation for the c-Si and a-Si modules at each site in 2008 by the direct parameter using equation (3) and by the approximate parameter using equations (5) or (6).
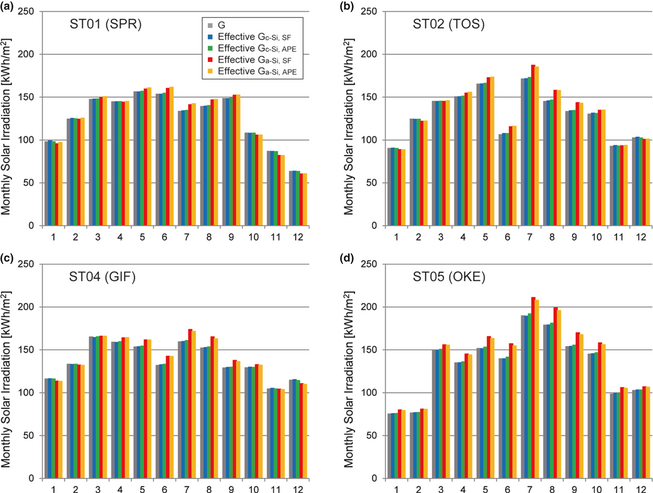
Figure 7 shows the monthly solar irradiation and effective solar irradiation at the optimum tilt angle, which is estimated by the direct and approximate parameters. The approximate estimation is in good agreement with the direct estimation. The effective solar irradiation for the c-Si module is almost equal to the solar irradiation all the year around. However, the effective solar irradiation for the a-Si module is higher and lower than the solar irradiation at Sapporo (Fig. 7A), Tosu (Fig. 7B), and Gifu (Fig. 7C) in summer and winter, respectively. Exceptionally, the effective solar irradiation for the a-Si module is always higher than the solar irradiance at Okinoerabu (Fig. 7D), which is located in the south of Japan.
|
|
|
Figure 7. Monthly solar irradiation (G) and effective solar irradiation at the optimum tilt angle in 2008, which is estimated by the direct parameter using equation (3) (Gc-Si, SF and Ga-Si, SF) and by the approximate parameter using equations (5) or (6) (Gc-Si, APE and Ga-Si, APE). |
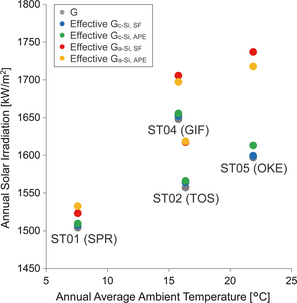
Finally, we estimate the annual effective solar irradiation. Figure 8 shows the annual average ambient temperature versus the annual solar irradiation or effective solar irradiation at the optimum tilt angle in 2008. The annual effective solar irradiation for the a-Si module at Okinoerabu is larger than that at Gifu, although the solar irradiation at Okinoerabu is smaller than that at Gifu. Table 1 shows the net effect of the solar spectrum on the annual energy yield of the c-Si and a-Si modules at each site. The results indicate that solar spectrum has little influence on the annual energy yield of the c-Si module. On the other hand, the spectral influence on the annual energy yield of the a-Si module increases with decreasing latitude. The effect of the solar spectrum would enhance the annual energy yield of a-Si modules by about 8% at Okinoerabu. The approximate estimation is in very good agreement with the direct estimation, whereas there is 1.2% difference between the estimations at most. As such, APE would be a useful index to quantify the effect of solar spectrum on the energy yield of PV systems simply and easily.
| ST01 (SPR) | ST02 (TOS) | ST04 (GIF) | ST05 (OKE) | |
|---|---|---|---|---|
| ||||
| Spectral effect for c-Si estimated by SF | +0.2% | +0.4% | +0.2% | +0.2% |
| Spectral effect for c-Si estimated by APE | +0.4% | +0.6% | +0.5% | +1.0% |
| Spectral effect for a-Si estimated by SF | +1.3% | +1.3% | +1.3% | +8.8% |
| Spectral effect for a-Si estimated by APE | +1.9% | +3.9% | +3.9% | +7.6% |
|
|
|
Figure 8. Relationship between the annual average ambient temperature and the annual solar irradiation or effective solar irradiation at the optimum tilt angle in 2008. |
Conclusions
In this study, we estimated the net effect of solar spectrum on the annual energy yield of PV modules by two parameters. The investigated data set of solar spectrum had been measured by JWA at four stations (Sapporo, Tosu, Gifu, and Okinoerabu) from 2008 to 2010. One parameter used the SF or MMF, which was directly calculated according to the definition in IEC 61853-3. We used APE for the other parameter. The relationship between APE and SF of c-Si and a-Si modules was investigated as the regression lines or curves by the least-squares method at each station. The results suggest that both regression lines and curves were almost similar among all stations. Consequently, we calculated the common regression line or curve for all stations from all solar spectra. The SF of the c-Si and a-Si modules was simply estimated as a function of APE using the common regression line or curve in the other parameter.
The effective solar irradiance of the c-Si and a-Si modules was calculated for the data set in 2008, in order to confirm the difference between the estimations by these parameters. The monthly effective solar irradiation estimated by the approximate parameter is in good agreement with that estimated by the direct parameter. Furthermore, the annual effective solar irradiation estimated by the approximate parameter is in very good agreement with that estimated by the direct parameter. As such, APE would be a useful index to estimate the effect of solar spectrum on the energy yield of PV modules simply and easily. As future work, it would be important to confirm whether the approximate parameter can be applicable to different climate regions, such as tropical or desert climate.
Acknowledgment
This study was financially supported by the New Energy and Industrial Technology Development Organization (NEDO) under the Ministry of Economy, Trade and Industry (METI).
Conflict of Interest
None declared.
References
- The European Photovoltaic Industry Association (EPIA). 2011. 2011 Annual Report. European Photovoltaic Industry Association, Brussels.
- Müllejans, H., T. Wagner, F. Merli, A. Jäger-Waldau, and E. D. Dunlop. 2004. Changes in spectral response with temperature and irradiance intensity. Thin Solid Films451–452:145–151. doi: 10.1016/j.tsf.2003.11.006
- Hibberd, C. J., F. Plyta, C. Monokroussos, M. Bliss, T. R. Betts, and R. Gottschalg. 2011. Voltage-dependent quantum efficiency measurements of amorphous silicon multi-junction mini-modules. Sol. Energy Mater. Sol. Cells95:123–126. doi: 10.1016/j.solmat.2010.03.039
- Monokroussos, C., M. Bliss, Y. N. Qiu, C. J. Hibberd, T. R. Betts, A. N. Tiwari, et al. 2011. Effects of spectrum on the power rating of amorphous silicon photovoltaic devices. Prog. Photovoltaics Res. Appl.19:640–648. doi: 10.1002/pip.1080
- International Electrotechnical Commission. 2008. Photovoltaic devices – Part 7: computation of the spectral mismatch correction for measurements of photovoltaic devices. IEC 60904-7 Edition 3.0. International Electrotechnical Commission, Geneva.
- International Electrotechnical Commission. Photovoltaic (PV) module performance testing and energy rating – Part 3: energy rating of PV modules. IEC 61853-3 Working Draft. International Electrotechnical Commission, Geneva.
- Gottschalg, R., D. G. Infield, and M. J. Kearney. 2003. Experimental study of variations of the solar spectrum of relevance to thin film solar cells. Sol. Energy Mater. Sol. Cells79:527–537. doi: 10.1016/S0927-0248(03)00106-5
- Fanni, L., A. Virtuani, and D. Chianese. 2011. A detailed analysis of gains and losses of a fully-integrated flat roof amorphous silicon photovoltaic plant. Sol. Energy85:2360–2373.
- Skoczek, A., A. Virtuani, T. Cebecauer, and D. Chianese. 2011. Energy yield prediction of amorphous silicon PV modules using full time data series of irradiance and temperature for different geographical locations. Pp. 3248–3252in Proceedings of the 26th European Photovoltaic Solar Energy Conference and Exhibition, Hamburg, Germany. doi: 10.4229/26thEUPVSEC2011-4DO.6.3
- Virtuani, A., and L. Fanni. 2013. Seasonal power fluctuations of amorphous silicon thin-film solar modules: distinguishing between different contributions. Prog. Photovoltaics Res. Appl. [Available online]. doi: 10.1002/pip.2257
- Wilson, H. R., and M. Hennies. 1989. Energetic relevance of solar spectral variation on solar cell short circuit current. Sol. Energy42:273–279.
- Nann, S., and K. Emery. 1992. Spectral effects on PV-device rating. Sol. Energy Mater. Sol. Cells27:189–216.
- Rüther, R., and J. Livingstone. 1994. Seasonal variations in amorphous silicon solar module outputs and thin film characteristics. Sol. Energy Mater. Sol. Cells36:29–43.
- Hirata, Y., and T. Tani. 1995. Output variation of photovoltaic modules with environmental factors – I. The effect of spectral solar radiation on photovoltaic module output. Sol. Energy55:463–468.
- Nakajima, A., M. Ichikawa, M. Kondo, K. Yamamoto, H. Yamagishi, and Y. Towada. 2004. Spectral effects of a single-junction amorphous silicon solar cell on outdoor performance. Jpn. J. Appl. Phys.43:2425–2431. doi: 10.1143/JJAP.43.2425
- Müllejans, H., A. Ioannides, R. Kenny, W. Zaaiman, H. Ossenbrink, and E. Dunlop. 2005. Spectral mismatch in calibration of photovoltaic reference devices by global sunlight method. Meas. Sci. Technol.16:1250–1254. doi: 10.1088/0957-0233/16/6/002
- Kenny, R. P., A. Ioannides, H. Müllejans, W. Zaaiman, and E. D. Dunlop. 2006. Performance of thin film PV modules. Thin Solid Films511–512:663–672. doi: 10.1016/j.tsf.2005.11.066
- Pérez-López, J. J., F. Fabero, and F. Chenlo. 2007. Experimental solar spectral irradiance until 2500 nm: results and influence on the PV conversion of different materials. Prog. Photovoltaics Res. Appl.15:303–315. doi: 10.1002/pip.739
- Tsutsui, J., and K. Kurokawa. 2008. Investigation to estimate the short circuit current by applying the solar spectrum. Prog. Photovoltaics Res. Appl.16:205–211. doi: 10.1002/pip.793
- Ishii, T., K. Otani, and T. Takashima. 2011. Effects of solar spectrum and module temperature on outdoor performance of photovoltaic modules in round-robin measurements in Japan. Prog. Photovoltaics Res. Appl.19:141–148. doi: 10.1002/pip.995
- Ishii, T., K. Otani, T. Takashima, and Y. Xue. 2013. Solar spectral influence on the performance of photovoltaic (PV) modules under fine weather and cloudy weather conditions. Prog. Photovoltaics Res. Appl. [Available online]. doi: 10.1002/pip.1210
- Jardine, C. N., T. R. Betts, R. Gottschalg, D. G. Infield, and K. Lane. 2002. Influence of spectral effects on the performance of multijunction amorphous silicon cells. Proceedings of the PV in Europe. From PV Technology to Energy Solutions Conference and Exhibition, Roma, Italy.
- Williams, S. R., T. R. Betts, T. Helf, R. Gottschalg, H. G. Beyer, and D. G. Infield. 2003. Modeling long-term module performance based on realistic reporting conditions with consideration to spectral effects. Pp. 1908–1911in Proceedings of the 3rd World Conference on Photovoltaic Energy Conversion, Osaka, Japan. doi: 10.1109/WCPEC.2003.1306312
- Betts, T. R., C. N. Jardine, R. Gottschalg, D. G. Infield, and K. Lane. 2003. Impact of spectral effects on the electrical parameters of multijunction amorphous silicon cells. Pp. 1756–1759in Proceedings of the 3rd World Conference on Photovoltaic Energy Conversion, Osaka, Japan. doi: 10.1109/WCPEC.2003.1306273
- Gottschalg, R., T. R. Betts, S. R. Williams, D. Sauter, D. G. Infield, and M. J. Kearney. 2004. A critical appraisal of the factors affecting energy production from amorphous silicon photovoltaic arrays in a maritime climate. Sol. Energy77:909–916. doi: 10.1016/j.solener.2004.06.015
- Minemoto, T., M. Toda, S. Nagae, M. Gotoh, A. Nakajima, K. Yamamoto, et al. 2007. Effect of spectral irradiance distribution on the outdoor performance of amorphous Si//thin-film crystalline Si stacked photovoltaic modules. Sol. Energy Mater. Sol. Cells91:120–122. doi: 10.1016/j.solmat.2006.07.014
- Minemoto, T., S. Nagae, and H. Takakura. 2007. Impact of spectral irradiance distribution and temperature on the outdoor performance of amorphous Si photovoltaic modules. Sol. Energy Mater. Sol. Cells91:919–923. doi: 10.1016/j.solmat.2007.02.012
- Otani, K., Y. Hishikawa, P. Sichanugrist, P. Supanich, and E. Hattha. 2008. Energy rating of various PV module technologies based on outdoor measurements in low latitude region, Thailand. Proceedings of Renewable Energy 2008, Busan, Korea, O-PV-044.
- Ishii, T., K. Otani, A. Itagaki, and K. Utsunomiya. 2012. A methodology for estimating the effect of solar spectrum on photovoltaic module performance by using average photon energy and a water absorption band. Jpn. J. Appl. Phys.51:10NF05. doi: 10.1143/JJAP.51.10NF05
- Cornaro, C., and A. Andreotti. 2013. Influence of Average Photon Energy index on solar irradiance characteristics and outdoor performance of photovoltaic modules. Prog. Photovoltaics Res. Appl. [Available online]. doi: 10.1002/pip.2194
- Gueymard, C. A. 2009. Daily spectral effects on concentrating PV solar cells as affected by realistic aerosol optical depth and other atmospheric conditions. P. 741007in Optical Modeling and Measurements for Solar Energy Systems III. Proceedings of SPIE, San Diego, CA. doi: 10.1117/12.826071
- Gueymard, C. A.2001. Parameterized transmittance model for direct beam and circumsolar spectral irradiance. Sol. Energy71:325–346.
- International Electrotechnical Commission. 2008. Photovoltaic devices – Part 3: measurement principles for terrestrial photovoltaic (PV) solar devices with reference spectral irradiance data. IEC 60904-3 Edition 2.0, International Electrotechnical Commission, Geneva.
Document information
Published on 01/06/17
Submitted on 01/06/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?