Application of the Stiffness-Force method to the analysis of a plate in tension with a central hole

1 Introducción

El método de la rigidez (SM), basado en las condiciones de equilibrio que derivan de la aplicación del principio del trabajo virtual, se utiliza exténsamente en el análisis por elementos finitos [1].

La otra aproximación básica en el análisis estructural es el método de las Fuerzas (FM) [2]. Este método se deriva de la aplicación del principio del trabajo virtual complementario. A partir de este método, Patnaik et al. desarrollaron el método de las fuerzas integrado dual (IFMD) [3], que tiene la misma ecuación de gobierno que el método de la rigidez. En el método IFMD se tienen en cuenta tanto las ecuaciones de equilibrio como las condiciones de compatibilidad. Por otro lado, Pian [4] introdujo el método híbrido (HM) y, recientemente, Adarraga et al. [5] indicaron que ambos métodos son equivalentes.

IFMD y HM se pueden obtener de la aplicación de los principios del trabajo virtual y del trabajo virtual complementario y satisfacen las ecuaciones de equilibrio como en SM y las condiciones de compatibilidad como en FM. Los autores denominan al método Rigidez-Fuerza con la intención de unificar la nomenclatura.

2 El método rigidez-fuerza (SFM)

2.1 Formulación

Las ecuaciones del SFM se obtienen de la aplicación de los principios del trabajo virtual y del trabajo virtual complementario:

${\textstyle \int _{V}^{~}{\left\{\delta \epsilon \right\}}^{T}\left\{\sigma \right\}dV={\left\{\delta a^{i}\right\}}^{T}\left\{P^{i}\right\}}$

(1)

${\textstyle \int _{V}^{~}{\left\{\delta \sigma \right\}}^{T}\left\{\epsilon \right\}dV={\left\{\delta P^{i}\right\}}^{T}\left\{a^{i}\right\}}$

(2)

donde {aⁱ} y {Pⁱ} son los vectores de desplazamientos y de fuerzas nodales respectivamente. A partir de los desplazamientos nodales, se pueden conocer los desplazamientos en cualquier punto del elemento [1]:

$\left\{u\right\}=\left[N\right]\left\{a^{i}\right\}$

(3)

donde [N] es la matriz de funciones de interpolación de desplazamientos.Una vez obtenidos los desplazamientos nodales se conocen también las deformaciones en el elemento:

$\left\{\epsilon \right\}=\left[L\right]\left[N\right]\left\{a^{i}\right\}=\left[B\right]\left\{a^{i}\right\}$

(4)

donde [L] es la matriz de operadores diferenciales y [B] es la matriz de forma. En el método SFM la interpolación de las tensiones y los desplazamientos es independiente [5]. Las tensiones en cualquier punto del elemento se interpolan a partir de los parámetros de tensión {F^j}:

$\left\{\sigma \right\}=\left[Y\right]\left\{F^{j}\right\}$

(5)

siendo [Y] la matriz de funciones de interpolación de tensiones. Por otro lado, el vector de tensiones se relaciona con el vector de deformaciones mediante la matriz de coeficientes de flexibilidad del material [S]:

$\left\{\sigma \right\}=\left[S\right]\left\{\epsilon \right\}$

(6)

Sustituyendo las ecuaciones (4) y (5) en el principio del trabajo virtual (1) resulta:

$\left({{\int }_{V}\left[B\right]}^{T}\left[Y\right]dV\right)\left\{F^{j}\right\}=\left\{P^{i}\right\}$

(7)

La matriz de equilibrio se define como:

$\left[E\right]={{\int }_{V}\left[B\right]}^{T}\left[Y\right]dV$

(8)

Por lo tanto, la ecuación de equilibrio (7) se expresa como:

$\left[E\right]\left\{F^{j}\right\}=\left\{P^{i}\right\}$

(9)

Al sustituir las ecuaciones (5), (6) y (9) en el principio del trabajo virtual complementario (2), resulta:

$\left({{\int }_{V}\left[Y\right]}^{T}\left[S\right]\left[Y\right]dV\right)\left\{F\right\}={\left[E^{e}\right]}^{T}\left\{a^{i}\right\}$

(10)

La matriz de flexibilidad se define como:

$\left[G\right]={{\int }_{V}\left[Y\right]}^{T}\left[S\right]\left[Y\right]dV$

(11)

La ecuación (10) se puede expresar como:

$\left[G\right]\left\{F^{j}\right\}={\left[E\right]}^{T}\left\{a^{i}\right\}$

(12)

De la ecuación (12) se obtienen los parámetros de tensiones del elemento {F^j}:

$\left\{F^{j}\right\}={\left[G\right]}^{-1}{\left[E\right]}^{T}\left\{a^{i}\right\}$

(13)

Multiplicando esta expresión en ambos lados por la matriz de equilibrio [E], el primer término de la ecuación (13) corresponde al vector de fuerzas externas aplicadas en los nodos, {Pⁱ}:

$\left\{P^{i}\right\}=\left[E\right]{\left[G\right]}^{-1}{\left[E\right]}^{T}\left\{a^{i}\right\}$

(14)

La ecuación (14) se puede escribir:

${\textstyle \left\{P^{i}\right\}=\left[K\right]\left\{a^{i}\right\}}$

(15)

En el método SFM la matriz de rigidez del elemento es: $\left[K^{e}\right]=\left[E\right]{\left[G\right]}^{-1}{\left[E\right]}^{T}$

(16)

La matriz de rigidez de la estructura se obtiene del ensamblaje de las matrices elementales, tal y como se hace en el método SM. Por lo tanto, la ecuación de gobierno del método SFM es:

${\textstyle \left[K\right]\left\{a^{l}\right\}=\left\{P^{l}\right\}}$

(17)

2.2 Elemento cuadrilateral de 4 nodos

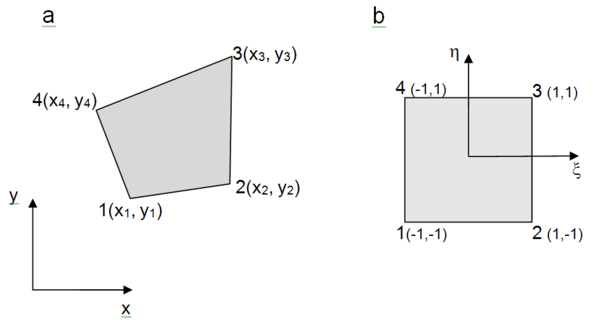
En esta sección se describe la formulación del método SFM correspondiente al elemento cuadrilateral isoparamétrico bidimensional de 4 nodos que se muestra en la figura 1.

Figura 1. Elemento cuadrilateral de 4 nodos: a) coordenadas globales; b) coordenadas naturales.

Conforme a lo descrito en la sección anterior, la matriz de rigidez del elemento se calcula a partir de las matrices de equilibrio y de flexibilidad.

En la formulación del elemento cuadrilátero isoparamétrico se emplean las mismas funciones de interpolación lineales que en el cuadrilátero general [N_i] que se utilizan en el método SM [1]:

${\textstyle {\begin{array}{c}x=\sum _{i=1}^{4}N_{i}x_{i}={\frac {1}{4}}{\sum }^{\mbox{​}}\left(1+\xi {\xi }_{i}\right)\left(1+\eta {\eta }_{i}\right)x_{i}\\\\y=\sum _{i=1}^{4}N_{i}y_{i}={\frac {1}{4}}{\sum }^{\mbox{​}}\left(1+\xi {\xi }_{i}\right)\left(1+\eta {\eta }_{i}\right)y_{i}\end{array}}}$

(18)

La matriz de deformación del elemento [B] se obtiene derivando la matriz de funciones de interpolación:

$\left[B\right]=\left[{\begin{array}{cc}{\frac {\partial N_{i}}{\partial x}}&0\\0&{\frac {\partial N_{i}}{\partial y}}\\{\frac {\partial N_{i}}{\partial y}}&{\frac {\partial N_{i}}{\partial x}}\end{array}}\right]$

(19)

En el caso de un cuadrilátero general esta matriz [B] varía con las coordenadas de cada punto.

Utilizando las funciones de interpolación de tensiones definidas en [6,7] la ecuación (5) resulta:

(20)

2.2.1 Matriz de Equilibrio [E]

La matriz de equilibrio de cada elemento se calcula mediante la siguiente expresión:

${\textstyle \left[E\right]=\int _{-1}^{1}\int _{-1}^{1}{\left[B\left(\xi ,\eta \right)\right]}^{T}\left[Y\right]\cdot \vert J\vert \cdot t\cdot d\xi d\eta }$

(21)

Donde t es el espesor del elemento y ${\textstyle \left|J\right|}$ el determinante del Jacobiano.

2.2.2 Matriz de Flexibilidad [G]

La matriz de flexibilidad de los elementos se obtiene según:

${\textstyle \left[G\right]=\int _{-1}^{1}\int _{-1}^{1}{\left[Y\right]}^{T}\left[S\right]\left[Y\right]\cdot \vert J\vert \cdot t\cdot d\xi d\eta }$

(22)

2.2.3 Matriz de Rigidez [K]

Una vez calculadas las matrices de equilibrio y de flexibilidad del elemento, la matriz de rigidez del elemento se obtiene mediante la ecuación (16).

Conocidas las matrices de rigidez elementales, la matriz de rigidez del sistema se obtiene ensamblando las matrices de rigidez de todos los elementos.

3 Análisis mediante SFM de una placa a tracción con un agujero circular central

La concentración de tensiones alrededor de agujeros tiene una gran importancia práctica, puesto que suelen ser causa de fallo. El análisis de placas agujereadas ha tenido una larga trayectoria y sigue vigente hoy en día. La solución de una placa infinita con un agujero circular central sometida a tracción uniaxial fue desarrollada por Kirsch [8]. Posteriormente Howland [9] obtuvo las tensiones alrededor del agujero en el caso de placas de ancho finito mediante una aproximación analítica. Tan [10] definió los factores de corrección debidos a ancho finito.

Existen en la bibliografía análisis experimentales [11,12] y gran variedad de aproximaciones analíticas [13,14,15,16-17], que se comparan con resultados obtenidos de modelos numéricos.

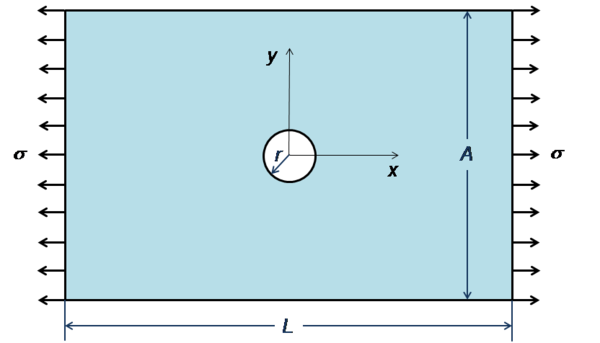
En el presente trabajo se pretende analizar la concentración de tensiones de una placa con un agujero circular central (ver figura 2) sometida a tracción uniaxial mediante el método SFM.

El análisis se ha realizado utilizando el programa de elementos finitos Abaqus. Para ello se ha escrito una subrutina de usuario, UEL, correspondiente al elemento cuadrilátero isoparamétrico y se ha implementado dicho código en el citado programa comercial Abaqus.

Figura 2. Placa a tracción con un agujero circular en su centro.

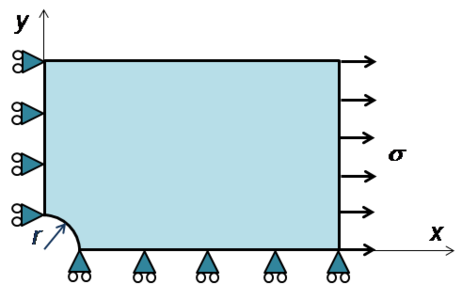
El modelo y las condiciones de contorno que se han utilizado en el análisis por elementos finitos se muestran en la figura 3.

Figura 3. Modelo y condiciones de contorno de la placa.

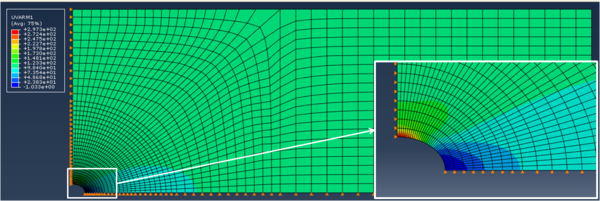
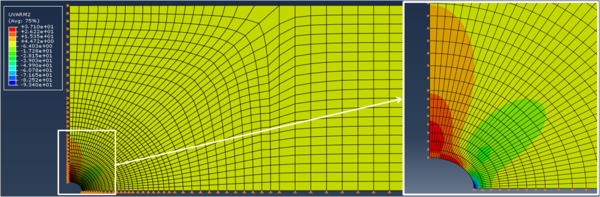
La distribución de tensiones horizontales σ_x y verticales σ_y se indican en las figuras 4 y 5, respectivamente.

Figura 4. Distribución de tensiones horizontales σ_x.

Figura 5. Distribución de tensiones verticales σ_y.

4 Conclusiones

La intención de este trabajo es analizar las concentraciones de tensiones generadas alrededor de un agujero circular central en composites mediante el método SFM. Para ello se ha escrito el código correspondiente a un cuadrilátero general y se ha implementado esa subrutina de usuario UEL en Abaqus.

5 Agradecimientos

Los autores agradecen a la Universidad del País Vasco (UPV/EHU) la financiación del Grupo de Investigación Mecánica de Materiales GIU 16/51 en la convocatoria de 2016.

Referencias

[1] E.Oñate, Structural analysis with the finite element method. Barcelona: International Center for Numerical Methods in Engineering (2009).

[2] J.Robinson, Integrated theory of finite element methods. London: John Wiley & Sons (1973).

[3] S.N.Patnaik, R.M.Coroneos, D.A.Hopkins, Advances in Engineering Software, 29, 3–6, pág. 463-474 (1998).

doi:http://dx.doi.org/10.1016/S0965-9978(97)00070-7

[4] T.H.H.Pian, AIAA Journal, 2, 7, pág. 1333-1336 (1964).

[5] I.Adarraga, M.A.Cantera, J.M.Romera, N.Insausti, F:Mujika, International Journal for Numerical Methods in Engineering, 98, 9, pág. 663-677 (2014). doi:10.1002/nme.4644

[6] T.H.H.Pian, K.Sumihara, International Journal for Numerical Methods in Engineering, 20, 9, pág. 1685-1695 (1984).

doi:10.1002/nme.1620200911

[7] C.Zhang, D.Wang, J.Zhang, W.Feng, Q.Huang, Finite Elements in Analysis and Design, 43, 4, pág. 321-332 (2007).

doi:http://dx.doi.org/10.1016/j.finel.2006.11.002

[8] S.P.Timoshenko, J.N.Goodier, Teoría de la elasticidad; S. Timoshenko y J.N. Goodier; traducido por Alberto Fuentes Pérez. Bilbao: Urmo (1968).

[9] R.C.J.Howland, Philosophical Transactions of the Royal Society of London.Series A, 229, 670-680, pág. 49-86 (1930).

doi:10.1098/rsta.1930.0002

[10] S.C.Tan, Journal of Composite Materials, 22, 11, pág. 1080-1097 (1988).

doi:10.1177/002199838802201105

[11] P.P.Camanho, P.Maimí, C.G.Dávila, Composites Science and Technology, 67, 13, pág. 2715-2727 (2007).

doi:https://doi.org/10.1016/j.compscitech.2007.02.005

[12] R.M.O’Higgins, M.A.McCarthy, C.T.McCarthy, Composites Science and Technology, 68, 13, pág. 2770-2778 (2008).

doi:https://doi.org/10.1016/j.compscitech.2008.06.003

[13] H.Wu, B.Mu, Composites Part B: Engineering, 34, 2, pág. 127-134 (2003).

doi:https://doi.org/10.1016/S1359-8368(02)00097-5

[14] P.P.Camanho, G.H.Erçin, G.Catalanotti, S.Mahdi, P.Linde, Composites Part A: Applied Science and Manufacturing, 43 , 8, pág. 1219-1225 (2012).

doi:https://doi.org/10.1016/j.compositesa.2012.03.004

[15]E.Martin, D.Leguillon, N.Carrère, International Journal of Solids and Structures, 49, 26, pág. 3915-3922 (2012).

doi:https://doi.org/10.1016/j.ijsolstr.2012.08.020

[16] R.M.Frizzell, M.A.McCarthy, C.T.McCarthy, Composite Structures, 110, pág. 51-61 (2014).

doi:https://doi.org/10.1016/j.compstruct.2013.11.003

[17] J.D.D.Melo, J.Bi, S.W.Tsai, Composite Structures, 159, pág. 44-52 (2017).

doi:https://doi.org/10.1016/j.compstruct.2016.09.055