Influence of mesh size on accuracy results in seismically excited water tanks

Abstract

The aim of this article is to present the influence of mesh spacing in the error parameters computed for rectangular tanks seismically excited. The potential flow theory is considered using the finite difference method to set a linear numerical formulation due to its simplicity and relatively low computation time, compared with those methods that try to solve directly the Navier–Stokes equations. Wave height on the free surface, as well as pressure, shear force and overturning moment at the tanks wall base are used as parameters for the error evaluation.

Keywords: tank, sloshing, error, mesh spacing

Introduction

Damage in water storage tanks caused by earthquakes can be a serious problem, especially for the ones that are used to supply drinking water to people. Design standards and guidelines such as [1–4], employ expressions based on models proposed by Housner [5] or Veletsos & Yang [6] to estimate the response of liquid sloshing and to design tanks. These models are based on simple assumptions and it is not uncommon that they lead to unrepresentative results of real phenomena.

In recent years, a wide variety of computational fluid dynamics (CFD) techniques have been proposed to solve the sloshing on tanks. Several approaches such as, finite difference method (FDM), finite volume method (FVM), finite difference method (FEM), and boundary element method (BEM), among many variations and modifications have been used to address the problem. All works mainly use two types of approaches to represent the fluid flow in the tank: (a) methods that try to solve directly the Navier–Stokes equations, and (b) methods that employ a potential flow theory.

Navier–Stokes is second order, nonlinear and unstable differential equations system; this is the main reason why the methods based on this approach are complex and tend to require a lot of computational effort. FEM and/or BEM are techniques commonly used for this approach; also, hybrid methodologies have been proposed, such as Lin et al. [7]. On the other hand, the use of potential flow theory facilitates the establishment of a solution to the fluid motion in the tank. To use this approach, various simplifying assumptions to the Navier–Stokes equations are required, such as: the fluid is homogeneous, incompressible, inviscid and irrotational. Thus, the use of potential flow theory is usually less complicated and results can be obtained in shorter time.

One of the CFD methods used to propose a solution for sloshing in tanks is the FDM, due to its simplicity and relatively easy way to create the equations systems to be solved. Several solutions have been proposed using the FDM, such as those established by Chen et al. [8] and Hernández–Barrios et al. [9, 10]. However, a systematic and extensive study to investigate the most advantageous mesh spacing using this method with adequate precision is lacking. Consequently, the main objective of this paper is to determinate the required mesh spacing to expect certain level of error in the parameters of interest using the FDM to solve rectangular tanks subjected to earthquake ground motions.

Numerical Model

Figure 1 2D physical domain tank

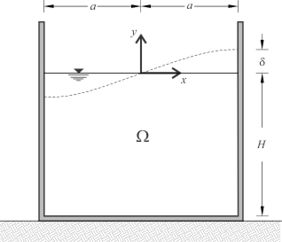
The equations of motion for the liquid–tank system depicted in Figure 1, which uses an inertial reference system (that moves with the tank) and considering a velocity potential Φ, are described below. Domain–wide continuity of the liquid is met using the Laplace equation defined by Eq. (1).

${\frac {{\partial }^{2}\phi }{\partial x^{2}}}+{\frac {{\partial }^{2}\phi }{\partial y^{2}}}=$$0$

(1)

On the walls, Eq. (2) below must be satisfied.

${\frac {\partial \phi }{\partial x}}=0$

(2)

And, on the bottom of the tanks the Eq. (3) must be met.

${\frac {\partial \phi }{\partial y}}=0$

(3)

On the surface ( ${\textstyle y=\delta }$ ) the movement of the fluid is governed by dynamic and kinematic conditions defined by Eqs. (4) and (5), respectively.

${\frac {\partial \phi }{\partial t}}+{\frac {1}{2}}\left[{\left({\frac {\partial \phi }{\partial x}}\right)}^{2}+\right.$$\left.{\left({\frac {\partial \phi }{\partial y}}\right)}^{2}\right]+$$\left\{{\begin{array}{cc}x&y\end{array}}\right\}\left\{{\begin{array}{c}a_{cx}\left(t\right)\\a_{cy}\left(t\right)\end{array}}\right\}+g\delta =0$

(4)

${\frac {\partial \delta }{\partial t}}+{\frac {\partial \phi }{\partial x}}{\frac {\partial \delta }{\partial x}}-$${\frac {\partial \phi }{\partial y}}=0$

(5)

Pressure is estimated from Bernoulli equation, expressed by Eq. (6), where ρ represents the fluid density; ${\textstyle a_{cx}(t)}$ and ${\textstyle a_{cy}(t)}$ represent respectively, the horizontal and vertical acceleration induced at tank base.

$p=-\rho \left[{\frac {\partial \phi }{\partial t}}+\left\{{\begin{array}{cc}x&y\end{array}}\right\}\left\{{\begin{array}{c}a_{cx}\left(t\right)\\a_{cy}\left(t\right)\end{array}}\right\}+{\frac {1}{2}}\left[{\left({\frac {\partial \phi }{\partial x}}\right)}^{2}+\right.\right.$$\left.\left.{\left({\frac {\partial \phi }{\partial y}}\right)}^{2}\right]+\right.$$\left.gy\right]$

(6)

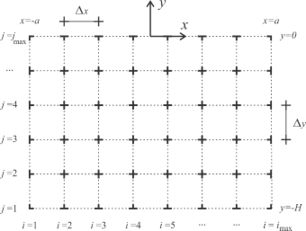
Discretizing in terms of second–order finite differences, and in correspondence with the scheme shown in Figure 2, on the walls the Eq. (2) is expressed according to Eqs. (7) and (8).

$-3{\phi }_{i,j}+4{\phi }_{i+1,j}-{\phi }_{i+2,j}=0{\mbox{ }}{\mbox{ }}i=$$1,{\mbox{ }}j\in \left[1,j_{max}\right]$

(7)

${\phi }_{i-2,j}-4{\phi }_{i-1,j}+3{\phi }_{i,j}=0{\mbox{ }}{\mbox{ }}i=$$i_{max},{\mbox{ }}j\in \left[1,j_{max}\right]$

(8)

Figure 2 Computational domain

On the bottom of the tank, the condition established by Eq. (3) is expressed according Eq. (9).

$-3{\phi }_{i,j}+4{\phi }_{i,j+1}-{\phi }_{i,j+2}=0{\mbox{ }}{\mbox{ }}i\in \left[2,i_{max-1}\right],{\mbox{ }}j=$$1$

(9)

For interior mesh points, the Laplace equation defined by Eq. (1) in its discretized form is expressed by Eq. (10).

$C_{1}{\phi }_{i,j-1}+{\phi }_{i-1,j}-2\left(1+C_{1}\right){\phi }_{i,j}+$${\phi }_{i+1,j}+C_{1}{\phi }_{i,j+1}=0{\mbox{ }}{\mbox{ }}i\in \left[2,i_{max-1}\right],{\mbox{ }}j\in \left[2,i_{max-1}\right]$

(10)

where ${\textstyle C_{1}={\left(\Delta x/\Delta y\right)}^{2}}$

On the surface, combining Eqs. (4) and (5), neglecting the higher order terms and using an implicit Crank–Nicholson scheme in time, the discretized expressions is shown in Eq. (11). Semi–viscous μ parameter is stated in 0.5% to simulate water viscosity, as recommended by Chen et al. [8].

${\mbox{ }}{\mbox{ }}C_{3}{\phi }_{i,j-2}^{\left(n+1\right)}-$$4C_{3}{\phi }_{i,j-1}^{\left(n+1\right)}+\left(1+3C_{3}+\right.$$\left.{\frac {1}{2}}\mu {\mbox{ }}\Delta t\right){\phi }_{i,j}^{\left(n+1\right)}=$$-C_{3}{\phi }_{i,j-2}^{\left(n\right)}+{\mbox{ }}4C_{3}{\phi }_{i,j-1}^{\left(n\right)}{\mbox{ }}+$${\mbox{ }}\left(1-3C_{3}-{\frac {1}{2}}\mu {\mbox{ }}\Delta t\right){\phi }_{i,j}^{\left(n\right)}{\mbox{ }}{\mbox{ }}-$${\frac {1}{2}}\Delta t\left(a_{cx}^{\left(n+1\right)}+\right.$$\left.a_{cx}^{\left(n\right)}\right)-\Delta t{\mbox{ }}g{\mbox{ }}{\delta }_{i,j}^{\left(n\right)}i\in \left[2,i_{max-1}\right],{\mbox{ }}j=$$j_{max}$

(11)

where ${\textstyle C_{3}={\frac {g{\left(\Delta t\right)}^{2}}{8{\mbox{ }}\Delta y}}}$

From the kinematic condition expressed by Eq. (5), neglecting the higher order terms and discretizing in finite difference terms, the wave height can be obtained from Eq. (12).

${\begin{array}{c}{\delta }_{i,j}^{\left(n+1\right)}={\delta }_{i,j}^{\left(n\right)}+{\frac {\Delta t}{2}}\left({\frac {{\phi }_{i,j-2}^{\left(n\right)}-4{\phi }_{i,j-1}^{\left(n\right)}+3{\phi }_{i,j}^{\left(n\right)}}{2\Delta y}}\right)+{\frac {\Delta t}{2}}\left({\frac {{\phi }_{i,j-2}^{\left(n+1\right)}-4{\phi }_{i,j-1}^{\left(n+1\right)}+3{\phi }_{i,j}^{\left(n+1\right)}}{2\Delta y}}\right)\\i\in \left[1,i_{max}\right],{\mbox{ }}j=j_{max}\end{array}}$

(12)

From Eq. (6), pressure can be estimated by Eq. (13).

$p_{i,j}^{\left(n+1\right)}=-\rho \left[{\frac {{\phi }_{i,j}^{\left(n+1\right)}-{\phi }_{i,j}^{\left(n\right)}}{\Delta t}}+\right.$$\left.{\frac {1}{2}}\left\{{\begin{array}{cc}x&y\end{array}}\right\}\left\{{\begin{array}{c}a_{cx}^{\left(n+1\right)}+a_{cx}^{\left(n\right)}\\a_{cy}^{\left(n+1\right)}+a_{cy}^{\left(n\right)}\end{array}}\right\}+gy\right]{\mbox{ }}{\mbox{ }}i\in \left[1,i_{max}\right],{\mbox{ }}j\in \left[1,j_{max}\right]$

(13)

Figure 3 Volcán de Cerro Prieto accelerogram (February 7, 1987) – Mexicali BC, Mexico

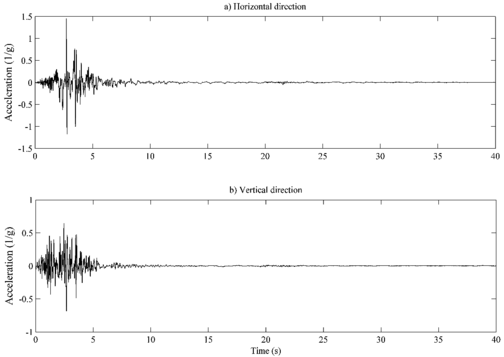
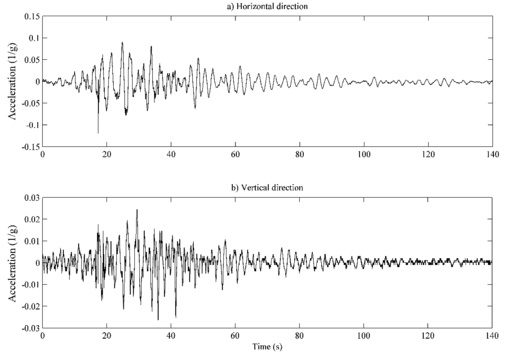
To assess the numerical model accuracy previously described, two very different seismic records are selected. The first one is the record Volcán de Cerro Prieto (VCP) showed in Figure 3, which is a seismic accelerogram with a great peak ground motion, close to 1.5 times gravity in its horizontal component. This record is selected to evaluate the response to a strong impulsive seismic acceleration. Additionally, this record has a strong vertical peak ground motion near to 0.7 times gravity. The second one is the record of Central de Abastos (CDA) which is shown in Figure 4. This record is selected because tends to cause high sloshing on tanks because it has a long dominant period, characteristic of soft soils.

Figure 4 Central de Abastos accelerogram (September 19, 1985) – Mexico City

Results

The numerical model previously described is used to evaluate wave height on the free surface, pressure, shear force and overturning moment at tank wall base. Wave height and pressure are obtained directly from Eqs. (12) and (13) respectively, while shear force and overturning moment are obtained using integration Simpson’s rule at the mesh point on the walls.

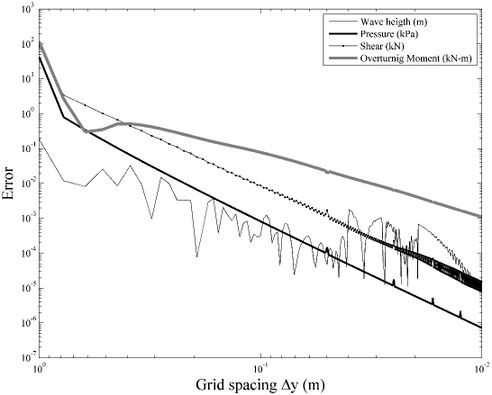
Initially, the maximum values of aforementioned parameters are computed with a gross mesh. Subsequently the number on mesh points in y direction is incremented by one. Seeking a regular mesh in x direction, the number of mesh divisions is determined by searching that C₁ in Eq. (10) is the closest to the unity, being always greater than one. The maximum values of each parameter are compared to those obtained from the previous mesh, where the estimated errors are the difference. Figure 5 shows the error evolution for a 100 m³ tank (2a = 6.25m, ${\textstyle H=}$ 3.1 m) subjected to VCP accelerogram. Similar analyses are performed for tank capacities from 100 m³ to 1500 m³ with typical dimensions showed in Table 1.

Figure 5 Error evolution for a 100 m³ tank

Many previous works report results just considering horizontal acceleration. Therefore, two sets of analyses for each accelerogram are computed, one set just with horizontal acceleration and another one that considers horizontal and vertical acceleration at the same time. Table 1 shows the maximum values obtained for VCP accelerogram for both sets of analyses, where a_cx implies that results are obtained with horizontal acceleration only, and a_cx + a_cy means that horizontal and vertical acceleration are considered. The presented values in Table 1 correspond to the densest mesh computed for each case because they are considered the most accurate results. As can be noted, wave heights are practically the same for both sets of analysis. However, for those results computed with horizontal and vertical acceleration, pressure, shear force, and overturning moment at the wall base are on average 17.8%, 14.4% and 3.3% greater respect to those obtained with horizontal acceleration only. On the other hand, if the same procedure is computed for CDA accelerogram, the obtained results are practically the same with or without vertical acceleration, having differences of 1.3% for pressure at most. This occurs because pressure, shear, and moment on VCP record are dominated by the impulsive induced motion, while for CDA accelerogram the motion is dominated by the sloshing effect, where vertical acceleration has a little influence. Additionally, vertical acceleration is considerably small for CDA accelerogram as can be shown in Figure 4.

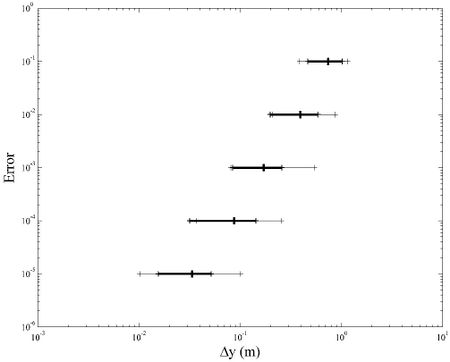
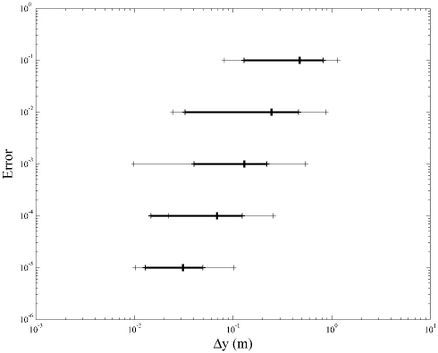
Note from Figure 5 that for the same grid spacing, several error values are obtained for each parameter. Considering that error evolution showed in Figure 5 is different for each tank geometry, a set of grid spacing values is obtained to achieve the same error. Figure 6 shows the distribution of required grid spacing to achieve several error levels for all tank dimensions and VPC accelerogram. Thin line joins the minimum and maximum grid spacing values, central mark indicates the average value, while the thick line joins the ± standard deviation around average. On Figure 6 only wave height and pressure are considered, because these parameters are obtained directly from the numerical model. Shear force and overturning moment are obtained from numerical integration, adding a numerical error, which leads to a smaller mesh spacing to achieve the same error. This can be observed in Figure 7, where required mesh spacing for all parameters is showed.

Table 1 Result values for Volcán de Cerro Prieto accelerogram

Capacity (m³)	Depth ${\textstyle H}$ (m)	Width ${\textstyle 2a}$ (m)	Wave Height (m)		Pressure (kPa)		Shear (kN)		Moment (kN–m)
			${\textstyle a_{cx}}$	${\textstyle a_{cx}+a_{cy}}$	${\textstyle a_{cx}}$	${\textstyle a_{cx}+a_{cy}}$	${\textstyle a_{cx}}$	${\textstyle a_{cx}+a_{cy}}$	${\textstyle a_{cx}}$	${\textstyle a_{cx}+a_{cy}}$
100	3.1	5.25	0.370	0.370	56.59	67.44	106.55	122.69	186.94	193.27
		6.25	0.400	0.400	58.35	69.13	110.27	126.41	191.74	198.07
300	3.6	8.25	0.496	0.496	69.05	81.53	152.26	174.02	301.16	311.07
		10.25	0.495	0.495	70.40	82.83	155.55	177.31	305.00	314.91
500	3.8	9.25	0.545	0.545	73.39	86.55	171.05	195.30	354.95	366.61
		14.25	0.440	0.440	75.16	88.25	175.56	199.80	360.25	371.90
800	4.35	11.30	0.483	0.407	84.55	99.60	226.04	257.82	532.22	549.70
		16.30	0.377	0.341	86.03	101.02	230.29	262.06	538.80	556.29
1000	4.5	12.30	0.370	0.370	87.81	103.37	243.00	277.00	590.41	609.77
		18.30	0.332	0.332	89.12	104.62	246.86	280.86	596.63	615.98
1500	4.6	16.30	0.373	0.373	90.85	106.71	257.25	292.78	635.93	656.60
		20.30	0.305	0.305	91.17	107.03	258.22	293.75	637.39	658.07

Figure 6 Grid spacing distribution for wave height and pressure for VCP accelerogram

Figure 7 Grid spacing distribution for all parameters and VCP accelerogram

Table 2 shows the recommended values of mesh separation Δy to get certain error level for both records considering horizontal and vertical acceleration at the same time. Suggestions are based on the average minus the standard deviation values showed in Figures 6 and 7 for VCP record. A same criterion is used for CDA record. As it can be observed from Table 2, for small errors, similar recommended values are obtained for both records, while mesh spacing is a little more conservative for VPC accelerogram for larger error levels. Thus, values shown in Table 2 can be used as reference to create the mesh for the desired error level when perform the described numerical model.

Table 2 Recommended mesh spacing to achieve the expected error

Error	Recommended mesh spacing (m)
	VCP record (impulsive motion)		CDA record (sloshing effect)
	Wave height & pressure	All parameters	Wave height & pressure	All parameters
10–1	0.45	0.13	0.50	0.20
10–2	0.20	0.06	0.25	0.08
10–3	0.08	0.04	0.08	0.03
10–4	0.03	0.02	0.03	0.02
10–5	0.02	0.01	0.02	0.01

Since reasonably similar recommended values are obtained even for two records that induce very different behavior in the liquid–tank system, it is expected that comparable results can be obtained for accelerograms which leads to an intermediate behavior respect to those here presented.

Conclusions

The suggested values of mesh separation Δy presented in Table 2 can be used as a guide to perform analysis of seismically excited water tanks. This can be done even of thanks are not rectangular, because normally an irregular mesh is transformed into a rectangular system to apply the FDM.

The forces magnitude on the walls appears to be directly related to the peak ground acceleration. Similarly, the influence of vertical acceleration on the results tends to be proportional to the magnitude of peak vertical acceleration, i.e.: if peak vertical acceleration is small, results tend not to be affected. Moreover, a large sloshing effect not necessarily induces large forces on tank boundaries.

Each analysis was performed in a computer with an Intel® Xeon® X5650 @ 2.67 GHz processor that never required more than two hours to solve the system for the entire accelerogram and meshes with smaller spacing, which have near 400 thousand points. The numerical model was coded in Fortran 95 using LU factorization algorithm with compressed sparse row storage scheme to solve the equations system. Whereas some commercial programs that solve the Navier–Stokes equations may require one of two days of execution to solve a similar problem, one or two hours of computational time (depending on the required precision) for the numerical model may only be needed. Therefore, numerical model presented can be and excellent alternative to simplified model used in design standards and guidelines to analyze and design water storage tanks.

Acknowledgements

The authors acknowledge the support of the Universidad de Guanajuato and the Universidad Michoacana de San Nicolás de Hidalgo to develop the presented paper. Also, the authors thank the reviewers for their comments and suggestions, which helped to improve this paper.

References

[1] American Waters Works Association (AWWA). Steel water storage tanks – Design, construction, maintenance and repair. McGraw–Hill, 2010.

[2] Priestley MJN, Davidson BJ, Honey GD, Hopkins DC, Martin RJ, Ramsey et al. editors. Seismic design of storage tanks – Recommendations from the New Zealand National Society of Earthquake Engineering. Wellington, New Zealand. 1986.

[3] Comisión Federal de Electricidad (CFE). Manual de Diseño de Obras Civiles – Diseño por Sismo. Instituto de Investigaciones Eléctricas, México. 2015.

[4] American Concrete Institute (ACI). Seismic Design of Liquid–Containing Concrete Structures and Commentary ACI 350.3–06, USA, 2006.

[5] Housner GW. The dynamic behavior of water storage tanks. Bulletin of Seismological Society of America 1963; 53:381–387.

[6] Veletsos AS, Yang JY. Earthquake response of liquid storage tanks. Proceeding of the 2^nd Annual Engineering Mechanics Division ASCE. 1977. 1–24

[7] Lin G, Liu J, Li J, Hu Z. A scaled boundary finite element approach for sloshing analysis of liquid storage tanks. Engineering Analysis with Boundary Elements 2015; 56:70–80.

[8] Chen W, Haroun MA, Liu F. Large amplitude liquid sloshing in seismically excited tanks. Earthquake Engineering & Structural Dynamics 1996. 25:653–669.

[9] Hernández–Barrios H, Heredia–Zavoni E, Aldama–Rodríguez AA. Nonlinear sloshing response of cylindrical tanks subjected to earthquake ground motion. Engineering Structures 2007. 29:3364–3376.

[10] Hernández–Barrios H, Hernández–Martínez A, Valdés–Vázquez JG. Non–linear sloshing effect on storage tanks subjected to high earthquake ground motion. Revista Internacional de Métodos Numéricos en Ingeniería 2015; 31:198–206.