Abstract
It is well known that the performance of solar cells may significantly suffer from local electric defects. Accordingly, infrared thermography (i.p. lock-in thermography) has been intensely applied to identify such defects as hot spots. As an imaging method, this is a fast way of module characterization. However, imaging leads to a huge amount of data, which needs to be investigated. An automatized image analysis would be a very beneficial tool but has not been suggested so far for lock-in thermography images. In this manuscript, we describe such an automatized analysis of solar cells. We first established a robust algorithm for segmentation (or recognition) for both, the PV-module and the defects (hot spots). With this information, we then calculated a parameter from the IR-images, which could be well correlated with the maximal power (Pmpp) of the modules. The proposed automatized method serves as a very useful foundation for faster and more thorough analyses of IR-images and stimulates the further development of quality control on solar modules.
Introduction
Energy supply by renewable sources such as solar modules (PV) will be a key issue for societies for the next decades. Common solar cells of the “first generation” (based on Silicon) contribute significantly to the electricity generation in various countries already today [1]. The success story of PV was heavily promoted by decreasing silicon-PV prices. However, solar cells based on thin film absorbers, such as CIGS, CdTe, or organic photovoltaics (OPV), start to gain larger parts of the market share. For illustration, about 10% of the installed modules today are based on thin film technology [2]. This is very promising as thin film solar modules have a strong potential for further substantial decrease in price, such enabling a further increase in green electricity production.
Solar cells based on organic compounds are definitely one of the most thrilling options when aiming for a huge decrease in production costs. One key aspect here is the possibility to print organic solar cells in large scale, which would decrease strongly the price of OPV. While the production of silicon PV is a rather mature process, processing of organic solar cells still exhibits room for improvement. One factor, which decreases the efficiency of organic solar cells, is electrical defects introduced during production. We want to point out that electrical defects also may and do occur when producing inorganic solar cells. The detrimental effect of “hot spots” has been reported in a various number of publications for different solar cell types (for example for silicon [3-10], CIGS [11-16], CdTe [17-19] and for OPV [20-23]). In any case, an automatized recognition and analysis of the defects is a highly desirable tool.
Electrical defects lead to local short circuit currents with heat being dissipated at the hot spot thereby reducing the performance of the solar cell [13, 24]. Origin of such local short circuits may be bad edge isolation or small electrical conductive contamination connecting locally front and back contact. Identification of such defects has been found to be an important task and, accordingly, the problem has been tackled in particular by fast imaging via IR cameras. The localization of even very small hot spots (showing only a minor temperature gradient) may be realized by applying lock-in thermography [25]. In this method, a pulsed excitation and a phase-sensitive detection increase the sensitivity vastly. The method is named dark lock-in thermography (DLIT) when applying electric current for excitation of the samples. By applying a voltage sweep (reverse and forward bias), DLIT enables a detailed defect characteristics [26]. Accordingly, DLIT is an important and commonly used tool in R&D labs of solar cell manufactures.
Processing conditions generally do vary over time when producing solar cells. These fluctuations most likely affect the composition, and the morphology of the module, as well as the number and types of defects. Hence, a large number of modules are studied and, in particular true for imaging methods, a large data set needs to be analyzed. IR-Images of the modules contain the foreground (the actual module) and a background. Furthermore, there may be hot spots on the foreground, which reduce the performance of the module. An algorithm, which automatically recognizes or detects both, the foreground and the defects, would be of great help to thoroughly analyze the huge amount of data obtained in R&D labs when aiming for a detailed characterization of defects on solar cells. This is, because an automatized analysis of the influence of defects on the module performance may be carried out with this information.
In this study, we describe an automatized analysis of lock-in thermography images and provide a proof-of-principle of its applicability for solar cell quality analysis. To do so, we establish an algorithm, which allows for an automatized segmentation of the module and an automatized segmentation of the defects. With segmentation we mean the recognition or detection of the according pixels of the digital image, that is, the pixels belonging to the solar module and the pixels belonging to hot spots. We then post-process the images and correlate the calculated image parameter with the crucial electrical module parameter for quality control, the maximum power of the module (Pmpp). The maximum power of a module is the key parameter for the price of module. Next to Pmpp, important parameters are the open circuit voltage Voc and the short circuit current Jsc. We focus our work on organic solar cells; however, the described method is not restricted at all to OPV.
Materials and Methods
We led the proof-of principle with innovative semitransparent test OPV modules produced in our lab (Fig. 1). The module substrate size was 16.5 cm × 16.5 cm consisting of 30 individual cells on an active area of 197 cm2. We processed four modules with the same processing parameters as described below.
|
|
|
Figure 1. Visible image of the investigated semitransparent modules. |
Inverted structure OPV devices were processed on fluorine-doped tin oxide (FTO) coated glass with the layer sequence ZnO nanoparticles/PBTZT-stat-BDTT-8: phenyl-C61-butyric acid methyl ester (PCBM)/poly(3,4-ethylenedioxythiophene)/polystyrene sulfonate (PEDOT:PSS)/silver nanowires (AgNW). FTO substrates were laser patterned to achieve P1 with a fluence of 0.41 J/cm2, 50% overlap and 0.9 J/cm2, 98% overlap, respectively. All layers were processed via slot-die coating with a 20 cm wide heatable slot-die head. ZnO nanoparticles dispersed in isopropyl alcohol (Nanograde AG, Zurich, Switzerland) were coated via slot-die coating optimizing coating and drying conditions to achieve a film thickness of 50 nm. Afterwards, the layer was dried at 80°C for 5 min. For the photoactive layer (PAL), PBTZT-stat-BDTT-8 was purchased from Merck Chemicals GmbH, Darmstadt, Germany and PCBM (technical grade 99%) from Solenne BV, Groningen, the Netherlands, and dissolved at a concentration of 35 mg/mL in a weight ratio 1:2 in o-xylene: tetrahydronaphthalene (9:1) and stirred for 12 h at 80°C before coating. The PAL was then slot die coated aiming at a dried film thickness of 290 nm. PEDOT:PSS (Clevios FHC) from Heraeus was diluted in deionized water (1:1 volume ratio) and then coated via slot-die coating aiming at a dried film thickness of 100 nm. The substrates were then annealed at 120°C for 5 min and afterwards patterned by laser ablation to achieve P2 (fluence of 0.08 J/cm2, 94% overlap, 3 times). The final wet film application completing the devices was done by slot-die coating AgNWs (Cambrios Advanced Materials Corp, Sunnyvale, CA, USA.) from aqueous solution which were afterwards annealed at 120°C for 5 min and laser patterned to achieve electrical separation (P3 – fluence of 0.08 J/cm2 and 94% overlap). Laser patterning was achieved with an LS 7xxP setup built by LS Laser Systems GmbH (München, Germany). The heart of the system is a femtoREGENTM UC- 1040–8000 fsec Yb SHG from High Q Laser GmbH (Rankweil, Austria) emitting at 1040 nm (fundamental wavelength) and 520 nm (first harmonic wavelength) with a pulse duration of <350 fsec at repetition rates up to 960 kHz. The devices were encapsulated in glass with DELO Katiobond LP655. Current–voltage (IV) characteristics were measured with a source measurement unit from Keysight (Santa Rosa, CA, USA) and a Tracer software (ReRa Tracer 3, ReRa Solutions, Nijmegen, The Netherlands). Illumination was provided by an LOT quantum device solar simulator Class A, AM1.5G spectra at 1000 W/m2.
After production, characterization of the samples was carried out by DLIT (dark lock-in thermography). In order to acquire lock-in IR-images, the IR-camera (Equus 327k; IRcam GmbH, Erlangen, Germany) sends a modulation signal to an electrical excitation. This way both devices are synchronized, which allows the application of a correlation function. The software of the camera then integrates (weighted average) over all captured images, in order to reduce the noise of the final output. The result is a phase-sensitive average of IR-images, commonly known lock-in thermography. When the measurement is done in the absence of illumination (electrical excitation instead), it is called dark lock-in thermography (DLIT). It is called illuminated lock-in thermography (ILIT) when pulsed light is used for excitation.
The measurements were performed at an excitation alternating between 0 V and 35 V. The applied voltage was in the low excitation regime to enhance shunt localization. The Stirling cooled InSb-detector of the camera is sensitive between 1 and 5 μm. The detector size is 640 × 512 pixels. Further settings of the camera were a lock-in frequency of 1 Hz, a frame integration time of 1 msec, and an image acquisition time of 15 min. The thickness of glass substrate was 3.2 mm and, at a frequency of 1 Hz, the captured signal dominantly stemmed from the active layer [27]. Amplitude and phase images were exported as raw data for further segmentation and image analysis.
Algorithm
Automatized recognition of diverse objects has been successfully implemented in machine vision, for example, in food industry [28] or in printed electronics [29]. Rather large noise makes object segmentation more difficult when applying infrared thermography [30, 31]. With segmentation, we mean the recognition of pixels belonging to a certain object in an image. Thus, the foreground may be separated from the background of an image, for example. Yet, a variety of algorithms has been proposed for standard thermography depending on the application, such as IR-surveillance [32-34] or target detection [35]. Unfortunately, the problem of low signal to noise ratio generally becomes much more challenging when applying highly sensitive lock-in thermography.
In a recent publication, we proposed an algorithm for automatized segmentation of PV-modules characterized by highly sensitive lock-in thermography [36]. This method was stimulated by algorithms developed to detect the background and foreground in images obtained by commercial scanners [37-39]. The method proved to work even under extremely low signal to noise ratio of 1.09 (for more details see [36], i.p. Fig. 3 of that reference). In short, the algorithm worked by identifying the four edges of the solar module individually by searching for the edge pixels. The edge pixels then represent the outer frame of the PV-module (this means all pixels inside the frame belong to the module or foreground). Searching was performed by a “moving standard deviation” process. The aim of this process is, simply speaking, to minimize the (relative) standard deviations of the two regions (background and foreground). The edge pixels are calculated by minimizing the standard deviation. For more details, the reader is referred to the original publication [36]. In the current paper, we apply the same algorithm to segment the foreground or active area of the solar modules. However, instead of using the amplitude images (as in the original paper), we use the phase image this time as the phase images exhibit a better contrast regarding the edges.
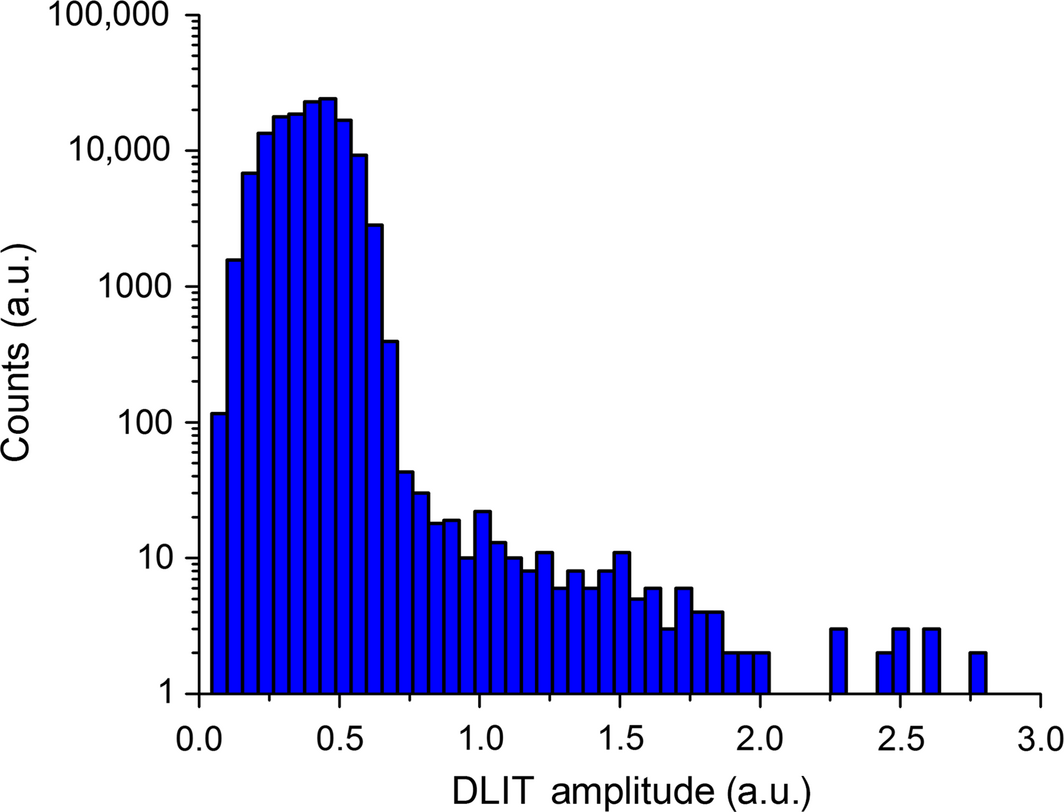
Next to the segmentation of the module (i.e., the identification of the foreground pixels), the segmentation of the defects (hot spots) is required for a successive quality analysis. The physical meaning of the identified hot spots is a large local short circuit current. Standard segmentation algorithms such as Otsus method [40] do not work properly as there is no bimodal distribution of the intensities. Figure 2 shows exemplarily a histogram of a DLIT image taken in this study (logarithmic scale). The peak corresponds to the foreground (PV module), while values significantly lower than the peak correspond to the background. As a remark, one can also directly see from this figure that such a bimodal global segmentation algorithm would not work to identify the foreground from the background.
|
|
|
Figure 2. Example of an intensity histogram of a dark lock-in thermography image (amplitude) recorded in this study (in a histogram, the x-axis resembles an intensity ranges or bins and the y-axis the number of pixels in the according bin). The histogram was calculated for 60 bins (rather low value for better visualization). |
Instead of a second peak, the hot spots are aligned in a very long and low tail in the histogram. Accordingly, two characteristics of the defects will be exploited for hot spot segmentation. Defects (1) show a large intensity in the image, and (2) they are rather sparsely distributed over the module. This leads obviously to the conclusion to search for outstandingly hot pixels and, at the same time, values, which have a low probability of occurrence.
The algorithm for defect identification is described in the following. We use the histogram information of the amplitude images for hot spot detection (see Fig. 2 as an example). P is the probability (of a certain intensity), which can be calculated by eq. (1), with N as number of total pixels of the image and n as numbers of pixels, or counts, in the respective bin (see Fig. 2, y-axis). The peak intensity is called Imax (eq. (2)). In our case, we apply the amplitude images, this means, the intensity is the DLIT amplitude. Only two parameters are required for the segmentation algorithm: the numbers of bins, nBins, typically 256, and a factor f (remark: in Fig. 2, we used only 60 bins for better visualization). The latter parameter characterizes the sensitivity (by defining the maximal threshold probability Pth, see eq. (3)) of the hot spot detection and was set to 0.1. The idea of “outstandingly hot pixels with low probability” is mathematically defined by eq. (4), the core of the rather simple but robust algorithm. BWdef denotes the binary image containing the defect pixels (hot spots) with x and y as coordinates of the image and I as the original intensity image (DLIT, amplitude). This means, pixels in the image BWdef with value 1 belong to a hot spot while pixels with value 0 do not belong to a hot spot. In summary, we use an additional probability threshold compared to conventional intensity thresholding.
|
|
(1) |
|
|
(2) |
|
|
(3) |
|
|
(4) |
Results
We examined four OPV modules produced in our lab. Figure 3 shows the phase images of the DLIT imaging on the left side and the amplitude images on the right side in gray values. First of all, we tested the segmentation of the foreground by the algorithm. The best results for this segmentation are found when applying the phase images. In doing so, all four modules were segmented correctly. The automatically segmented edges are marked as yellow rectangles in Figure 3. All pixels inside the yellow rectangle belong to the module and their intensities are referred to as Imodule in this paragraph.
|
|
|
Figure 3. Dark lock-in thermography images of the four different modules. On the left side the phase images are depicted, on the right side the amplitude images. Yellow lines indicate the segmentation of the PV-module (foreground) which was carried out on the phase images. Module segmentation may be applied also to the amplitude image (both images are recorded simultaneously). The red lines indicate the segmented hot spots (or defects), which was carried out with the amplitude images. |
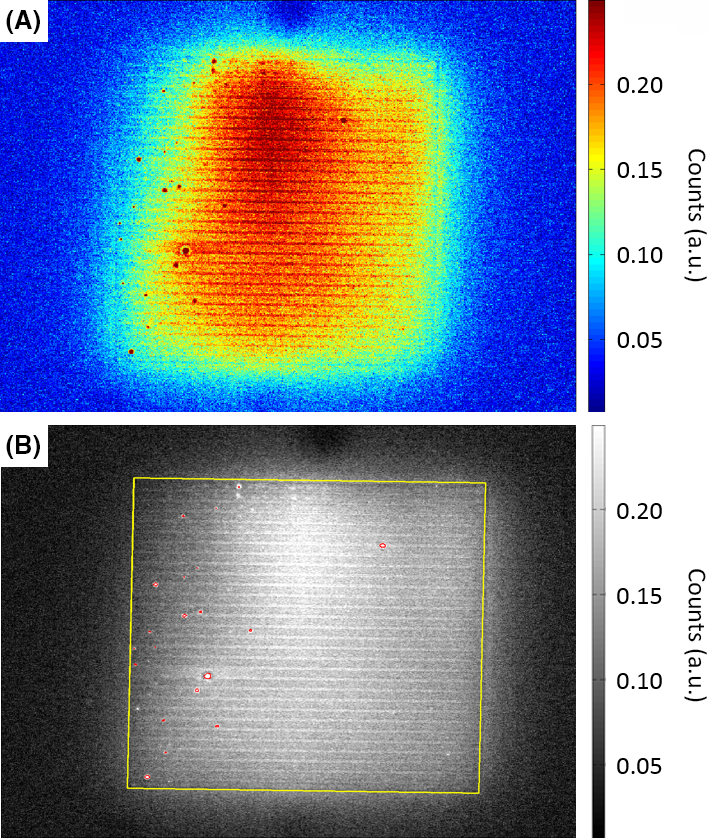
Next, we tested the algorithm for segmentation of the hot spots. Rather few hot spots were detected as already mentioned in the section “algorithm”, see also the histogram in Figure 2. The defects were identified in the amplitude images, see the red indicated pixels in Figure 3, right. The pixels inside the red boundary lines recognized as hot spots and their intensities are referred to as Idef. The edge of the module, indicated in yellow, may be copied from the phase image as both images are calculated from the same phase-sensitive transient lock-in measurement. Accordingly, the module cannot be moved unintentionally in between recording both images. Therefore, the yellow frame has exactly the same position in the amplitude image and phase image. The number of detected “hot pixels” varied between 86 (sample number 2) and 411 (sample number 1). Sample 3 exhibited 131 defect pixels and sample 4 showed 134 defect pixels. The defect pixels are hard to distinguish by eye when looking at the grey scale images in Figure 3, right. To verify that the identified pixels are hot spots, Figure 4 compares the DLIT-amplitude image of one sample displayed in a colored intensity scale (Fig. 4A) and in grey scale values (Fig. 4B). The hot spots can more easily be located by eye in the colored image and were correctly identified by the algorithm, compare Figure 4B. The colored image, though, has the disadvantage of a more difficult identification of the module edges by eye. This example illustrates the large gradients in temperature and the difficulty of setting the “correct” contrast. Also, by looking at the “freckles” in the images in Figure 4, one can get an impression of the noise present in the highly sensitive lock-in thermography images.
|
|
|
Figure 4. (A) Dark lock-in thermography (amplitude) image of sample 4 in color-coded scale and (B) in grey scale. Yellow lines indicate the PV-module edge and the right lines indicate the detected hot spots by the algorithm. |
After recognition of the foreground (active PV module area) and the hot spots, a parameter (scalar value) describing or “summarizing” the DLIT image may be determined. The aim is to correlate this parameter with electrical parameters for quality analysis. One of the most crucial parameters in terms of quality control is the maximum power, Pmpp. Previous work [13, 25] showed that a promising IR-parameter candidate is the ratio of the intensity of the hot spots and the intensity of the module (as a kind of base signal). The parameter is calculated according to eq. (5). The IR-parameter basically quantifies a contrast between the hot spots and the module normal active area signal. Here, Idef denotes the intensity vector of the hot pixels, Imodule the intensity vector of the module (foreground), Adef the area (or number of pixels) of the defect vector, and Amodule the area (or number of pixels) of the module vector.
|
|
(5) |
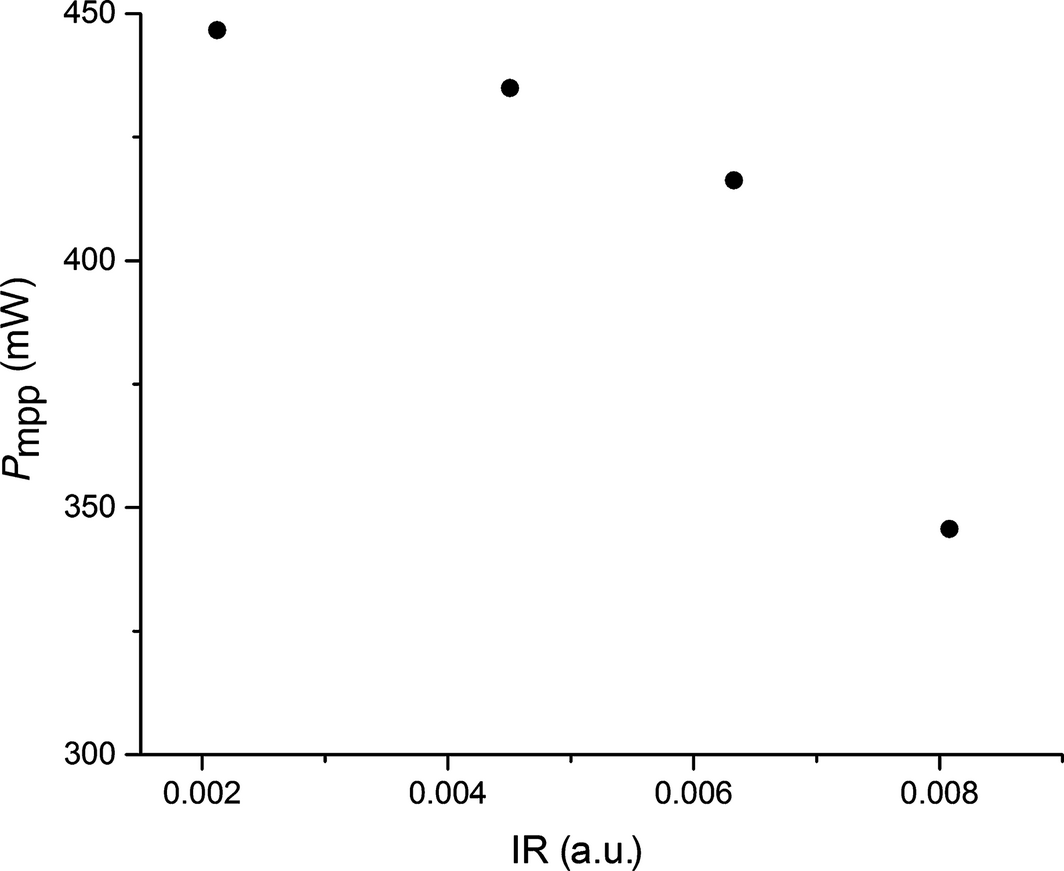
We correlate this parameter with Pmpp measured by the JV-curve at standard measurement conditions (STM). Figure 5 shows the result with the IR parameter on the x-axis and Pmpp on the y-axis. A clear dependency between the IR-parameter and Pmpp is observed. In our proof of principle, we found a highly nonlinear decrease in Pmpp with increasing value of the IR-parameter. This behavior depends on various influences, such as the thickness of the encapsulation glass, IR-camera, camera calibration or, of course, the choice of the IR-parameter. Accordingly, different relations between Pmmp may be found when applying the proposed analysis to a different PV-module types and/or using a different imaging setup. In any case, our results strongly illustrate the suitability of this analysis method for automatized quality control. In the current work, we proofed that the automatized analysis works even for encapsulated modules. Segmentation of IR-images of nonencapsulated samples (taken for example directly in the production line) is much easier due to larger thermal gradients (as glass is a thermal insulator). Previous work based on a manual analysis proved also the applicability of ILIT (illuminated lock-in thermography) as a potential contactless measurement tool for quality control [11]. Accordingly, a transfer of this analysis to ILIT images, and therefore a contactless quality control tool, is straight forward.
|
|
|
Figure 5. Maximal power (Pmpp) of the modules depending on the IR-parameter (calculated according to eq. (5)) derived from the dark lock-in thermography amplitude images. Segmentation of the PV-module and the hot spots was carried out prior to this analysis. |
Conclusions
We present a combined approach of an automatized segmentation of a PV-module and the defects (hot spots) on the module. Both, segmentation of the module and the hot spots, were carried out successfully for all investigated four encapsulated OPV modules. In previous work [36], module detection worked also for all 10 investigated CIGS modules (samples without front cover glass). We applied the segmentation algorithm to 10 CIGS mini-module, and all defects (hot spots) and the boundaries of the modules were determined correctly (by using the same values of the parameters of the algorithm, f and Nbins). Accordingly, we believe that the algorithm is robust and may be applied to any kind of thin film solar cells. The transfer of the method is straight forward, though, in some cases an adaptation of the algorithm parameters might be necessary. The automatized segmentation is an important step toward a thorough analysis of IR-images (and also potentially for luminescence images). We successfully correlated an IR-parameter calculated from the lock-in thermography images with the maximum power (Pmpp) of the modules as a proof-of-principle.
The presented approach may be utilized as foundation of adapted (and if necessary more sophisticated) automatized evaluation of large data sets obtained by imaging of PV. The presented (or similar) algorithm facilitates a thorough statistical analysis of a large number of samples also under different working conditions. This strongly helps to improve tools for quality control and also helps to better understand the photo-physical impact of defects on solar modules. While the effect of single defects on the solar module performance have been successfully investigated [13, 41, 42], many open questions remain when studying whole modules with several defects.
Acknowledgments
We gratefully acknowledge the German Ministry of Economy and Energy (OptiCIGS, 0325724C) for funding. Andreas Vetter received funding through the “Bavaria on the move initiative” (Energie Campus Nürnberg) by the State of Bavaria. We thank Viktor Antlitz and Andre Karl for helping with the experimental work. Andre Karl gratefully acknowledges funding by the German Research Foundation (DFG, “Entwicklung von bildgebenden Verfahren zur Defekterkennung in Tandem Solarzellen”).
Conflict of Interest
None declared.
References
- Cumulative installed solar photovoltaics capacity in leading countries and the world, 2000–2013. Earth Policy Institute, Washington, DC. 2015
- Forstner, H., S. Bandil, M. Zweegers, R. Bollen, G. Coletti, W. Sinke. 2013 Results. International Technology Roadmap for Photovoltaic (ITRPV). VDMA Photovoltaic Equipment, Frankfurt, Germany.
- Breitenstein, O., J. P. Rakotoniaina, and M. H. Al Rifai. 2003. Quantitative evaluation of shunts in solar cells by lock-in thermography. Prog. Photovolt. Res. Appl.11:515–526.
- Breitenstein, O., J. P. Rakotoniaina, M. H. Al Rifai, and M. Werner. 2004. Shunt types in crystalline silicon solar cells. Prog. Photovolt.12:529–538.
- Michl, B., M. Padilla, I. Geisemeyer, S. T. Haag, F. Schindler, M. C. Schubert et al. 2014. Imaging techniques for quantitative silicon material ans solar cell analysis. IEEE J. Photovolt.4:2156–3381.
- Johnston, S., H. Guthrey, F. Yan, K. Zaunbrecher, M. Al-Jassim, P. Rakotoniaina et al. 2014. Correlating multicrystalline silicon defect types using photoluminescence, defect-band emission, and lock-in thermography imaging techniques. IEEE J. Photovolt.4:348–354.
- Rißland, S., T. M. Pletzer, H. Windgassen, O. Breitenstein, and A. S. Preparation. 2013. Local thermographic efficiency analysis of multicrystalline and cast-mono silicon solar cells. IEEE J. Photovolt.3:1192–1199.
- Geisemeyer, I., F. Fertig, W. Warta, S. Rein, and M. C. Schubert. 2014. Prediction of silicon PV module temperature for hot spots and worst case partial shading situations using spatially resolved lock-in thermography. Sol. Energy Mater. Sol. Cells120:259–269.
- Shen, C., K. Wang, and M. A. Green. 2014. Fast separation of front and bulk defects via photoluminescence on silicon solar cells. Sol. Energy Mater. Sol. Cells128:260–263.
- Augarten, Y., T. Trupke, M. Lenio, J. Bauer, J. W. Weber, M. Juhl et al. 2013. Calculation of quantitative shunt values using photoluminescence imaging. Prog. Photovolt. Res. Appl.21:933–941.
- Vetter, A., F. Fecher, J. Adams, R. Schaeffler, J.-P. Theisen, C. J. Brabec et al. 2013. Lock-in thermography as a tool for quality control of photovoltaic modules. Energy Sci. Eng.1:12–17.
- Adams, J., A. Vetter, F. Hoga, F. Fecher, J. P. Theisen, C. J. Brabec et al. 2014. The influence of defects on the cellular open circuit voltage in CuInGaSe2 thin film solar modules-An illuminated lock-in thermography study. Sol. Energy Mater. Sol. Cells123:159–165.
- Vetter, A., F. S. Babbe, B. Hofbeck, P. Kubis, M. Richter, S. J. Heise et al. in press. Visualizing the performance loss of solar cells by IR-thermography - an evaluation study on CIGS with artificially induced defects. Prog. Photovolt. Res. Appl.24:1001–1008.
- Misic, B., B. E. Pieters, U. Schweitzer, A. Gerber, and U. Rau. 2015. Thermography and electroluminescence imaging of scribing failures in Cu(In, Ga)Se-2 thin film solar modules. Phys. Status Solidi. A Appl. Mater. Sci.212:2877–2888.
- Johnston, S., T. Unold, I. Repins, A. Kanevce, K. Zaunbrecher, F. Yan et al. 2012. Correlations of Cu(In, Ga)Se-2 imaging with device performance, defects, and microstructural properties. J. Vac. Sci. Technol., A30:111–114.
- Gerber, A., V. Huhn, T. M. H. Tran, M. Siegloch, Y. Augarten, B. E. Pieters et al. 2015. Advanced large area characterization of thin-film solar modules by electroluminescence and thermography imaging techniques. Sol. Energy Mater. Sol. Cells135:35–42.
- McMahon, T. J., T. J. Berniard, and D. S. Albin. 2005. Nonlinear shunt paths in thin-film CdTe solar cells. J. Appl. Phys.97:054503.
- Johnston, S., T. Unold, I. Repins, R. Sundaramoorthy, K. M. Jones, B. To et al. 2010. Imaging characterization techniques applied to Cu(In,Ga)Se[sub 2] solar cells. J. Vac. Sci. Technol.28:665.
- Katz, N., M. Patterson, K. Zaunbrecher, S. Johnston, and J. Hudgings. 2013. High-resolution imaging of defects in CdTe solar cells using thermoreflectance. Electron. Lett.49:1559–1560.
- Hoppe, H., J. Bachmann, B. Muhsin, K.-H. Druee, I. Riedel, G. Gobsch et al. 2010. Quality control of polymer solar modules by lock-in thermography. J. Appl. Phys.107:014505.
- Bachmann, J., C. Buerhop-Lutz, R. Steim, P. Schilinsky, J. A. Hauch, E. Zeira et al. 2012. Highly sensitive non-contact shunt detection of organic photovoltaic modules. Sol. Energy Mater. Sol. Cells101:176–179.
- Roesch, R., D. M. Tanenbaum, M. Jorgensen, M. Seeland, M. Baerenklau, M. Hermenau et al. 2012. Investigation of the degradation mechanisms of a variety of organic photovoltaic devices by combination of imaging techniques-the ISOS-3 inter-laboratory collaboration. Energy Environ. Sci.5:6521–6540.
- Roesch, R., F. C. Krebs, D. M. Tanenbaum, and H. Hoppe. 2012. Quality control of roll-to-roll processed polymer solar modules by complementary imaging methods. Sol. Energy Mater. Sol. Cells97:176–180.
- Straube, H., J.-M. Wagner, J. Schneider, and O. Breitenstein. 2011. Quantitative evaluation of loss mechanisms in thin film solar cells using lock-in thermography. J. Appl. Phys.110:084513.
- Breitenstein, O., W. Warta, and M. Langenkamp. 2010. Lock-in thermography, basics and use for evaluating electronic devices and materials, 2nd ed. Springer, Berlin.
- Breitenstein, O.. 2012. Local efficiency analysis of solar cells based on lock-in thermography. Sol. Energy Mater. Sol. Cells107:381–389.
- Straube, H., and O. Breitenstein. 2011. Infrared lock-in thermography through glass substrates. Sol. Energy Mater. Sol. Cells95:2768–2771.
- Brosnan, T., and D.-W. Sun. 2004. Improving quality inspection of food products by computer vision – a review. J. Food Eng.61:3–16.
- Wu, W. Y., M. J. J. Wang, and C. M. Liu. 1996. Automated inspection of printed circuit boards through machine vision. Comput. Ind.28:103–111.
- Lin, C.-L., C.-W. Kuo, C.-C. Lai, M.-D. Tsai, Y.-C. Chang, and H.-Y. Cheng. 2011. A novel approach to fast noise reduction of infrared image. Infrared Phys. Technol.54:1–9.
- Zhu, B., X. Fan, Z. D. Cheng, D. Wang, Y. Q. Fang, and X. S. Chen. 2015. An IR strong clutter background suppression algorithm based on sparse kernel method. Tien Tzu Hsueh Pao/Acta Electron. Sin.43:716–721.
- Elguebaly, T., and N. Bouguil. 2013. Finite asymmetric generalized Gaussian mixture models learning for infrared object detection. Comput. Vis. Image Underst.117:1659–1671.
- Bankman, D. J., and T. M. Neighoff. 2008. Pattern recognition for detection of human heads in infrared images. Opt. Eng.47:046404.
- Han, J., A. Gaszczak, R. Maciol, S. E. Barnes, and T. P. Breckon. 2013. Human pose classification within the context of near-IR imagery tracking. Proc. SPIE Int. Soc. Opt. Eng.8901:89010E.
- Wang, X., G. Lv, and L. Xu. 2012. Infrared dim target detection based on visual attention. Infrared Phys. Technol.55:513–521.
- Vetter, A., J. Hepp, and C. J. Brabec. 2016. Automatized segmentation of photovoltaic modules in IR-images with extreme noise. Infrared Phys. Technol.76:439–443.
- Herley, C.. 2004. Efficient inscribing of noisy rectangular objects in scanned images. Proc. Int. Conf. Image Process. ICIP, 4:2399–2402.
- Guerzhoy, M., and Z. Hui. 2008. Segmentation of rectangular objects lying on an unknown background in a small preview scan image. Proceedings of the 5th Canadian Conference on Computer and Robot Vision, CRV 2008, 369–375.
- Kurilin, I. V., I. V. Safonov, M. N. Rychagov, H. Lee, and S. H. Kim. 2014. High-performance automatic cropping and deskew of multiple objects on scanned images. Proc. SPIE Int. Soc. Opt. Eng., 9016:90160B.
- Otsu, N.1979. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man. Cybern.9:62–66.
- Konovalov, I. E., O. Breitenstein, and K. Iwig. 1997. Local current-voltage curves measured thermally (LIVT): a new technique of characterizing PV cells. Sol. Energy Mater. Sol. Cells48:53–60.
- Fecher, F. W., A. P. Romero, C. J. Brabec, and C. Buerhop-Lutz. 2014. Influence of a shunt on the electrical behavior in thin film photovoltaic modules – a 2D finite element simulation study. Sol. Energy105:494–504.
Document information
Published on 01/06/17
Submitted on 01/06/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?