Effect of elbow implant design parameters on loosening: A finite element analysis

Abstract

Loosening of an implant is the main complication after total elbow arthroplasty. The design parameters of the implant are a factor that contributes to the loosening of the implant. In this study, the correlation of loosening and geometry of the elbow implant component was investigated using the finite element method. Image processing software was used to construct elbow bones. Humeral and ulnar components were modeled with various cross-sections and flanges using modeling computer-aided design software. Modeling of all stems was based on conventional cemented fixation. Axial torsion and Anterior-posterior force were applied to the articular surface. Zero-displacement was applied to the proximal humerus and distal ulna. Bone graft was used between the flange and distal humerus bone. The stress shielding of bones and micro-motion were obtained in cement-implant-bone interfaces. Results showed that humeral and ulnar stems with modified diamond cross-section observed less micro-motion in the cement-bone-implant interfaces and as well as the least stress shielding in the distal humerus and proximal ulna compared to others. Furthermore, the modified flange, concave, transferred the least micro-motion to the bone-cement-implant interface and less stress shielding in distal humerus in comparison with trapezium and rectangular ones. This computational analysis represented a step in quantifying the role of interface micro-motion stress shielding of bone in initiating elbow implant loosening. A reduction of micro-motion and stress shielding through design modifications may improve the clinical outcomes.

Keywords: Micro-motion, stress shielding, lossening, elbow implant, finite element analysis

1. Introduction

Despite the wide range of advances in designing of elbow implants, loosening is the most common cause of long-term failure after total elbow arthroplasty (TEA) [1,2,3]. Loosening occurs due to three reasons: (1) Stress shielding of the bone (2) Implant-cement-bone micro-motion, and (3) articular surfaces wear [2,4,5]. Loosening is the most important reason to revise cemented elbow implants after surgery. Loosening is a mechanical incident which results in the failure of the bond between the implant and bone bed.

Micro-motion happens at the interface of mating components that belongs to one mechanical system. This phenomenon results in the displacement of a component relative to another one. Micro-motion is considered an engineering issue that points to the demand for replacing or revising the implant. Micro-motion results in the formation of micro-gaps between the surfaces, therefore it should be minimized in the interfaces. This micro-motion causes movement between surfaces and consequently loss of adhesion. With the increase of micro-motion, boundaries in interfaces would widen, which leads to migration of implant components and loosening.

Partial unloading of the bone occurs around implanted elbow components. This is due to the fact that stiffness of bone is less than the implant material. Herein, the stress distribution is changed in bone by remodeling which results in bone resorption and increment of the movement between the implant and bone (loosening) [6,7]. This phenomenon is called stress shielding. Hence, loss of distal humerus, owing to stress-shielding, must be diminished, as it may cause loosening. Therefore, in order to prevent loosening stress shielding and micro-motion must be reduced.

The geometry of the implant is a factor that contributes to the loosening of the implant. Generally, implant parameters such as stem cross-section and flange shape) affect the amount of load transfer from the implant to the bone [8,9,10]. Achievement of elbow implants is related to the way mechanical factors are transferred to the surrounding interfaces and bone. This is because the amount of transferred load to the bone is increased by implant design parameters and causes rising of stress shielding and micro-motion. The healing of interfacial tissues is related to the micro-motion in interfaces; there are harmful outcomes at higher micro-motion range (e.g. interfacial fibrous tissue formation) however, at the lower range, there is an affirmative effect (e.g. stimulation of interfacial bone formation) [6,7]. The many modifications have been carried out in the elbow implant after the first TEA. Modification of implants prepares longer survival and better functionality of previous designs [11,12,13].

Many studies have investigated the implant design to discover more knowledge of the biomechanics of the elbow. The basis of the majority of the original designs was a plain hinge joint; consequently, the complete constraint of the articulation resulted in the loosening. The modern implants are categorized in unlinked and linked hinge [14,15,16,17,18]. Linked implants are influenced by more loosening than unlinked ones. The linked implants are designed based on hinged principle. The snap-fit bushings or pins, as connection parts between humeral and ulnar components, present a semi-constrained structure which permits a small laxity in various directions (rotational, lateral, and medial planes). The loose hinge precisely simulates the normal kinematics elbow. Due to the transfer of a higher rate of stress from the interfaces, the chance of loosening is significantly higher in linked implants than unlinked ones due to receiving higher forces [19,20].

From the clinical point of view, implant component migration and advanced widening of boundaries in implant-cement-bone interfaces are radiographic indications of loosening. Duparc et al. [21] reported investigated loosening of attributed in a 2 years follow-up. The whole revised stems were loosened and 60% of them showed micro-motion [21]. The loosening process and micro-motion pattern of an elbow implant were evaluated in a clinical study. The results showed that eight of eighteen humeral components were at risk of loosening; however ulnar components were not at risk of loosening. A lateral flange was recommended flange to improve the rotational stability of the transverse and longitudinal axes [22]. A study investigated the rotation and migration of ulnar/humeral components using radiostereometric (RSA) analysis. Early micro-motion was observed for ulnar and humeral stems [23]. The effect of the various hollow-stemmed implant was assessed to minimize loosening and the impact of stress shielding using FEA by Gross et al. [36]. It was seen the growth of stress in the proximal bone at 15% for the hollow stem compared to stems with a similar outside diameter [24]. This shows using different stem shapes may decrease stress shielding and finally loosening. Huiske et al. [25] studied the relationship between bone resorption and implant flexibility using strain-adaptive bone-remodeling theory compared with FEA [25]. The bone adaptation to stress shielding was found as the result of the resorptive bone which contributes to the raise of loosening. This loosening was occurred due to interfaces micro-motion and interface debonding. Loosening does not appear with clinical symptoms in its primary stages at the present, the examination of physical evaluation and periodically radiographic are only clinically methods to define the implant loosening [2].

Studies on the state of loosening in terms of micro-motion and stress shielding due to elbow implantation are very limited according to the author's knowledge. Therefore, the purpose of present study was to investigate the mechanical loosening of an elbow implant using finite element analysis (FEA). More precisely, the study intended to determine the effect of elbow implant design parameters including flange shape and cross-section on micro-motion and stress shielding of bone. To accomplish these goals, a methodology was developed to perform FEA of elbow implant components. Image processing software was used to construct bones. A computer-aided design (CAD) and computer-aided engineering (CAE) software were used to model implant components with various flanges and cross-sections. The analysis was carried out to obtain the stress shielding of bones and micro-motion in implant-cement-bone interfaces. We hypothesized that modification of an elbow implant would lead to the reduction of implant loosening

2. Materials and Methods

2.1 Modeling of elbow bones

Mimics software (Ver.10, Materialise NV., Belgium), through computed tomography (CT), was used to construct elbow bones. CT data set involved the slice thickness of 0.7mm and the resolution of 0.477mm (Figure 1). Then, the constructed elbow bones were imported into SolidWorks. In this study, SolidWorks software was used for simulated surgery and modeling all components of the linked elbow implant. Simulated surgery of humerus and ulna bones was carried out to insert modeled implant into the constructed bone. Therefore, a hole was made in humerus/ulna bones and the implant left these bones with a hole. The initial step to prepare of the humerus was bone resection from the midportion of the capitellum and trochlea (Figure 2). As a result, the center axis of flexion-extension was identified. If the capitellum is assumed a circle and sighted from the lateral position of the elbow, the center axis of rotation is placed in the center of the circle. A similar procedure was carried out to prepare ulna (Figure 3). The ulnar component was inserted into the ulna to ensure a good fit before cementing. Conventional cemented fixation was the basis of modeling of all stems therefore, they had smooth surfaces. The optimum thickness of cement (between 1.0 and 1.5mm) was considered to avoid high failure in the cement-bone [26].

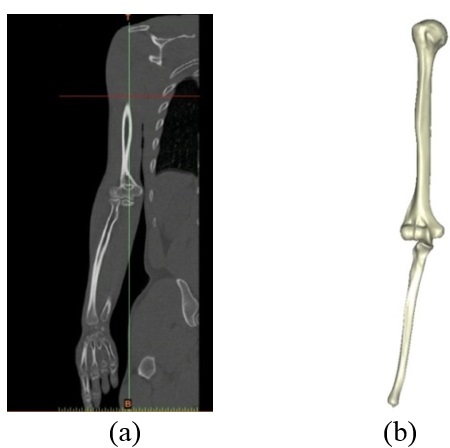
Figure 1. (a) CT data. (b) Constructed bone

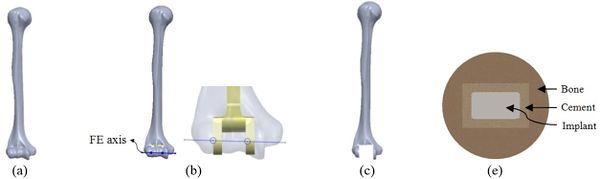
Figure 2. Simulated surgery of humerus. (a) Constructed bone. (b) Placement of implant. (c) After surgery. (d) Cement used around stem

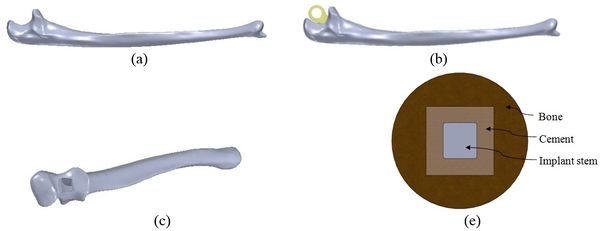
Figure 3. Simulated surgery of ulna. (a) Constructed ulna.(b) Placement of implant. (c) After surgery. (d) Cement used around stem

2.2 Modeling of Implant components

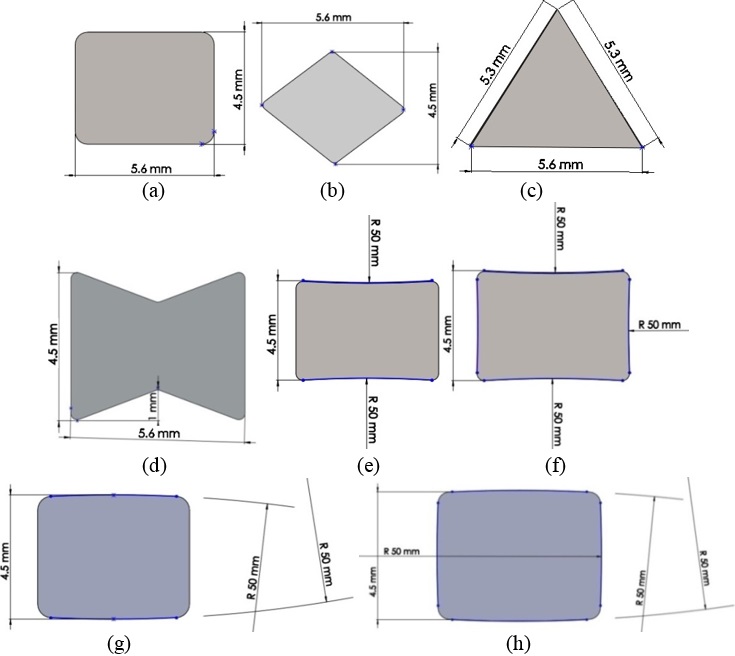
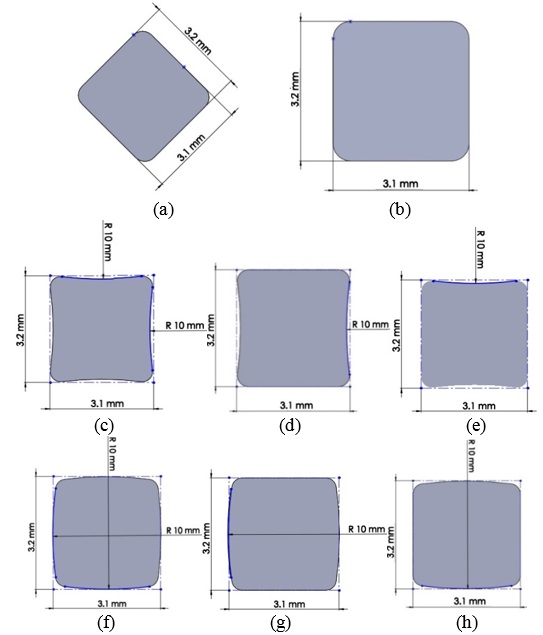
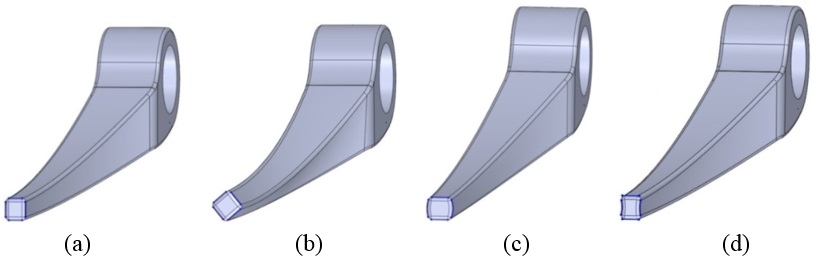
Many studies have carried out to analyze the ideal stem cross-sectional to control implant loosening. Dimension for modeling elbow implant was obtained from a real Coonrad-Morrey implant. Various shapes were modeled to modify a proper cross-section for the humeral component. The cross-sections included diamond, rectangular, triangular, width triangular, concave, and convex. The length of the humeral stem was the same for all cross-sections at 150mm (Figure 4). Several sub-designs were noticed for the concave cross-section including width concave with variant radiuses (25mm to 70mm) and all sides concave. In the same way, different sub-designs were assumed for convex cross-section, including width convex with the different radiuses (25mm to 70mm) and all sides convex (Figure 5). Furthermore, various cross-sections including concave, rectangular, convex, diamond modeled to develop a sufficient ulnar component (Figure 6). Several sub-designs were used for concave cross-section including height concave, all sides concave, and width concave (radius from 8mm to 12mm). Similarly, different sub-designs were considered for convex cross-section including width convex with various (radius of 8mm to 12mm), all sides convex, and height concave (Figure 7).

Figure 4. Different humeral stem cross-sections. (a) Rectangular. (b) Triangular. (c) Diamond. (d) Width triangular. (e) Convex. (f) Concave

Figure 5. Modelled humeral components with different cross-sections. (a) Rectangular.(b) Diamond. (c) Triangular. (d) Width triangular. (e) Width concave. (f) All sides concave. (g) Width convex. (h) All sides convex

Figure 6. Different ulnar stem cross-sections. (a) Rectangular. (b) Diamond. (c) Convex. (d) Concave

Figure 7. Modelled ulnar component with different cross-sections. (a) Diamond. (b) Rectangular. (c) All sides concave. (d) Height concave. (e) Width concave. (f) All sides convex. (g) Height convex. (h) Width convex

The anterior flange transfers a portion of the load through the elbow prosthesis stem to the distal region of the humerus, which diminishes the probability of humeral loosening [27,28]. Therefore, the flange was modeled with various shapes including concave, trapezium and rectangular. CT data of distal humerus was used to determine the curve angle of the trapezium model. The angle of where the flange faces distal humerus was nearly 7.3°. These three models were analyzed under the same cross-section (rectangular), the same humeral stem length (150mm), and similar dimensions (Figure 8). Bone graft was used between the distal humerus and flange. AP compression force (1N) and axial torsion (1N.cm) were applied to the articular surface of the humeral component.

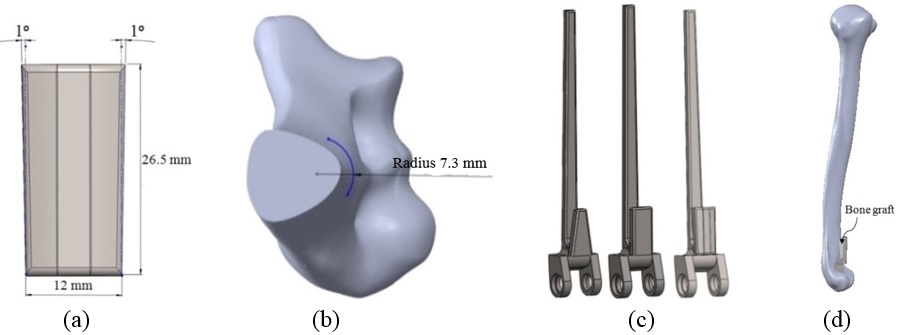
Figure 8. (a) Modelled concave flange. (b) Distal humerus angle. (c) Three various flange shapes. (d) Implanted humerus

2.3 Boundary conditions and loading

Loading levels compared to the actual physiological loads are considerably less in the majority of FEA models. Mostly, only static joint forces are applied and the rest forces (owing to the activity of ligaments, tendons, and muscles) are omitted [29,30]. In this study considers AP compression and axial torsion for FEA. An equal dual force was applied to the implant head (articular surface). AP compression (1 N) and torque (1 N.cm) were applied in distal humerus and proximal ulna (Figures 9 and 10). The proximal end of the humerus and distal end of ulna were fixed [31]. Isotropic, homogeneous, and linear elastic materials were considered for interfaces and implant (Table 1) [27,28,31,32].

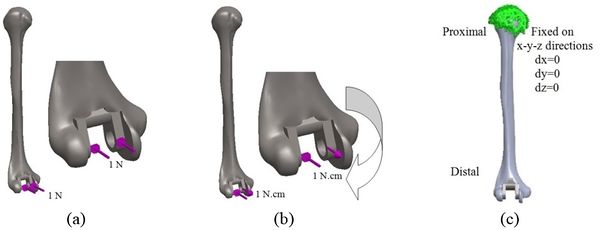
Figure 9. Humeral components. (a) Applied AP compression force. (b) Applied axial torsion force. (c) Boundary conditions

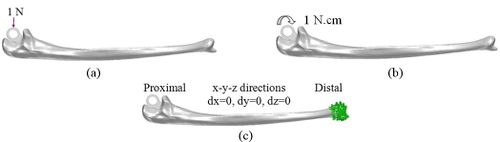
Figure 10. Ulnar component. (a) AP compression force. (b) Axial torsion force. (c) Boundary conditions

Table 1. Mechanical property of materials

Material	Elastic module (GPa)	Poison ratio
Humeral/Ulnar component (Titanium)	110	0.3
Bone	16.7	0.3
Cement	2.28	0.3

2.4 Mesh convergence

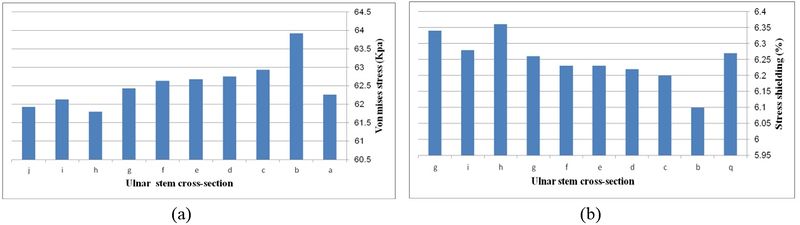
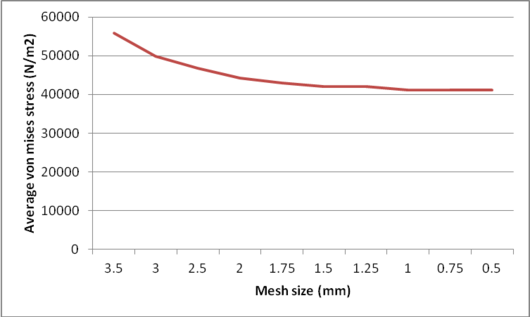
An ulnar stem was used to investigate mesh convergence. For this purpose, a series of runs were accomplished with similar conditions except for the size of the element, which was reduced between each run. Tetrahedron element sizes from 4mm to 0.5mm were utilized to mesh model (Figure 11). Average Von Mises stress in the ulnar stem is shown in Figure 12. It was seen a considerable diversity between the refined models and coarsest ones. The mesh sizes of 1mm (41.14 kPa), 0.75mm (41.15 kPa) and 0.5mm (41.19 kPa) presented approximately the same stresses. Undoubtedly, more time was spent running the analysis with the mesh size of 0.5mm and 0.75mm than the size of 1mm while, the results were similar. Hence, convergence was reached when there was no qualitative change in the stresses. Consequently, this study was used a mesh size of 1mm.

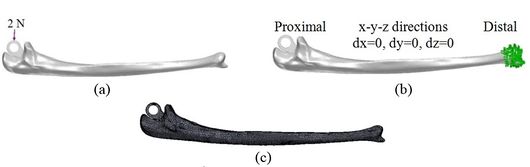
Figure 11. (a) Implanted ulna. (b) Boundary conditions. (c) Meshed bone

Figure 12. Average Von Mises stress for ulnar stem

2.5 Finite element analysis to predict micro-motion and stress shielding

The method of relative motion measurement is a significant difference between experimental and finite element predictions of micro-motion. FEA method presents the amount of sliding which happens at the interface through subtracting displacement of outer cement surface from the bone surface and also the displacements at cement surface from the outer surface of the stem. However, experimentally, micro-motion is obtained through displacement transducers mounted on the outer cortex of the bone. The outcomes are generally compared, and low micro-motion is preferred to high micro-motion. Hence, initially, displacement was obtained in cement (${\textstyle {\delta }_{c})}$, implant (prosthesis) stem ${\textstyle \,({\delta }_{p)}}$, and bone ${\textstyle \,({\delta }_{b})}$. Next, the displacement results were put in Eqs. (1) and (2) to calculate micro-motion in bone-cement and cement-implant interfaces. To obtain stress shielding, we applied AP compression force in intact humerus and ulna bones. The same load was applied in the implanted humerus and ulna bones with different stem lengths and cross-sections. Then, firstly, stress was obtained in distal and proximal of intact humerus and ulna bones respectively. Afterward, stress was obtained for implanted humerus and ulna with different parameters in the same locations. Finally, stress shielding was obtained for all models using Eqs. (3)

Micro-motion in implant-cement interface:

${\textstyle \quad {\delta }_{cp}=}$${\sqrt {{\delta }_{x,cp}^{2}}}+{\delta }_{y,cp}^{2}+{\delta }_{z,cp}^{2}$

(1)

Micro-motion in cement-bone interface:

${\textstyle \,{\delta }_{cb}=}$${\sqrt {{\delta }_{x,cb}^{2}}}+{\delta }_{y,cb}^{2}+{\delta }_{z,cb}^{2}\quad$

(2)

${\textstyle \%{\hbox{ Stress shielding }}=\,\left[\displaystyle {\frac {({\sigma }_{b}{)}_{n}}{\displaystyle {\frac {{E}_{b}}{{E}_{p}}}{\,\sigma }_{p}}}\right]\times 100\%}$

(3)

where ${\textstyle ({\sigma }_{b}{)}_{n}}$ is the normal level of stress for un-implanted and ${\textstyle {\sigma }_{i}}$ stands for the stress of implanted humerus and ulna bones. ${\textstyle {E}_{b}}$ and ${\textstyle {E}_{i}}$ are elastic modules of bone and implant respectively. This equation presents the reduction of force in the bone due to the removal of normal stress in bone bone by an implant.

3. Results

3.1 Effect of implant cross-section on micro-motion

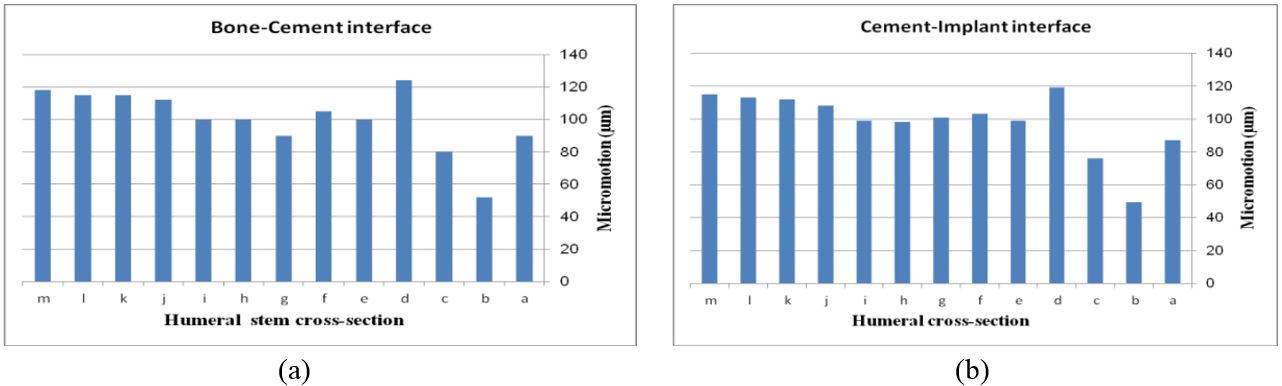
The impact of humeral cross-section on micro-motion (under AP compression force) is presented in Figure 13. In the cement-bone interface, the lowest micro-motion was seen at $80\,\mu$m (triangular stem) and $52\,\mu$m (diamond stem). However, the highest micro-motion was observed at $124\,\mu$m (concave $R=25$mm) and $118\,\mu$m (all sides convex). The same amount was observed at $100\,\mu$m for (i) and (h). Among all concave cross-sections, all sides concave presented the lowest micro-motion at $90\,\mu$m. For the implant-cement interface, the lowest micro-motion was seen at $51\,\mu$m for the diamond cross-section. After the diamond, the triangular stem presented less micro-motion at $76\,\mu$m. Approximately, concave stems indicated less micro-motion than convex models.

Figure 13. Micro-motion for different humeral stem cross-sections under AP compression force. (a) Bone-cement interface. (b) Cement-implant interface: (a) Rectangular. (b) Diamond.(c) Triangular. (d) Concave $R=25$mm. (e) Concave $R=50$mm. (f) Concave $R=70$mm. (g) All sides concave. (h) Two sides triangular (1mm). (i) Two sides triangular (0.5mm). (j) Convex $R=25$mm. (k) Convex $R=50$mm. (l) Convex $R=70$mm. (m) All sides convex

The effect of cross-section on micro-motion of the humeral stem (under torsion force) is shown in Figure 14. In the cement-bone interface, diamond ($34\,\mu$m) and triangular ($90\,\mu$m) stems showed the highest and the lowest micro-motions respectively. Two sides triangular (0.5mm) and concave $R=50$mm stems presented the same micro-motion at $74\,\mu$m, which was considerably higher than stems with concave $R=50$mm, triangular, convex $R=25$, convex $R=50$, and convex $R=70$mm cross-sections. In the implant-cement interface, the smallest micro-motion was observed in diamond and convex $R=50$mm stems at $52\,\mu$m and $42\,\mu$m respectively while rectangular and all sides concave experienced micro-motion at $103\,\mu$m. Figures were slightly increased from convex $R=70$ ($54\,\mu$m) to $89\,\mu$m for the two sides triangular (1mm). All sides concave stem showed higher micro-motion ($89\,\mu$m) than concave $R=70$mm and $R=50$mm at $81\,\mu$m.

Figure 14. Micro-motion for different humeral stem cross-sections under torsion force in (a) Bone-cement interface. (b) Cement-implant interface: (a) Rectangular. (b) Diamond. (c) Triangular. (d) Concave $R=25$mm. (e) Concave $R=50$mm. (f) Concave $R=70$mm. (g) All sides concave. (h) Two sides triangular (1mm). (i) Two sides triangular (0.5mm). (j) Convex $R=25$mm. (k) Convex $R=50$mm. (l) Convex $R=70$mm. (m) All sides convex

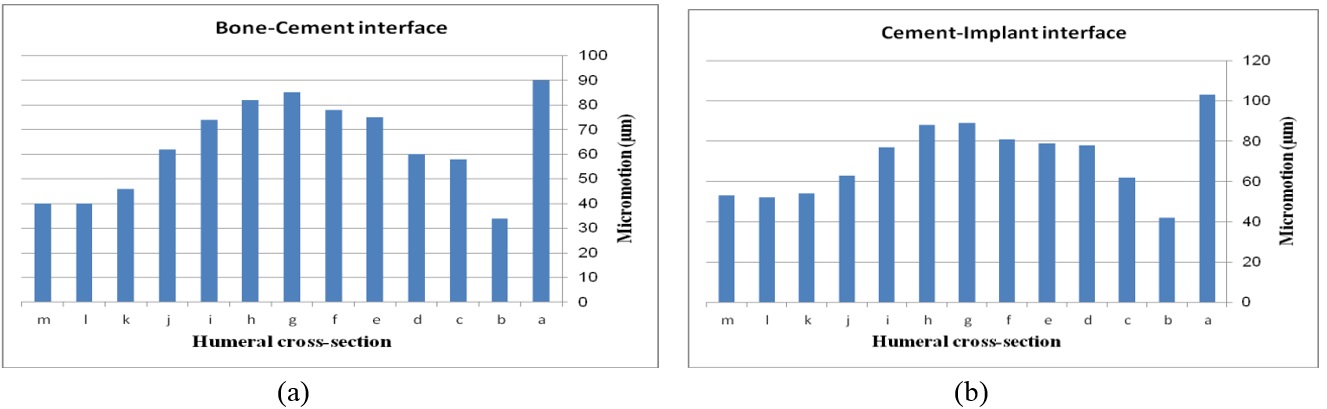
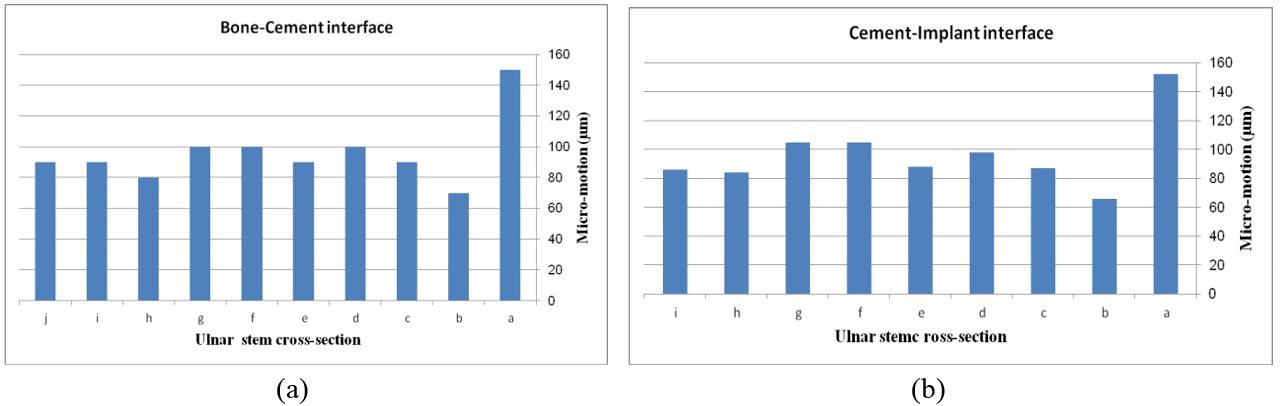
The effect of cross-section on micro-motion of the ulnar stem (under AP compression force) is shown in Figure 15. Results showed a moderate fluctuation in micro-motion. In the cement-bone interface, the highest micro-motion was seen at $150\,\mu$m for the rectangular stem, which was double than diamond. The width concave, height concave, and concave $R=10$mm stem experienced the same micro-motion at $100\,\mu$m. In a similar way, it was seen the same micro-motion at $90\,\mu$m for height convex, width convex, and concave $R=8$mm stems. In the cement-implant interface, the lowest and highest micro-motions were seen for the diamond stem ($66\,\mu$m) and rectangular stem ($152\,\mu$m) respectively. Totally, concave cross-sections transferred higher micro-motion to stems than convex cross-sections. It was seen micro-motion at $105\,\mu$m for height and width concave stems, which was considerably higher compared with the width convex and the height at $86\,\mu$m.

Figure 15. Micro-motion for different ulnar stem cross-sections under the AP force. (a) Bone-cement interface. (b) Cement-implant interface: (a) Rectangular. (b) Diamond. (c) All sides concave $R=8$mm. (d) All sides concave $R=10$mm. (e) All sides concave $R=12$mm. (f) With concave. (g) Height concave. (h) All sides convex $R=10$mm. (i) With convex. (j) Height convex

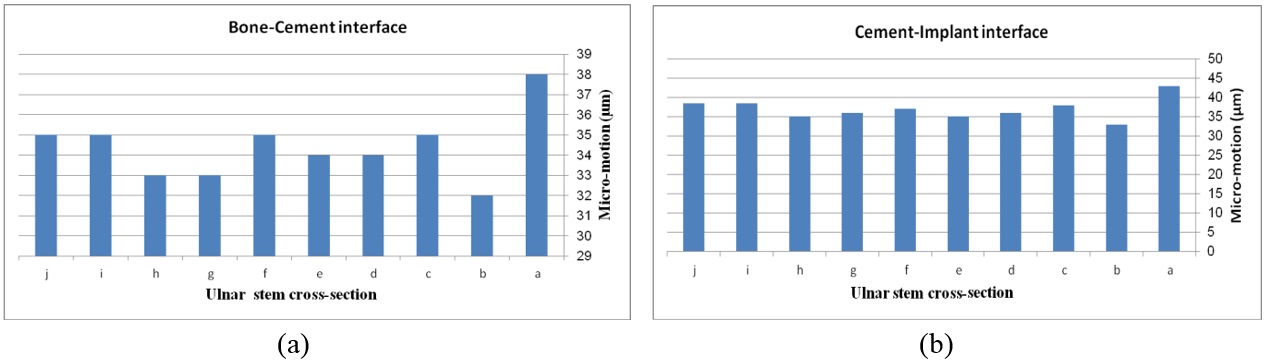
The impact of ulnar cross-section on micro-motion (under torsion force) is shown in Figure 16. A remarkable fluctuation was observed for different cross-sections in the cement-bone interface. The concave $R=10$mm and diamond stems showed the lowest micro-motion at $34\,\mu$m and $33\,\mu$m respectively, while the highest micro-motion was registered for the rectangular stem at 38 µm. The same micro-motion was presented for the height and width convex stems at $35\,\mu$m. In the implant-cement interface, figures were seen a relatively different trend. Width and height convex stems presented the second highest micro-motion at $39\,\mu$m, which was significantly higher than the rectangular stem at $43\,\mu$m. The lowest micro-motion was observed for the diamond stem at $33\,\mu$m following by all sides concave $R=12$mm, height concave, and all sides convex $R=10$mm at the $35\,\mu$m, and consequently, concave $R=12$2 and concave $R=10$mm at $36\,\mu$m.

Figure 16. Micro-motion for different ulnar stem cross-sections under torsion force. (a) Bone-cement interface. (b) Cement-implant interface: (a) Rectangular. (b) Diamond. (c) All sides concave $R=8$mm. (d) All sides concave $R=10$mm. (e) All sides concave $R=12$mm. (f) With concave. (g) Height concave. (h) All sides convex $R=10$mm. (i) With convex. (j) Height convex

3.2 Effect of flange design on micro-motion

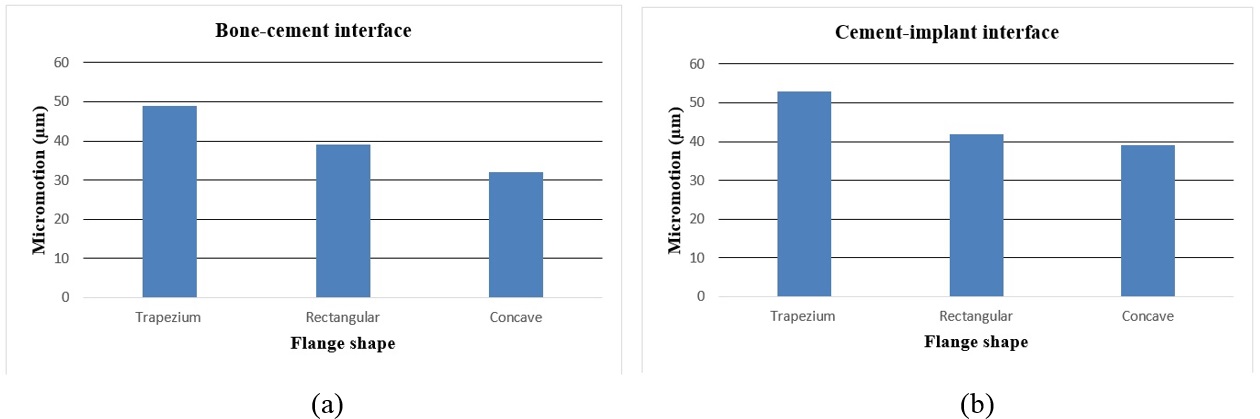
The effect of various flanges on micro-motion of the distal humeral stem (under torsion force) is shown in Figure 17. Under the torsion force, a reduction trend was seen in micro-motion from the trapezium to concave flanges. In the cement-bone interface, trapezium flange presented micro-motion at $49\,\mu$m. Then, the rectangular flange showed slightly less micro-motion at $39\,\mu$m. It was seen the same micro-motion at $32\,\mu$m for concave flanges. In the cement-implant interface, micro-motion saw a reduction trend from the trapezium ($53\,\mu$m) to concave 3˚ ($39\,\mu$m).

Figure 17. Micro-motion of the implanted humerus bone with different flange shapes under the torsion force. (a) Bone-implant interface. (b) Cement-implant interface

3.3 Effect of implant cross-section on stress shielding

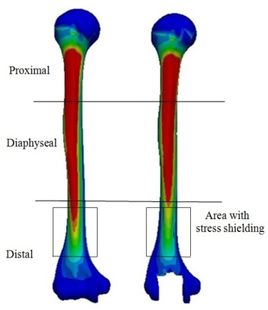
Figure 18 presents the Von Mises stress distribution in the implanted and intact humerus (intact humerus acts as a reference) under AP compression. The humerus was assigned into three regions of interest (ROI): distal, diaphyseal, and proximal. Reduction of stress expresses a decrease reduction in the load and consequently the growth of the stress shielding. No effective changes were seen for stress distribution between implanted and intact humerus in diaphyseal and proximal areas. Stress shielding occurred in the distal region. The anterior of the distal area showed stress at 72.90 kPa in the intact humerus.

Figure 18. Von Mises stress in intact humerus bone (left). Implanted humerus bone with rectangular stem cross-section (right)

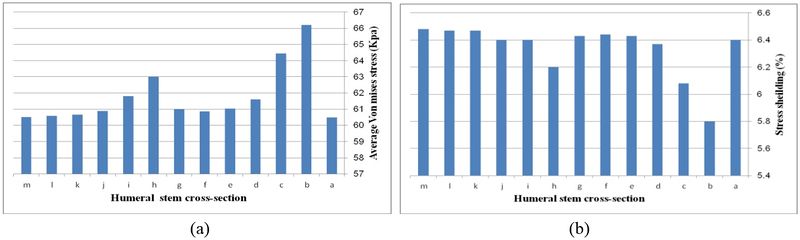
Figure 19 (a) presents average stress in the distal region of the implanted humerus for different cross-sections. The diamond stem showed the highest stress at 66.2 kPa, while all sides convex and rectangular stems experienced the least micro-motion at 60.5 kPa. Triangular stem experienced less stress than the diamond stem (64.45 kPa). Two sides triangular (1mm) and (0.5mm) stems presented higher stress compared to convex and concave at 61.8 kPa and 63 kPa respectively. The stress shielding for the humeral stem with different cross-sections is shown in Figure 19 (b). Triangular (6.0%) and diamond (5.8%) stems presented the lowest stress shielding. Approximately, it was seen the same stress shielding at 6.4% for concaves $R=50$mm, $R=70$mm, rectangular and sides concave stems. Concave stems experienced slightly less stress shielding than convex stems. However, two sides triangular (1mm), at 6.2%.stem, presented moderately less than two sides triangular (0.5mm) stem at 6.4%.

Figure 19. (a) Average Von Mises stress for different humeral stem cross sections under AP compression force. (b) Stress shielding for different humeral stem cross sections under AP compression force: (a) Rectangular, (b) Diamond, (c) Triangular, (d) Concave $R=25$mm, (e) Concave $R=50$mm, (f) Concave $R=70$mm, (g) All sides concave, (h) Width triangle (1mm), (i) Width triangle (0.5mm), (j) Convex $R=25$mm, (k) Convex $R=50$mm, (l) Convex $R=70$mm, (m) All sides convex

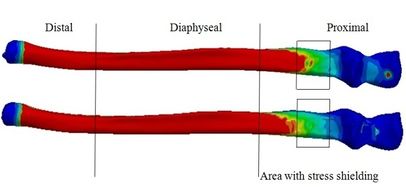
Figure 20 presents the stress distribution in the implanted and intact ulna (intact ulna acts as a reference) under AP compression. It was observed the stress distribution in diaphyseal and distal regions. The proximal part experienced stress shielding. In anterior of the proximal area, intact ulna experienced stress at 70.68 kPa. The Von Mises stress distribution in proximal of the implanted ulna is shown in Figure 21 (a). The lowest stress was seen in width concave and all sides concave $R=10$mm stems (61.9 kPa), while the highest stress was observed in the diamond stem at 63.9 kPa. Concave stem ($R=8$) showed the second highest stress at 62.9 kPa. All sides concave $R=12$mm and $R=10$mm stems experienced stress at the same amount at 62.8 kPa, while the rectangular stem presented at 62.2 kPa. The effect of cross-section on the stress shielding (under AP compression force) in the ulnar stem is Figure 21 (b). Moderate growth in stress shielding was seen from 6.2% for all sides concave $R=8$mm stem to nearly 6.4% for convex $R=10$mm stem which presented the highest amount than all models. The lowest stress shielding was registered for the diamond stem at 6.1%. The similar stress shielding was observed for width convex and rectangular stems at approximately 6.3%.

Figure 20. Von Mises stress in intact ulna bone (up), and implanted ulna bone with a rectangular cross-section (down)

Figure 21. (a) Average Von Mises stress. (b) Stress shielding in the proximal region of implanted ulna bone for different ulnar stem cross-sections under AP compression force for different humeral stem cross sections under AP compression force: (a) Rectangular, (b) Diamond, (c) All sides concave $R=8$mm, (d) All sides concave $R=10$mm, (e) All sides concave $R=12$mm, (f) Width concave, (g) Height concave, (h) All sides convex $R=10$mm, (i) Width convex, (j) Height convex

4. Discussion

Since the inception of TEA, many designs of elbow implants have been evolved. Design features have been altered owing to different clinical and radiographic problems and eventually failures after TEA. Some modifications in designs should be considered to achieve a sufficient outcome. FEA is a considerable approach to examine implants previous to clinical application. In order to modify an elbow implant, an understanding of different implant features on loosening would be useful. In this study effect of elbow implant parameters on loosening was assessed using FEA.

In order to control implant loosening, a wide range of efforts has been directed to achieve ideal stem cross-section. Although many cross-sections have been studied, concave, convex, and diamond cross-sections have not examined for elbow implants [3,36,37,38]. Yongpravat et al. used a delta-wing shaped stem was to resist torsional forces [39]. Gschwend et al. was developed a long ribbed, four edged stems to achieve rotation stability [40]. The data from the analysis of the hip stem may be suitable to modify the elbow stem. As an example, smooth stem edges were chosen rather than sharp ones to hinder stress increase in the interfaces. Therefore, in the current study, the development of stems was on conventional cemented fixation basis; eventually, all stems possessed smooth surfaces.

According to our results, stem with concave cross-section presented higher micro-motions than stem with the convex cross-section in the implant-cement-bone interfaces. In addition, the lowest micro-motion was recorded for the humeral stem with a diamond cross-section at the implant-cement-bone interface under both torsion and AP forces than other cross-sections. A similar outcome was seen for ulnar stem under both torsion and AP forces. The obtained values for micro-motion (diamond cross-section) were in the range of the optimum one to decrease loosening. Now, the question is how diamond cross-section causes lower loosening compared to other cross-sections?

The lack of cement-bone-implant bonding causes loosening which is a consequence of the mechanical failure of implant components. Debonding is the loss of adhesion between two surfaces, which were originally bonded. The growth of the movement in surfaces persuades the loss of adhesion. The cause of this movement is micro-motion. Hence, higher micro-motion causes more loss of adhesion, movement, and loosening. Clearly, less movement between interfaces requires a longer time to loosen bone against the implant. Boundaries in interfaces are widened through higher movement, which results in migration of implant components (clinically is known as loosening) [1,4].

Applied axial torsion caused the stem to rotate around an axis perpendicular to the articular surface. Under axial torsion, the anterior-posterior plane plays a more significant role than the mediolateral one. Hence, a number of contact fixation points in frontal and posterior planes are the key to resist torsion. Diamond cross-section presented two fixation points with both bone and cement in the anterior-posterior plane however; the other models presented one point. Diamond cross-section fits the humerus canal in both frontal and posterior planes. It causes self-locking to the endosteal bone through two corners of diamond shape along the whole stem in frontal and posterior planes. This feature results in less movement in interfaces. Therefore, a better distal fit was achieved by having an anterior-posterior point (act as two wings) claiming to improve stability. Hence, diamond cross-section presented considerably less micro-motion compared to rectangular.

The load is comprised of torsional and bending components and it not considered only axial compression. Therefore, a little micro-motion occurs between stem and cement interface during sequential loads, thus, this motion (interface slip) is distributed non-homogenously over the stem due to stem shapes. Motion at the implant-bone interface mostly results in the growth of fibrous around the implant. Clinically, this issue makes implants unstable. It has been found that interfaces micro-motion affects the longevity of implants loosening [41,42].

Another reason for loosening is the stress shielding of bone by the implant [8]. Based on obtained results, diamond cross-section transferred the lowest stress shielding in the proximal ulna and distal humerus. Stress shielding enhances bone loss surrounding an implant as a result of changed (reduced) mechanical stress. The bone resorption occurred in areas where force transferred across the implant bypasses a portion of the bone. External loads are carried all by an intact elbow. However, the capacity of load-carrying is shared by the implant in the implanted bone. Consequently, stress is decreased in bone; therefore, stress is shielded [43].

Diamond cross-section leads implanted ulna and humerus to experience stress closer to the intact bones (natural situation). Therefore, based on Wolff’s Law, humerus and ulna carry less stress shielding. In other words, the reduction in compression/tension loads by the living bones reduces the thickness of bone thickness and bone mass, which finally causes bone resorption. Ulna and humerus are deposited at locations with higher stresses and are resorbed at locations with little stresses. The decrease of stress relevant to the natural situation ends in bone remodeling (getting thinner). Now, ulna and humerus are resorbed. Here, postoperatively, a lack of sufficient bones for implant stability causes implant migration and loosening [8,44].

In this study, the different stresses were seen between implanted and intact models, which shows a risk of bone resorption by stress shielding in the proximal ulna and distal humerus. Remedios et al. reviewed 25 cemented Kudo implants for 5 years. Two elbows presented a bone loss in the humerus, which does not deny the potential risks found by this study [45]. Similarly, in the present study, the decrease in stress in the distal humerus compared with the intact one induces bone resorption. This finding is in agreement with the clinical studies following TEA [46,47]. The difference in stress distributions between the implanted intact ulna and humerus begins the failure of the cement or bone in the stem-tip.

Some studies have investigated the torsional stability of implant stems. Mann et al. and Chang et al. showed that circular stem induces less resistance to torsion [48,49]. Also, a few studies have suggested rectangular stems [50]. Kedgley et al. showed the influence of the stem cross-section (triangular, circular, oval, rectangular) on stability and loosening. Stem shape was impressively affected stability and loosening [51]. However, in this study, the modified cross-section (diamond) presented higher resistance to torsion than rectangular. In the current study, all dimensions used for cross-section were the same as those available commercially. This study prepared a fundamental for development and modification of stems under torsion, compression, and other more complex loading modes.

The flange protects the implant-bone-cement interfaces and affects mechanical factors and consequently reduction of implant loosening. Herren et al. studied the influences of an anterior flange to the GSB III humeral component [52]. No significant diversities were observed in displacements or the stress distribution, indicating the flange had a small influence on this design. Quenneville et al. studied the impact of a flange on strains in the distal region of the humerus. It was seen that strains are affected by a flange using different geometric [53]. In a similar way, our study proved that micro-motion is affected by the change of flange shape.

Our results showed that a concave flange transfers the lowest micro-motion to the implant-bone-cement interface compared with rectangular and trapezium. Theoretically, the flange increases the rotational stability of the humeral component. The flange affects the transmission of micro-motion to the distal region of humeral stem. Increased micro-motion leads to more movement between surfaces, which widen the boundaries in interfaces and the migration of implant components. Clinically, this migration is seen as radiolucency surrounding the stem. If radiolucency is increased to more than 2mm, loosening probably occurs. Hence, less micro-motion transferred by the concave flange to interfaces may cause lower loosening. Although the effect of the introduced flange in this study, concave, on micro-motion is little, it probably decreases loosening in a long time. The concave flange may decrease more stress shielding in distal humerus bone rather than other flanges.

Several limitations were observed in this study. Only one elbow sample was considered for this study. Considering a wide range of elbow bones with different sizes may deliver more accurate results. Furthermore, considering complex loading in the implanted elbow may present more reliable results. It is hoped that future studies may be able to accommodate these deficiencies which may or may not play an important role in the more accurate design of elbow implants. Many different recommendations can be stated for future extensions of the introduced approach in this study. Investigating the effect of changing the flexion-extension axis in micro-motion transferred to the bone-cement-implant interfaces can develop the approach further. Furthermore, using the same approach, remodeling of the humerus and ulna bones can be investigated after surgery. As well as, future work can concern the kinematic of intact and elbow replaced by the modified implant.

There are a large number of studies on hip and knee implantation. Nevertheless, TEA suffers from a lack of computational research in contributing design implant parameters to reduce loosening, therefore, related problems have not been completely coped. This computational analysis represented a step in quantifying the role-of stress shielding of bones and micro-motion in the cement-bone-implant interfaces to initiate implant loosening. Analyzing factors that could compromise the loosening of an elbow implant is important to its success. A reduction of micro-motion and stress shielding, through modification of the design, may improve the clinical outcomes.

Acknowledgement

We acknowledge Global College of Engineering and Technology (Oman) for supporting this study.

References

[1] Chafik D., O’Driscoll S., King G.W. Yamaguchi K. Total elbow arthroplasty-convertible. Operative Techniques Orthop., 20(1):58-67, 2010.

[2] Ren K., Dusad A., Zhang Y., Wang D. Therapeutic intervention for wear debris-induced aseptic implant loosening. Acta Pharmaceutica Sinica, 3(2):76-85, 2013.

[3] Gregory J.J., Ennis O., Hay S.M., Total elbow arthroplasty. Current Orthop., 22:80-89, 2008.

[4] Antuna S., Vallina V. Elbow arthroplasty: design, indications and results. Rev. Ortop. Traumatol., 50(1):55-67, 2006.

[5] Bahraminasab M., Sahari B.B., Edwards K.L., Farahmand F., Hong T.S., Naghibi H. Material tailoring of the femoral component in a total knee replacement to reduce the problem of aseptic loosening. Materials and Design, 52:441-451, 2013.

[6] Yang D. Bone/cement interface in total hip arthroplasty:an in vitro study of bone surface preparation, fatigue and interface mechanics. PhD Thesis, University of Maryland, College Park, 2006.

[7] Ozan O., Turkyilmaz I., Ersoy A.E., McGlumpby E.A., Rosenstiel S.F. Clinical accuracy of 3 different types of computed tomography-derived stereolithographic surgical guides in implant placement. J. Oral Maxillofacial Surg., 67(2):394-401, 2009.

[8] Bahraminasab M., Sahari B.B., Edwards K.L., Farahmand F., Arumugam M., Hong T.S. Aseptic loosening of femoral components- A review of current and future trends in materials used. Materials and Design, 2:459-470, 2012.

[9] Sabatini A.L., Goswami T. Hip implants VII: Finite element analysis and optimization of cross-sections. Materials and Design, 29(7):1438-1446, 2008.

[10] Austman R.L., Beaton B.J.B., Quenneville C.E., King G.J.W., Gordon K.D., Dunning C.E. The effect of distal ulnar implant stem material and length on bone strains. J. Hand Surg., 32(6):848–854, 2007.

[11] Ericson A., Olivecrona H., Stark A., Maguire G.Q., Zeleznik M.P., Arndt A. Computed tomography an analysis of radiostereometric data to determine flexion axes after total joint replacement: Application to the elbow joint. J. Biomech., 43(10):1947-1952, 2010.

[12] Hastings H., Minimally constrained elbow implant arthroplasty: The discovery elbow system. Tech. Hand Up Extrem Surg., 8(1):34-50, 2004.

[13] Szekeres M., King G.J. Total elbow arthroplasty. J. Hand Ther., 19:245-253, 2006.

[14] Heidari M., Harun M.N., Syahrom A. Influence of polyethylene thickness on axis pin in linked elbow implant. Advanced Materials Research, 845:194-198, 2014.

[15] Heidari M., Harun M.N., Kadir M.R.A., Kashani J., Syahrom A. Effect of humeral stem shape on displacement in elbow implant. Applied Mechanics and Materials, 393:467-471, 2013.

[16] Heidari M., Kadir M.R.A., Kashani J., Fallahiarezoodar A., Alizadeh M., Robson et al. Influences of rheumatoid arthritis on elbow: A finite element analysis. J. Advanced Science Letters, 19(11):3219-3222, 2013.

[17] Heidari M., Kadir M.R.A., Fallahiarezoodar A., Harun M.N., Alizadeh M., Kashani J. Biomechanical assessment of unconstrained elbow prosthesis after total elbow replacement: A finite element analysis. Applied Mechanics and Materials, 234:7-10, 2012.

[18] Trigg S.D. Total elbow arthroplasty: current concepts. Northeast Florida Med., 57(3):37-40, 2006.

[19] Sotelo JS. Total elbow arthroplasty. J. Open Orthop., 5:115-123, 2011.

[20] An K.N., Morrey B.F. Biomechanics of the elbow. In Morrey B.F. The elbow and its disorders, W.B. Saunders (Ed.), Philadelphia, 2000.

[21] Duparc J., Massin P. Results of 203 total hip replacements using a smooth, cementless femoral component. J. Bone and Joint Sur. (Br.), 74(2):251-256, 1992.

[22] Valstar E.R., Eric V.H., Rozing P.M. Micromotion of the souter-strathclyde total elbow prosthesis in patients with rheumatoid arthritis 21 elbows followed for 2 years. Acta Orthop. Scand., 73(3):264-272, 2002.

[23] Nuttall] D.,  Trail I.A., Stanley, J.K., Micromotion of the acclaim total elbow arthroplasty using radiosteremetry. J. Bone Joint Surg. Br., 91:256, 2009.

[24] Gross S., Abel E.W., A finite element analysis of hollow stemmed hip prostheses as a means of reducing stress shielding of the femur. J. Biomechanics, 34:995-1003, 2001.

[25] Huiskes P., Weinans H., Rietbergen B.V. The relationship between stressshielding and bone resorption around total hip stems and the effects of flexible materials. Clinical Orthopaedics and Related Research 274:124-34, 1992.

[26] Day J.S. The clinical performance of UHMWPE in elbow replacements. UHMWPE Biomaterials Handbook, Academic Press (USA), Chapter 10, 2nd Edition, pp. 137-152, 2009.

[27] Amarasinghe R.S., Rupasinghe R.A.M., Anurathan P., Herath S.R. Effects of geometry of the interamedullary stem of the ulna component of hinged elbow joint prostheses on the bone and implant bendingstress. J. Mechanics in Med. Biology, 11(5):1271-293, 2011.

[28] Prasad N., Dent C. Outcome of total elbow replacement for rheumatoid arthritis: single surgeon’s series with Souter-Strathclyde and Coonrad-Morrey prosthesis. J. Shoulder Elbow Surg., 19(3):376-83, 2010.

[29] Takatori K., Hashizume H., Wake H., Inoue H., Nagayama N. Analysis of stress distribution in the humeroradial joint. J. Orthop. Sci., 7(6):650-657, 2002.

[30] Cheung E.V., O’Driscoll S.W. Total elbow prosthesis loosening caused by ulnar component pistoning. J. Bone Joint Surg. Am., 89(6):1269-1274, 2007.

[31] Goel V.K., Lee I.I-K., Blair W.F. Effect of the Coonrad elbow prosthesis on stresses in the humerus. J. Clin. Biomech., 4(1):11-l6, 1989.

[32] Completo A., Pereira J., Fonseca F., Ramos A., Relvas C., Simões J. Biomechanical analysis of total elbow replacement with unlinked iBP prosthesis: An in vitro and finite element analysis. Clin. Biomechan., 26(10):990-997, 2011.

[33] Stokdijk M., Meskers C.G.M., Veeger H.E.J., de Boer Y.A., Kozing P.M. Determination of the optimal elbow axis for evaluation of placement of prostheses. Clin. Biomechan., 14:177-184, 1999.

[34] Godest A.C., Beaugonin M., Haug E., Taylor M., Gregson P.J. Simulation of a knee joint replacement during a gait cycle using explicit finite element analysis. J. Biomech., 35(2):267-275, 2002.

[35] Halloran J.P., Petrella A.J., Rullkoetter P.J. Explicit finite element modelling of total knee replacement mechanics. J. Biomech., 38(2):323-331, 2005.

[36] Gross S., Abel E.W. A finite element analysis of hollow stemmed hip prostheses as a means of reducing stress shielding of the femur. J. Biomechanics., 34(8):995-1003, 2001.

[37] Gregory J.J., Ennis O., Hay S.M. Total elbow arthroplasty. Current Orthop., 22(2):80-89, 2008.

[38] Huiskes P., Weinans H., Rietbergen B.V. The relationship between stressShielding and bone resorption around total hip stems and the effects of flexible materials. Clinical Orthopaedics and Related Research, 274:124-34, 1992.

[39] Yongpravat C., Kim H.M., Gardner T.R., Bigliani L.U., Levine W.N., Ahmad G.S. Glenoid implant orientation and cement failure in total shoulder arthroplasty: a finite element analysis. J. Shoulder Elbow Surg., 22(7):940-947, 2013.

[40] Gschwend N. Present state of art in elbow arthroplasty. Acta Orthopædica Belgica, 68(2):100-117, 2002.

[41] Chong D.Y., Hansen U.N., Amis A.A., Analysis of bone-prosthesis interface micromotion for cementless tibial prosthesis fixation and the influence of loading conditions. J. Biomech., 19(43):1074-1080, 2010.

[42] Burke D.K., O’connor D., Zalenski E.B., Jasty M., Harris W.H. Micromotion of cemented and uncemented femoral components. J. Bone Joint Surg., 73(1):33-37, 1991.

[43] Chanlalit C., Shukla D.R., Fitzsimmons J.S., An K.N., O’Driscoll S.W. Stress shielding around radial head prostheses. J. Hand Surg., 37(10): 2118-2125, 2012.

[44] Wang A., Sun D.C., Stark C., Dumbleton J.H. Wear mechanisms of UHMWPE in total joint replacements. Wear, 181-183:241-249, 1995.

[45] Remedios C., Chantelot C., Giraud F., Migaud H., Fontaine C. Results with Kudo elbow prostheses in non-traumatic indications: A study of 36 cases. Acta Orthop. Belg., 71(3):273-288, 2005.

[46] Figgie H.E., Inglis A.E., Christopher B.S. Total elbow arthroplasty in the face of significant bone stock or soft tissue losses. J. Arthroplasty 1(2):71-81, 1986.

[47] Wixson R.L., Elasky N., Lewis J.L. Mechanical properties of proximal tibia1 cancellous bone in arthritic knees. Trans. ORS, 33-50, 1987.

[48] Chang P.B., Mann K.A., Bartel D.L. Cemented femoral stem performance. Effects of proximal bonding, geometry, and neck length. Clin. Orthop. Relat. Res., 355:57-69, 1998.

[49] Mann K.A., Bartel D.L., Ayers D.C. Influence of stem geometry on mechanics of cemented femoral hip components with a proximal bond. J. Orthop. Res., 15(5):700-706, 1997.

[50] Huiskes R., Verdonschot N., Nivbrant B. Migration, stem shape, and surface finish in cemented total hip arthroplasty. Clin. Orthop. Relat. Res., 355:103-112, 1998.

[51] Kedgley A.E., Lang P., Dunning C.E. The effect of cross-sectional stem shape on the torsional stability of cemented implant components. J. Biomech. Eng., 129(3):310-314, 2007.

[52] Herren D.B., Ploeg H., Hertig D., Klabunde R. Modeling and finite element analysis of a new revision implant for the elbow. Clin Orthop., 420:292-297, 2004.

[53] Quenneville C.E., Austman R.L., King G.W., Johnson J.A., Dunning C.A. Role of an anterior flange on cortical strains through the distal humerus after total elbow arthroplasty with a latitude implant. J. Hand Surg., 33(6):927-931, 2008.