Abstract
In this study, a simple and high accurate series-based method called Differential Transformation Method (DTM) is used for solving the coupled nonlinear differential equations in fluids mechanic problems. The concept of the DTM is briefly introduced, and its application on two different cases, natural convection of a non-Newtonian nanofluid between two vertical plates and Newtonian nanofluid flow between two horizontal plates, has been studied. DTM results are compared with those obtained by a numerical solution (Fourth-order Runge–Kutta) to show the accuracy of the proposed method. Results reveal that DTM is very effective and convenient which can achieve more reliable results compared to other analytical methods in solving some engineering and sciences problems.
Keywords
Coupled nonlinear differential equations; Differential Transformation Method; Natural convection; Newtonian and non-Newtonian nanofluids
1. Introduction
The nonlinear problems and phenomena can be modeled by ordinary or partial nonlinear differential equations to find their physical behavior in certain cases. Most of these described physical and mechanical problems have a set of coupled nonlinear differential equations. For example, heat transfer by natural convection which commonly occurs in many physical and engineering applications such as geothermal systems, chemical catalytic reactors, and heat exchangers has a system of coupled nonlinear differential equations. One of the simple and reliable methods for solving the system of coupled nonlinear differential equations is analytical solution which recently is widely used in solving many problems [1], [2], [3], [4], [5], [6], [7] and [8]. Ziabakhsh and Domairry [9] have studied the natural convection of a non-Newtonian fluid between two infinite parallel vertical flat plates by Homotopy Analysis Method (HAM) which is a general form of the HPM.
An analytical method called Differential Transformation Method (DTM) has also been introduced for nonlinear problem solution. DTM is an analytical method based on Taylor series. It constructs an analytical solution in the form of a polynomial. Actually, DTM is different from the traditional high order Taylor series method, which requires symbolic calculation of the necessary derivatives of the data functions. This method was firstly applied in the engineering field by Zhou [10] and its abilities attracted many authors to use this method for solving the nonlinear equations. DTM or improved shape forms of it (Ms-DTM and Hybrid-DTM) can solve any coupled nonlinear equations set. They can also be used for three dimensional problems. Ghafoori et al. [11] solved a nonlinear oscillation equation by DTM and they revealed that DTM results are more accurate than HPM and VIM (Variation Iteration Method). Yahyazadeh et al. [12] evaluated the natural convection flow of a nanofluid over a linearly stretching sheet in the presence of magnetic field using DTM. Also, Biazar and Eslami [13] considered DTM to solve the quadratic Riccati differential equation and the derived results by DTM were compared with the results of HAM and ADM (adomian decomposition method). They showed that DTM results are more effective and favorable than HAM and ADM results. Gokdogan et al. [14] acquired an approximate analytical solution of the chaotic Genesio system by a modified DTM. Ayaz [15] studied two-dimensional differential transform method for solving an initial value problem in partial differential equations (PDEs). In another application of DTM, the natural frequencies and critical flow velocities of pipes conveying fluid with several typical boundary conditions were obtained by Ni et al. [16]. Although many analytical methods have been presented in the literature, DTM is expected to find more valuable applications due to the following advantages:
- Unlike perturbation techniques, DTM is independent of any small parameter such as p in HPM. DTM can thus be applied no matter if governing equations and boundary/initial conditions of a given nonlinear problem contain small or large quantities or not.
- DTM does not need to calculate auxiliary parameter through h-curves against Homotopy Analysis method (HAM).
- DTM does not need to determine auxiliary function, auxiliary parameter or guess suitable initial values. Unlike HAM, it can solve the equations directly.
- DTM provides us with great freedom to express solutions of a given nonlinear problem by means of Pade approximant and Ms-DTM.
This paper aimed to apply DTM for system of coupled nonlinear equations and testify the reliability of DTM by comparing its results with HPM. For showing the accuracy of DTM in described problems, two cases of problems, natural convection of a non-Newtonian fluid between two vertical plates and Newtonian fluid flow analysis between two horizontal plates, were solved. As an important result, it was found that the DTM results are more accurate than those obtained by HPM in some areas. After this verification, the effects of some physical parameters were analyzed to show the efficiency of DTM for this type of the problems.
2. Problems description
The study of the fluid flow between parallel plates has many applications in industries which motivated the researchers to investigate. Ziabakhsh and Domairry [9] investigated the natural convection of non-Newtonian fluid between vertical parallel plates using HAM, and based on their work, Hatami and Ganji [18] studied the effect of sodium alginate (SA) non-Newtonian nanofluid between parallel plates. Also, Rajagopal and Na [19] presented a numerical solution for the natural convection of non-Newtonian fluids between vertical plates. In the following section, two cases of problems in fluid flow between parallel plates with coupled nonlinear differential equations will be introduced. It is aimed to investigate the efficiency of DTM in comparison with numerical solution.
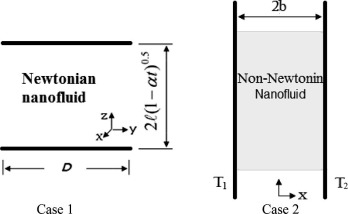
2.1. Case 1
In first case the heat transfer analysis in the unsteady two-dimensional squeezing nanofluid flow between the infinite parallel plates (Fig. 1, left). The two plates are placed at . For , the two plates are squeezed until they touch where and for the two plates are separated. The viscous dissipation effect, the generation of heat due to friction caused by shear in the flow, is retained. This effect is quite important in the case when the fluid is largely viscous or flowing at a high speed. This behavior occurs at high Eckert number (≫1). The symmetric nature of the flow is adopted. The fluid is a water based nanofluid containing Cu (copper) nanoparticles. The nanofluid is a two component mixture with the following assumptions: incompressible; no-chemical reaction; negligible viscous dissipation; negligible radiative heat transfer; nano-solid-particles and the base fluid are in thermal equilibrium and no slip occurs between them. The governing equations for momentum and energy in unsteady two dimensional flow of a nanofluid are as follows [17]:
|
|
(1) |
|
|
(2) |
|
|
(3) |
|
|
(4) |
Here u and v are the velocities in the x and y directions respectively, T is the temperature, P is the pressure, and effective density , the effective dynamic viscosity , the effective heat capacity and the effective thermal conductivity of the nanofluid are defined as follows [7]:
|
|
(5) |
The relevant boundary conditions are as follows:
|
|
(6) |
We introduce these parameters:
|
|
(7) |
Substituting the above variables into (2) and (3) and then eliminating the pressure gradient from the resulting equations give
|
|
(8) |
Using (7), Eqs. (3) and (4) reduces to the following differential equations:
|
|
(9) |
Here and are constants given by
|
|
(10) |
With these boundary conditions:
|
|
(11) |
where S is the squeeze number, Pr is the Prandtl number and Ec is the Eckert number, which are defined as follows:
|
|
(12) |
|
|
|
Fig. 1. Schematic of the two cases of problems with coupled nonlinear equations in fluids mechanic. |
2.2. Case 2
The second case (Fig. 1, right) consists of two vertical flat plates separated by a distance of 2b . A non-Newtonian fluid flows between them due to natural convection. The walls at and are held at constant temperatures and , respectively, where . This difference in temperature causes the fluid near the wall at to rise and the fluid near the wall at to fall. The fluid is a non-Newtonian Sodium Alginate (SA) based nanofluid containing Cu and Ag nanoparticles. It is assumed that the base fluid and the nanoparticles are in thermal equilibrium and no slip occurs between them. The effective density , the effective dynamic viscosity , the heat capacitance and the thermal conductivity of the nanofluid are given as follows [7]:
|
|
(13) |
|
|
(14) |
|
|
(15) |
|
|
(16) |
Here, is the solid volume fraction. By definition following are the similarity variables:
|
|
(17) |
Under these assumptions and following the nanofluid model proposed by Maxwell–Garnett (MG) model [9], the Navier–Stokes and energy equations can be reduced to the following pair of ordinary differential equations:
|
|
(18) |
|
|
(19) |
where Prandtl number (Pr), Eckert number (Ec ), dimensionless non-Newtonian viscosity () and have the following forms:
|
|
(20) |
|
|
(21) |
The appropriate boundary conditions are as follows:
|
|
(22) |
3. Principle of analytical methods
3.1. Differential Transformation Method (DTM)
For understanding the concept of DTM, we suppose that is an analytic function in domain D , and represents any point in the domain. The function is then represented by one power series whose center is located at . The Taylor series expansion function of is in form of
|
|
(23) |
The Maclaurin series of can be obtained by taking in Eq. (23) as follows:
|
|
(24) |
As explained in Ref. [10], the differential transformation of the function is defined as follows:
|
|
(25) |
where represents the transformed function and is the original function. The differential spectrum of is confined within the interval , where H is a constant value and it can be assumed as unity in common DTM, but for multi-step DTM it should be considered as the length of t steps. When the methods no longer work and Pade approximation should be applied. More information about H can be found in Ref. [20]. The differential inverse transform of is defined as follows:
|
|
(26) |
It is clear that the concept of differential transformation is based upon the Taylor series expansion. The values of function at values of argument k are referred to as discrete, i.e. is known as the zero discrete, as the first discrete, etc. The more the discrete available, the more precise it is possible to restore the unknown function. The function consists of the T -function , and its value is given by the sum of the T -function with as its coefficient. In real applications, with the right choice of constant H, the larger values of argument k will lead to rapid reduction of the discrete of spectrum. The function is expressed by a finite series and Eq. (26) can be written as follows:
|
|
(27) |
where n is the number of statements of the DTM. Generally, by increasing n, DTM accuracy will be increased, but it depends on H and time step’s length [20]. Actually, H depends on the time steps which for classical DTM is considered unity, but for Multi step DTM or Ms-DTM it is equal to the time step value. Some important mathematical operations performed by differential transform method are listed in Table 1. As described before, one of the most advantages of DTM is its independence of small parameter, linearization or perturbation. Also, it does not need to determine auxiliary function, auxiliary parameter or suitable initial guess against other analytical methods.
| Origin function | Transformed function |
|---|---|
4. Application of analytical methods on the problem
4.1. Application of DTM on case 1
Now Differential Transformation Method has been applied into the governing equations. Taking the differential transforms of Eqs. (8), (9) and (10) with respect to and considering H = 1 gives:
|
|
(28) |
|
|
(29) |
|
|
(30) |
|
|
(31) |
where and are the differential transforms of and are constants which can be obtained through boundary condition. This problem can be solved as follows:
|
|
(32) |
|
|
(33) |
The above process is continuous. By substituting Eqs. (32) and (33) into the main equation based on DTM, it can be obtained that the closed form of the solutions is as follows:
|
|
(34) |
|
|
(35) |
by substituting the boundary condition from Eq. (11) into Eqs. (34) and (35) in point the values of can be obtained. By substituting obtained into Eqs. (34) and (35), the expression of and can be obtained. For example for Cu–water nanofluid when Pr = 6.2, Ec = 0.05, , S = 0.1 and following equations will be obtained:
|
|
(36) |
|
|
(37) |
4.2. Application of DTM on case 2
Similarly, DTM is applied to Eqs. (18) and (19). Their transformed form will be as follows:
|
|
(38) |
The boundary conditions can be written as follows:
|
|
(39) |
In ith step, by solving the set of coupled Eq. (38), and can be determined. For example using boundary condition and Eq. (22) second terms will be
|
|
(40) |
where and represent the DTM transformed form of and V respectively and and d are unknown coefficients that after specifying and and applying boundary condition (Eq. (22)) into it, will be determined. For example when and for Cu–SA following values were determined for and d coefficients.
|
|
(41) |
Finally, and when and can be defined as follows:
|
|
(42) |
As seen in terms of above equation, although for increasing the accuracy, the number of statements has been increased, convergence of DTM is completely evident.
5. Results and discussion
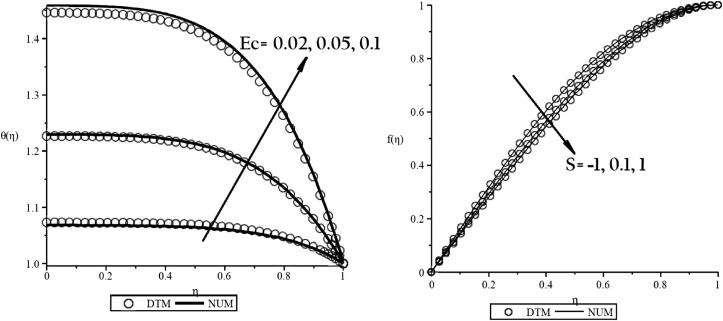
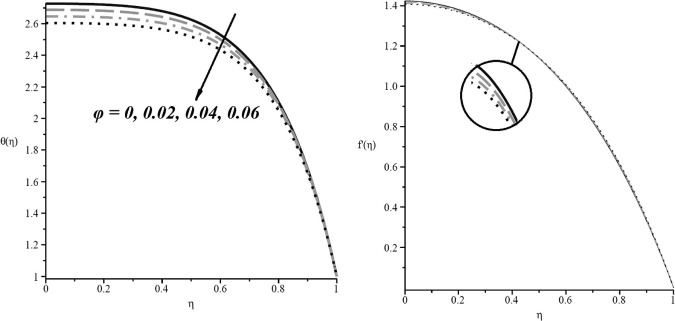
As has been discussed, Newtonian and non-Newtonian nanofluids can be found in many industrial applications [21], [22], [23], [24], [25], [26], [27] and [28]. Their analysis and treatment can be performed by well-known analytical and numerical methods. Some of these methods have been employed for solving the engineering problems [29], [30], [31] and [32]. In our study, efficiency of DTM for solving these kinds of problems is examined through two different problems as introduced in the previous sections. Our DTM solutions will be compared to numerical solution presented in the literature [19]. As mentioned before, in first case, heat transfer and nanofluid flow analysis in the unsteady squeezing nanofluids between parallel plates are studied using Differential Transformation Method (DTM) and results are compared with forth-order Runge–Kutta numerical method. Fig. 2 shows the results of DTM for solving the Eqs. (8) and (9) in different Eckert and squeeze numbers. As seen in these figures, DTM has a good agreement with numerical method in wide range of Ec and S numbers. Effect of Nanoparticles volume fraction on velocity and temperature profiles is shown in Fig. 3. Adding nanoparticles into the base fluid leads to increase in thermal boundary layer thickness while it has no significant effect on velocity boundary layer thickness. It is obvious that when nanoparticles were added into base fluid, heat transfer will increase due to their high thermal conductivity, and so temperature profiles will be decreased.
|
|
|
Fig. 2. Comparison of DTM and numerical results for (a) when Pr = 6.2, S = 0.1, , and (b) when Pr = 6.2, Ec = 0.05, , . |
|
|
|
Fig. 3. Effect of nanoparticles volume fraction () on (a) temperature profile and (b) velocity profile when Pr = 6.2, Ec = 0.5, , S = 1.0. |
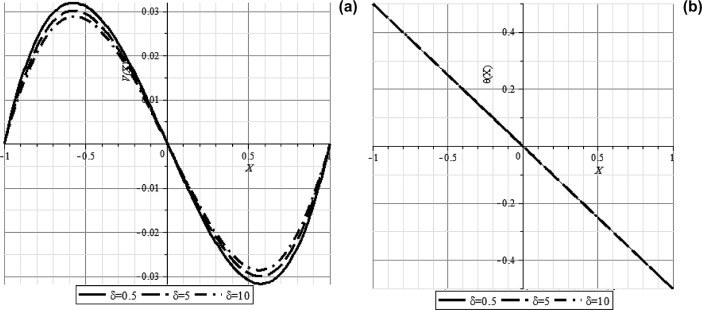
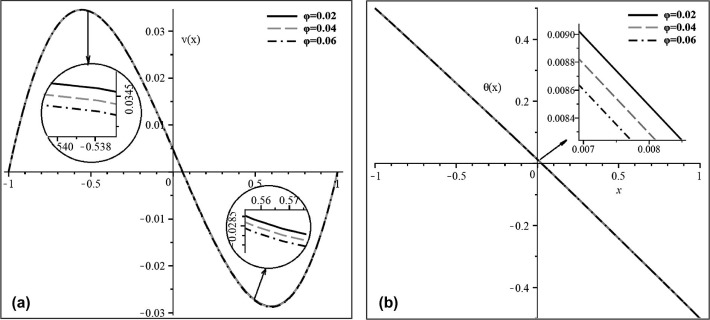
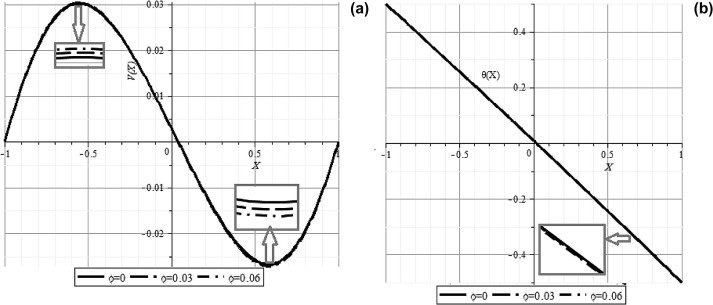
For the second case, the base fluid is considered as a non-Newtonian fluid containing sodium alginate (SA) and two types of nanoparticles namely silver (Ag) and copper (Cu) are added. For showing the efficiency of analytical applied method (DTM), Table 2 and Table 3 presented values and errors for Ag–SA, respectively. These tables also confirm the accuracy of DTM for solving such kinds of problems. The effect of number on non-dimensional velocity and temperature of the nanofluid is investigated through Fig. 4(a) and (b). These figures confirm that has no effect on temperature variations but it reduces velocity values. The same phenomenon was also observed by Ziabakhsh and Domairry [9]. Fig. 5 confirms that when nanoparticles volume fraction increases, velocity profiles increase but temperature values decrease due to increase in heat transfer. Fig. 5 shows the effect of nanoparticles volume fraction () on velocity profile and temperature distribution for SA–TiO2 nanofluid when , while Fig. 6 depictesthe effect of volume fraction of copper nanoparticles.
Table 2.
Velocity and temperature profile values by applied methods for Ag–SA nanofluid profiles when , .
| X | V(X) | (X) | ||
|---|---|---|---|---|
| Numerical | DTM | Numerical | DTM | |
| −1.0 | 0.00 | 2 × 10−11 | 0.50 | 0.50 |
| 0.45059686 | −0.9 | 0.013888702 | 0.01402428 | 0.45043148 |
| −0.8 | 0.023620556 | 0.02368182 | 0.40071897 | 0.40113389 |
| −0.7 | 0.029489465 | 0.02945437 | 0.35094362 | 0.35161056 |
| −0.6 | 0.031888322 | 0.03182368 | 0.30114965 | 0.30202640 |
| −0.5 | 0.031279886 | 0.03127150 | 0.25135346 | 0.25238090 |
| −0.4 | 0.028164333 | 0.02827959 | 0.20155266 | 0.20267356 |
| −0.3 | 0.023053394 | 0.02332968 | 0.15173412 | 0.15290389 |
| −0.2 | 0.016454874 | 0.01690353 | 0.10188071 | 0.10307139 |
| −0.1 | 0.008866496 | 0.00948289 | 0.05197647 | 0.05317557 |
| 0.0 | 0.000776279 | 0.00154951 | 0.002010267 | 0.00321593 |
| 0.1 | −0.007333249 | −0.00641485 | −0.04802206 | −0.04680801 |
| 0.2 | −0.014979179 | −0.01392846 | −0.09811697 | −0.09689681 |
| 0.3 | −0.021672314 | −0.02050956 | −0.14826378 | −0.14705093 |
| 0.4 | −0.026912911 | −0.02567640 | −0.19844679 | −0.19727080 |
| 0.5 | −0.030190188 | −0.02894723 | −0.24864875 | −0.24755700 |
| 0.6 | −0.030988255 | −0.02984030 | −0.29885599 | −0.29791001 |
| 0.7 | −0.028801308 | −0.02787389 | −0.34906512 | −0.34833031 |
| 0.8 | −0.023159274 | −0.02256617 | −0.39929111 | −0.39881842 |
| 0.9 | −0.013660270 | −0.01343546 | −0.44957637 | −0.44937485 |
| 1.0 | 0.00 | −2 × 10−11 | −0.50 | −0.50 |
| X | V(X) | (X) |
|---|---|---|
| DTM | DTM | |
| −1.0 | 0.00 | 0.00 |
| −0.9 | 0.00976 | 0.00037 |
| −0.8 | 0.00259 | 0.00104 |
| −0.7 | 0.00119 | 0.0019 |
| −0.6 | 0.002027 | 0.00291 |
| −0.5 | 0.000268 | 0.00409 |
| −0.4 | 0.00409 | 0.00556 |
| −0.3 | 0.01198 | 0.00771 |
| −0.2 | 0.02727 | 0.01169 |
| −0.1 | 0.06952 | 0.02307 |
| 0.0 | 0.99607 | 0.59975 |
| 0.1 | 0.125238 | 0.025281 |
| 0.2 | 0.070145 | 0.012436 |
| 0.3 | 0.053652 | 0.00818 |
| 0.4 | 0.045945 | 0.005926 |
| 0.5 | 0.041171 | 0.004391 |
| 0.6 | 0.037045 | 0.003165 |
| 0.7 | 0.032201 | 0.002105 |
| 0.8 | 0.02561 | 0.001184 |
| 0.9 | 0.016457 | 0.000448 |
| 1.0 | 0.00 | 0.00 |
|
|
|
Fig. 4. Effect of number on (a) velocity profile (V(X )) and (b) temperature profile ((X )) for Cu–SA nanofluid when , . |
|
|
|
Fig. 5. Effect of nanoparticles volume fraction () on (a) velocity profile (V(X )) and (b) temperature distribution ((X)) for SA–TiO2 nanofluid when . |
|
|
|
Fig. 6. Effect of nanoparticles volume fraction on (a) velocity profile (V(X )) and (b) temperature profile () for Cu–SA nanofluid when . |
6. Conclusion
In present work, Differential Transformation Method (DTM) is applied for solving the coupled nonlinear differential equations in fluids mechanic to show the validity and simplicity of this method. For this aim, two cases of problems in nanofluid mechanics which have coupled nonlinear differential equations were selected and DTM was applied on them. For illustrating the accuracy of described method, a numerical method was also used to solve the problems. A very good agreement between these two methods was observed in both problems. Compared to previous works, DTM has a better agreement with numerical method compared to other analytical and perturbation methods. This DTM accuracy is due to independency to small parameter (p) compared to perturbation methods and direct solving of the equation without linearization or discretization.
Acknowledgments
D. Jing gratefully acknowledges the financial support from the National Natural Science Foundation of China (Nos. 51422604 and 21276206) and China Fundamental Research Funds for the Central Universities.
References
- [1] S.A. Atouei, K. Hosseinzadeh, M. Hatami; Heat transfer study on convective–radiative semi-spherical fins with temperature-dependent properties and heat generation using efficient computational methods; Appl. Therm. Eng., 89 (2015), pp. 299–305
- [2] M. Hatami, G.R.M. Ahangar, D.D. Ganji; Refrigeration efficiency analysis for fully wet semi-spherical porous fins; Energy Convers. Manage., 84 (84) (2014), pp. 533–540
- [3] M. Hatami, D.D. Ganji; Thermal behavior of longitudinal convective–radiative porous fins with different section shapes and ceramic materials (SiC and Si3N4); Ceram. Int., 40 (2014), pp. 6765–6775
- [4] M. Hatami, D.D. Ganji; Motion of a spherical particle on a rotating parabola using Lagrangian and high accuracy multi-step differential transformation method; Powder Technol., 258 (2014), pp. 94–98
- [5] M. Hatami, D.D. Ganji; Natural convection of sodium alginate (SA) non-Newtonian nanofluid flow between two vertical flat plates by analytical and numerical methods; Case Stud. Thermal Eng. (2014)
- [6] A. Ahmadi, Kh. Hosseinzadeh, M. Hatami, D.D. Ganji; A comprehensive analysis of the flow and heat transfer for a nanofluid over an unsteady stretching flat plate; Powder Technol. (2014)
- [7] G. Domairry, M. Hatami; Squeezing Cu–water nanofluid flow analysis between parallel plates by DTM-Padé Method; J. Mole. Liq. (2014)
- [8] M. Hatami, D.D. Ganji; Thermal analysis of convective fin with temperature-dependent thermal conductivity and heat generation; Case Stud. Thermal Eng. (2014)
- [9] Z. Ziabakhsh, G. Domairry; Analytic solution of natural convection flow of a non-Newtonian fluid between two vertical flat plates using homotopy analysis method; Commun. Nonlinear Sci. Numer. Simul., 14 (2009), pp. 1868–1880
- [10] J.K. Zhou; Differential Transformation Method and its Application for Electrical Circuits; Hauzhang University Press, Wuhan, China (1986)
- [11] S. Ghafoori, M. Motevalli, M.G. Nejad, F. Shakeri, D.D. Ganji, M. Jalaal; Efficiency of differential transformation method for nonlinear oscillation: comparison with HPM and VIM; Curr. Appl. Phys., 11 (2011), pp. 965–971
- [12] H. Yahyazadeh, D.D. Ganji, A. Yahyazadeh, M. Taghi Khalili, P. Jalili, M. Jouya; Evaluation of natural convection flow of a nanofluid over a linearly stretching sheet in the presence of magnetic field by the differential transformation method; Therm. Sci., 16 (5) (2012), pp. 1281–1287
- [13] J. Biazar, M. Eslami; Differential transform method for quadratic Riccati differential equation; Int. J. Nonlinear Sci., 9 (4) (2010), pp. 444–447
- [14] A. Gokdogan, M. Merdan, A. Yildirim; The modified algorithm for the differential transform method to solution of Genesio systems; Commun. Nonlinear Sci. Numer. Simul., 17 (2012), pp. 45–51
- [15] F. Ayaz; On the two-dimensional differential transform method; Appl. Math. Comput., 143 (2003), pp. 361–374
- [16] Q. Ni, Z.L. Zhang, L. Wang; Application of the differential transformation method to vibration analysis of pipes conveying fluid; Appl. Math. Comput., 217 (2011), pp. 7028–7038
- [17] D.D. Ganji, S.H. Hashemi Kachapi; Progress in Nonlinear Science: Analysis of Nonlinear Equations in Fluids; Asian Academic Publisher Limited, Hong Kong, China (2011)
- [18] M. Hatami, D.D. Ganji; Natural convection of sodium alginate (SA) non-Newtonian nanofluid flow between two vertical flat plates by analytical and numerical methods; Case Stud. Thermal Eng., 2 (2014), pp. 14–22
- [19] K.R. Rajagopal, T.Y. Na; Natural convection flow of a non-Newtonian fluid between two vertical flat plates; Acta Mech., 54 (1985), pp. 39–46
- [20] C. Bervillier; Status of the differential transformation method; Appl. Math. Comput., 218 (2012), pp. 10158–10170
- [21] M. Hatami, D.D. Ganji; Heat transfer and flow analysis for SA–TiO2 non-Newtonian nanofluid passing through the porous media between two coaxial cylinders; J. Mole. Liq., 188 (2013), pp. 155–161
- [22] M. Hatami, J. Hatami, D.D. Ganji; Computer simulation of MHD blood conveying gold nanoparticles as a third grade non-Newtonian nanofluid in a hollow porous vessel; Comput. Meth. Prog. Biomed., 113 (2) (2014), pp. 632–641
- [23] G. Domairry, M. Hatami; Squeezing Cu–water nanofluid flow analysis between parallel plates by DTM-Padé Method; J. Mole. Liq. (2014)
- [24] M. Hatami, D.D. Ganji; Thermal and flow analysis of microchannel heat sink (MCHS) cooled by Cu–water nanofluid using porous media approach and least square method; Energy Convers. Manage., 78 (2014), pp. 347–358
- [25] M. Hatami, R. Nouri, D.D. Ganji; Forced convection analysis for MHD Al2O3–water nanofluid flow over a horizontal plate; J. Mole. Liq., 187 (2013), pp. 294–301
- [26] M. Sheikholeslami, M. Hatami, D.D. Ganji; Analytical investigation of MHD nanofluid flow in a semi-porous channel; Powder Technol., 246 (2013), pp. 327–336
- [27] M. Sheikholeslami, M. Hatami, D.D. Ganji; Nanofluid flow and heat transfer in a rotating system in the presence of a magnetic field; J. Mole. Liq., 190 (2013), pp. 112–120
- [28] M. Hatami, M. Sheikholeslami, D.D. Ganji; Laminar flow and heat transfer of nanofluid between contracting and rotating disks by least square method; Powder Technol., 253 (2014), pp. 769–779
- [29] M. Hatami, D.D. Ganji; Thermal performance of circular convective–radiative porous fins with different section shapes and materials; Energy Convers. Manage., 76 (2013), pp. 185–193
- [30] M. Hatami, A. Hasanpour, D.D. Ganji; Heat transfer study through porous fins (Si3N4 and AL) with temperature-dependent heat generation; Energy Convers. Manage., 74 (2013), pp. 9–16
- [31] M. Hatami, D.D. Ganji; Investigation of refrigeration efficiency for fully wet circular porous fins with variable sections by combined heat and mass transfer analysis; Int. J. Refrig. (2013) http://dx.doi.org/10.1016/j.ijrefrig.2013.11.002
- [32] M. Hatami, G. Domairry; Transient vertically motion of a soluble particle in a Newtonian fluid media; Powder Technol., 253 (2014), pp. 481–485
Document information
Published on 12/04/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?