A numerical approximation for build the stress/strain diagram with just the maximum load obtained

Abstract

One of the fundamental features in the design of rigid pavements is the rupture modulus, which value is obtained experimentally using a bending test and indicates the maximum load that a concrete beam can support. To determine this value is expensive and impractical since the tests require rather large stress values, there is always a risk of producing brittle fractures in the probes used. For this reason, it is proposed in this paper an implementation of a numerical estimation for the deformations due to the maximum load through a simple interpolation model that allows the generation of the stress/strain diagram using the only data available: the maximum load. The results show that it is possible to calculate the maximum deformation value in the beam previous to the failure. Also, it is possible to generate the stress/strain diagram and distinguish the elastic and elastoplastic areas of the concrete.

Keywords: Finite Element Analysis; Concrete; Blends; Approximation

2 Introduction

Nowadays, concrete is one of the most used materials in construction. It is used for various important reasons like its ability to be moldable in almost any shape compared to other materials, nevertheless, it requires fast and reliable quality control tests [1].

That is why the laboratories of materials which are responsible for checking quality control are an important factor for this kind of materials, forming part of the important decisions as they continue with the implementation of a product, change it or modify it and for this reason, the area of material resistance is particularly important. Usually, one of the most requested destructive tests is the simple compression test, in which, to determine the ${\textstyle f'c}$ (specified compressive stress) values is the goal. Other important tests are the ${\textstyle Mr}$ (rupture modulus) and the Test Method for Splitting Tensile Strength. The flexion test in concrete is applied to prismatic or rectangular specimens to obtain the break modulus values [2]. A thorough analysis of the test results is required due to the importance of these parameters in the design of rigid pavements, on which the bearing surface is made of concrete [3]. Obtaining the deformations that are generated in this kind of element is not a simple task, because it requires adequate instrumentation to measure a small displacement that occurs in a short lapse of time previous to a brittle fracture. Therefore, we need to implement an efficient method to obtain accurate information, for this reason, a numerical analysis such as those given by the finite element analysis [4] can be useful to calculate the deformations generated by the applied load. The finite element analysis requires to discretize the structure making a complete analysis of the behavior of the structure [5]. The modeling is essential to study the fundamentals processes that occur in materials to predicted real performance on the structures of concrete and to use both to improve the design [6]. Also, the numerical methods in conjunction with lab results are fundamental to improve the analysis. This paper contains information about ${\textstyle f'c}$ (specified compressive stress) values of a different blend of concrete elaborated under controlled conditions in the lab, the aggregates used in this study were obtained from Morelia Michoacán area. The cement used was a product of the Holcim trademark, the simple compressive strength of the design was 35 Mpa. For this analysis, prismatic elements were made with the elaborated blend and they were used in bending stress test to obtain the maximum load that can be held.

The study is based on the elaboration of the deformation stress/strain diagram obtaining only the maximum load in the bending test made in the laboratory. These data have become a benchmark for structures as rigid pavements. The dynamic problems of fracture can be classified into stationary and those with propagation cracks. In both cases, the tension fields and displacements around the crack are time-dependent. This value is 35 ${\textstyle Mpa}$, where the design of the blend was based on the methodology American Concrete Institute. Prismatic specimens of 15 cm ${\textstyle \times }$ 15 cm ${\textstyle \times }$ 60 cm were made and they were demolded and cured, where the beams are doubly supported, there are studies for dynamic cases as mentioned in[7] or for beam cantilever cases [8]. The dynamic problems of fracture can be classified into stationary and those with propagation cracks. In both cases, the tension fields and displacements around the crack depending on the time. [9] and [10] studied stress fields and displacement of dynamic problems of stationary cracks in isotropic materials [11], Nishioka and Atluri [12] also, studied the tension fields and displacement of the dynamic propagation of cracks with high speed in isotropic materials. The results were obtained monitoring for different ages of tests which were 60, 90, 140 and 180 days taking the arithmetic mean as the predominant value and also the maximum load recorded by the laboratory equipment as the value for each numerical analysis [13].

Each result obtained comes from static linear analysis with finite elements in a flat stress condition, considering infinitesimal deformations and applying a vertical displacement on the upper half face of the beam [14]. This paper contains information about the results of rupture modulus of concrete tested at different ages and one way to generate the stress/strain diagram using numerical methods.

3 Description of the Test

American Standard Test Method C 78-00 [15] establishes the test method for determination of the concrete bending strength, using by third-point loading method. When using molded specimens, turn the test specimen on its side concerning its position as molded and center it on the support blocks. When using sawed specimens, place the specimen so that the tension face corresponds to the top or bottom of the specimen as cut from the parent material. In Figure (1) the description of the elements involved in the test is shown.

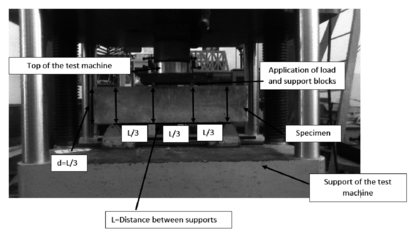
Figure 1: Flexural strength test with load in the thirds of the beam

In the bending test, it can be determined important values that characterize the concrete such as the rupture modulus, which is given by the Eq. 1

$R={\dfrac {P~L}{b~d^{2}}},$

(1)

where, ${\textstyle R}$ is the rupture modulus in ${\textstyle kpa}$, ${\textstyle P}$ is the maximum load applied in ${\textstyle kg}$, ${\textstyle L}$ is the distance between supports in ${\textstyle cm}$, ${\textstyle b}$ is the average width of the specimen in ${\textstyle cm}$, ${\textstyle d}$ is the average thickness in ${\textstyle cm}$.

The parameters involved in Eq. (1) can be obtained through direct methods of measurement on the specimen except for ${\textstyle P}$; the value of ${\textstyle P}$ is the maximum load obtained by the test. The information that can be obtained from this test is often limited to the instrumentation available, and doing post-processing turns out complicated, since only the rupture modulus is measured. One of the aims of this paper is to provide a tool for post-processing using the displacement values in the test; these deformations are very difficult to calculate in practice due to its cost. The use of other instruments as micrometers is impractical because the failure occurs in a fragile way (i.e., happens very fast), and the micrometer can be damaged when the failure occurs, making the readings almost impossible to read. Another problem is the fact that the deformations are located in a minimal range (${\textstyle \thicksim 10^{-4}m}$). This is the main reason for using the Finite Element analysis that can solve this problem and help to get enough information about a test that only provides scarce information and it allows to generate the stress/strain diagram to have a general overview of the behavior of the element in the the study.

3.1 Procedure Test "in situ"

This paper makes the analysis, the model, the calculation of the deformations and the calculation of the static elasticity module for a specific case, which was studied in Morelia, Michoacán, Mexico. The known feature for this concrete is the resistance to simple design compression whose value is 39.2266 ${\textstyle MPa}$. The test comprises setting loads to the element in 4 stages, the first stage comprises an applied load of 250 ${\textstyle kg}$, the second of 500 ${\textstyle kg}$, 750 ${\textstyle kg}$ and 1000 ${\textstyle kg}$ are the last 2 stages of load. Once the load is applied, the stabilization of the readings in the micrometers is expected to obtain the deformation data, the data are registered until the last load. For this case, just a maximum load of 1000 ${\textstyle kg}$ is placed.

One aim is to compare the analytical solution in tests measured in situ, and verify the approximation, to establish the consistency of the model. The model performs the calculation of the deformations and the deformation stress/strain diagram just with the maximum load got in the bending test in the laboratory, and for this purpose, the test was performed to establish if the model represents the measurements made in real experiments.

In Figure (2) the implementation for get the deformations generated is shown, which one result from the applied load.

Figure 2: Procedure and implementation of the test

Table (1) presents the loads measured in different stages.

Table. 1 Applied loads stages

Loading stages	load (${\textstyle kg}$)
1st load	250
2nd load	500
3rd load	750
4th load	1000

4 Finite Element analysis

In this article, two-dimensional Euler-Bernoulli beam bilinear finite elements to produce a matching of the local and global coordinates are used. This methodology is characterized by suitable piecewise polynomials and, the problem analyzed is adequate for these conditions.

The deformation of a beam must haven't continuous slope as well as continuous deflection at any two neighboring beam elements. To satisfy this continuity requirement each node has both deflection, ${\textstyle \upsilon }$ and slope ${\textstyle \theta _{i}}$ as nodal variables. In this case, any two neighboring beam elements have common deflection and slope at the shared nodal point.

The Euler Bernoulli beam equation is based on the assumption that the plane normal to the neutral axis before deformation remains normal to the neutral axis after deformation [16].

In this work, an efficient numerical approach to calculate the deformation generated by an applied load on a beam is proposed. The load is taken as the maximum value registered by the bending test. The process starts by proposing the number of nodes in the beam that will be discretized, the moment of inertia is calculated according to its cross-section, and the elasticity module is proposed for the initial tests. Then, the domain is discretized, and the connectivity table of the elements involved is generated, the number of elements will depend on the number of nodes previously established.

Evaluating the system ${\textstyle K*U=F}$ and substituting the respective values the stiffness matrix for the system is obtained, as shown in the following expression:

$K={\begin{bmatrix}1.6554e+09&2.0693e+07&-1.6554e+09&2.0693e+07\\2.0693e+07&3.4488e+05&-2.0693e+07&1.7244e+05\\-1.6554e+09&-2.0693e+07&1.6554e+09&-2.0693e+07\\2.0693e+07&1.7244e+05&-2.0693e+07&3.4488e+05\\\end{bmatrix}}.$

From this information is made the assembly of the global stiffness matrix, which was solved, considering the expression ${\textstyle K*U=F}$ the system has the form below.

${\begin{bmatrix}1.6554e+09&2.0693e+07&-1.6554e+09&2.0693e+07\\2.0693e+07&3.4488e+05&-2.0693e+07&1.7244e+05\\-1.6554e+09&-2.0693e+07&1.6554e+09&-2.0693e+07\\2.0693e+07&1.7244e+05&-2.0693e+07&3.4488e+05\\\end{bmatrix}}{\begin{Bmatrix}\upsilon _{1}\\\theta _{1}\\\upsilon _{2}\\\theta _{2}\\\vdots \\\upsilon _{i}\\\theta _{i}\end{Bmatrix}}={\begin{Bmatrix}V_{1}\\M_{1}\\V_{2}\\M_{2}\\\vdots \\V_{i}\\M_{i}.\end{Bmatrix}}$

Lastly, the system is solved, the deformations are obtained efficiently and, with this data, it is possible to build different diagrams.

It is very important to notice that the calculation of the maximum deformation is derived from the analysis of the previously mentioned set of equations, which shows that the inputs of the vector of terms independent of each other correspond to values of ${\textstyle V_{i}}$ and ${\textstyle M_{i}}$, deformations and moments respectively. In this case by convention twenty-five nodes are computed, i.e., ${\textstyle n=arbitrary}$ ${\textstyle odd}$ ${\textstyle value}$ so that ${\textstyle F\in {\mathbb {R} }^{2nx2n}}$ and the entries of the vector ${\textstyle F}$ will be of value ${\textstyle 2n}$ i.e., has an independent vector of fifty entries, where the entry ${\textstyle n}$ corresponds to the maximum deflection and the entry ${\textstyle n+1}$ corresponds to the maximum moment, considering that the initial entry is equal to zero ${\textstyle (F(1,1)=0)}$, and thus, these increase until the highest value, from the entry ${\textstyle (n+1)}$ the values begin to decrease with the same magnitude with which it grew until reaching zero in the last of the entries of the system, that is ${\textstyle F(2n,1)=0}$. In this case, it is considered that the number of nodes chosen is sufficient for the flexibility of the solution since elevating the number of nodes for this case does not impact the solution and the representation, unless the objective would be to carry out a deep discretization. The information can be represented as ${\textstyle V_{max}=F(n,1)}$ and ${\textstyle M_{max}=(F(n+1),1).}$ The aforementioned discretization was implemented in MATLAB 2018b [17] using a personal computer (Windows 10 Pro, processor Intel (R) Core(TM) i5-3210M CPU @ 2.50GHz RAM: 8 GB). The crucial steps to solve this system are shown, and it also shows the idealization of the mesh with the finite element analysis in Figure (3) to solve the problem.

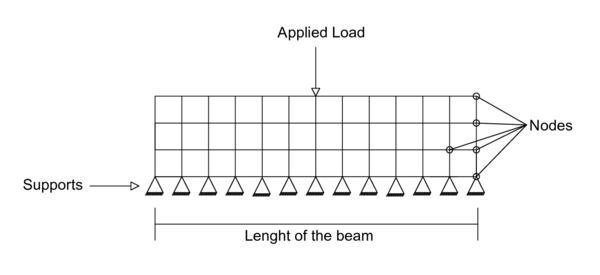
Figure 3: Idealized mesh

The methodology aforementioned is used for analyzing the behavior of a concrete element, and this kind of analysis it's important for the trend in different materials[18]. This element was tested to flexion, and the information obtained was introduced as input data for the finite element analysis.

Usually, this method requires many amounts of operations and in this work is proposed an algorithm elaborated in MATLAB, which solves this problem in an efficient way[19]. One of the principal problem with this kind of analysis is the sensibility and precision of results and this depends on the number of nodes that discretized the structure of the system.

This algorithm allows to input values that equal to features such as inertia moment, maximum load, which is obtained in the flexural strength test, length of the element, in this case, the length of the beam, the number of nodes that discretized the system and if it is possible the elasticity modulus. To the right is shown the principal structure of the algorithm after mentioned.

5 Numerical Tests

The blends of concrete used in the bending tests were made according to the ${\textstyle ACI}$ methodology [20], and the design resistance to simple compression chosen ${\textstyle 35~Mpa}$. The blends are prepared during the dry season. The specimens were developed and tested under controlled conditions in the laboratory, mainly the flexure test must be carried out at uniform speed, in such a way that the stress increase of the extreme fibers does not exceed 980 ${\textstyle Kpa/min}$ or ${\textstyle 10~kgf/cm^{2}}$ per minute, allowing higher speeds 50% before to the estimated load of rupture.

One must determine the average width, the thickness, and the location of the failure line, using the average of three measures: one in the middle, and two on the edges of the specimen. All of them must be precise, up to ${\textstyle 1~mm}$. The resulting data as shown in table (2).

Table. 2 Results of the flexure test in the laboratory

Test days	Maximum load registered(kn)	Rupture modulus(Mpa)
60	39.8640	5.42
90	41.1879	5.60
140	41.9334	5.70
180	43.1100	5.86

For the finite element analysis, distribution of twenty-five nodes equispaced along the beam and a moment of inertia of ${\textstyle 60e^{-6}~m}$ was considered, this moment is calculated as a function of the sectional area and an elasticity modulus of ${\textstyle 35.9253}$ ${\textstyle Mpa}$, this modulus is obtained from the resonant frequency test made in laboratory [21]. The number of nodes depends on the approximation required, in this case, twenty-five nodes are used, so the computing time is relatively short for this number, and the maximum deformation generated by the maximum load can be represented with one unique value.

For this problem, it is considered a value of time ${\textstyle t=0}$ for the quasi-static case. Since the crack occurs very fast in the bending test, it is to say, the time to get the crack is up to three seconds, which is quite short to measure deformations. Different analyses were performed corresponding to four test ages, the first test shows the maximum load to 60 days, the second age is for 90 days with the maximum load obtained in that test and it is the same case for the other test ages. For this reason, four diagrams are shown, one for each test age with a maximum load for each one.

It is important to mention that the results measured with the approximations obtained are data that were not generated in the test due to the restriction and difficulty of equipment implementation for taking data in this kind of test, therefore the results obtained are approximations and estimation of data that do not exist in physical tests, however, due to the conditions of this type of elements, their performance is partially known and thus the results generate a good approximation to the aforementioned performance, i.e., the approximation to an analytical solution is generated, in addition to the availability of data to be analyzed.

6 Results

For the construction of the previous graphs, the quasi-static case was considered, where even though the tests are compared at different ages, time is not considered a factor that directly influences the calculation of the deformations, this procedure is known as batch calculation. In the batch calculation, it is considered the set data that is in that stage, and it is compared with the set data that is in another stage. In this case, the test ages are considered as the different stages.

The deformations were calculated using the finite element analysis, for the construction of the previously diagrams all data obtained in the numerical solution is used, for diagrams shown in the Figures (4 - 6), it can be seen the length of the beam in the horizontal axis, which is 0.60 meters, such measure is the length of all specimens. In the vertical axis, the displacements (in meters) calculated with the ${\textstyle FEM}$ are shown. These Figures show the deformations that occurred by the effect of an applied load, and it is essential to say that the maximum deformation occurs with the maximum load registered in the test of bending in the laboratory. Notice that as the days go by the resistance increases, therefore, the deformations increase for each case, and we can conclude that the deformations have a direct connection with the applied load. The computed deflection and slip profiles have been compared with test results of the continuous composite beam at the specific load states, however, this is not informative to verify the computational results.[22]. At the early loading stages, both curves will increase linearly.

Figure (6) shows all deformations obtained by the numerical solution.

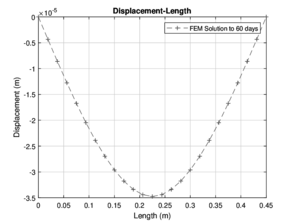
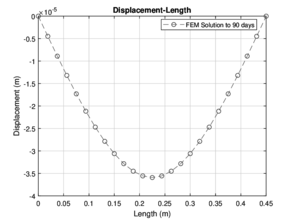
Figure 4: Numerical solution for 60 and 90 days

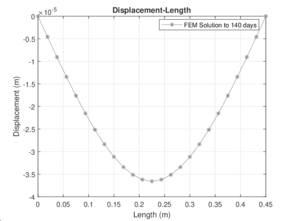
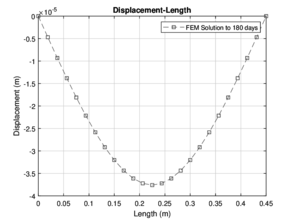
Figure 5: Plots of numerical solution for 140 and 180 days

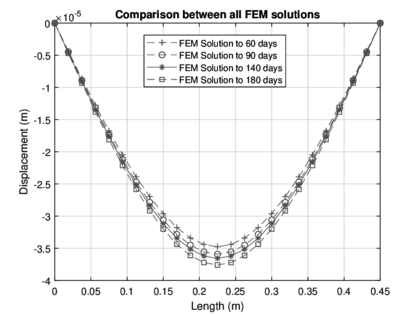
Figure 6: Plot of displacement for all test days

Based on the displacements generated through ${\textstyle FEM}$, it is possible to generate the stress/strain diagram, since there is the necessary information to do so. It is important to mention that in this part the interpretation of the results obtained by ${\textstyle FEM}$ will be the factor to be able to generate the diagrams successfully. Once the information obtained is worked on, the stress/strain diagram is generated for each of the test ages. It is important to highlight how these diagrams were generated, the procedure is described below.

First, the straight line is made between the initial deformation which is a zero value, and the final deformation, this straight line is shown in the stress/strain diagram was traced joining the origin and the point corresponding to the maximum deformation, which is the cause of the maximum load applied.

For the aforementioned diagram, it is impossible to give more information as these are the only data obtained from this test, which is elaborated in the laboratory. Using the finite element analysis, it is possible to generate the second trajectory in each one of the test ages, these make an approximation to the deformation of each element, these deformations were calculated by the previous process and with this data, it's possible to generate the corresponding stress/strain diagram. Using the deformations obtained by the ${\textstyle FEM}$, it is possible to construct a continuous linear function in fragments, which represents the connection of each one of the deformations calculated, since the initial deformation, which is zero until the final deformation, and in the same way, the value its equal to zero. The interesting part is that the intermediary values are the ${\textstyle FEM}$ data.

This data is converted in a linear function, whit known values, the initial and final deformations, therefore the constructed lines could be named such as C' function, i.e., a continuous function in pieces. One of the principal application with this data it's the analysis of the elastic zone and the plastic zone for each of the beams, this information can be identified and thus perform further analysis, that allows generating a piece of crucial information about of development and performance of this important material.

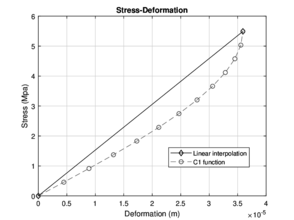
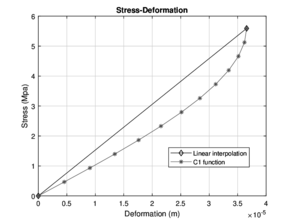
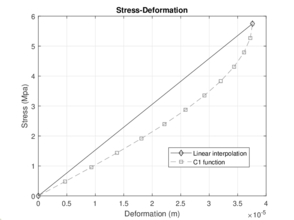
The results obtained from the analysis are shown below in Figures (fig:solutioninterp - 8).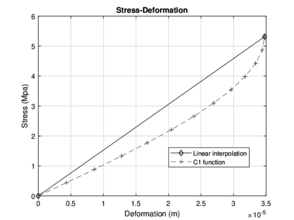

Figure 7: Solution of the linear interpolation model for 60 days and 90 days

Figure 8: Solution of the linear interpolation model for 140 days and 180 days

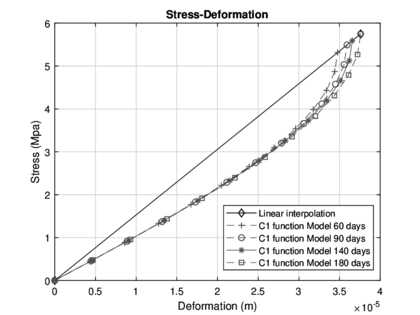
Figure 9: Comparison of the model at different test ages vs linear interpolation

This paper is characterized by a numerical analysis, which is based on unique data, which is the maximum load obtained from the bending test. The displacements generated by the load through the finite element analysis are approximated from it and it is possible to generate the stress/strain diagram with the analysis of equations type C1. The governing equation is the differential partial equation of the fourth order of Eule-Bernoulli. An efficient way to make an approximation for the determination of the displacements generated by the load is to use the formulation of Lagrange, where it is possible to use a polynomial of a lower order, for this case, a polynomial of second-order is the solution.

$f_{2}(x)={\dfrac {(x-x_{1})(x-x_{2})}{(x_{0}-x_{1})(x_{0}-x_{2})}}f(x_{0})+{\dfrac {(x-x_{0})(x-x_{2})}{(x_{1}-x_{0})(x_{1}-x_{2})}}f(x_{1})+{\dfrac {(x-x_{0})(x-x_{1})}{(x_{2}-x_{0})(x_{2}-x_{1})}}f(x_{2})$

Where ${\textstyle x_{0}}$ and ${\textstyle f(x_{0})}$ are considered as the origin (0,0), the variables ${\textstyle x_{2}}$ and ${\textstyle f(x_{2})}$ correspond to the length of the element and to the last displacement respectively, which in this case the length of the element is the length of the beam subjected to the bending test and the last displacement is equal to 0 since it is considered that the beam could reach its original form before it reaches the maximum load.

Performing the above consideration ${\textstyle x_{1}}$ is equal to the length of half of the beam since it is considered only the distance to the central axis and ${\textstyle f(x_{1})}$ is the maximum deformation, deformation obtained by the analysis of the finite element analysis. Therefore, it is possible to make an approximation of the estimation of the deformations based on a simple configuration such as Lagrange's adaptation. The result of the aforementioned approximation is shown in the Figures (10) and (11)

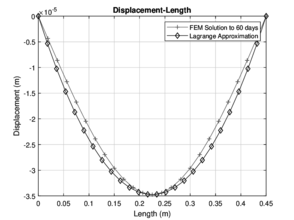
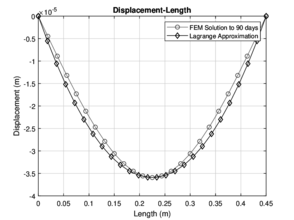
Figure 10: Numerical approximation with Lagrange for 60 and 90 days

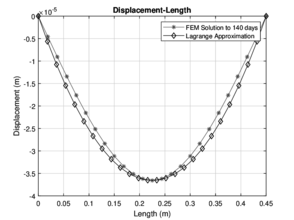
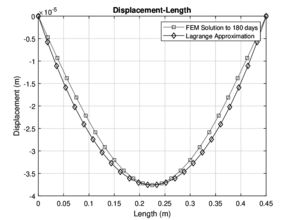
Figure 11: Numerical approximation with Lagrange for 140 and 180 days

6.1 Test in situ

The deformations obtained with the micrometers and their respective approximations are shown in Figures (12 and fig_deformations2). Figures (fig:carga1,2) and (fig:3,4) show the comparative among the precision obtained by Lagrange methodology and the FEM in each applied load.

Table. 3 Results of test in situ

Applied load (${\textstyle Kg}$)	Deformation (mm)
250	0.006858
500	0.019050
750	0.027940
1000	0.037592

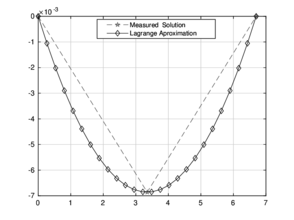
Figure 12: Measured solution and his Lagrange Approximation

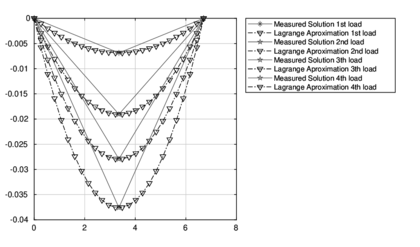
Figure 13: Measured solution and his Lagrange Approximation

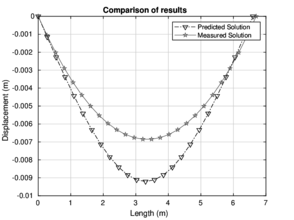
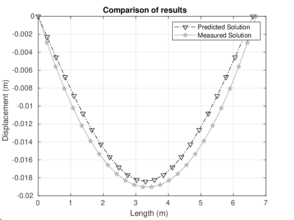
Figure 14: Behavior at 250 and 500 $kg$, respectively

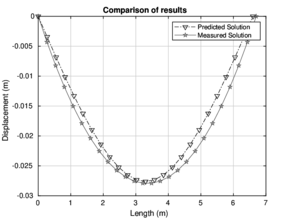
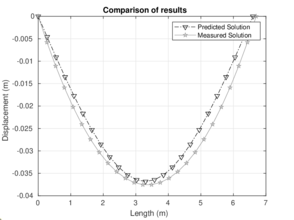
Figure 15: Behavior at 750 and 1000 $kg$, respectively

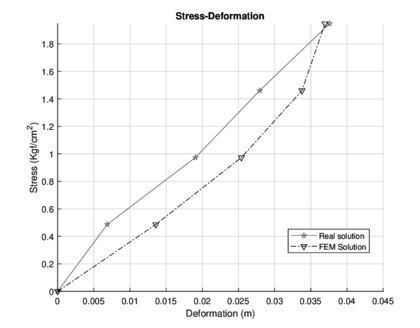
Figure 16: Stress/strain diagram for both solutions

7 Conclusions.

An important advantage of this procedure is an efficient way to obtain deformation stress/strain diagrams without the use of equipment such as micrometers or laser devices. Furthermore, this allows us to know each of the deformations within the length of the specimen in the bending test and to consider a number n of deformations since this amount of values will be limited by the computational cost and not by physical factors. This type of data must be analyzed since the deformations establish crucial parameters for the design of slabs and the design of rigid pavements since currently the analysis of this type of structure is not carried out with the detail that must be done.

The hardened concrete tests performed in the laboratory usually provide only limited specific data of the existing instrumentation, and a post-process of the information is not possible. One of the main ideas of this paper is to propose a method to compute the deformations in a concrete beam which is subject to flexure stresses using only the maximum load, by proposing a procedure to calculate the deformations generated in the beam. Thus, a stress/strain diagram can be generated to estimate the elasticity module [23].

The results obtained in this work model the behavior of an element under the application of a load. Such data can be useful for further analysis related to the performance of concrete. The methodology proposed here can be used to provide useful technical information for the construction community.

To make a stress/strain diagram using results from the laboratory, it would be necessary for a considerable number of micrometers placed along the beam to measure the deformations. The data obtained would be enough to sketch the diagram, but the performance of such measures is impractical since the instrumentation is not easy to implement. The proposal of this work is to use a numerical method to solve this problem. The finite element analysis allows us to calculate the displacements generated in this test, the typology of a doubly-supported beam with a load in the center. This phenomenon is known as the problem of the Euler-Bernoulli beam equation. It is important to mention that the concrete used is a block of concrete without reinforcing steel and for this reason, the modulus of elasticity is almost zero, but with the numerical analysis, we found the little values of that elasticity.

Once the problem is solved with this method, the diagrams of displacements along the length of the beam can be generated. The calculation of these displacements is essential to construct the deformation stress/strain diagram since the intermediate displacements previous to the maximum displacement are used in such construction. It is important to remark that this analysis is performed in situ or in the laboratory, and it provides a general overview of the performance of a certain concrete blend.

Numerical and laboratory tests allow predicting the behavior and performance of a concrete blend. It is vital to perform this analysis in an efficient way, since gathering this data may take more time and requires skill. The programming language used for this work is Matlab. One of the advantages of the proposed method is its simplicity to handle boundary conditions and it is possible to obtain extra information from the run.

The analysis with this kind of methodology is with the goal to found an efficient way the numerical solution about deformations generated by the load applied in the element. This work is just the application of the model in one a blend of concrete but can be applied in other blends and can be compared the numerical performance.

8 Acknowledgments.

The authors wish to thank the information provided to the materials laboratory Ing. Luis Silva Ruelas for providing the necessary equipment to obtain data. Thanks to Conacyt, CIC, and Aula-CIMNE for funding this research.

BIBLIOGRAPHY

[1] Lopez-Calvo, HZ and Montes-Garcia, P and Alonso-Guzmán, EM and Martinez-Molina, W and Bremner, TW and Thomas, MDA. (2017) "Effects of corrosion inhibiting admixtures and supplementary cementitious materials combinations on the strength and certain durability properties of HPC", Volume 44. NRC Research Press. Canadian Journal of Civil Engineering 11 918–926

[2] Ghadimi, Siamak and Kourehli, Seyed Sina. (2018) "Multi cracks detection in Euler-Bernoulli beam subjected to a moving mass based on acceleration responses". Taylor & Francis. Inverse Problems in Science and Engineering 1–21

[3] Bustamante, Fernando Olivera. (2002) "Estructuración de vías terrestres: vías terrestres y pavimentos". Compañía Editorial Continental

[4] Ariaei, A and Ziaei-Rad, S and Ghayour, M. (2009) "Vibration analysis of beams with open and breathing cracks subjected to moving masses", Volume 326. Elsevier. Journal of sound and vibration 3-5 709–724

[5] Cifuentes, Arturo O. (1989) "Dynamic response of a beam excited by a moving mass", Volume 5. Elsevier. Finite Elements in Analysis and Design 3 237–246

[6] Jing, Lanru and Hudson, JA. (2002) "Numerical methods in rock mechanics", Volume 39. Elsevier. International Journal of Rock Mechanics and Mining Sciences 4 409–427

[7] Gökda, Hakan. (2013) "A crack identification approach for beam-like structures under moving vehicle using particle swarm optimization", Volume 55. Carl Hanser Verlag. Materials Testing 2 114–120

[8] Ghadimi, Siamak and Kourehli, Seyed Sina. (2017) "Multiple crack identification in Euler beams using extreme learning machine", Volume 21. Springer. KSCE journal of Civil Engineering 1 389–396

[9] Chen, EP. (1978) "Sudden appearance of a crack in a stretched finite strip", Volume 45. American Society of Mechanical Engineers. Journal of Applied Mechanics 2 277–280

[10] Baker, BR. (1962) "Dynamic stresses created by a moving crack", Volume 29. American Society of Mechanical Engineers. Journal of Applied Mechanics 3 449–458

[11] Adams, George G. (1999) "Dynamic motion of two elastic half-spaces in relative sliding without slipping", Volume 121. American Society of Mechanical Engineers. Journal of tribology 3 455–461

[12] Nishioka, T and Atluri, SN. (1983) "Path-independent integrals, energy release rates, and general solutions of near-tip fields in mixed-mode dynamic fracture mechanics", Volume 18. Pergamon. Engineering Fracture Mechanics 1 1–22

[13] Del Valle Moreno, A and Guzmán Torres, JA and Alonso Guzmán, EM and Martínez Molina, W and Torres Acosta, AA and Terán Guillén, J and Montes Zea, MA and Torres Murillo, AI and Martínez Madrid, M. (2015) "Solicitaciones mecánicas y estáticas a concreto hidráulico simple elaborado con agregados pétreos redondeados y adicionados con fibras deshidratadas de cactus opuntia". Publicación Técnica 448

[14] Graffe, Rubén and Linero, Dorian. (2010) "Simulación numérica del proceso de fractura en modo I de vigas de concreto con trayectoria de fisuración conocida mediante un modelo discreto de fisura cohesiva", Volume 25. Pontificia Universidad Católica de Chile. Departamento de Ingeniería y Gestión de la Construcción. Revista ingeniería de construcción 3 399–418

[15] ASTM, C. (2000) "78-00,“". Standard Test Method for Flexural Strength of Concrete (Using Simple Beam with Third-Point Loading),” American Society for Testing and Materials

[16] Kwon, Young W and Bang, Hyochoong. (2018) "The finite element method using MATLAB". CRC press

[17] Lowell. (2018) "MATLAB. Matlab user manual.". MA: Mathwork Inc.

[18] Nour, Ali and Massicotte, Bruno and Yildiz, Emre and Koval, Viacheslav. (2007) "Finite element modeling of concrete structures reinforced with internal and external fibre-reinforced polymers", Volume 34. NRC Research Press. Canadian Journal of Civil Engineering 3 340–354

[19] Cohen, Michael and Monteleone, Agostino and Potapenko, Stanislav. (2018) "Finite element analysis of intermediate crack debonding in fibre reinforced polymer strengthened reinforced concrete beams", Volume 45. NRC Research Press. Canadian Journal of Civil Engineering 10 840–851

[20] Kosmatka, Steven H and Panarese, William C and Bringas, Manuel Santiago. (1992) "Diseño y control de mezclas de concreto". Instituto Mexicano del Cemento y del Concreto

[21] ASTM, C. (2000) "125 (2000)". Standard Terminology Relating to Concrete and Concrete Aggregates, ASTM International, PA

[22] Gu, Ping and Sheng, Bo and Chen, Shiming. (2012) "Discussion of “Nonlinear behaviour of steel–concrete composite bridges: finite element modelling and experimental verification”", Volume 39. NRC Research Press. Canadian Journal of Civil Engineering 10 1171–1172

[23] Zheng, Yong-Ping and Choi, APC and Ling, HY and Huang, Yan-Ping. (2009) "Simultaneous estimation of Poisson's ratio and Young's modulus using a single indentation: a finite element study", Volume 20. IOP Publishing. Measurement science and technology 4 045706