Valuation of the China internet company under a real option approach

Abstract

The objective of the paper is description, application and verification of the real option methodology in financial decision-making of the internet company in China. There is the real option methodology described. Subsequently financial characterisation of internet Baidu company is given. Crucial part consists in calculation of the company value under several scenarios and real option alternatives. We conclude that generalised real option methodology is suitable method of valuation of the internet company under China economical conditions.

JEL classification

C4 ; C02 ; G3 ; G11

Keywords

Real options ; Internet company ; Option valuation methods

Introduction

Valuation of the company is very important problem in financial decision making. One of the well developed methodologies is a real option approach. The internet industry and Chinese market is full of uncertainty and flexibility. The objective of the paper is description, application and verification of the real option methodology in financial decision-making of the internet company Baidu in China.

Valuation procedure of an American real option

The generalised principle of valuation is called the martingale principle see e.g. (Luenberger, 1998 ). The principle is being defined so that a value has to be equal to the expected future value, implying the random process is without trend. In the case of the risk neutral approach this category is ratio of random value and risk-free asset, so after rearranging

$V_{t}=e^{-r\cdot dt}\cdot {\overset {\frown }{E}}(V_{t+dt}){\mbox{,}}$

( 2.1)

here V_t is value, r is risk-free rate, dt   is time interval, ${\textstyle {\overset {\frown }{E}}(V_{t+dt})}$ is risk neutral expected value. We can gain the same result for complete market under replication valuation strategy or arbitrage principle.

One of the basic approaches of derivatives valuation under complete market is replication strategy; see e.g. (Smith and Nau, 1995 , p. 795; Amram et al., 1999 , Barnett, 2005 , Boer, 2002 , Brandao and Dyer, 2005 , Carlsson and Fuller, 2003 , Chevalie-Roignant and Trigeorgis, 2011 , Cox et al., 1979 , Čulík, 2004 , Čulík, 2006 , Čulík, 2008 , Čulík, 2010 , Damodaran, 2001 , Dixit and Pindyck, 1994 , Dluhošová, 2004 , Driouchi et al., 2012 , Guthrie, 2009 , Junyan Guo, 2015 , Muzzioli and Torricelli, 2004 , Shockley, 2007 , Smit and Trigeorgis, 2004 , Triantis, 2001 , Trigeorgis and Schwartz, 2001 , Viebig et al., 2008 , Yoshida, 2002 , Yoshida, 2003 , Zmeškal, 1999 , Zmeškal, 2001 , Zmeškal, 2005 , Zmeškal, 2006 , Zmeškal, 2008 , Zmeškal, 2010a , Zmeškal, 2010b , Zmeškal, 2011  and Zmeškal, 2012 ). Having derived the replication strategy, we suppose a compact (effective) market, asset-bearing the incomes (dividends, coupons, etc.) proportional to an asset price. The replication strategy is based on creation a portfolio from underlying asset S and risk-free asset B so, for every situation the derivative value is to be replicated; it means a derivative value equals a portfolio value.

Portfolio value in appraising a moment t   is ${\textstyle \Pi _{t}\equiv a\cdot S_{t}+B_{t}=f_{t}}$ ; portfolio value in a moment ${\textstyle t+dt}$ for growing price is ${\textstyle \Pi _{t+dt}\equiv a\cdot S_{t+dt}^{u}+B_{t}\cdot e^{r\cdot dt}=f_{t+dt}^{u}}$ ; the portfolio value in a moment for declining price, ${\textstyle \Pi _{t+dt}\equiv a\cdot S_{t+dt}^{d}+B_{t}\cdot e^{r\cdot dt}=f_{t+dt}^{d}}$ ; where ${\textstyle \Pi _{t}}$ is portfolio value, S is underlying asset value, a is a amount of underlying asset, B is risk-free asset value, f is derivative value, r is continuous risk-free rate, u (d   ) are indexes of growth (fall) of underlying asset, ${\textstyle S_{t+dt}^{u}}$ , ${\textstyle S_{t+dt}^{d}}$ are their prices in up-movements (down-movements).

By solution of three equations for variables a , B , f_t , we can get a general formula for derivative price,

${\begin{array}{l}\displaystyle f_{t}=e^{-r\cdot dt}\cdot \left\{f_{t+dt}^{u}\cdot \left[{\frac {e^{r\cdot dt}\cdot S_{t}-S_{t+dt}^{d}}{S_{t+dt}^{u}-S_{t+dt}^{d}}}\right]+f_{t+dt}^{d}\cdot \right.\\\left.\displaystyle \cdot \left[{\frac {S_{t+dt}^{u}-e^{r\cdot dt}\cdot S_{t}}{S_{t+dt}^{u}-S_{t+dt}^{d}}}\right]\right\}{\mbox{.}}\end{array}}$

( 2.2)

The derivative price is determined as a present value of expected value in a following period. This is the general formula for European derivative price valuation by the replication strategy, which should be written as follows,

${\begin{array}{l}\displaystyle f_{t}=e^{-r\cdot dt}\cdot [f_{t+dt}^{u}\cdot ({\overset {\frown }{p}})+f_{t+dt}^{d}\cdot (1-{\overset {\frown }{p}})]\\\displaystyle {\mbox{   }}{\mbox{or}}{\mbox{   }}f_{t}=e^{-r\cdot dt}\cdot {\overset {\frown }{E}}(f_{t+dt}){\mbox{.}}\end{array}}$

( 2.3)

In the case of the American derivative type, formula is following,

${\begin{array}{l}\displaystyle f_{t}=max\lbrace g_{t};e^{-r\cdot dt}\cdot [f_{t+dt}^{u}\cdot ({\overset {\frown }{p}})+f_{t+dt}^{d}\cdot (1-{\overset {\frown }{p}})]\rbrace \\\displaystyle {\mbox{   }}{\mbox{or}}{\mbox{   }}f_{t}=max[g_{t};e^{-r\cdot dt}\cdot {\overset {\frown }{E}}(f_{t+dt})]\end{array}}$

( 2.4)

where g_t is payoff value.

Symbol ${\textstyle {\overset {\frown }{p}}}$ implies the risk-neutral probability of up-movement and ${\textstyle {\overset {\frown }{E}}(f_{t+dt})}$ is the risk-neutral expected value,

${\overset {\frown }{p}}={\frac {e^{r\cdot dt}\cdot S_{t}-S_{t+dt}^{d}}{S_{t+dt}^{u}-S_{t+dt}^{d}}}{\mbox{,}}$

( 2.5)

This probability can be considered neither a market growth nor a subjective probability. Due to (2.3) the derivative price is equal to the present value of risk-neutral expected value of subsequent period, which coincides with generalised martingale principle, see (2.1) .

We can express the underlying asset price, under the proportional continuous income c , due to Geometric Browns process as follows,

${\begin{array}{l}\displaystyle S_{t+dt}^{u}=S_{t}\cdot U;{\mbox{   }}S_{t+dt}^{d}=S_{t}\cdot D,{\mbox{   }}{\mbox{where}}{\mbox{   }}U=e^{\sigma \cdot {\sqrt {dt}}},{\mbox{   }}D=e^{-\sigma \cdot {\sqrt {dt}}}\\\displaystyle {\mbox{   }}(1+C)^{-1}=e^{-c\cdot {\sqrt {dt}}}{\mbox{,}}\end{array}}$

( 2.6)

then after substitution to (2.5) and after re-arranging we get particular risk-neutral probability formula

${\overset {\frown }{p}}={\frac {((1+R)/(1+C))-D}{U-D}}{\mbox{.}}$

This formula can be generalised substituting ${\textstyle (1+R)/(1+C)=G}$ as follows ${\textstyle {\overset {\frown }{p}}=(G-D)/(U-D)}$ .

There exist several type of financial option. One of them is financial (debt) real option with payoff function,

$g=max(A-D;0){\mbox{,}}$

( 2.7)

where A is asset value, D is debt value.

The option to expand can be used as an American option, which allowed expanding project at any time during the projects life, payoff function is as follows,

$g=max(A\cdot x-INV_{exp};0){\mbox{,}}$

( 2.8)

where x   is the scale of possibility, ${\textstyle INV_{exp}}$ is investment (CAPEX) of expansion.

The option to contract can be used like American option, with following payoff,

$g=max(INV_{con}-A\cdot y;0){\mbox{,}}$

( 2.9)

here ${\textstyle INV_{con}}$ deinvestment, y is percentage of contraction.

Another type of option is multiple option combining several types of the option. If we combine expansion and contraction options, we get this payoff function,

$g=max(A\cdot x-INV_{exp};INV_{con}-A\cdot y;0)$

( 2.10)

Characterisation of internet Baidu Inc. company

Over the past twenty years, the internet has truly transformed China. There are more than 600 million internet users in China, which indicate almost a half of Chinese are living with internet. In this huge market, Baidu occupies more than 75% revenue share in the internet search market, and 30% market share in online advertising area until 2013. At the same time, it has approximately 753,000 active online marketing customers. Its online marketing customers not only be individuals, but also consist of small and medium enterprises (SMEs) throughout China, large domestic companies and Chinese divisions or subsidiaries of large, multinational companies.

Baidu is founded in 2000, at beginning it was an internet search engine website. And then with the development of technology and expansion of market scale, Baidu extended its service from simple search to mobile and cloud, location based services, consumer products and international operations. Its products include web pages, news, images, multimedia files, music, movies and it is also the first one in China to offer Wireless Application Protocol and personal digital assistant based mobile search. Web search is the main business of the companys online productions, which may deliver the most useful and relevant search. And based on this successful service, Baidu sell advertising and get profit efficiently. Besides, it has invested in other entities, for example computer game company. Variety products successfully attracted consumers loyalty. According to a recent survey by China Internet Network Information Centre, there are 470 million active search internet users in China in 2013 and 86% of them identified Baidu as their favourite internet service company.

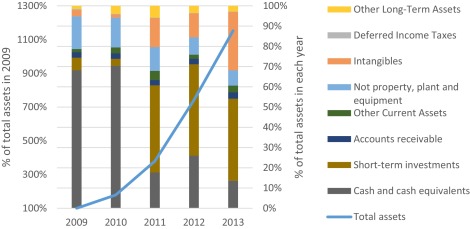
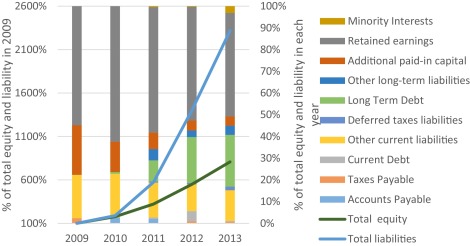
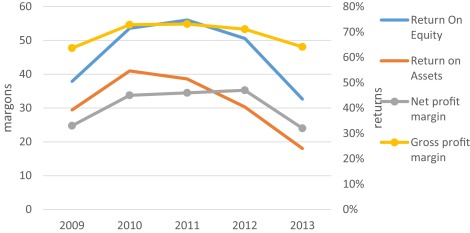
In 2005, Baidu was listed in NASDAQ (NASDAQ: BIDU) as the largest Chinese company. At the initial public day, Baidu opened at $66, more than double its initial public offering price $27, the highest price reached to $151.21 and ended at $122.54, which went up by 354%. Baidu became the IPO markets biggest splash in at least five years. In 2007, Baidu became the first Chinese company to be included in the NASDAQ-100 index (Fig. 1 , Fig. 2  and Fig. 3 ).

Fig. 1. Horizontal–vertical common-size analysis of assets.

Fig. 2. Horizontal–vertical common-size analyses of liability and equity.

Fig. 3. Growth of profitability ratios.

Baidu valuation under flexibility

Internet companies are more complex to evaluate than traditional companies. Because the internet industry is still in fast development period around the world and the growth of internet companies is one of the key factors in valuation. There is too much uncertainty in internet industry, and traditional methods are unable to reflect accurate value of enterprise. And the valuation criteria of internet companies, such as customer effects, time effects, innovation effects and brand effects, are also difficult to measure.

By mapping out both uncertainties and decisions over time, real options methods provide an appropriate way to track value creation and risk profile. In many case, real options is used only if the firm actually executes the plan. If the plan proceeds unsuccessful, manager has the right to give up the decision and avoid loss. But if the plan progress goes well, manager also has the right to make optimistic decisions.

In this section, we discuss value of Baidu with option to expand, option to contract, and option to expand or contract. In order to analyse influence of different expansion rate and contraction rate, we apply basic scenario, optimistic scenario, middle scenario and pessimistic scenario in each option. For valuation Eqs. (2.4)  and (2.5) are applied. And real options are calculated due to (2.8) expand, (2.9) contract and (2.10) multiple.

Input parameters

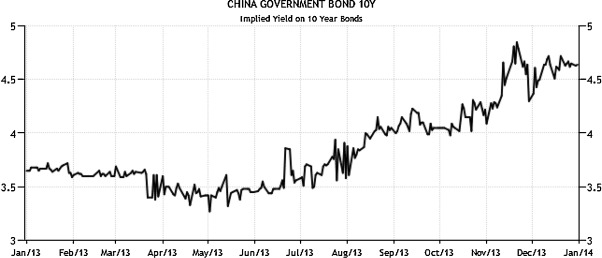
We consider and estimate following input valuation parameters. The typical risk free rate is long term government bond. And we adopted interest rate of China 10 years government bond as risk free rate ( Fig. 4 ).

Fig. 4. China 10 years government bond yield curve.

We focus on the interest rate of government bond during 2013, it increased to 4.6 percent in December from 3.3 percent in April. And because investors always prefer higher interest rates from long term government bonds, we decide to choose 4.6 percent as risk free rate, R_f for prediction.

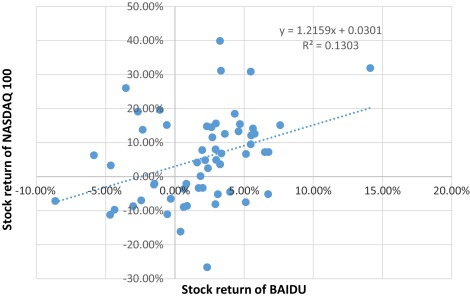
Beta parameter is a kind of market sensitivity, and it is also the correlation between a companys stock return and markets return. We use common regression model to build trend line between return of index and return of Baidu stock to estimate beta ( Fig. 5 ).

Fig. 5. Scatter diagram of indexs return and Baidu stocks return.

We choose monthly price of NASDAQ100 from 2009 to 2013 as our observation index, and adopt monthly stock price of Baidu from the same time period as independent variable. Fig. 5 illustrates the equation y  = 1.2159x  + 0.0301 explains 13.03% of changes in Baidus stock return is caused by NASDAQ100s return. And if return of NASDAQ100 increases by one percent, then return of Baidu grows up approximately by 1.21 percent. So we defined β as 1.2. Because typical betas is between 0 and 2, Baidus stock is riskier than typical stock but also has higher rewards.

Before getting assets value, we need to calculate Baidus free cash flow as passive state in 2013, and cost of capital. If perpetuity is assumed, we can defined Baidus asset value (A ) as follows, A  = FCF /WACC .

Free cash flow can be defined as the cash flow which is generated after investment but before interest payment. Here we employed free cash to the firm. The function is written as follows, FCFF = NOPAT  + D&A  − ΔNWC  − Capex . Here FCFF represents free cash flow to the firm, NOPAT means net operating profit after tax, D&A is depreciation and amortisation, ΔNWC is the change of net working capital and Capex is capital expenditures. In fiscal 2013, Baidus operating income was 11,706 million CNY and total taxes was 1756 million CNY, as the result, its NOPAT can be counted as 9950 million CNY. And D&A was 2652 million CNY, ΔNWC was −914 million CNY, and Capex was 2800 million CNY. Consequently, FCFF should be 10,716 million CNY in 2013.

We apply Capital Asset Pricing Model (CAPM model) to estimate weighted average cost of capital WACC . The weighted average cost of capital is determined by cost of debt Rd, cost of equity E (R_i ), income tax rate T , target level of debt to asset D /A and target level of equity to asset E /A , which is written as follows,

$WACC={\frac {E}{A}}\cdot R_{E}+{\frac {D}{A}}\cdot R_{D}{\mbox{.}}$

From Baidus annual reports and China tax policy, we have already know that corporate income tax rate is 15%. Next we will discuss estimation of other components of WACC.

Market approach is used to estimate cost of debt, which includes interest expenses in relation to debt. In 2003, interest expenses of Baidu were 447 million CNY and total debt was 16,644 million CNY. Therefore, we estimate cost of debt as 2.69%.

The cost of equity has three components: the risk free rate, the risk premium and risk adjustment. We known that risk free rate is 4.6%, and risk adjustment beta is 1.2. And risk premium is calculated by the difference between the market expected return and risk free rate. Since average annual ten years return of NASDAQ100 in the end of 2014, 9.03%, is reported as market return, we get 4.43% as risk premium. According to CAPM model, expected rate of equity return equals the risk free rate adds risk adjustment beta times risk premium, which is written as follows, E (R_i ) = R_f  + β [E (R_m ) − R_f ]. Here E (R_i ) is expected return of security, and is also defined as cost of capital; E (R_m ) represents market expected return. As a consequence, cost of equity is equal to 9.92%.

Target level of debt to asset and target level of equity to asset can be calculated by market debt, market equity, and market capital. However, market value of debt is difficult to estimate; here we use book value of debt in the calculation. It is written in annual report that total debt of Baidu was 166,44 million CNY in 2013. And market value of equity is also called market capitalisation, which is calculated by share outstanding multiplying stock price. At December 31 2013, total share outstanding of Baidu is 350 million, and the closed price is $177.88. Consequently, market capitalisation is $62,258 million. Consider of foreign exchange rate between USD and CNY, we adopt the exchange rate on December 31 2013, 6.05. Therefore the market capitalisation of Baidu is 376,824.25 million CNY. And then we assume market value of capital is calculated as the sum of market value of equity and debt, which is 393,468.25 million CNY. So target level of equity to asset is 95.77%, and weight of debt is 4.23%. Finally, we can get WACC based on the function (4.3), and the result is 9.59%. And the asset value of our case is 111,741 million CNY.

Importatnt input financial term is debt . The nature of companys limited liability gives shareholders rights to decide residual value of the company. Shareholders can get the rest value after companys asset covering debt, which is similar like options. Strike price is stable regardless of the type of option and maturity time. In real options method, face value of debt is strike price. Nevertheless, Chinese bond market is not mature and complete, we decide to use book value of debt as strike price, which is 16,644 million CNY.

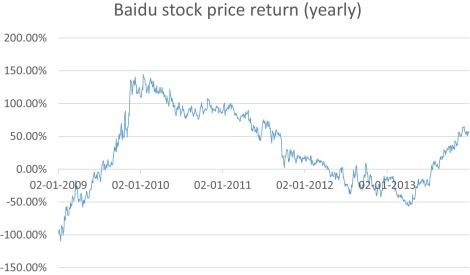
We can consider the volatility to be crucial option input parameter. There are two ways to estimate volatility, one is backward looking, and another is forward looking. Calculation of backward looking volatility depends on historical returns, and calculation of forward looking volatility depends on present value of options. Here we employ backward looking method with historical stock price of Baidu from January 1, 2008 to December 31, 2013.

Based on historical stock, we get yearly return (logarithm) from 2009 to 2013 at first, which we can see from Fig. 6 . And then standard deviation of yearly return is computed as 49.15%. Therefore we assume that the volatility of Baidu is 49%.

Fig. 6. Yearly return of Baidus stock from 2009 to 2013.

Typically speaking, the company with high profit each year has more potential to keep high investment. In order to get growth rate of future investment, we suppose that it equals to growth rate of revenues. Based on market approach, we find total revenue of Chinese search engine companies from 2009 to 2013 at first. And then calculate change in each year, with the weight we assumed, we can get the change of relative market revenues 33.22%. At last by adding growth of Chinese GDP 7.67%, we get the final change of relevant market 40.89%. As a result, growth of revenue 45.24% is the sum of changes of market revenues and changes of Baidus market share. And in our assumption, the growth of investment x is also 45.24%.

Consider the previously parameters we have already estimated, we supposed the coefficient of up movements u and coefficient of down movements d , which are based on the volatility, are 1.74 and 0.56. We determine the risk neutral probability of up movement p is 0.4 and probability of down movement q is 0.6.

Scenarios supposed description

We assume that according to economy development four scenarios are possible: basic, middle, optimistic and pessimistic ones. Under them contraction and expansion coefficients are estimated, see Table 1 .

Table 1. Scenarios alternatives and expansion or contraction parameters.

		2013	2014	2015	2016	2017	2018
Basic scenario	Expansion rate	45%	45%	45%	45%	45%	45%
	Contraction rate	20%	20%	20%	20%	20%	20%
Middle scenario	Expansion rate	20%	30%	45%	30%	20%	10%
	Contraction rate	30%	20%	10%	20%	30%	45%
Optimistic scenario	Expansion rate	10%	20%	30%	35%	40%	45%
	Contraction rate	45%	40%	35%	30%	20%	10%
Pessimistic scenario	Expansion rate	45%	40%	35%	30%	20%	10%
	Contraction rate	10%	20%	30%	35%	40%	45%

Results and discussion

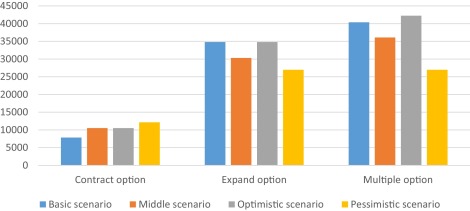
Results showing the flexibility values are presented in Fig. 7 and Table 2 . Compared to simple options, multiple options have higher value in our case, and it is not the aggregation of each simple option. In our research, price of each scenario in multiple options is lower than the sum prices of expand option and contract option. When measuring price of multiple options, we should consider about the correlation between expand option and contract option.

Fig. 7. Results of the flexible investment in different scenarios (million, CNY).

Table 2. Option prices in different scenarios (million, CNY).

	Basic scenario	Middle scenario	Optimistic scenario	Pessimistic scenario
Contract option	7850	10,521	10,521	12,149
Expand option	34,792	30,312	34,792	26,961
Multiple options	40,370	36,092	42,231	26,961

Both table and figure illustrate that in the multiple options, the price in optimistic scenario presents the highest level, 42,231 million CNY, and the price in pessimistic scenario is the lowest, 26,961 million CNY. In the option to expand, the highest price 34,792 million CNY is located in optimistic scenario and basic scenario simultaneously, and the lowest one is in pessimistic scenario, which is 26,961 million CNY. And in the option to contract, price in pessimistic scenario, 12,149 million CNY, is the highest one, and the price in basic scenario maintains the lowest level, 7850 million CNY.

From the results, we find that future development trend is an important factor in real options method. For example, the option to expand the project is a positive right to enlarge companys business scale and get more profit, and the option to contract the project can be seen as a negative right to cut more costs and scale back investment. Therefore price of expand option is always higher than the price of contract option.

This conclusion can be also used in scenario approach. We distinguish each scenario by different expansion rate and contraction rate. When we discuss four scenarios in expand option, it is interesting to discover there are two same results in basic scenario and optimistic scenario. In our assumption, due to the excellent investment environment, the company keeps a stable expansion rate 45% in basic scenario and an increasing expansion rate from 10% to 45% in optimistic scenario. Both of these two scenarios demonstrate the same positive develop trend in the future, and they have the same expansion rate at maturity time by coincidence. Therefore, the final option values are same.

Meanwhile, there are two identical results in the option to contract, and one is from middle scenarios, and another is from optimistic scenario. Since 2016, options in these two scenarios move in the same contraction rate, which is from 30% to 10%. It indicates that after 2016, the company will contract the investment in the same trend from middle scenario and optimistic scenario. Consequently, option prices of these scenarios are same.

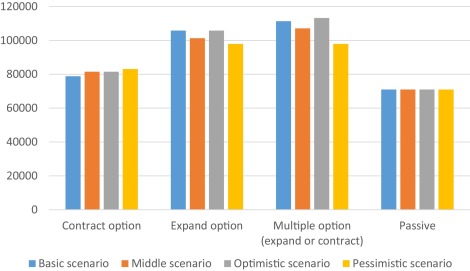
Due to the fact that the passive asset value of Baidu is 70,986 million CNY in 2013, the total asset values of Baidu in different flexibilities are summarised in Table 3 and Fig. 8 .

Table 3. Passive and flexibility asset valuation results (million, CNY).

Component		Total value	Flexibility
Passive value		70,986	0
Contract option	Basic scenario	78,836	7850
	Middle scenario	81,507	10,521
	Optimistic scenario	81,507	10,521
	Pessimistic scenario	83,135	12,149
Expand option	Basic scenario	105,778	34,792
	Middle scenario	101,298	30,312
	Optimistic scenario	105,778	34,792
	Pessimistic scenario	97,947	26,961
Multiple options (expand or contract)	Basic scenario	111,356	40,370
	Middle scenario	107,078	36,092
	Optimistic scenario	113,217	42,231
	Pessimistic scenario	97,947	26,961

Fig. 8. The relationship between passive and flexible asset value of Baidu.

As is exhibited in the Table 3 and Fig. 8 , Baidus total asset value with flexibility is higher than the account passive value. The total asset value with the option to contract in basic scenario is 78,836 million CNY, in middle scenario and passive scenario is 81,507 million CNY and in passive scenario is 83,135 million CNY. The total asset value with the option to expand in basic scenario and optimistic scenario is 105,778 million CNY, in middle scenario is 101,298 million CNY, and in pessimistic scenario is 97,947 million CNY. And the total asset value of Baidu with the option to expand or contract in basic scenario is 111,356 million CNY, in middle scenario is107,078 million CNY, in optimistic scenario is 113,217 million CNY and in pessimistic scenario is 97,947 million CNY.

By contrast, the highest total asset value is with multiple options in optimistic scenario, 11,317 million CNY. In such a situation, Baidu will have the best environment and innovation awareness in the next five years. And the company can simultaneously continue the operation with no changes, expand or contract the project. The lowest asset value with flexibility is with contract option in basic scenario, 78,836 million CNY. In this situation, future expectations are negative and impossible to improve. Hence, expectations regarding long-term performance influence not only early growth investment, but also total asset value with real options.

Conclusion

The paper is devoted to possibilities of real option method application in valuation internet company, Baidu company in detail. We can see usefulness of the methodology because of big volatility and uncertainty and flexibility of internet industry. The Cines market is in the specific big grow and volatility suitable for real option methodology and we can find the flexibility value which is not negligible. We verified that application method described is very fruitful and demanded in valuation under significant uncertainty and flexibility.

Conflict of interest

The authors declare that there is no conflict of interest.

Acknowledgements

The research was supported by the European Social Fund within the project CZ.1.07/2.3.00/20.0296.

The paper has been also elaborated in the framework of the IT4Innovations Centre of Excellence project, reg. no. CZ.1.05/1.1.00/02.0070 supported by Operational Programme ‘Research and Development for Innovations’ funded by Structural Funds of the European Union and state budget of the Czech Republic.

References

1. Amram et al., 1999 M. Amram, N. Kulatilaka; Real Option Managing Strategic Investment in an Uncertain World; , 0-87584-845-1Harvard Business School Press, Boston (1999)
2. Barnett, 2005 M.L. Barnett; Paying attention to real options; R&D Manage., 35 (2005), pp. 61–72
3. Boer, 2002 F.P. Boer; The Real Option Solution: Finding Total Value in a High-risk World; , 0-471-20998-8John Wiley & Sons, New York (2002)
4. Brandao and Dyer, 2005 L.E. Brandao, J.S. Dyer; “Decision Analysis and real options”: a discrete time approach to real option valuation; Ann. Oper. Res., 135 (2005), p. 21
5. Carlsson and Fuller, 2003 C. Carlsson, R. Fuller; A fuzzy approach to real option valuation; Fuzzy Sets Syst., 139 (2003), pp. 297–312
6. Chevalie-Roignant and Trigeorgis, 2011 B. Chevalie-Roignant, L. Trigeorgis; Competitive Strategy: Options and Games; Massachusetts Institute of Technology, USA (2011)
7. Cox et al., 1979 J.C. Cox, S.A. Ross, R. Mark; Option pricing: a simplified approach; J. Financ. Econ., 7.3 (1979), pp. 229–263
8. Čulík, 2004 M. Čulík; Valuing of real options portfolio and its influence on project value; 22nd International Conference on Mathematical Methods in Economics (2004), pp. 56–62
9. Čulík, 2006 M. Čulík; Real option application for modular project valuation; 24th International Conference on Mathematical Methods in Economics (2006), pp. 123–130
10. Čulík, 2008 M. Čulík; Emissions trading: investment decision-making and real option analysis (simulation approach); 4th International Scientific Conference on Managing and Modelling of Financial Risk, Ostrava (2008), pp. 11–18
11. Čulík, 2010 M. Čulík; Flexibility and project value: interactions and multiple real options; 3rd Global Conference on Power Control and Optimization, Gold Coast, Australia. Power Control and Optimization Book Series: AIP Conference Proceedings, vol. 1239 (2010), pp. 326–334
12. Damodaran, 2001 A. Damodaran; The Dark Side of Valuation: Valuing Old Tech, New Tech and New Economy Companies; , 0-13-040652-XFT Press, London (2001)
13. Dixit and Pindyck, 1994 A.K. Dixit, R.S. Pindyck; Investment under Uncertainty; Princeton University Press (1994)
14. Dluhošová, 2004 D. Dluhošová; An analysis of financial performance using EVA method; Finance a úvěr – Czech J. Econ. Financ., 54 (11–12) (2004), pp. 541–559
15. Driouchi et al., 2012 T. Driouchi, D.J. Bennett; Real options in management and organization strategy: a review of decision-making and performance implications; Int. J. Manage. Rev., 14 (2012), pp. 39–62
16. Guthrie, 2009 G. Guthrie; Real Options in Theory and Practice; Oxford University Press (2009)
17. Junyan Guo, 2015 Junyan Guo; Application of the Real Option Methods in BAIDU Company Valuation; (Diploma dissertation) Faculty of Economics, VSB-Technical University of Ostrava, Czech Republic (2015)
18. Luenberger, 1998 D.G. Luenberger; Product of trees for investment analysis; J. Econ. Dyn. Control, 22 (1998), pp. 1403–1417
19. Muzzioli and Torricelli, 2004 S. Muzzioli, C. Torricelli; A multi-period binomial model for pricing options in a vague world; J. Econ. Dyn. Control, 28 (2004), pp. 861–887
20. Shockley, 2007 R.L. Shockley Jr.; An Applied Course in Real Options Valuation; , 0-324-25963-8Thomson South-Western, Mason (2007)
21. Smit and Trigeorgis, 2004 Smit H.T.J., L. Trigeorgis; Strategic Investment: Real Options and Games; Princeton University Press, United Kingdom (2004)
22. Smith and Nau, 1995 J.E. Smith, R.F. Nau; Valuing risky projects: Option pricing theory and decision analysis; Manage. Sci., 14 (1995), p. 795
23. Triantis, 2001 A. Triantis; Real options: state of the practice; J. Appl. Corpor. Financ., 14.2 (2001), pp. 8–14
24. Trigeorgis and Schwartz, 2001 L. Trigeorgis, E.S. Schwartz; Real Options and Investment Under Uncertainty; , 0-262-19446-5The MIT Press, London (2001)
25. Viebig et al., 2008 J. Viebig, T. Poddig, A. Varmaz; Equity Valuation: Models from Leading Investment Banks; , 978-0-470-03149-0John Wiley & Sons, Chichester (2008)
26. Yoshida, 2002 Y. Yoshida; A discrete-time model of American put option in an uncertain environment”; Eur. J. Oper. Res., 151 (2002), pp. 153–166
27. Yoshida, 2003 Y. Yoshida; The valuation of European options in uncertain environment; Eur. J. Oper. Res., 145 (2003), pp. 221–229
28. Zmeškal, 1999 Z. Zmeškal; Fuzzy-stochastic estimation of a firm value as a call option; Finance a úvěr – Czech J. Econ. Financ., 3 (1999), pp. 168–175
29. Zmeškal, 2001 Z. Zmeškal; Application of the fuzzy-stochastic methodology to appraising the firm value as a European call option; Eur. J. Oper. Res., 135/2 (2001), pp. 303–310
30. Zmeškal, 2005 Z. Zmeškal; Approach to real option model application on soft binomial basis fuzzy-stochastic approach; 23rd International Conference on Mathematical Methods in Economics (2005), pp. 433–439
31. Zmeškal, 2006 Z. Zmeškal; Real option applications based on the generalised multinomial flexible switch options methodology; 24th International Conference on Mathematical Methods in Economics, Plzeň (2006), pp. 545–553
32. Zmeškal, 2008 Z. Zmeškal; Application of the American real flexible switch options methodology a generalized approach; Finance a Úvěr – Czech J. Econ. Financ., 58 (2008), pp. 261–275
33. Zmeškal, 2010a Z. Zmeškal; Real compound sequential and learning options modelling; 28th International Conference on Mathematical Methods in Economics (2010), pp. 688–693
34. Zmeškal, 2010b Z. Zmeškal; Generalised soft binomial American real option pricing model (fuzzy-stochastic approach); Eur. J. Oper. Res., 207/2 (2010), pp. 1096–1103 http://dx.doi.org/10.1016/j.ejor.2010.05.045
35. Zmeškal, 2011 Z. Zmeškal; Investigation of the real switch option value sensitivity; 29th International Conference on Mathematical Methods in Economics (2011), pp. 774–779
36. Zmeškal, 2012 Z. Zmeškal; Modelling the sequential real options under uncertainty and vagueness (fuzzy-stochastic approach); 30th International Conference on Mathematical Methods in Economics (2012), pp. 1027–1032