Impact of ENSO events on the interannual variability of Hadley circulation extents in boreal winter

Abstract

The interannual variability of the boreal winter Hadley circulation extents during the period of 1979–2014 and its links to El Niño-Southern Oscillation (ENSO) were investigated by using reanalysis datasets. Results showed that the El Niño (La Niña) events can induce the shrinking (expansion) of Hadley circulation extent in the Southern Hemisphere. For the Northern Hemisphere, El Niño (La Niña) mainly leads to shrinking (expansion) of the Hadley circulation extent in the middle and lower troposphere and expansion (shrinking) of the Hadley circulation extent in the upper troposphere. The ENSO associated meridional temperature gradients have close relationship with the Hadley circulation extents in both Hemispheres. But in the Northern Hemisphere, the ENSO associated eddy momentum flux divergence plays more important role in affecting the Hadley circulation extent than the meridional temperature gradient because of the small local Rossby number. In the Southern Hemisphere, as the ENSO induced eddy momentum flux divergence is small, the meridional temperature gradient dominates the change of the Hadley circulation extent.

Keywords

Hadley circulation ; Extents ; Meridional temperature gradient ; ENSO

1. Introduction

Hadley circulation (HC) is a large-scale thermal driven meridional circulation in the tropics. As the HC is related to the water vapor, energy and angular momentum transport, it plays important roles in the climate system (Li et al., 2015  and Hou, 1998 ), which has attracted a lot of focuses (Li et al., 2013  and Quan et al., 2004 ).

Among the previous studies, HC expansion is one of the most important research aspects. It has been found that the HC suffered poleward expansion since 1979 (Fu et al., 2006 , Hu and Fu, 2007  and Feng et al., 2011 ). Subsequently, some studies focused on more evidences of the long-term widening of the HC (Seidel and Randel, 2007  and Nguyen et al., 2013 ) and the causes (Adam and Schneider, 2014 , Lu et al., 2009  and Polvani et al., 2011 ).

Most of the above mentioned studies are focused on the long-term trends of HC width, but some studies also analyzed the interannual variability of HC width (Adam and Schneider, 2014  and Nguyen et al., 2013 ). These studies revealed that the interannual variability of the HC extent (HCE) may reach to a deviation of 5 latitude degrees, which is even larger than the widening trend during last three decades. As the long-term trend of HC widening may induce expansion of subtropical drought areas (Fu et al., 2006 ), the interannual variability of the HCE may also cause such impacts on interannual time scale. Therefore, it is important to figure out the interannual variability of HCEs and its causes.

There are several factors affecting HCEs, such as the radiative effect caused by ozone change (Polvani et al., 2011 , Waugh et al., 2015  and Staten et al., 2012 ), the sea surface temperature (SST) change (Son et al., 2010  and Adam and Schneider, 2014 ), and the greenhouse gas (GHG) emission (Lu et al., 2009 ). Among these factors, the El Niño-Southern Oscillation (ENSO) is one of the most robust interannual signals in the tropics. Many studies revealed that the changes of HC spatial structure and strength on interannual time scale are closely related to ENSO (Ma and Li, 2008 , Feng et al., 2013  and Feng and Li, 2013 ). Using diagnosing methods, Nguyen et al. (2013) pointed out that interannual variability of HCEs has close relationship with ENSO, but no further mechanism is discussed in their study. Some previous studies demonstrate that the extratropical eddy is mainly related to the HCE changes (Ceppi and Hartmann, 2013 ), and ENSO can influence the eddy activity (Caballero and Anderson, 2009 ). Thus, ENSO may be an important factor that affects HCE on the interannual time scale. At present it is not quite clear how ENSO affects HCE.

Because ENSO signals are most robust in boreal winter season (December–February, DJF), and have close links to the principal modes of DJF HC (Ma and Li, 2007  and Ma and Li, 2008 ). In this paper, the interannual variability of boreal winter HCEs and its relationship with ENSO will be investigated. As the remainder of this manuscript is arranged as follows: Section 2 described the reanalysis datasets and methods; Section 3 presents the results; Discussion and conclusions are given in Section 4.

2. Data and methods

The atmospheric variables employed in this work are taken from the Interim European Centre for Medium-Range Weather Forecasts (ECMWF) Re-Analysis (ERAI) (Dee et al., 2011 ), the National Centers for Environmental Prediction (NCEP)–National Center for Atmospheric Research (NCAR) reanalysis (NCEP1) (Kalnay et al., 1996 ) and the NCEP–Department of Energy (DOE) Atmospheric Model Intercomparison Project (AMIP)-II Reanalysis (NCEP2) data (Kanamitsu et al., 2002 ). All the reanalysis datasets have 2.5° × 2.5° horizontal resolutions. The ERAI has 37 vertical levels and the other two have 17 vertical levels. The ERAI and NCEP2 cover the period of 1979–2016 and the NCEP1 covers the period of 1948–2016. The overlapped period of 1979–2014 is chosen in this study. The SST data used in this study is from the monthly mean Extended Reconstruction of Historical Sea Surface Temperature version 3b (ERSST v3b) dataset, which has a 2.0° × 2.0° horizontal resolution and covers the period of 1854–2016 (Smith et al., 2008 ).

In this study, the mass stream function (MSF) is used to depict the HC. The MSF is calculated by vertically integrating the zonal mean meridional wind (Holton, 1992  and Li, 2001 ). The HCE has several definitions, such as by using tropopause height (Seidel and Randel, 2007 ), the latitude of outgoing long-wave radiation (OLR) equaling to 250 W m⁻² (Hu and Fu, 2007  and Johanson and Fu, 2009 ), the latitude of precipitation minus evaporation equaling zero (Quan et al., 2014 ) and the latitude of MSF at 500 hPa equaling to zero (Hu and Fu, 2007 ). As the MSF = 0 is more commonly used to define the HCE in previous studies (Hu and Fu, 2007  and Quan et al., 2014 ), it was also used in this study to define the HCE. The linear trends of the variables were removed in order to analyze the interannual variability.

3. Results

3.1. Interannual variability of HCE

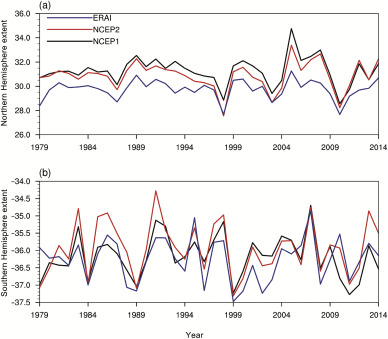
Fig. 1 shows the changes of DJF HCE in both Hemispheres during the period of 1979–2014. It can be observed that both the northern and southern HCEs show obvious interannual variabilities, and the results from the three datasets are consistent in the variability. The correlation coefficients among the three datasets are greater than 0.85 (significant at 99% confidence level) for the Northern Hemisphere HCE and 0.66 (significant at 99% confidence level) for the Southern Hemisphere HCE. It also can be seen that the year-to-year deviation of the HCEs can reach to about 5 latitude degrees (Fig. 1 b).

Fig. 1. Time series of the December to February Hadley circulation extent (HCE) in (a) the Northern Hemisphere and (b) the Southern Hemisphere during 1979–2014 based on ECMWF Re-Analysis (ERAI) (blue line), NCEP2 (red line) and NCEP1 (black line).

It is also worth noting that there are slight differences in the variances of the HCE among different datasets. Of all the datasets, the variances of HCEs in the Northern Hemisphere ranges from 0.63 to 1.34, which are larger than those in the Southern Hemisphere. The values of HCE from ERAI are systematically lower than those of NCEP1 and NCEP2 (Fig. 1 b).

3.2. Relationship between HCE and the tropical SST

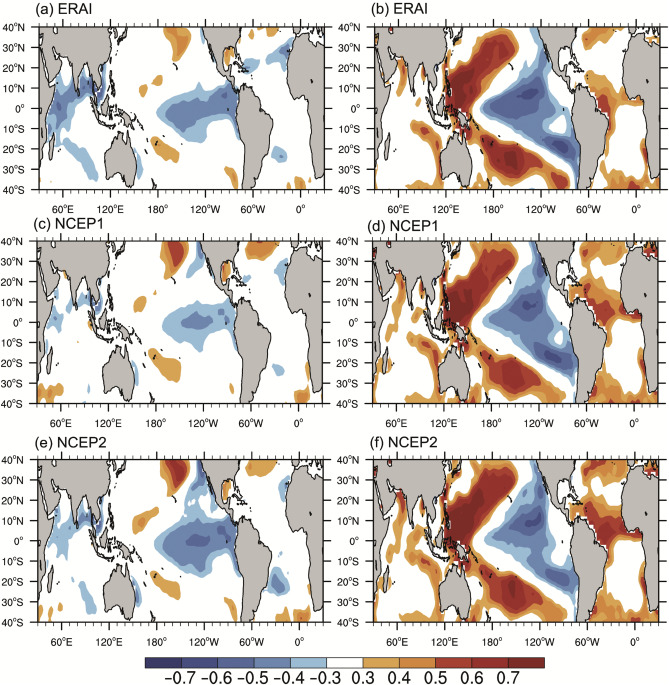
Fig. 2 shows the correlation patterns between the HCEs and the tropical SST anomalies (SSTA) based on ERAI, NCEP1 and NCEP2. The Southern Hemisphere HCE has been multiplied by −1 for the discussion convenience. It can be seen that of all the three datasets significant correlations between the HCEs and the SSTA are observed in the middle and eastern Pacific, which resemble the ENSO cold pattern. The correlation patterns for the Northern Hemisphere HCE is relatively weaker than that of the Southern Hemisphere. For the Northern (Southern) Hemisphere HCE, the correlation coefficients over the middle and eastern Pacific can reach 0.4 (0.7), exceeding 95% confidence level. The possible reason why the Northern Hemisphere HCE is less connected to ENSO might be that the Northern Hemisphere has more complex land-sea distribution. For the correlation patterns of the Southern Hemisphere HCE, three datasets show consistent spatial structures, while for the Northern Hemisphere HCE, the NCEP2 has the strongest correlations in mid-eastern Pacific, while those of NCEP1 is the weakest among the three datasets. Additionally, the HCE in the Northern Hemisphere is also connected with the SST over the tropical Indian Ocean, which may be because the Indian Ocean SSTA is connected to the Pacific Ocean in ENSO events. In general, both the Northern and Southern Hemisphere HCEs are closely related to ENSO.

Fig. 2. Correlation map between the sea surface temperature (SST) and (a) Hadley circulation extent (HCE) in the Northern Hemisphere, (b) HCE in the Southern Hemisphere based on ECMWF Re-Analysis (ERAI) during 1979–2014. (c–d) and (e–f) are the same as (a–b), but for NCEP1 and NCEP2, respectively. The HCE in Southern Hemisphere is multiplied by −1, for discussion convenience. The shading indicates the correlation coefficients exceeding 95% confidence level.

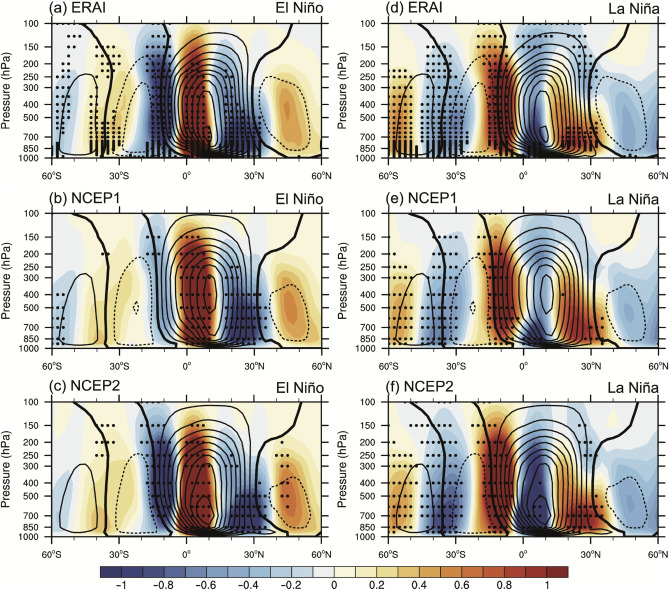
Fig. 3 further shows the composite anomaly of MSF based on the positive and negative ENSO phases by using the three reanalysis datasets. The positive (negative) ENSO years are defined as the years when standardized Niño3.4 index (defined as the areal mean SSTA over the area of 5°S–5°N, 170°W–120°W) is larger (less) than 1 (−1) standard deviation. The positive phase (El Niño) years are 1982/1983, 1986/1987, 1991/1992, 1994/1995, 1997/1998, 2002/2003, 2009/2010; and the negative phase (La Niña) years are 1988/1989, 1999/2000, 2007/2008, 2010/2011. Fig. 3 also shows the DJF climatological MSF, which displays two cells in each hemisphere. The northern cell extends to the Southern Hemisphere and also is much stronger than the southern cell. The climatological HCEs in the two hemispheres locate at about 30°N and 38°S, respectively.

Fig. 3. The boreal winter climatological mass stream function (contours) and composite anomalies (shading) for El Niño periods based on (a) ECMWF Re-Analysis (ERAI), (b) NCEP1 and (c) NCEP2 during 1979–2014. (d–f) Same as (a–c), but for La Niña periods. The stippled areas indicate the composite anomalies exceeding 95% confidence level. The contours intervals are 2 × 1010  kg s−1 .

Of all the three datasets, in El Niño years, there exist negative MSF anomalies around 30°N, and positive MSF anomalies around 38°S (Fig. 3 a–c). Both the northern and southern MSF anomalies have reversed sign compared with the climatological MSF. This means that in El Niño years the HCEs would move toward the equator, which may lead to a narrower HC width than normal years. In La Niña years the MSF anomalies around 30°N (38°S) is positive (negative), which is in the same sign to the climatological MSF. It implies that the HC in La Niña years tend to be wider than normal years.

It is worth noting that in the Southern Hemisphere, the ENSO related MSF anomalies over the subtropics are barotropic, i.e. the MSF anomalies in the whole troposphere have uniform structure (Fig. 3 ). This would lead to a consistent movements of the Southern Hemisphere HCEs both in the upper and lower levels.

But in the Northern Hemisphere, the MSF anomalies in the upper and lower levels are different. In El Niño cases (Fig. 3 a–c), there are negative MSF anomalies over subtropics in the middle and lower troposphere, but there is slightly positive MSF anomaly in the upper troposphere. In La Niña cases (Fig. 3 d–f), there are negative MSF anomalies above 300 hPa, while positive MSF anomalies in the middle and lower levels (bellow 400 hPa). The reversed signs of the MSF anomaly between upper and lower troposphere will lead to different direction of movements for the HCEs in different levels, especially in La Niña cases. Thus, the definition of HCE by the latitude of MSF = 0 at 500 hPa may has shortcomings. It can only represent the change of HCE in the middle troposphere. Although some previous studies pointed out that the expansion trends of HC in the layers from 700 hPa to 300 hPa are approximately consistent (Johanson and Fu, 2009 ), but in view of the results in this study, the HCE defined by MSF = 0 at 500 hPa should be treated with caution. Therefore, in the following analysis, HCE is defined as the latitude where the mean MSF = 0 between 850 hPa and 200 hPa.

There are also slight differences in the statistical significance among different datasets. In El Niño periods, the significant confidence level of the composed MSF for NCEP1 is lower than 90% in most regions of the Southern Hemisphere, and for NCEP2, only those in the upper troposphere exceed 90% confidence level. In the Northern Hemisphere, all three datasets consistently exceed 90% confidence level in middle and lower troposphere (Fig. 3 a–c). In La Niña periods, all three datasets show consistent significant level in the Southern Hemisphere, while in the Northern Hemisphere, both ERAI and NCEP2 are consistent and significant at 90% confidence level over the subtropics. The NCEP1 is lower than 90% confidence level nearly through the whole troposphere in subtropical region. Overall, results of ERAI and NCEP2 are more consistent with each other (Fig. 3 d–f). In spite of the difference of the significance levels, the spatial structure of the composed MSF, especially the baroclinic structure in the Northern Hemisphere, are consistent in all three datasets, indicating that the results are reliable. The following analysis will be based on ERAI.

3.3. Possible mechanism

The time and zonal mean momentum in the upper troposphere is approximately balanced by meridional advection and eddy momentum flux divergence. The equation can be written as follows:

$\left(f+{\overline {\zeta }}\right){\overline {v}}=\left(1-\right.$$\left.R\right)f{\overline {v}}\approx S.$

( 1)

Where f is the Coriolis parameter; ζ is the relative vorticity; v   is meridional wind; ${\textstyle R=-{\overline {\zeta }}/f}$ is the local Rossby number; S is the eddy momentum flux divergence; “−” indicates time and zonal mean ( Walker and Schneider, 2006 ).

In the zonal mean momentum balance Eq. (1) , the vertical advection of the momentum term is omitted because of its small magnitude compared with other terms. As the mass stream function is calculated by integrating the meridional wind, v in Eq. (1) can represent the HC. According to Eq. (1) , when R →0, v   can be decided by eddy momentum flux divergence, i.e. ${\textstyle {\overline {v}}\approx S/f}$ . When R →1, HC is angular conservation system in which the motion of the air is determined by the diabatic forcing, especially the meridional temperature gradient, and the HCE is proportional to the meridional temperature gradient ( Held and Hou, 1980 ).

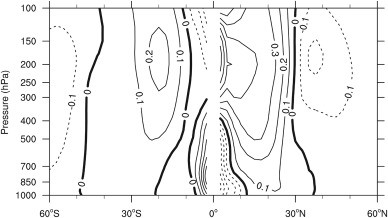
In order to investigate the impacts of ENSO on the HCEs, both occasions of R →0 and R →1 need to be considered, because ENSO may affect the HC via both diabatic forcing and eddies. The DJF climatological R increases dramatically when approaching to the equator ( Fig. 4 ). R is close to zero at about 30°N and 35°S, which implies that the HCEs in both Hemispheres may be affected by eddy momentum flux divergence.

Fig. 4. December to February climatology of the local Rossby number based on the period of 1979–2014.

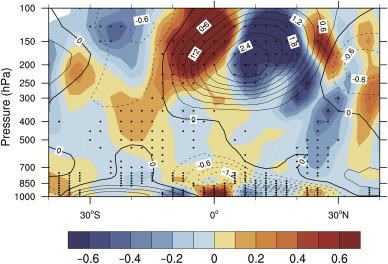
As the composite circulation anomalies based on El Niño and La Niña events are approximately reversed in sign, the following analysis will consider the composite difference between El Niño and La Niña. Displayed in Fig. 5 is the DJF climatology of the zonal mean meridional wind and the composite difference of the eddy momentum flux divergence based on ENSO. In the Northern Hemispheric subtropics, we can see positive eddy momentum flux divergence anomaly above 300 hPa in 20°N–30°N, while in the middle and lower troposphere over the same latitude bands, there are negative eddy momentum flux divergence anomalies (Fig. 5 ).

Fig. 5. Composite difference of the eddy momentum flux divergence (shading, unit: 10−5  m s−2 ) based on positive and negative ENSO phases. The contours indicate the December to February climatology of meridional wind (m s−1 ) during the period of 1979–2014. The stippled areas indicate that the values exceeds 90% confidence level.

The above eddy momentum flux divergence anomalies can results in a vertical shear of anomalous meridional wind based on Eq. (1) . Specifically, the positive eddy momentum flux divergence anomaly in the upper troposphere will induce anomalous southerly there, while negative eddy momentum flux divergence anomaly in the middle and lower troposphere will induce southerly there. Because the DJF climatological zonal mean meridional wind above 850 hPa is southerly, which approaches to zero around 30°N corresponding to the HCE in the upper level. Therefore, the southerly anomaly in the upper troposphere can expand the HCE in the upper level, while the northerly anomaly in the middle and lower troposphere can shrink the HCE in the lower levels. These results indicate that the ENSO influences the Northern Hemispheric HCE mainly via influencing the subtropical eddy momentum flux divergence, which is consistent with the composite anomaly of MSF shown in Fig. 3 .

However, the situation is different in the Southern Hemisphere. The MSF anomaly in associated with ENSO events in Fig. 3 presents a nearly barotropic structure. It indicates that in the Southern Hemisphere, the HCEs in all levels have consistent shrinking or expansion anomaly in associated with ENSO events. But the ENSO related eddy momentum flux divergence in the southern tropics is quite small and not statistically significant. Question arises that how ENSO affects the HCE in the Southern Hemisphere.

As discussed in Eq. (1) , ENSO may affect HCEs via two ways: 1) eddy momentum flux divergence, which has been discussed in analyzing the Northern Hemisphere HCE; 2) the meridional temperature gradient (MTG), which is a key role in the angular momentum conservation system (Held and Hou, 1980 ).

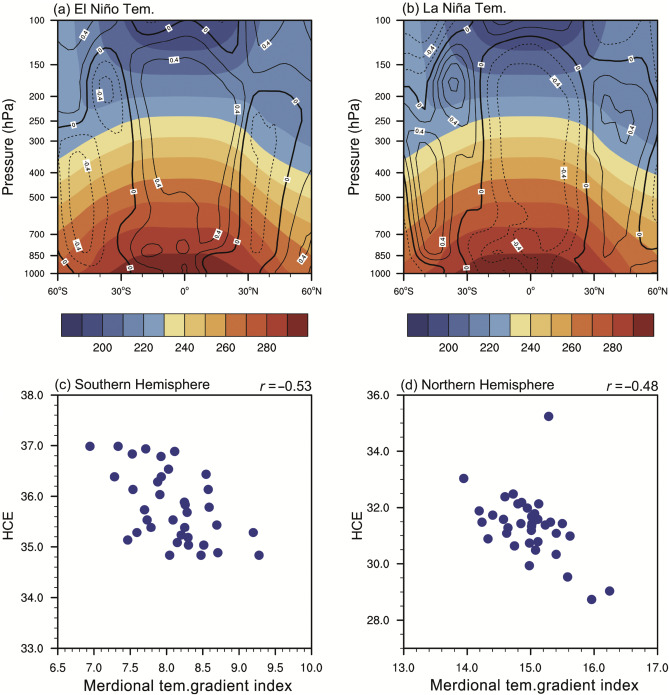
Shown in Fig. 6 are the climatology and composite anomaly of the zonal mean temperature based on El Niño and La Niña and the scatter plots of HCE and MTG. In El Niño cases, the tropical troposphere is generally warmer than that in the normal years, while the subtropical troposphere is suffered cold anomalies (Fig. 6 a). But in La Niña cases, the tropical troposphere cools, while the subtropical troposphere warms (Fig. 6 b). The climatological temperature field shows an apparent with higher temperature in the tropics and lower temperature over the mid-latitudes (Fig. 6 a–b). That means in El Niño (La Niña) years, the MTG increases (decreases). It is also worth noting that both the climatology and the ENSO related anomaly of the MTG in troposphere are nearly barotropic. According to Held and Hou (1980) the HCE is proportional to the pole-equator temperature difference. Specifically, the increasing (decreasing) of the MTG can shrink (expand) the HCEs. To quantitatively estimate the MTG, an MTG index is defined as:

$I_{{\mbox{MTG}},{\mbox{SH}}}=T_{\left[0-20{\mbox{°}}S;850-200hPa\right]}-$$T_{\left[50{\mbox{°}}S-30{\mbox{°}}S;850-200hPa\right]}{\mbox{,}}$

( 2)

$I_{{\mbox{MTG}},{\mbox{NH}}}=T_{\left[0-20{\mbox{°}}{\mbox{N}};850-200hPa\right]}-$$T_{\left[30{\mbox{°}}{\mbox{N}}-50{\mbox{°}}{\mbox{N}};850-200hPa\right]}{\mbox{.}}$

( 3)

Where I_MTG,SH and I_MTG,NH are the meridional gradient indices in Southern and Northern Hemispheres, respectively; T is the temperature; “[]” represents the cross-section where the areal mean is performed.

Fig. 6. Climatology (shading) and composite anomalies (contours) of the December to February temperature (K) based on (a) El Niño and (b) La Niña events during the period of 1979–2014. (c) The scatter plot of Hadley circulation extent (HCE) in the Southern Hemisphere and the meridional temperature gradient index. (d) As in (c), but for the Northern Hemisphere. The values at the top-right corners in (c) and (d) indicate the correlation coefficients between HCEs and the meridional temperature gradient index. The HCE is defined as the latitude at which the vertical mean of mass stream function (MSF) between 850 hPa and 200 hPa equals to zero in the corresponding hemisphere.

The relationships between MTG and the HCE in both Hemispheres are shown in Fig. 6 c–d. Each dot represents a different year. We can see that robust correlations between HCE and MTG in both Hemispheres are evident. The HCE and MTG have higher correlation coefficient (r  = −0.54) in the Southern Hemisphere than that in the Northern Hemisphere (r  = −0.45). Note that the HCE is negatively correlated with MTG, i.e. when the MTG enlarges (diminishes), the HCE will move equatorward (poleward).

Therefore, El Niño (La Niña) enhances (weakens) the MTG (Fig. 6 a–b), which can result in shrinking (expansion) of the HCE in both Hemispheres. But in the Northern Hemisphere the eddy momentum flux divergence plays a more important role than the MTG in modulating the HCE because of the smallness of the Rossby number. Although the Rossby number in the Southern Hemisphere subtropics is also small, but the ENSO induced eddy momentum flux divergence is small there. Thus, the MTG plays a dominant role in affecting HCE in the Southern Hemisphere.

4. Discussion and conclusions

In this study, the interannual variability of the HCEs was investigated. The links between HCE change and ENSO were also analyzed via diagnostic methods. The results show that El Niño (La Niña) events can induce the shrinking (expansion) of HCE in the Southern Hemisphere. In the Northern Hemisphere, El Niño (La Niña) leads to shrinking (expansion) of the HCEs in the middle and lower troposphere and expansion (shrinking) of the HCE in the upper troposphere.

The ENSO associated MTG is closely correlated with the HCEs in both Hemispheres. But in the northern subtropics, the Rossby number is small and eddy momentum flux divergence plays a more important role than the MTG in affecting HCE. ENSO can induce opposite eddy momentum flux divergence between the upper and lower troposphere in the northern subtropics and then an opposite direction of the HCE movement in the Northern Hemisphere. In the Southern Hemisphere, in spite of the smallness of Rossby number, the ENSO related eddy momentum flux divergence is also small, thus the MTG plays dominant role in affecting HCE. Because the MTG is nearly barotropic, the movements of HCE in varies levels are consistent.

Several other issues about the HCE change need to be further addressed. Firstly, the inconsistency movements of HCEs in the upper and lower troposphere in response to ENSO draws our attention to the definition of HCE. A lot of previous studies investigated the long-term trend of HCE by defining it as the latitude of MSF = 0 at 500 hPa. Although some studies pointed out that the width of HC is not sensitive to either a single level or a vertical average (Johanson and Fu, 2009  and Stachnik and Schumacher, 2011 ), the results in these studies show the inconsistency of HCE in different levels in response to ENSO. Therefore, the commonly used definition of HCE (MSF = 0 at 500 hPa) should be treated with caution.

Another issue is that ENSO has equatorial symmetric SST distribution, but the responses of eddy to the SST changes are asymmetric. The meridional SST gradient can influence the tropospheric wave activity through changing the zonal wind (Hu et al., 2014 ). But in DJF, the zonal wind in the both Hemispheres are asymmetric, which may lead to asymmetric wave activity. Additionally, the asymmetry of land-sea distribution in the two Hemispheres may also lead to different wave responses.

There are still more interesting questions, such as how ENSO is related to the local HCE change? Is there an interaction between the HCE and the momentum balance over the subtropics? These questions will be investigated in the future works.

Acknowledgment

We thank the editor and the two anonymous reviewers for their helpful and constructive comments on the manuscript. This work was supported by the National Natural Science Foundation of China (41530424 ).

References

1. Adam and Schneider, 2014 O. Adam, T. Schneider; Role of changes in mean temperatures versus temperature gradients in the recent widening of the Hadley circulation; J. Clim., 27 (2014), pp. 7450–7461
2. Caballero and Anderson, 2009 R. Caballero, B.T. Anderson; Impact of midlatitude stationary waves on regional Hadley cells and ENSO; Geophys. Res. Lett., 36 (2009), p. L17704
3. Ceppi and Hartmann, 2013 P. Ceppi, D.L. Hartmann; On the speed of the eddy-driven jet and the width of the Hadley cell in the southern hemisphere; J. Clim., 26 (2013), pp. 3450–3465
4. Dee et al., 2011 D.P. Dee, S.M. Uppala, A.J. Simmons, et al.; The ERA-Interim reanalysis: configuration and performance of the data assimilation system; Quart. J. Roy. Meteor. Soc., 137 (2011), pp. 553–597
5. Feng and Li, 2013 J. Feng, J.-P. Li; Contrasting impacts of two types of ENSO on the boreal spring Hadley circulation; J. Clim., 26 (2013), pp. 4773–4789
6. Feng et al., 2011 R. Feng, J.-P. Li, J.-C. Wang; Regime change of the boreal summer Hadley circulation and its connection with the tropical SST; J. Clim., 24 (2011), pp. 3867–3877
7. Feng et al., 2013 J. Feng, J.-P. Li, F. Xie; Long-term variation of the principal mode of boreal spring Hadley Circulation linked to SST over the Indo-Pacific Warm Pool; J. Clim., 26 (2013), pp. 532–544
8. Fu et al., 2006 Q. Fu, C.M. Johanson, J.M. Wallace, et al.; Enhanced mid-latitude tropospheric warming in satellite measurements; Science, 312 (2006), p. 1179
9. Held and Hou, 1980 I.M. Held, A.Y. Hou; Nonlinear axially symmetric circulations in a nearly inviscid atmosphere; J. Atmos. Sci., 37 (1980), pp. 515–533
10. Holton, 1992 J.R. Holton; An Introduction to Dynamic Meteorology; (third ed.)Academic Press, San Diego, Calif (1992)
11. Hou, 1998 A.Y. Hou; Hadley circulation as a modulator of the extratropical climate; J. Clim., 55 (1998), pp. 2437–2457
12. Hu et al., 2014 D.-Z. Hu, W.-S. Tian, F. Xie, et al.; Effects of meridional sea surface temperature changes on stratospheric temperature and circulation; Adv. Atmos. Sci., 31 (2014), pp. 1–13
13. Hu and Fu, 2007 Y.-Y. Hu, Q. Fu; Observed poleward expansion of the Hadley circulation since 1979; Atmos. Chem. Phys., 7 (2007), pp. 5229–5236
14. Johanson and Fu, 2009 C.M. Johanson, Q. Fu; Hadley cell widening: model simulations versus observations; J. Clim., 22 (2009), pp. 2713–2725
15. Kalnay et al., 1996 E. Kalnay, M. Kanamitsu, R. Kistler, et al.; The NCEP/NCAR 40-year reanalysis project; Bull. Amer. Meteor. Soc., 77 (1996), pp. 437–472
16. Kanamitsu et al., 2002 M. Kanamitsu, W. Ebisuzaki, J. Woollen, et al.; NCEP–DOE AMIP-II reanalysis (R-2); Bull. Amer. Meteor. Soc., 83 (2002), pp. 1631–1643
17. Li, 2001 J.-P. Li; Atlas of Climate of Global Atmospheric Circulation I China; Meteorology Press, Beijing (2001) (in Chinese)
18. Li et al., 2013 J.-P. Li, R.-C. Ren, Y.-Q. Qi, et al.; Progress in air–land–sea interactions in Asia and their role in global and Asian climate change; Chin. J. Atmos. Sci., 37 (2) (2013), pp. 518–538 (in Chinese)
19. Li et al., 2015 X.-F. Li, J.-P. Li, Y. Li; Recent winter precipitation increase in the middle–lower Yangtze River Valley since the late 1970s: a response to warming in the tropical Indian Ocean; J. Clim., 28 (2015), pp. 3857–3879
20. Lu et al., 2009 J. Lu, C. Deser, T. Reichler; Cause of the widening of the tropical belt since 1958; Geophys. Res. Lett., 36 (2009), p. L03803
21. Ma and Li, 2007 J. Ma, J.-P. Li; Strengthening of the boreal winter Hadley circulation and its connection with ENSO; Prog. Nat. Sci., 17 (2007), pp. 1327–1333
22. Ma and Li, 2008 J. Ma, J.-P. Li; The principal modes of variability of the boreal winter Hadley cell; Geophys. Res. Lett., 35 (2008), p. L01808
23. Nguyen et al., 2013 H. Nguyen, A. Evans, C. Lucas, et al.; The Hadley circulation in reanalyses: climatology, variability, and change; J. Clim., 26 (2013), pp. 3357–3376
24. Polvani et al., 2011 L.M. Polvani, D.W. Waugh, G.J.P. Correa, et al.; Stratospheric ozone depletion: the main driver of 20th century atmospheric circulation changes in the Southern Hemisphere; J. Clim., 24 (2011), pp. 795–812
25. Quan et al., 2004 X.-W. Quan, H.F. Diaz, M.P. Hoerling; Change in the tropical Hadley cell since 1950; H.F. Diaz, R.S. Bradley (Eds.), The Hadley Circulation: Past, Present, and Future, Cambridge University Press, New York (2004), pp. 85–120
26. Quan et al., 2014 X.-W. Quan, M.P. Hoerling, J. Perlwitz, et al.; How fast are the tropics expanding?; J. Clim., 27 (2014), pp. 1999–2013
27. Seidel and Randel, 2007 D.J. Seidel, W.J. Randel; Recent widening of the tropical belt: evidence from tropopause observations; J. Geophys. Res., 112 (2007), p. D20113
28. Smith et al., 2008 T.M. Smith, R.W. Reynolds, T.C. Peterson, et al.; Improvements NOAAs historical merged land-ocean temp analysis (1880–2006); J. Clim., 21 (2008), pp. 2283–2296
29. Son et al., 2010 S.W. Son, E.P. Gerber, J. Perlwitz, et al.; Impact of stratospheric ozone on Southern Hemisphere circulation change: a multimodel assessment; J. Geophys. Res., 115 (2010), p. D00M07
30. Stachnik and Schumacher, 2011 J.P. Stachnik, C. Schumacher; A comparison of the Hadley circulation in modern reanalyses; J. Geophys. Res., 116 (2011), p. D22102
31. Staten et al., 2012 P.W. Staten, J.J. Rutz, T. Reichler, et al.; Breaking down the tropospheric circulation response by forcing; Clim. Dyn., 39 (2012), pp. 2361–2375
32. Walker and Schneider, 2006 C.C. Walker, T. Schneider; Eddy influences on Hadley circulations: simulations with an idealized GCM; J. Atmos. Sci., 63 (2006), pp. 3333–3350
33. Waugh et al., 2015 D.W. Waugh, C.I. Garfinkel, L.M. Polvani; Drivers of the recent tropical expansion in the Southern Hemisphere: changing SSTs or ozone depletion?; J. Clim., 28 (2015), pp. 6581–6586