Risk efficiency of hedging strategy in China financial market

Summary

This paper presents the analysis of China financial market and method of hedging optimization for compute expected shortfall risk based on attitude towards risk under the Black–Scholes model. The application demonstrates an example of the efficient hedging strategy for call option in the Black–Scholes model based on geometric Brownian motion with loss function. The data of illustrations which applies in China financial market. The resulting efficient hedges allow the investor to interpolate in a systematic way extreme of partial hedging (between no hedge and full hedge) that depend on the accepted level of shortfall risk.

JEL classification

D81 ; G1 ; G32

Keywords

Hedging strategy ; Risk measure ; Black–Scholes model ; China financial market

Introduction

This paper is going to describe the general invest environment of China financial market. Consider risk management has become progressively more important for corporations. It will use the risk measure analysing a call option to demonstrate how active trading in China financial market. Furthermore, in particular calculate the cases of lower partial moments, linear and risk-taking that considers the attitude towards risk, the result presents the efficient hedge for call option in Black–Scholes model. The objective of this paper is risk measure analysis which for Value at Risk (VaR) and distinguish between VaR and expected shortfall (ES) in China financial market and analyse partial hedge of estimate the expected shortfall risk in the Black–Scholes model. Risk measure and hedging which are two concepts investor used and considered every daily life. But how much should be hedged 0–50–100% (no hedge–partial hedge–full hedge)? Depends on exposure and risk attitude towards. Risk attitude is a complex area, it can measure in variety ways, though not perfect and entirely accurate, but it is progressing. The paper is interested in the approach of partial hedge of estimate risk measures ES risk in the Black–Scholes model based on different risk attitude towards.

Analysis of China financial market

As the fastest growing and one of the largest economies of the world, China has witnessed a magical transformation from a stagnant command economy to a dynamic market economy. In this section is presents the overview of China financial market and risk measure analysis in China financial market.

Overview of China financial market

The Chinese stock market has promoted the reform of state-owned enterprises and the change of their systems, and enabled a stable transition between the two systems. On the strength of the stock market in the past decade, many large state-owned enterprises have realized system change. The change also has stimulated medium and small-sized state-owned enterprises to adopt the shareholding system, thus solving the most important issue – the system problem – during the transition from planned to a market economy. As for ordinary citizens, bank deposit is not the only way to put their money. The stock market has become one of the most important channels for investment. Following Table 1 presents the Chinese stock market statistics in 2014.

Table 1. Chinese stock market statistics in 2014.

	Q1	Q2	Q3	Q4
Total funds raised (100 million yuan)	1344	1221	1262	3232
Turnover of trading (100 million yuan)	121,903	94,691	190,646	335,146
Quarter-end volume of stock issued (100 million shares)	34,224	35,483	36,239	36,795
Quarter-end market capitalization (100 million yuan)	236,625	244,129	239,548	372,547
Quarter-end numbers of companies listed	2537	2540	2569	2613
Quarter-end close index
Shanghai stock exchange composite index (December 19, 1990 = 100)	2033	2048	2364	3235
Shenzhen stock exchange component index (July 20, 1994 = 1000)	7190	7343	8080	11,015

Source : The Peoples Bank, 2014  and The Peoples Bank, 2015 .

Methods of stock trading are constantly being improved. Today, a network system for securities exchange and account settlement has been formed, with the Shanghai and Shenzhen exchanges as the powerhouse, radiating to all parts of the country (see china.org.cn).

China has three stock exchanges, two of them (Shanghai stock exchange, Shenzhen stock exchange) are located in mainland of China, one is located in Hong Kong. Also there are four futures exchanges in mainland of China. Zhengzhou Commodity Exchange (ZCE) which established in 1993. Dalian Commodity Exchange (DCE) which established in February 1993. Shanghai Futures Exchange (SHFE) which established in 1999. China Financial Futures Exchange (CFFEX) which established in Shanghai in September 2006. There are two futures exchanges in Hong Kong which are Hong Kong Exchanges and Clearing (HKEx) and Hong Kong Mercantile Exchange (HKMEx). Following Table 2 presents the Chinese futures market statistics in 2014.

Table 2. Chinese futures market statistics in 2014.

	Q1	Q2	Q3	Q4
Transaction volume (10 thousand lots)	49,192	55,102	65,011	81,280
Turnover of trading (100 million yuan)	573,161	583,577	674,833	1,088,312
Quarter-end position (10 thousand lots)	803	986	1004	910

Source : The Peoples Bank, 2014  and The Peoples Bank, 2015 .

Outlook of China options market

China launched simulated trading in stock index option on 8th November 2013, as regulators move to enhance risk hedging options to support further financial reforms. The first stock options launched on the Shanghai Stock Exchange on 2014, offering investors a new hedging tool for trading index heavyweights, which regulators long have hoped to boost. The options are based on the exchange-trade fund (ETF) that tracks the SSE50 index, composed of the 50 most heavily weighted stocks on the bourse. Regulators are essentially guiding investors into blue chips, which most retail investors have avoided in favour of smaller firms, whose valuations have been pushed up.

Risk measure analysis in China financial market

General there are two basic but often use measures of risk that are VaR and ES. To comparison them, a measure that can produce better incentives for traders than VaR is ES. This is also sometimes referred to as conditional VaR, conditional tail expectation, or expected tail loss.

ES has better properties than VaR in that it encourages diversification. In spite of its weaknesses, VaR has become the most popular measure of risk among both regulators and risk managers. Because the disadvantage of ES are it does not have the simplicity of VaR and as a result is more difficult to understand, and it is more difficult to back-test a procedure for calculating ES than it is to back-test a procedure for VaR.

Example of risk measure comparison between VaR and ES in financial asset (options) in the China financial market (HKEx). Following Table 3 illustrates the normal distribution VaR, Historical VaR and ES for the PING AN (2318.HK) call option.

Table 3. Normal distribution value at risk, historical value at risk and expected shortfall.

Normal distribution value at risk
Mean return	0.004608
Standard deviation of returns	0.018692278
Value at Risk (%)
Bottom 5%	−0.019347118
Bottom 10%	−0.026138061

Historical Value at Risk		Expected shortfall
n	29	90% confidence	−0.02556
Bottom 10%	4th return
Bottom 3rd return	−0.012600229
Bottom 2nd return	−0.016203704
Bottom 2.9th return	0.016227568 (10% Value at Risk)
Bottom 5%	1.45th return	95% confidence	−0.03204
Bottom 2nd return	−0.016203704
Bottom 1st return	−0.047869185
Bottom 1.45th return	−0.033619719 (5%Value at Risk)

According to the results, it is calculate the normal distribution VaR and historical VaR, and compare the results of historical VaR and ES under confidence of 90% (10% VaR) and 95% (5% VaR). The result of 5% VaR is −0.019347118, 95% confidence ES is −0.03204. The result of 10% VaR is −0.026138061, 90% confidence ES is −0.02556.

Methodology of hedging strategy under the Black–Scholes model

The optimal hedging ${\textstyle {\tilde {\phi }}\in {\mathfrak {R}}}$ is ${\textstyle min_{\phi \in {\mathfrak {R}}}E[l((1-\phi )H)]}$ , s.t. ${\textstyle sup_{p{_{\ast }}\in {\mathfrak {R}}}E{_{\ast }}[\phi H]\leq {\tilde {V}}_{0}}$ , l   is strictly convex, on ${\textstyle \lbrace H>0\rbrace }$ . General considering the case of lower partial moments based on the optimal hedging which the loss function ${\textstyle l(x)=(x^{p}/P)}$ for ${\textstyle P>1}$ .

Proposition 1.

The optimal hedge consists in hedging the modified claim

$\phi _{p}H=H-c_{p}(\rho \ast )^{1/p-1}\wedge H$

( 2.1)

where the constant c_pis determined  ${\textstyle E{_{\ast }}[\phi _{p}H]={\tilde {V}}_{0}}$ .

In the Black–Scholes model with constant volatility ${\textstyle \sigma >0}$ the underlying discounted price process is given by a geometric Brownian motion ${\textstyle dX_{t}=X_{t}(\sigma dW_{t}+mdt)}$ , where ${\textstyle E(X_{t})=X_{0}\cdot e^{[(m/\sigma )-((1/2)\cdot (m/\sigma ))^{2}\cdot (T-t)]}}$ .

With initial value ${\textstyle X_{0}=x_{0}}$ , where W is a Wiener process under P and m   is a constant. If assume that ${\textstyle m>0}$ . The unique equivalent martingale measure P * is given by

${\frac {dP^{_{\ast }}}{dP}}=\rho ^{_{\ast }}=exp\left(-{\frac {m}{\sigma }}W_{T}-{\frac {1}{2}}\left({\frac {m}{\sigma }}\right)^{2}T\right)=const{\mbox{ }}X_{T}^{-\alpha }$

( 2.2)

where it set ${\textstyle \alpha =(m/\sigma ^{2})}$ .

The process W   * defined by ${\textstyle W_{t}^{_{\ast }}=W_{t}+(m/\sigma )t}$ , is a Brownian motion under P *.

A European call payoff function ${\textstyle H_{T}=(X_{T}-K)^{+}}$ can be hedged perfectly if it provides the initial capital

$H_{0}=E^{_{\ast }}[H]=x_{0}\Phi (d_{+})-K\Phi (d_{-})$

( 2.3)

where ${\textstyle d_{\pm }(x_{0},K)=((ln{\mbox{ }}x_{0}-ln{\mbox{ }}K)/\sigma {\sqrt {T}})\pm (1/2)\sigma {\sqrt {T}}}$ , and ${\textstyle \Phi }$ denotes the distribution function of the standard normal distribution.

Suppose it use only an initial capital ${\textstyle {\tilde {V}}_{0}}$ which is smaller than the Black–Scholes price H₀ . Under this constraint to minimize the shortfall risk ${\textstyle E[l((H-V_{T})^{+})]}$ where l is given loss function satisfying the assumptions. Lower partial moments and the linear case are modified claims and strategies determined and compare to the Black–Scholes perfect hedging strategy, see Föllmer and Leukert (2000) .

Proposition 2.

Lower partial moments modified claims and strategy for  ${\textstyle p\rightarrow \infty }$.

${\begin{array}{l}\displaystyle \epsilon _{p}(t,x)={\frac {\partial }{\partial x}}F_{p}(t\\\displaystyle x)=\Phi \left({\frac {ln{\mbox{ }}x-ln{\mbox{ }}L}{\sigma {\sqrt {\tau }}}}+{\frac {1}{2}}\sigma {\sqrt {\tau }}\right)+{\frac {\alpha }{p-1}}{\frac {L^{\alpha /(p-1)}(L-K)}{x^{(}\alpha /(p-1))+1}}\times exp\left[{\frac {1}{2}}\sigma ^{2}\tau {\frac {\alpha }{p-1}}\left({\frac {\alpha }{p-1}}+\right.\right.\\\left.\left.\displaystyle +1\right)\right]\times \Phi \left({\frac {ln{\mbox{ }}x-ln{\mbox{ }}L}{\sigma {\sqrt {\tau }}}}-\sigma {\sqrt {\tau }}\left({\frac {\alpha }{p-1}}+{\frac {1}{2}}\right)\right)\end{array}}$

( 2.4)

Let ${\textstyle \tau =T-t}$ , ${\textstyle \alpha =(m/\sigma ^{2})}$ .

Hence the function F_p by following equation

${\begin{array}{l}\displaystyle F_{p}(t,x)=x\Phi (d_{+}(x,L))-K\Phi (d_{-}(x\\\displaystyle L))-{\frac {L^{\alpha /(p-1)}(L-K)}{x^{\alpha }/(p-1)}}\times exp\left[{\frac {1}{2}}\sigma ^{2}\tau {\frac {\alpha }{p-1}}\left({\frac {\alpha }{p-1}}+1\right)\right]\Phi \left(d_{-}(x\right.\\\left.\displaystyle L)-{\frac {\alpha \sigma {\sqrt {\tau }}}{p-1}}\right)\end{array}}$

( 2.5)

The constant L   is modified claim of option prices which determined by the equation ${\textstyle {\tilde {V}}_{0}=F_{p}(0,x_{0})}$ . Let determine ${\textstyle {\tilde {V}}_{0}}$ equal 1, which means when ${\textstyle t=0}$ , calculate by the following equation

${\begin{array}{l}\displaystyle F_{p}(0\\\displaystyle x)=x\Phi \left({\frac {ln{\mbox{ }}x-ln{\mbox{ }}L}{\sigma {\sqrt {T}}}}+{\frac {1}{2}}\sigma {\sqrt {T}}\right)-K\Phi \left({\frac {ln{\mbox{ }}x-ln{\mbox{ }}L}{\sigma {\sqrt {T}}}}-{\frac {1}{2}}\sigma {\sqrt {T}}\right)-\\\displaystyle -{\frac {L^{\alpha /(p-1)}(L-K)}{x^{\alpha }/(p-1)}}\times exp\left[{\frac {1}{2}}\sigma ^{2}T{\frac {\alpha }{p-1}}\left({\frac {\alpha }{p-1}}+1\right)\right]\Phi \left({\frac {ln{\mbox{ }}x-ln{\mbox{ }}L}{\sigma {\sqrt {T}}}}-{\frac {1}{2}}\sigma {\sqrt {T}}\right)-\\\displaystyle -\left({\frac {\alpha \sigma {\sqrt {T}}}{p-1}}\right)={\tilde {V}}_{0}=1\end{array}}$

( 2.6)

Resulting of L input calculate Eq. (2.5) for call option with strike corresponding to the Black–Scholes, see Föllmer and Leukert (2000) .

Application of efficient hedging strategy

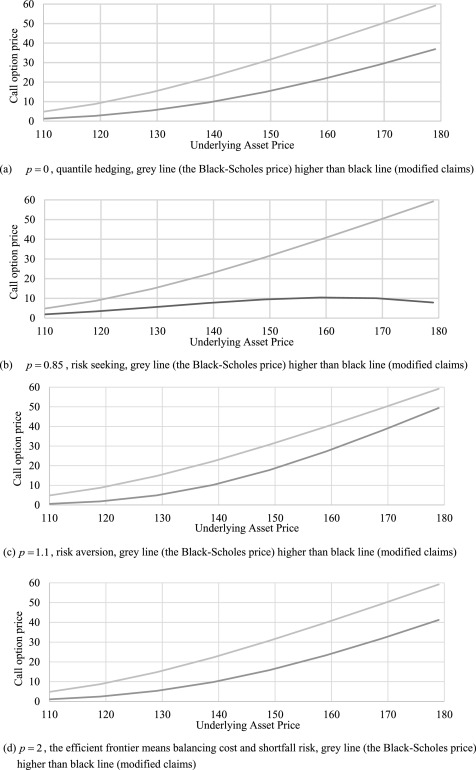
Example of the financial asset (call option) for modified claims and strategies determined the Black–Scholes efficient hedging strategy in China financial market (HKEx). Following Table 4 presents the parameters of call option TENCENT (0700.HK) under the Black–Scholes model.

Table 4. Parameters call option under the Black–Scholes model.

V0	H0	K	T  − t	m	α
1	4.4	120	0.15	0.1	0.664257626

Hence, V₀ denotes initial capital, H₀ denotes the Black–Scholes price, K is strike price, X is underlying asset price. Following Fig. 1 presents the Black–Scholes call option efficient hedging strategy.

Figure 1. The Black–Scholes call option efficient hedging strategy.

It was illustrated the approach of partial hedge of estimate the ES risk in the Black–Scholes model, the efficient hedges for call option in the geometric Brownian motion with known volatility and for the loss function based on different risk attitude towards. Because risk profiling is not an exact science, risk attitude is a complex area, but it can measure in variety ways, even each of ways measurement has their own advantages and disadvantages. Based on Fig. 1 to summarize different attitudes towards shortfall risk are reflected in different shapes of the modified claims and of the resulting hedging strategies by following special case when ${\textstyle p\rightarrow \infty }$ means risk free; when ${\textstyle p=1}$ means risk neutral; when ${\textstyle p=0}$ means quantile hedging; when ${\textstyle p=0.85}$ means risk seeking; when ${\textstyle p=1.1}$ means risk aversion; when ${\textstyle p=2}$ the efficient frontier means balancing cost and shortfall risk.

Conclusion

The paper describes the outlook and risk analysis (VaR and ES) in China financial market. Resulting of compare between VaR and ES that risk measure can produce better incentives for traders than VaR is ES. The objective of this paper is method of efficient hedging for call option in the Black–Scholes model based on geometric Brownian motion. The illustration determined of application is the Black–Scholes efficient hedging strategy in a call option data which from China financial market. The resulting of efficient hedges allow the investor to interpolate in a systematic way extremes of partial hedging which depend on the accepted level of shortfall risk attitude towards.

Conflict of interest

The author declares that there is no conflict of interest.

Acknowledgments

The research was supported by the SGS project of VSB-TU Ostrava under no. SP2015/15. This paper has been also elaborated in the framework of the Operational Programme Education for Competitiveness – Project No. CZ.1.07/2.3.00/20.0296.

References

1. Föllmer and Leukert, 2000 H. Föllmer, P. Leukert; Efficient hedging: cost versus shortfall risk; Financ. Stochast., 4 (2000), pp. 117–146
2. The Peoples Bank, 2014 The Peoples Bank of China Annual Report 2014.
3. The Peoples Bank, 2015 The Peoples Bank of China. http://www.pbc.gov.cn/ .