Robotics to develop computational thinking in early Childhood Education

Pulsa aquí para ver la versión en Español (ES)

Abstract

The development of programming skills is currently promoting from an early school age, trying to get children to take an active and creative role in the use of technologies. The objective of this article is to verify the repercussion of educational robotics activities on kindergarten students in the acquisition of computational thinking and programming skills. The research design is quasi-experimental, with pre-test and post-test measures, using experimental and control groups. The sample consists of 131 students from the second cycle of early education (between 3 and 6 years old), all from the same Spanish school. Computational thinking is measured through three dimensions: sequences (algorithms), action-instruction correspondence and debugging. The intervention sessions, as well as the structure of the challenges that were used in the pre- and post-test evaluations, were designed based on the reference program of robotics studies called “TangibleK”. The intervention, carried out doing learning activities using educational robotics resources, presents positive results in relation to the computational thinking skills achieved. The differences between the pre-test and the post-test in the experimental and control groups are statistically significant, in that children engaged in robotics program achieves a greater advance in the three dimensions of computational competence through this method.

Download the PDF version

1. Introduction and state of the question

The current digital situation calls for the development of strategies to modernize learning processes, including initiatives for the acquisition of digital skills to enable all citizens to function in a digitalised society. In this context, there is a growing trend promoting the development of programming skills from early school age to ensure that people acquire an active and creative role in the use of technologies, through the mastery of new cognitive skills and practices such as code-literacy.

1.1. Robotics for educational purposes

Currently, robotics is incorporated as highly valuable educational resources in the development of technical and social skills. Educational Robotics (ER) finds its main sustenance in constructivist and constructionists learning theories (Bravo & Forero, 2012; Schwabe, 2013). According to Papert, knowledge is achieved to the extent that the individual interacts with the object of study (Bers, Flannery, Kazakoff, & Sullivan, 2014); in this sense, the ER allows individuals to achieve this level of interaction. Through learning activities based on the design and construction of prototypes, students develop significant knowledge, moving from the abstract to the tangible (Pittí, Curto-Diego, & Moreno-Rodilla, 2010). Educational robotics can be integrated into the teaching-learning process through various practical approaches, one of which is its adoption as the main object of learning (Goodgame, 2018; Karampinis, 2018); a second approach would be as a means of learning (Koning, Faber, & Wierdsma, 2017; Kucuk & Sisman, 2017); the third would be to use it to support learning developments (Moro, Agatolio, & Menegatti, 2018). In the first two approaches, the orientation is aimed at the construction and programming of robots, using gear parts, sensors, actuators, and coding instructions according to the syntax of a programming language. Currently the main educational initiatives with robotics, are in these two approaches, by means of the development of training activities through courses and workshops (Buss & Gamboa, 2017; Ozcinar, Wong, & Ozturk, 2017); an example is the First Lego League, an international challenge that promotes interest in science and technology.

In the third approach, robots are used within the classroom, as a didactic resource (Bruni & Nisdeo, 2017; Serholt, 2018). In this way, learning can be facilitated by inquiry, where the occurrence of errors is taken as a learning opportunity. We find some initiatives developed in countries such as the United Kingdom, one of the pioneering nations in the development of programming skills and computational thinking from a formal curricular perspective, which has incorporated the subject “Computing” into its school curriculum.

1.2. Computational thinking

New theories on code-literacy (Zapata-Ros, 2015), which allow individuals to communicate with devices through instructions in computer languages, trigger a great interest by the computational thinking processes (Liu, Perera, & Klein, 2017). Jeanette Wing used this term for the first time in 2006, arguing that this type of thinking “involves solving problems, designing systems and understanding human behavior, based on the fundamental concepts of informatics” (Wing, 2006: 33). Subsequently, it was considered as a basic competence that every citizen would have to acquire to function in the digital society. In addition, she argued that computational thinking is neither routine nor mechanical, but a way of solving problems intelligently and imaginatively (Wing, 2008).

In 2009, the National Science Foundation funded the project “Leveraging Thought Leadership for Computational Thinking in PK-12”. This was a joint program between the Association of Computer Science Teachers and the International Society for Technology in Education. The purpose of this initiative was to make computational thinking concepts accessible to educators by providing an operational definition, shared vocabulary and meaningful examples appropriate for the age of the students. The project linked educational objectives with classroom practices (Barr, Harrison, & Conery, 2011).

In Europe, we find similar projects; one is Erasmus+ KA2 “TACCLE3 – Coding. The contents presented through the project's website (http://taccle3.eu/), are an example of successful educational practices and experiences in the process of incorporation and promotion of these skills (García-Peñalvo et al., 2016). A significant contribution to the conceptual framework on computational thinking has been made by researchers Karen Brennan (Harvard University) and Mitch Resnick (MIT) formulating an alternative model on this style of thinking. The model was proposed within the research project that resulted in the creation of Scratch, a visual programming platform “by blocks” that allows children and young people to make their own interactive stories with animations and simulations in a playful environment. The model of computational thinking formulated by Brennan and Resnick (2012) is based on three dimensions: computational concepts, practices, and perspectives.

From our point of view, computational thinking could be defined as the ability and capacity to solve problems using programming and the fundamentals of computational science. In recent years, an approach which is increasingly used has been developed, aimed at improving children's technological literacy and making computational thinking a relevant competency in school environments (Caballero & García-Valcárcel, 2017; Liu, Perera, & Klein, 2017). Some research provides evidence that shows the positive changes that occur in students immersed in training courses in programming skills and computational thinking using programmable robots (Chen, Shen, Barth-Cohen, Jiang, Huang, & Eltoukhy, 2017; Durak & Saritepeci, 2018). In the Spanish context, programs are increasingly targeted at children in the early stages of education on mathematical content, such as algebra, with the use of robotic devices adapted to children for the development of computational thinking skills successfully (Alsina & Acosta, 2018).

The integration of robotics during the first school stages takes advantage of the fact that in this period new ideas are created based mainly on experiences and concepts previously learned; there is a great influence of the family environment (Seppänen, Schaupp, & Wahlström, 2018; Wong, Jiang, & Kong, 2018). Learning, therefore, occurs when children, using information captured by their senses, share ideas, test their limits and receive feedback. In these actions, imagination and creativity play an important role in the production of new knowledge (Buitrago, Casallas, Hernández, Reyes, Restrepo, & Danies 2017). In addition, the development of programming and computational thinking skills through robots capitalizes on the playful characteristics of the resource and context, which represents a positive impact, according to Froebel’s approach to games (Resnick & Rosenbaum, 2013).

2. Material and method

Considering the theoretical framework exposed and considering there are still few empirical studies that prove the impact of educational robotics on the development of computational thinking in young children, this study aims to test the influence of a training program based on learning activities with educational robotics on the acquisition of computational thinking skills in early childhood education.

At present, there are several resources of educational robotics that allow the introduction of programming at early ages. The Bee-Bot® robotics kit is used for this research. This is a bee-shaped floor robot with a structure that combines resilience and subtlety at the same time. Other factors in its favor are its dimensions, which allow for easy handling. In addition, its colors, sounds, and movements make it a suitable resource for use with young children between the ages of 3 and 7.

On the other hand, its manufacturer, the English company TTS, has a recognized trajectory in the design and construction of educational resources for which this robot represents a mature educational technology with a high level of confidence and checked quality. The robot has buttons to program the sequence of movements it must perform: advance, reverse, turn left or right, start to move, pause the movements and delete the previous commands. The robot displaces in 15 cm movements, makes 90º turns and stores up to 40 instructions in its memory. For the study, a series of rugs or mats that were designed explicitly for research according to the objectives of the training activities were used. In addition, a story was elaborated for each rug that among its characters involved the Bee-Bot® robot itself. This story was presented to the children before they were shown the challenge they had to solve. The purpose of the story was to present the challenges in a playful and motivating context adapted to the children’s age.

2.1. Research design

The research questions used for this study are the following:

1) Is it possible to develop the computational thinking of children in the early childhood education stage (3-6 years) through robotic activities in the classroom?

2) Can children improve their ability to sequence actions by responding to a challenge through programming activities using educational robots?

3) Can children improve their ability to relate the instructions they give to a robot to the action it performs?

4) Can children improve their ability to identify and correct existing errors in a programming sequence?

With these questions in mind, the objective of this research focuses on assessing the students’ performance when facing these computational challenges, both initially and once they have completed a training program with robotic activities, thus, assessing the effectiveness of the program in terms of the skills developed by participants.

As a starting hypothesis, it was established that the integration of a program of learning activities with educational robotics would significantly contribute to the acquisition of computational thinking skills in Early Childhood Education schoolchildren.

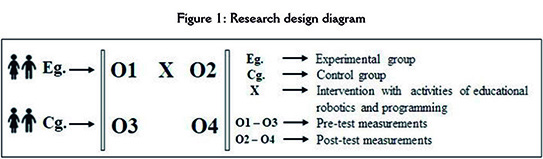
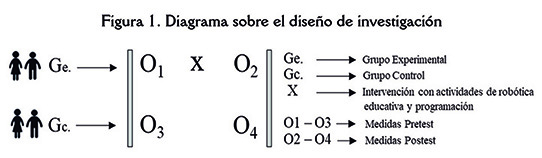
The study was developed using a quasi-experimental design (Campbell & Stanley, 1993; Hernández & Maquilón, 2010), with pre-test and post-test measurements in two groups (experimental and control), as shown in the diagram in Figure 1. The students are divided into two groups, experimental (Eg), whose members would perform the training program, and control group (Cg), comprised of subjects who would not participate in robotics activities (Kandlhofer & Steinbauer, 2016). The allocation of students to groups could not be done randomly since the intervention allowed by the school required working with intact groups formed according to criteria inherent to the school itself and independent of the study. Following the methodological criteria of this type of research design, measures were collected from everyone (experimental and control group), before and after the intervention.

2.2. Variables

Two types of variables were defined in the research design: independent and dependent (Hernández & al., 2014: 238). The independent variable was one that was manipulated to measure its effect on the dependent variable. Thus, the educational robotics training program was the independent variable. The dependent variable was defined as the students' computational thinking and programming skills, considering three dimensions, which could be evaluated through the robotics kit:

1) Sequences: ability to sequence actions by responding to a challenge through programming activities.

2) Action-instruction correspondence: ability to relate the instructions given to a robot with the action it performs.

3) Debugging: ability to identify and correct existing errors in a programming sequence.

Brennan y Resnick (2012) described the sequences as a series of steps that must be taken for a task to succeed.

Computational thinking action-instruction refers to the execution to be performed by the robot each instruction was provided with (Bers, Flannery, Kazakoff, & Sullivan, 2014). The practical dimension of debugging corresponds to the performance of a task by means of the trial and error method, learning from mistakes.

2.3. Participants

The sample was made up of 131 children from a subsidized center located in Salamanca, during the 2016-2017 academic year. All the participants were informed of the objectives of the study, and the informed consent of the minors’ parents/guardians was compiled with the collaboration of the school. The age range of the participants was between 3 and 6 years old (70% between 4 and 5 years old). The distribution of participants in groups was 67 for the experimental group (51% of the entire sample) and 64 in the control group (49% of the entire sample), with a gender-balanced proportion observed. Girls represented 45% of the subjects in the experimental group and 48% in the control group.

2.4. Procedure

The research was structured based on three stages: the first involved the initial measurement of the dependent variable (pre-test), the second developed the training program (intervention), and the third repeated the administration of the evaluation test (post-test).

The intervention consisted of the development of 7 working sessions with the children in the experimental group. The first was an introduction to the use of the devices, and in the following 6 sessions the children explored concepts and carried out practices on programming. The intervention sessions were designed using the TangibleK robotics curriculum –created by the DevTech research group at Tufts University in Boston, directed by teacher Umaschi Bers– as a reference (Bers, 2010).

Planning for the training session was done in agreement with the teachers, whose function was to introduce the researcher to the class group in a familiar setting, to supervise the activities developed in class and to evaluate the performance of the children together with the researcher. Each session took place during a school day, with an approximate duration of four hours per day, integrating robotics activities in the curriculum to enhance logical-mathematical skills. During the course of the activities, the students worked in small groups (4-5 members) collaboratively. The sessions were organized based on the planned objectives:

• In the introductory session, called ‘My first steps in robotics,' students had the opportunity to use the Bee-Bot® robot, exploring its characteristics and achieving a general understanding of the resource's functionalities.

• In sessions 1 and 2 they worked on the Sequence dimension. The children had to create sequences of instructions to have the robot move across the mat. First, simple forward movements were programmed. Left and right turns were then included.

• Sessions 3 and 4 focused on the Action-instruction correspondence dimension. Cards were used to enable the children to program the way they wanted the robot to move and then they were checked against the robots’ movements.

• Sessions 5 and 6 were focused on the debugging dimension. In these sessions, children were provided with simple sequences containing errors that they had to detect and correct to successfully complete the challenge.

The third phase began once the training sessions were over. At this point, a new measurement was developed through the application of Solve-it tests (programming challenges accompanied by ludic stories) that allow for the evaluation of the participants’ acquired learning in the experimental and control groups. The evaluation tests were carried out individually.

2.5. Instruments

The evaluation instrument used to assess the level of performance achieved by the children is an adaptation of the “SSS” rubric used in the TangibleK program (Bers, 2010). The researcher and the teacher applied the rubric together and agreed on the evaluation results for each student.

Each dimension was evaluated through the resolution of two challenges posed to children. Each challenge received a score of 0 to 5 points, depending on the autonomy of the subject to solve the challenge and the success achieved (performance). The criteria formulated in the rubric was valued with a maximum score of 5 if the child completely achieved the assigned challenge without any help from the researcher. If the student almost achieved the assigned challenge with minimum help from the researcher, the achievement obtained was scored with a 4. If the development of the challenge was moderately satisfactory, receiving periodic aid from the researcher, but not step-by-step, the value assigned was 3 points. When the child displayed a minimal response to the assigned challenge, obtaining step-by-step help from the researcher in the process, he or she was assigned a 2. In the case of a student initiating the development of the challenge, but not completing it, a score of 1 was assigned, and when the participant did not attempt to solve the challenge, the assigned score was 0. For this study, a value of 4 was set as the objective level of achievement to overcome each challenge satisfactorily.

2.6. Data analysis

To verify the influence of educational robotics activities on the acquisition of computational thinking skills in school children, the results obtained in the pre-test and post-test were analyzed, distinguishing the dimensions: sequences, action-instruction correspondence and debugging.

First, the normality of the sample was determined using the Kolmogorov-Smirnov normality test. The use of this type of test is recommended when the study is performed on a sample of more than 30 individuals, as it was our case. This test is important because it enables the determination of whether to use parametric or nonparametric tests in the analyses for statistical hypothesis contrast. In the statistical analyses that were carried out, ?<0.05 was established as a critical value.

The Kolmogorov-Smirnov test data on pre-test results in the experimental and control groups leads to the conclusion that these data do not follow a normal distribution. The asymptotic significance value calculated for each dimension of computational thinking and the total is less than the confidence level established for the analyses. This leads to the use of nonparametric contrast tests such as the U of Mann-Whitney and the W of Wilcoxon.

3. Results

3.1. Study of the equivalence of the experimental and control groups in the pre-test

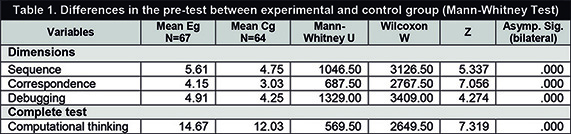
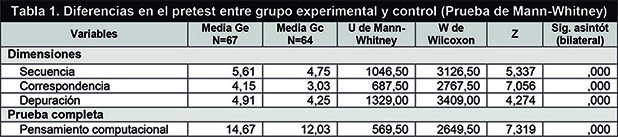
First, the pre-test results in the experimental (Eg) and control (Cg) groups were compared to verify their equivalence. The data obtained show that the groups were not equivalent, as significant differences can be observed between both groups when comparing the means of all dimensions and the total score (complete test), with more positive results seen in the experimental group (see Table 1). The lack of equivalence in the experimental and control groups is an issue that could not be foreseen a priori since the school formed the groups before beginning the research, and group modification were not allowed. The verification of this situation was considered when selecting the most appropriate data analysis strategy, since, although this is not a desirable situation to establish the comparison between the control and experimental groups, it is not an insurmountable barrier, as specific methods of analysis offer a solution to this (non-equivalent control group designs).

3.2. Analysis of post-test results

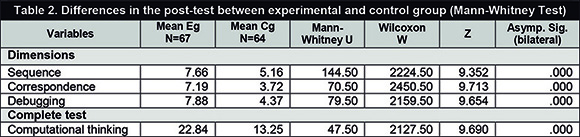
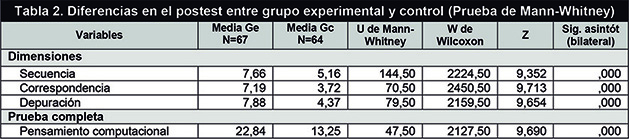
The data obtained in the post-test also show significant differences (p<.001) between the experimental group and the control group in all the variables studied (dimensions and complete test), as it can be seen in Table 2. However, since these are not initially equivalent groups, these differences are not directly attributable to the intervention; thus it is necessary to deepen the analysis.

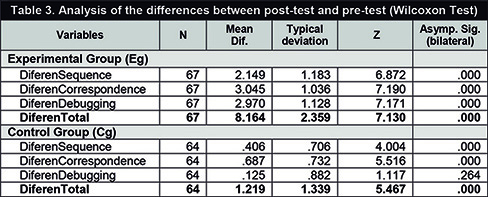
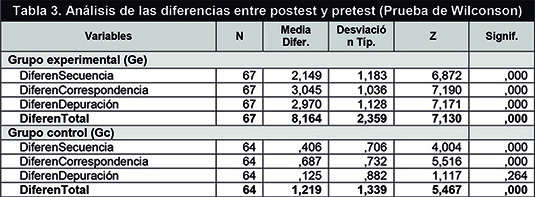
Following the guidelines of non-equivalent control group designs (Campbell & Stanley, 1993; Tejedor, 2000) to find the incidence of the independent variable in the dependent variable, the significance of the differences produced between the pre- and post-test scores in each of the dimensions of the dependent variable was analyzed for both the experimental and control groups (see Table 3 on the next page). To this end, new variables are defined: DiferenSequence, DiferenCorrespondence, DiferenDebugging, and DiferenTotal, which are obtained by calculating the difference between the pre- and post-test scores. It can be observed that the difference between the pre-test and the post-test in the experimental group is more than 2 points in all dimensions, reaching 8.16 points in the complete test (DiferenTotal). However, in the control group, the scores in the final test increased less the differences being less than 1 point in all dimensions and 1.22 in the complete test. If we observe the statistical significance of the differences pointed out, only in one case it is not significant: the debugging dimension in the control group. In this variable, there was no increase in the abilities of children in the control group. While, for the rest of the variables, even in the control group, there were significant differences that can be explained as an instrumentation effect (due to the administration of the initial test or pre-test, which may have implied some learning) as well as the maturation effect (due to the maturation of the children during the months of intervention, given that at these young children learn new abilities constantly and very quickly).

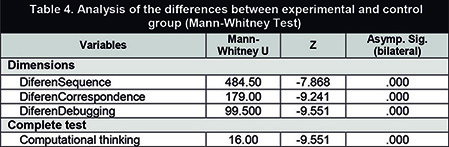
Additionally, with the data generated from the differences between the post-test and the pre-test, other statistical analyses were carried out, such as the non-parametric Mann-Whitney U test for independent samples, to confirm whether the learning gains in the experimental group are significantly higher than those in the control group. Defining the gain as the increase in the post-test score concerning the pre-test, the test results reflected an asymptotic significance of less than .01 (Table 4) for each of the variables. Therefore, the results obtained in the final tests show significant differences between the two groups (experimental and control); it can be argued that the children in the experimental group obtained greater abilities than those in the control group thanks to the intervention conducted, demonstrating a greater progress (statistically significant) in post-test scores.

The size of the effect has been estimated for the complete test by calculating the Cohen’s value. This is extraordinarily high (1.84), much higher than the value 0.80 established as very high. This value reaffirms the difference in the achievements made by the children according to the group to which they were assigned, being greater in the group that carried out the training.

3.3. Graphical analysis of differences between experimental and control groups

Finally, we show the existing differences in the experimental and control groups through a graphical analysis using the ROC curves (García-Valcárcel & Tejedor, 2017). We did this taking as study variables the differences between the pre-test and post-test scores in each of the dimensions for the dependent variable, and in the total variable called computational thinking skills. As a classification or state variable, the group variable is considered with two possible values: experimental group and control. For the analysis, the members of the experimental group have been considered as positive cases and have been represented in the graph.

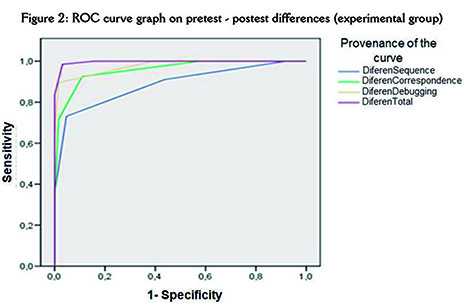
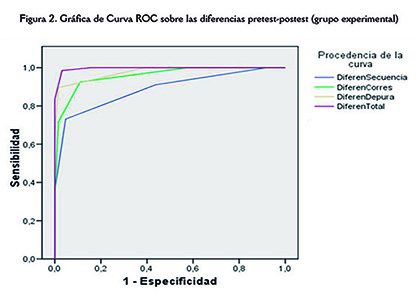
Figure 2 (see next page) shows the pairs of values (1- specificity, sensitivity) generated by the graph of ROC curves for each of the study variables (DiferenSequence, DiferenCorrespondence, DiferenDebugging, and DiferenTotal). It can be observed that all the curves are above the reference value (diagonal of the area). This is because the scores of the students in the experimental group are much higher than those of the students in the control group in all the analysis variables, as it is also shown in the preceding tables.

4. Discussion and conclusions

The development of educational robotics activities oriented to the acquisition of computational thinking skills presents positive results, corroborating that the training program facilitates the development of thinking skills in the following dimensions: sequences, action-instruction correspondence and debugging. The significant differences found between the members of the experimental and control groups demonstrate the existence of greater learning in the experimental group for each of the variables analyzed. The children in the control group also showed better skills in the post-test, which can be attributed to the maturation effect, the learning attributed to the pre-test, and to the fact that during the period of time in which the intervention took place, progress continued in the curricular program, specifically in the area of logic and mathematics, which generated greater knowledge linked to the skills evaluated.

Children who participated in the program acquired new skills to design and develop programming sequences using tangible objects (robots). These new skills allowed them to experimentally check the consequences and accuracy of the designed instructions, as well as detect errors in the programming sequences. The methodology used also supports the acquisition of social skills, such as communication, collaborative work, creativity, autonomy, and leadership. This form of learning is related to active learning methodologies and constructionist learning theories that postulate that knowledge is achieved through the interaction of the subject with the object of study (Bers, Flannery, Kazakoff, & Sullivan, 2014).

This study shows that it is possible to develop these thinking skills from early school stages, as program participants were between 3 and 6 years of age, and these children responded to the study expectations, allowing the initial hypothesis to be tested. The research also shows the impact of incorporating robotics in the development of significant learning in digital competencies related to programming. At the same time, it lays the foundations for the implementation of more complex technological learning scenarios at higher school levels.

The results achieved coincide with the conclusions of other research projects (Lee, Sullivan, & Bers, 2013; Elkin, Sullivan, & Bers, 2014) that show the positive effects of the introduction of robotic resources to promote the development of skills and interests linked to the STEM knowledge areas (Science, Technology, Engineering and Mathematics).

We consider it pertinent to highlight some limitations of the study carried out that must have to do with the size of the sample. It could have been wider if there had been more schools interested in participating in the study, as well as the equivalence of groups that could have been achieved with a random assignment of the participants to the groups which was not possible in this study due to the school organization. In this regard, the limitations of the researchers and the conditions established by the educational centers for the development of this type of studies must be considered. We consider that the results presented can be interpreted as an approximation to the subject, although more studies are required to consolidate the conclusions.

Funding Agency

National Secretariat of Science, Technology and Innovation (SENACYT) and Institute for Training and Use of Human Resources (IFARHU) of the Panama Republic.

References

Alsina, A., & Acosta, Y. (2018). Iniciación al álgebra en Educación Infantil a través del pensamiento computacional: Una experiencia sobre patrones con robots educativos programables. Revista Iberoamericana de Educación Matemática, 52, 218-235. https://bit.ly/2PC1hLt

Barr, D., Harrison, J., & Conery, L. (2011). Computational Thinking: A digital age skill for everyone. Learning and Leading with Technology, 38(6), 20-23.

Berrocoso, J., Sánchez, M., & Arroyo, M. (2015). El pensamiento computacional y las nuevas ecologías del aprendizaje. Red, 46, 1-18. https://doi.org/10.6018/red/46/3

Bers, M.U. (2010). The TangibleK Robotics program: Applied computational thinking for young children. Early Childhood Research & Practice, 12(2). https://bit.ly/2RZ3B11

Bers, M.U., Flannery, L., Kazakoff, E.R., & Sullivan, A. (2014). Computational thinking and tinkering: Exploration of an early childhood robotics curriculum. Computers & Education, 72, 145-157. https://doi.org/10.1016/j.compedu.2013.10.020

Bravo, F.A., & Forero, A. (2012). La robótica como un recurso para facilitar el aprendizaje y desarrollo de competencias generales. Teoría de la Educación. 13(2), 120-136. https://bit.ly/2EtOVnJ

Brennan, K., & Resnick, M. (2012). New frameworks for studying and assessing the development of computational thinking. In Proceedings of the 2012 Annual Meeting of the American Educational Research Association (AERA) (pp. 1-25), Vancouver, Canada.

Bruni, F., & Nisdeo, M. (2017). Educational robots and children’s imagery: A preliminary investigation in the first year of primary school. Research on Education and Media, 9(1), 37-44. https://doi.org/10.1515/rem-2017-0007

Buitrago, F., Casallas, R., Hernández, M., Reyes, A., Restrepo, S., & Danies, G. (2017). Changing a generation’s way of thinking: Teaching computational thinking through programming. Review of Educational Research, 87(4), 834-860. https://doi.org/10.3102/0034654317710096

Buss, A., & Gamboa, R. (2017). Teacher transformations in developing computational thinking: Gaming and robotics use in after-school settings. In P.J. Rich & C.B. Hodges (Eds.), Emerging research, practice, and policy on computational thinking (pp. 189-203). Switzerland: Springer International Publishing. https://doi.org/10.1007/978-3-319-52691-1_12

Caballero, Y.A., & García-Valcárcel, A. (2017). Development of computational thinking skills and collaborative learning in initial education students through educational activities supported by ICT resources and programmable educational robots. In F.J. García-Peñalvo (Ed.), Proceedings of the 5th International Conference on Technological Ecosystems for Enhancing Multiculturality (p. 103). New York: ACM. https://doi.org/10.1145/3144826.3145450

Campbell, D., & Stanley, J. (1993). Disen?os experimentales y cuasiexperimentales en la investigacio?n social. Buenos Aires: Amorrortu.

Chen, G., Shen, J., Barth-Cohen, L., Jiang, S., Huang, X., & Eltoukhy, M.M. (2017). Assessing elementary students’ computational thinking in everyday reasoning and robotics programming. Computers and Education, 109, 162-175. https://doi.org/10.1016/j.compedu.2017.03.001

Durak, H.Y., & Saritepeci, M. (2018). Analysis of the relation between computational thinking skills and various variables with the structural equation model. Computers & Education, 116, 191-202. https://doi.org/10.1016/j.compedu.2017.09.004

Elkin, M., Sullivan, A., & Bers, M.U. (2014). Implementing a robotics curriculum in an early childhood Montessori classroom. Journal of Information Technology Education: Innovations in Practice, 13, 153-169. https://doi.org/10.28945/2094

García-Peñalvo, F.J., Rees, A.M., Hughes, J., Jormanainen, I., Toivonen, T., & Vermeersch, J. (2016). A survey of resources for introducing coding into schools. Proceedings of the Fourth International Conference on Technological Ecosystems for Enhancing Multiculturality (TEEM’16) (pp.19-26). Salamanca, Spain, November 2-4, 2016. New York: ACM. https://doi.org/10.1145/3012430.3012491

García-Valcárcel, A., & Tejedor, F.J. (2017). Percepción de los estudiantes sobre el valor de las TIC en sus estrategias de aprendizaje y su relación con el rendimiento. Educación XX1, 20(2), 137-159. https://doi.org/10.5944/educxx1.19035

Goodgame, C. (2018). Beebots and Tiny Tots. In E. Langran, & J. Borup (Eds.). Society for Information Technology & Teacher Education International Conference (pp. 1179-1183). Association for the Advancement of Computing in Education (AACE).

Herna?ndez-Sampieri, R., Ferna?ndez-Collado. C., & Baptista-Lucio. P. (2014). Metodologi?a de la investigacio?n. Me?xico: McGraw-Hill Education.

Kandlhofer, M., & Steinbauer, G. (2016). Evaluating the impact of educational robotics on pupils’ technical-and social-skills and science related attitudes. Robotics and Autonomous Systems, 75, 679685. https://doi.org/10.1016/j.robot.2015.09.007

Karampinis, T. (2018). Robotics-based learning interventions and experiences from our implementations in the RobESL framework. International Journal of Smart Education and Urban Society, 9(1), 13-24. https://doi.org/10.4018/ijseus.2018010102

Koning, J.I., Faber, H.H., & Wierdsma, M.D. (2017). Introducing computational thinking to 5 and 6 years old students in dutch primary schools: An educational design research study. In C. Suero, & M. Joy (Eds.), Proceedings of the 17th Koli Calling Conference on Computing Education Research Calling Conference on Computing Education Research (pp. 189-190). New York: ACM. https://doi.org/10.1145/3141880.3141908

Kucuk, S., & Sisman, B. (2017). Behavioral patterns of elementary students and teachers in one-to-one robotics instruction. Computers & Education, 111, 31-43. https://doi.org/10.1016/j.compedu.2017.04.002

Lee, K.T., Sullivan, A., & Bers, M.U. (2013). Collaboration by design: Using robotics to foster social interaction in kindergarten. Computers in the Schools, 30(3), 271-281. https://doi.org/10.1080/07380569.2013.805676

Liu, H.P., Perera, S.M., & Klein, J.W. (2017). Using model-based learning to promote computational thinking education. In P.J. Rich, & C.B. Hodges (Eds.), Emerging research, practice, and policy on computational thinking (pp. 153-172). Switzerland: Springer International Publishing. https://doi.org/10.1007/978-3-319-52691-1_10

Moro, M., Agatolio, F., & Menegatti, E. (2018). The RoboESL Project: Development, evaluation and outcomes regarding the proposed robotic enhanced curricula. International Journal of Smart Education and Urban Society, 9(1), 48-60. https://doi.org/10.4018/ijseus.2018010105

Ozcinar, H., Wong, G., & Ozturk, H.T. (Eds.) (2017). Teaching computational thinking in primary education. USA: IGI Global. https://doi.org/10.4018/978-1-5225-3200-2

Pittí, K., Curto-Diego, B., Moreno-Rodilla, V. (2010). Experiencias construccionistas con robótica educativa en el Centro Internacional de Tecnologías Avanzadas. Education in the Knowledge Society, 11(1), 310-329. https://bit.ly/2MNPwls

Resnick, M., & Rosenbaum, E. (2013). Designing for tinkerability. In M. Honey & D.E. Kanter (Eds.), Design, make, play: Growing the next generation of STEM innovators (pp.163-181). New York: Routledge.

Schwabe, R.H. (2013). Las tecnologías educativas bajo un paradigma construccionista: un modelo de aprendizaje en el contexto de los nativos digitales. Revista Iberoamericana de Estudos em Educação, 8(3), 738-746. https://doi.org/10.5860/choice.51-1612

Seppänen, L., Schaupp, M., & Wahlström, M. (2018). Enhancing learning as theoretical thinking in robotic surgery. Nordic Journal of Vocational Education and Training, 7(2), 84-103. https://doi.org/10.3384/njvet.2242-458x.177284

Serholt, S. (2018). Breakdowns in children's interactions with a robotic tutor: A longitudinal study. Computers in Human Behavior, 81, 250-264. https://doi.org/10.1016/j.chb.2017.12.030

Tejedor, F.J. (2000). El diseño y los diseños en la evaluación de programas. Revista de Investigación Educativa, 18(2), 319-339.

Wing, J.M. (2006). Computational thinking. Communications of the ACM, 49(3), 33-35. https://doi.org/10.1145/1118178.1118215

Wing, J.M. (2008). Computational thinking and thinking about computing. Philosophical Transactions. Series A, Mathematical, Physical, and Engineering Sciences, 366(1881), 3717-3725. https://doi.org/10.1098/rsta.2008.0118

Wong, G., Jiang, S., & Kong, R. (2018). Computational thinking and multifaceted skills: A qualitative study in primary schools. in teaching computational thinking in primary education (pp. 78-101). USA: IGI Global. https://doi.org/10.4018/978-1-5225-3200-2.ch005

Zapata-Ros, M. (2015). Pensamiento computacional: Una nueva alfabetización digital. RED, 46, 1-47. https://doi.org/10.6018/red/45/4

Click to see the English version (EN)

Resumen

Actualmente se promueve el desarrollo de habilidades de programación desde una edad escolar temprana, tratando de que los niños adquieran un rol activo y creativo en el uso de las tecnologías. El objetivo de este trabajo es comprobar la repercusión del desarrollo de actividades de robótica educativa en la adquisición de habilidades de pensamiento computacional y programación en escolares de educación infantil. El diseño de la investigación es de tipo cuasi-experimental, con medidas pretest y postest, utilizando grupo experimental y control. La muestra la conforman 131 estudiantes del segundo ciclo de educación infantil (entre 3 y 6 años de edad) de un centro educativo español. El pensamiento computacional se mide a través de tres dimensiones: secuencias (algoritmos), correspondencia acción-instrucción y depuración. Las sesiones de intervención, así como la estructura de los retos que se utilizaron en las evaluaciones pre y postest fueron diseñadas tomando como base el programa de estudios en robótica denominado «TangibleK». La intervención, centrada en actividades de aprendizaje mediante recursos de robótica educativa, presenta resultados positivos en relación a las habilidades de pensamiento computacional logradas. Las diferencias encontradas entre el pre y postest en el grupo experimental son estadísticamente significativas y superiores a las presentadas en el grupo control, de modo que se concluye que los niños que realizan el programa de robótica consiguen un mayor avance en las tres dimensiones de la competencia computacional.

Descarga aquí la versión PDF

1. Introducción y estado de la cuestión

El escenario digital actual exige el desarrollo de estrategias que modernicen los procesos de aprendizaje, incluyendo iniciativas para la adquisición de competencias digitales que permitan a todos los ciudadanos desenvolverse en una sociedad altamente tecnificada. En este contexto tiene cada vez más presencia una corriente que promueve el desarrollo de habilidades de programación desde una edad escolar temprana para lograr que las personas adquieran un rol activo y creativo en el uso de las tecnologías, mediante el dominio de nuevas habilidades cognitivas y prácticas como la código-alfabetización.

1.1. Robótica con propósitos educativos

Actualmente, se incorpora la robótica como un recurso educativo altamente valioso en el desarrollo de competencias técnicas y sociales. La Robótica Educativa (RE) encuentra sus principales sustentos en las teorías de aprendizaje constructivistas y construccionistas (Bravo & Forero, 2012; Schwabe, 2013). De acuerdo con Papert, el conocimiento se logra en la medida en que el individuo interacciona con el objeto de estudio (Bers, Flannery, Kazakoff, & Sullivan, 2014); en este sentido, la RE permite lograr este nivel de interacción. Mediante la realización de actividades de aprendizaje basadas en el diseño y construcción de prototipos, los estudiantes logran desarrollar conocimientos significativos, pasando de lo abstracto a lo tangible (Pittí, Curto-Diego, & Moreno-Rodilla, 2010).

La robótica educativa se puede integrar en el proceso enseñanza-aprendizaje mediante diversos enfoques prácticos, uno de éstos es su adopción como objeto principal de aprendizaje (Goodgame, 2018; Karampinis, 2018), un segundo enfoque sería como medio de aprendizaje (Koning, Faber, & Wierdsma, 2017; Kucuk & Sisman, 2017) y, el tercero, consistiría en utilizarla como apoyo al desarrollo de aprendizajes (Moro, Agatolio, & Menegatti, 2018). En los primeros dos enfoques la orientación va dirigida a la construcción y programación de robots, empleando piezas de engranajes, sensores, actuadores y codificando instrucciones de acuerdo a la sintaxis propia de un lenguaje de programación.

Actualmente las principales iniciativas educativas con robótica, se ubican en estos dos enfoques, mediante el desarrollo de actividades de formación a través de cursos y talleres (Buss & Gamboa, 2017; Ozcinar, Wong, & Ozturk, 2017); un ejemplo es la First Lego League que supone un desafío internacional que despierta el interés por la ciencia y la tecnología.

En el tercer enfoque, los robots se emplean dentro de la clase, como un recurso didáctico (Bruni & Nisdeo, 2017; Serholt, 2018). De esta manera, se puede facilitar el aprendizaje por indagación, donde la ocurrencia de errores es tomada como una oportunidad de aprendizaje. En esta línea de acciones, encontramos iniciativas en Inglaterra para trabajar el desarrollo de habilidades de programación y pensamiento computacional desde una perspectiva curricular formal, incorporando la asignatura «Computing».

1.2. Pensamiento computacional

Las nuevas teorías sobre código-alfabetización (Zapata-Ros, 2015) que permiten a los individuos comunicarse con dispositivos a través de instrucciones en lenguajes informáticos, desencadenan un gran interés por los procesos de pensamiento computacional (Liu, Perera, & Klein, 2017). Jeanette Wing utilizó este término por primera vez en el año 2006, argumentando que este tipo de pensamiento «implica resolver problemas, diseñar sistemas y comprender el comportamiento humano, basándose en los conceptos fundamentales de la informática» (Wing, 2006: 33). Posteriormente, fue considerada como una competencia básica que todo ciudadano tendría que adquirir para desenvolverse en la sociedad digital. Además, sostuvo que el pensamiento computacional no es rutinario ni mecánico, sino una forma de resolver problemas de manera inteligente e imaginativa (Wing, 2008).

En 2009 la National Science Foundation costeó el proyecto: Leveraging Thought Leadership for Computational Thinking in PK-12. Este fue un desarrollo conjunto entre la Asociación de Profesores de Ciencias de la Computación y la Sociedad Internacional de Tecnología en Educación. El propósito de esta iniciativa era lograr que los conceptos de pensamiento computacional fueran accesibles a los educadores, proporcionando una definición operativa, un vocabulario compartido y ejemplos significativos adecuados a la edad de los estudiantes. En el proyecto se vinculaban los objetivos educativos y las prácticas de aula (Barr, Harrison, & Conery, 2011).

En Europa encontramos proyectos encaminados en este mismo sentido; uno es Erasmus+ KA2 “TACCLE3 – Coding. Los contenidos presentados a través del sitio web del proyecto (http://taccle3.eu), son un referente de prácticas y experiencias educativas de éxito en el proceso de incorporación y fomento de estas competencias (García-Peñalvo & al., 2016). Un aporte significativo al marco conceptual sobre el pensamiento computacional lo han realizado los investigadores Karen Brennan (Universidad de Harvard) y Mitch Resnick (MIT) formulando un modelo alternativo sobre este estilo de pensamiento. Este lo plantearon dentro del proyecto de investigación que dio como resultado la creación de Scratch, una plataforma visual de programación ‘por bloques’ que permite a los niños y jóvenes realizar sus propias historias interactivas, con animación, simulaciones y un ambiente lúdico. El modelo sobre pensamiento computacional que formularon Brennan y Resnick (2012), se articula en base a tres dimensiones: los conceptos computacionales, las prácticas y las perspectivas.

Desde nuestro punto de vista, se podría definir el pensamiento computacional como la habilidad y capacidad para resolver problemas utilizando la programación y los fundamentos de las ciencias computacionales. En los últimos años se ha desarrollado un enfoque creciente orientado a mejorar la alfabetización tecnológica de los niños y hacer que el pensamiento computacional sea una competencia relevante en los entornos escolares (Caballero & García-Valcárcel, 2017; Liu, Perera, & Klein, 2017). Algunas investigaciones al respecto aportan evidencias que demuestran que se producen cambios positivos en los estudiantes inmersos en programas de formación en habilidades de programación y pensamiento computacional empleando robots programables (Chen, Shen, Barth-Cohen, Jiang, Huang, & Eltoukhy, 2017; Durak & Saritepeci, 2018).

En el contexto español se está empezando a trabajar con los niños de las primeras etapas educativas sobre contenidos matemáticos como álgebra con el uso de dispositivos robóticos adaptados a los niños para el desarrollo de habilidades de pensamiento computacional (Alsina & Acosta, 2018) con buenos resultados.

La integración de la robótica durante las primeras etapas escolares aprovecha que en este periodo se crean nuevas ideas basadas principalmente en experiencias y conceptos aprendidos previamente; existiendo una gran influencia del entorno familiar (Seppänen, Schaupp, & Wahlström, 2018; Wong, Jiang, & Kong, 2018). Por consiguiente, el aprendizaje se produce cuando los niños, haciendo uso de la información capturada por sus sentidos, comparten ideas, prueban sus límites y obtienen retroalimentación. En estas acciones, la imaginación y la creatividad juegan un papel importante en la producción de nuevos conocimientos (Buitrago, Casallas, Hernández, Reyes, Restrepo, & Danies, 2017). Además, el desarrollo de habilidades de programación y pensamiento computacional mediante robots capitaliza las características lúdicas del recurso y el contexto, lo que representa un impacto positivo de acuerdo al enfoque de juego planteado por Froebel (Resnick & Rosenbaum, 2013).

2. Material y métodos

A la luz del marco teórico expuesto, y considerando que todavía son escasos los estudios empíricos que prueban el impacto de la robótica educativa en el desarrollo del pensamiento computacional de los niños pequeños, se planifica un estudio con el objetivo de comprobar la influencia de un programa de formación basado en actividades de aprendizaje con robótica educativa en la adquisición de habilidades de pensamiento computacional en escolares de educación infantil.

En la actualidad son diversos los recursos de robótica educativa que permiten introducir la programación en edades tempranas. Para esta investigación se ha utilizado el kit de robótica Bee-Bot®. Este es un robot de piso en forma de abeja con una estructura que combina resistencia y sutileza al mismo tiempo. Otros factores a su favor son sus dimensiones, que permiten una fácil manipulación. Además, sus colores, sonidos y movimientos lo hacen un recurso adecuado para utilizarse con niños pequeños entre los 3 y 7 años. Por otro lado, su fabricante, la empresa inglesa TTS, posee una reconocida trayectoria en el diseño y construcción de recursos educativos por lo que este robot representa una tecnología educativa madura existiendo un nivel de confianza y calidad comprobada. El robot cuenta con botones para programar la secuencia de movimientos que él deberá realizar: avanzar, retroceder, girar a la izquierda o derecha, comenzar a moverse, pausar los movimientos y borrar los comandos anteriores. El robot se desplaza en movimientos de 15 cm, realiza giros de 90º y almacena en memoria hasta 40 instrucciones. Para el estudio se opta por utilizar una serie de tapetes o alfombrillas que fueron diseñados de forma específica para la investigación en función de los objetivos de las actividades de formación. Además, se elabora para cada tapete una historia que involucraba entre sus personajes al propio robot Bee-Bot®. Esta narración se presenta a los niños antes de exponer el reto que debían resolver. El propósito de la historia era presentar los retos bajo un contexto lúdico y motivador adaptado a la edad de los niños.

2.1. Diseño de investigación

Las preguntas de investigación de las que se parten son las siguientes:

1) ¿Se puede desarrollar el pensamiento computacional de los niños de la etapa educativa de Infantil (3-6 años) a través de actividades de robótica en el aula?

2) ¿Pueden mejorar los niños su capacidad de secuenciar acciones para dar respuesta a un desafío a través de actividades de programación usando robots educativos?

3) ¿Pueden mejorar los niños su capacidad de relacionar las instrucciones que dan a un robot con la acción que éste desempeña?

4) ¿Pueden mejorar los niños su habilidad para identificar y corregir los errores existentes en una secuencia de programación?

Los objetivos del trabajo, relacionados con estas preguntas de investigación, se centran en evaluar el desempeño de los estudiantes ante retos en los que tienen que demostrar estas habilidades computacionales, inicialmente y una vez que han completado un programa formativo con actividades de robótica. Y de este modo, valorar la eficacia del programa en función de las capacidades desarrolladas en los sujetos.

Como hipótesis de partida se establece que mediante la integración de un programa de actividades de aprendizaje con robótica educativa se contribuirá significativamente a la adquisición de habilidades de pensamiento computacional en escolares de educación infantil.

El estudio se desarrolla mediante un diseño de tipo cuasi-experimental (Campbell & Stanley, 1993; Hernández & Maquilón, 2010), con medidas pretest y postest en dos grupos (experimental y control), como se observa en el diagrama de la figura 1. Los estudiantes se dividen en dos grupos, experimental (Ge), cuyos integrantes realizarán el programa formativo, y grupo de control (Gc), formado por los sujetos que no participarán en las actividades de robótica (Kandlhofer & Steinbauer, 2016). La asignación de los sujetos a los grupos no se puede realizar de forma aleatoria, ya que la intervención permitida por el centro educativo exigía trabajar con los grupos intactos formados de acuerdo a criterios inherentes al propio colegio e independientes del estudio. Siguiendo los criterios metodológicos de este tipo de diseño de investigación, se recolectan medidas de cada individuo (grupos experimental y control), antes y después de la intervención.

2.2. Variables

En el diseño de la investigación se definen dos tipos de variables: independiente y dependiente (Hernández & al., 2014: 238). La variable independiente es aquella que se manipula a fin de medir su efecto en la variable dependiente. Así pues, el programa de formación sobre robótica educativa es la variable independiente.

La variable dependiente se define como las habilidades de pensamiento computacional y programación de los estudiantes, considerando tres dimensiones, las cuales pueden ser evaluadas a través del kit de robótica:

1) Secuencias: capacidad de secuenciar acciones para dar respuesta a un desafío a través de actividades de programación.

2) Correspondencia acción-instrucción: capacidad de relacionar las instrucciones que dan a un robot con la acción que desempeña.

3) Depuración: habilidad para identificar y corregir los errores existentes en una secuencia de programación.

Brennan y Resnick (2012) describen las secuencias como una serie de pasos que deben realizarse para que una tarea en particular se desarrolle con éxito. La acción-instrucción del pensamiento computacional, se refiere a la ejecución que deberá hacer el robot de cada instrucción que se le proporciona (Bers, Flannery, Kazakoff, & Sullivan, 2014). La dimensión práctica depuración corresponde a la realización de una tarea mediante el método de ensayo y error, aprendiendo de los errores.

2.3. Participantes

La muestra la conformaron 131 estudiantes de educación infantil de un centro concertado ubicado en Salamanca, durante el curso académico 2016-2017. Todos los participantes son informados de los objetivos del estudio y se recopilaron los consentimientos informados de los padres/tutores de los menores con la colaboración del centro escolar. El rango de edad de los participantes estuvo entre los 3 y 6 años (el 70% entre 4 y 5 años). La distribución de los participantes en los grupos es de 67 para el grupo experimental (51% de toda la muestra) y 64 en el grupo control (49% de toda la muestra), observándose una proporción equilibrada en función del género). Las niñas representan el 45% de los sujetos del grupo experimental y el 48% del grupo control.

2.4. Procedimiento

La investigación se estructuró en base a tres etapas: La primera supone la medición inicial de la variable dependiente (pretest), en la segunda se desarrolla el programa formativo (intervención) y en la tercera se repite la aplicación de la prueba de evaluación (postest).

La intervención consistió en el desarrollo de siete sesiones de trabajo con los niños del grupo experimental. La primera es de iniciación al uso de los dispositivos y en las siguientes seis sesiones los niños pudieron explorar conceptos y realizar prácticas sobre programación. Las sesiones de intervención fueron diseñadas tomando como referencia el programa de estudios en robótica TangibleK (Bers, 2010), creado por el grupo de investigación DevTech de la universidad Tufts en Boston, bajo la dirección de la profesora Umaschi Bers.

La planificación de las sesiones formativas se realizó de acuerdo con las maestras, cuya función fue lograr la familiaridad del investigador con el grupo de clase, supervisar las actividades desarrolladas en la clase y evaluar el desempeño de los niños junto con el investigador. Cada sesión se desarrolla a lo largo de una jornada escolar, con un tiempo aproximado de cuatro horas por jornada, integrando las actividades de robótica en el desarrollo curricular con el fin de potenciar habilidades lógico-matemáticas. Durante el desarrollo de las actividades los estudiantes trabajaron en pequeños grupos (4-5 integrantes) de forma colaborativa. Las sesiones se organizaron en base a los objetivos previstos:

• En la sesión de iniciación, denominada Mis primeros pasos en Robótica, los estudiantes tuvieron la oportunidad de utilizar el robot Bee-Bot®, explorando sus características y logrando una comprensión general de las funcionalidades del recurso.

• En la sesión 1 y 2 se trabaja la dimensión de Secuencia. Los niños tienen que crear secuencias de instrucciones para desplazar el robot a través del tapete. En primer lugar, se programan movimientos simples hacia delante. Posteriormente se incluyen giros a izquierda y derecha.

• Las sesiones 3 y 4 se centraron en la dimensión Correspondencia acción-instrucción. Se utilizan tarjetas para que los niños programen los movimientos que quieren que el robot realice y posteriormente se comprueban con los robots.

• Las sesiones 5 y 6 se orientaron a trabajar la dimensión Depuración. En éstas se les proporcionan secuencias simples con errores que deben detectar y corregir para conseguir el reto planteado.

Una vez concluidas las sesiones de formación, se inicia la tercera fase, en la cual se realiza una nueva medición mediante la aplicación de pruebas Solve-it (retos de programación acompañados de historias lúdicas) que permiten evaluar los aprendizajes adquiridos en los integrantes de los grupos experimental y control. La aplicación de las pruebas de evaluación se realiza de forma individual.

2.5. Instrumentos

El instrumento de evaluación utilizado para valorar el nivel de desempeño que alcanzaron los niños es una adaptación de la rúbrica SSS empleada en el programa TangibleK (Bers, 2010). La rúbrica es aplicada por el investigador y la maestra de forma conjunta, consensuando la valoración de los resultados obtenidos por cada uno de los estudiantes.

Cada dimensión es evaluada a través de la resolución de dos retos planteados a los niños. Cada reto recibe una puntuación de 0 a 5 puntos, en función de la autonomía del sujeto para resolver el reto y el éxito alcanzado (desempeño). Los criterios formulados en la rúbrica implican valorar con el puntaje máximo 5, si el niño/a logra completamente el reto asignado sin ninguna ayuda del investigador. En el caso de que el estudiante logre de forma significativa el reto asignado; es decir, con mínimas ayudas del investigador, se puntúa el logro obtenido con un 4. Si el desarrollo del reto resulta medianamente satisfactorio, recibiendo ayudas periódicas del investigador, pero no paso a paso, el valor asignado es de 3 puntos. Cuando el niño/a presenta una respuesta mínima al reto asignado, obteniendo del investigador ayuda paso a paso durante el desarrollo, se le asigna un 2. En el caso de que el estudiante inicia el desarrollo del reto, pero no lo completa, se asigna un puntaje de 1 y cuando el participante no intenta resolver el reto asignado, la valoración asignada es de 0 puntos. Para el presente estudio se fijó el valor 4, como el nivel de logro objetivo para superar satisfactoriamente cada reto.

2.6. Análisis de datos

Para comprobar la influencia de las actividades de robótica educativa en la adquisición de habilidades de pensamiento computacional en los escolares, se efectúa el análisis de los resultados obtenidos en las pruebas pretest y postest, distinguiendo las dimensiones: secuencias, correspondencia instrucción-acción y depuración.

En primer lugar, se realiza el estudio de normalidad de la muestra poblacional empleando para esto el test de normalidad Kolmogorov-Smirnov. El uso de este tipo de prueba se recomienda cuando el estudio se realiza en una muestra superior a 30 individuos, como es nuestro caso. Este test es importante porque permite determinar las pruebas a utilizar, de tipo paramétricas o no paramétricas, en los análisis para contraste de hipótesis estadísticas. En los análisis estadísticos que se efectúan se establece como valor crítico ?<0.05.

Los datos de la prueba Kolmogorov-Smirnov sobre los resultados del pretest en los grupos experimental y control, permite concluir que estos datos no siguen una distribución normal. El valor de significación asintótica calculado para cada dimensión del pensamiento computacional y para el total es menor al nivel de confianza establecido para los análisis. Esto lleva a utilizar pruebas de contraste no paramétricas como la U de Mann-Whitney y la W de Wilcoxon.

3. Resultados

3.1. Estudio de la equivalencia de los grupos experimental y control en el pretest

En primer lugar, se comparan los resultados del pretest entre el grupo experimental (Ge) y control (Gc) para verificar su equivalencia. Los datos obtenidos muestran que los grupos no son equivalentes, observándose diferencias significativas entre ambos grupos en las medias de todas las dimensiones y la puntuación total (prueba completa) a favor del grupo experimental (ver tabla 1). La falta de equivalencia en los grupos experimental y control es una cuestión que no se ha podido prever a priori, ya que los grupos están formados por el colegio previamente al inicio de la investigación y no se ha permitido su modificación. La constatación de esta situación es tenida en cuenta para seleccionar la estrategia de análisis de datos más adecuada, ya que, si bien no es la situación deseable para establecer la comparación de los grupos control y experimental, tampoco es una barrera insalvable, pues existen métodos de análisis que ofrecen una solución (diseños de grupo control no equivalente).

3.2. Análisis de resultados del postest

Los datos obtenidos en el postest también evidencian diferencias significativas (p<,001) entre el grupo experimental y control en todas las variables estudiadas (dimensiones y prueba completa) como se puede apreciar en la tabla 2. Sin embargo, por no ser grupos equivalentes inicialmente, estas diferencias no son atribuibles directamente al tratamiento, es necesario profundizar en el análisis.

Siguiendo las pautas de los diseños de grupo control no equivalentes (Campbell y Stanley, 1993; Tejedor, 2000) y con objeto de conocer la incidencia de la variable independiente en la variable dependiente, se decide analizar la significatividad de las diferencias producidas entre las puntuaciones del pretest y las obtenidas en el postest en cada una de las dimensiones de la variable dependiente, para los dos grupos experimental y control (Tabla 3). Para ello son definidas nuevas variables denominadas: DiferenSecuencia, DiferenCorrespondencia, DiferenDepuración y DiferenTotal; las cuales se obtienen calculando la diferencia entre la puntuación en el postest y la del pretest.

Se puede observar que la diferencia entre el pretest y el postest en el grupo experimental es de más de 2 puntos en todas las dimensiones, alcanzando 8,16 puntos en la prueba completa (DiferenTotal), mientras que en el grupo control las puntuaciones en la prueba final han añadido menos ganancia, siendo las diferencias menores a 1 punto en todas las dimensiones y de 1,22 en la prueba completa.

Si observamos la significación estadística de las diferencias apuntadas, tan solo en un caso no resulta significativa, se trata de la dimensión Depuración en el grupo control. En dicha variable no ha habido una ganancia en las habilidades de los niños del grupo control, mientras que en el resto de las variables, aun tratándose del grupo control, se han producido diferencias significativas que se pueden explicar como efecto de instrumentación (debido a la propia aplicación de la prueba inicial o pretest, que ha podido suponer un cierto aprendizaje) así como al efecto maduración (debido a la propia maduración de los niños en los meses que dura el tiempo de intervención, dado que a estas edades tempranas los niños aprenden nuevas habilidades constantemente y de forma muy rápida).

Adicionalmente, con los datos que se han generado a partir de las diferencias entre el postest y el pretest se realizan otros análisis estadísticos como la prueba no paramétrica U de Mann-Whitney para muestras independientes, con objeto de confirmar si las ganancias de aprendizaje en el grupo experimental son significativamente mayores que las habidas en el grupo control. Entendiendo la ganancia como el aumento de la puntuación en el postest con respecto al pretest. Los resultados de la prueba muestran para cada una de las variables una significancia asintótica menor al 0,01 (Tabla 4).

Por tanto, se puede decir que los resultados alcanzados en las pruebas finales presentan diferencias significativas entre ambos grupos (experimental y control); se puede argumentar que los niños del grupo experimental obtienen mayores habilidades que los niños del grupo control, gracias a la intervención realizada, mostrando un mayor avance (estadísticamente significativo) en las puntuaciones del postest.

Se ha estimado el tamaño del efecto para la prueba completa calculando el valor ? de Cohen y resulta extraordinariamente alto (1,84), por ser muy superior al valor 0,80 establecido para considerarse muy alto. Este valor reafirma la diferencia de los logros conseguidos por los niños en función del grupo al que ha sido asignado, siendo mayor en el grupo que ha realizado la formación.

3.3. Análisis gráfico de las diferencias entre los grupos experimental y control

Finalmente, mostramos, mediante un análisis gráfico utilizando las curvas ROC (García-Valcárcel & Tejedor, 2017), las diferencias existentes en los grupos experimental y control. Lo haremos tomando como variables de estudio las diferencias producidas entre las puntuaciones del pretest y las del postest en cada una de las dimensiones de la variable dependiente, y en la variable total denominada habilidades de pensamiento computacional. Como variable de clasificación o de estado se toma la variable grupo, con dos posibles valores: grupo experimental y control. Para el análisis se ha considerado como caso positivo a los integrantes del grupo experimental, los cuales han sido representados en la gráfica.

En la Figura 2 observamos los pares de valores (1- especificidad, sensibilidad) que generan el grafico de curvas ROC para cada una de las variables de estudio (DiferenSecuencia, DiferenCorrespondencia, DiferenDepuración y DiferenTotal). Se puede apreciar que todas las curvas están por encima del valor de referencia (diagonal del área). Esto ocurre así porque las puntuaciones de los estudiantes pertenecientes al grupo experimental son mucho más altas que las de los estudiantes del grupo control en todas las variables de análisis, tal como ya se había puesto de manifiesto en las tablas precedentes.

4. Discusión y conclusiones

El desarrollo de actividades de robótica educativa orientadas a la adquisición de habilidades de pensamiento computacional presenta resultados positivos que corroboran que el programa formativo ha facilitado la formación de habilidades de pensamiento relacionadas con las dimensiones: secuencias, correspondencias instrucción-acción y depuración. Las diferencias significativas encontradas entre los integrantes de los grupos experimental y control demuestran la existencia de un mayor aprendizaje en cada una de las variables analizadas en el grupo que realizó las actividades de robótica. Los niños del grupo control también demuestran mejores habilidades en la prueba postest, lo que se atribuye al efecto maduración, el aprendizaje debido a la prueba pretest y a que el tiempo que ha durado la intervención se ha seguido avanzando en el programa curricular, y específicamente en el área de lógica y matemática, lo que genera mayores conocimientos relacionados con las habilidades evaluadas.

Los niños que han participado en el programa han adquirido nuevas habilidades para diseñar y construir secuencias de programación utilizando objetos tangibles (robots), pudiendo comprobar de forma experimental las consecuencias y exactitud de las instrucciones elaboradas, así como detectar errores en las secuencias de programación. La metodología empleada apoya también la adquisición de habilidades sociales, como la comunicación, el trabajo colaborativo, la creatividad, la autonomía y el liderazgo. Esta forma de aprendizaje se relaciona con las metodologías activas de aprendizaje y las teorías del aprendizaje construccionistas que postulan que el conocimiento se logra a través de la interacción del sujeto con el objeto de estudio (Bers, Flannery, Kazakoff, & Sullivan, 2014).

Este estudio demuestra que es posible desarrollar estas habilidades de pensamiento desde etapas escolares tempranas, ya que se ha trabajado con estudiantes de 3 a 6 años y los niños han respondido a las expectativas del estudio, pudiéndose comprobar la hipótesis de partida. La investigación pone de manifiesto el impacto que tiene la incorporación de la robótica en el desarrollo de aprendizajes significativos, en referencia a la formación de competencias digitales relacionadas con la programación. A la vez, sienta las bases para la implementación de escenarios de aprendizaje tecnológicos más complejos en futuros niveles escolares.

Los resultados alcanzados coinciden con las conclusiones de otras investigaciones (Lee, Sullivan, & Bers, 2013; Elkin, Sullivan, & Bers, 2014) que manifiestan los efectos positivos de la introducción de recursos de robótica para fomentar el desarrollo de habilidades e intereses vinculados a las áreas de conocimiento STEM (Science, Technology, Engineering and Mathematics).

Consideramos pertinente poner de manifiesto algunas limitaciones del estudio realizado que tienen que ver con el tamaño de la muestra, la cual podría ser más amplia si se hubiera contado con más centros educativos interesados en participar en el estudio, así como la equivalencia de los grupos, que podría conseguirse con una asignación aleatoria de los sujetos a los grupos, lo cual no ha sido posible debido a la organización escolar. Al respecto, se deben tener en cuenta las limitaciones de los investigadores y las condiciones que establecen los centros educativos para el desarrollo de este tipo de estudios. Consideramos que los resultados expuestos pueden interpretarse como una aproximación al tema si bien se requieren más estudios que permitan consolidar las conclusiones.

Apoyos

Secretaría Nacional de Ciencia, Tecnología e Innovación (SENACYT) e Instituto para la Formación y Aprovechamiento de los Recursos Humanos (IFARHU) de la República de Panamá.

Draft Content 289623138-71778 ov-es017.jpg

Draft Content 289623138-71778 ov-es018.jpg

Draft Content 289623138-71778 ov-es019.jpg

Draft Content 289623138-71778 ov-es020.jpg

Draft Content 289623138-71778 ov-es021.jpg

Draft Content 289623138-71778 ov-es022.jpg

Referencias